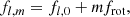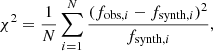| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 11 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201935478 | |
| Published online | 21 January 2020 | |
Pulsational properties of ten new slowly pulsating B stars
1
Institute of Physics, Faculty of Science, P. J. Šafárik University, Park Angelinum 9, Košice 040 01, Slovak Republic
e-mail: miroslav.fedurco@student.upjs.sk
2
Department of Theoretical Physics and Astrophysics, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic
3
American Association of Variable Star Observers (AAVSO), 49 Bay State Rd., Cambridge, MA 02138, USA
4
Bundesdeutsche Arbeitsgemeinschaft für Veränderliche Sterne e.V. (BAV), 12169 Berlin, Germany
Received:
15
March
2019
Accepted:
5
December
2019
Context. Slowly pulsating B (SPB) stars are upper main-sequence multi-periodic pulsators that show non-radial g-mode oscillations driven by the κ mechanism acting on the iron bump. These multi-periodic pulsators have great asteroseismic potential and can be employed for the calibration of stellar structure and evolution models of massive stars.
Aims. We collected a sample of ten hitherto unidentified SPB stars with the aim of describing their pulsational properties and identifying pulsational modes.
Methods. Photometric time series data from various surveys were collected and analyzed using diverse frequency search algorithms. We calculated astrophysical parameters and investigated the location of our sample stars in the log Teff vs. log L/L⊙ diagram. Current pulsational models were calculated and used for the identification of pulsational modes in our sample stars. An extensive grid of stellar models along with their g-mode eigenfrequencies was calculated and subsequently cross-matched with the observed pulsational frequencies. The best-fit models were then used in an attempt to constrain stellar parameters such as mass, age, metallicity, and convective overshoot.
Results. We present detected frequencies, corresponding g-mode identifications, and the masses and ages of the stellar models producing the best frequency cross-matches. We partially succeeded in constraining stellar parameters, in particular concerning mass and age. Where applicable, rotation periods have been derived from the spacing of triplet component frequencies. No evolved SPB stars are present in our sample. We identify two candidate high-metallicity objects (HD 86424 and HD 163285), one young SPB star (HD 36999), and two candidate young SPB stars (HD 61712 and HD 61076).
Conclusions. We demonstrate the feasibility of using ground-based observations to perform basic asteroseismological analyses of SPB stars. Our results significantly enlarge the sample of known SPB stars with reliable pulsational mode identifications, which provides important input parameters for modeling attempts aiming to investigate the internal processes at work in upper main-sequence stars.
Key words: asteroseismology / stars: early-type / stars: variables: general
© ESO 2020
1. Introduction
Slowly pulsating B (SPB) stars were first described as a class by Waelkens (1991). They are main-sequence (MS) stars of spectral types B2 to B9 (i.e., 22 000–11 000 K), which show non-radial g-mode oscillations driven by the κ mechanism acting on the iron bump (Gautschy & Saio 1993). These SPB stars are multi-periodic pulsators whose observed periods range from 0.3 d to about 5 d (De Cat 2007).
Several fast-rotating SPB stars have been described; the majority, however, seem to be comparably slow rotators (De Cat 2007; Degroote et al. 2011). There also exist very slowly rotating SPB stars like KIC 10526294 (rotation period of about 188 d; Pápics et al. 2014). This is remarkable as the mean projected rotational velocity (υ sin i) of B-type stars well exceeds 100 km s−1 (Abt et al. 2002), which induces strong meridional circulation and mass loss (Dolginov & Urpin 1983).
Stars of the upper MS are characterized by a convective core and a radiative envelope. The asteroseismic potential of SPB stars has been recognized early on (De Cat 2007). These stars are perfect test laboratories of ill-understood processes that have a significant influences, such as diffusion and internal differential rotation, on the lifetime of a star. Asteroseismic analyses of SPB stars are therefore expected to contribute to the calibration of stellar structure and evolution models of massive stars, for which the observed mass distribution significantly contradicts theoretical predictions (Castro et al. 2014). In addition, these analyses can be employed to determine and calibrate internal parameters such as the convective overshoot parameter or envelope mixing (Moravveji et al. 2015, 2016), which are not directly observable but have a significant influence on stellar structure and evolution (Pápics et al. 2015; Buysschaert et al. 2018). Furthermore, nonrigid rotational profiles can be studied by determining the spacing between rotationally split modes (Pápics et al. 2017; Triana et al. 2015).
Current asteroseismic modeling attempts are mainly based on quasi-uninterrupted observational data from space telescopes such as Convection, Rotation and planetary Transit (CoRoT) (Auvergne et al. 2009) or Kepler (Borucki 2016) because their continuity and precision enable reliable mode identification and help to constrain basic stellar parameters such as mass, luminosity, and effective temperature with great precision (Szewczuk & Daszyńska-Daszkiewicz 2018). However, owing to their long-period, gravity-driven oscillations, SPB stars lend themselves perfectly for asteroseismic modeling using ground-based survey data with rather low cadence.
Pulsation in pre-MS (PMS) stars is of special interest as it allows the investigation of the short-lived early phases of stellar evolution with oscillations (Zwintz et al. 2015), thereby providing valuable constraints and input parameters for theoretical considerations. Dedicated effort has led to the discovery of γ Doradus and, in particular, δ Scuti pulsation in PMS objects (e.g., Zwintz et al. 2013; Ripepi et al. 2015), but the situation is less clear for SPB stars. Gruber et al. (2012) identify two SPB stars in the vicinity of the young open star cluster NGC 2244; however, the available proper motion and radial velocity data were insufficient to confirm their cluster membership. Zwintz et al. (2009) discovered ten SPB variables in the field of NGC 2264, another young open cluster. Later on, Zwintz et al. (2017) investigate four SPB variables belonging to NGC 2264 in detail. Interestingly, despite the derived ages between one and six million years, the authors find that all stars seem to be early zero age MS (ZAMS) objects that have already left the PMS phase. The search for PMS SPB pulsators, therefore, has not yielded any conclusive results yet, and identifying suitable candidates remains of special interest.
In this paper, we present photometric time series analysis of ten newly identified SPB stars together with an asteroseismic analysis aimed at the identification of pulsational modes. These results significantly add to our knowledge of the pulsational properties of these stars and allow us to constrain astrophysical parameters, which helps to throw more light on the internal processes at work in upper MS stars.
2. Target selection, photometric data sources, reduction, and analysis
The following sections give details on the sample selection, the employed photometric time series data, and our methods of analysis.
2.1. Target selection and data sources
For the sample selection, we resorted to The International Variable Star Index (VSX; Watson et al. 2006), which is the most up-to-date and accurate variable star database available. To identify new SPB stars, we systematically investigated suspected and known variable stars with periods typical for SPB stars and a spectral type of B or A. The extension to spectral type A was deemed necessary to identify objects that had been spectroscopically misclassified.
In the given spectral type range on the MS, SPB stars coexist with other types of photometric variables such as Be stars (Rivinius et al. 2013) and rotationally variable CP2/4 stars (Preston 1974). While Be stars usually exhibit complex variability on timescales ranging from a few minutes to decades, the latter objects, which are also known as α2 Canum Venaticorum (ACV) variables (Samus et al. 2017), exhibit surface abundance patches or spots and variability periods in the same range as SPB stars. Their variability, however, is strictly monoperiodic (Netopil et al. 2017) and can therefore be easily distinguished from SPB type pulsation.
After the collection of an initial sample list, we searched for the availability of photometric observations in the databases of the following surveys: All Sky Automated Survey (ASAS; Pigulski 2014), All-Sky Automated Survey for Supernovae (ASAS-SN; Kochanek et al. 2017), HIPPARCOS (van Leeuwen et al. 1997), Optical Monitoring Camera (OMC; Alfonso-Garzón et al. 2015), and Wide Angle Search for Planets (SuperWASP; Street et al. 2003). In this way, a sample of ten newly identified SPB variables boasting extensive time series photometry was collected (cf. Table 1).
Astrophysical parameters of our sample stars.
HD 48497, HD 61076, HD 61712, HD 86424, HD 115067, HD 163285, and HD 168121 were first reported as variables on the basis of HIPPARCOS data (ESA 1997; Koen & Eyer 2002). Nichols et al. (2010) report the variability of HD 66181 using the pointing control camera of the Chandra X-ray Observatory. However, all these stars lack deeper studies and their variability types have not been determined. Consequently, the stars are listed as variable stars of unspecified type (type VAR) in the VSX. HD 36999 and HD 97895 are listed as suspected variable stars in the GCVS and VSX.
2.2. Photometric data reduction and analysis
Only data from the third phase of the All Sky Automated Survey project (ASAS-3) were taken into account; measurements with quality assignments “C” and “D” were excluded. Mean V magnitudes were calculated as the weighted average of the values provided in the five different apertures available. To check the feasibility of this approach, we subsequently restricted our analysis to the “best” aperture as indicated by the ASAS-3 system for any given star. No significant differences were found between the two approaches. Finally, a basic 5σ clipping was performed to clean the light curves from outliers.
The ASAS-SN measurements are taken with different cameras, which we treated separately. The mean for each individual data set was calculated, and data points were deleted on a 5σ basis. After that, the data of the individual cameras were merged. In the case of HIPPARCOS and OMC data, a 5σ clipping algorithm was applied.
Measurements with an error larger than 0.05 mag were excluded from the SuperWASP data sets. Each camera was treated separately and the mean for each individual data set was derived; data points were deleted on a 5σ basis. The data of the individual cameras were then merged. Applying this procedure also corrects for the different offsets of the cameras. However, for larger data sets, we also separately investigated the measurements from each camera.
The resulting light curves were examined in more detail using the program package PERIOD04 (Lenz & Breger 2005), which performs a discrete Fourier transform. An iterative pre-whitening procedure was used to extract all significant frequencies with a signal-to-noise ratio above 4. The results from PERIOD04 were checked with the CLEANEST and phase dispersion minimization (PDM) algorithms as implemented in the program package PERANSO (Paunzen & Vanmunster 2016). The same results were obtained within the derived errors, which depend on the time series characteristics, i.e., the distribution of measurements over time and the photon noise. All significant frequencies are listed in Table 2. Amplitude spectra and residuals, as derived with PERIOD04, are given in the appendix (Fig. A.1).
All detected frequencies along with the corresponding g-modes characterized by angular degree ℓ, radial order ng, and azimuthal order m.
3. Log Teff vs. log L/L⊙ diagram
To check whether our sample stars fall within the regime of known SPB stars, we collected a control sample of well-established SPB variables (i.e., stars with a detailed asteroseismic analysis available) that also boast uvbyβ photometry (Paunzen 2015). We gleaned the BV magnitudes from the compilation by Kharchenko (2001), who compiled an all-sky catalog of more than 2.5 million stars and transformed the available HIPPARCOS/TychoBV magnitudes to Johnson BV using a homogenized transformation law. Corresponding I magnitudes were taken from the HIPPARCOS catalog; JHKs magnitudes are from the 2MASS 6X Point Source Working Database (Skrutskie et al. 2006).
The final Teff values were derived in two different steps. First, we relied on the calibration by Napiwotzki et al. (1993) on the basis of uvbyβ photometry. For the stars without uvbyβ photometry, Teff was derived from the updated relations for MS stars published by Pecaut & Mamajek (2013). A mean value of the calibrated values from (B − V)0, (V − I)0, and (V − Ks)0 was calculated. To test all calibrated values, the VOSA (VO Sed Analyzer) tool v6.0 (Bayo et al. 2008) was applied to fit the spectral energy distribution (SED) to the available photometry. No outliers were detected, which provides confidence in our results. In addition, a propagation of uncertainties was performed for the photometric observations, from which we deduce a precision of approximately 200 K for the derived Teff values.
We calculated the luminosity based on the parallax, apparent magnitude, reddening, and bolometric correction (BC). Parallaxes were taken from Gaia DR2 (Lindegren et al. 2018). We interpolated reddening values for stars without any uvbyβ photometry within the corresponding maps published by Green et al. (2018) using the distances from Bailer-Jones et al. (2018). Employing the derived Teff values, the BC was calculated from the relations listed by Flower (1996). Finally, we used the bolometric magnitude of the Sun (+4.75 mag) to derive luminosities and errors. For the latter, a complete error propagation was applied. The derived astrophysical parameters of our sample stars are listed in Table 1.
Spectral types were taken from the catalog of Skiff (2014), who made a careful assessment of the literature. Almost all classifications originate from the Michigan catalog of two-dimensional spectral types for the HD Stars (Houk & Swift 1999) and are thus based on photographic plates. This likely explains why two stars (HD 61076 and HD 168121) are listed with giant luminosities (luminosity class III) but are not located in this region of the HRD. Their spectral types, however, are consistent with the derived Teff values.
In Fig. 1, the log Teff vs. log L/L⊙ diagram for our sample stars and the control sample of well-established SPB variables is shown. Also indicated are isochrones from the ZAMS to 160 Myr with a spacing of 20 Myr, which were calculated with the Modules for Experiments in Stellar Astrophysics (MESA; Paxton et al. 2011, 2013, 2015, 2018) code. No evolved SPB variables are present in both samples, and there is a noticeable lack of SPB pulsators at or very close to the ZAMS; this fact was already noticed before Zwintz et al. (2017) but which is not yet understood. With our work, we add at least two very young SPB stars (HD 36999 and HD 61712) to the overall sample. The star HD 61076 deserves special mention, as it is located way below the ZAMS.
 |
Fig. 1. Log Teff vs. log L/L⊙ diagram for our sample stars (red symbols) and a control sample of well-established SPB stars from the literature (black symbols) with available uvbyβ photometry. Also indicated are isochrones from the ZAMS to 160 Myr with a spacing of 20 Myr. |
4. Grid of stellar models
We used the MESA and GYRE nonadiabatic oscillation codes (Townsend & Teitler 2013; Townsend et al. 2018) to identify modes of oscillation in our sample stars. An extensive grid of MS stellar models was calculated with four free parameters: initial mass, initial metallicity, age, and overshooting. Initial masses of the stellar models were set within the range 3–5.5 M⊙, with a step-size of ΔM = 0.1 M⊙. Since stellar evolution on the MS does not progress evenly, the time-step Δt was parameterized by the maximum allowed rate of change in overall relative hydrogen abundance dX/X = 0.001. Initial metallicities of our stellar models range from 0.003 to 0.03, with a step-size of ΔZ = 0.003 and additional nodes at Z = 0.019 and 0.02. We also took into account the impact of the overshooting parameter fov and calculated models with overshooting parameters in the range 0–0.04, with a step-size of Δfov = 0.002. In this way, over 85 000 stellar models were computed. The detailed MESA inlist used in our calculations is given in Appendix B.
As the next step, eigenfrequencies of low-degree g-modes were calculated for each stellar model using the GYRE code. As a consquence of visibility issues with high-angular degree modes (Aerts et al. 2010) and computational time limitations, eigenfrequencies were calculated only for low-degree g-modes with ℓ = 1, 2. Furthermore, we decided to restrict our calculations to frequencies above 0.3 c/d for ℓ = 1 and 0.6 c/d for ℓ = 2. Below these corresponding frequency thresholds, the frequency spacing of high-order modes is insufficient to prevent misidentification of modes due to uncertainties in the derived stellar parameters. The complete GYRE inlist can also be found in Appendix B.
Stellar model eigenfrequencies were calculated on nonrotating stellar models, which caused degeneracy in modes with the same angular degree l but different azimuthal order m. If necessary, this degeneracy was lifted by introducing rotational splitting for a given mode multiplet, i.e.,
where frot is the rotational frequency of the star.
5. Mode identification
Once the grid of stellar models with their g-mode eigenfrequencies was completed, synthetic frequencies of low-degree g-modes calculated with GYRE were compared to the observed frequencies obtained by the frequency analysis described in Sect. 2.2. In our search algorithm, the accuracy of the fit of a given g-mode combination and the corresponding stellar model was evaluated using the function
where N is the total number of detected frequencies viable for cross-match, fobs is the observed frequency, and fsynth is its supposed synthetic counterpart.
To reduce the number of stellar models to be checked for each object, the original grid of models was cropped to a subgrid of models with luminosities and effective temperatures within 1σ to 3σ of our target. To find the best-fit stellar model, we calculated χ2 for possible combinations of g-mode eigenfrequencies and each stellar model. Finally, the mode combination scoring the highest χ2 value within a 3σ error box was selected.
Initially, eigenfrequencies for non-rotating models were used in the search algorithm. If no satisfactory solution was found, rigid-body rotation was introduced using Eq. (1). The rotational period was searched for heuristically either by searching for equidistant spacing in the observed frequencies or by assuming that certain couples of frequencies are wings of a dipole triplet where the central peak was not detected. The rotational period was finally derived by a linear fit of Eq. (1) to the detected triplet. A 2D slice of the grid search procedure is shown in Fig. 2.
 |
Fig. 2. Hertzsprung–Russell diagram (HRD) illustrating a 2D slice of the grid search procedure for the star HD 48497, using the best-fit mode combination (see Table 2). Also shown are evolutionary tracks with initial metallicity and overshooting parameter that provided the best fit of the models to the observed frequencies. The underlying heat map indicates the interpolated χ2 values on a logarithmic scale. Corresponding isochrones are overlayed in 10 Myr increments. The location of HD 48497 is indicated by the black dot, which is surrounded by the corresponding 1σ, 2σ, and 3σ error boxes. |
Table 2 lists the detected frequencies and, where applicable, the corresponding modes. In case a frequency multiplet was detected, we also identified the azimuthal order m. The rotational periods derived from the frequency spacing of triplet component frequencies are provided in Table 3.
In the case of HD 168121, the spacing between the different overtones n is relatively small for ℓ = 1 modes. Furthermore, the three detected frequencies are closely but not symmetrically spaced, which means that they do not belong to an ℓ = 1 triplet or the triplet is asymmetric because Eq. (1) is no longer valid for fast rotators (Cowling & Newing 1949). Another possible explanation is that two frequencies are the product of rotational splitting of the same mode and the third frequency is a member of a different mode. Because of the lack of any additional frequencies outside the problematic region and our model assuming triplets to be symmetric because of the size of the grid, none of the detected frequencies in this star could be reliably identified.
6. Results
In the following, the results on the individual stars are discussed. Figure C.1 provide a discussion of the properties of the best-fit stellar models.
HD 36999. This star, which is listed as a young stellar object (a star in its earliest stages of development, i.e., either a protostar or a PMS) in SIMBAD (Wenger et al. 2000), is a member of the Orion OB association (Tian et al. 1996) with an estimated age of 2.2 Myr (Wolff et al. 2004), which is well in line with our results. This makes HD 36999 a particular interesting object because it is located on, or slightly below, the ZAMS. As has been pointed out (cf. Sect. 1), only very few SPB stars of comparable age are known so far (Gruber et al. 2012; Zwintz et al. 2017).
To investigate the evolutionary status of this object, we checked the available LAMOST DR5 spectrum (Zhao et al. 2012; Cui et al. 2012) for the presence of emission lines or other telltale signs of PMS stars. Interestingly, the spectrum clearly shows numerous strong emission lines, for instance, O II 3728 Å, Hβ 4863 Å, O III 4960 Å, O III 5007 Å, Hα 6563 Å, and S II 6716,6731 Å. This is in agreement with the emission profile of the nebula that pervades the corresponding sky region and apparently contaminates the LAMOST spectrum of HD 36999 and the spectra of numerous other stars in the vicinity. Contamination of LAMOST spectra by H II regions is a known issue (Hou et al. 2016). We assume that this may be caused by fiber drift, issues with the pipeline software responsible for the background substraction, or by sampling the background during the integration while the seeing is excellent.
Because of the higher luminosity derived from Gaia DR2 data, we determined that the best-fit model boasts a mass of 3.6 M⊙ and an age of 25 Myr; these values are somewhat higher than those given by Wolff et al. (2004) of 3.26 M⊙ and 2.2 Myr. Our analysis suggests a rather low value of fov < 0.01. We achieved best results by regarding frequencies f1 and f2 as side lobes of a rotationally split triplet. Owing to the non-detection of the central peak of this supposed triplet and underestimated frequency uncertainties provided by PERIOD04, we were unable to properly estimate the uncertainty of the rotation period.
HD 48497. Niemczura et al. (2009) presented a detailed abundance analysis of this star, which has a very low υ sin i value of 13 km s−1 and underabundances of Cr, Sr, and Ni of about 0.5 dex as compared to the solar values. Therefore, Yushchenko et al. (2015) include HD 48497 in their list of possible λ Bootis star candidates. These stars constitute a small group of A- to F-type stars characterized by the depletion of Fe-peak elements of up to 2 dex (Murphy & Paunzen 2017). However, HD 48497 is too hot and does not show the typical elemental abundance pattern of λ Bootis stars. It therefore cannot be considered a member of this group. From our analysis, we find that the models with a mass of 4.2 M⊙ and an age of 25 Myr provide the best fit to the observed frequencies. It is noteworthy that during the analysis, we discovered that frequency f1 is a side lobe of the 1 d alias frequency that is ubiquitous in ground-based observations. Consequently, this frequency was disregarded during the grid search procedure.
HD 61076. The available HIPPARCOS parallax of 0.96(78) mas led to the conclusion that this star is a giant with a luminosity of 910 L⊙ (Hohle et al. 2010). The Gaia DR2 parallax, on the other hand, places this star well below the ZAMS. We find that, for the given luminosity, a Teff difference of 1000 K is needed to shift HD 61076 to the ZAMS for models with a metallicity of Z = 0.02. The published spectral type of B5/7 might indicate some peculiarities that render the temperature estimation uncertain. We strongly suspect that the Teff determination based on the Gaia DR2 parallax is erroneous; however, only further photometric or spectroscopic data can shed more light on this issue and the nature of this star.
Since our grid consists of stellar models with a wide range of metallicity and overshooting parameter values, we performed a grid search for the best-fit g-mode combination despite the apparently peculiar nature of this star. As expected, low-metallicity models with Z < 0.01 were able to shift the ZAMS sufficiently toward the position of our object in the HRD. The best-fit model indicates a 3.2 M⊙ object near the ZAMS (2 Myr) with an initially low metallicity of Z = 0.009 and the rather high value of fov > 0.03. However, the high value of fov, the age of the object, and its peculiar location in the HRD cast doubt on the reliability of fov. Lack of time on the ZAMS should prevent fov from having any significant impact on the internal structure of the star. In addition, if we exclude models outside the 1σ confidence interval, the previously stated constraint on fov vanishes (see Fig. C.1). Despite these uncertainties, the scarcity of very young SPB stars and the apparently peculiar nature of this object warrant a closer look at HD 61076 in future studies.
HD 61712. Mannings & Barlow (1998) presented evidence that this star might be a PMS star with significant IR excess. An inspection of the SED of the object with the VOSA tool clearly confirms the presence of IR excess. However, a PMS nature cannot be unambiguously established by this criterion alone because similar excesses have been observed in stars that have already reached the MS (Montesinos et al. 2009). One definite diagnostic criterion would be the presence of emission lines; however, to the best of our knowledge, no spectrum of this object is available. Our analysis failed to provide an unambiguous age estimation because multiple stellar models with similar values of χ2 were obtained for the best-fit g-mode combination. However, these models uniformly point to a mass of 3.6 M⊙. In summary, HD 61712 is a candidate young SPB star worthy of further attention.
HD 66181. No detailed investigations of this object are available in the literature. Unfortunately, although the best-fit g-mode combination was found, we were unable to put constraints on the mass of the object. However, from the detection of a dipole triplet, the rotational period could be calculated (see Table 3).
HD 86424. This star is a visual binary with a magnitude difference of the components (HD 86424 and CD−41 5479B) of 2.3 mag and a separation of 9 7 (Sinachopoulos 1988). Using the available Gaia DR2 parallaxes, Bailer-Jones et al. (2018) estimate distances between 547 and 573 pc for HD 86424 and 585 and 607 pc for CD−41 5479B. The two stars, therefore, do not form a physical system. Assuming an identical reddening value and the given distance, we derive an absolute magnitude of about +2.5 mag for the fainter component. This is typical for a F0 V star, which is also compatible with the available optical and near-infrared colors. In this spectral region is situated the blue border of the γ Doradus instability strip (Bradley et al. 2015), which is populated by g-mode pulsators with periods between 0.5 and 5 d. We are not able to rule out that CD−41 5479B is the source of the detected variability because both stars are covered by the apertures of the employed data sources. The parameters of the two best-fit models point to a mass of 2.5 M⊙ and an approximate age of 50 Myr. However, it has to be pointed out that the best-fit stellar models within the 1σ confidence interval boast a rather high metallicity of Z = 0.027. As we do not have any additional information about the metallicity of HD 86424, we are unable to confirm the validity of our models.
7 (Sinachopoulos 1988). Using the available Gaia DR2 parallaxes, Bailer-Jones et al. (2018) estimate distances between 547 and 573 pc for HD 86424 and 585 and 607 pc for CD−41 5479B. The two stars, therefore, do not form a physical system. Assuming an identical reddening value and the given distance, we derive an absolute magnitude of about +2.5 mag for the fainter component. This is typical for a F0 V star, which is also compatible with the available optical and near-infrared colors. In this spectral region is situated the blue border of the γ Doradus instability strip (Bradley et al. 2015), which is populated by g-mode pulsators with periods between 0.5 and 5 d. We are not able to rule out that CD−41 5479B is the source of the detected variability because both stars are covered by the apertures of the employed data sources. The parameters of the two best-fit models point to a mass of 2.5 M⊙ and an approximate age of 50 Myr. However, it has to be pointed out that the best-fit stellar models within the 1σ confidence interval boast a rather high metallicity of Z = 0.027. As we do not have any additional information about the metallicity of HD 86424, we are unable to confirm the validity of our models.
HD 97895. With a Galactic latitude of +29° and low radial velocity (Kordopatis et al. 2013), this star is an unusual hot B-type star because it is situated most certainly in the thick disk and is characterized by a metallicity significantly different from the solar value (Miranda et al. 2016). The SPB stars of such metallicities are valuable testbeds for the calibration of pulsational models (Miglio et al. 2007). The observed frequencies can be closely matched by dipole modes on 50 Myr old 4.8 M⊙ stellar models. From the rotational splitting of one of the observed frequencies, we were able to determine the rotational period. Despite our expectations, our best-fit models do not indicate metallicities significantly different from the solar value. Models with a low value of fov produce a more accurate fit to the observed frequencies.
HD 115067. With an age of about 90 Myr, this is the most evolved star in our sample. Otherwise, no detailed investigations are available in the literature. Unfortunately, in the case of this object, only one frequency suitable for cross-identification was available, which is insufficient to perform a grid search. Table 2 contains a lower estimate on the radial order of the observed frequency f1 under the assumption that it corresponds to a dipole mode.
HD 163285. No detailed investigations of this object are available in the literature. High-metallicity stellar models with a mass of 3.8 M⊙ and an age of 40 Myr provide the best fit to the observed frequencies. The value fov can be constrained within the range from 0.024 to 0.030.
HD 168121. No detailed investigations of this object are available in the literature.
7. Conclusions
We collected and analyzed extensive sets of photometric time series data of ten hitherto unidentified SPB stars with the aim of describing their pulsational properties and identifying pulsational modes. Astrophysical parameters were calculated and the location of our sample stars in the log Teff vs. log L/L⊙ diagram was investigated. We calculated current pulsational models to identify pulsational modes in our sample stars. An extensive grid of stellar models and its corresponding eigenfrequencies were calculated.
For eight objects, the observed frequencies were successfully cross-matched with a best-fit g-mode combination using our grid search algorithm. From the best-fit stellar model, we were able to constrain the astrophysical properties of our sample stars. In the case of five objects (HD 48497, HD 61076, HD 61712, HD 86424, and HD 163285), we were able to constrain masses down to the resolution limit of the grid, i.e., 0.1 M⊙. Employing the ages of the corresponding best-fit models (see Table 2), we were also able to derive information on the age of seven stars. HD 36999 is a particular interesting object because it is located on, or slightly below, the ZAMS. HD 61712 is another candidate young SPB star. A special case is HD 61076, which may be a very young and low-metallicity object, according to the best-fit models. On the opposite side, the best-fit models for HD 86424 and HD 163285 indicate a higher than average metallicity of 0.027. In accordance with our expectations, no evolved SPB stars are present in our sample.
As far as overshooting parameter fov is concerned, our results can be divided into three groups. The first group consists of HD 48497, HD 61712, HD 66181, and HD 86424, and boasts a wide range of best-fit values of fov, which demonstrates the need to better constrain this parameter using g-mode pulsations in stars with convective cores. In the second group of objects (HD 36999 and HD 97895), there is a clear tendency for models with low values of fov to produce better frequency cross-matches. Finally, in the third group of objects (HD 61076 and HD 163285), the best-fit models confined fov to intervals above 0.02 (see Fig. C.1).
With the present study, we significantly enlarge the sample of known SPB stars with reliable pulsational mode identifications. We furthermore demonstrate the feasibility of using ground-based observations to perform basic asteroseismological analyses of SPB stars. While our results do not reach the accuracy of previous studies based exclusively on space photometry (e.g., Szewczuk & Daszyńska-Daszkiewicz 2018), they nevertheless constitute a significant improvement on the constraints provided by the uncertainties in Teff and luminosity derived from photometry and Gaia data. In theory, the presented approach can also be used with space-based observations. However, owing to the much higher number of frequencies detected in these data, the grid search algorithm should be replaced by a more refined and less computationally heavy cross-matching algorithm. Such effort may lead to much tighter constraints on stellar parameters, which will help to shed more light on the internal processes at work in upper MS stars.
Acknowledgments
The research of M.F. was supported by the Slovak Research and Development Agency under the contract No. APVV-15-0458 and internal grant No. VVGS-PF-2018-758 of the Faculty of Science, P. J. Šafárik University in Košice. This work presents results from the European Space Agency (ESA) space mission Gaia. Gaia data are being processed by the Gaia Data Processing and Analysis Consortium (DPAC). Funding for the DPAC is provided by national institutions, in particular the institutions participating in the Gaia MultiLateral Agreement (MLA). The Gaia mission website is https://www.cosmos.esa.int/gaia. The Gaia archive website is https://archives.esac.esa.int/gaia. This research has made use of the SIMBAD database and the VizieR catalog access tool, operated at CDS, Strasbourg, France.
References
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Netherlands: Springer), 15 [Google Scholar]
- Alfonso-Garzón, J., Domingo, A., & Mas-Hesse, J. M. 2015, in Highlights of Spanish Astrophysics VIII, eds. A. J. Cenarro, F. Figueras, C. Hernández-Monteagudo, J. Trujillo Bueno, & L. Valdivielso, 435 [Google Scholar]
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J. 2016, Rep. Progr. Phys., 79, 036901 [Google Scholar]
- Bradley, P. A., Guzik, J. A., Miles, L. F., et al. 2015, AJ, 149, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Buysschaert, B., Aerts, C., Bowman, D. M., et al. 2018, A&A, 616, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cowling, T. G., & Newing, R. A. 1949, ApJ, 109, 149 [Google Scholar]
- Cui, X.-Q., Zhao, Y.-H., Chu, Y.-Q., et al. 2012, Res. Astron. Astrophys., 12, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- De Cat, P. 2007, Commun. Asteroseismol., 150, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Degroote, P., Acke, B., Samadi, R., et al. 2011, A&A, 536, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolginov, A. Z., & Urpin, V. A. 1983, Ap&SS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- ESA 1997, in The HIPPARCOS and TYCHO Catalogues. Astrometric and Photometric Star Catalogues Derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gautschy, A., & Saio, H. 1993, MNRAS, 262, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Gruber, D., Saio, H., Kuschnig, R., et al. 2012, MNRAS, 420, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Hohle, M. M., Neuhäuser, R., & Schutz, B. F. 2010, Astron. Nachr., 331, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, W., Luo, A.-L., Hu, J.-Y., et al. 2016, Res. Astron. Astrophys., 16, 138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houk, N., & Swift, C. 1999, Michigan Spectral Survey, 5 [Google Scholar]
- Kharchenko, N. V. 2001, Kinematika i Fizika Nebesnykh Tel, 17, 409 [NASA ADS] [Google Scholar]
- Kochanek, C. S., Shappee, B. J., Stanek, K. Z., et al. 2017, PASP, 129, 104502 [NASA ADS] [CrossRef] [Google Scholar]
- Koen, C., & Eyer, L. 2002, MNRAS, 331, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Gilmore, G., Steinmetz, M., et al. 2013, AJ, 146, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannings, V., & Barlow, M. J. 1998, ApJ, 497, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Montalbán, J., & Dupret, M.-A. 2007, MNRAS, 375, L21 [CrossRef] [Google Scholar]
- Miranda, M. S., Pilkington, K., Gibson, B. K., et al. 2016, A&A, 587, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montesinos, B., Eiroa, C., Mora, A., & Merín, B. 2009, A&A, 495, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moravveji, E., Aerts, C., Pápics, P. I., Triana, S. A., & Vandoren, B. 2015, A&A, 580, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moravveji, E., Townsend, R. H. D., Aerts, C., & Mathis, S. 2016, ApJ, 823, 130 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Murphy, S. J., & Paunzen, E. 2017, MNRAS, 466, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., Schoenberner, D., & Wenske, V. 1993, A&A, 268, 653 [Google Scholar]
- Netopil, M., Paunzen, E., Hümmerich, S., & Bernhard, K. 2017, MNRAS, 468, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Nichols, J. S., Henden, A. A., Huenemoerder, D. P., et al. 2010, ApJS, 188, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Niemczura, E., Morel, T., & Aerts, C. 2009, A&A, 506, 213 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pápics, P. I., Moravveji, E., Aerts, C., et al. 2014, A&A, 570, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pápics, P. I., Tkachenko, A., Aerts, C., et al. 2015, ApJ, 803, L25 [Google Scholar]
- Pápics, P. I., Tkachenko, A., Van Reeth, T., et al. 2017, A&A, 598, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E. 2015, A&A, 580, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paunzen, E., & Vanmunster, T. 2016, Astron. Nachr., 337, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Pigulski, A. 2014, in Precision Asteroseismology, eds. J. A. Guzik, W. J. Chaplin, G. Handler, & A. Pigulski, IAU Symp., 301, 31 [NASA ADS] [Google Scholar]
- Preston, G. W. 1974, ARA&A, 12, 257 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ripepi, V., Balona, L., Catanzaro, G., et al. 2015, MNRAS, 454, 2606 [NASA ADS] [CrossRef] [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Samus, N. N., Kazarovets, E. V., Durlevich, O. V., Kireeva, N. N., & Pastukhova, E. N. 2017, Astron. Rep., 61, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Sinachopoulos, D. 1988, A&AS, 76, 189 [NASA ADS] [Google Scholar]
- Skiff, B. A. 2014, VizieR Online Data Catalog: B/mk [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Street, R. A., Pollaco, D. L., Fitzsimmons, A., et al. 2003, in Scientific Frontiers in Research on Extrasolar Planets, eds. D. Deming, & S. Seager, ASP Conf. Ser., 294, 405 [NASA ADS] [Google Scholar]
- Szewczuk, W., & Daszyńska-Daszkiewicz, J. 2018, MNRAS, 478, 2243 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, K. P., van Leeuwen, F., Zhao, J. L., & Su, C. G. 1996, A&AS, 118, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D., Goldstein, J., & Zweibel, E. G. 2018, MNRAS, 475, 879 [Google Scholar]
- Triana, S. A., Moravveji, E., Pápics, P. I., et al. 2015, ApJ, 810, 16 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 1997, in Hipparcos– Venice ’97, eds. R. M. Bonnet, E. Høg, P. L. Bernacca, et al., ESA SP, 402, 19 [NASA ADS] [Google Scholar]
- Waelkens, C. 1991, A&A, 246, 453 [NASA ADS] [Google Scholar]
- Watson, C. L., Henden, A. A., & Price, A. 2006, Soc. Astron. Sci. Ann. Symp., 25, 47 [NASA ADS] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolff, S. C., Strom, S. E., & Hillenbrand, L. A. 2004, ApJ, 601, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Yushchenko, A. V., Gopka, V. F., Kang, Y.-W., et al. 2015, AJ, 149, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, Res. Astron. Astrophys., 12, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Zwintz, K., Hareter, M., Kuschnig, R., et al. 2009, A&A, 502, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwintz, K., Fossati, L., Ryabchikova, T., et al. 2013, A&A, 550, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwintz, K., Fossati, L., & Ryabchikova, T. 2015, in Physics and Evolution of Magnetic and Related Stars, eds. Y. Y. Balega, I. I. Romanyuk, & D. O. Kudryavtsev, ASP Conf. Ser., 494, 157 [NASA ADS] [Google Scholar]
- Zwintz, K., Moravveji, E., Pápics, P. I., et al. 2017, A&A, 601, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Amplitude spectra
 |
Fig. A.1. Results of the frequency analysis of the light curves of our sample stars. The top panels of each plot illustrate the original amplitude spectra. Significant frequencies, as listed in Table 2, are identified. The bottom panels shows the residuals after subtracting the indicated frequencies and corresponding aliases. |
Appendix B: MESA and Gyre inlists
The grid of stellar models was produced using the following MESA inlist file. Empty parameter values were filled sequentially for each node of the grid.
&star_job
create_pre_main_sequence_model = .false.
write_profile_when_terminate = .false.
show_log_description_at_start = .false.
change_lnPgas_flag = .true.
change_initial_lnPgas_flag = .true.
new_lnPgas_flag = .true.
change_Z = .true.
change_initial_Z = .true.
new_z =
/ !end of star_job namelist
&controls
write_profiles_flag = .true.
profile_interval = 15
history_interval = 3
write_header_frequency = 999999
terminal_interval = 999999
photo_interval = 5000000
log_directory =
initial_mass =
mixing_length_alpha = 1.73
set_min_D_mix = .true.
min_D_mix = 0
overshoot_f_above_burn_h_core =
overshoot_f0_above_burn_h_core = 0.005
dX_div_X_hard_limit = 1d-3
delta_lg_XH_cntr_max = -1
delta_lg_XH_cntr_limit = 0.05
alpha_semiconvection = 0.01
write_pulse_data_with_profile = .true.
pulse_data_format = "GYRE"
add_center_point_to_pulse_data = .true.
add_double_points_to_pulse_data = .true.
calculate_Brunt_N2 = .true.
xa_central_lower_limit_species(1) = "h1"
xa_central_lower_limit(1) = 1d-3
when_to_stop_rtol = 1d-3
when_to_stop_atol = 1d-3
mixing_D_limit_for_log = 1d-4
use_Ledoux_criterion = .true.
D_mix_ov_limit = 0d0
which_atm_option = "photosphere_tables"
cubic_interpolation_in_Z = .true.
! test with "Gold Standard" tolerances
threshold_grad_mu_for_double_point = 10.
newton_iterations_limit = 20
max_tries = 20
iter_for_resid_tol2 = 30
tol_residual_norm1 = 1d-9
tol_max_residual1 = 1d-7
tol_correction_norm = 1d-9
tol_max_correction = 1d-7
/ ! end of controls namelist
After the grid of stellar models was created, each stellar model was then used to calculate the frequencies of dipole and quadrupole g-modes using the following GYRE inlist:
/ &model model_type = ’EVOL’ file = file_format = ’MESA’ uniform_rot = .TRUE. Omega_units = ’CYC_PER_DAY’ Omega_rot = 0.0 repair_As = .TRUE. / &constants / &mode l = 1 n_pg_min = -25 tag = ’l=1’ / &mode l = 2 n_pg_min = -30 tag = ’l=2’ / &osc nonadiabatic = .TRUE. / &num diff_scheme = ’COLLOC_GL4’ / &scan grid_type = ’INVERSE’ freq_min_units = ’CYC_PER_DAY’ freq_max_units = ’CYC_PER_DAY’ freq_min = 0.321 freq_max = 10.0 n_freq = 100 tag_list = ’l=1’ / &scan grid_type = ’INVERSE’ freq_min_units = ’CYC_PER_DAY’ freq_max_units = ’CYC_PER_DAY’ freq_min = 0.6 freq_max = 10.0 n_freq = 100 tag_list = ’l=2’ / &grid alpha_osc = 10 alpha_exp = 2 n_inner = 5 / &nad_output summary_file = freq_units = ’CYC_PER_DAY’ summary_file_format = ’TXT’ summary_item_list = ’M_star,R_star,l,m,n_pg, n_p,n_g,freq,freq_units,E,E_norm,eta’ /
Appendix C: χ2 distributions for the best-fit g-mode combinations
 |
Fig. C.1. χ2 values of stellar models within 1σ (blue points) and 3σ (gray points) of the given target. Represented χ2 values were calculated for the best-fit g-mode combination as listed in Table 2. Each figure shows the χ2 distribution across all free parameters of the stellar model grid, i.e., initial mass (top left), age (top right), metallicity (bottom left), and overshooting (bottom right). |
 |
Fig. C.1. continued. |
All Tables
All detected frequencies along with the corresponding g-modes characterized by angular degree ℓ, radial order ng, and azimuthal order m.
All Figures
 |
Fig. 1. Log Teff vs. log L/L⊙ diagram for our sample stars (red symbols) and a control sample of well-established SPB stars from the literature (black symbols) with available uvbyβ photometry. Also indicated are isochrones from the ZAMS to 160 Myr with a spacing of 20 Myr. |
| In the text | |
 |
Fig. 2. Hertzsprung–Russell diagram (HRD) illustrating a 2D slice of the grid search procedure for the star HD 48497, using the best-fit mode combination (see Table 2). Also shown are evolutionary tracks with initial metallicity and overshooting parameter that provided the best fit of the models to the observed frequencies. The underlying heat map indicates the interpolated χ2 values on a logarithmic scale. Corresponding isochrones are overlayed in 10 Myr increments. The location of HD 48497 is indicated by the black dot, which is surrounded by the corresponding 1σ, 2σ, and 3σ error boxes. |
| In the text | |
 |
Fig. A.1. Results of the frequency analysis of the light curves of our sample stars. The top panels of each plot illustrate the original amplitude spectra. Significant frequencies, as listed in Table 2, are identified. The bottom panels shows the residuals after subtracting the indicated frequencies and corresponding aliases. |
| In the text | |
 |
Fig. C.1. χ2 values of stellar models within 1σ (blue points) and 3σ (gray points) of the given target. Represented χ2 values were calculated for the best-fit g-mode combination as listed in Table 2. Each figure shows the χ2 distribution across all free parameters of the stellar model grid, i.e., initial mass (top left), age (top right), metallicity (bottom left), and overshooting (bottom right). |
| In the text | |
 |
Fig. C.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.