| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | L11 | |
| Number of page(s) | 5 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201936827 | |
| Published online | 10 December 2019 | |
Letter to the Editor
Jupiter formed as a pebble pile around the N2 ice line
Leiden Observatory, Leiden University, PO Box 9513, 2300 Leiden, The Netherlands
e-mail: arbos@umich.edu
Received:
2
October
2019
Accepted:
22
November
2019
Context. The region around the H2O ice line, due to its higher surface density, seems to be the ideal location to form planets. The core of Jupiter, as well as the cores of close-in gas giants are therefore thought to form in this region of the disk. Nevertheless, constraining the formation location of individual planets has proven to be difficult.
Aims. We aim to use the nitrogen abundance in Jupiter, which is around four times solar, in combination with Juno constraints on the total mass of heavy elements in Jupiter to narrow down its formation scenario.
Methods. Different pathways of enrichment of the atmosphere of Jupiter are considered, such as the accretion of enriched gas, pebbles, and planetesimals, and their implications for the oxygen abundance of Jupiter are discussed.
Results. The super-solar nitrogen abundance in Jupiter necessitates the accretion of extra N2 from the proto-solar nebula. The only location of the disk where this can happen is outside or just inside the N2 ice line. These constraints favor a pebble accretion origin of Jupiter, from the perspective of composition and planet formation. We predict that Jupiter’s oxygen abundance is between 3.6 and 4.5 times solar.
Key words: astrochemistry / planets and satellites: formation / planets and satellites: individual: Jupiter
© ESO 2019
1. Introduction
There are currently three theories that deal with the formation of gas giants in the Solar System. The classical picture is the core-accretion scenario, in which kilometer-sized planetesimals grow through mutual collisions, eventually leading to a core of a few Earth masses which can start to efficiently capture a gaseous atmosphere. (Pollack et al. 1996; Kokubo & Ida 2002; Ida & Lin 2004). For planetesimal accretion to work on a reasonable timescale, within the few-million-year lifetime of the gas disk, high surface densities of planetesimals are needed. As such planetesimal accretion is most efficient in forming giant planets at small radii. An increase in the surface density of planetesimals at the H2O ice line at a few AU makes this the preferred location for the formation of Jupiter in this scenario (Stevenson & Lunine 1988; Ciesla & Cuzzi 2006; Schoonenberg & Ormel 2017). Further migration due to interactions with the gas disk and resonances with Saturn would then put Jupiter at its current location (Walsh et al. 2011).
An alternative to the model of core accretion is the paradigm of pebble accretion, in which planetesimals grow by accreting millimeter- and centimeter-sized pebbles that flow radially through the disk. As a planet migrates as it is accreting its gas, its core needs to form at larger radii, outside of 15 AU, to end up at a few AU when the gas disk has dissipated (Bitsch et al. 2015, 2019; Cridland et al. 2019). Finally there is the possibility of forming giant planets through gravitational instabilities in the outer disk. In this scenario, Jupiter would form by direct gravitational collapse of a clump in the cold outer regions of the solar nebula before migrating inwards (Boss 1997, 2002; Boley et al. 2010).
This sets up a dichotomy of the origin of Jupiter: either formation around the water ice line, or formation at large radii. These different formation histories should leave an imprint on the composition of the planet, especially on the C/O ratio (Öberg et al. 2011). While a lot of effort has been put into constraining the atmosphere of Jupiter (Atreya et al. 2003, 2016; Bolton et al. 2017), there is a consensus that the oxygen abundance measurement by the Galileo mission is not representative of the bulk atmospheric abundance of oxygen in Jupiter, and therefore the C/O ratio cannot be used (Niemann et al. 1998; Atreya et al. 2003). These studies found however that both carbon and nitrogen are enhanced above solar levels (see Table 1, Asplund et al. 2009; Atreya et al. 2016). The enhancement of nitrogen is interesting, as nitrogen in the interstellar medium (ISM) is extremely volatile because the main carrier, N2, does not freeze-out until temperatures below ∼20 K are reached (Bisschop et al. 2006). Furthermore, the next most abundant nitrogen carrier, NH3, generally does not contain more than 10% of the total nitrogen budget (Lodders et al. 2009; Boogert et al. 2015; Cleeves et al. 2018; Pontoppidan et al. 2019; Altwegg et al. 2019). This potentially makes the nitrogen content of a planet a powerful probe of its formation location. In this Letter we use recent insights into planet formation theory and new constraints from the Juno mission to put Jupiter in an astrochemical context. This approach brings forward a couple of formation scenarios for Jupiter that can explain the abundance of elemental N in its atmosphere.
Elemental abundances relative to H.
During the development of this work, Öberg & Wordsworth (2019) published a similar line of argument as discussed here. We share their conclusion, that Jupiter must have formed outside of the N2 iceline. Enrichment of Jupiter’s atmosphere by N2 is critical in both studies, but whereas Öberg & Wordsworth (2019) use the relative enrichment pattern of volatile species to constrain the composition and formation temperature of the enriching bodies, we use the total heavy element mass to constrain Jupiter’s most likely formation location.
2. Enriching Jupiter with nitrogen
Generally speaking there are three methods to enrich the atmosphere of a gas giant planet with a specific element: through the accretion of enriched gas, through the accretion of solids during core or atmosphere formation, or through the late accretion of solids after the planet has accreted its atmosphere (see Fig. 1). Recently there have been multiple studies that have looked at the effect of disk evolution, especially the growth and drift of icy grains, and at the effect this has on the gas-phase elemental abundances (Ciesla & Cuzzi 2006; Booth et al. 2017; Stammler et al. 2017; Bosman et al. 2018; Krijt et al. 2018; Booth & Ilee 2019). In general, it is found that enrichments above solar abundances in a certain element can happen just inside an ice line if radial drift is efficient and the ice line corresponds to a species that is an abundant (≳10%) carrier of that element.
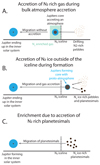 |
Fig. 1. Different scenarios for the origin of nitrogen in Jupiter’s atmosphere. In scenario A (top), the nitrogen is accreted during the bulk of the atmosphere accretion from the part of the disk that is rich in N2 gas close to the N2 ice line. The gas is enriched by rapidly drifting pebbles from outside the N2 ice line. In scenario B (middle), nitrogen is brought in with the solid material that accretes onto Jupiter while it is in the cold outer disk. This limits core formation to outside the N2 ice line, leaving the location of gas accretion unconstrained. In scenario C (bottom), Jupiter forms somewhere inside the N2 ice line, as far in as the H2O ice line, the classical location of Jupiter formation. Dinitrogen then has to be brought in on planetesimals that originate outside of the N2 ice line and migrate towards the location of the forming Jupiter. This scenario leaves almost no room for solids other than the N2-rich solids to be accreted by Jupiter after the initial core has formed. Scenario B seems to be the most reasonable scenario. |
In the case of nitrogen, Booth & Ilee (2019) find an enrichment of elemental nitrogen up to a factor of two above solar both within the NH3 ice line and in an annulus just within the N2 ice line. The high elemental nitrogen abundances within the NH3 ice line are strongly dependent on the initial NH3 abundance. Booth & Ilee (2019) assume that 33% of elemental nitrogen is in the form of NH3. Such high NH3 abundances have not been seen in observations of the cold ISM (Boogert et al. 2015), proto-planetary disks (Cleeves et al. 2018; Pontoppidan et al. 2019), or Solar System objects (Lodders et al. 2009; Altwegg et al. 2019), indicating that in all these environments N2 is the dominant carrier, containing ∼90% of the elemental nitrogen. With the low NH3 ice abundances observed, a super-solar nitrogen abundance due to the sublimation of NH3 is unlikely, suggesting that if Jupiter’s atmospheric enhancements are due to the accretion of enriched gas (Fig. 1, scenario A), it must have accreted most of its mass just within the N2 ice line.
The second and third scenarios depend on enrichment by solids that deposit nitrogen in the atmosphere. For simplicity, we assume that Jupiter accreted a solar N/H ratio from the gas, and that all of the extra nitrogen was brought in by solids. We further assume that the solids that were accreted onto Jupiter deposited their full nitrogen reservoir into the atmosphere. With these assumptions it is possible to calculate the mass of refractories (silicates and metals) that Jupiter needs to accrete as a function of the nitrogen-to-refractory mass ratio for the accreting solid bodies.
In Fig. 2 we show this relation along with mass constraints based on the known properties of Jupiter and the Solar System. The relative solid nitrogen mass and refractory mass is based on the nitrogen-to-refractory mass ratio, assuming that the volatile and refractory elemental abundances add up to the proto-solar abundance of Asplund et al. (2009). We assume that the refractories contain all of the sulfur, iron, magnesium, and silicon available in the ISM. Furthermore, we assume that the silicon is in equal parts enstatite and forsterite (e.g. Meeus et al. 2009), resulting in an average of 3.5 oxygen atoms per silicon in the refractories. Finally, we follow Pontoppidan et al. (2014) and Bergin et al. (2015) and place 25% of the total carbon in the refractory phase. This leads to a gas-to-refractory mass ratio of 186 and a nitrogen-to-refractory mass ratio of 0.2, the effective upper limit to the amount of nitrogen that can be added to the solid phase. Above this mass ratio, the outer disk would have had to be more enhanced in nitrogen than what is seen in the solar photosphere, a scenario we find unlikely. In the outer parts of the disk, where all non-noble elements heavier than hydrogen are in solids, the total gas-to-solid ratio drops to 77, and so the total solid mass in these regions is about twice the available refractory mass.
 |
Fig. 2. Nitrogen-to-refractory mass ratio of enriching solids necessary to reach Jupiter’s Nitrogen content as a function of total refractory mass added to Jupiter. It is assumed that Jupiter has accreted solar composition gas and that the excess nitrogen was brought in frozen on solids. The upper limit to the total heavy element mass is taken to be 27 M⊕ (Wahl et al. 2017). This can be in the form of ice-poor or ice-rich bodies; for ice-poor bodies the refractory mass is assumed to be the total mass of heavy elements, for ice-rich bodies, assuming H2O and CO are frozen out, as would be expected for a very N2-rich body, the heavy element mass is around two times the refractory mass, meaning that only ∼12 M⊕ of refractories can be accreted. The nitrogen-to-refractory mass ratios of ISM grains without N2 ice (Boogert et al. 2015), comets (Altwegg et al. 2019), or CI chondrites (Lodders et al. 2009) have been added for comparison. None of these have a high-enough nitrogen fraction to enhance Jupiter’s atmosphere. |
The gravitational moments measured by Juno (Bolton et al. 2017; Folkner et al. 2017; Iess et al. 2018) limit the total mass of heavy elements in the planet to be between 24 and 27 Earth masses (Wahl et al. 2017). Therefore, we can immediately neglect any refractory source that would need to accrete masses ≳27 M⊕. Furthermore, assuming that Jupiter accretes near the N2 snow line, the pebbles that are incorporated into the planet will also carry a significant portion of H2O and CO ice.
The combination of the accreted heavy element mass and the available nitrogen strongly limit the amount and composition of the solids that have enriched Jupiter’s atmosphere. In the case of enrichment by H2O and CO ice-poor bodies, it is required that these bodies contain > 25% of the available nitrogen budget. However, for ice-rich bodies, the total heavy element mass (which includes the ice) is about twice the refractory mass, which further rules out the enrichment of Jupiter by nitrogen-poor bodies and moves the minimum solid nitrogen fraction required to more than ∼75% of the total available nitrogen. Comets and meteorites are strongly ruled out as carriers of the nitrogen enhancement of Jupiter’s atmosphere as they contain far too little nitrogen (Lodders et al. 2009; Altwegg et al. 2019). Since we require at least 75% of the proto-solar nitrogen budget to be in the solid phase, to explain the N-enrichment of Jupiter’s atmosphere, it must have accreted this mass in the form of N2 ice.
This low-temperature origin of the building blocks of Jupiter was also proposed by Owen et al. (1999) and Owen & Encrenaz (2006). However, as new observations have constrained the total amount of enriching solids, we need the majority of the N2 to be in the ice, and thus temperatures below 20 K (Bisschop et al. 2007), instead of a smaller fraction of N2 trapped in a water-rich ice, in which case N2 can be trapped in the ice up to temperatures of 40 K (Lunine & Stevenson 1985; Collings et al. 2004).
3. Implications of Jupiter’s nitrogen enrichment
3.1. Enrichment during formation
The high nitrogen abundance in Jupiter necessitates the accretion of N2 rich gas or solids. Enrichment of Jupiter during its formation means that the nitrogen was from a local source. The accretion of highly nitrogen-enriched gas can only happen just inside the N2 ice line, at 60 AU (Fig. 1A). At the same time, enrichment of the atmosphere by accretion of small bodies necessitates the presence of N2 ice, which similarly requires early atmosphere growth outside of the N2 ice line (Fig. 1B). Finally, nitrogen outgassing from the core would necessitate a N2 rich core and thus core formation outside of the N2 ice line. The exact location of the N2 ice line in the early Solar System is hard to constrain and estimates of the N2 ice line in protoplanetary disks around solar mass stars vary greatly, ranging between 20 and 80 AU (Huang et al. 2016; van Terwisga et al. 2019; Qi et al. 2019).
Forming Jupiter’s core of around 10 Earth masses (e.g. Lambrechts & Lega 2017) at these radii is very hard to do by planetesimal accretion (Bitsch et al. 2015) and would point toward a pebble accretion or gravitational instability origin for Jupiter.
Pebble accretion seems especially promising as building a core from pebbles would leave the N2 on the pebbles until it is captured within the gravitational influence. Models by Bitsch et al. (2019) show that as long as the pebble flux is high enough in the outer disk, it is possible to form a cold Jupiter starting core growth as far out as 50 AU. Taking an optimistic estimate for both the pebble accretion efficiency (10% Ormel & Liu 2018) and the total mass of pebbles accreted onto the proto-Jupiter (7.5 M⊕) indicates a pebble reservoir of 75 M⊕ of refractories, or equivalently 0.05 M⊙ of gas, outside the N2 iceline. This translates into disks with radii of between 30 and 100 AU, assuming a surface density power-law slope between −1 and −0.5 (Tazzari et al. 2016). The total amount of dust necessary to form these pebbles in the model is even larger (Bitsch et al. 2019), indicating an even larger and more massive disk would be necessary. This puts the proto-solar nebula among the largest and most massive disks currently observed (Tazzari et al. 2016; van Terwisga et al. 2019).
In the case of formation by gravitational instability of the gas disk, the energy released by the collapse of gas would locally heat the disk and evaporate the N2 ice off the grains, hampering the accretion of N-enhanced material (Ilee et al. 2017). The large transport rates in a gravitationally unstable disk would quickly smooth any pre-exisiting overdensities in the gas or dust, making it difficult to build a nitrogen-enriched object (Kratter & Lodato 2016). In all of the cases discussed above, N2 needs to be frozen out in the part of the disk where Jupiter is forming. This indicates that the disk needs to be large and cold, and is thus likely to be in either the late class I or early class II stage, as the younger, still embedded disks are too warm to have CO, and therefore N2, frozen out (van ’t Hoff et al. 2018).
3.2. Enrichment after formation
It could also be possible that the atmosphere of Jupiter was enriched after it had formed and had accreted the majority of its atmosphere. This would require the N-enriched bodies to be formed at large radii, and Jupiter to be formed at smaller radii, for example at the water ice line. The enriching bodies in this case need to be large, roughly kilometres in size, as they need to be able to hold on to their N2 while traveling to Jupiter. If enrichment happens in the disk stage, these bodies need to be big enough not to be trapped in the pressure maximum caused by Jupiter, but not too big. As N2 is very volatile, any internal heating by large impacts or through radioactive decay (e.g. Prialnik et al. 1987) will lead to lower N2 abundances in the solids.
This scenario requires a very strict set of circumstances: assuming a core of around 10 M⊕ is needed to start gas accretion (Lambrechts & Lega 2017), then this leaves at most 15 M⊕ of heavy elements, namely ice and refractories, that can be added. The minimal amount of refractories needed, assuming Jupiter manages to capture all the available N2, is 7.5 M⊕. If Jupiter formed at the water ice line, there is a part of the disk (∼15 AU wide) that does not contribute to the enrichment of Jupiter’s atmosphere, while a significant amount of mass from the outer disk (≳20 AU) makes it to Jupiter with its volatile component intact. This seems highly unlikely – which further argues for a young Jupiter forming very close to or even beyond the N2 ice line.
4. Discussion
4.1. Nitrogen-rich bodies in the Solar System
Until now, little evidence has been found of bodies incorporating the bulk of the proto-solar N2 as ice in the Solar System (Glein & Waite 2018). Pluto might have incorporated a significant amount of N2 ice at its formation, but without a measurement of the nitrogen isotopic ratio its origin is open to speculation (Mandt et al. 2017). Finding bodies that incorporated and still contain a significant fraction of the primordial nitrogen would point to a possible reservoir of Jupiter-enriching bodies, and their current orbits could be indicative of the formation location of Jupiter. Both the very CH3OH-rich 2014 MU69 (Stern et al. 2019) and the comet C/2016 R2, which has a high measured N2/CO ratio (Opitom et al. 2019), could be one of these bodies. This indicates that bodies rich in N2 exist outside the orbit of Neptune.
The 14N/15N nitrogen isotopic ratio can be used to look at the origin of nitrogen in other bodies as well. There is a large discrepancy between the solar nitrogen isotopic ratio and the isotopic ratio found in many comets (e.g. Mumma & Charnley 2011). This is most likely due to fractionation processes either in the ISM or in the proto-planetary disk enriching HCN and NH3 and derivatives in 15N (Terzieva & Herbst 2000; Visser et al. 2018). As these species are less volatile than N2, ices above the sublimation temperature of N2 can easily be enriched in 15N.
The nitrogen isotopic ratio in Jupiter is the same as the one measured in the solar wind, implying that Jupiter’s nitrogen indeed comes from the bulk nitrogen reservoir of the proto-solar nebula (Fletcher et al. 2014). Saturn has a similar nitrogen isotopic ratio to Jupiter as well as a similar overabundance of total nitrogen over the sun, indicating that Saturn likely inherited its nitrogen from the same source as Jupiter (Fletcher et al. 2014; Atreya et al. 2016). The measured isotopic ratios of other bodies are up to a factor three lower than the solar value (Niemann et al. 2010; Mandt et al. 2014, 2017; Bockelée-Morvan et al. 2015), which includes meteorites, comets, and Titan, indicating that these bodies did not accrete their nitrogen from the bulk N2 reservoir.
4.2. Carbon and oxygen in Jupiter
Working with the assumption that Jupiter did not accrete a significant amount of solids after accreting most of its gas, it is possible to use the different formation scenarios and measured carbon contents for the planet to predict the oxygen content of Jupiter. These predictions depend critically on what is assumed to happen with the refractory carbon (here 25% of total carbon Pontoppidan et al. 2014; Bergin et al. 2015) and oxygen contained in refractories. Assuming silicates are in a 50–50 mix of SiO3 and SiO4 ions and iron not in the form of iron oxides, about 23% of the oxygen is refractory (Costantini et al. 2005; Meeus et al. 2009). For simplicity, as would be representative of gas in the inner regions of disks (Pontoppidan et al. 2014), we assume that all available volatile carbon is in CO, which then contains 40% of the total oxygen, with the remaining 37% of the oxygen in H2O. As such we are ignoring the few to tens of percent of carbon that can be contained within CO2 in the ice (Pontoppidan et al. 2014; Boogert et al. 2015; Le Roy et al. 2015).
Table 2 shows the oxygen and carbon abundances in Jupiter as predicted from different enrichment scenarios. In the case that N2 is accreted from N2-enriched gas, we assume that this gas is also enriched in CO by the same factor, which leads to an enrichment in both oxygen and carbon. The extra carbon cannot explain the full carbon enrichment observed in Jupiter’s atmosphere and therefore additional carbon from the refractory reservoir is necessary. Here one can assume that only the water ice on these grains enriches the atmosphere in oxygen, or that both the water ice and the silicates deposit oxygen in the atmosphere. In all cases a super solar C/O ratio is found.
Carbon and oxygen abundances relative to solar, predicted for Jupiter’s atmosphere assuming different contributing sources.
In the case that excess N2 was accreted as solid N2 on top of a 1 MJup solar composition atmosphere, it is safe to assume that all of the ices on the grains would also enrich the atmosphere. Again this does not match the carbon enrichment in the atmosphere and an additional carbon source is necessary. However, including all of the refractory carbon that is brought in by these grains would raise the carbon abundance in Jupiter to a value higher than the nominal measured value, but still within the range of observations. Finally adding enrichment by the full release of oxygen from the silicates brings the oxygen enhancement up to 4.5 times solar and the C/O ratio back to solar. Therefore, we predict a solar or slightly super-solar C/O ratio for Jupiter.
5. Conclusions
The nitrogen enrichment in Jupiter’s atmosphere makes it likely that Jupiter formed at much larger radii than is observed now. At these radii, core formation due to pebble accretion onto a planetesimal seems to be the most likely scenario as it would naturally bring in a lot of nitrogen-rich ice. This would nevertheless require a cold, massive, and large disk with a sufficiently massive N2 ice reservoir to enrich Jupiter’s atmosphere and enough pebbles flowing in these cold regions to be able to form Jupiter itself. The proto-solar nebula would therefore likely have resembled the most massive and largest proto-planetary disks that are currently observed.
This formation scenario necessitates the formation of Jupiter’s core at a time when the disk was cool enough to have N2 as an ice. Furthermore, the mass of pebbles necessary to enrich Jupiter’s atmosphere implies that formation of Jupiter took place in a large, massive disk, implying that the proto-solar disk was analogous to the largest proto-planetary disks currently observed. Jupiter’s atmosphere should be enriched in oxygen; in this case with a O/H below 4.5 times solar, with the preferred models predicting O/H between 3.6 and 4.5 times solar.
Acknowledgments
The authors thank the referee for a constructive report that improved the quality of the paper. Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA). This project has made use Matplotlib (Hunter 2007).
References
- Altwegg, K., Balsiger, H., & Fuselier, S. A. 2019, ARA&A, 57, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Atreya, S. K., Mahaffy, P. R., Niemann, H. B., Wong, M. H., & Owen, T. C. 2003, Planet. Space Sci., 51, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Atreya, S. K., Crida, A., Guillot, T., et al. 2016, ArXiv e-prints [arXiv:1606.04510] [Google Scholar]
- Bergin, E. A., Blake, G. A., Ciesla, F., Hirschmann, M. M., & Li, J. 2015, Proc. Natl. Acad. Sci., 112, 8965 [NASA ADS] [CrossRef] [Google Scholar]
- Bisschop, S. E., Fraser, H. J., Öberg, K. I., van Dishoeck, E. F., & Schlemmer, S. 2006, A&A, 449, 1297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bisschop, S. E., Fuchs, G. W., van Dishoeck, E. F., & Linnartz, H. 2007, A&A, 474, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Izidoro, A., Johansen, A., et al. 2019, A&A, 623, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelée-Morvan, D., Calmonte, U., Charnley, S., et al. 2015, Space Sci. Rev, 197, 47 [CrossRef] [Google Scholar]
- Boley, A. C., Hayfield, T., Mayer, L., & Durisen, R. H. 2010, Icarus, 207, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, S. J., Adriani, A., Adumitroaie, V., et al. 2017, Science, 356, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Boogert, A. C. A., Gerakines, P. A., & Whittet, D. C. B. 2015, ARA&A, 53, 541 [Google Scholar]
- Booth, R. A., & Ilee, J. D. 2019, MNRAS, 487, 3998 [NASA ADS] [CrossRef] [Google Scholar]
- Booth, R. A., Clarke, C. J., Madhusudhan, N., & Ilee, J. D. 2017, MNRAS, 469, 3994 [NASA ADS] [CrossRef] [Google Scholar]
- Bosman, A. D., Tielens, A. G. G. M., & van Dishoeck, E. F. 2018, A&A, 611, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boss, A. P. 1997, Science, 276, 1836 [NASA ADS] [CrossRef] [Google Scholar]
- Boss, A. P. 2002, Earth Planet. Sci. Lett., 202, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J., & Cuzzi, J. N. 2006, Icarus, 181, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Öberg, K. I., Wilner, D. J., et al. 2018, ApJ, 865, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Collings, M. P., Anderson, M. A., Chen, R., et al. 2004, MNRAS, 354, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Costantini, E., Freyberg, M. J., & Predehl, P. 2005, A&A, 444, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cridland, A. J., Bosman, A. D., & van Dishoeck, E. F. 2019, A&A, submitted [Google Scholar]
- Fletcher, L. N., Greathouse, T. K., Orton, G. S., et al. 2014, Icarus, 238, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Folkner, W. M., Iess, L., Anderson, J. D., et al. 2017, Geophys. Res. Lett., 44, 4694 [NASA ADS] [CrossRef] [Google Scholar]
- Glein, C. R., & Waite, J. H. 2018, Icarus, 313, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J., Öberg, K. I., & Andrews, S. M. 2016, ApJ, 823, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 604, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Iess, L., Folkner, W. M., Durante, D., et al. 2018, Nature, 555, 220 [NASA ADS] [CrossRef] [Google Scholar]
- Ilee, J. D., Forgan, D. H., Evans, M. G., et al. 2017, MNRAS, 472, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 2002, ApJ, 581, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Kratter, K., & Lodato, G. 2016, ARA&A, 54, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Krijt, S., Schwarz, K. R., Bergin, E. A., & Ciesla, F. J. 2018, ApJ, 864, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Lega, E. 2017, A&A, 606, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Roy, L., Altwegg, K., Balsiger, H., et al. 2015, A&A, 583, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H. P. 2009, Landolt Börnstein, 4B, 712 [Google Scholar]
- Lunine, J. I., & Stevenson, D. J. 1985, ApJS, 58, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Mandt, K. E., Mousis, O., Lunine, J., & Gautier, D. 2014, ApJ, 788, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Mandt, K., Luspay-Kuti, A., Hamel, M., et al. 2017, MNRAS, 472, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Meeus, G., Juhász, A., Henning, T., et al. 2009, A&A, 497, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Niemann, H. B., Atreya, S. K., Carignan, G. R., et al. 1998, J. Geophys. Res., 103, 22831 [NASA ADS] [CrossRef] [Google Scholar]
- Niemann, H. B., Atreya, S. K., Demick, J. E., et al. 2010, J. Geophys. Res. (Planets), 115, E12006 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., Boogert, A. C. A., Pontoppidan, K. M., et al. 2011, ApJ, 740, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Öberg, K. I., & Wordsworth, R. 2019, AJ, 158, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Opitom, C., Hutsemékers, D., Jehin, E., et al. 2019, A&A, 624, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Liu, B. 2018, A&A, 615, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, T., & Encrenaz, T. 2006, Planet. Space Sci., 54, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, T., Mahaffy, P., Niemann, H. B., et al. 1999, Nature, 402, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Bergin, E. A., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 363 [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Banzatti, A., et al. 2019, ApJ, 874, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., Bar-Nun, A., & Podolak, M. 1987, ApJ, 319, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Qi, C., Öberg, K. I., Espaillat, C. C., et al. 2019, ApJ, 882, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Schoonenberg, D., & Ormel, C. W. 2017, A&A, 602, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stammler, S. M., Birnstiel, T., Panić, O., Dullemond, C. P., & Dominik, C. 2017, A&A, 600, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stern, S. A., Weaver, H. A., Spencer, J. R., et al. 2019, Science, 364, 6441 [Google Scholar]
- Stevenson, D. J., & Lunine, J. I. 1988, Icarus, 75, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Tazzari, M., Testi, L., Ercolano, B., et al. 2016, A&A, 588, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terzieva, R., & Herbst, E. 2000, MNRAS, 317, 563 [NASA ADS] [CrossRef] [Google Scholar]
- van ’t Hoff, M. L. R., Tobin, J. J., Harsono, D., & van Dishoeck, E. F. 2018, A&A, 615, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Terwisga, S. E., van Dishoeck, E. F., Cazzoletti, P., et al. 2019, A&A, 623, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., Bruderer, S., Cazzoletti, P., et al. 2018, A&A, 615, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wahl, S. M., Hubbard, W. B., Militzer, B., et al. 2017, Geophys. Res. Lett., 44, 4649 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Carbon and oxygen abundances relative to solar, predicted for Jupiter’s atmosphere assuming different contributing sources.
All Figures
 |
Fig. 1. Different scenarios for the origin of nitrogen in Jupiter’s atmosphere. In scenario A (top), the nitrogen is accreted during the bulk of the atmosphere accretion from the part of the disk that is rich in N2 gas close to the N2 ice line. The gas is enriched by rapidly drifting pebbles from outside the N2 ice line. In scenario B (middle), nitrogen is brought in with the solid material that accretes onto Jupiter while it is in the cold outer disk. This limits core formation to outside the N2 ice line, leaving the location of gas accretion unconstrained. In scenario C (bottom), Jupiter forms somewhere inside the N2 ice line, as far in as the H2O ice line, the classical location of Jupiter formation. Dinitrogen then has to be brought in on planetesimals that originate outside of the N2 ice line and migrate towards the location of the forming Jupiter. This scenario leaves almost no room for solids other than the N2-rich solids to be accreted by Jupiter after the initial core has formed. Scenario B seems to be the most reasonable scenario. |
| In the text | |
 |
Fig. 2. Nitrogen-to-refractory mass ratio of enriching solids necessary to reach Jupiter’s Nitrogen content as a function of total refractory mass added to Jupiter. It is assumed that Jupiter has accreted solar composition gas and that the excess nitrogen was brought in frozen on solids. The upper limit to the total heavy element mass is taken to be 27 M⊕ (Wahl et al. 2017). This can be in the form of ice-poor or ice-rich bodies; for ice-poor bodies the refractory mass is assumed to be the total mass of heavy elements, for ice-rich bodies, assuming H2O and CO are frozen out, as would be expected for a very N2-rich body, the heavy element mass is around two times the refractory mass, meaning that only ∼12 M⊕ of refractories can be accreted. The nitrogen-to-refractory mass ratios of ISM grains without N2 ice (Boogert et al. 2015), comets (Altwegg et al. 2019), or CI chondrites (Lodders et al. 2009) have been added for comparison. None of these have a high-enough nitrogen fraction to enhance Jupiter’s atmosphere. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


