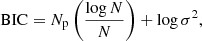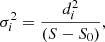| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A119 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201936698 | |
| Published online | 13 December 2019 | |
Asteroseismological analysis of the ultra-massive ZZ Ceti stars BPM 37093, GD 518, and SDSS J0840+5222
1
Grupo de Evolución Estelar y Pulsaciones, Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: acorsico@fcaglp.unlp.edu.ar
2
Instituto de Astrofísica La Plata, IALP (CCT La Plata), CONICET-UNLP, Argentina
Received:
13
September
2019
Accepted:
16
October
2019
Context. Ultra-massive (≳1 M⊙) hydrogen-rich (DA) white dwarfs are expected to have a substantial portion of their cores in a crystalline state at the effective temperatures characterising the ZZ Ceti instability strip (Teff ∼ 12 500 K) as a result of Coulomb interactions in very dense plasmas. Asteroseismological analyses of these white dwarfs can provide valuable information related to the crystallisation process, the core chemical composition, and the evolutionary origin of these stars.
Aims. We present a thorough asteroseismological analysis of the ultra-massive ZZ Ceti star BPM 37093, which exhibits a rich period spectrum, on the basis of a complete set of fully evolutionary models that represent ultra-massive oxygen/neon (ONe) core DA white dwarf stars harbouring a range of hydrogen (H) envelope thicknesses. We also carry out preliminary asteroseismological inferences on two other ultra-massive ZZ Ceti stars that exhibit fewer periods, GD 518, and SDSS J0840+5222.
Methods. We considered g-mode adiabatic pulsation periods for ultra-massive ONe-core DA white dwarf models with stellar masses in the range 1.10 ≲ M⋆/M⊙ ≲ 1.29, effective temperatures in the range 10 000 ≲ Teff ≲ 15 000 K, and H-envelope thicknesses in the interval −10 ≲ log(MH/M⋆)≲ − 6. We explored the effects of employing different H-envelope thicknesses on the mode-trapping properties of our ultra-massive ONe-core DA white dwarf models and performed period-to-period fits to ultra-massive ZZ Ceti stars with the aim of finding an asteroseismological model for each target star.
Results. We find that the trapping cycle and trapping amplitude are larger for thinner H envelopes, and that the asymptotic period spacing is longer for thinner H envelopes. We find a mean period spacing of ΔΠ ∼ 17 s in the data of BPM 37093, which is likely to be associated with ℓ = 2 modes. However, we are not able to put constraints on the stellar mass of BPM 37093 using this mean period spacing due to the simultaneous sensitivity of ΔΠ with M⋆, Teff, and MH, which is an intrinsic property of DAV stars. We find asteroseismological models for the three objects under analysis, two of them (BPM 37093 and GD 518) characterised by canonical (thick) H envelopes, and the third one (SDSS J0840+5222) with a thinner H envelope. The effective temperature and stellar mass of these models are in agreement with the spectroscopic determinations. The percentage of crystallised mass for these asteroseismological models is 92%, 97%, and 81% for BPM 37093, GD 518, and SDSS J0840+5222, respectively. We also derive asteroseismological distances which differ somewhat from the astrometric measurements of Gaia for these stars.
Conclusions. Asteroseismological analyses like the one presented in this paper could lead to a more complete understanding of the processes occurring during crystallisation inside white dwarfs. Also, such analyses could make it possible to deduce the core chemical composition of ultra-massive white dwarfs and, in this way, to infer their evolutionary origin, such as the correlation between a star’s ONe core and its having originated through single-star evolution or a carbon/oxygen (CO) core indicating the star is the product of a merger of the two components of a binary system. However, in order to achieve these objectives, it is necessary to find a greater number of pulsating ultra-massive WDs and to carry out additional observations of known pulsating stars to detect more pulsation periods. Space missions such as TESS can provide a great boost towards achieving these aims.
Key words: stars: oscillations / stars: interiors / stars: evolution / white dwarfs
© ESO 2019
1. Introduction
ZZ Ceti (also called DAV stars) stars are the most numerous and best-studied class of pulsating white dwarf (WD) stars. They are normal DA WDs with effective temperatures between ∼10 400 K and ∼12 400 K and logarithm of surface gravities in the range of [7.5 − 9.1]. These stars exhibit brightness variations due to non-radial g (gravity) modes with low harmonic degree (ℓ ≤ 2) with periods in the interval [70 − 1500] s (Winget & Kepler 2008; Fontaine & Brassard 2008; Althaus et al. 2010b; Córsico et al. 2019). The first object of this class, HL Tau 76, was discovered to be pulsating by Landolt (1968). From then until now, a large number of ZZ Ceti stars have been discovered, initially through specific efforts with observations of bright targets from the ground (Fontaine & Brassard 2008), then from the Sloan Digital Sky Survey (SDSS; York et al. 2000), and, more recently, with the Kepler space telescope (Borucki 2016), and the Kepler’s second mission K2 (Van Cleve et al. 2016). Currently, there are 260 ZZ Ceti stars known (Córsico et al. 2019), and it is expected that the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014) will be useful in raising this number substantially.
Asteroseismology is a powerful technique that offers the exciting prospect of deducing the internal structure of stars by studying their natural frequencies. In the case of pulsating WDs, the first asteroseismic studies of ZZ Ceti stars that compared the observed periods with the theoretical periods computed on a large grid of realistic DA WD models (the so-called “forward method”) were carried out by Bradley (1998, 2001). These pioneering works showed that it would be possible, in principle, to infer the internal chemical structure, the stellar mass, surface gravity, effective temperature, luminosity, radius, seismological distance, and rotation rate of ZZ Ceti stars on the basis of the observed pulsation periods. Since then, more detailed asteroseismological studies of DAV stars have been carried out, either through the use of fully evolutionary models (Romero et al. 2012, 2013, 2017; De Gerónimo et al. 2017, 2018), or of static/parametric models (Bischoff-Kim et al. 2008; Fu et al. 2013; Bognár et al. 2016; Giammichele et al. 2017a,b). Both methods have their respective strengths and weaknesses but, ultimately, their results offer complementary findings (see discussion in Córsico et al. 2019).
A matter of particular interest in this paper is the asteroseismological analysis of rare ultra-massive ZZ Ceti stars (M⋆ ≳ 1 M⊙). At variance with average-mass (0.50 ≲ M⋆/M⊙ ≲ 0.70) and massive (0.70 ≲ M⋆/M⊙ ≲ 1.0) ZZ Ceti stars which are likely to have CO cores1, ultra-massive ZZ Ceti stars are expected to harbour cores made mostly of O and Ne if they are the result of single-star evolution. However, it cannot be ruled out that ultra-massive WDs could have CO cores if they are the result of the merger of two WDs (García-Berro et al. 2012). By virtue of their very high masses, these stars are expected to have a large fraction of their cores crystallised at the effective temperatures that characterise the ZZ Ceti instability strip. The crystallisation process is attributed to Coulomb interactions in very dense plasmas. This process was theoretically predicted to take place in the cores of WDs six decades ago (Kirzhnits 1960; Abrikosov 1961; Salpeter 1961; van Horn 1968) but it was not until recently that the existence of crystallised WDs was inferred from the study of WD luminosity function of stellar clusters (Winget et al. 2009; García-Berro et al. 2010), and the galactic field (Tremblay et al. 2019). The effects of crystallisation on the pulsational properties of ZZ Ceti star models have been studied by Montgomery & Winget (1999), Metcalfe et al. (2004), Córsico et al. (2004, 2005), Brassard & Fontaine (2005).
In the specific case of ultra-massive WDs with ONe cores, the first attempt at studying their pulsational properties from a theoretical perspective was undertaken by Córsico et al. (2004), who showed that the forward and mean period spacing of ONe-core WDs are markedly different from those of CO-core WDs. De Gerónimo et al. (2019) recently revisited the topic by assessing the adiabatic pulsation properties of ultra-massive DA WDs with ONe cores on the basis of a new set of fully evolutionary models generated by Camisassa et al. (2019). These models incorporate the most updated physical ingredients for modelling the progenitor and WD evolution. Specifically, the chemical profiles of the WD models of Camisassa et al. (2019), adopted from Siess (2010), are consistent with the predictions of the progenitor evolution with stellar masses in the range of 9.0 < MZAMS/M⊙ < 10.5 from the zero age main sequence (ZAMS) to the end of the super asymptotic giant branch (S-AGB) phase. In addition, these models consider, for the first time, changes in the core chemical composition that result from phase separation due to crystallisation according to the predictions of the phase diagram suitable for 16O and 20Ne plasma of Medin & Cumming (2010).
In this paper, we perform the first detailed asteroseismological analysis of the ultra-massive ZZ Ceti stars known to date carried out on the basis of the new grid of ONe-core WD models presented in Camisassa et al. (2019). At present, there are four objects of this class known: BPM 37093 (M⋆ = 1.1 M⊙; Kanaan et al. 1992), GD 518 (M⋆ = 1.24 M⊙; Hermes et al. 2013), SDSS J084021 (M⋆ = 1.16 M⊙; Curd et al. 2017), and WD J212402 (M⋆ = 1.16 M⊙; Rowan et al. 2019). The location of these stars in the spectroscopic Hertzsprung–Russell (HR) diagram is shown in Fig. 1, along with the evolutionary tracks of Camisassa et al. (2019). The observed pulsation periods of these stars are shown in Tables 1, 3, 5, and 7. The star with the richest pulsation spectrum, BPM 37093 (Table 1), allows for a detailed asteroseismological analysis. This star is the main object of our paper. The remaining stars exhibit just three periods (GD 518 and SDSS J084021: Tables 3 and 5, respectively) and only one period (WD J212402: Table 7). In view of this, for GD 518 and SDSS J084021 it is only possible to carry out a preliminary seismological analysis, whereas for WD J212402, it is not possible at present to carry out any asteroseismological inference. The stellar models upon which we base our study consider time-dependent element diffusion and crystallisation with chemical rehomogeneization due to phase separation. In order to have a set of models suitable for a detailed asteroseismological analysis, we have expanded our set of models by generating new sequences of WD models characterised by H envelopes thinner than the (thick) canonical envelopes. In this way, we extend the parameter space covered by our asteroseismological analysis.
 |
Fig. 1. Evolutionary tracks (red solid lines) of ultra-massive DA WD models computed by Camisassa et al. (2019) in the Teff − log g plane. Blue dashed lines indicate 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95 and 99% of crystallised mass. Locations of ultra-massive DA WD stars (Kleinman et al. 2013; Kepler et al. 2016; Curd et al. 2017) are indicated with black star symbols. Black circles indicate the location of known ultra-massive ZZ Ceti stars: BPM 37093 (Nitta et al. 2016), SDSS J084021 (Curd et al. 2017), GD 518 (Hermes et al. 2013), and WD J212402 (Rowan et al. 2019). |
Independent frequencies and periods in the data of BPM 37093 from Metcalfe et al. (2004), along with the theoretical periods, harmonic degrees, radial orders, and period differences of the best-fit model described in Sect. 4.3.
The paper is organized as follows: a brief description of the numerical codes and the evolutionary models that we employed is provided in Sect. 2. In Sect. 3 we present a brief description of the pulsation properties of our models. In Sect. 4 we perform a detailed asteroseismological analysis of the ultra-massive ZZ Ceti star BPM 37093, and in Sect. 5 we carry out period-to-period fits to the stars GD 518 and SDSS J084021. Finally, in Sect. 6 we summarize the main findings of this work.
2. Numerical codes and evolutionary models
2.1. Evolutionary and pulsational codes
The ultra-massive DA WD evolutionary models employed in this work were computed using the LPCODE evolutionary code (see Althaus et al. 2005b, 2010a; Renedo et al. 2010; Miller Bertolami 2016, for a detailed physical description). This numerical tool has been employed to study multiple aspects of the evolution of low-mass stars (Wachlin et al. 2011; Althaus et al. 2013, 2015), the formation of horizontal branch stars (Miller Bertolami et al. 2008), extremely low-mass WDs (Althaus et al. 2013), AGB and post-AGB evolution (Miller Bertolami 2016), the evolution of DA WDs (Camisassa et al. 2016) and H-defficient WDs (Camisassa et al. 2017), among others. More recently, the code has been employed to assess the impact of the uncertainties in progenitor evolution on the pulsation properties and asteroseismological models of ZZ Ceti stars (De Gerónimo et al. 2017, 2018). The input physics of the version of the LPCODE evolutionary code employed in this work is described in Camisassa et al. (2019) (see that paper for more details). An aspect of particular importance in this study is the treatment of crystallisation. Theoretical models predict that cool WD stars must crystallise due to the strong Coulomb interactions in their very dense interiors (van Horn 1968). The two additional energy sources induced by crystallisation, namely, the release of latent heat and the gravitational energy associated with changes in the chemical profiles induced by crystallisation, are consistently taken into account. The chemical redistribution due to phase separation and the associated release of energy have been considered following Althaus et al. (2010c), appropriately modified by Camisassa et al. (2019) for ONe plasmas. To assess the enhancement of 20Ne in the crystallised core, we used the azeotropic-type phase diagram of Medin & Cumming (2010).
The pulsation code used to compute the nonradial g-mode pulsations of our complete set of models is the adiabatic version of the LP-PUL pulsation code described in Córsico & Althaus (2006). We did not consider torsional modes, since these modes are characterised by very short periods (up to 20 s; see Montgomery & Winget 1999) which have never been observed in ZZ Ceti stars. To account for the effects of crystallisation on the pulsation spectrum of g modes, we adopted the “hard-sphere” boundary conditions (Montgomery & Winget 1999; Córsico et al. 2005), which assume that the amplitude of the radial displacement of g modes is drastically reduced below the solid-liquid boundary layer because of the non-shear modulus of the solid, as compared with the amplitude in the fluid region (Montgomery & Winget 1999). The squared Brunt–Väisälä frequency (N2) for the fluid part of the models was computed as per Tassoul et al. (1990). The Ledoux term B, which explicitly contains the contributions of the chemical interfaces to the Brunt–Väisälä frequency, has been appropriately generalized in order to include the presence of transition regions in which multiple nuclear species vary in abundance.
2.2. The grid of ultra-massive ONe-core WD models
The asteroseismological analysis presented in this work is based on a set of four evolutionary sequences of ultra-massive WD models with stellar masses M⋆ = 1.10, 1.16, 1.22, and 1.29 M⊙ resulting from the complete evolution of the progenitor stars through the S-AGB phase (Camisassa et al. 2019). The core and inter-shell chemical profiles of our models at the start of the WD cooling phase were derived from Siess (2010). The cores are composed mostly of 16O and 20Ne and smaller amounts of 12C, 23Na, and 24Mg (see Figs. 2 and 3 of Camisassa et al. 2019). Since element diffusion and gravitational settling operate throughout the WD evolution, our models develop pure H envelopes. The helium (He) content of our WD sequences is given by the evolutionary history of progenitor star, however, the H content of our canonical (thick) envelopes [log(MH/M⋆)∼ − 6] was set by imposing that further evolution does not lead to H thermonuclear flashes on the WD cooling track. We expanded our grid of models by artificially generating new sequences harbouring thinner H envelopes [log(MH/M⋆) = − 7, −8, −9, −10], for each stellar-mass value. This artificial procedure was done at high-luminosity stages of the WD evolution. The resulting transitory effects of this procedure become irrelevant much before the models reach the ZZ Ceti regime. Details on the method for computing the chemical rehomogeneization at the core regions during crystallisation are given in Camisassa et al. (2019) and De Gerónimo et al. (2019). Temporal changes of the chemical abundances due to element diffusion were assessed by using a new full-implicit treatment for time-dependent element diffusion described in detail in Althaus et al. (2019).
In Fig. 2 we show the 1H, 4He, 12C, 16O, 20Ne, 23Na, and 24Mg chemical profiles in terms of the fractional mass for 1.29 M⊙ ONe-core WD models at Teff ∼ 12 000 K and H envelope thicknesses log(MH/M⋆) = − 6, −7, −8, −9, and −10. Note that a pure He buffer develops as we consider thinner H envelopes (from the top to the bottom panel). At this effective temperature, the chemical rehomogeneization due to crystallisation has already been completed, giving rise to a core where the abundance of 16O increases (20Ne decreases) outward. In Fig. 3 we show the logarithm of the squared Brunt–Väisälä frequency corresponding to the same models shown in Fig. 2. The step at the triple chemical transition between 12C, 16O, and 20Ne seen in Fig. 2 [−log(1 − Mr/M⋆)∼1.4] is within the solid part of the core and, thus, it is irrelevant for the mode-trapping properties of these models. This is because according to the hard-sphere boundary conditions adopted for the pulsations, the eigenfunctions do not penetrate the solid region (gray zone). In view of this, the mode-trapping properties of the models illustrated in Figs. 2 and 3 are entirely determined by the presence of the He/H transition and the associated bump in the Brunt-Väisälä frequency, which is located in more external regions for thinner H envelopes (see more in the next section).
 |
Fig. 2. Abundances by mass of 1H, 4He, 12C, 16O, 20Ne, 23Na, and 24Mg as a function of the fractional mass, corresponding to ONe-core WD models with M⋆1.29 M⊙, Teff ∼ 12 000 K and log(MH/M⋆) = − 6, −7, −8, −9, and −10 (from top to bottom). Models were computed by taking into account time-dependent element diffusion, along with latent heat release and chemical redistribution caused by phase separation during crystallisation. The solid part of the models is emphasized with a gray tone. The crystallised mass fraction (in percentage) is 99.5%. |
 |
Fig. 3. Logarithm of squared Brunt–Väisälä frequency, corresponding to the same ONe-core WD models with M⋆ = 1.29 M⊙, Teff ∼ 12 000 K and log(MH/M⋆) = − 6, −7, −8, −9, and −10 shown in Fig. 2. They gray zone corresponds to the crystallised part of the models. |
3. Pulsation calculations
We computed adiabatic pulsation periods of ℓ = 1, 2 g modes in a range of periods covering the period spectrum that is typically observed in ZZ Ceti stars (70 s ≲Π ≲ 1500 s). We briefly examine the impact of the inclusion of thin H envelopes on the mode-trapping properties of our ultra-massive WD models. Mode trapping of g modes in WDs is a well-studied mechanical resonance for the mode propagation that results from the presence of density gradients induced by chemical transition regions. Specifically, chemical transition regions which involve non-negligible jumps in density act like reflecting walls that partially trap certain modes, forcing them to oscillate with greater amplitudes in specific regions and with smaller amplitudes outside those regions (for details, see Brassard et al. 1992a,b; Bradley et al. 1993; Córsico et al. 2002). From an observational point of view, a possible signature of mode trapping in a WD star is the departure from uniform period spacing. According to the asymptotic theory of stellar pulsations, in the absence of chemical gradients, the pulsation periods of g modes with high radial order k (long periods) are expected to be uniformly spaced with a constant period separation given by (Tassoul et al. 1990):
where
Actually, the period separation in chemically-stratified WD models like the ones considered in this work is not constant except for very high radial-order modes. We define the forward period spacing as ΔΠk = Πk + 1 − Πk. The left panels of Fig. 4 show Πk − ΔΠk diagrams for the same WD models depicted in Figs. 2 and 3. These models are characterised by M⋆ = 1.29 M⊙ at Teff ∼ 12 500 K and by different thicknesses of the H envelope. In each panel, the horizontal dashed line corresponds to the asymptotic period spacing computed with Eqs. (1) and (2). Models with decreasing H envelope thicknesses are displayed from top to bottom, starting with the case of the canonical envelope. In examining the plots, several aspects are worth mentioning. Firstly, the asymptotic period spacing increases for decreasing H envelope thickness. This is because the integral in Eq. (2) for the quantity Π0 is smaller for thinner H envelopes because the bump in the Brunt–Väisälä frequency induced by the He/H chemical interface becomes progressively narrow in the radial coordinate r as this interface is located at more external layers. Since Π0 is larger for thinner H envelopes, the asymptotic period spacing increases (Eq. (1)). 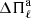 experiences an increase between 37% and 60% when we go from the canonical envelope [log(MH/M⋆) = − 6] to the thinnest envelope [log(MH/M⋆) = − 10] for this sequence. Another notable feature in the left panels of Fig. 4 is connected with the changes in mode-trapping properties when we consider H envelopes that are progressively thinner. Indeed, we note that for thick envelopes, including the canonical one, the period-spacing distribution of g modes shows a regular pattern of mode trapping with a very short trapping cycle – the k interval between two trapped modes. When we consider thinner H envelopes, the trapping cycle and the trapping amplitude increase. A common feature for all the values of log(MH/M⋆) considered in this study is that the mode-trapping signatures exhibited by ΔΠk vanish for very large radial orders (very long periods), in which case ΔΠk approaches
experiences an increase between 37% and 60% when we go from the canonical envelope [log(MH/M⋆) = − 6] to the thinnest envelope [log(MH/M⋆) = − 10] for this sequence. Another notable feature in the left panels of Fig. 4 is connected with the changes in mode-trapping properties when we consider H envelopes that are progressively thinner. Indeed, we note that for thick envelopes, including the canonical one, the period-spacing distribution of g modes shows a regular pattern of mode trapping with a very short trapping cycle – the k interval between two trapped modes. When we consider thinner H envelopes, the trapping cycle and the trapping amplitude increase. A common feature for all the values of log(MH/M⋆) considered in this study is that the mode-trapping signatures exhibited by ΔΠk vanish for very large radial orders (very long periods), in which case ΔΠk approaches 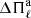 , as predicted by the asymptotic theory.
, as predicted by the asymptotic theory.
 |
Fig. 4. Left panels: forward period spacing, ΔΠk, in terms of the pulsation periods, Πk, for WD models with M⋆ = 1.29 M⊙, Teff ∼ 12 000 K and different thicknesses of the H envelope. Thin horizontal dashed lines correspond to the value of the asymptotic period spacing, ΔΠa. Right panels: oscillation kinetic energy versus the periods for the same WD models shown in the left panel. Normalization, (δr/r)r = R⋆ = 1 (δr being the radial displacement), has been assumed to compute the kinetic energy values. |
Mode-trapping effects also translate into local maxima and minima in the kinetic energy of oscillation Ekin, which are usually associated to modes that are partially confined to the core regions and modes that are partially trapped in the envelope. This can be appreciated in the right panels of Fig. 4. The behaviour described above for ΔΠk is also found in the case of Ekin, that is, the mode-trapping cycle and amplitude increase with decreasing H envelope thickness.
4. Asteroseismological analysis of BPM 37093
Kanaan et al. (1992) made the discovery of the first ultra-massive ZZ Ceti star, BPM 37093. This star is characterised by Teff = 11 370 K and log g = 8.843 (Nitta et al. 2016). Detailed theoretical computations carried out by Winget et al. (1997), Montgomery (1998), and Montgomery & Winget (1999) suggest that BPM 37093 should have a crystallised core. This star has been the target of two multi-site observing campaigns of the Whole Earth Telescope (WET; Nather et al. 1990). The preliminary results of these campaigns were published by Kanaan et al. (2000). The 1998 observations (XCov 16) revealed a set of regularly spaced pulsation frequencies in the range of 1500–2000 μHz. The 1999 observations (XCov 17) revealed a total of four independent modes, including two new modes and two that had been seen in the previous campaign. By comparing pulsation amplitudes in the UV to the optical spectra, Nitta (2000) identified the harmonic degree of the BPM 37093 pulsation modes, concluding that they can not be ℓ = 3 and that most of the modes must be ℓ = 2. Metcalfe et al. (2004) obtained new single-site observations of BPM 37093 from the Magellan 6.5 m telescope over three nights in February 2003. These data showed evidence of five independent modes, all of which had been detected in the two previous multi-site campaigns. Kanaan et al. (2005) reported on WET observations of BPM 37093 obtained in 1998 and 1999. On the basis of a simple analysis of the average period spacing, they concluded that a large fraction of the total stellar mass of the star should be crystallised. On the basis of asteroseismological techniques, Metcalfe et al. (2004) reported their “measurement” of the crystallized mass fraction for BPM 37093 and determined a value ∼90%. However, by employing similar asteroseismological methods, Brassard & Fontaine (2005) questioned those conclusions, suggesting instead that the percentage of crystallised mass of BPM 37093 should probably be between 32% and 82%. In the following sections, we carry out a detailed astroseismological analysis that involves the assessment of a mean period spacing and its comparison with the theoretical values, along with period-to-period fits undertaken with the intention of finding an asteroseismological model.
4.1. Period spacing
For the asteroseismological analysis of this star, we adopt the set of eight modes considered by Metcalfe et al. (2004) (see Table 1). This list of periods is based on the set of periods detected by Nitta (2000). We searched for a constant period spacing in the data of BPM 37093 by using the Kolmogorov-Smirnov (K-S; see Kawaler 1988), the inverse variance (I-V; see O’Donoghue 1994), and the Fourier Transform (F-T; see Handler et al. 1997) significance tests. In the K-S test, any uniform or, at least, any systematically non-random period spacing in the period spectrum of the star will appear as a minimum in Q. In the I-V test, a maximum of the inverse variance indicates a constant period spacing. Finally, in the F-T test, we calculated the Fourier transform of a Dirac comb function (created from the set of observed periods) and then we plotted the square of the amplitude of the resulting function in terms of the inverse of the frequency. Once again, a maximum in the square of the amplitude indicates a constant period spacing. In Fig. 5, we show the results of applying the tests to the set of periods of Table 1. The three tests indicate the existence of a mean period spacing of about 17 s. According to our set of models, the asymptotic period spacing (Eq. (1)) for ultra-massive DA WDs with masses between 1.10 and 1.29 M⊙ and effective temperatures within the ZZ Ceti instability strip (13 500K − 10 500 K) varies between ∼22 s and ∼34 s for ℓ = 1, and between ∼12 s and ∼19 s for ℓ = 2. Clearly, the period spacing evidenced by the 3 tests for BPM 37093 corresponds to modes ℓ = 2. This indicates that the period spectrum of this star is dominated by quadrupole modes, which is in concordance with the finding of Nitta (2000). By averaging the period spacing derived from the three statistical tests, we found ΔΠℓ = 2 = 17.3 ± 0.9 s.
 |
Fig. 5. I-V (upper panel), K-S (middle panel), and F-T (bottom panel) significance tests applied to the period spectrum of BPM 37093 to search for a constant period spacing. The periods used here are the same eight periods shown in Table 1. |
Nitta et al. (2016) expanded the set of periods of Nitta (2000) for BPM 37093 by employing Gemini South time-series combined with simultaneous time-series photometry from Mt. John (New Zealand), SAAO, PROMPT, and Complejo Astronómico El Leoncito (CASLEO, Argentina), providing a list of 13 periods (see their Table 1). Averaging two pairs of periods, the list gives 11 periods, of which eight are the same as in Metcalfe et al. (2004), and the remaining three periods are new periods with values 624.2 s, 641.0 s, 660.8 s. We applied the three statistical tests to this expanded list of periods but we did not find a clear period spacing. This is because the three new periods do not fit well into the regular pattern of periods with ℓ = 2 shown in Table 1.
4.2. Average of the computed period spacings
In principle, the stellar mass of pulsating WDs can be derived by comparing the average of the period spacings (or the asymptotic period spacing2) computed from a grid of models with different masses, effective temperatures, and envelope thicknesses with the mean period spacing exhibited by the star, if present. This method takes full advantage of the fact that the period spacing of DBV (pulsating DB WDs) and GW Vir stars (pulsating PG1159 stars) primarily depends on the stellar mass and the effective temperature, and very weakly on the thickness of the He envelope in the case of DBVs (see, e.g. Tassoul et al. 1990) and the thickness of the C/O/He envelope in the case of GW Vir stars (Kawaler & Bradley 1994). In the case of ZZ Ceti stars, however, the the average of the period spacings and the asymptotic period spacing depends on the stellar mass, the effective temperature, and the thickness of the H envelope with a comparable sensitivity. Consequently, the method is not, in principle, directly applicable to ZZ Ceti stars due to the intrinsic degeneracy of the dependence of ΔΠ with the three parameters M⋆, Teff, and MH (Fontaine & Brassard 2008).
In spite of this caveat, we tried to derive the stellar mass of BPM 37093 from the measured quadrupole period spacing. To this end, we assessed the average quadrupole period spacings computed for our models as 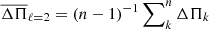 , where ΔΠk is the forward period spacing for ℓ = 2 modes and n is the number of theoretical periods considered from the model. For BPM 37093, the observed periods are in the range of [511,635] s. In computing the averaged period spacings for the models, however, we considered the range [500, 1400] s, that is, we adopted a longer upper limit of this range of periods in order to obtain a better sample of the period spacing of modes within the asymptotic regime. In Fig. 6, we show the run of the average of the computed period spacings (ℓ = 2) in terms of the effective temperature for our ultra-massive DA WD evolutionary sequences for all the thicknesses of the H envelope, along with the observed period spacing for BPM 37093. As can be seen in the figure, it is not possible in this instance to put very strong constraints on the mass of BPM 37093 and the only thing that can be ascertained is that the mass of the star could be M⋆ = 1.16 M⊙ with a thick (canonical) H envelope [log(MH/M⋆) = − 6] but it could also be as massive as M⋆ = 1.29 M⊙ and with a H envelope 100 times thinner [log(MH/M⋆) = − 8]. This degeneracy of the solutions could be eliminated with the help of period-to-period fits. We address this issue in the next section.
, where ΔΠk is the forward period spacing for ℓ = 2 modes and n is the number of theoretical periods considered from the model. For BPM 37093, the observed periods are in the range of [511,635] s. In computing the averaged period spacings for the models, however, we considered the range [500, 1400] s, that is, we adopted a longer upper limit of this range of periods in order to obtain a better sample of the period spacing of modes within the asymptotic regime. In Fig. 6, we show the run of the average of the computed period spacings (ℓ = 2) in terms of the effective temperature for our ultra-massive DA WD evolutionary sequences for all the thicknesses of the H envelope, along with the observed period spacing for BPM 37093. As can be seen in the figure, it is not possible in this instance to put very strong constraints on the mass of BPM 37093 and the only thing that can be ascertained is that the mass of the star could be M⋆ = 1.16 M⊙ with a thick (canonical) H envelope [log(MH/M⋆) = − 6] but it could also be as massive as M⋆ = 1.29 M⊙ and with a H envelope 100 times thinner [log(MH/M⋆) = − 8]. This degeneracy of the solutions could be eliminated with the help of period-to-period fits. We address this issue in the next section.
 |
Fig. 6. Comparison between quadrupole (ℓ = 2) period spacing derived for BPM 37093 (ΔΠ = 17.3 ± 0.9 s) and the average of the computed ℓ = 2 period spacings, |
4.3. Period-to-period fits
Here we search for a pulsation model that best matches the individual pulsation periods of BPM 37093. The aptness of the match between the theoretical pulsation periods (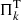 ) and the observed individual periods (
) and the observed individual periods (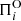 ) is measured by means of a merit function defined as:
) is measured by means of a merit function defined as:
where N is the number of observed periods. The WD model that shows the lowest value of χ2, if exists, is adopted as the “best-fit model”. We assess the function χ2 = χ2(M⋆, MH, Teff) for stellar masses of 1.10, 1.16, 1.22, and 1.29 M⊙. For the effective temperature, we cover a range of 15 000 ≳ Teff ≳ 10 000 K. Finally, for the H-envelope thickness we adopt the values of log(MH/M⋆) = − 6, −7, −8, −9, −10. The quality of our period fits is assessed by means of the average of the absolute period differences, 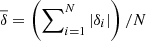 , where
, where 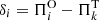 , and by the root-mean-square residual,
, and by the root-mean-square residual, 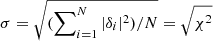 .
.
We assumed two possibilities for the mode identification: (i) that all of the observed periods correspond to g modes associated with ℓ = 1, and (ii) that the observed periods correspond to a mix of g modes associated with ℓ = 1 and ℓ = 2. We first considered the eight periods employed by Metcalfe et al. (2004) (see Table 1). The case (i) did not show clear solutions compatible with BPM 37093 in relation to its spectroscopically-derived effective temperature. Instead, the case (ii) in which we allow the periods of the star to be associated to a combination of ℓ = 1 and ℓ = 2 modes resulted in a clear seismological solution for a WD model with M⋆ = 1.16 M⊙, Teff = 11 650 K and log(MH/M⋆) = − 6, as can be seen in Fig. 7. In Table 1, we show the periods of the best-fit model along with the harmonic degree, the radial order, and the period differences. For this model, we obtain 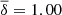 s and σ = 1.28 s. In order to have an indicator of the quality of the period fit, we computed the Bayes Information Criterion (BIC; Koen & Laney 2000):
s and σ = 1.28 s. In order to have an indicator of the quality of the period fit, we computed the Bayes Information Criterion (BIC; Koen & Laney 2000):
 |
Fig. 7. Inverse of the quality function of the period fit in the case when we allow the periods to be associated to ℓ = 1 and ℓ = 2 modes in terms of the effective temperature for the ultra-massive DA WD model sequences with different stellar masses (M⋆) and H envelope thicknesses [log(MH/M⋆)], as indicated. Vertical dashed line and gray strip correspond to the spectroscopic effective temperature of BPM 37093 and its uncertainties (Teff = 11 370 ± 500 K). We note the strong maximum in (χ2)−1 for M⋆ = 1.16 M⊙ and log(MH/M⋆) = − 6 at Teff ∼ 11 650 K. This corresponds to our “best-fit” model (see text for details). |
where Np is the number of free parameters in the models and N is the number of observed periods. The smaller the value of BIC, the better the quality of the fit. In our case, Np = 3 (stellar mass, effective temperature, and thickness of the H envelope), N = 8, and σ = 1.28 s. We obtain BIC = 0.55, which means that our fit is very good. In Table 2, we list the main characteristics of the best-fit model. The seismological stellar mass is in good agreement with the spectroscopic inference based on the evolutionary tracks of Camisassa et al. (2019). The quadrupole (ℓ = 2) mean period spacing of our best fit model is 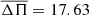 s, which is in excellent agreement with the mean period spacing derived for BPM 37093 (ΔΠ = 17.3 ± 0.9 s). Figure 8 depicts the chemical profiles (upper panel) and the propagation diagram (lower panel) corresponding to the best-fit model of BPM 37093. Our best-fit model has ∼92% of its mass in a crystalline state.
s, which is in excellent agreement with the mean period spacing derived for BPM 37093 (ΔΠ = 17.3 ± 0.9 s). Figure 8 depicts the chemical profiles (upper panel) and the propagation diagram (lower panel) corresponding to the best-fit model of BPM 37093. Our best-fit model has ∼92% of its mass in a crystalline state.
Main characteristics of BPM 37093.
 |
Fig. 8. Internal chemical structure (upper panel) and squared Brunt–Vaïsälä and Lamb frequencies for ℓ = 1 and ℓ = 2 (lower panel) corresponding to our best-fit ultra-massive DA WD model for BPM 37093 with a stellar mass M* = 1.16 M⊙, an effective temperature Teff = 11 653 K, a H envelope mass of log(MH/M*)∼ − 6, and a crystallised mass fraction of Mcr = 0.92M⋆. |
We repeated the process of period fit considering the preliminary set of 13 periods observed by Nitta et al. (2016), but we did not find a clear seismological solution when we considered the case (i) nor when we adopted the case (ii).
4.4. Internal uncertainties
We assessed the uncertainties in the stellar mass (σM⋆), the thickness of the H envelope (σMH), and the effective temperature (σTeff) of the best-fit model by employing the expression (Zhang et al. 1986; Castanheira & Kepler 2008):
where 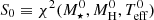 is the minimum of χ2 which is reached at
is the minimum of χ2 which is reached at 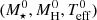 corresponding to the best-fit model and S is the value of χ2 when we change the parameter i (in this case, M⋆, MH, or Teff) by the amount di, keeping the other parameters fixed. The quantity di can be evaluated as the minimum step in the grid of the parameter i. We obtain the following uncertainties: σM⋆ ∼ 0.014 M⊙, σMH ∼ 6.3 × 10−7M⋆, and σTeff ∼ 40 K. The uncertainty in L⋆ is derived from the width of the maximum in the function (1/χ2) in terms of L⋆. We obtain σL⋆ ∼ 5.8 × 10−4 L⊙. The uncertainties in R⋆ and g are derived from the uncertainties in M⋆, Teff, and L⋆.
corresponding to the best-fit model and S is the value of χ2 when we change the parameter i (in this case, M⋆, MH, or Teff) by the amount di, keeping the other parameters fixed. The quantity di can be evaluated as the minimum step in the grid of the parameter i. We obtain the following uncertainties: σM⋆ ∼ 0.014 M⊙, σMH ∼ 6.3 × 10−7M⋆, and σTeff ∼ 40 K. The uncertainty in L⋆ is derived from the width of the maximum in the function (1/χ2) in terms of L⋆. We obtain σL⋆ ∼ 5.8 × 10−4 L⊙. The uncertainties in R⋆ and g are derived from the uncertainties in M⋆, Teff, and L⋆.
Table 2 includes the parameters of the best-fit model along with the uncertainties derived above. These are formal uncertainties related to the process of searching for the asteroseismological model and, therefore, they can be considered “internal” uncertainties inherent to the asteroseismological process.
4.5. Asteroseismological distance
We employed the effective temperature and gravity of our best-fit model to infer the absolute G magnitude (MG) of BPM 37093 in the Gaia photometry (Koester, priv. comm.). We find MG = 13.53 mag. On the other hand, we obtain the apparent magnitude mG = 13.8 mag from the Gaia Archive3. According to the well-known expression log d = (mG − MG + 5)/5, we obtain d = 11.38 ± 0.06 pc and a parallax π = 87.87 ± 0.40 mas. These asteroseismological distance and parallax are somewhat different as compared with those provided directly by Gaia, that is, d = 14.81 ± 0.01 pc and π = 67.52 ± 0.04 mas. However, we note that the uncertainties in the asteroseismological distance and parallax come mainly from the uncertainties in the effective temperature and the logarithm of the gravity of the best-fit model (∼40 K and ∼0.025), which are, admittedly, small because they are solely attributed to internal errors. Realistic estimates of these errors are probably much higher. That said, we believe that with more realistic estimates of the uncertainties in Teff and log g, and, thus, in the errors in the asteroseismological distance and parallax, the agreement with the astrometric values could substantially improve.
4.6. Rotation period
If the stellar rotation is slow and rigid, the rotation frequency Ω of the WD is connected with the frequency splitting δν through the coefficients Ck, ℓ – which depend on the details of the stellar structure – and the values of m (−ℓ,…, − 1, 0, +1, …, +ℓ) by means of the expression δν = m(1 − Ck, ℓ) Ω (Unno et al. 1989). The period at 564.1 s in Table 1 is actually the average of two very close observed periods which are assumed to be the components m = −1 (562.6 s) and m = +1 (565.5 s) of a rotationally split ℓ = 2 mode (see Nitta et al. 2016). Here it is assumed that the remainder components of the quintuplet (m = −2, 0, +2) are not visible for some unknown reason. Based on this hypothesis, we derive a frequency splitting of δν = 4.55 μHz. Making the same assumption for the pair of observed periods at 633.5 s and 636.7 s (see Nitta et al. 2016), which, when averaged, give the period 635.1 s (Table 1), we have δν = 3.95 μHz. For our best-fit model for BPM 37093, we find that the 564 s and 635 s modes have Ck, ℓ = 2 ∼ 0.166. Using this value for Ck, ℓ, and the averaged frequency splitting, 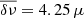 Hz, we obtain a rotation period of ∼55 h. This rotation period is consistent with the rotation-period values inferred from asteroseismology for WD stars (see Table 10 of Córsico et al. 2019). We can also estimate what the rotation period would be if these periods were the components m = −1 and m = +1 of ℓ = 1 modes instead of ℓ = 2 modes. In that case, we would have Ck, ℓ = 2 ∼ 0.498 from the best-fit model, and then the rotation period should be ∼33 h.
Hz, we obtain a rotation period of ∼55 h. This rotation period is consistent with the rotation-period values inferred from asteroseismology for WD stars (see Table 10 of Córsico et al. 2019). We can also estimate what the rotation period would be if these periods were the components m = −1 and m = +1 of ℓ = 1 modes instead of ℓ = 2 modes. In that case, we would have Ck, ℓ = 2 ∼ 0.498 from the best-fit model, and then the rotation period should be ∼33 h.
4.7. Comparison with previous analyses
Metcalfe et al. (2004) carried out a parametric asteroseismological analysis on BPM 37093 on the basis of the eight periods listed in the first column of Table 1. These authors employed DA WD models characterised by chemical transition regions resulting from the assumption of diffusive equilibrium. The free parameters of the analysis are the crystallised mass fraction (that is, the location of the inner boundary conditions for the pulsations, which coincides with the liquid/solid interface), the He and H envelope thickness, and the effective temperature. The authors consider pure C- and O-core WDs, and three fixed stellar-mass values. They obtain a family of asteroseismological models characterised by different stellar parameters, but all of them with 90% of the mass crystallised. A second parametric asteroseismological analysis of BPM 37093 was performed independently by Brassard & Fontaine (2005), who employed DA WD models with some improved aspects; for example, updated opacities, chemical transitions resulting from time-dependent element diffusion, and cores made of CO in addition to pure C and O cores. In addition, the models of Brassard & Fontaine (2005) do not consider the crystallised mass fraction as a free parameter but, instead, the value is fixed for each model and results from the predictions of the EoS. The results of this analysis largely differ from those of Metcalfe et al. (2004). Indeed, Brassard & Fontaine (2005) found a set of optimal asteroseismological models characterised by a percentage of crystallised mass in the range 32–82%. These authors emphasize that the information contained in the eight periods employed in both analyses is not enough to unravel the core chemical structure nor to derive the percentage of crystallised mass of this star due to the fact that the modes are characterised by high radial orders and, therefore, they are in the asymptotic regime of g-mode pulsations. The strong differences among the results in the works by Metcalfe et al. (2004) and Brassard & Fontaine (2005) could be attributed to the fact that Metcalfe et al. (2004) only varied the crystallised mass fraction in increments of 10 % (i.e., 10%, 20%, 30%, …, 80%, 90%). Using a finer grid in the increments of the crystallised mass fraction could result in many other possible best-fit solutions, which could potentially be in better agreement with the larger set of solutions found by Brassard & Fontaine (2005).
The DA WD models employed in the present paper are substantially different as compared with those employed by Metcalfe et al. (2004) and Brassard & Fontaine (2005), particularly with regard to the core chemical structure and composition. In fact, while those authors consider cores made of pure C, pure O, and mixtures of 50% of C and 50% of O, in the present analysis we consider cores made of O and Ne with evolving chemical structures as predicted by fully evolutionary computations. In addition, our asteroseismological approach, which is based on fully evolutionary models, largely differs from the one adopted in the aforementioned works, namely, the employment of structure models with a number of adjustable free parameters aiming to search for more optimal asteroseismological models. It is for these reasons that a direct comparison of our results with those of Metcalfe et al. (2004) and Brassard & Fontaine (2005) is not possible. However, we can emphasize that our analysis favours a WD model with a large fraction of mass in solid phase (∼92%), which is more in line with the results of Metcalfe et al. (2004). Also, the identification of the harmonic degree ℓ and the radial order k of the pulsation modes for the asteroseismological solutions are similar. Indeed, our analysis predicts that most of the modes are quadrupole modes, except for the modes with periods at 531.1 s and 613.5 s, which are dipole modes. In the case of Metcalfe et al. (2004), most of the the modes are ℓ = 2, except modes with periods 582.0 s and 613.5 s which are ℓ = 1 modes. Finally, Brassard & Fontaine (2005) predict that most of the modes are ℓ = 2, except the mode with period 613.5 s, which is a ℓ = 1 mode. Regarding the radial order of the modes, in our case we obtain 29 ≤ k ≤ 36, whereas both Metcalfe et al. (2004) and Brassard & Fontaine (2005) analyses predict 28 ≤ k ≤ 35. The surprising agreement of the identification of the radial order k of the modes according to Metcalfe et al. (2004) and Brassard & Fontaine (2005) as with the current analysis (differing only by 1) could be due to the fact that our best-fit model for BPM 37093 has a large fraction of its mass crystallised, so that g-mode pulsations are insensitive to the ONe-core chemical features and, thus, the pulsational properties of the model resemble those of a model with a similar mass but with a CO core.
5. Other ultra-massive ZZ Ceti stars
There are three other pulsating ultra-massive ZZ Ceti stars known to date, apart from BPM 37093. They are GD 518, SDSS J084021.23+522217.4, and J212402.03−600100.0. In contrast to BPM 37093, these three stars show only a few pulsation periods (see Tables 3, 5, and 7), which prevents us from finding a period spacing for these stars. Also, the scarcity of such periods inhibits us from carrying out a detailed asteroseismological analysis as in the case of BPM 37097. Thus, we limit ourselves a preliminary analysis of period-to-period fits for GD 518 and SDSS J084021.23+522217.4. The star J212402.03−600100.0 is excluded from this analysis because it only has a single detected period.
Independent frequencies in the data of GD 518 from Hermes et al. (2013) along with the theoretical periods, harmonic degrees, radial orders, and period differences of the best-fit model.
5.1. GD 518
Pulsations in WD J165915.11+661033.3 (GD 518) were first detected by Hermes et al. (2013). Model-atmosphere fits to this star indicate that it is located in the ZZ Ceti instability strip with Teff ∼ 12 030 K and log g ∼ 9.08, which would correspond to a mass of 1.20 M⊙ if the ONe-core WD models from Althaus et al. (2005a) are used, or 1.23 M⊙ if the CO-core WD models from Wood (1995) are employed. The value of the stellar mass of the star is M⋆ = 1.198 M⊙ if the evolutionary tracks of ONe-core WD models of Camisassa et al. (2019) are adopted. To date, no asteroseismological analysis has been performed to this star. Our period-to-period fits for this star indicate that our best fit model – the one which minimizes the merit function from Eq. (3) – is characterised by a value of χ2 = 0.56, 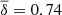 s, σ = 0.75 s, and BIC = 0.22, and has a stellar mass of 1.22M⊙ and Teff = 12 060 K (see Table 4 and Fig. 9). The stellar mass of the asteroseismological model is consistent with the spectroscopic mass derived from the evolutionary tracks of Camisassa et al. (2019).
s, σ = 0.75 s, and BIC = 0.22, and has a stellar mass of 1.22M⊙ and Teff = 12 060 K (see Table 4 and Fig. 9). The stellar mass of the asteroseismological model is consistent with the spectroscopic mass derived from the evolutionary tracks of Camisassa et al. (2019).
 |
Fig. 10. Same as in Fig. 8, but for the asteroseismological best-fit model of SDSS J084021.23+522217.4. |
Independent frequencies in the data of SDSS J084021.23+522217.4 from Curd et al. (2017), along with the theoretical periods, harmonic degrees, radial orders, and period differences of the best-fit model.
The asteroseismological distance and parallax inferred for GD 518, derived in the same way as for BPM 37093, are d = 49.80 ± 0.06 pc and π = 20.08 ± 0.03 mas. These values are somewhat different than those provided by Gaia (that is, d = 64.57 ± 0.3 pc and π = 15.48 ± 0.08 mas). The agreement between these sets of values could improve if we could employed more realistic values for the uncertainties in Teff and log g of the asteroseismological model for GD 518, in a similar way as for BPM 37093 (see discussion at the end of Sect. 4.5).
5.2. SDSS J084021.23+522217.4
This ultra-massive ZZ Ceti star was discovered by Curd et al. (2017) from a sample of DA WD from the SDSS DR7 and DR10. Model-atmosphere fits indicate Teff ∼ 12 160 K, log g ∼ 8.93 and M⋆ ∼ 1.16 M⊙. These results are in good agreement with the preliminary asteroseismological analysis performed by the same authors, where their best-fit CO-core WD model has M⋆ = 1.14 M⊙, MH = 5.8 × 10−7M⋆, MHe = 4.5 × 10−4M⋆, 0.50 ≤ Mcr/M⋆ ≤ 0.70 and 11 850 ≤ Teff ≤ 12 350 K.
Our best-fit model is characterised by χ2 = 0.14, 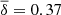 s, σ = 0.38 s, and BIC = − 0.37 with one period (797.4 s) identified as a ℓ = 2 mode, and the remaining periods identified as ℓ = 1 modes. The derivation of the stellar parameters gives Teff = 12 550 K, M⋆ = 1.10 M⊙, MH/M⋆ = 1.02 × 10−7, MHe/M⋆ = 3.0 × 10−4, Mcr/M⋆ = 0.81, with a central 20Ne abundance of 0.52. The stellar mass derived from the asteroseismological model is somewhat smaller than the value derived spectroscopically on the basis of the evolutionary tracks of Camisassa et al. (2019). On the other hand, the disagreement regarding the mass of the crystallised part of the core as compared with the result found by Curd et al. (2017) is due to our employment of ONe-core WD models here, whereas those authors employed CO-core WD models. When searching for the best-fit model with all periods assumed to be associated with ℓ = 1 modes, we found the same best-fit model as in the previous analysis, but with a poorer quality function (χ2 = 1.56).
s, σ = 0.38 s, and BIC = − 0.37 with one period (797.4 s) identified as a ℓ = 2 mode, and the remaining periods identified as ℓ = 1 modes. The derivation of the stellar parameters gives Teff = 12 550 K, M⋆ = 1.10 M⊙, MH/M⋆ = 1.02 × 10−7, MHe/M⋆ = 3.0 × 10−4, Mcr/M⋆ = 0.81, with a central 20Ne abundance of 0.52. The stellar mass derived from the asteroseismological model is somewhat smaller than the value derived spectroscopically on the basis of the evolutionary tracks of Camisassa et al. (2019). On the other hand, the disagreement regarding the mass of the crystallised part of the core as compared with the result found by Curd et al. (2017) is due to our employment of ONe-core WD models here, whereas those authors employed CO-core WD models. When searching for the best-fit model with all periods assumed to be associated with ℓ = 1 modes, we found the same best-fit model as in the previous analysis, but with a poorer quality function (χ2 = 1.56).
The asteroseismological distance and parallax inferred for this star are d = 89.95 ± 0.08 pc and π = 11.12 ± 0.01 mas, which differ from the Gaia values (d = 138.50 ± 4.0 pc and π = 7.22 ± 0.21 mas). Again, a better estimate of the uncertainties of the effective temperature and gravity of the asteroseismological model could contribute to bringing the asteroseismological distance and parallax values closer to those derived by Gaia.
5.3. WD J212402
The variability of WD J212402 was discovered by Rowan et al. (2019) from time-series GALEX space-telescope observations. This star has Teff = 12 510 K and log g = 8.98 (Gentile Fusillo et al. 2019). The stellar mass of the star is M⋆ = 1.16 M⊙ and the crystallised mass fraction should be of Mcr/M⋆ ∼ 0.90 according to the evolutionary tracks of Camisassa et al. (2019). Unfortunately, only a single period has been detected (Table 7), preventing us from attempting an asteroseismological analysis. It would be very important to have additional observations of this star to detect more pulsation periods.
6. Summary and conclusions
In this paper, we conduct the first asteroseismological study of the ultra-massive ZZ Ceti stars known to date by employing an expanded set of grid of ONe-core WD models presented in Camisassa et al. (2019). The stellar models this study is based on consider crystallisation with chemical rehomogeneization due to phase separation. We include ultra-massive WD models with different thicknesses of the H envelope with the aim of expanding the parameter space in our asteroseismological exploration.
For the ultra-massive ZZ Ceti star BPM 37093, we carried out a detailed asteroseismological analysis that includes the derivation of a mean period spacing of ∼17 s, which is associated to ℓ = 2 g modes. We have not been able, however, to infer the stellar mass of the star by comparing the observed period spacing with the averaged theoretical period spacings. This is due to the intrinsic degeneracy of the dependence of ΔΠ with the three parameters M⋆, Teff, and MH. On the other hand, we derived a best-fit model for the star by considering their individual pulsation periods. This model is characterised by Teff = 11 650 K, M⋆ = 1.16M⊙, log(MH/M⋆) = − 6, and Mcr/M⋆ = 0.92 (see Table 2). In addition, we derived an asteroseismological distance of 11.38 pc, which differs somewhat from the astrometric distance measured by Gaia, of 14.81 pc. Finally, we inferred a rotation period of 55 h under the assumption that the modes that exhibit frequency splittings are associated with ℓ = 2 modes. For the ultra-massive ZZ Ceti stars GD 518 and SDSS J084021, which exhibit only three periods, we performed period-to-period fits and we find the asteroseismological models whose characteristics are listed in Tables 4 and 6. In particular, this analysis predicts that the crystallised mass fraction of these stars is Mcr/M⋆ = 0.97 for GD 518 and Mcr/M⋆ = 0.81 for SDSS J084021. The asteroseismological distances inferred for these stars (50 pc and 90 pc, respectively) are somewhat different to the distances measured by Gaia (65 pc and 139 pc, respectively). Finally, for the ultra-massive ZZ ceti star WD J212402, which exhibits one single period, it is not possible to do any kind of asteroseismological inference at this stage.
Single frequency in the data of WD J212402.03−600100.0 from Rowan et al. (2019).
Tables 2, 4, and 6 include the parameters of the best-fit models for BPM 37093, GD 518, and SDSS J084021.23+522217.4, respectively. We note that for two of the three stars studied (BPM 37093 and GD 518), the percentage of crystallisation is larger than 90% by mass, which is larger than the mass of the ONe core. Thus, since g-mode pulsations only sample the non-crystallised regions and since these regions are dominated by O, C, He and H, it is not surprising that the best-fit seismological models are consistent with prior studies which assume CO cores, particularly in the case of BPM 37093.
In Tables 2, 4, and 6 we include the formal uncertainties related to the process of searching for the asteroseismological model and, therefore, they can be considered as internal uncertainties inherent to the asteroseismological process. An estimation of more realistic uncertainties in the structural quantities that characterise the asteroseismological models of these stars (Teff, M⋆, MH, MHe, R⋆, etc) is very difficult to obtain since they depend on the uncertainties affecting the physical processes of the progenitor evolution. An estimate of the impact of the uncertainties in the prior evolution on the structural parameters of the asteroseismological models was carried out by De Gerónimo et al. (2017, 2018) for ZZ Ceti stars of intermediate masses harbouring CO cores. These authors derive typical uncertainties of ΔM⋆/M⋆ ≲ 0.05, ΔTeff ≲ 300 K and a factor of two in the thickness of the H envelope. While we cannot directly extrapolate these results to our analysis of ultra-massive DA WD models with ONe cores, we can adopt them as representative of the real uncertainties affecting the parameters of our asteroseismological models for BPM 37093, GD 518, and SDSS J084021.23+522217.4.
In this paper, we assumed that ultra-massive WDs (M⋆ ≳ 1 M⊙) come from single-star evolution and must have ONe cores. However, we cannot discard the possibility that these objects are the result of mergers of two WDs (the so-called “double degenerate scenario”; see, e.g. García-Berro et al. 2012; Schwab et al. 2012) in a binary system, in the case of which they are expected to have CO cores. The study of the evolutionary and pulsational properties of ultra-massive WDs resulting from WD+WD mergers is beyond the scope of the present paper and will be the focus of a future investigation.
We conclude our paper by calling attention to the need for new photometric observations from the ground or from space (e.g. TESS) in the aim of finding more variable ultra-massive WDs and also to re-observe already-known objects (for instance WD J212402) in pursuit of more pulsation periods. This will result in reliable asteroseismological analyses that could yield valuable information about the crystallisation processes in WDs. In addition, it could be possible to derive the core chemical composition and, in turn, to infer their evolutionary origin as either a single-star evolution or binary-star evolution with the merger of two WDs.
Generally, the use of the asymptotic period spacing (computed according to Eq. (1)) instead of the average of the computed period spacings can lead to an overestimation of the stellar mass, except for stars that pulsate with very high radial orders, such as PNNV stars (Althaus et al. 2008).
Acknowledgments
We wish to acknowledge the suggestions and comments of the anonymous referee that strongly improved the original version of this work. We gratefully acknowledge Prof. Detlev Koester for providing us with a tabulation of the absolute magnitude of DA WD models in the Gaia photometry. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, and by the PIP 112-200801-00940 grant from CONICET. This research has made use of NASA’s Astrophysics Data System.
References
- Abrikosov, A. A. 1961, Sov. Phys. JETP, 12, 1254 [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., & Córsico, A. H. 2005a, A&A, 441, 689 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005b, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Kepler, S. O., & Miller Bertolami, M. M. 2008, A&A, 478, 175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010a, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010b, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010c, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Uzundag, M., et al. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201936346 [Google Scholar]
- Bischoff-Kim, A., Montgomery, M. H., & Winget, D. E. 2008, ApJ, 675, 1505 [NASA ADS] [CrossRef] [Google Scholar]
- Bognár, Z., Paparó, M., Molnár, L., et al. 2016, MNRAS, 461, 4059 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J. 2016, Rep. Progr. Phys., 79, 036901 [Google Scholar]
- Bradley, P. A. 1998, ApJs, 116, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, P. A. 2001, ApJ, 552, 326 [NASA ADS] [CrossRef] [Google Scholar]
- Bradley, P. A., Winget, D. E., & Wood, M. A. 1993, ApJ, 406, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., & Fontaine, G. 2005, ApJ, 622, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., Wesemael, F., & Hansen, C. J. 1992a, ApJS, 80, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., Fontaine, G., Wesemael, F., & Tassoul, M. 1992b, ApJS, 81, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2016, ApJ, 823, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Rohrmann, R. D., et al. 2017, ApJ, 839, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2019, A&A, 625, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castanheira, B. G., & Kepler, S. O. 2008, MNRAS, 385, 430 [Google Scholar]
- Córsico, A. H., & Althaus, L. G. 2006, A&A, 454, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Benvenuto, O. G., & Serenelli, A. M. 2002, A&A, 387, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Montgomery, M. H., García-Berro, E., & Isern, J. 2005, A&A, 429, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., García-Berro, E., Althaus, L. G., & Isern, J. 2004, A&A, 427, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., & Kepler, S. O. 2019, A&ARv, 27, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Curd, B., Gianninas, A., Bell, K. J., et al. 2017, MNRAS, 468, 239 [NASA ADS] [CrossRef] [Google Scholar]
- De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., & Kepler, S. O. 2017, A&A, 599, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Gerónimo, F. C., Althaus, L. G., Córsico, A. H., Romero, A. D., & Kepler, S. O. 2018, A&A, 613, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Gerónimo, F. C., Córsico, A. H., Althaus, L. G., Wachlin, F. C., & Camisassa, M. E. 2019, A&A, 621, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, J.-N., Dolez, N., Vauclair, G., et al. 2013, MNRAS, 429, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- García-Berro, E., Lorén-Aguilar, P., Aznar-Siguán, G., et al. 2012, ApJ, 749, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Gentile Fusillo, N. P., Tremblay, P.-E., Gänsicke, B. T., et al. 2019, MNRAS, 482, 4570 [NASA ADS] [CrossRef] [Google Scholar]
- Giammichele, N., Charpinet, S., Brassard, P., & Fontaine, G. 2017a, A&A, 598, A109 [Google Scholar]
- Giammichele, N., Charpinet, S., Fontaine, G., & Brassard, P. 2017b, ApJ, 834, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Handler, G., Pikall, H., O’Donoghue, D., et al. 1997, MNRAS, 286, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Kepler, S. O., Castanheira, B. G., et al. 2013, ApJ, 771, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Kanaan, A., Kepler, S. O., Giovannini, O., & Diaz, M. 1992, ApJ, 390, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Kanaan, A., Nitta-Kleinman, A., Winget, D. E., et al. 2000, Baltic Astron., 9, 87 [NASA ADS] [Google Scholar]
- Kanaan, A., Nitta, A., Winget, D. E., et al. 2005, A&A, 432, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawaler, S. D. 1988, in Advances in Helio- and Asteroseismology, eds. J. Christensen-Dalsgaard, & S. Frandsen, IAU Symp., 123, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kawaler, S. D., & Bradley, P. A. 1994, ApJ, 427, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O., Pelisoli, I., Koester, D., et al. 2016, MNRAS, 455, 3413 [NASA ADS] [CrossRef] [Google Scholar]
- Kirzhnits, D. A. 1960, Sov. Phys. JETP, 11, 365 [Google Scholar]
- Kleinman, S. J., Kepler, S. O., Koester, D., et al. 2013, ApJs, 204, 5 [Google Scholar]
- Koen, C., & Laney, D. 2000, MNRAS, 311, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1968, ApJ, 153, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Medin, Z., & Cumming, A. 2010, Phys. Rev. E, 81, 036107 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Montgomery, M. H., & Kanaan, A. 2004, ApJ, 605, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montgomery, M. H., & Winget, D. E. 1999, ApJ, 526, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, M. H. 1998, PhD Thesis, The University of Texas at Austin [Google Scholar]
- Nather, R. E., Winget, D. E., Clemens, J. C., Hansen, C. J., & Hine, B. P. 1990, ApJ, 361, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, A. 2000, PhD Thesis, The University of Texas at Austin [Google Scholar]
- Nitta, A., Kepler, S. O., Chené, A.-N., et al. 2016, IAU Focus Meeting, 29B, 493 [Google Scholar]
- O’Donoghue, D. 1994, MNRAS, 270, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, Proc. SPIE, 9143, 914320 [Google Scholar]
- Romero, A. D., Córsico, A. H., Althaus, L. G., et al. 2012, MNRAS, 420, 1462 [Google Scholar]
- Romero, A. D., Kepler, S. O., Córsico, A. H., Althaus, L. G., & Fraga, L. 2013, ApJ, 779, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Romero, A. D., Córsico, A. H., Castanheira, B. G., et al. 2017, ApJ, 851, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan, D. M., Tucker, M. A., Shappee, B. J., & Hermes, J. J. 2019, MNRAS, 486, 4574 [NASA ADS] [CrossRef] [Google Scholar]
- Salpeter, E. E. 1961, ApJ, 134, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Schwab, J., Shen, K. J., Quataert, E., Dan, M., & Rosswog, S. 2012, MNRAS, 427, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L. 2010, A&A, 512, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
- Tremblay, P.-E., Fontaine, G., Fusillo, N. P. G., et al. 2019, Nature, 565, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
- Van Cleve, J. E., Howell, S. B., Smith, J. C., et al. 2016, PASP, 128, 075002 [NASA ADS] [CrossRef] [Google Scholar]
- van Horn, H. M. 1968, ApJ, 151, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., Kepler, S. O., Campos, F., et al. 2009, ApJ, 693, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Kepler, S. O., Kanaan, A., Montgomery, M. H., & Giovannini, O. 1997, ApJ, 487, L191 [NASA ADS] [CrossRef] [Google Scholar]
- Wood, M. A. 1995, in White Dwarfs, eds. D. Koester, & K. Werner (Berlin: Springer Verlag), Lecture Notes in Physics, 443, 41 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
- Zhang, E. H., Robinson, E. L., & Nather, R. E. 1986, ApJ, 305, 740 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Independent frequencies and periods in the data of BPM 37093 from Metcalfe et al. (2004), along with the theoretical periods, harmonic degrees, radial orders, and period differences of the best-fit model described in Sect. 4.3.
Independent frequencies in the data of GD 518 from Hermes et al. (2013) along with the theoretical periods, harmonic degrees, radial orders, and period differences of the best-fit model.
Independent frequencies in the data of SDSS J084021.23+522217.4 from Curd et al. (2017), along with the theoretical periods, harmonic degrees, radial orders, and period differences of the best-fit model.
Single frequency in the data of WD J212402.03−600100.0 from Rowan et al. (2019).
All Figures
 |
Fig. 1. Evolutionary tracks (red solid lines) of ultra-massive DA WD models computed by Camisassa et al. (2019) in the Teff − log g plane. Blue dashed lines indicate 0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 95 and 99% of crystallised mass. Locations of ultra-massive DA WD stars (Kleinman et al. 2013; Kepler et al. 2016; Curd et al. 2017) are indicated with black star symbols. Black circles indicate the location of known ultra-massive ZZ Ceti stars: BPM 37093 (Nitta et al. 2016), SDSS J084021 (Curd et al. 2017), GD 518 (Hermes et al. 2013), and WD J212402 (Rowan et al. 2019). |
| In the text | |
 |
Fig. 2. Abundances by mass of 1H, 4He, 12C, 16O, 20Ne, 23Na, and 24Mg as a function of the fractional mass, corresponding to ONe-core WD models with M⋆1.29 M⊙, Teff ∼ 12 000 K and log(MH/M⋆) = − 6, −7, −8, −9, and −10 (from top to bottom). Models were computed by taking into account time-dependent element diffusion, along with latent heat release and chemical redistribution caused by phase separation during crystallisation. The solid part of the models is emphasized with a gray tone. The crystallised mass fraction (in percentage) is 99.5%. |
| In the text | |
 |
Fig. 3. Logarithm of squared Brunt–Väisälä frequency, corresponding to the same ONe-core WD models with M⋆ = 1.29 M⊙, Teff ∼ 12 000 K and log(MH/M⋆) = − 6, −7, −8, −9, and −10 shown in Fig. 2. They gray zone corresponds to the crystallised part of the models. |
| In the text | |
 |
Fig. 4. Left panels: forward period spacing, ΔΠk, in terms of the pulsation periods, Πk, for WD models with M⋆ = 1.29 M⊙, Teff ∼ 12 000 K and different thicknesses of the H envelope. Thin horizontal dashed lines correspond to the value of the asymptotic period spacing, ΔΠa. Right panels: oscillation kinetic energy versus the periods for the same WD models shown in the left panel. Normalization, (δr/r)r = R⋆ = 1 (δr being the radial displacement), has been assumed to compute the kinetic energy values. |
| In the text | |
 |
Fig. 5. I-V (upper panel), K-S (middle panel), and F-T (bottom panel) significance tests applied to the period spectrum of BPM 37093 to search for a constant period spacing. The periods used here are the same eight periods shown in Table 1. |
| In the text | |
 |
Fig. 6. Comparison between quadrupole (ℓ = 2) period spacing derived for BPM 37093 (ΔΠ = 17.3 ± 0.9 s) and the average of the computed ℓ = 2 period spacings, |
| In the text | |
 |
Fig. 7. Inverse of the quality function of the period fit in the case when we allow the periods to be associated to ℓ = 1 and ℓ = 2 modes in terms of the effective temperature for the ultra-massive DA WD model sequences with different stellar masses (M⋆) and H envelope thicknesses [log(MH/M⋆)], as indicated. Vertical dashed line and gray strip correspond to the spectroscopic effective temperature of BPM 37093 and its uncertainties (Teff = 11 370 ± 500 K). We note the strong maximum in (χ2)−1 for M⋆ = 1.16 M⊙ and log(MH/M⋆) = − 6 at Teff ∼ 11 650 K. This corresponds to our “best-fit” model (see text for details). |
| In the text | |
 |
Fig. 8. Internal chemical structure (upper panel) and squared Brunt–Vaïsälä and Lamb frequencies for ℓ = 1 and ℓ = 2 (lower panel) corresponding to our best-fit ultra-massive DA WD model for BPM 37093 with a stellar mass M* = 1.16 M⊙, an effective temperature Teff = 11 653 K, a H envelope mass of log(MH/M*)∼ − 6, and a crystallised mass fraction of Mcr = 0.92M⋆. |
| In the text | |
 |
Fig. 9. Same as in Fig. 8, but for the asteroseismological best-fit model of GD 518. |
| In the text | |
 |
Fig. 10. Same as in Fig. 8, but for the asteroseismological best-fit model of SDSS J084021.23+522217.4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



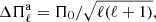
![$$ \begin{aligned} \Pi _0= 2 \pi ^2 \left[\int _{\rm fluid} \frac{N}{r} \mathrm{d}r\right]^{-1}. \end{aligned} $$](/articles/aa/full_html/2019/12/aa36698-19/aa36698-19-eq2.gif)
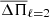
![$$ \begin{aligned} \chi ^2(M_{\star }, M_{\rm H}, T_{\rm eff})= \frac{1}{N} \sum _{i=1}^{N} \min [(\Pi _i^\mathrm{O}- \Pi _k^\mathrm{T})^2], \end{aligned} $$](/articles/aa/full_html/2019/12/aa36698-19/aa36698-19-eq9.gif)