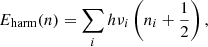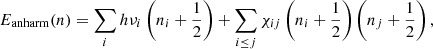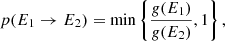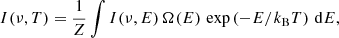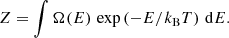| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A71 | |
| Number of page(s) | 16 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201936310 | |
| Published online | 02 December 2019 | |
The infrared bands of polycyclic aromatic hydrocarbons in the 1.6–1.7 μm wavelength region
1
School of Engineering Sciences in Chemistry, Biotechnology and Health, Department of Theoretical Chemistry and Biology, Royal Institute of Technology, 10691 Stockholm, Sweden
e-mail: taochen@kth.se
2
Hefei National Laboratory for Physical Science at the Microscale, Department of Chemical Physics, School of Chemistry and Materials Science, University of Science and Technology of China, Hefei 230026 Anhui, PR China
e-mail: luo@kth.se
3
Department of Physics and Astronomy, University of Missouri, Columbia, MO 65211, USA
e-mail: lia@missouri.edu
Received:
14
July
2019
Accepted:
13
October
2019
Context. The 3.3 μm aromatic C–H stretching band of polycyclic aromatic hydrocarbon (PAH) molecules seen in a wide variety of astrophysical regions is often accompanied by a series of weak satellite bands at ∼3.4–3.6 μm. One of these sources, IRAS 21282+5050, a planetary nebula, also exhibits a weak band at ∼1.68 μm. While the satellite features at ∼3.4–3.6 μm are often attributed to the anharmonicities of PAHs, it is not clear whether overtones or combination bands dominate the 1.68 μm feature.
Aims. In this work, we examine the anharmonic spectra of eight PAH molecules, including anthracene, tetracene, pentacene, phenanthrene, chrysene, benz[a]anthracene, pyrene, and perylene, to explore the origin of the infrared bands in the 1.6–1.7 μm wavelength region.
Methods. Density functional theory (DFT) in combination with the vibrational second-order perturbation theory (VPT2) was used to compute the anharmonic spectra of PAHs. To simulate the vibrational excitation process of PAHs, the Wang–Landau random walk technique was employed.
Results. All the dominant bands in the 1.6–1.7 μm wavelength range and in the 3.1–3.5 μm C–H stretching region are calculated and tabulated. It is demonstrated that combination bands dominate the 1.6–1.7 μm region, while overtones are rare and weak in this region. We also calculate the intensity ratios of the 3.1–3.5 μm C–H stretching features to the bands in the 1.6–1.7 μm region, I3.1 − 3.5/I1.6 − 1.7, for both ground and vibrationally excited states. On average, we obtain ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈12.6 and ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈17.6 for PAHs at ground states and at vibrationally excited states, respectively.
Key words: astrochemistry / molecular data / ISM: molecules / ISM: lines and bands / infrared: general / molecular processes
© ESO 2019
1. Introduction
The broad infrared (IR) emission bands at 3.3, 6.2, 7.7, 8.6, and 11.3 μm observed in a wide variety of Galactic and extragalactic objects are generally attributed to polycyclic aromatic hydrocarbon (PAH) molecules (Leger & Puget 1984; Allamandola et al. 1989). These bands account for ∼10–20% of the total IR emission of the Milky Way and star-forming galaxies (Tielens 2008). Besides these five prominent bands, a few minor bands are also widely observed, for example the band at ∼3.4 μm which is often attributed to the C–H stretch of aliphatic hydrocarbons (Pendleton & Allamandola 2002), superhydrogenated PAHs (Bernstein et al. 1996; Sandford & Bernstein 2013), or anharmonicity (Barker et al. 1987), and in some objects, multiple weaker features at 3.46, 3.51, and 3.56 μm are also observed, with a tendency to decrease in strength with increasing wavelength (Geballe et al. 1985; Jourdain de Muizon et al. 1986; Joblin et al. 1996). In addition, a weak band at ∼1.68 μm is seen in IRAS 21282+5050, a planetary nebula (Geballe et al. 1994)1.
There is debate over the origin of the bands in the 1.6–1.7 μm wavelength region. Brenner & Barker (1992) predicted the intensity ratio of the 1.68 μm band to the 3.4 μm band to be I1.68/I3.4 ≈ 1/6, provided that the 3.4 μm feature arises from the ν = 2 → 1 transition while the 1.68 μm feature arises from the ν = 2 → 0 overtone emission, where ν is the vibrational quantum number. However, observationally, Siebenmorgen & Peletier (1993) derived I1.68/I3.4 ≲ 1/48 and Magazzù & Strazzulla (1992) derived I1.68/I3.4 ≲ 1/45. Duley (1994) argued that the 1.68 μm feature could not be attributed to the overtones of the C–H stretch, and that instead it could result from combination bands. On the other hand, experimentally, Reddy et al. (1982) detected a band at ∼1.67 μm in the spectra of highly vibrationally excited benzene and attributed it to the overtone transition.
The theoretical anharmonic spectra of PAHs contain detailed information about each vibrational mode (Mackie et al. 2015, 2016, 2018a), which ought to provide conclusive evidence regarding the essence of the bands in the 1.6–1.7 μm wavelength region. Anharmonic spectra can be calculated with ab initio methods, which in theory has been well established for decades (Clabo et al. 1988; Allen et al. 1990; Amos et al. 1991; Maslen et al. 1992; Martin et al. 1995; Assfeld et al. 1995). However, due to high computational costs, in practice, the calculation of anharmonic spectra for large molecules, such as PAHs for example, has only recently been achieved.
Maltseva et al. (2015, 2016, 2018) measured the IR absorption spectra at very low temperature (∼4 K) by means of the UV-IR ion dip spectroscopy, allowing them to obtain high-resolution IR spectra of PAHs. Nevertheless, such spectra cannot be interpreted by harmonic models. To interpret the measured spectra, Mackie et al. (2015, 2016, 2018a) calculated the ground-state anharmonic IR spectra for linear, non-linear, hydrogenated, and methylated PAHs using second-order vibrational perturbations theory (VPT2). Although for most of the bands their calculated spectra accurately match the high-resolution experimental spectra, Maltseva et al. (2015) noticed that there are several intensive bands still missing in the C–H stretch region of the calculated spectra. Chen (2018) accounted for the missing bands through the inclusion of the 1-3 and 2-2 Darling-Dennison resonances in the VPT2 calculations. To model the astronomical environments and interpret the observations, Mackie et al. (2018b) and Chen et al. (2018) incorporated vibrational excitation into the calculations of the anharmonic spectra using the Wang–Landau random walk technique. This approach generated reasonable emission spectra in comparison with the experimental spectra measured by the Berkeley Single Photon InfraRed Emission Spectrometer (Schlemmer et al. 1994; Wagner et al. 2000).
In this work, we compute the ground-state and vibrationally excited anharmonic spectra of a number of PAH species to explore the origin of the bands in the 1.6–1.7 μm wavelength region and compare the strengths of the bands in this region with that of the C–H stretch in the 3.1–3.5 μm region.
2. Computational details
The anharmonic vibrational spectra are calculated using the density of functional theory (DFT) as implemented in the Gaussian 16 package (Frisch et al. 2016). The functional of B3LYP (Becke 1992; Lee et al. 1988) in combination with the polarized double-ζ basis set, N07D (Barone et al. 2014), are used for the calculations. It has been shown that such a combination produces more accurate spectra in comparison with other DFT methods (Mackie et al. 2018a; Chen 2018).
The geometry optimisations are performed with a very tight convergence criterion and a very fine integration grid (Int = 200 974) for numerical integrations. For the resonant calculation, the generalized VPT2 (GVPT2) approach (Barone et al. 2014) is used. GVPT2 involves a two-step procedure: first, resonant terms are identified by means of an ad hoc test (Martin et al. 1995) and are successively removed, which is called deperturbed VPT2 (DVPT2). In the second step, the discarded terms are reintroduced through a variational treatment. This approach has been shown to give accurate results (Maslen et al. 1992; Boese & Martin 2004; Barone et al. 2014; Mackie et al. 2015, 2016; Martin et al. 1995).
To balance the computational costs and accuracy of anharmonic IR spectra, only 1-2 Fermi resonances and 1-1 and 2-2 Darling-Dennison resonances are taken into account. The maximum resonant thresholds are set to 200 cm−1 for both types of resonances, and the minimum thresholds are all set to 0 cm−1. Such settings have been evaluated and shown to produce reasonable spectra (Chen 2018).
3. Results and discussion
The molecules studied in this work are shown in Fig. 1. They can roughly be divided into three groups: (i) linear PAHs including anthracene (C14H10), tetracene (C18H12), and pentacene (C22H14); (ii) non-linear PAHs including phenanthrene (C14H10), chrysene (C18H12), and benz[a]anthracene (C18H12); and (iii) compact or pericondensed PAHs including pyrene (C16H10) and perylene (C20H12). The symmetries of these molecules are as follows: naphthalene (D2h), anthracene(D2h), tetracene (D2h), phenanthrene (C2v), chrysene (C2h), benz[a]anthracene (Cs), pyrene (D2h), and perylene (D2h).
 |
Fig. 1. Molecules studied in this work. Anthracene, tetracene, and pentacene are linear PAHs. Phenanthrene, chrysene, and benz[a]anthracene are non–linear PAHs. Pyrene and perylene are compact PAHs. |
3.1. The importance of anharmonicity
For harmonic oscillators, the vibrational states are equally separated on a symmetric closed parabolic potential energy surface. The vibrational energies at each state can be calculated from the following equation:
where νi is the frequency of the ith vibrational mode and n ≡ (n1, n2,...) represents the quantum number of each vibrational state. The fundamental vibrational energy corresponds to the transition from the ground (n = 0) to the first vibrational state (n = 1), i.e., E(1) = (3/2)∑ihνi. The calculated fundamental bands for the studied molecules in the 1.5–3.5 μm wavelength region are shown in Fig. 2. The insets in Fig. 2 expand the 1.6–1.7 μm region. It is clear that the fundamental bands for PAHs are only present in the C–H stretch region at ∼3.1–3.5 μm and no bands are seen in the 1.6–1.7 μm region.
 |
Fig. 2. Calculated harmonic fundamental bands of anthracene, tetracene, pentacene, phenanthrene, chrysene benz[a]anthracene, pyrene, and perylene. The insets zoom in the 1.6–1.7 μm region. |
According to Eq. (1), a molecule bonded by harmonic potential might reach infinite energy E(n → ∞) without bond breaking. However, this is not the case in reality. Molecules do dissociate at highly excited vibrationally states (Chen et al. 2015; Chen & Luo 2019). The potential energy surface is not a symmetric parabolic shape; in contrast, it is a non-symmetric open well (anharmonic potential), which allows a molecule to break at a certain vibrationally state. On an anharmonic potential energy surface, the energy levels are unequally separated, which can be computed as follows:
where χij represents the anharmonic coupling which describes the interactions (mode couplings) or resonances among various vibrational modes and is usually given by a two-dimensional matrix. Since most of the elements of χij are negative, the anharmonic energy levels Eanharm(n) are lower than the corresponding harmonic energy levels Eharm(n). Therefore, with anharmonic potential, the positions and intensities of the fundamental bands differ from that of harmonic potential. Moreover, due to mode couplings, combination bands (i.e., two or more fundamental vibrations are excited simultaneously) show up in the spectra (Mackie et al. 2015; Maltseva et al. 2015).
Figure 3 shows the anharmonic spectra of the studied PAHs. Due to anharmonic effects, more bands (e.g., combination bands) appear in the C–H stretch region and the fundamental bands systemically shift to longer wavelengths in comparison with Fig. 2. The insets in Fig. 3 amplify the 1.6–1.7 μm region. Unlike Fig. 2, multiple weak bands show up in this region. The mode numbers, wavelengths, and absolute intensities for the C–H stretch and 1.6–1.7 μm regions are given in Appendix A. In addition, the mode descriptions (including frequencies, symmetries, and displacement vectors) for the modes contributing to these two regions can also be found in Appendix A. One can see that the 1.6–1.7 μm region is dominated by the combination bands and no intensive overtone can be found in this region for linear (e.g., anthracene, tetracene, and pentacene) or compact (e.g., pyrene and perylene) PAHs, since the first overtones (for the fundamental bands in the C–H stretch region) are electric-dipole-forbidden (Duley 1994).
 |
Fig. 3. Calculated anharmonic IR spectra (including fundamental bands, combination bands, and overtones) of anthracene, tetracene, pentacene, phenanthrene, chrysene benz[a]anthracene, pyrene, and perylene at ground states. The insets zoom in the 1.6–1.7 μm region. |
Only a few overtones can be seen for non-linear PAHs (e.g., phenanthrene, benz[a]anthracene). The highest intensity of the overtones among all the studied molecules is ∼2.683 km mol−1 which comes from the 1.66 μm band of benz[a]anthracene, and it corresponds to the overtone of the fundamental band ν10. The second highest overtone comes from phenanthrene with an intensity of ∼1.434 km mol−1, which corresponds to the overtone of the fundamental band ν9.
3.2. Vibrational excitations
Molecules in the ISM are mostly excited by starlight (i.e., UV and visible photons). Following the internal conversion, the absorbed energies are rapidly transferred to nuclear degrees of freedom, that is vibrational excited states. At a vibrationally excited state, the IR spectrum differs significantly from that of the ground state (Chen et al. 2018; Mackie et al. 2018b). Moreover, PAHs may dissociate to smaller fragments or isomerize to multiple structures at a high vibrational state, in which anharmonicity plays a key role (Chen & Luo 2019). To incorporate the vibrational excitations, the vibrational microcanonical density of states (DoS) is calculated following the Wang–Landau random walk model (Wang & Landau 2001). In the model, the initial density of states g(E) is set to 1 for all possible energies E. A random walk in energy space is then begun by forming trial states, each of which is produced by randomly picking a quanta ni and randomly changing its value (+1, 0, or −1). In general, if E1 and E2 are energies before and after a quanta set is changed, the transition probability from energy E1 to E2 is
which implies that if g(E2)≤g(E1), the state with energy E2 is accepted, otherwise it is accepted with a probability g(E1)/g(E2). In addition, the maximum vibrational states have to be considered. The vibrational quantum number is chosen such that the associated energy remains in the increasing region.
The vibrational DoS provides the weights needed to achieve flat-histogram sampling in energy space (Basire et al. 2009). Following the trend of the DoS, second random walks in the space of quantum numbers are performed to build the accumulated absorption I(ν, E) at the wavelength ν and for a given internal energy. The absorption intensity I(ν, T) at finite temperature T can be derived by a standard Laplace transformation of the accumulated absorption I(ν, E):
where Ω(E) represents the DoS, kB is the Boltzmann constant, and Z is the partition function:
Figure 4 shows the anharmonic IR spectra of eight molecules at 1000 K. At such high temperature, the bands are combined to several broad bands.
 |
Fig. 4. Calculated anharmonic IR spectra of anthracene, tetracene, pentacene, phenanthrene, chrysene, benz[a]anthracene, pyrene, and perylene at 1000 K. |
3.3. The band-intensity ratios of I3.1 − 3.5/I1.6 − 1.7
As shown in Appendix A, there are a large number of combination bands located in the 1.6–1.7 μm region. However, their average intensities are much lower than the bands in the C–H stretching region. To quantify the differences between these two regions, we compute, I3.1 − 3.5/I1.6 − 1.7, that is, the intensity ratios of the C–H stretch region and the 1.6–1.7 μm region. In the calculations, the C–H stretch region is measured from 2800 to 3200 cm−1, that is, 3.125–3.571 μm, while the 1.6–1.7 μm region is measured from 5900 to 6300 cm−1, that is, 1.587–1.695 μm.
Table 1 shows the ratios calculated from the intensities in both regions. At ground vibrational states, pentacene shows the highest ratio (∼13.27). At excited vibrational states, the highest ratio comes from perylene. No general trend as a function of molecular size or structure is found; however, for linear molecules at ground state, the ratio appears to increase with the number of aromatic rings. The average ratio of the studied molecules at ground states are ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈12.6. For vibrationally excited states, the average ratio is ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈17.6. We notice that the ratios increase ∼10–50% going from ground states to excited states. Hence, for PAHs, the band ratio of 12.6 ought to be a lower limit.
Intensity ratio, I3.1 − 3.5/I1.6 − 1.7, of the C–H stretch to the bands in the 1.6–1.7 μm region (with 0 K for ground states and 1000 K for vibrational excited states).
4. Conclusions
Using DFT in combination with the VPT2 method, the 1.6–1.7 μm region of the IR spectra of PAHs is investigated. The calculations reveal that anharmonicity and mode couplings are crucial for this region, in which combination bands are more intensive and abundant than the overtones. Only two of the eight molecules considered here exhibit overtones in this region (i.e., phenanthrene and benz[a]anthracene, with a maximum intensity of ∼2.683 km mol−1).
To model the vibrational excitations of these molecules, the Wang–Landau random walk algorithm is incorporated. The model shows that due to anharmonicity and vibrational excitations, the fundamental and combination bands (at the ground state) are merged to several inseparable broad bands. The C–H stretching region at 3.1–3.5 μm is compared to the 1.6–1.7 μm region. The average band intensity ratios are ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈12.6 and ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈17.6 at ground states and at vibrationally excited states respectively. Since the band intensity ratio I3.1 − 3.5/I1.6 − 1.7 goes up as the molecule gets excited, ⟨I3.1 − 3.5/I1.6 − 1.7⟩≈12.6 should be the lower limit for PAHs.
Attempts to search for the 1.68 μm feature in the planetary nebula Hb 5 (Magazzù & Strazzulla 1992), the protoplanetary nebula HD 44179, the planetary nebula He 2–177, and the photodissociated region Orion bar (Siebenmorgen & Peletier 1993) have been made but only upper limits have been placed.
Acknowledgments
We thank the anonymous referee for their very helpful comments which considerably improved the presentation of this work. This work is supported by the Swedish Research Council (Contract No. 2015–06501). The calculations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC). A. L. is supported in part by NSF AST-1816411 and NASA 80NSSC19K0572.
References
- Allamandola, L., Tielens, A., & Barker, J. 1989, ApJS, 71, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, W. D., Yamaguchi, Y., Császár, A. G., et al. 1990, Chem. Phys., 145, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Amos, R. D., Handy, N. C., Green, W. H., et al. 1991, J. Chem. Phys., 95, 8323 [NASA ADS] [CrossRef] [Google Scholar]
- Assfeld, X., Almlöf, J. E., & Truhlar, D. G. 1995, Chem. Phys. Lett., 241, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Barker, J. R., Allamandola, L., & Tielens, A. 1987, ApJ, 315, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Barone, V., Biczysko, M., & Bloino, J. 2014, Phys. Chem. Chem. Phys., 16, 1759 [CrossRef] [Google Scholar]
- Basire, M., Parneix, P., Calvo, F., Pino, T., & Bréchignac, P. 2009, J. Phys. Chem. A, 113, 6947 [CrossRef] [PubMed] [Google Scholar]
- Becke, A. D. 1992, J. Chem. Phys., 96, 2155 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, M. P., Sandford, S. A., & Allamandola, L. J. 1996, ApJ, 472, L127 [CrossRef] [Google Scholar]
- Boese, A. D., & Martin, J. M. 2004, J. Phys. Chem. A, 108, 3085 [CrossRef] [Google Scholar]
- Brenner, J., & Barker, J. R. 1992, ApJ, 388, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, T. 2018, ApJS, 238, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, T., & Luo, Y. 2019, MNRAS, 486, 1875 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, T., Gatchell, M., Stockett, M. H., et al. 2015, J. Chem. Phys., 142, 144305 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, T., Mackie, C., Candian, A., Lee, T. J., & Tielens, A. G. G. M. 2018, A&A, 618, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clabo, D. A., Allen, W. D., Remington, R. B., Yamaguchi, Y., & Schaefer, H. F. 1988, Chem. Phys., 123, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. 1994, ApJ, 429, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M., Trucks, G., Schlegel, H., et al. 2016, Gaussian 09, Revision E.01, Wallingford CT [Google Scholar]
- Geballe, T., Lacy, J., Persson, S., McGregor, P., & Soifer, B. 1985, ApJ, 292, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T., Joblin, C., d’Hendecourt, L., et al. 1994, ApJ, 434, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Joblin, C., Tielens, A., Allamandola, L., & Geballe, T. 1996, ApJ, 458, 610 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jourdain de Muizon, M., Geballe, T., d’Hendecourt, L., et al. 1986, ApJ, 306, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C., Yang, W., & Parr, R. G. 1988, Phys. Rev. B, 37, 785 [Google Scholar]
- Leger, A., & Puget, J. 1984, A&A, 137, L5 [NASA ADS] [Google Scholar]
- Mackie, C. J., Candian, A., Huang, X., et al. 2015, J. Chem. Phys., 143, 224314 [NASA ADS] [CrossRef] [Google Scholar]
- Mackie, C. J., Candian, A., Huang, X., et al. 2016, J. Chem. Phys., 145, 084313 [NASA ADS] [CrossRef] [Google Scholar]
- Mackie, C. J., Candian, A., Huang, X., et al. 2018a, Phys. Chem. Chem. Phys., 20, 1189 [CrossRef] [Google Scholar]
- Mackie, C. J., Chen, T., Candian, A., Lee, T. J., & Tielens, A. G. G. M. 2018b, J. Chem. Phys., 149, 134302 [NASA ADS] [CrossRef] [Google Scholar]
- Magazzù, A., & Strazzulla, G. 1992, A&A, 263, 281 [NASA ADS] [Google Scholar]
- Maltseva, E., Petrignani, A., Candian, A., et al. 2015, ApJ, 814, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Maltseva, E., Petrignani, A., Candian, A., et al. 2016, ApJ, 831, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Maltseva, E., Mackie, C. J., Candian, A., et al. 2018, A&A, 610, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, J. M., Lee, T. J., Taylor, P. R., & François, J.-P. 1995, J. Chem. Phys., 103, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Maslen, P. E., Handy, N. C., Amos, R. D., & Jayatilaka, D. 1992, J. Chem. Phys., 97, 4233 [NASA ADS] [CrossRef] [Google Scholar]
- Pendleton, Y. J., & Allamandola, L. J. 2002, ApJS, 138, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, K., Heller, D. F., & Berry, M. J. 1982, J. Chem. Phys., 76, 2814 [NASA ADS] [CrossRef] [Google Scholar]
- Sandford, S. A., & Bernstein, M. P. 2013, ApJS, 205, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Schlemmer, S., Cook, D., Harrison, J., et al. 1994, Science, 265, 1686 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Siebenmorgen, R., & Peletier, R. 1993, A&A, 279, L45 [NASA ADS] [Google Scholar]
- Tielens, A. G. G. M. 2008, ARA&A, 46, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, D., Kim, H., & Saykally, R. 2000, ApJ, 545, 854 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Wang, F., & Landau, D. 2001, Phys. Rev. Lett., 86, 2050 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Appendix A: Additional tables and figures
Dominant bands (with intensity ≳0.2 km mol−1) in C–H stretching region and 1.6–1.7 μm region for anthracene, tetracene, and pentacene.
Same as Table A.1 but for phenanthrene, chrysene, and benz[a]anthracene.
Same as Table A.1 but for pyrene and perylene.
 |
Fig. A.1. 1.6–1.7 μm region of the anharmonic IR spectra of ground-state anthracene, tetracene, pentacene, phenanthrene, chrysene benz[a]anthracene, pyrene, and perylene. |
 |
Fig. A.2. 1.6–1.7 μm region of the vibrationally excited spectra of anthracene, tetracene, pentacene, phenanthrene, chrysene, benz[a]anthracene, pyrene, and perylene at 1000 K. |
 |
Fig. A.3. Anthracene: harmonic frequencies, symmetries and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.4. Tetracene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.5. Pentacene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.6. Phenanthrene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.7. Chrysene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.8. Benz[a]anthracene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.9. Pyrene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
 |
Fig. A.10. Perylene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
All Tables
Intensity ratio, I3.1 − 3.5/I1.6 − 1.7, of the C–H stretch to the bands in the 1.6–1.7 μm region (with 0 K for ground states and 1000 K for vibrational excited states).
Dominant bands (with intensity ≳0.2 km mol−1) in C–H stretching region and 1.6–1.7 μm region for anthracene, tetracene, and pentacene.
All Figures
 |
Fig. 1. Molecules studied in this work. Anthracene, tetracene, and pentacene are linear PAHs. Phenanthrene, chrysene, and benz[a]anthracene are non–linear PAHs. Pyrene and perylene are compact PAHs. |
| In the text | |
 |
Fig. 2. Calculated harmonic fundamental bands of anthracene, tetracene, pentacene, phenanthrene, chrysene benz[a]anthracene, pyrene, and perylene. The insets zoom in the 1.6–1.7 μm region. |
| In the text | |
 |
Fig. 3. Calculated anharmonic IR spectra (including fundamental bands, combination bands, and overtones) of anthracene, tetracene, pentacene, phenanthrene, chrysene benz[a]anthracene, pyrene, and perylene at ground states. The insets zoom in the 1.6–1.7 μm region. |
| In the text | |
 |
Fig. 4. Calculated anharmonic IR spectra of anthracene, tetracene, pentacene, phenanthrene, chrysene, benz[a]anthracene, pyrene, and perylene at 1000 K. |
| In the text | |
 |
Fig. A.1. 1.6–1.7 μm region of the anharmonic IR spectra of ground-state anthracene, tetracene, pentacene, phenanthrene, chrysene benz[a]anthracene, pyrene, and perylene. |
| In the text | |
 |
Fig. A.2. 1.6–1.7 μm region of the vibrationally excited spectra of anthracene, tetracene, pentacene, phenanthrene, chrysene, benz[a]anthracene, pyrene, and perylene at 1000 K. |
| In the text | |
 |
Fig. A.3. Anthracene: harmonic frequencies, symmetries and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.4. Tetracene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.5. Pentacene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.6. Phenanthrene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.7. Chrysene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.8. Benz[a]anthracene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.9. Pyrene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
 |
Fig. A.10. Perylene: harmonic frequencies, symmetries, and displacement vectors for the modes which contribute to the combination bands or overtones in the 1.6–1.7 μm and C–H stretching regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.