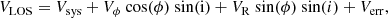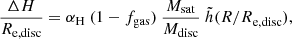| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935898 | |
| Published online | 21 October 2019 | |
The survey of planetary nebulae in Andromeda (M 31)
II. Age–velocity dispersion relation in the disc from planetary nebulae
1
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
e-mail: sbhattac@eso.org
2
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA
3
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
4
NRC Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
5
European Southern Observatory, Alonso de Córdova 3107, Santiago de Chile, Chile
6
UCO/Lick Observatory, Department of Astronomy & Astrophysics, University of California Santa Cruz, 1156 High Street, Santa Cruz, California 95064, USA
7
Research School of Astronomy and Astrophysics, Mount Stromlo Observatory, Cotter Road, 2611 Weston Creek, ACT, Australia
Received:
16
May
2019
Accepted:
20
September
2019
Context. The age–velocity dispersion relation is an important tool to understand the evolution of the disc of the Andromeda galaxy (M 31) in comparison with the Milky Way.
Aims. We use planetary nebulae (PNe) to obtain the age–velocity dispersion relation in different radial bins of the M 31 disc.
Methods. We separate the observed PNe sample based on their extinction values into two distinct age populations in the M 31 disc. The observed velocities of our high- and low-extinction PNe, which correspond to higher- and lower-mass progenitors, respectively, are fitted in de-projected elliptical bins to obtain their rotational velocities, Vϕ, and corresponding dispersions, σϕ. We assign ages to the two PN populations by comparing central-star properties of an archival sub-sample of PNe, that have models fitted to their observed spectral features, to stellar evolution tracks.
Results. For the high- and low-extinction PNe, we find ages of ∼2.5 and ∼4.5 Gyr, respectively, with distinct kinematics beyond a deprojected radius RGC = 14 kpc. At RGC = 17–20 kpc, which is the equivalent distance in disc scale lengths of the Sun in the Milky Way disc, we obtain σϕ, 2.5 Gyr = 61 ± 14 km s−1 and σϕ, 4.5 Gyr = 101 ± 13 km s−1. The age–velocity dispersion relation for the M 31 disc is obtained in two radial bins, RGC = 14–17 and 17–20 kpc.
Conclusions. The high- and low-extinction PNe are associated with the young thin and old thicker disc of M 31, respectively, whose velocity dispersion values increase with age. These values are almost twice and three times that of the Milky Way disc stellar population of corresponding ages, respectively. From comparison with simulations of merging galaxies, we find that the age–velocity dispersion relation in the M 31 disc measured using PNe is indicative of a single major merger that occurred 2.5–4.5 Gyr ago with an estimated merger mass ratio ≈1:5.
Key words: galaxies: individual: M 31 / galaxies: kinematics and dynamics / planetary nebulae: general
© ESO 2019
1. Introduction
Discs in late-type galaxies contain two distinct dynamical populations: the “cold” thin disc and the “hot” thick disc, as found in the Milky Way (MW; e.g. Gilmore & Reid 1983) and nearby edge-on galaxies (Yoachim & Dalcanton 2006; Comerón et al. 2019). The thin-disc stars are younger with rotational velocities close to that of the collisional gas (Roberts 1966). The thick-disc stars are older and through dynamical heating, via secular evolution of the disc (Sellwood 2014) or mergers with satellite galaxies (Quinn & Goodman 1986), their rotational velocity decreases and velocity dispersion increases. In the solar neighbourhood, velocity dispersion appears to increase monotonically with age (Delhaye 1965; Casagrande et al. 2011), but it is not known if that is representative of the entire MW disc. A major part of the MW thick disc is also found to be chemically distinct from its dominant thin disc (see review by Bland-Hawthorn & Gerhard 2016). While mergers of satellite galaxies can dynamically heat galactic discs, the cold MW disc does not seem to have undergone any major merger event in the last 10 Gyr.
The Andromeda (M 31) galaxy is the closest giant spiral galaxy to the MW. A number of substructures have been observed in the inner halo of M 31 (McConnachie et al. 2018) that may have resulted from a recent merger (Fardal et al. 2013; Hammer et al. 2018). This may also be linked to an observed burst of star formation ∼2 Gyr ago (Bernard et al. 2015; Williams et al. 2017). It is well known that the velocity dispersion of a disc stellar population increases with age (Strömberg 1925; Wielen 1977). Dorman et al. (2015; hereafter D15) estimated the age–velocity dispersion relation (AVR) for the M 31 disc with kinematics of stars from the SPLASH spectroscopic survey (Guhathakurta et al. 2005, 2006). D15 assigned ages to stars based on their position on the colour-magnitude diagram (CMD; see their Fig. 6) from the PHAT survey (Dalcanton et al. 2012). While their main sequence (MS) stars are well separated in this CMD, the red giant branch (RGB) and asymptotic giant branch (AGB) loci overlap, resulting in a more ambiguous age separation. D15 construct the line-of-sight (LOS) velocity dispersion (σLOS) vs. radius profiles for the different populations. Their Fig. 16 shows a general trend of increasing σLOS with age, although with significant overlap of these profiles among populations and radii. On the basis of this trend, D15 state that the RGB population in M 31 has a velocity dispersion that is nearly three times that of the MW.
Planetary nebulae (PNe) are discrete tracers of stellar populations and their kinematics have been measured in galaxies of different morphological types (e.g. Coccato et al. 2009; Cortesi et al. 2013; Pulsoni et al. 2018; Aniyan et al. 2018). Planetary nebulae in M 31 have negligible contamination from MW PNe or background galaxies (Bhattacharya et al. 2019). A number of PN properties are related to the mass, luminosity, and age of their progenitor stars. For example, from the central star properties derived from modelling nebular emission lines of PNe in the Magellanic clouds and M 31, Ciardullo & Jacoby (1999) find a correlation between PN circumstellar extinction and the mass of their central star. Dust production of stars in the AGB phase scales exponentially with their initial progenitor masses for the 1 ∼ 2.5 M⊙ range after which it remains roughly constant (Ventura et al. 2014). Additionally, PNe with dusty high-mass progenitors evolve faster (Miller Bertolami 2016) and so their circumstellar matter has little time to disperse, while PNe with lower central star masses evolve sufficiently slowly that a larger fraction of dust is dissipated from their envelopes (Ciardullo & Jacoby 1999). Kinematics of young and old stellar populations are well-traced by high- and low-mass giant stars, respectively, in the MW through their rotational velocity and velocity dispersion (e.g. Aniyan et al. 2016). In the M 31 disc, different kinematics of younger and older stellar populations are expected to correlate with high- and low-extinction PNe, respectively.
In this letter, we identify PNe populations based on their extinction for the first time, allowing us to obtain two distinct age populations for the M 31 disc. The data used in this work are described in Sect. 2. In Sect. 3, we first discuss classification of PNe based on their extinction values. We then obtain the rotational velocity curve and rotational velocity dispersion for the M 31 disc high- and low-extinction PNe. We assign ages to the two PNe populations by comparing modelled central star properties in Kwitter et al. (2012; hereafter Kw+12) to the Miller Bertolami (2016) stellar evolution tracks. We then obtain the AVR for the M 31 disc in Sect. 4 and compare it with previous determinations in M 31 and the MW. From the comparison with simulated galaxies, we estimate the mass ratio of a possible merger event in the M 31 disc. We summarise our results and conclude in Sect. 5.
2. Data description
Bhattacharya et al. (2019) identified PN candidates in a 16 deg2. imaging survey of M 31 with MegaCam at the CFHT, covering the disc and inner halo. Spectroscopic observations of a complete subsample of these PN candidates were carried out with the Hectospec multifibre positioner and spectrograph on the Multiple Mirror Telescope (MMT; Fabricant et al. 2005). The Hectospec 270 gpm grating was used and provided spectral coverage from 3650 to 9200 Å at a resolution of ∼5 Å. Each Hectospec fibre subtends 1.5″ on the sky and was positioned on the PN candidates in each field. On September 15, 2018, and October 10, 2018, with an exposure time of 9000 s each, two fields in the southwest region of the M 31 disc were observed, while on December 4, 2018, with an exposure time of 3600 s, one field covering the northern part of the M 31 disc and the Northern Spur substructure was observed. Of the 343 observed PNe candidates, 129 had confirmed detection of the [O III] 4959/5007 Å emission lines. Of these observed PNe, 92 showed the Hβ line and their extinctions (AV) could be determined from the Balmer decrement. Details of the spectroscopic observations of the PNe along with the extinction determination and chemical abundances will be presented in a forthcoming paper (Bhattacharya et al., in prep.; hereafter Bh+19b).
Sanders et al. (2012; hereafter San+12) also studied PNe and H II regions in the M 31 disc and outer bulge using Hectospec on the MMT. These latter authors observed 407 PNe; 321 of them with the Hβ line detected and subsequent reliable extinction measurements. The combined sample of PNe with extinction measurements in M 31 from San+12 and Bh+19b therefore consists of 413 PNe.
3. Analysis
3.1. Classification of planetary nebulae based on extinction measurements
The distribution of the M 31 PNe extinction values (see Fig. 1) exhibits a sharp drop at AV = 0.75 mag, increases again at AV = 1–1.25 mag, and drops off gradually at larger values of AV. Figure 1 also shows the distribution of the LMC PNe extinction values (Reid & Parker 2010), shifted such that their peak (originally in the AV = 0.75–1 mag bin) is coincident with the distribution of the M 31 PNe extinction values (AV = 0.25–0.5 mag bin). The shifted distribution of the LMC PNe extinction values also shows a sharp drop at AV = 0.75 mag and gradually falls off while that of the M 31 disc PNe shows a secondary peak at AV = 1–1.25 mag. The distribution of M 31 PNe extinction values around the first higher peak possibly results from an older parent stellar population (numerically more prevalent), spawning PNe having lower circumstellar extinction values (further discussions in Sect. 3.3), while the secondary peak at higher circumstellar extinction values would indicate the presence of a younger parent stellar population.
 |
Fig. 1. Histogram showing the distribution of extinction values for the San+12 and Bh+19b PNe. The high- and low-extinction PNe lie in the blue and red shaded regions, respectively. The distribution of extinction values of the LMC PNe observed by Reid & Parker (2010), shifted such that its peak corresponds to that of the M 31, is shown in yellow. |
We therefore classify M 31 PNe with extinction values higher and lower than AV = 0.75 mag as high- and low-extinction PNe, respectively. Our PNe sample is then divided into 145 high- and 268 low-extinction PNe, which are expected to be associated with younger and older parent stellar populations, respectively. We note that using a different extinction value within the AV = 0.65 − 0.85 mag range for the classification of the two PN populations has negligible effect on the rotation curves obtained in Sect. 3.2. The high-extinction PNe classification is not biased by the LOS dust attenuation in M 31 according to our investigation in Appendix A. Figure 2 shows the spatial distribution of the PNe in the M 31 disc.
 |
Fig. 2. Position on sky of San+12 PNe (squares) and Bh+19b PNe (circles). The high-extinction PNe are shown in blue while the low-extinction PNe are shown in red. The PNe are divided into elliptical bins to obtain rotation curves. |
3.2. Rotation curves
For both San+12 and Bh+19b PNe, the LOS velocities (LOSVs) are obtained from full spectral fitting, resulting in an uncertainty of 3 km s−1. The PNe are de-projected on to the galaxy plane based on the position angle (PA = 38°) and inclination (i = 77°) of M 31 in the planer disc approximation. They are then binned into seven elliptical bins (Fig. 2) with the first six bins covering 3 kpc each starting at a deprojected major axis radius RGC = 2 kpc from the centre of M 31 and the final bin covering RGC = 20–30 kpc. Planetary nebulae observed outside RGC = 30 kpc probably belong to the inner halo substructures, possibly the Northern Spur, and are hence not included in the analysis. The position of the PNe in each bin can be described using cylindrical coordinates, with the z = 0 kpc plane as the local plane of the galaxy, r = 0 kpc as the galactic centre, and ϕ measured counterclockwise from the position angle of M 31. The LOSV for the PNe, VLOS, in each bin is then fitted by the following equation:
where Vsys is the systemic velocity of M 31, assumed to be −309 km s−1 (Merrett et al. 2006); Vϕ is the rotational velocity in the plane of the galaxy; VR is the radial streaming motion that can be inwards or outwards; i is the inclination of M 31 mentioned previously; and Verr = 3 km s−1 is the uncertainty in measurement. LOSVs for the high- and low-extinction PNe are fitted separately in each elliptical bin using LMFIT (Newville et al. 2014) to obtain Vϕ, VR, and ϕ as the parameters describing the mean motion of the PNe populations in each bin. We note that VZ, the off-plane motion in the z direction, is considered to be zero as no net off-plane motion is expected for PNe in the disc.
The obtained Vϕ rotation curves for the high- and low-extinction PNe are shown in blue and red, respectively, in Fig. 3. The uncertainty in the fitted VR is relatively high and their values are close to zero in each bin. Thus, no clear evidence of radial streaming motion is found in either PN population. Setting VR = 0 km s−1 also has a negligible effect on the rotation curves. The difference in rotational velocities between the gas and the stellar population in a disc is a measure of the asymmetric drift and is higher for older stellar populations that have more non-circular orbits as a result of dynamical heating (Strömberg 1946). Outside RGC = 14 kpc, the high-extinction PNe have a rotational velocity closer to that of the H I gas derived by Chemin et al. (2009), indicative of a dynamically young population, while that of the low-extinction PNe is much further away from that of the H I gas, indicative of a dynamically older population (Strömberg 1946).
 |
Fig. 3. Rotational velocities for the high- and low-extinction PNe are shown in blue and red, respectively. The black line shows the H I rotation velocity from Chemin et al. (2009). The co-rotation radius (black dotted line) and outer Lindblad resonance (OLR; black dashed line) of the M 31 bar are as found by the models of Blaña et al. (2018). The grey shaded region is possibly influenced by different dynamical heating events and is not discussed here. |
We estimate the rotational velocity dispersion, σϕ, as the standard deviation with respect to the fitted Vϕ in each bin. The σϕ profiles for the high- and low-extinction PNe are shown in Fig. 4. Outside RGC = 14 kpc, σϕ is lower for the high-extinction PNe – as expected for a dynamically young population – than that measured for low-extinction PNe, a dynamically older population. In the outermost bin, σϕ increases sharply for the low-extinction PNe population. This may be due to the presence of PNe associated with the M 31 inner halo substructures like the Northern Spur or the NGC 205 loop at this distance from the M 31 centre. Within 14 kpc, both the high- and low-extinction PNe samples show an overall reversal in the Vϕ rotation curves and in σϕ, but both populations are dynamically hot. While this might be linked to the interaction of the disc with the bar in M 31 as modelled by Blaña et al. (2018) for the inner two bins, other sources of dynamical heating may be at play for RGC = 8 − 14 kpc, either stemming simply from the secular evolution of the disc and/or through a merger event. This will be investigated in a forthcoming paper (Bhattacharya et al., in prep.). Given the large values of σϕ ≈ 130 km s−1 for the low-extinction PNe, their parent stellar population may be distributed as a flattened spheroid, rather than a planer disc. Given the inclination of the M 31 disc, deprojecting these PNe as a planer disc may result in an overestimate of their RGC values, leading to a bias in the estimated σϕ. We investigate the effect of disc thickness in Appendix B. We find that the scale height of the low-extinction PNe is HLow ext ≈ 0.86 kpc. Within our 3 kpc bin sizes, only ∼10% of the low-extinction PNe may be included in a different bin. The effect on the estimated σϕ values of these ∼10% PNe in different bins is within the measurement uncertainties.
 |
Fig. 4. Rotational velocity dispersion for the high- and low-extinction PNe are known in blue and red, respectively. The black lines and grey shaded region are the same as in Fig. 3. |
3.3. Ages of the M 31 disc planetary nebulae
Kw+12 observed sixteen PNe in the outer disc of M 31 to measure various emission lines and determine chemical abundances. They used the CLOUDY photoionization codes (Ferland et al. 1998) to estimate the bolometric luminosity (L/L⊙) and effective temperature (Teff) of the central stars of these PNe. Figure 5 shows their estimated log(L/L⊙) vs. log(Teff), coloured by their extinction classification (high-extinction: blue; low-extinction: red). The post-AGB stellar evolution tracks from Miller Bertolami (2016) for a metallicity Z0 = 0.01 are also plotted in Fig. 5. It is clear that the high-extinction PNe in this subsample lie either around the tracks corresponding to an initial progenitor mass of 1.5 M⊙ and age (τMS + AGB; lifetime in main-sequence and AGB phases) of 2.3 Gyr or are even younger with higher initial progenitor masses. The low-extinction PNe in this sub-sample, barring one, are older than 4.2 Gyr with initial progenitor mass lower than 1.25 M⊙. We note that these ages could be uncertain up to ∼1 Gyr based on the estimations by Kw+12. We may therefore assign the mean ages corresponding to the Kw+12 high- (∼2.5 Gyr) and low- (∼4.5 Gyr) extinction PNe to those with the corresponding extinction values in the San+12 and Bh+19b PNe populations.
 |
Fig. 5. High- and low-extinction PNe observed by Kw+12 are shown in blue and red, respectively in the log(L/L⊙) vs. log(Teff) plot. The stellar evolution tracks from Miller Bertolami (2016) corresponding to metallicity, Z0 = 0.01, are shown in black. The initial stellar mass and τMS + AGB are also labelled. |
4. Age–velocity dispersion relation
4.1. The observed age–velocity dispersion relation in M 31
We obtain the AVR in M 31 for two elliptical bins with RGC = 14–17 and 17–20 kpc. These are presented in Fig. 6, clearly showing the increase in the velocity dispersion with age. In Fig. 6, we also present the age–velocity dispersion value for the MS (∼30 Myr age), σϕ, MS = 30 ± 10 km s−1, obtained by D15 in the RGC = 14–17 kpc bin.
 |
Fig. 6. Age–velocity dispersion relation for PNe in the M 31 disc at RGC = 14–17 and 17–20 kpc is shown in magenta and cyan, respectively. The assigned age is shown in log scale with the MS (∼30 Myr age; D15) in the RGC = 14–17 kpc bin shown at 0.8 Gyr for visual clarity. The AVR obtained in the solar neighbourhood in the MW (Nordström et al. 2004) is shown in grey for comparison. Their total velocity dispersion is shown with squares while the velocity dispersion in the space velocity components (U, V, W) is shown with filled circles, open circles, and filled triangles, respectively. We also present, with open triangles, the velocity dispersion in the W component from Aniyan et al. (2018) for only those MW stars with [Fe/H] < −0.3, showing a flattening in the MW AVR at older ages. |
Based on models fitting the star formation rate, gas profiles, and metallicity distributions of the M 31 and MW discs, Yin et al. (2009) find that RGC = 19 kpc in the M 31 disc is the equivalent distance, in disc scale lengths, of the Sun (R⊙ = 8 kpc) in the MW disc. We therefore compare the velocity dispersion of the MW disc obtained in the solar neighbourhood by Nordström et al. (2004) to our σϕ in the RGC = 17–20 kpc bin, where σϕ, 2.5 Gyr = σϕ, High ext = 61 ± 14 km s−1 and σϕ, 4.5 Gyr = σϕ, Low ext = 101 ± 13 km s−1. Nordström et al. (2004) describe the MW velocity dispersion in space-velocity components (U, V, W), defined in a right-handed Galactic system with U pointing towards the Galactic centre, V in the direction of rotation, and W towards the north Galactic pole (Fig. 6). The equivalent in the MW disc for the σϕ in the M 31 disc would be some combination of σMW, U and σMW, V with a value intermediate between the two (D15). We compare our obtained σϕ of the M 31 disc with the σMW, U, which is ∼29 km s−1 and ∼35 km s−1 for 2.5 Gyr and 4.5 Gyr old populations, respectively. In the RGC = 17–20 kpc bin, the σϕ of the 2.5 Gyr and 4.5 Gyr old populations in M 31 are about twice and three times that of the σMW, U of the 2.5 Gyr and 4.5 Gyr old MW thin disc populations, respectively.
4.2. Comparison with previously measured and simulated age–velocity dispersion relations
The AVR in M 31 was previously estimated by D15 from the σLOS of stars whose classification in different age bins suffered from ambiguity. Their observations were also limited to the PHAT survey footprint, covering about a quarter of the M 31 disc along its major axis out to RGC ∼ 18 kpc. Our observed PNe sample covers the entire M 31 disc out to RGC = 30 kpc, and the high- and low-extinction PNe are well separated in age (Fig. 5). The σϕ values for the high- and low-extinction PNe agree within errors with that obtained by D15 for older AGB (∼2 Gyr old) and RGB (∼4 Gyr old) stars, respectively. Quirk et al. (2019) fitted the rotation curves for stellar populations identified by D15. In the RGC = 14 − 17 kpc bin, Vϕ for the high-extinction PNe is in good agreement with that obtained by Quirk et al. (2019) for older AGB stars, but for the low-extinction PNe it is lower than that of RGB stars by ∼30 km s−1. This is possibly due to their RGB population being contaminated by younger AGB stars, resulting in a Vϕ value that is closer to that of the HI gas.
The AVR for the M 31 disc shows a steep slope in the 0–2.5 Gyr age range and an even steeper slope in the 2.5–4.5 Gyr age range than those for the MW disc in similar age bins. The AVR of the MW disc is considered to be driven by secular evolution channels (see review by Sellwood 2014). An AVR with velocity dispersion increasing gradually with age is also measured in simulated disc galaxies with similarly quiescent merger histories (from zoom-in cosmological simulations by House et al. 2011; Martig et al. 2014). However, simulated disc galaxies undergoing a single merger show a significant increase in velocity dispersion for stellar populations older than the end of the merger (Martig et al. 2014, see their Fig. 2), with larger velocity dispersion for higher merger mass ratios. After the end of the merger, it takes ∼2 Gyr for stellar populations to form with velocity dispersion values similar to those for quiescent discs. The high σϕ, 4.5 Gyr values in the M 31 disc are reminiscent of those seen in populations older than the merger event in simulated galaxies. The lower σϕ, 2.5 Gyr values in the M 31 disc are reminiscent of the lower values predicted by simulations some time after the end of the merger. Finally, the velocity dispersion for the MS in M 31 is akin to that for quiescent discs, also observed at least ∼2 Gyr after the merger event in the simulated galaxies. Therefore, we may deduce from the observed AVR in the M 31 disc that a single merger event took place 2.5–4.5 Gyr ago.
4.3. Estimation of the merger mass ratio
In the framework of a single merger in the M 31 disc, we estimate the merger mass ratio and satellite mass required to produce the dynamically hot 4.5 Gyr-old population with disc scale height H4.5 Gyr = HLow ext ≈ 0.86 kpc (Appendix B). We use the relation between disc scale height (H) and satellite-to-disc-mass ratio (Msat/Mdisc) described by Hopkins et al. (2008) for a satellite galaxy (assumed to be a rigid body) that merged with a disc galaxy (assumed to be a thin disc) on an in-plane prograde radial orbit. The relation in the case of a satellite merging with a Mestel (1963) disc galaxy, having constant circular velocity Vc, disc, is as follows:
where ΔH gives the increase in scale height in the disc galaxy following the merger; 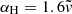 is a derived constant with
is a derived constant with 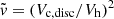 , Vh being the halo circular velocity; fgas is the gas fraction in both the disc galaxy and satellite (assumed to be equal) before the merger; R is the galactocentric radius of the population with scale height H; and Re, disc is the disc effective radius.
, Vh being the halo circular velocity; fgas is the gas fraction in both the disc galaxy and satellite (assumed to be equal) before the merger; R is the galactocentric radius of the population with scale height H; and Re, disc is the disc effective radius.
We assume that the M 31 disc evolved by secular evolution prior to the merger event. Therefore, we adopt the scale height of the old thin disc of the MW as measured in the solar neighbourhood, HMW ≈ 300 pc (see Bland-Hawthorn & Gerhard 2016, and references therein), as the pre-merger scale height Hpre-merger for the M 31 disc. Thus, Hpre-merger ≈ HMW ≈ 0.3 kpc and ΔH = H4.5 Gyr − Hpre-merger ≈ 0.56 kpc. R = 18.5 is the median of the RGC = 17–20 kpc bin, which is the equivalent disc scale length in M 31 to the solar neighbourhood. From Blaña et al. (2018), we adopt Vc, disc = 250 km s−1, Re, disc = 9.88, and Vh = 182 km s−1. The present-day gas fraction in M 31 is ∼9% (Yin et al. 2009) but M 31 is observed to have undergone a burst of star formation ∼2 Gyr ago which produced ∼10% of its mass (Williams et al. 2017). Assuming that the stellar mass formed in this burst was present as gas mass before the merger, we adopt fgas = 0.19. Plugging these values into Eq. (2), we obtain Msat/Mdisc ≈ 0.21 or Msat : Mdisc ≈ 1 : 5. Given that the total mass of the M 31 disc is 7 × 1010 M⊙ (Yin et al. 2009), a 1.4 × 1010 M⊙ satellite is required to dynamically heat the M 31 disc.
5. Summary and conclusion
We classify the observed sample of PNe based on their measured extinction values into high- and low-extinction PNe which are associated with 2.5 Gyr and 4.5 Gyr parent populations, respectively. By fitting rotation curves to the two PNe populations in de-projected elliptical bins, we find that the high- and low-extinction PNe are dynamically colder and hotter, respectively, especially at RGC = 14 − 20 kpc (Figs. 3 and 4). We thus obtain the AVR at these radii and find that σϕ increases with age in the M 31 disc, which is dynamically much hotter than the stars in the MW disc of corresponding ages.
There is an interesting timescale coincidence between the age of the high-extinction PNe and the ∼2 Gyr old burst of star formation observed both in the stellar disc and inner halo of M 31 (Bernard et al. 2015; Williams et al. 2017). We speculate that most of the high-extinction PNe, causing the secondary peak in the extinction distribution (Fig. 1), are those whose progenitors formed during the ∼2 Gyr old star formation burst, while the low-extinction PNe were likely formed earlier. The high-extinction PNe are kinematically tracing the younger thin disc of M 31 outside RGC = 14 kpc from the centre and are clearly separated, both in Vϕ and σϕ, from the dynamically hotter low-extinction PNe which may be associated with the thicker disc. Some low-extinction PNe may also be associated with the old thin disc and inner halo of M 31.
Using hydrodynamical simulations, Hammer et al. (2018) argue that a single major merger 2–3 Gyr ago, where the satellite eventually coalesced to build up the M 31 bulge after multiple passages, can explain the dynamical heating of the M 31 disc. These latter authors also predict a merger with a mass ratio of at least 1:4.5 from their simulations, and also a decreasing trend in the velocity dispersion with radius, as observed, albeit within errors, in Fig. 4. Such a merger could also explain the burst of star formation ∼2 Gyr ago and the presence of the M 31 inner halo substructures. Fardal et al. (2013) also use hydrodynamical simulations to predict the formation of the giant stream from a merger ∼1 Gyr ago with a ∼3.2 × 109 M⊙ satellite. The AVR measured in the M 31 disc using PNe is indicative of a single merger occurring 2.5–4.5 Gyr ago with a merger mass ratio ≈1:5, with a 1.4 × 1010 M⊙ satellite galaxy. Such a galaxy would have been the third largest member of the local group, more massive than M 33 (Kam et al. 2017). This is consistent with the prediction from Hammer et al. (2018). In conclusion, the kinematics of the M 31 disc PNe have been able to shed light on the recent dynamical evolution of M 31. Our next step is to use PNe to further investigate the interface of the disc and inner halo of M 31.
Acknowledgments
SB acknowledges support from the IMPRS on Astrophysics at the LMU Munich. We are grateful to the anonymous referee for the constructive comments that improved the manuscript. Based on observations obtained at the MMT Observatory, a joint facility of the Smithsonian Institution and the University of Arizona. Based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT). This research made use of Astropy – a community-developed core Python package for Astronomy (Astropy Collaboration 2013), Numpy (Oliphant 2015) and Matplotlib (Hunter 2007). This research also made use of NASA’s Astrophysics Data System (ADS (https://ui.adsabs.harvard.edu)).
References
- Aniyan, S., Freeman, K. C., Gerhard, O. E., Arnaboldi, M., & Flynn, C. 2016, MNRAS, 456, 1484 [NASA ADS] [CrossRef] [Google Scholar]
- Aniyan, S., Freeman, K. C., Arnaboldi, M., et al. 2018, MNRAS, 476, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Chapman, S. C., et al. 2015, MNRAS, 453, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, S., Arnaboldi, M., Hartke, J., et al. 2019, A&A, 624, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaña, M., Gerhard, O., Wegg, C., et al. 2018, MNRAS, 481, 3210 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chemin, L., Carignan, C., & Foster, T. 2009, ApJ, 705, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Ciardullo, R., & Jacoby, G. H. 1999, ApJ, 515, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Coccato, L., Gerhard, O., Arnaboldi, M., et al. 2009, MNRAS, 394, 1249 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, S., Salo, H., Knapen, J. H., & Peletier, R. F. 2019, A&A, 623, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortesi, A., Arnaboldi, M., Coccato, L., et al. 2013, A&A, 549, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Lang, D., et al. 2012, ApJS, 200, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Dalcanton, J. J., Fouesneau, M., Hogg, D. W., et al. 2015, ApJ, 814, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Delhaye, J. 1965, Solar Motion and Velocity Distribution of Common Stars (Chicago: University of Chicago Press), 61 [Google Scholar]
- Dorman, C. E., Guhathakurta, P., Seth, A. C., et al. 2015, ApJ, 803, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., Aniano, G., Krause, O., et al. 2014, ApJ, 780, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Fata, R., Roll, J., et al. 2005, PASP, 117, 1411 [NASA ADS] [CrossRef] [Google Scholar]
- Fardal, M. A., Weinberg, M. D., Babul, A., et al. 2013, MNRAS, 434, 2779 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Gilmore, G., & Reid, N. 1983, MNRAS, 202, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Guhathakurta, P., Ostheimer, J. C., Gilbert, K. M., et al. 2005, ArXiv e-prints [arXiv:astro-ph/0502366] [Google Scholar]
- Guhathakurta, P., Rich, R. M., Reitzel, D. B., et al. 2006, AJ, 131, 2497 [NASA ADS] [CrossRef] [Google Scholar]
- Hammer, F., Yang, Y. B., Wang, J. L., et al. 2018, MNRAS, 475, 2754 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., Younger, J. D., & Besla, G. 2008, ApJ, 688, 757 [NASA ADS] [CrossRef] [Google Scholar]
- House, E. L., Brook, C. B., Gibson, B. K., et al. 2011, MNRAS, 415, 2652 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kam, S. Z., Carignan, C., Chemin, L., et al. 2017, AJ, 154, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kwitter, K. B., Lehman, E. M. M., Balick, B., & Henry, R. B. C. 2012, ApJ, 753, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Martig, M., Minchev, I., & Flynn, C. 2014, MNRAS, 443, 2452 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W., Ibata, R., Martin, N., et al. 2018, ApJ, 868, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Merrett, H. R., Merrifield, M. R., Douglas, N. G., et al. 2006, MNRAS, 369, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1963, MNRAS, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newville, M., Stensitzki, T., Allen, D. B., & Ingargiola, A. 2014, https://doi.org/10.5281/zenodo.11813 [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliphant, T. E. 2015, Guide to NumPy, 2nd edn. (USA: CreateSpace Independent Publishing Platform) [Google Scholar]
- Pulsoni, C., Gerhard, O., Arnaboldi, M., et al. 2018, A&A, 618, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quinn, P. J., & Goodman, J. 1986, ApJ, 309, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Quirk, A., Guhathakurta, P., Chemin, L., et al. 2019, ApJ, 871, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, W. A., & Parker, Q. A. 2010, MNRAS, 405, 1349 [NASA ADS] [Google Scholar]
- Roberts, M. S. 1966, ApJ, 144, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, N. E., Caldwell, N., McDowell, J., & Harding, P. 2012, ApJ, 758, 133 [Google Scholar]
- Sellwood, J. A. 2014, Rev. Mod. Phys., 86, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Strömberg, G. 1925, ApJ, 61, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Strömberg, G. 1946, ApJ, 104, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Dell’Agli, F., Schneider, R., et al. 2014, MNRAS, 439, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R. 1977, A&A, 60, 263 [NASA ADS] [Google Scholar]
- Williams, B. F., Dolphin, A. E., Dalcanton, J. J., et al. 2017, ApJ, 846, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoachim, P., & Dalcanton, J. J. 2006, AJ, 131, 226 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Effect of line-of-sight dust attenuation in extinction-based selection of planetary nebulae
The PNe are separated into high- and low-extinction samples considering that the measured extinction values for high-extinction PNe are dominated by their circumstellar extinction, with LOS dust attenuation equally affecting both samples. Any spatial correlation between higher LOS dust attenuation in the galaxy and the position of high-extinction PNe would result in PNe with low circumstellar extinction being misclassified. The dust in the M 31 disc and IGM was mapped by Draine et al. (2014) using near-infrared data from the Spitzer Space Telescope. This was used by Blaña et al. (2018) to obtain the LOS extinction map of the inner disc of M 31 shown in Fig. A.1, also showing the de-projected positions of the high- (blue) and low- (red) extinction PNe. It is clear that there is no preferential selection of the high-extinction PNe at the regions of high LOS extinction in the disc. Both the high- and low-extinction PNe are not spatially correlated with the distribution of LOS extinction.
 |
Fig. A.1. High- (blue) and low- (red) extinction PNe overlaid on the de-projected LOS extinction (AV) map of the inner region of M 31 from Blaña et al. (2018). The elliptical rings show 5 (dotted), 10 (dashed), and 15 (solid) kpc de-projected distances from the centre of M 31. Both the high- and low-extinction PNe are not spatially correlated with the distribution of LOS extinction in the M 31 disc. |
To further investigate this issue, we check whether the high-extinction PNe are preferentially found in the dustier regions of the M 31 disc by taking in to account the geometry of its dust attenuation. The northeast (NE) half of the M 31 disc has higher LOS dust attenuation than the southwest (SW) half (Draine et al. 2014). We thus divide the PNe sample into two halves corresponding to these two regions of the M 31 disc, as shown in Fig. A.2. The cumulative number of PNe is obtained along their deprojected major-axis distances (XPC), with the negative values assigned to the southern side of M 31, for the high-extinction PNe (solid) and all PNe (dashed), for both the NE (orange) and SW (green) halves for the M 31 disc (Fig. A.3). The cumulative distribution of both high-extinction PNe and the entire PNe sample clearly follow a similar distribution in both halves of the M 31 disc with a slightly higher number of PNe observed in the NE half. A KS test shows that the high-extinction PNe in both halves follow the same distribution with a p-value = 0.99. We classify 2% more PNe as high extinction in the SW half of M 31 which is anti-correlated with the expected effects from the LOS dust attenuation. We thus conclude that the LOS dust attenuation effects do not drive the extinction-based classification of our PN populations.
 |
Fig. A.2. Position in space of high- and low-extinction PNe marked with filled and open circles respectively. The black line indicates the major axis of M 31, dividing the PNe into the northeastern (NE) and southwestern (SW) halves of the M 31 disc shown in orange and green, respectively. The black ellipses show RGC = 10 kpc (inner), 20 kpc (middle), and 30 kpc (outer). North is up, east is right. |
 |
Fig. A.3. Cumulative sum of high-extinction PNe (solid lines) and all PNe (dotted lines) for the NE (orange) and SW (green) along the deprojected major-axis distances, XGC. Southern side of M 31 is assigned negative values. |
Appendix B: Validity of the planar disc assumption for the low-extinction planetary nebulae
At the inclination of M 31, deprojecting the low-extinction PNe at high z on a planer disc may result in assigned RGC values which are different from the true ones. We first estimate the scale height of the low-extinction PNe (HLow ext). In order to establish an extinction map of M 31 RGB stars found by the PHAT survey, Dalcanton et al. (2015) modelled the geometry of the M 31 thicker disc to describe the distribution of RGB (∼4 Gyr old; D15) and red clump stars in low-extinction regions. These latter authors found that this thicker disc has a ratio of vertical to horizontal exponential scale heights of hz/hr = 0.15. From IRAC 3.6 μm band images of M 31, Blaña et al. (2018) find that the M 31 disc scale length hr = 5.71 ± 0.08 kpc. Thus, hz = 0.86 ± 0.01 for the M 31 thicker disc. Since the RGB stars have mean age and kinematics close to that of the low-extinction PNe (see Sects. 3.3 and 4.2 for details), HLow ext = hz ≈ 0.86 kpc.
Given the inclination of M 31, PNe at z ∼ 0.86 kpc may be deprojected with an estimated RGC that is ∼0.2 kpc different from its true RGC value. For an exponentially decreasing stellar density (ρ) profile of the low-extinction PNe with z, 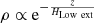 , 1/4 of the low-extinction PNe in any bin may lie at z ∼ 0.86 kpc. Given the 3 kpc bin sizes used to determine σϕ, Low ext, only ∼10% of the low-extinction PNe may be included in a different bin. The measured σϕ values have ∼10% error, as in Fig. 4. Thus the planar disc assumption for PNe does not bias the Vϕ and σϕ profiles within the estimated errors.
, 1/4 of the low-extinction PNe in any bin may lie at z ∼ 0.86 kpc. Given the 3 kpc bin sizes used to determine σϕ, Low ext, only ∼10% of the low-extinction PNe may be included in a different bin. The measured σϕ values have ∼10% error, as in Fig. 4. Thus the planar disc assumption for PNe does not bias the Vϕ and σϕ profiles within the estimated errors.
All Figures
 |
Fig. 1. Histogram showing the distribution of extinction values for the San+12 and Bh+19b PNe. The high- and low-extinction PNe lie in the blue and red shaded regions, respectively. The distribution of extinction values of the LMC PNe observed by Reid & Parker (2010), shifted such that its peak corresponds to that of the M 31, is shown in yellow. |
| In the text | |
 |
Fig. 2. Position on sky of San+12 PNe (squares) and Bh+19b PNe (circles). The high-extinction PNe are shown in blue while the low-extinction PNe are shown in red. The PNe are divided into elliptical bins to obtain rotation curves. |
| In the text | |
 |
Fig. 3. Rotational velocities for the high- and low-extinction PNe are shown in blue and red, respectively. The black line shows the H I rotation velocity from Chemin et al. (2009). The co-rotation radius (black dotted line) and outer Lindblad resonance (OLR; black dashed line) of the M 31 bar are as found by the models of Blaña et al. (2018). The grey shaded region is possibly influenced by different dynamical heating events and is not discussed here. |
| In the text | |
 |
Fig. 4. Rotational velocity dispersion for the high- and low-extinction PNe are known in blue and red, respectively. The black lines and grey shaded region are the same as in Fig. 3. |
| In the text | |
 |
Fig. 5. High- and low-extinction PNe observed by Kw+12 are shown in blue and red, respectively in the log(L/L⊙) vs. log(Teff) plot. The stellar evolution tracks from Miller Bertolami (2016) corresponding to metallicity, Z0 = 0.01, are shown in black. The initial stellar mass and τMS + AGB are also labelled. |
| In the text | |
 |
Fig. 6. Age–velocity dispersion relation for PNe in the M 31 disc at RGC = 14–17 and 17–20 kpc is shown in magenta and cyan, respectively. The assigned age is shown in log scale with the MS (∼30 Myr age; D15) in the RGC = 14–17 kpc bin shown at 0.8 Gyr for visual clarity. The AVR obtained in the solar neighbourhood in the MW (Nordström et al. 2004) is shown in grey for comparison. Their total velocity dispersion is shown with squares while the velocity dispersion in the space velocity components (U, V, W) is shown with filled circles, open circles, and filled triangles, respectively. We also present, with open triangles, the velocity dispersion in the W component from Aniyan et al. (2018) for only those MW stars with [Fe/H] < −0.3, showing a flattening in the MW AVR at older ages. |
| In the text | |
 |
Fig. A.1. High- (blue) and low- (red) extinction PNe overlaid on the de-projected LOS extinction (AV) map of the inner region of M 31 from Blaña et al. (2018). The elliptical rings show 5 (dotted), 10 (dashed), and 15 (solid) kpc de-projected distances from the centre of M 31. Both the high- and low-extinction PNe are not spatially correlated with the distribution of LOS extinction in the M 31 disc. |
| In the text | |
 |
Fig. A.2. Position in space of high- and low-extinction PNe marked with filled and open circles respectively. The black line indicates the major axis of M 31, dividing the PNe into the northeastern (NE) and southwestern (SW) halves of the M 31 disc shown in orange and green, respectively. The black ellipses show RGC = 10 kpc (inner), 20 kpc (middle), and 30 kpc (outer). North is up, east is right. |
| In the text | |
 |
Fig. A.3. Cumulative sum of high-extinction PNe (solid lines) and all PNe (dotted lines) for the NE (orange) and SW (green) along the deprojected major-axis distances, XGC. Southern side of M 31 is assigned negative values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.