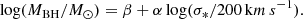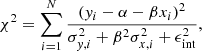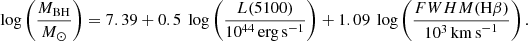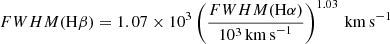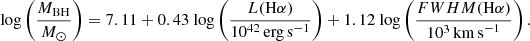| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 11 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935398 | |
| Published online | 17 October 2019 | |
Properties of radio-loud quasars in the Sloan Digital Sky Survey⋆
1
Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatory, Chinese Academy of Sciences, 80 Nandan Road, Shanghai 200030, PR China
e-mail: harry.gaur31@gmail.com
2
Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, Nainital 263002, India
3
Indian Institute of Astrophysics, Koramangala, Bangalore 560 034, India
4
Department of Astronomy, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
5
National Center for Supercomputing Applications, University of Illinois at Urbana-Champaign, 605 East Springfield Avenue, Champaign, IL 61820, USA
Received:
5
March
2019
Accepted:
22
August
2019
We present a study of a sample of 223 radio-loud quasars (up to redshift < 0.3) in order to investigate their spectral properties. Twenty-six of these radio-loud quasars are identified as flat-spectrum radio quasars (FSRQs), and 54 are identified as steep-spectrum radio quasars (SSRQs) based on their radio spectral index. We study the [O III] line properties of these quasars to investigate the origin and properties of blue wings (shift of the profile toward lower wavelengths) and blue outliers (shift of the whole spectroscopic feature). Most of the quasars show blue wings with velocities of up to 420 km s−1. We find that about 17% of the quasars show outliers whose velocities span from 419 to −315 km s−1. Finally, we revisit the MBH − σ relation of our sample using the [S II]λ 6716,6731 and [O III] line widths as surrogates for stellar velocity dispersions, σ, to investigate their location on the MBH − σ relation for quiescent galaxies. Because [S II] is strongly blended with Hα, we were able to estimate σ[S II] for only 123 quasars. We find that the radio-loud quasars do not show a relationship between MBH and σ[S II]/[O III] up to a redshift of 0.3, although they cluster around the local relation. We find an overall offset of 0.12 ± 0.05 dex of our sample of radio-loud quasars from the MBH − σ relation of quiescent galaxies. Quasars in our highest redshift bin (z = 0.25 − 0.3) show a deviation of ∼0.33 ± 0.06 dex from the local relation. Implications of the results are discussed.
Key words: Galaxy: general / galaxies: active / galaxies: jets / quasars: emission lines
Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A46
© ESO 2019
1. Introduction
Quasars are classified into radio-loud and radio-quiet objects. The radio-loudness parameter (R) is conventionally defined as the ratio of the radio luminosity at 5 GHz to the optical luminosity at 4400 Å (Kellermann et al. 1994). Based on this, 10–15% of the quasars are called radio loud, with R ≥ 10. Radio-loud quasars possess powerful radio jets that extend from subparsecs to well outside a galaxy and sometimes to megaparsec scales. The remaining sources are radio quiet, with much weaker radio jets that are mostly confined within the host galaxy when they are detected at all (Kellermann et al. 2016; Padovani 2016).
Radio-loud quasars are further divided into compact flat-spectrum radio quasars (FSRQ; α > −0.5) and extended steep-spectrum radio quasars (SSRQ; α < −0.5), where the spectral index α is defined as fν ∝ ν−α, and fν is the flux density at frequency ν. A radio-loud quasar consists of a compact central core and two extended lobes. The spectrum of the central core is flat and the spectra of the lobes are steep. The radio-loud quasar therefore appears as an FSRQ when it is core dominated and as an SSRQ when it is lobe dominated. The relativistic beaming model for radio sources unifies core-dominated and lobe-dominated sources by means of orientation (Blandford & Rees 1974), where core-dominated objects are viewed close to the jet axis, and lobe-dominated objects are viewed at larger angles.
Radio-loud quasars usually have powerful jets. Although the mechanism of jet formation is still debated, it has been proposed that the jet provides substantial feedback that could affect the circumnuclear environment at the galaxy scale and even at larger galaxy cluster scales (McNamara & Nulsen 2007). Recent observations show evidence for feedback from active galactic nuclei (AGN) in the form of massive large-scale outflows (Fabian 2012; Greene et al. 2012; Scannapieco et al. 2012; Zakamska & Greene 2014). The discovery of many massive molecular outflows has also given support to AGN feedback models (Feruglio et al. 2010; Aalto et al. 2012; Maiolino et al. 2012) and found relations between outflow rates and various AGN properties. Cicone et al. (2014) found that outflow rates correlate with the AGN power. The [O III] emission line shows asymmetry and blueshifts, indicating that the narrow-line region (NLR) is undergoing an organized outflow (Zakamska & Greene 2014; Xu & Komossa 2009). The [O III] line profiles are generally characterized by two distinct components. The first component represents the line core. It has almost the same redshift as the host galaxy. The second component is systematically blueshifted (sometimes redshifted) and has a higher full width at half-maximum (FWHM) than the core component. The second component is usually called a blue wing (BW) and is associated with a gas outflow in the NLR (Komossa et al. 2008). Blue wings are thought to be generated by strong winds in the sources with high Eddington ratios (Proga et al. 2002). Sometimes, the first component also shows blueshift with respect to the rest frame wavelength (Zamanov et al. 2002), and such sources are called blue outliers (BOs; Komossa et al. 2008).
The formation of these BOs are not well understood in AGNs, but in radio-loud quasars, powerful relativistic jets might interact with the NLR and lead to these BOs. Previous studies have found that larger widths of narrow lines are found in AGNs with which powerful radio jets are associated (Peterson 1997). The fast relativistic jet could accelerate the gas and release part of its energy into thermal energy of the surrounding gas (Pedlar & Muxlow 1995). However, simulations (Wagner & Bicknell 2011; Wagner et al. 2012) have shown that only powerful jets can affect the gas kinematics in the NLR and thereby generate BOs.
It is well known that galaxies with massive bulges contain central supermassive black holes (SMBHs). The correlation between the mass of the SMBH, MBH, and the host stellar velocity dispersion, σ, which is called the MBH − σ relation, is of fundamental importance for understanding galaxy formation and evolution. Earlier studies found a close connection between the black hole mass and the stellar velocity dispersion of the bulge (Ferrarese & Merritt 2000; Gebhardt et al. 2000a; Tremaine et al. 2002; Lauer et al. 2007; Kormendy & Ho 2013; Shen et al. 2015, and references therein), as well as a close link between the mass of the black hole and bulge formation and growth (Marconi & Hunt 2003; Häring & Rix 2004; Haehnelt & Kauffmann 2000).
The updated MBH − σ relation for local inactive galaxies is given by Kormendy & Ho (2013) for classical bulges or elliptical galaxies as
The location of AGNs on the MBH − σ plane of quiescent galaxies is of great importance because it would provide strong constraints on their evolution. Various classes of AGNs, such as narrow-line Seyfert 1 galaxies, radio-quiet and radio-loud quasars, and intermediate SMBH, were sometimes found to lie on the relation and sometimes away from it (Nelson 2000; Boroson 2003; Shields et al. 2003; Grupe & Mathur 2004; Bonning et al. 2005; Salviander et al. 2007; Komossa & Xu 2007; Shen et al. 2008; Gu et al. 2009; Ramya et al. 2011; Woo et al. 2013; Salviander & Shields 2013; Bennert et al. 2015; Subramanian et al. 2016).
To firmly establish the MBH − σ relation for different samples, accurate and uniform estimates of both MBH and σ are required; however, this is often difficult to achieve. MBH is commonly estimated by combining the measured line width of broad emission lines such as Hα, Hβ, Mg II, and C IV with the continuum and/or the line luminosity. The empirical relation between the radius of the broad line region (BLR) and the continuum and/or the line luminosity is based on reverberation mapping measurements (Kaspi et al. 2000; Greene & Ho 2005; Peterson et al. 2004). In AGNs, the nuclei are usually much brighter than the host galaxy itself. The fundamental limitation therefore is that the stellar velocity dispersions cannot be directly measured, except in a few low-luminosity AGNs (Greene & Ho 2005; Shen et al. 2015, and references therein). Instead of directly measuring σ, the line width of the narrow [O III]λ 5007 line is commonly used as a surrogate for σ (Komossa & Xu 2007; Gu et al. 2009; Salviander & Shields 2013). The correlation between NLR gas and the gravitational potential of bulge of the host galaxy is significant (Nelson 2000), but the σ[O III] shows more scatter than the stellar velocity σ on the Faber–Jackson relation (Nelson & Whittle 1996; Bonning et al. 2005; Xiao et al. 2011).
Previous studies have found that the radio-loud quasars deviate from the MBH − σ relation for quiescent galaxies (Bian & Zhao 2004; Bonning et al. 2005; Bian et al. 2008; Shen et al. 2008; Gu et al. 2009). Radio-loud quasars mostly settle above the relation, that is, they may have higher black hole masses for a given stellar velocity dispersion. Previously, the [O III] line width was used as surrogate for the stellar velocity dispersion, which means that it can include quasars up to 0.8 redshift. We know that the [O III] line is often asymmetrical in the line profile and has a strong blueshifted wing component due to outflows (e.g., Boroson 2005; Bae & Woo 2014). The uncertainty of this proxy can therefore be very large, as is shown by the direct comparison between the [O III] line width and the measured stellar velocity dispersion (Woo et al. 2006; Xiao et al. 2011). This illustrates that in order to use the [O III] line width as a proxy for σ in active galaxies, the blue wing should be properly removed. It has also been proposed that because of the complexity and asymmetry of this line, other low-ionization emission lines such as [S II]λ 6716,6731, [N II]λ 6584,6548 and [O I]λ 6300 from the NLR can be used as proxies for σ (Nelson & Whittle 1996; Greene & Ho 2005). Because the [N II] line is usually blended with strong Hα (e.g., Zhou et al. 2006) and [O I] is usually weak, the [S II] line was proposed to be a better indicator of σ (Greene & Ho 2005).
We here study a sample of radio-loud quasars to investigate their spectral properties with the aim to determine the distribution of black hole mass, Eddington ratio, radio luminosity, etc. By calculating the radio spectral index, we classify the sample of radio-loud quasars into FSRQs and SSRQs. We also investigate the spectral properties of the [O III] lines of our sample to determine whether BOs are present in radio-loud quasars, and if so, whether relativistic jets produce them. Finally, we revisit the MBH − σ relation for radio-loud quasars using the [S II] and [O III] line widths as surrogates of σ, to investigate their location on the MBH − σ relation for quiescent galaxies. We study whether there is difference in the location of FSRQs and SSRQs on the MBH − σ relation. The cosmological parameters H0 = 70 km s−1 Mpc−1, Ωm = 0.3, Ωλ = 0.7 are used throughout the paper. The sample selection and data reduction are described in Sects. 2 and 3, respectively. The results are presented in Sect. 4, and a discussion and our conclusions are given in Sect. 5.
2. Sample selection
We selected our sample of radio-loud quasars from the Sloan Digital Sky Survey (SDSS) Data Release (DR10) quasar catalog, which consists of 105 783 bona fide quasars brighter than Mi = −22.0 and has at least one broad emission line width larger than 1000 km s−1 (Schneider et al. 2010). The SDSS optical spectra cover the wavelength range 3800 − 9200 Å with a spectral resolution of ∼1850 − 2200 (Schneider et al. 2010). The radio flux densities at 1.4-GHz are tabulated from the Faint Images of the Radio Sky (FIRST) radio catalog (Becker et al. 1995) and the radio-loudness parameter R = f6 cm/f2500 was then estimated, where f6 cm and f2500 are the flux densities at 6 cm and 2500 Å at the rest frame of the source, respectively (see details in Shen et al. 2011).
We selected radio-loud quasars with redshift z ≤ 0.3 based on the criterion that R ≥ 10 as given in Shen et al. (2011). To estimate R, we computed the 5 GHz flux density from the FIRST-integrated flux density assuming a power-law slope of 0.5, as done in Shen et al. (2011). This way of calculating the radio loudness can be questioned because the effect of relativistic beaming affects both radio and optical emission, especially for FSRQs, and can do so differentially. However, an accurate correction for an individual object is rather difficult.
The flux limit of FIRST (1 mJy) means that some radio-loud quasars may not be found through cross matching because they cause biases against high-z sources. In order to determine this bias, we plot the percentage of sources detected by FIRST (sources detected with FIRST/total sources observed in this redshift range) along the redshift, to determine whether the fraction decreases with increasing redshift. Figure 1 shows no correlation between the percentage of sources detected with FIRST vs. redshift (up to z = 0.3). It is therefore difficult to conclude that the sample is biased against more distant objects. To determine whether the sources that are not detected by FIRST are indeed at R < 10, we also calculated the upper limits of the radio loudness (R) of non-detected sources by measuring F5 GHz using the limiting flux of FIRST (i.e., 1 mJy). We found that the radio loudness of all sources is lower than 10.
 |
Fig. 1. Percentage of sources detected with FIRST vs. redshift. |
We know that [S II] lines are lower ionization lines and that a high signal-to-noise ratio (S/N) is required to decompose them. Therefore we extracted only quasars with a mean S/N > 10. These two steps resulted in a sample of 230 quasars. In many spectra, the [S II] lines are strongly blended with the Hα emission line, therefore we were only able to estimate σ[S II] for 123 quasars. Most broader Hα profiles are associated with more massive quasars, which could lead to a selection bias in the way that we probably excluded some of the most massive galaxies. In radio-loud quasars, broader Hα profiles affect the estimation of the [S II] line widths. We therefore also estimated the [O III] line widths for the whole sample. We excluded seven spectra upon visual inspection because of spectral defects in the region of [O III]. This left a total of 223 spectra. Only 80 of these 223 quasars have well-measured 5 GHz flux densities that allow us to determine uniform radio spectral indices. For these we obtained the 5 GHz fluxes by cross-correlating them with the Green Bank 6 cm (GB6) catalog (Gregory et al. 1996). In this useful subsample, 26 quasars are identified as FSRQs with α1.4 − 5 GHz ≤ 0.5, and 54 objects are SSRQs with α1.4 − 5 GHz > 0.5.
3. Spectral analysis
The SDSS spectra were corrected for Galactic extinction using the reddening map of Schlegel et al. (1998). These spectra were then shifted to their rest wavelength by adopting the redshift from the header of the SDSS spectra. In order to fit the power-law continuum, we chose the wavelength range that was not affected by prominent emission lines. We used the optical Fe II template from Véron-Cetty et al. (2004), which covers the wavelength range of 3535 − 7534 Å. The continuum and Fe II components were fit on the line-free spectral windows by minimizing χ2, and were then subtracted from the spectra (see details in Chen et al. 2009). In our sample of radio-loud quasars, the nuclei are relatively bright with respect to the host galaxy. We therefore ignored the contribution of the host galaxy to the spectrum.
In order to estimate flux and velocity dispersion of [S II] and [O III] from the continuum-subtracted spectra, we fit local regions around Hα and Hβ following the procedure of Shen et al. (2011). For Hα, we fit the wavelength range of 6000 − 7180 Å. The narrow components of Hα, [N II]λλ 6548,6584 and [S II]λλ 6717,6713 were modeled with a single-Gaussian profile and their line widths were tied to the same. The flux ratios of the [N II] doublets were fixed to 2.96 (Osterbrock 1989). Following Hao et al. (2005), we imposed an upper limit on the line width of the narrow components, FWHM < 1200 km s−1. The broad Hα component was modeled with multi-Gaussian components, that is, starting with a single Gaussian with FWHM > 1200 km s−1 up to three multiple Gaussians, each with FWHM > 1200 km s−1. New Gaussian components were added one at a time if they led to a reduction of > 20% in χ2 following Xiao et al. (2011). Generally, one or two Gaussians were sufficient to fit the broad Hα profile. However, quasars with asymmetric double-peaked profiles or very broad wings required more than two Gaussian components.
Similar fitting was performed for the Hβ and [O III] lines in the wavelength range 4200 − 5300 Å. Each of the [O III]λλ 4959,5007 lines were model with a double-Gaussian model, that is a core (with higher flux) and a mostly blueshifted wing component (with lower flux) (e.g., Heckman et al. 1981; Greene & Ho 2005; Komossa et al. 2008). The FWHM of the narrow Hβ line was tied to that of the [O III] core, with an upper limit of 1200 km s−1. The flux ratio of [O III]λ 4959 to [O III]λ 5007 was constrained to be 1:3 (Osterbrock 1989). As for Hα, the broad Hβ component was model with multi-Gaussian components (up to three), each with FWHM > 1200 km s−1. In adding a new Gaussian component, we followed the method adopted in Greene & Ho (2005), Sect. 3.2. We also manually checked the fitting results of some spectra using an F-test while we added new Gaussian components and found that the F-test values were significant when a new χ2 led to a reduction of > 20%. We therefore adopted this more stringent criterion to facilitate the fitting model, and a new Gaussian profile was added only when the χ2 was reduced by > 20% (Xiao et al. 2011). Another method to fit the asymmetric profiles of the Hβ component is to use a Gauss-Hermite series (van der Marel & Franx 1993). The broad component of the Hβ line was fit using a sixth-order Gauss-Hermite series. More details are given in Park et al. (2012). We fit a few quasars in our sample using this method and found that both methods yield very similar results (Shen et al. 2011).
Asymmetric profiles are clearly seen in [O III] but are not detected in [S II] profiles. We used the code MPFITFUN of IDL to fit the emission lines employing the GUASS1 program. The parameters that were required to be fit for each Gaussian are centroid, peak value, and sigma. To estimate uncertainties in the measured quantities from single-epoch spectra, we generated 100 mock spectra by adding Gaussian noise to the original spectrum using the flux density errors. Then, we fit these simulated spectra using the fitting procedure described above. We estimated the standard deviation of the distribution of measurements from these 100 simulated spectra as the measurement uncertainty. Uncertainties on fluxes were estimated by adding errors of peak and sigma in quadrature. Examples of the emission line profile fits in the Hα and Hβ regions are shown in the upper and lower panels of Fig. 2, respectively.
 |
Fig. 2. Examples of fits to the spectra in Hα (upper panel) and Hβ regions (lower panel), respectively. Black lines in both panels indicate the observed spectrum, and thick red lines indicate the complete fit to the spectra including all the Gaussian components. The power-law continuum and the Fe II template are shown by red and orange lines, respectively. Broad and narrow Hα are shown in the upper panel by magenta and blue lines, respectively. The [S II] and [N II] lines are shown by green and orange lines, respectively. Broad and narrow Hβ are shown in the lower panel by magenta and blue lines, respectively. The narrow core of [O III] is shown by a green line, and the wing component is represented by a red line. The fit residuals are shown in the lower panels of both panels. |
4. Results
4.1. Estimating the black hole mass
Black hole masses have been derived using different methods in the literature (i.e., Czerny & Nikołajuk 2010; Shen 2013, for recent reviews). For quiescent galaxies, MBH has been estimated through simulations of galaxy stellar dynamics (e.g., Gebhardt et al. 2000b). For AGN, the reverberation mapping method is the most accurate method for measuring MBH (Blandford & McKee 1982). This method assumes that the BLR is virialized and that the motion of the emitting clouds is dominated by the gravitational field of the SBH (e.g., Ho 1999; Wandel et al. 1999),
where G is the gravitational constant, RBLR is the radius of the BLR, VBLR is the rotational velocity of the ionized gas, and f is a dimensionless factor that accounts for the unknown geometry and orientation of the BLR. When the continuum flux, which arises from the accretion disk or very close to it, varies with time, this is later echoed by changes in flux of the BLR, assuming that the BLR is powered by photoionization from the central source. Therefore, RBLR is obtained by cross-correlation of the light curves, which provides the time delay between the continuum variations and the BLR variations. VBLR is estimated from the width of the Doppler-broadened emission lines. This reverberation mapping technique requires high-quality spectrophotometric monitoring of AGNs over an extended period of time. Values of MBH for over 50 AGNs have been estimated using this method (Kaspi et al. 2000; Peterson et al. 2004; Bentz et al. 2009). The uncertainty in the MBH calculation through the reverberation mapping method is between 0.4 and 0.5 dex (Shen 2013).
The single-epoch virial methods assume that the BLR gas is virialized and follows a radius–luminosity relation of the form RBLR ∝ Lα. The coefficients of this relation are determined from estimates of a sample of AGNs for which reverberation mapping data are available. VBLR in this method is estimated from the FHWM of broad Hα or Hβ emission lines. RBLR is estimated using the monochromatic continuum luminosity of the host galaxy at 5100 Å. Because the continuum luminosity is correlated with LHα and LHβ (Greene & Ho 2005), the mass of the black hole can be estimated using FWHM and luminosities of either of the Balmer lines. Greene & Ho (2005) provide equations for the SMBH masses in terms of the Hα and Hβ lines,
and
The FWHM of the combined profile of the broad Hα is commonly used to calculate the black hole mass because its S/N is typically higher than that of Hβ. The empirical relation between the radius of the BLR and the continuum luminosity at 5100 Å is also generally used to estimate the black hole mass (e.g., Kaspi et al. 2000). In radio-loud quasars, the optical continuum might be contaminated by synchrotron radiation from relativistic jets that might be partly beamed, particularly in FSRQs. Under such circumstances, the optical continuum might be boosted by the nonthermal jet emission, which could overestimate the true thermal component and in turn systematically overestimate the black hole masses (Kaspi et al. 2000; Greene & Ho 2005; Chen et al. 2009). This is illustrated in the relationship between the 5100 Å continuum luminosity L5100 and broad Hα luminosity LHα in Fig. 3. The solid line represents the relation of LHα–L5100 given by Greene & Ho (2005) derived for radio-quiet AGNs. While many quasars follow the relation of radio-quiet AGNs, a significant number of quasars lie below the line with a higher L5100 at fixed LHα than radio-quiet AGNs. This is likely due to contamination of nonthermal jet emission continuum luminosity in L5100.
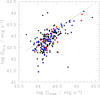 |
Fig. 3. Correlation between LHα and L5100 of the radio-loud sample. The solid line represents the relation of LHα–L5100 given by Greene & Ho (2005) derived for radio-quiet AGNs. Unclassified radio-loud quasars, FSRQs, and SSRQs from our AGN sample are represented by black, red, and blue symbols, respectively. |
In addition to the contamination of the jet emission by the continuum emission, black hole mass estimates may also be affected by BLR geometry. It has been argued that the BLR in radio-loud AGNs can have a more disk-like geometry (Wills & Browne 1986; Vestergaard et al. 2000). In this scenario, for smaller jet viewing angles, narrower broad lines will be observed, and thus the black hole masses will be underestimated. This probably is a particular issue for FSRQs, where the jet moves toward us at a fairly small viewing angle (Jackson & Wall 1999; Lacy et al. 2001; McLure & Dunlop 2002). It is typically difficult to correct the BLR inclination for each source because no information of their orientation is commonly available (Shen & Ho 2014).
In our sample of radio-loud quasars, we therefore estimated MBH with the empirical relation that uses the FWHM and luminosity of Hα. A newer empirical relation for calculating the black hole mass using the line width and luminosity of the broad Hα line is given by Reines et al. (2013). They updated Eq. (4) of Greene & Ho (2005) using the modified radio–luminosity relationship of Bentz et al. (2013). The modified empirical relation is
where ϵ is the scale factor that depends on the BLR geometry and spans a range of ∼0.75 − 1.4 (e.g., Onken et al. 2004; Grier et al. 2013). Here, we assumed ϵ = 1.
Shen (2013) estimated the uncertainty in calculating the black hole mass using the single-epoch (SE) virial Black Hole mass estimators and found that the dominant uncertainty in log MBH is the systematic uncertainty, which can be ∼0.5 dex.
The BLR luminosity LBLR was derived following Celotti et al. (1997) by scaling the strong broad emission lines Hβ to the quasar template spectrum of Francis et al. (1991), in which Lyα is used as a flux reference of 100. From the BLR luminosity, we estimated the disk bolometric luminosity as Lbol = 30 LBLR (Xu et al. 2009). The bolometric luminosity of our sample of quasars varies between log(Lbol) = 44.69 − 46.38 (±0.005) (erg s−1). Black hole masses, radio loudness, and Eddington ratio distributions of the whole sample of quasars, as well as those that were identified as FSRQs and SSRQs, are shown in the top and bottom panels of Fig. 4.
 |
Fig. 4. Histograms of the logarithms of the sample parameters. The top row shows the entire sample, MBH (left); the radio loudness (middle); and the Eddington ratio (right). The bottom row shows FSRQs (red) and SSRQs (blue): MBH (left); radio loudness (middle); and Eddington ratio (right). |
Black hole masses range between 106 and 109.5 M⊙ for the whole sample. The black hole masses of FSRQs range between 107.38 and 109.40 M⊙, and the range is 106.37 − 109.45 M⊙ for SSRQs. However, as mentioned above, because of the systematic uncertainty of ∼0.5 dex in the MBH estimation, there is likely no significant difference between the MBH ranges quoted for flat-spectrum and steep-spectrum quasars. The logarithms of the radio-loudness parameter of FSRQs range between 1.044 and 3.814 and of SSRQs between 1.011 and 4.340. The Eddington ratio log(Lbol/LEdd) values for FSRQs are between −2.292 and −0.251, and SSRQs are found to lie between −2.411 and −0.519. Table A.1 lists all the values and estimates from the optical measurements of our radio-loud sample.
4.2. [O III] line properties
As described above, the [O III] profiles were modeled with two Gaussians, and the lower wavelength peaked Gaussian in both [O III] lines represents the wing component. We calculated the shift of the [O III] core with respect to the rest frame wavelength, vc (in km s−1). Some of the quasars have shown blueshifts as well as redshifts of the [O III] lines. As defined in Komossa et al. (2008) for narrow-line Seyfert galaxies, a source is defined as a BO when its velocity v[O III] < −150 km s−1. In some of the quasars, the [O III] lines are shifted toward higher wavelength, and they are called red outliers. The measurement of the velocity shifts of [O III] profiles should be done relative to the galaxy rest frame, which is usually found by measuring stellar absorption features. However, in our sample of AGNs, these are very weak or absent. The redshift is also provided by the SDSS pipeline from which it is determined based on all strong emission lines. It might therefore influence the velocity shift of the [O III] profiles. We accordingly measured the redshift based on the narrow lines of Hβ. In our sample of radio-loud quasars, 31 quasars are BOs, and 7 of the quasars are red outliers. This means that about 17% of the quasars in our sample show outliers. In previous studies of narrow-line Seyfert 1 galaxies (NLS1s), Zamanov et al. (2002) and Komossa et al. (2008) found that they occur for between 4 and 16%. The outlier velocities attained by these quasars lie between 419 and −315 km s−1.
Strong turbulence in the NLR might lead to such outliers. Radio luminosity might also affect the gas kinematics in such a way that powerful relativistic jets can be linked with the outlier velocities (Tadhunter et al. 2001; Nesvadba et al. 2008). Here, we investigate whether the shift of [O III] is clearly connected to the accretion rate of radio-loud quasars. We searched for correlations of vc with MBH, Lrad, the Eddington ratio, and L[O III] core; they are shown in Fig. 5. The solid line represents the minimal value for outliers, which is −150 km s−1 as defined in Komossa et al. (2008) for NLS1s. The panels show no significant correlation among these quantities.
 |
Fig. 5. Relation of the absolute velocity of the [O III] wing (in km s−1) in the abscissa with the black hole mass (top left), radio luminosity (top right), Eddington ratio (bottom left), and luminosity of [O III]c (bottom right). |
The velocity of the wing component, vw, was calculated with respect to the core component. All of the quasars in our radio-loud sample show blue wings with velocities of up to 420 km s−1. A substantial subset (51) of the quasars also shows red wings with velocities of up to −316 km s−1. We searched for a correlation between velocity of the wing component with the Eddington ratio, as the components are thought to originate in outflows induced by high Eddington ratios (Komossa et al. 2008). We also tested the correlations of vw with MBH, Lrad, and FWHM [OIII]core. The results are shown in Fig. 6. We did not find any significant correlation between these quantities. We then separated outliers from regular sources and searched for a correlation between these quantities. Only a weak correlation (r = 0.236 with p = 0.0092) was found between vw and FWHM [OIII]core for outliers in our sample, which indicates that a turbulent outflow is generated in the gas. This turbulence results in a high FWHM [OIII]core.
 |
Fig. 6. Relation of absolute velocity shift of [O III] (core) in the abscissa with the black hole mass (top left), radio luminosity (top right), Eddington ratio (bottom left), and FWHM [OIII]core (bottom right). |
We also find a weak correlation between L1.4 GHz and the luminosity of the [O III] core, L[O III] core with a Spearman correlation coefficient of rs = 0.253 at a confidence level of 99.6% (see Fig. 7). This indicates a possible relation between radio jets and NLR. After removing the common dependence on redshift using a partial correlation analysis, we still find a correlation value of ps = 0.225 at a confidence level of 98.9%. This might be explained with the shock excitation model, where the NLR emission could be powered by radio-emitting jets(Bicknell et al. 1997; Meléndez et al. 2008). The flux limit of GB6 is much higher than that of FIRST, therefore the source classification, especially those steep-spectrum objects, is heavily biased toward objects with high flux density at 1.4 GHz. This probably explains the predominance of unclassified objects at the low L1.4 GHz side of Fig. 7.
 |
Fig. 7. Relation of the radio luminosity, log L1.4 GHz (erg s−1) to the luminosity of [O III]c. The color symbols are same as in Fig. 2. |
Previous studies (Mullaney et al. 2013) have found that the radio luminosity affects the [O III] line profile. In order to investigate this effect, we performed a correlation analysis between L1.4 GHz and the FWHM of the core component, FWHM [OIII]core. However, we did not find any significant correlation between these quantities.
We also calculated the R5007 parameter, which is defined as the ratio between the [O III]λ 5007 line and the whole Hβ flux. Because Hβ is formed in the inner part of the BLR and [O III] is formed in the NLR, this ratio could be used to evaluate whether the jet interaction is different in BLR and NLR. We therefore searched for a possible correlation between R5007 and the wing velocity because fast [O III] wings lead to a reduction of the covering factor in the NLR, which leads to a reduction of the flux of the [O III] lines. For our sample of radio-loud quasars we did not find a significant correlation between these quantities, however.
4.3. MBH − σ relation
We used the NLR gas velocity dispersions of [S II] and [O III] as surrogates for the stellar velocity dispersion,
where σobs = FWHM[SII], or [O III]/2.35 and z is the redshift (Bian et al. 2008). For the SDSS spectra, the mean value of the instrument resolution, σins, is about 56 km s−1 and 60 km s−1 for [S II] and [O III], respectively (Greene & Ho 2005).
The MBH − σ relation for our sample is shown in Fig. 8 using the [S II] (upper panel) and [O III] (lower panel) line width as surrogate for the stellar velocity dispersion. Unclassified radio loud quasars, FSRQs, and SSRQs are shown. The Kormendy & Ho (2013) relation for classical bulge or elliptical galaxies (KH13, Eq. (1)), the relation in Tremaine et al. (2002; T02) and the relation in McConnell & Ma (2013) for late-type galaxies are also shown in the figure.
 |
Fig. 8. MBH − σ[S II] relation for radio-loud quasars (upper panel), FSRQs, SSRQs, and unclassified radio loud quasars are represented by red, blue, and black symbols, respectively. MBH–σ[O III] relation of radio-loud quasars (lower panel). In both panels, black, red, and blue solid lines represent the MBH − σ relations for quiescent galaxies by Kormendy & Ho (2013), Tremaine et al. (2002), and McConnell & Ma (2013), respectively. For [O III], the core of the line is used after decomposing the asymmetric blue wings. |
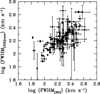 |
Fig. 9. Correlations between the FWHM of [S II] and [O III] (Spearman Correlation coefficient, r = 0.7527 with p = 2.2e−16). |
The figure shows that the radio-loud quasars of our sample do not show any correlation between MBH and σ, although they do cluster around the relation for local inactive galaxies, though with some outliers.
In order to determine the overall offset of our sample of radio-loud quasars from the local relation of inactive galaxies, we fit the log MBH as a function of log σ*:
Here y = log(MBH/M⊙), x = log(σ*/200 km s−1), and α and β are the slope and intercept of the regression, respectively. In order to perform the linear regression, we adopted two methods: FITEXY (Tremaine et al. 2002) and LINMIX_ERR (Kelly 2007).
The FITEXY (Press et al. 1992), modified by Tremaine et al. (2002), was implemented in our work in IDL using the mpfit (Markwardt 2009) Levenberg–Marquardt least-squares minimization routine. Our implementation is similar to that provided in Williams et al. (2010)1. It performs the linear regression by minimizing
where α and β are the regression coefficients, σx and σy are standard deviation in measurement errors, and 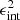 is the intrinsic variance. The value of ϵint is iteratively adjusted as an effective additional y error by repeating the fit until χ2/(N − 2) = 1 is obtained (i.e., following the suggested iterative procedure given in Bedregal et al. 2006 and Bamford et al. 2006). If after the initial iteration the reduced χ2 is lower than one, no further iterations occur and ϵint = 0. ϵ is set to properly account for the intrinsic scatter. Thus the best-fit slope is not biased by a few points with small measurement errors (e.g., see the discussion in Tremaine et al. 2002). We only considered the measurement errors of log MBH and σ in the fit, and the intrinsic scatter ϵ therefore includes the contribution from the systematic errors in log MBH and σ. We also tried to add the systematic errors on both log MBH and σ, but did not find significantly different results of slopes and intercept (as also found in Shen et al. 2015).
is the intrinsic variance. The value of ϵint is iteratively adjusted as an effective additional y error by repeating the fit until χ2/(N − 2) = 1 is obtained (i.e., following the suggested iterative procedure given in Bedregal et al. 2006 and Bamford et al. 2006). If after the initial iteration the reduced χ2 is lower than one, no further iterations occur and ϵint = 0. ϵ is set to properly account for the intrinsic scatter. Thus the best-fit slope is not biased by a few points with small measurement errors (e.g., see the discussion in Tremaine et al. 2002). We only considered the measurement errors of log MBH and σ in the fit, and the intrinsic scatter ϵ therefore includes the contribution from the systematic errors in log MBH and σ. We also tried to add the systematic errors on both log MBH and σ, but did not find significantly different results of slopes and intercept (as also found in Shen et al. 2015).
We did not find any correlation between MBH and σ, probably because of systematic uncertainties on both parameters, but points are clustered around the local relation. In order to find the overall offset of our sample of radio-loud quasars with respect to the local relation, we followed the approach of Sheinis & López-Sánchez (2017) and fixed α (to the slope of KH13) in our regressions. The results of the regression are summarized in Table 1. We estimated our results with the alternative regression method, which uses the Bayesian linear regression routine, linmix_err, developed by Kelly (2007). It is available in the NASA IDL astronomy user library2. We did not find significantly different results for slope and intercept using these two methods and therefore quote regression results from the previous method.
Linear regression results for the radio-loud sample with α fixed at 4.38.
In this regression analysis, we fixed α = 4.38 (the slope of the KH13 relation) and left the intercept as a free parameter. The results of this regression for σ of [S II], [O III] and for various redshift bins are provided in Table 1. When the [SII] lines are used as σ*, the radio-loud sample shows an intrinsic scatter of 0.74 around the local relation with an intercept of 8.41. The sample consisting of σ[S II] involves a selection bias, however, because we removed most of the broader Hα profiles where the [S II] lines were blended. For these quasars, the [S II] line widths could therefore not be calculated and were removed from the sample. For the sample consisting of the [O III] line width, the intrinsic scatter decreases to ∼0.60 with an overall deviation of ∼0.12 ± 0.05 dex from the local relation. However, when we take the systematic uncertainties on MBH and σ into account, these deviations are not significant. Our results are in accordance with those of previous studies, where the MBH − σ relation for active galaxies appeared to be flatter than for quiescent galaxies (Woo et al. 2013; Shen et al. 2015). Shen et al. (2015) have argued that the flattening of the MBH − σ relation of active galaxies at high redshift is due to the various selection biases that cause the sample to contain more luminous and massive systems. This shifts the most massive black holes above the quiescent galaxy relation (Woo et al. 2016; Salviander & Shields 2013; Brotherton et al. 2015), and hence the MBH − σ relation for quasars in individual samples may change with redshift.
To determine the offset of our sample of MBH − σ relation from quiescent galaxies at different redshifts, we divided whole sample into three redshift bins of 0.1–0.2, 0.2–0.25, and 0.25–0.3 in such a way that nearly equal numbers of quasars fall in each bin. The parameters in Table 1 show a significant offset of ∼0.33 ± 0.06 dex for the quasars that lie in highest redshift bin (0.25–0.3). The intrinsic scatter decreases from the lowest to the highest bin.
4.3.1. Comparison of MBH with an alternative method
In Sect. 3.1 we used the empirical relation of Reines et al. (2013) to calculate the virial black hole mass. As mentioned in Sect. 3.1, this is based on the method outlined in Greene & Ho (2005), but was derived with the modified radius–luminosity relationship of Bentz et al. (2013). As compared to estimating MBH using Eq. (4) of Greene & Ho (2005), this modification of the radius–luminosity relation causes an increase in the estimate of MBH by a factor of ∼1.6. The estimated range of the black hole mass lies between MBH = 107.1–109.2 M⊙ (in Sect. 4.1).
Wang et al. (2009) presented a new formalism of the empirical relation using Hβ lines and the updated BH mass measurements from reverberation mapping. This new formalism has shown improved internal scatter between the single-epoch estimators and the mass estimators based on reverberation mapping, but it systematically deviates from some of the commonly used MBH estimators in the literature. It involves MBH ∝ FWHM1.09 instead of MBH ∝ FWHM2 that is commonly used in the literature, which gives progressively higher and lower MBH values toward the low- and high-mass ends, respectively. Collin et al. (2006) also reported results that are consistent with those of the Wang et al. (2009) formalism over a relatively wide mass range. The discrepancy between previously used mass estimators and those Wang et al. (2009) therefore arises because more recently recalibrated and updated reverberation mapping MBH measurements from the literature are used (i.e., Peterson et al. 2004; Bentz et al. 2007; Grier et al. 2008) as well as a best-fitting value of γ instead of fixed γ = 2 in MBH ∝ FWHMγ. To determine whether this systematic bias described by Wang et al. (2009) can affect the intrinsic scatter in the MBH estimation of our radio-loud sample, we reestimated the MBH of our sample using the formalism of Wang et al. (2009), which reads
The line luminosity and FWHM of Hα are better suited to estimate MBH of radio-loud quasars (for the reasons described in Sect. 3.1). To transform Eq. (9) into the line luminosity and FWHM of Hα, we therefore used the empirical relations provided by Greene & Ho (2005) between the FWHM of Hα and Hβ, and between the broad Hα luminosity and continuum luminosity at 5100 Å, L5100 and inserted them into Eq. (9),
By inserting these relations into Eq. (9), we obtain the formula
Now we reestimated MBH using Eq. (12), and we repeat the plot of the MBH − σ relation using these newly estimated MBH values in Fig. 10. The MBH range is slightly reduced to 107.1–108.8 M⊙. The scatter is indeed reduced, as pointed out by Wang et al. (2009). However, we find that the newly estimated MBH values do not change our main results.
 |
Fig. 10. MBH − σ[O III] relation of radio-loud quasars using the formalism of Wang et al. (2009) given in Eq. (9). FSRQs, SSRQs, and unclassified radio-loud quasars are represented by red, blue, and black symbols, respectively. The black, red, and blue lines represent the MBH–σ relation of quiescent galaxies by Kormendy & Ho (2013), Tremaine et al. (2002), and McConnell & Ma (2013), respectively. |
4.3.2. Biases and uncertainties
The intrinsic scatter along the vertical direction in the MBH − σ relation of radio-loud quasars can be partly accounted for by the uncertainties in the estimation of the black hole masses, which can be under- or overestimated due to the BLR geometry and Doppler boosting, respectively. The Doppler-boosting effect has been avoided by replacing the continuum luminosity with the line luminosity in BLR radius–luminosity empirical relation. The similar black hole mass distributions between FSRQs and SSRQs show that the BLR geometry effect is probably not severe in our sample. In addition to these two effects, the single-epoch virial BH mass estimators are still subject to a number of uncertainties that are propagated from the measurement errors in FWHM and line luminosity and by the different methods that are adopted to estimate the line widths and luminosities, leading to various discrepancies (Shen et al. 2008). The dominant uncertainty is the systematic uncertainty, however, which is ∼0.5 dex (Shen 2013).
An uncertainty is also present in the estimation of σ. We described above that the FWHM of the [S II] and [O III] emission lines were used as a surrogate for the stellar velocity dispersion σ. These lines were used as σ in previous studies to explore the MBH − σ relation (i.e., Gu et al. 2009; Salviander et al. 2007; Salviander & Shields 2013; Brotherton et al. 2015, and references therein), and large scatter was found. The uncertainty of this substitution is large, as is shown by the direct comparison between the [O III] line width and the stellar σ (Xiao et al. 2011; Woo et al. 2016; Sheinis & López-Sánchez 2017). For type 2 AGNs, Woo et al. (2016) found an uncertainty of 0.19 dex in the direct comparison of the [O III] line width and σ. The actual uncertainty for this substitution is not known for radio-loud quasars. We therefore assumed a lower limit of 0.19 dex in the substitution of σ[O III]. Along with these uncertainties, the estimation of σ[O III] can also be affected by the outflows that can be noted through the moderate correlation between σ[O III] and the velocity width of the outflowing gas (shown in Fig. 11).
 |
Fig. 11. Relation of σ[O III] to the velocity of the outflowing gas, V[O III] wing. The color symbols are the same as in Fig. 4. |
Now we discuss the other potential biases (in addition to the uncertainties in the measurements of MBH and σ) that could lead to the observed intrinsic scatter in our sample of radio-loud quasars. This includes the intrinsic scatter in the MBH − σ relation of inactive galaxies of 0.31 dex for early-type galaxies and 0.44 dex for all galaxy types, based on the locally observed sample of galaxies (Gültekin et al. 2009). However, the magnitude of intrinsic scatter in the MBH − σ relation of AGN samples is not known.
Salviander et al. (2007) simulated the effect of a Malmquist-like bias that arises from correlations between quasar luminosity, MBH, and redshift. Lauer et al. (2007) also suggested that because there is intrinsic scatter in the MBH − σ relation, the samples that are selected based on a threshold in quasar luminosity will preferentially select overmassive BHs with respect to the stellar velocity dispersion. Shen & Kelly (2010) and Shen (2013) found that because single-epoch virial mass estimates depend on luminosity, quasar samples with high threshold luminosity are biased toward high virial masses. Shen & Kelly (2010) estimated a bias of 0.2−0.3 dex in MBH for Lbol > 1046 erg s−1. Recently, Shen et al. (2015) performed simulations to show that these biases lead to a flattening in the slope of the MBH − σ relation because the undermassive BHs are more easily lost because their luminosity threshold is high. The effects of these statistical biases are more severe at high redshifts.
5. Discussion and conclusions
We studied a sample of 223 radio-loud quasars out to z < 0.3. We investigated their black hole mass, radio luminosity, and Eddington ratio distributions. We calculated the radio spectral indices and were able to classify 26 of the quasars as FSRQs and 56 as SSRQs.
We investigated the [O III] properties of our radio-loud sample and found that about 17% of these quasars show outliers. The typical velocity attained by these outliers lies between 419 and −315 km s−1. These outliers are thought to originate either from strong turbulence in the NLR or the influence of powerful relativistic jets. We failed to find any significant correlation of the velocity shift of [O III] to L1.4 GHz, Eddington ratio, etc. All the [O III] profiles also show blue wings with velocities of up to 420 km s−1. Blue wings are also believed to originate in outflows that are induced by a high Eddington ratio, but we did not find any significant correlation between these quantities.
The correlation between L1.4 GHz and L[O III] core indicates a possible relation between radio jets and NLRs. We find only a weak correlation between these quantities.
Quasars with broader σ[O III] core are associated with field with a high outflow velocity. The effect of outflows might therefore affect the true estimate of σ[O III] by broadening the [O III] line profiles (Dopita & Sutherland 1995; Nelson & Whittle 1996; Komossa & Xu 2007).
We revisited the MBH − σ relation for our sample of radio-loud SDSS quasars using [O III] and [S II]λ 6716,6731 σ as surrogate for the stellar velocity dispersion. We find that the radio-loud quasars do not show a relationship between MBH and σ, which is expected because of the systematic uncertainties on them (described above), but they cluster instead around the MBH − σ relation for inactive galaxies.
Some recent works have shown that the MBH − σ relation for active galaxies appears to be shallower or flatter than for inactive or quiescent galaxies (Woo et al. 2013; Shen et al. 2015). The studies of Woo et al. and Shen et al. involved measurements of stellar absorption features, based on which the teams calculated the stellar velocity dispersion. Woo et al. (2013) found different slopes of the MBH − σ relation for quiescent and active galaxies, which could be due to the real physical difference of the BH-galaxy coevolution. However, Shen et al. (2015) also found a flattening of the MBH − σ relation of active galaxies at high redshift, but they argued that this might be caused by the various selection biases and BH mass uncertainties in luminosity-threshold quasar samples. As the redshift increases, most of the selection criteria cause the sample to contain more luminous and massive systems, which shifts the most massive black holes above the quiescent galaxy relations (Woo et al. 2010, 2013; Salviander & Shields 2013; Shen et al. 2015; Brotherton et al. 2015), and the MBH − σ relation of quasars in individual samples may therefore change with redshift. Our sample is restricted to z ≤ 0.3 because the [S II] line was used. We find an overall offset of 0.12 ± 0.05 of our sample of radio-loud quasars from the local relation of quiescent galaxies. When the quasars in the highest redshift bin (0.22–0.3) are considered, an overall offset of 0.33 ± 0.06 is found. These results are used with caution because systematic uncertainties were not taken into account when they were calculated. A detailed study of the MBH − σ relation of radio-loud quasars at higher redshift is required, which will be presented in our future work.
Acknowledgments
We are grateful to the anonymous referee for the insightful comments. We are indebted to Gregory Shields and Paul J. Wiita for carefully reading the manuscript and providing very valuable suggestions. We are grateful to Arun Mangalam and J. H. Woo for their useful discussions and comments on the work. HG acknowledges Xiaobo Dong and Ting Xiao for helpful discussions of the analysis and data reduction. HG thanks Liao Mai for help in this work. HG is sponsored by the Chinese Academy of Sciences Visiting Fellowship for Researchers from Developing Countries, CAS President’s International Fellowship Initiative (grant No. 2014FFJB0005), supported by the NSFC Research Fund for International Young Scientists (grant 11450110398) and supported by the China Postdoctoral Science Foundation Grant (grant 2016T90393). HG acknowledges the financial support from the Department of Science and Technology, India, through INSPIRE faculty award IFA17-PH197 at ARIES, Nainital. MFG acknowledges support from the National Science Foundation of China (grants 11873073 and U1531245). This work makes extensive use of SDSS-I/II data. The SDSS website is at http://www.sdss.org/.
References
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bae, H.-J., & Woo, J.-H. 2014, ApJ, 795, 30 [Google Scholar]
- Bamford, S. P., Aragón-Salamanca, A., & Milvang-Jensen, B. 2006, MNRAS, 366, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Bedregal, A. G., Aragón-Salamanca, A., & Merrifield, M. R. 2006, MNRAS, 373, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, V. N., Treu, T., Auger, M. W., et al. 2015, ApJ, 809, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Denney, K. D., Cackett, E. M., et al. 2007, ApJ, 662, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Peterson, B. M., Pogge, R. W., & Vestergaard, M. 2009, ApJ, 694, L166 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Denney, K. D., Grier, C. J., et al. 2013, ApJ, 767, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Rees, M. J. 1974, MNRAS, 169, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, W., & Zhao, Y. 2004, MNRAS, 347, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, W.-H., Chen, Y.-M., Hu, C., Huang, K., & Xu, Y. 2008, Chin. J. Astron. Astrophys., 8, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Bicknell, G. V., Dopita, M. A., & O’Dea, C. P. O. 1997, ApJ, 485, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Bonning, E. W., Shields, G. A., Salviander, S., & McLure, R. J. 2005, ApJ, 626, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, T. A. 2003, ApJ, 585, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, T. 2005, AJ, 130, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Brotherton, M. S., Singh, V., & Runnoe, J. 2015, MNRAS, 454, 3864 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., Padovani, P., & Ghisellini, G. 1997, MNRAS, 286, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Z., Gu, M., & Cao, X. 2009, MNRAS, 397, 1713 [NASA ADS] [CrossRef] [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Czerny, B., & Nikołajuk, M. 2010, Mem. Soc. Astron. It., 81, 281 [NASA ADS] [Google Scholar]
- Dopita, M. A., & Sutherland, R. S. 1995, ApJ, 455, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Francis, P. J., Hewett, P. C., Foltz, C. B., et al. 1991, ApJ, 373, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000a, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Kormendy, J., Ho, L. C., et al. 2000b, ApJ, 543, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 627, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Zakamska, N. L., & Smith, P. S. 2012, ApJ, 746, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., Scott, W. K., Douglas, K., & Condon, J. J. 1996, ApJS, 103, 427 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Pancoast, A., Barth, A., et al. 2008, ApJ, 688, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Grier, C. J., Martini, P., Watson, L. C., et al. 2013, ApJ, 773, 90 [CrossRef] [Google Scholar]
- Grupe, D., & Mathur, S. 2004, ApJ, 606, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M., Chen, Z., & Cao, X. 2009, MNRAS, 397, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Haehnelt, M. G., & Kauffmann, G. 2000, MNRAS, 318, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, L., Strauss, M. A., Tremonti, C. A., et al. 2005, AJ, 129, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Miley, G. K., van Breugel, W. J. M., & Butcher, H. R. 1981, ApJ, 247, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C. 1999, in Observational Evidence for Black Holes in the Universe, ed. S. K. Chakarbarti (Dordrecht: Kluwer), 157 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, C. A., & Wall, J. V. 1999, MNRAS, 304, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Sramek, R. A., Schmidt, M., Green, R. F., & Shaffer, D. B. 1994, AJ, 108, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Condon, J. J., Kimball, A. E., Perley, R. A., & Ivezic, Z. 2016, ApJ, 831, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C. 2007, ApJ, 665, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., & Xu, D. 2007, ApJ, 667, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Xu, D., Zhou, H., Storchi-Bergmann, T., & Binette, L. 2008, ApJ, 680, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Lacy, M., Laurent-Muehleisen, S. A., Ridgway, S. E., Becker, R. H., & White, R. L. 2001, ApJ, 551, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Faber, S. M., Richstone, D., et al. 2007, ApJ, 662, 808 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
- McConnell, N. J., & Ma, C.-P. 2013, ApJ, 764, 184 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Dunlop, J. S. 2002, MNRAS, 331, 795 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Meléndez, M., Kraemer, S. B., Armentrout, B. K., et al. 2008, ApJ, 682, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Fine, S., et al. 2013, MNRAS, 433, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C. H. 2000, ApJ, 544, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C. H., & Whittle, M. 1996, ApJ, 465, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., Gilbert, A. M., & van Breugel, W. 2008, A&A, 491, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Onken, C. A., Ferrarese, L., Merritt, D., et al. 2004, ApJ, 615, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley, CA: University Science Books) [CrossRef] [Google Scholar]
- Padovani, P. 2016, A&ARv, 24, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Park, D., Kelly, B. C., Woo, J. H., & Treu, T. 2012, ApJS, 203, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Pedlar, A., & Muxlow, T. W. B. 1995, Ap&SS, 233, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 1997, An Introduction to Active Galactic Nuclei (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in C, 2nd edn. (New York: Cambridge University Press) [Google Scholar]
- Proga, D., Stone, J. M., & Kallman, T. R. 2002, ApJ, 543, 686 [Google Scholar]
- Ramya, S., Prabhu, T. P., & Das, M. 2011, MNRAS, 418, 789 [NASA ADS] [CrossRef] [Google Scholar]
- Reines, A. E., Greene, J. E., & Geha, M. 2013, ApJ, 775, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Salviander, S., & Shields, G. A. 2013, ApJ, 764, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Salviander, S., Shields, G. A., Gebhardt, K., & Bonning, E. W. 2007, ApJ, 662, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., Wadepuhl, M., Parry, O. H., et al. 2012, MNRAS, 423, 1726 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A., Gebhardt, K., Salviander, S., et al. 2003, ApJ, 583, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Sheinis, A. I., & López-Sánchez, Á. R. 2017, AJ, 153, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., Berk, D. E. V., Schneider, D. P., & Hall, P. B. 2008, AJ, 135, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y. 2013, Bull. Astron. Soc. India, 41, 61 [NASA ADS] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Kelly, B. C. 2010, ApJ, 713, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Greene, J. E., Ho, L. C., et al. 2015, ApJ, 805, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Subramanian, S., Ramya, S., Das, M., et al. 2016, MNRAS, 455, 3148 [NASA ADS] [CrossRef] [Google Scholar]
- Tadhunter, C., Wills, K., Morganti, R., Oosterloo, T., & Dickson, R. 2001, MNRAS, 327, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Franx, M. 1993, ApJ, 407, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M.-P., Joly, M., & Véron, P. 2004, A&A, 417, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vestergaard, M., Wilkes, B. J., & Barthel, P. D. 2000, ApJ, 538, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, A. Y., & Bicknell, G. V. 2011, ApJ, 728, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, A. Y., Bicknell, G. V., & Umemura, M. 2012, ApJ, 757, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Wandel, A., Peterson, B. M., & Malkan, M. A. 1999, ApJ, 526, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J.-G., Dong, X.-B., Wang, T.-G., et al. 2009, ApJ, 707, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, M. J., Bureau, M., & Cappellari, M. 2010, MNRAS, 409, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Wills, B. J., & Browne, I. W. A. 1986, ApJ, 302, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Treu, T., Malkan, M. A., & Blandford, R. D. 2006, ApJ, 645, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J. H., Treu, T., Barth, A. J., et al. 2010, ApJ, 716, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Schulze, A., Park, D., et al. 2013, ApJ, 772, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Bae, H.-J., Son, D., & Karouzos, M. 2016, ApJ, 817, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, T., Barth, A. J., Greene, J. E., et al. 2011, ApJ, 739, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y.-D., Cao, X., & Wu, Q. 2009, ApJ, 694, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D., & Komossa, S. 2009, ApJ, 705, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Zakamska, N. L., & Greene, J. E. 2014, MNRAS, 442, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R., Marziani, P., Sulentic, J. W., et al. 2002, ApJ, 576, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Yuan, W., et al. 2006, ApJS, 166, 128 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Percentage of sources detected with FIRST vs. redshift. |
| In the text | |
 |
Fig. 2. Examples of fits to the spectra in Hα (upper panel) and Hβ regions (lower panel), respectively. Black lines in both panels indicate the observed spectrum, and thick red lines indicate the complete fit to the spectra including all the Gaussian components. The power-law continuum and the Fe II template are shown by red and orange lines, respectively. Broad and narrow Hα are shown in the upper panel by magenta and blue lines, respectively. The [S II] and [N II] lines are shown by green and orange lines, respectively. Broad and narrow Hβ are shown in the lower panel by magenta and blue lines, respectively. The narrow core of [O III] is shown by a green line, and the wing component is represented by a red line. The fit residuals are shown in the lower panels of both panels. |
| In the text | |
 |
Fig. 3. Correlation between LHα and L5100 of the radio-loud sample. The solid line represents the relation of LHα–L5100 given by Greene & Ho (2005) derived for radio-quiet AGNs. Unclassified radio-loud quasars, FSRQs, and SSRQs from our AGN sample are represented by black, red, and blue symbols, respectively. |
| In the text | |
 |
Fig. 4. Histograms of the logarithms of the sample parameters. The top row shows the entire sample, MBH (left); the radio loudness (middle); and the Eddington ratio (right). The bottom row shows FSRQs (red) and SSRQs (blue): MBH (left); radio loudness (middle); and Eddington ratio (right). |
| In the text | |
 |
Fig. 5. Relation of the absolute velocity of the [O III] wing (in km s−1) in the abscissa with the black hole mass (top left), radio luminosity (top right), Eddington ratio (bottom left), and luminosity of [O III]c (bottom right). |
| In the text | |
 |
Fig. 6. Relation of absolute velocity shift of [O III] (core) in the abscissa with the black hole mass (top left), radio luminosity (top right), Eddington ratio (bottom left), and FWHM [OIII]core (bottom right). |
| In the text | |
 |
Fig. 7. Relation of the radio luminosity, log L1.4 GHz (erg s−1) to the luminosity of [O III]c. The color symbols are same as in Fig. 2. |
| In the text | |
 |
Fig. 8. MBH − σ[S II] relation for radio-loud quasars (upper panel), FSRQs, SSRQs, and unclassified radio loud quasars are represented by red, blue, and black symbols, respectively. MBH–σ[O III] relation of radio-loud quasars (lower panel). In both panels, black, red, and blue solid lines represent the MBH − σ relations for quiescent galaxies by Kormendy & Ho (2013), Tremaine et al. (2002), and McConnell & Ma (2013), respectively. For [O III], the core of the line is used after decomposing the asymmetric blue wings. |
| In the text | |
 |
Fig. 9. Correlations between the FWHM of [S II] and [O III] (Spearman Correlation coefficient, r = 0.7527 with p = 2.2e−16). |
| In the text | |
 |
Fig. 10. MBH − σ[O III] relation of radio-loud quasars using the formalism of Wang et al. (2009) given in Eq. (9). FSRQs, SSRQs, and unclassified radio-loud quasars are represented by red, blue, and black symbols, respectively. The black, red, and blue lines represent the MBH–σ relation of quiescent galaxies by Kormendy & Ho (2013), Tremaine et al. (2002), and McConnell & Ma (2013), respectively. |
| In the text | |
 |
Fig. 11. Relation of σ[O III] to the velocity of the outflowing gas, V[O III] wing. The color symbols are the same as in Fig. 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




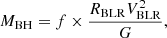
![$$ \begin{aligned} M_{\rm BH}&= (3.6\pm 0.2)\times 10^6 \times \left(\frac{L_{\mathrm{H}\beta }}{10^{42}\,\mathrm{erg\,s}^{-1}}\right)^{(0.56\pm 0.02)} \nonumber \\&\quad \times \left(\frac{{FWHM}_{\mathrm{H}\beta }}{10^3\,\mathrm{km\,s}^{-1}}\right)^2 \quad [M_{\odot }], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35398-19/aa35398-19-eq3.gif)
![$$ \begin{aligned} M_{\rm BH}&= 2.0^{+0.4}_{-0.3}\times 10^6 \times \left(\frac{L_{\mathrm{H}\alpha }}{10^{42}\,\mathrm{erg\,s}^{-1}}\right)^{(0.55\pm 0.02)}\nonumber \\&\quad \times \left(\frac{{FWHM}_{\mathrm{H}\alpha }}{10^3\,\mathrm{km\,s}^{-1}}\right)^{(2.06\pm 0.06)} \quad [M_{\odot }]. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35398-19/aa35398-19-eq4.gif)
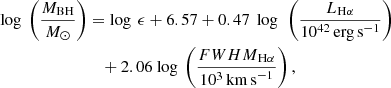
![$$ \begin{aligned} \sigma = \sqrt{\sigma _{\mathrm{obs}}^{2} - [\sigma _{\mathrm{ins}}/ (1+ z)]^{2}}, \end{aligned} $$](/articles/aa/full_html/2019/11/aa35398-19/aa35398-19-eq6.gif)