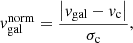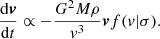| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A16 | |
| Number of page(s) | 7 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201834689 | |
| Published online | 11 October 2019 | |
Fossil group origins
X. Velocity segregation in fossil systems
1
IRFU, CEA, Université Paris-Saclay, 91191 Gif-sur-Yvette, France
e-mail: stefano.zarattini@cea.fr
2
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité, 91191 Gif-sur-Yvette, France
3
Instituto de Astrofísica de Canarias, calle Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
4
Departamento de Astrofísica, Universidad de La Laguna, Avenida Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Spain
5
INAF-Osservatorio Astronomico di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
6
Dipartimento di Fisica, Università degli Studi di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
7
Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, Vicolo dell’Osservatorio 3, 35122 Padova, Italy
8
INAF-Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 2, 35122 Padova, Italy
9
Astronomy Department, University of Wisconsin, 475 N Charter Street, Madison, WI 53706, USA
10
Harvard Center for Astrophysics, 60 Garden Str., 02138 Cambridge, MA, USA
Received:
20
November
2018
Accepted:
19
July
2019
Aims. We aim to study how the velocity segregation and the radial profile of the velocity dispersion depend on the prominence of the brightest cluster galaxies (BCGs).
Methods. We divided a sample of 102 clusters and groups of galaxies into four bins of magnitude gap between the two brightest cluster members. We then computed the velocity segregation in bins of absolute and relative magnitude. Moreover, for each bin of magnitude gap we computed the radial profile of the velocity dispersion.
Results. When using absolute magnitudes, the segregation in velocity is limited to the two brightest bins and no significant difference is found for different magnitude gaps. However, when we use relative magnitudes, a trend appears in the brightest bin: the larger the magnitude gap, the larger the velocity segregation. We also show that this trend is mainly due to the presence, in the brightest bin, of satellite galaxies in systems with small magnitude gaps: in fact, if we study central galaxies and satellites separately, this trend is mitigated and central galaxies are more segregated than satellites for any magnitude gap. A similar result is found in the radial velocity dispersion profiles: a trend is visible in central regions (where the BCGs dominate) but, if we analyse the profile using satellites alone, the trend disappears. In the latter case, the shape of the velocity dispersion profile in the centre of the systems with different magnitude gaps shows three types of behaviour: systems with the smallest magnitude gaps have an almost flat profile from the centre to the external regions; systems with the largest magnitude gaps show a monothonical growth from the low values of the central part to the flat ones in the external regions; and finally, systems with 1.0 < Δm12 ≤ 1.5 show a profile that peaks in the centre and then decreases towards the external regions.
Conclusions. We suggest that two mechanisms could be responsible for the observed differences in the velocity segregation of the BCGs: an earlier formation of systems with a larger magnitude gap or a more centrally concentrated halo. However, the radial profiles of the velocity dispersion confirm that central galaxies are more relaxed, but that the satellite galaxies do not seem to be affected by the magnitude gap.
Key words: galaxies: clusters: general / galaxies: groups: general
© S. Zarattini et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
It is well known that the galaxy population in the field is different from that in clusters. Many authors (Melnick & Sargent 1977; Whitmore et al. 1993, amongst others) have shown that red early-type galaxies are located in the central (denser) regions of nearby galaxy clusters, whereas blue star-forming late-type galaxies are found at larger radii where the density is lower. Dressler (1980) showed that there is a correlation between the fraction of galaxies of different morphological types and the local projected galaxy density. He then concluded that the presence of different morphological types in different regions of the clusters is not dependent on the global conditions related to the environment of the cluster, but that it is more connected with the local clustering. However, Sanroma & Salvador-Sole (1990) showed that this morphological trend is driven by the projected radius and not by the surface density.
A phenomenon that is related to this spatial segregation of galaxies is their segregation in the velocity space. The study of this latter segregation requires a greater observational effort, since deep spectroscopy is needed. However, various studies have been conducted on this topic and significant differences in the velocity distribution are found for different galaxy populations. As an example, a difference in velocity dispersion measures using red and passive galaxies or blue star-forming galaxies in clusters was found by many authors (Moss & Dickens 1977; Sodre et al. 1989; Biviano et al. 1992, 1996, 1997; Scodeggio et al. 1995; Goto 2005; Sánchez-Janssen et al. 2008). Another type of known segregation is that of massive and luminous galaxies, which are found to be segregated in velocity with respect to smaller and fainter galaxies. This effect was reported for the first time by Rood & Turnrose (1968) and then further analysed by other authors (e.g. Biviano et al. 1992, and references therein). These authors showed that only the most luminous galaxies are segregated and that brighter galaxies have lower velocities. The result was confirmed more recently by Adami et al. (1998), Girardi et al. (2003), Goto (2005), and Ribeiro et al. (2013) and it is generally explained by invoking physical processes that are able to transfer the kinetic energy of galaxies mainly to the dark matter (DM) particles. The process responsible for this effect is usually identified with dynamical friction (Chandrasekhar 1943; Sarazin 1986): a massive galaxy that is falling into a cluster interacts with other, smaller galaxies. The smaller galaxies gain energy and momentum in the interaction at the expense of the massive galaxy. Moreover, the falling galaxy suffers a dynamical friction from the DM halo of the cluster. On the contrary, the process of violent relaxation is expected to produce a velocity distribution that is independent of galaxy mass (Lynden-Bell 1967).
The existence of velocity segregation in galaxy clusters was also considered as a sign of dynamical evolution (Coziol et al. 2009). In fact, dynamical friction requires a long time to produce its effect on the more massive galaxies. However, Skibba et al. (2011) showed that between 25% and 40% of the brightest galaxies are satellites rather than central. We already showed (Zarattini et al. 2016; hereafter Paper VII) that the majority of the brightest cluster galaxies (BCGs) located in fossil groups (FGs) seem to lie at the centre of the potential well, not showing a significant peculiar velocity, a result recently confirmed by Gozaliasl et al. (2019). This could be interpreted as velocity segregation, but to really address this issue we also have to study the peculiar velocities of satellite galaxies. In addition, as in Zarattini et al. (2015; hereafter Paper V), we now have enough statistics to understand if there is a dependence between the magnitude gap and the velocity segregation of galaxies.
Moreover, we also focus our attention on how the radial velocity dispersion profiles vary with the magnitude gap. These profiles, together with the projected number density and mass profiles, are able to provide hints on the type of orbits that dominate a cluster (Biviano & Katgert 2004; Aguerri et al. 2017). In the context of this work, we are interested in studying whether or not different orbits are found in systems with different magnitude gaps. Biviano & Katgert (2004) showed that the velocity dispersion profiles can be distinct for different galaxy populations: early-type galaxies show a decreasing radial profile towards the centre of the clusters, whereas late-type galaxies show a clear increase in the centre. This is supposed to be connected with different types of orbits: isotropic for early-type galaxies and more radial for late-type ones. Recently, Aguerri et al. (2017) also confirmed that there is a segregation of orbits depending on the luminosity of galaxies: more luminous galaxies are in less radial orbits than fainter galaxies. A similar orbital difference for galaxies of different mass was found by Annunziatella et al. (2016), but in only the inner regions of clusters.
This work is part of the Fossil Group Origins (FOGO) project, a program presented in Aguerri et al. (2011) in which we studied different aspects of FGs, a particular type of galaxy aggregation dominated at optical wavelengths by a massive and luminous central galaxy, at least two magnitudes brighter than the second brightest member in the r-band (Δm12 ≥ 2). The detailed study of the sample was presented in Zarattini et al. (2014; hereafter Paper IV). The project studied the properties of the BCGs in FGs (Méndez-Abreu et al. 2012), the X-ray-versus-optical scaling relations (Girardi et al. 2014), the global X-ray scaling relations (Kundert et al. 2017; hereafter Paper VI), the dependence of the luminosity function on the magnitude gap (Paper V), the presence of substructures in FGs (Paper VII), and the stellar populations in FG BCGs (Corsini et al. 2018). Moreover, we presented the case of a transitional fossil system in Aguerri et al. (2018).
The present paper is structured as follows: in Sect. 2 we present the sample used for this work, in Sect. 3 we present the results on both the velocity segregation and the radial velocity dispersion profiles, in Sect. 4 we discuss the results, and in Sect. 5 we draw our conclusions.
The cosmology adopted in this paper, as in the rest of the FOGO papers, is H0 = 70 km s−1 Mpc−1, ΩΛ = 0.7, and ΩM = 0.3.
2. Sample
We build our sample by combining two different datasets, as done for the study of the dependence of the luminosity function on the magnitude gap (Paper V). In the first sample (hereafter S1) we have the 34 FG candidates proposed by Santos et al. (2007) and analysed by the FOGO team in Paper IV. The spectroscopic completeness of the S1 sample is more than 70% down to mr = 17 and more than 50% down to mr = 18. For the S1 sample we have a total of 1244 available velocities (26 clusters), of which 579 turned out to be members of the respective cluster. We refer the reader to Paper IV for detailed information of the S1 sample. We were able to confirm that 15 out of 34 are genuine FGs, 7 are non-FGs, and the other 12 remain to be confirmed. We defined as “genuine fossil” a group or cluster of galaxies that adheres to one of the two following definitions: (i) it has a magnitude gap of at least two magnitudes between its 2 brightest member galaxies (Δm12 ≥ 2) in the r band within half the virial radius, or (ii) it has a magnitude gap of at least 2.5 mag between the first and the fourth brightest members (Δm14 ≥ 2.5) in the r band within half the virial radius (see Paper IV for details). For this work we use only systems with z ≤ 0.25. This cut in redshift allows us to reach the dwarf regime in all the clusters. After its application the number of clusters in the S1 sample reduces to 26. In this sample, the BCGs are the starting point for the selection of the sample and are taken from the Sloan Digital Sky Survey (SDSS) luminous red galaxies sample. Details on the selection criteria can be found in Santos et al. (2007). The median mass of clusters in the S1 sample, computed from the line-of-sight velocity dispersion using Eq. (1) from Munari et al. (2013), is log M200 = 14.21 ± 0.42 dex.
The S1 sample is biased towards systems with large magnitude gaps, since it was selected to find new FGs. In particular, the mean value of the Δm12 parameter is Δm12 ∼ 1.5 and only four systems have Δm12 ≤ 0.5. We therefore add a second sample (hereafter S2) taken from Aguerri et al. (2007). These systems were selected as clusters with z ≤ 0.1 from the catalogues of Zwicky et al. (1961), Abell et al. (1989), Voges et al. (1999), and Böhringer et al. (2000). They were observed in the SDSS Data Release 4 (SDSS-DR4; Adelman-McCarthy et al. 2006). The S2 sample consists of 88 clusters, but we only used those whose Δm12 was spectroscopically confirmed. This criterion reduced the number of systems in the S2 sample to 76, with a mean Δm12 ∼ 0.7. The spectroscopic completeness of the S2 sample is more than 85% down to mr = 17 and more than 60% down to mr = 18. In the S2 sample, there are a total of 5977 velocities available, of which 3886 turned out to be members. In S2, the centre of the cluster was determined using the peak of the X-ray emission (when available) or the peak of the galaxy distribution. The BCG was then selected to be the brightest galaxy of the central region. The mean difference between the centre of the cluster and the selected BCG is 150 kpc (see Aguerri et al. 2007, for details). The median mass of clusters in the S2 sample, computed as for S1, is log M200 = 14.27 ± 0.37 dex. A detailed comparison between S1 and S2 was presented in Paper V and references therein. The number of clusters obtained by combining S1+S2 and applying the described cut in redshift is thus 102. We stress that these are exactly the same systems used in Paper V and that there is no intersection between the two samples.
3. Results
In this section we present the results of the study of the dependence of the velocity segregation (Sect. 3.1) and of the velocity dispersion profile (Sect. 3.2) on the magnitude gap.
3.1. Dependence of the velocity segregation on the magnitude gap
Following what we did in Paper V, we divide our sample of 102 clusters and groups in four subsamples of different Δm12. In particular, the first subsample includes all clusters with Δm12 ≤ 0.5, the second one those with 0.5 < Δm12 ≤ 1.0, the third subsample those with 1.0 < Δm12 ≤ 1.5, and finally the last subsample has all the systems with Δm12 > 1.5. According to this division, we have 31, 24, 26, and 21 systems in the first, second, third, and fourth subsamples, respectively. The values of the magnitude gaps used to divide the sample are arbitrary and chosen to have more that 20 systems per bin in order to obtain robust statistical results. The median velocity dispersion of the four different subsamples are 557 ± 171 km s−1, 617 ± 159 km s−1, 587 ± 200 km s−1, and 545 ± 206 km s−1, respectively. The corresponding median M200 masses (given in logarithmic units) are 14.27 ± 0.38 dex, 14.40 ± 0.35 dex, 14.33 ± 0.40 dex, and 14.21 ± 0.48 dex.
For each member galaxy, we have a velocity that comes from our own spectroscopy or SDSS and magnitudes from SDSS-DR7. In particular, throughout the paper we use the model magnitude in the r band and all absolute magnitudes are K-corrected following Chilingarian et al. (2010).
For each cluster of the S1 sample, R200 was obtained from X-ray data and members were selected using a two-step procedure applied to the galaxies in the region within R200. First, we used DEDICA (Pisani 1993, 1996), which is an adaptive kernel procedure that works under the assumption that a cluster corresponds to a local maximum in the density of galaxies. We then adopted the likelihood ratio test (Materne 1979) to assign a membership probability to each single galaxy relative to an identified cluster. The details on these procedures are described in Paper IV. For the clusters in the S2 samples, Aguerri et al. (2007) also adopted a two-step procedure in which the first step was the gapping procedure proposed by Zabludoff et al. (1990). They also applied the KMM algorithm (Ashman et al. 1994) to estimate the statistical significance of bi-modality in the main peak identified in the first step. Once the members of the clusters are identified, they are used to compute the value of R200 for each cluster. Details of this procedure can be found in Aguerri et al. (2007). The two procedures applied to the S1 and S2 samples are robust to interlopers, thus granting a reliable measure of the cluster global properties. Once R200 and member galaxies were known, we computed the distance of each galaxy from the centre of the cluster (defined as the BCG position), which was used to compute the velocity dispersion profile in Sect. 3.2.
The velocity segregation is computed in bins of absolute magnitude. For each galaxy we compute its normalised velocity as
where vgal is the recessional velocity of the galaxy itself, whereas vc and σc are the mean velocity and the velocity dispersion of the corresponding cluster computed within at least 0.5 R200 and after removing velocity interlopers (see Zarattini et al. 2014, for details). Subsequently, for each absolute-magnitude bin we compute the mean value of the normalised velocity for all the clusters that have at least a galaxy with the required magnitude.
We present in Fig. 1 the dependence of the velocity segregation on magnitude gap. The plot is computed using all galaxies within the virial radius. It can be seen that the segregation in velocity appears only in the two most luminous magnitude bins. No significant trend appears with the magnitude gap, although the systems with the larger gaps seem to show a larger segregation. It is worth noting that clusters with Δm12 ≤ 0.5 do not have galaxies in the brightest magnitude bin (e.g. no galaxies with −24.5 ≤ r ≤ −23.5). The Spearman rank correlation test confirms that a correlation is present in each of the four subsamples. Moreover, in order to assess the significance of the segregation, we shuffle the magnitude gaps among the four subsamples 100 times and recompute vnorm(Mr > −23)−vnorm(Mr < −23) for each case. We find that in only 10% of the cases is the velocity segregation as high as the one found for the Δm12 > 1.5 subsample.
 |
Fig. 1. Dependence of the velocity segregation on luminosity in bins of the magnitude gap for galaxies within R200. We show with black filled squares those clusters with Δm12 ≤ 0.5, with red filled hourglasses those with 0.5 < Δm12 ≤ 1.0, with violet filled bow ties those with 1.0 < Δm12 ≤ 1.5, and with green filled circles those systems with Δm12 ≥ 1.5. The error bars show the uncertainties of the mean, computed as the standard deviation of the normalised velocity divided by the square root of the total number of galaxies in each absolute-magnitude bin. |
As we did in Paper V, we compute also the relative velocity segregation by subtracting the magnitude of the central galaxy to all the magnitudes. As a result, all the BCGs are located in the same bin, independently of their magnitude and on the mass of their hosting group or cluster. This is useful when comparing objects with different masses as clusters and groups in order to highlight differences that originate directly from the magnitude gap. In fact, as we showed in Paper V, the central galaxies of groups are fainter than those of clusters and they can lie in a region where there are a lot of intermediate-mass galaxies in clusters. For this reason, in Fig. 1 the impact of the magnitude gap can be mitigated.
We present the relative velocity segregation in Fig. 2. In the top left panel, we show the result obtained within R200: the color code is the same as in Fig. 1 and we can see that the segregation in velocity seems to be limited to galaxies that are as bright as the BCGs. Moreover, it seems that there can be a trend in the first magnitude bin: here galaxies located in clusters with larger magnitude gaps seem to be more segregated. However, the trend is not strong. We then compute the same quantities within 0.5 R200 and show the results in the top right panel of Fig. 2. Now the trend with magnitude gap is stronger because the magnitude gap is computed for galaxies within 0.5 R200, while in the left panels we include also galaxies out to R200. This suggests that it is possible that other galaxies as bright as the BCGs can be found at distances larger that 0.5 R200, not affecting the magnitude gap but affecting the observed segregation. The trend shows that the larger the gap, the more segregated the (central) galaxies in velocity. As we found for the LFs, there is a statistical difference larger that 3σ between the two most extreme cases (namely, Δm12 ≤ 0.5 and Δm12 > 1.5), with the other two magnitude-gap bins located in the middle and following the trend set by the magnitude gap itself.
 |
Fig. 2. Dependence of the velocity segregation with the magnitude gap obtained using relative magnitudes. Top left panel: result obtained with all the galaxies within 1 R200, whereas in top right panel we use only galaxies within 0.5 R200. Lower panels: same results, but separating central galaxies (filled stars) from satellites. The remaining symbols and color code are the same as in Fig. 1. |
Again, as we did for Fig. 1, we compute the difference in velocity between the two brightest bins for the subsample of clusters with Δm12 ≥ 1.5. This difference is the largest that we found (in Fig. 2, this is the difference between the two leftmost green points in the top-right panel) and it is measured to be 0.6. We then shuffle the magnitude gap of each cluster 100 times, recomputing the resulting relative velocity segregation for the four subsamples (that have no relation with the magnitude gap at this point) each time. Thus, for each subsample we compute the velocity segregation for the first two bins and compare it with our reference value, finding that the new values are never larger than 0.6.
We also show the same results in the two lower panels of Fig. 2, but splitting the galaxy population of each cluster in two components: the BCGs and the satellite galaxies. The two most interesting results in these panels are that (i) the trend in the first magnitude bin is still visible, although it is weaker and limited to BCGs alone, and that (ii) satellites do not seem to suffer from velocity segregation, independently of their magnitude. In fact, the bottom right panel of Fig. 2 clearly shows that satellite galaxies located in the two brightest magnitude bins have the same normalised velocity as satellite galaxies in the fainter magnitude bins. On the other hand, when comparing the top and bottom panels it can be seen that the velocity segregation in the brightest magnitude bin is stronger when using only BCGs (bottom panels) than when satellites are also included. This is particularly evident for the first subsample, where massive satellites can be found in the brightest bin. However, a trend in velocity segregation is also visible in the bottom panels, but it is mitigated, especially within 0.5 R200.
3.2. Dependence of the velocity dispersion profile on the magnitude gap
We also study the cumulative and differential velocity dispersion profiles, 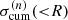 and
and 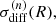 respectively, in the different magnitude-gap bins. The differential quantities are computed at R = 0.025 R200, R = 0.05 R200, R = 0.1 R200, R = 0.2 R200, R = 0.5 R200, and R = 1 R200. The cited quantities and the 68% uncertainties are computed using the biweight estimator of the ROSTAT package (Beers et al. 1990).
respectively, in the different magnitude-gap bins. The differential quantities are computed at R = 0.025 R200, R = 0.05 R200, R = 0.1 R200, R = 0.2 R200, R = 0.5 R200, and R = 1 R200. The cited quantities and the 68% uncertainties are computed using the biweight estimator of the ROSTAT package (Beers et al. 1990).
Figure 3 presents the results. A trend seems to appear in the very central part: the clusters with the largest Δm12 have a lower value of velocity dispersion in the centre. However, the trend is not as clear as it was for the velocity segregation, because clusters with 1.0 < Δm12 ≤ 1.5 have a small velocity dispersion in the centre, which roughly triples at 0.07 R200. A difference remains in the two most-extreme cases. It can be seen that at large radii all the velocity dispersion profiles become flatter at a value that is close to unity, which is the value of the velocity dispersion computed using all the galaxies in the sample. However, the way in which the different subsamples selected using the magnitude gap reach this limit is different: clusters with Δm12 ≤ 0.5 reach it faster and the “jump” between the most central values and the plateau is smaller than that of clusters with Δm12 > 1.5. It is worth noting that the first (left-most) points of Fig. 3 confirm the results presented in Fig. 2 for the BCGs.
 |
Fig. 3. Cumulative (upper panel) and differential (lower panel) velocity dispersion profiles for clusters in different magnitude-gap bins. The colour code is the same as in Fig. 1 and shaded areas represent 1σ uncertainties. The small vertical lines represent the radii at which the differential quantities are computed. |
In Fig. 4 we show the same analysis, but for satellite galaxies only. Here the trend disappears and we can identify three different behaviours: systems in which also the satellite galaxies have a small velocity dispersion in the centre of the clusters (clusters with 0.5 < Δm12 ≤ 1.0 and Δm12 > 1.5), systems with an almost flat profile (Δm12 ≤ 0.5), and systems with a higher velocity dispersion in the centre than in the more external parts (clusters with 1 < Δm12 ≤ 1.5).
4. Discussion
We show in Sect. 2 that there is a dependence of the velocity segregation on the magnitude gap. In particular, there is a trend for systems with larger magnitude gaps to have more highly segregated bright galaxies. Moreover, the segregation is clearly limited to the central galaxies alone. These two results suggest that there is some connection between the magnitude gap and the consequences it has on the evolution of the BCGs, but that this connection does not affect satellite galaxies. A possible explanation is that the DM halos in systems with larger magnitude gaps are found to be more centrally concentrated (D’Onghia et al. 2005; von Benda-Beckmann et al. 2008; Ragagnin et al. 2019). Those halos can thus create a deeper potential well, able to enhance the dynamical friction with the central galaxy. In fact, it is known (e.g. Adhikari et al. 2016) that a DM subhalo orbiting inside a larger halo will experience dynamical friction due to the density of DM particles in the host halo, with a rate of
In this equation, M is the mass of the subhalo, v is its relative velocity with respect to the host, ρ is the local density of the host halo, and f(v|σ) is the fraction of field particles with velocity less than |v|. The result is that a massive halo going through a more centrally concentrated host should experience a stronger deceleration and it would end at the bottom of the potential well in a shorter time than the same halo in a sparser host (see also Jiang et al. 2008).
A similar argument can be used if systems with large magnitude gaps form at an earlier epoch than systems with smaller magnitude gaps. In fact, in this case the former would have more time to slow down the central galaxies, without the need to assume more centrally concentrated DM halos. This early formation was predicted using hydrodynamical simulations by D’Onghia et al. (2005) and von Benda-Beckmann et al. (2008), but more recent simulations question this point. In particular, in Paper VI we showed, using the Illustris cosmological hydrodynamical simulation, that the early mass-assembly history of fossil systems (e.g. systems with Δm12 ≥ 2) is the same as for non-fossil systems. Differences rise at z < 0.4, when fossil systems stop accreting galaxies and have enough time to merge the big satellites into their BCG, thus creating the gap. In particular, using semi-analytical modelling, Farhang et al. (2017) noticed that FGs evolve faster than non-FGs in the redshift range 0.4 > z > 0.1 and they then evolve as non-FGs from z = 0.1. On the other hand, it is worth noting that our results seem to confirm that systems with small gaps could be cluster mergers as suggested for example by Trevisan & Mamon (2017).
Recently, Barsanti et al. (2016) studied a sample of 41 clusters in the range 0.4 ≤ z ≤ 1.5 and looked for luminosity segregation in velocity space. These latter authors found evidence of segregation for all those galaxies brighter than the third most luminous galaxy in each cluster. Moreover, they found that the more luminous the galaxy, the lower its velocity. This result is also in agreement with that reported for a local sample by Biviano et al. (1992). Our systems are divided into magnitude gap bins and the growing of the gap can also affect velocity segregation: in fact, the larger the gap, the more luminous (and massive) the BCG and, as a consequence, the more segregated the BCG should be in velocity. However, our findings show that only the BCGs are strongly segregated in velocity. No hints are found that bright and massive satellites suffer velocity segregation.
Unfortunately, the result of the dependence of the velocity segregation on the magnitude gap is not able to favour one of the two scenarios proposed in the last paragraph with respect to the other. Thus, we also study the radial velocity dispersion profile in order to obtain more information and try to find reasons to favour one of the previous scenarios over the other. From a theoretical point of view, the computation of the “inverted” Jeans equation, which is used to compute the velocity-anisotropy profile (see Biviano & Katgert 2004, for details), depends on the number density of galaxies, the mass, and velocity dispersion profiles. Therefore, assuming the same mass profile for all the clusters, the observed differences in the velocity dispersion profiles can depend on the spatial distribution, on different orbits of galaxies, or on different dark matter concentration.
We then compute the spatial distribution of galaxies in the four subsamples and present the result in Fig. 5. There seems to be a small trend in which objects with larger Δm12 have steeper galaxy densities. However, the individual points for the different subsamples are all in agreement within the uncertainties and we also perform a linear fit to the spatial distribution of the different subsamples, finding no differences in the slopes at 1σ level. We also calculate the cluster number concentration for our four subsamples. To do so, we firstly compute the radial completeness profiles for each cluster separately. These were obtained by selecting all galaxies with and without redshift in the chosen magnitude range (the upper quartile of the magnitude distribution of members), binning the two in radii, and calculating the number ratio in each bin. We then assign to each member galaxy the completeness value that corresponds to the radial bin that includes the galaxy itself. Subsequently, we stack the clusters according to their Δm12 and we fit a projected Navarro–Frenk–White profile (NFW; Navarro et al. 1997) to the stacked profiles, taking the radial completeness correction into account. The fits are done out to R200, since at larger radii not all the clusters contribute. The concentrations that we find are c1 = 2.0 ± 0.1, c2 = 2.1 ± 0.2, c3 = 1.9 ± 0.2, and c4 = 2.5 ± 0.4 for the four subsamples of different Δm12. These values are quite low compared to theoretical predictions for the concentration of DM, also considering that Biviano et al. (2017) found that galaxies and DM concentrations are similar for nearby clusters. On the other hand, the values we find are in relatively close agreement with other observational works, like Lin et al. (2004; c = 2.9 ± 0.2), Van der Burg et al. (2015; c = 2.03 ± 0.2), and references therein. Although the DM concentrations we found for our four subsamples are compatible with one another, it is worth noting that systems with larger mass seem to have higher concentrations. This result was already found in Farhang et al. (2017): in particular, in their Fig. 8, they show that systems with a large magnitude gap have a systematically higher concentration than their control sample.
 |
Fig. 5. Surface density profiles of galaxies in the different subsamples. The colour code is the same as in Fig. 1. |
We can therefore conclude that the spatial distribution of galaxies does not strongly depend on Δm12. As a consequence, the observed differences in the velocity dispersion profiles should reflect different orbits. This is in agreement with earlier findings by Girardi & Mezzetti (2001), who showed that a peak in the velocity dispersion profile is expected when moderate radial orbits are included, and Biviano & Katgert (2004) who demonstrated that the central peak can be generated by the presence of late-type galaxies, whereas the profiles of bright ellipticals showed a clear decrease toward the centre.
This theoretical framework, in which differences in the velocity dispersion profiles are connected to different types of orbits, is able to explain in a convincing way the results we found. However, the velocity dispersion profiles of satellite galaxies seem to exclude a link between the orbits and the magnitude gap. In fact, a trend is visible only when including BCGs, whereas it disappears when satellite galaxies alone are analysed. If we compare clusters with the smallest and largest Δm12 alone (the two most-extreme cases), the former clearly show a lower velocity dispersion in the centre. But if we include the two intermediate cases, the situation changes significantly: the clusters with 1.0 < Δm12 ≤ 1.5 show a clear peak in the central part that excludes any possible trend.
It is worth noting that clusters with 1.0 < Δm12 ≤ 1.5 are dominated by Abell 85. This cluster has 257 members and the total number of galaxies used in this magnitude-gap bin is 1042. The second most numerous cluster in the bin is FGS31 with 79 members and the mean number of members per cluster (excluding Abell 85) is 35. The velocity dispersion profile of Abell 85 was already studied in Aguerri et al. (2007) and the authors also found that it peaks in the central part to a value that is larger than that in the external regions. Thus, a possible explanation for the peculiar shape of the velocity dispersion profile for the clusters in the magnitude-gap bin 1.0 < Δm12 ≤ 1.5 is that the subsample is dominated by Abell 85. To test this scenario, we removed this cluster from our sample and recomputed the velocity dispersion profile. The result does not change, meaning that Abell 85 is not the only cluster in this magnitude-gap bin to show this behaviour. We must therefore conclude that the peak in the central part of the velocity dispersion profile is a characteristic of these systems and is not caused by a single peculiar case.
The radial velocity dispersion profile was also analysed by Ribeiro et al. (2010). In particular, they studied a sample of galaxy groups and divided them into two categories: groups with Gaussian velocity distribution (e.g. relaxed) and groups with non-Gaussian velocity distribution (e.g. non relaxed). Non-relaxed clusters were found to have an increasing velocity dispersion profile from the centre to R200, while relaxed clusters were found to have a flat velocity dispersion profile in the same radial range. On the other hand, Cava et al. (2017) found the opposite result, the velocity dispersion profiles of irregular clusters declines from the centre to R200 more rapidly than that of regular ones. The velocity dispersion profile of the systems in our sample with largest magnitude gaps also show an increasing trend from the centre but only out to 0.2 * R200. Thus, the similarity with the results of Ribeiro et al. (2010) for the irregular clusters is only apparent (compare our Fig. 3 with their Fig. 2) and it would be erroneous to conclude from this similarity that our large magnitude-gap systems are irregulars. As a matter of fact we showed in Paper VII of this series that the fraction of systems with substructures (i.e. irregular systems) is the same in fossil and non-fossil samples.
5. Conclusions
We divide a sample of 102 clusters and groups of galaxies into four bins of magnitude gap (Δm12) in order to study the dependence of the velocity segregation of their galaxies and of their radial velocity dispersion profiles on the Δm12 parameter. The results we find can be summarised as follows:
-
Velocity segregation only appears in the two brightest bins when it is computed in bins of absolute magnitudes.
-
Velocity segregation only appears in the brightest bin of relative magnitudes.
-
Velocity segregation is limited to central galaxies alone. Satellite galaxies show no segregation independently of their magnitude and of the magnitude gap of their host cluster.
-
The radial profile of the velocity dispersion shows a trend in the central part with the magnitude gap. Furthermore, the larger the magnitude gap, the smaller the velocity dispersion at the centre.
-
The differences in the radial profiles are concentrated within 0.15 R200. At larger radii, no significant difference is found.
-
The trend disappears if we exclude the BCGs from the computation of the radial profile of the velocity dispersion. This means that the trend is due to central galaxies alone.
-
A different behaviour appears in the central part of the profiles computed with satellites alone for clusters with 1.0 < Δm12 ≤ 1.5: the central velocity dispersion is higher in the centre than at large radii, whereas all other systems show an almost monotonic growth.
These results show that there is a link between the magnitude gap of the hosting cluster and its central galaxy, but on the other hand the satellite population seems to show peculiar behaviours not linked to the gap itself. For the BCGs the difference could lie in an earlier formation epoch of the host halo as well as in a more centrally concentrated halo of the host cluster. These scenarios could favour the relaxation of the central galaxy in the centre of the potential well, because they offer a way to accelerate this process: a longer time for dynamical friction to act (in the former scenarios) or a stronger drag due to a larger amount of mass located in the very centre of the cluster halo (latter scenario). On the other hand, the differences in the satellite population could originate from different orbits. We plan to study the orbits of galaxies in FGs in a forthcoming paper of this series.
Acknowledgments
We would like to thank the referee, Gary Mamon, for his suggestions that helped us to improve the way we present our results. The research leading to these results received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n. 340519. Moreover, SZ acknowledges financial support from the University of Trieste through the program “Finanziamento di Ateneo per progetti di ricerca scientifica (FRA2015)” and from the grant PRIN INAF2014-1.05.01.94.02. J. A. L. A. thanks the support from the Spanish Ministerio de Economia y Competitividad (MINECO) through the grant AYA2013-43188-P. EMC acknowledges financial support from Padua University through grants DOR1699945, DOR1715817, DOR1885254, and BIRD164402. ED acknowledges the hospitality of the Institute for Theory and Computation (ITC) at Harvard University, where part of this work has been completed.
References
- Abell, G. O., Corwin, Jr., H. G., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adami, C., Biviano, A., & Mazure, A. 1998, A&A, 331, 439 [NASA ADS] [Google Scholar]
- Adelman-McCarthy, J. K., Agüeros, M. A., Allam, S. S., et al. 2006, ApJS, 162, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Adhikari, S., Dalal, N., & Clampitt, J. 2016, JCAP, 2016, 022 [CrossRef] [Google Scholar]
- Aguerri, J. A. L., Sánchez-Janssen, R., & Muñoz-Tuñón, C. 2007, A&A, 471, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguerri, J. A. L., Girardi, M., Boschin, W., et al. 2011, A&A, 527, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguerri, J. A. L., Agulli, I., Diaferio, A., & Dalla Vecchia, C. 2017, MNRAS, 468, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Aguerri, J. A. L., Longobardi, A., Zarattini, S., et al. 2018, A&A, 609, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Annunziatella, M., Mercurio, A., Biviano, A., et al. 2016, A&A, 585, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] [Google Scholar]
- Barsanti, S., Girardi, M., Biviano, A., et al. 2016, A&A, 595, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Biviano, A., & Katgert, P. 2004, A&A, 424, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1992, ApJ, 396, 35 [CrossRef] [Google Scholar]
- Biviano, A., Durret, F., Gerbal, D., et al. 1996, A&A, 311, 95 [NASA ADS] [Google Scholar]
- Biviano, A., Katgert, P., Mazure, A., et al. 1997, A&A, 321, 84 [NASA ADS] [Google Scholar]
- Biviano, A., Moretti, A., Paccagnella, A., et al. 2017, A&A, 607, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Cava, A., Biviano, A., Mamon, G. A., et al. 2017, A&A, 606, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1943, ApJ, 97, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Chilingarian, I. V., Melchior, A.-L., & Zolotukhin, I. Y. 2010, MNRAS, 405, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Corsini, E. M., Morelli, L., Zarattini, S., et al. 2018, A&A, 618, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coziol, R., Andernach, H., Caretta, C. A., Alamo- Martínez, K. A., & Tago, E. 2009, AJ, 137, 4795 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Sommer-Larsen, J., Romeo, A. D., et al. 2005, ApJ, 630, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Farhang, A., Khosroshahi, H. G., Mamon, G. A., Dariush, A. A., & Raouf, M. 2017, ApJ, 840, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., & Mezzetti, M. 2001, ApJ, 548, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Rigoni, E., Mardirossian, F., & Mezzetti, M. 2003, A&A, 406, 403 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Girardi, M., Aguerri, J. A. L., De Grandi, S., et al. 2014, A&A, 565, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goto, T. 2005, MNRAS, 359, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Gozaliasl, G., Finoguenov, A., Tanaka, M., et al. 2019, MNRAS, 483, 3545 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, C. Y., Jing, Y. P., Faltenbacher, A., Lin, W. P., & Li, C. 2008, ApJ, 675, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Kundert, A., D’Onghia, E., & Aguerri, J. A. L. 2017, ApJ, 845, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-T., Mohr, J. J., & Stanford, S. A. 2004, ApJ, 610, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Materne, J. 1979, A&A, 74, 235 [NASA ADS] [Google Scholar]
- Melnick, J., & Sargent, W. L. W. 1977, ApJ, 215, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Barrena, R., et al. 2012, A&A, 537, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, C., & Dickens, R. J. 1977, MNRAS, 178, 701 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, E., Biviano, A., Borgani, S., Murante, G., & Fabjan, D. 2013, MNRAS, 430, 2638 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] [Google Scholar]
- Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Ragagnin, A., Dolag, K., Moscardini, L., Biviano, A., & D’Onofrio, M. 2019, MNRAS, 486, 4001 [NASA ADS] [CrossRef] [Google Scholar]
- Ribeiro, A. L. B., Lopes, P. A. A., & Trevisan, M. 2010, MNRAS, 409, L124 [NASA ADS] [Google Scholar]
- Ribeiro, A. L. B., Lopes, P. A. A., & Rembold, S. B. 2013, A&A, 556, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rood, H. J., & Turnrose, B. E. 1968, ApJ, 152, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Janssen, R., Aguerri, J. A. L., & Muñoz- Tuñón, C. 2008, ApJ, 679, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Sanroma, M., & Salvador-Sole, E. 1990, ApJ, 360, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, W. A., Mendes de Oliveira, C., & Sodré, Jr., L. 2007, AJ, 134, 1551 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1986, Rev. Mod. Phys., 58, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Solanes, J. M., Giovanelli, R., & Haynes, M. P. 1995, ApJ, 444, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., van den Bosch, F. C., Yang, X., et al. 2011, MNRAS, 410, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Sodre, Jr., L., Capelato, H. V., Steiner, J. E., & Mazure, A. 1989, AJ, 97, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Trevisan, M., & Mamon, G. A. 2017, MNRAS, 471, 2022 [NASA ADS] [CrossRef] [Google Scholar]
- Van der Burg, R. F. J., Hoekstra, H., Muzzin, A., et al. 2015, A&A, 577, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- von Benda-Beckmann, A. M., D’Onghia, E., Gottlöber, S., et al. 2008, MNRAS, 386, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmore, B. C., Gilmore, D. M., & Jones, C. 1993, ApJ, 407, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., Huchra, J. P., & Geller, M. J. 1990, ApJS, 74, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zarattini, S., Barrena, R., Girardi, M., et al. 2014, A&A, 565, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zarattini, S., Aguerri, J. A. L., Sánchez-Janssen, R., et al. 2015, A&A, 581, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zarattini, S., Girardi, M., Aguerri, J. A. L., et al. 2016, A&A, 586, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwicky, F., Herzog, E., Wild, P., Karpowicz, M., & Kowal, C. T. 1961, Catalogue of Galaxies and of Clusters of Galaxies, Vol. I (Pasadena: California Institute of Technology) [Google Scholar]
All Figures
 |
Fig. 1. Dependence of the velocity segregation on luminosity in bins of the magnitude gap for galaxies within R200. We show with black filled squares those clusters with Δm12 ≤ 0.5, with red filled hourglasses those with 0.5 < Δm12 ≤ 1.0, with violet filled bow ties those with 1.0 < Δm12 ≤ 1.5, and with green filled circles those systems with Δm12 ≥ 1.5. The error bars show the uncertainties of the mean, computed as the standard deviation of the normalised velocity divided by the square root of the total number of galaxies in each absolute-magnitude bin. |
| In the text | |
 |
Fig. 2. Dependence of the velocity segregation with the magnitude gap obtained using relative magnitudes. Top left panel: result obtained with all the galaxies within 1 R200, whereas in top right panel we use only galaxies within 0.5 R200. Lower panels: same results, but separating central galaxies (filled stars) from satellites. The remaining symbols and color code are the same as in Fig. 1. |
| In the text | |
 |
Fig. 3. Cumulative (upper panel) and differential (lower panel) velocity dispersion profiles for clusters in different magnitude-gap bins. The colour code is the same as in Fig. 1 and shaded areas represent 1σ uncertainties. The small vertical lines represent the radii at which the differential quantities are computed. |
| In the text | |
 |
Fig. 4. Same as Fig. 3, but restricted to satellite galaxies. |
| In the text | |
 |
Fig. 5. Surface density profiles of galaxies in the different subsamples. The colour code is the same as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.