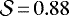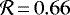| Issue |
A&A
Volume 630, October 2019
Rosetta mission full comet phase results
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935517 | |
| Published online | 20 September 2019 | |
Dynamic field line draping at comet 67P/Churyumov-Gerasimenko during the Rosetta dayside excursion
1
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstr. 6,
8042 Graz, Austria
e-mail: martin.volwerk@oeaw.ac.at
2
Institute for Geophysics and Extraterrestrial Physics, Technische Universität Braunschweig, Braunschweig, Germany
3
Swedish Institute of Space Physics,
Kiruna, Sweden
4
Swedish Institute of Space Physics,
Uppsala, Sweden
5
Laboratoire de Physique et Chimie de l’Environnement et de l’Espace (LPC2E),
Orléans, France
6
South West Research Institute,
San Antonio, USA
Received:
22
March
2019
Accepted:
9
May
2019
Context. The Rosetta dayside excursion took place in September–October 2015 when comet 67P/Churyumov-Gerasimenko (67P/CG) was located at ~1.36 AU from the Sun after it had passed perihelion on 13 August 2015 at ~1.25 AU. At this time, the comet was near its most active period, and its interaction with the solar wind was expected to be at its most intense, with ion pickup and magnetic field line draping. The dayside excursion was planned to move through different regions that were expected upstream of the cometary nucleus, and to possibly detect the location of the bow shock.
Aims. The goal of this study is to describe the dynamic field line draping that takes place around the comet and the plasma processes that are connected to this.
Methods. The data from the full Rosetta Plasma Consortium (RPC) were used to investigate the interaction of solar wind and comet, starting from boxcar-averaged magnetic field data in order to suppress high-frequency noise in the data. Through calculating the cone and clock angle of the magnetic field, we determined the draping pattern of the magnetic field around the nucleus of the comet. Then we studied the particle data in relation to the variations that are observed in the magnetic field.
Results. During the dayside excursion, the magnetic field cone angle changed several times, which means that the magnetic field direction changes from pointing sunward to anti-sunward. This is caused by the changing directions of the interplanetary magnetic field that is transported toward the comet. The cone-angle direction shows that mass-loading of the interplanetary magnetic field of the solar wind leads to dynamic draping. The ion velocity and the magnetic field strength are correlated because the unmagnetized ions are accelerated more (less) strongly by the increasing (decreasing) magnetic field strength. There is an indication of an anticorrelation between the electron density and the magnetic field strength, which might be caused by the magnetized electrons being mirrored out of the strong field regions. The Rosetta RPC has shown that (dynamic) draping also occurs as mildly active comets, as was found at highly active comets such as 1P/Halley and 21P/Giacobini-Zinner, but also that determining both dynamic and nested draping will require a combination of fast flybys and slow excursions for future missions.
Key words: comets: individual: 67P/Churyumov-Gerasimenko / magnetic fields / plasmas / methods: data analysis
© ESO 2019
1 Introduction
Comets are well known for their luminous tails, both the curved dust tail and the ion tail that points radially away from the Sun. It was the behavior of the ion tails that caused Biermann (1951) to posit that corpuscular radiation was required to come from the Sun to accelerate cometary ions. A few years later, Alfvén (1957) used his magnetohydrodynamics (MHD) theory to show that frozen-in magnetic fields in the solar wind would drape themselves around the active cometary nucleus, thereby creating the ion tail. This process has been well studied with flybys of comets 1P/Halley (Riedler et al. 1986; Raeder et al. 1987) and 21P/Giacobini-Zinner (Slavin et al. 1986a,b; Cowley 1987; McComas et al. 1987a,b; Perez-de-Tejada 1990).
With the arrival of Rosetta (Glassmeier et al. 2007a) at comet 67P/Churyumov-Gerasimenko (67P/CG), it became for the first time possible to accompany a comet on its path from the outer solar system (6 August 2014, orbit insertion at ~3.6 astronomical units, AU) through perihelion (13 August 2015 at ~ 1.25 AU) until end of operations (30 September 2016 at ~3.8 AU). Owing to spacecraft operations and instrument limitations, Rosetta mainly stayed in the so-called terminator orbits around comet 67P/CG at distances below 30 km. This allowed a very detailed study of the inner part of interaction region (e.g., Nilsson et al. 2015a; Goetz et al. 2016a; Glassmeier 2017). However, the terminator orbits (i.e., confined to the plane perpendicular to the Sun-comet direction) were not suitable to investigate the large-scale structure of the induced magnetosphere, which is many times larger, as the bow shock (BS) location was expected to be farther away than 1000 km from the nucleus (Koenders et al. 2013).
Fortunately, two far excursions took place during the cometary operations, one in the dayside direction (22 September until 11 October 2015) with comet 67P/CG at ~1.36 AU from the Sun. This is the topic of this paper. Another excursion was made to the nightside (24 March until 10 April 2016) with comet 67P/CG at ~2.7 AU from the Sun, discussed by Volwerk et al. (2018) for the Fluxgate Magnetometer in the Rosetta Plasma Consortium (RPC-MAG) measurements and by Behar et al. (2018) for observations made with the Ion Composition Analyzer (ICA) of the RPC.
Some aspects of the dayside excursion have been discussed in earlier papers. Mandt et al. (2016) studied different plasma regions around comet 67P/CG, and found that two regions are separated by an ion-neutral collisionopause (also referred to as ion exobase): one that characterized by an enhanced electron density in the presence of lesser magnetic field pile up and low-energy water group ions – the inner region – and another characterized by a reduced electron density in the presence of stronger magnetic field pile up and accelerated water-group ions acclerated to energies above 100 eV – the outer region. The location of the collisionopause is estimated to be at about 575 ≤ R ≤ 750 km.
Edberg et al. (2016) used the dayside excursion to investigate the influence of a coronal mass ejection (CME) impacting the induced magnetosphere around comet 67P/CG. They showed that the magnetic field becomes compressed during the impact and that the solar wind ion signature in the plasma instruments, which had disappeared since early May 2015 (at ~1.7 AU from the Sun), returned in the observations. Strong spikes in the magnetic field were identified as flux ropes, possibly created by reconnection in the cometary coma.
One interesting aspect of the dayside excursion is that the BS was not observed in the data (Mandt et al. 2016; Simon Wedlund et al. 2017), indicating that it is farther away than 1500 km from the nucleus (see also Goetz et al. 2017). The reason for this discrepancy between observations and the numerical model may be that the cometary production rate in the numerical model was assumed to be too low. Nilsson et al. (2018a) hypothesized that a shock like structure might be located at a distance of 4000 km from the nucleus. The authors based this on remote observations (from the shock) of ion signatures. However, Gunell et al. (2018) recently reported indications of an “infant bow shock” on 7 March 2015 (at 2.2 AU) and on 24 February 2016 (at 2.4 AU), at which time comet 67P/CG had low activity rate and Rosetta was closer than 100 km, slightly upstream, to the nucleus.
One of the main effects of an active comet in the solar wind is mass-loading through ionization of the outgassed neutrals from the cometary nucleus, the slowing-down of the solar wind through momentum conservation, and eventually, the draping of the solar wind magnetic field around the cometary nucleus (Biermann 1951; Alfvén 1957). This draping changes the direction of the magnetic field from the average Parker spiral (Parker 1958) toward a more radial direction with respect to the Sun. If the interplanetary magnetic field (IMF) changes direction, for example, because it passes a sector boundary, and if the diffusion time of the magnetic field through the plasma environment of the nucleus is long enough, the so-called nested draping can occur (see Riedler et al. 1986; Raeder et al. 1987; Volwerk et al. 2017). The IMF is transported faster than the diffusion, which causes layers of differently oriented magnetic field directions to form an onion-like structure around the nucleus. This can well be observed with a snapshot (i.e., a very fast flyby) of the magnetic environment around the comet, as was done by VEGA 1 (Riedler et al. 1986) and Giotto (Raeder et al. 1987) at comet 1P/Halley.
During the Rosetta mission, however, it was found that the magnetic field line draping at a mildly active comet behaves differently at small distances (≲50 km) than was observed at comet 1P/Halley, for instance. Because of the mass-loading close to the comet, the solar wind is deflected in the direction opposite to the convectional electric field (Broiles et al. 2015). The magnetic field is pulled along with the deflected solar wind and thereby drapes in the Z-direction perpendicular to the equatorial plane in which the draping usually is found (Koenders et al. 2016).
The Rosetta dayside excursion, up to 1500 km away from the nucleus, is an excellent opportunity to study the dynamics of field line draping around a mildly active comet. The slow speed of the spacecraft (~ 1 m s−1) will allow us to observe the decelerated solar wind, IMF, and any boundaries to pass over it, thereby giving a clear view of the dynamics of field line draping.
In this paper the large-scale structure of the magnetic field and the associated plasma behavior are studied during the dayside excursion. First the data of all RPC (Carr et al. 2007) instruments are presented, then the field line draping is studied together with the dynamic features that were observed. Then the connection between the magnetic field and the ions and electrons is studied, with a discussion and conclusions at the end.
2 Data
The observations of the full RPC (Carr et al. 2007), that is, the MAG (Glassmeier et al. 2007b), the ICA (Nilsson et al. 2007), the Langmuir Probe intercalibrated with the Mutual Impedance Probe (LAP and MIP; Eriksson et al. 2006; Trotignon et al. 2006) and the Ion and Electron Spectrometer (IES; Burch et al. 2006), were used to study the dayside excursion between 22 September and 11 October 2015. The MAG data have been processed and calibrated (Goetz et al. 2016b) and are presented in the cometary solar equatorial (CSEQ)1 coordinate system. These are not the 1 Hz magnetometer data, but are boxcar averaged over 512 s with a shift of 30 s, such that the high-frequency signals are filtered out to focus on the large-scale draping structure of the magnetic field along the dayside excursion. The 512 s, or data points, were chosen for spectral analysis purposes, which is not used in this current paper.
The ICA data have been processed to obtain the density and the bulk velocity under the assumption that all ions are H2O+ (see Behar 2018, for details). As the ICA instrument can work in different modes (low time-resolution full energy spectrum versus high time-resolution for only low-energy channels), there is no continuous monitoring of the bulk velocity vi. The high-resolution data were removed before the analysis in this paper.
The data from IES are mainly used in their time-energy spectrograms for electrons and ions.
The MIP/LAP plasma density was obtained from an intercalibration between MIP density and LAP Sun-comet (S/C) potential measurements, when density is high, as well as between LAP-sweep derived density and the LAP S/C potential, when the density is low. Continuity between the two regimes was ensured. The cross-calibration also took electron temperature variations into account (see, e.g., Heritier et al. 2017; Breuillard et al. 2019).
Figure 1 shows a three-dimensional view of the dayside excursion, with the magnetic field direction plotted along the orbit every hour, and projections onto the three different orthogonal planes. From the projections it is clear that the excursion went onto a ~45° inclined orbit in all of the three planes. This means that the orbit is ideally suited for investigating the field line draping around the comet.
In Fig. 2 we show the magnetic field data from RPC-MAG as well as the radial distance of Rosetta with respect to 67P/CG, the ICA ion velocity and density with the MIP electron density overplotted, the IES electron and ion time-energy spectrograms, and the time-shifted OMNI solar wind data (shifted by six days, determined by the ballistic propagation model developed by Opitz et al. 2009, 2010) and the combined cone angle of Rosetta and the solar wind magnetic field. The two red lines in the figure indicate the time interval that the induced magnetosphere of comet 67P/CG interacted with a CME (Edberg et al. 2016), and the solid black line shows the time at which Rosetta was farthest from the comet and turned around.
 |
Fig. 1 Three-dimensional view of the dayside excursion. In blue we show the orbit of Rosetta, with hourly magnetic field vectors in green. In black we show the orbit projected on the three orthogonal planes. The projections show that the orbit was inclined by ~ 45° in each plane, making it very useful for the investigation of nested draped magnetic fields. |
3 Field line draping
The solar wind magnetic field is draped around the outgassing cometary nucleus (see Alfvén 1957), creating a bilobal magnetotail (see Slavin et al. 1986a). In Fig. 3, adapted from Volwerk et al. (2017), we show a schematic of nested field line draping. The IMF, with changing magnetic field direction, is transported toward the active cometary nucleus. Forcomet 67P/CG, the solar wind plasma may have crossed a bow wave or shock, although there are no direct observations of this structure during the dayside excursion. Putative evidence for the development of a BS, however, was presented by Gunell et al. (2018) during two intervals a few months before and after perihelion. Nilsson et al. (2018a) deduced from ICA ion spectra that there might be a BS at comet 67P/CG as far away as 4000 km.
The orbit of Rosetta is drawn into the schematic, showing that the different magnetic regions along the dayside excursion can be differentiated by looking at the X-component of the magnetic field, which indicates whether the field points sunward or antisunward. Therefore, the cone angle is calculated, defined by
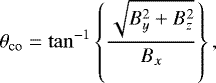 (1)
(1)
where θco = 0° indicates sunward and θco = 180° antisunwardmagnetic field. In Fig. 2J we plot the cone angle as a time-line in blue, together with the cone angle of the IMF shifted by six days. There does not seem to be a common pattern in the two cone angles, which might be caused by the fact that comet 67P/CG was located almost at the far side of the Sun from Earth.
For studying field line draping, it is convenient to consider the cone angle of the magnetic field as defined above in Eq. (1). The result for the dayside excursion is shown in Fig. 4A as a two-dimensional histogram showing the number of data points in bins of 5° in cone angle and 50 km in radial distance of Rosetta from comet 67P/CG. The left panel shows the outbound leg (22 September until 30 September), and the right panel shows the inbound leg of the excursion (1 October until 11 October).
During the outbound leg, Fig. 4A-left, there are three groups of cone angles within R ≤ 400 km at θco ≈ 30°, then there is a jump, and for 400 km ≤ R ≤ 600 km the cone angle is θco ≈ 140°. Then another jump occurs, and from R ≈ 600 km until apoapsis, the cone angle is θco ≈ 60°.
After apoapsis, when Rosetta returned to the comet on the inbound leg, Fig. 4A-right, the cone angle first remains at θco ≈ 60° until a radial distance of R ≈ 1400 km, after which again a jump occurs. Between 700 km ≤ R ≤ 1400 km, the cone angle returns to θco ≈ 130°. At a radial distance of ~700 km, the interaction of the induced magnetosphere of the comet with a CME takes place (the two white lines, Edberg et al. 2016), after which the cone angle again jumps to θco ≈ 50° with a rather large spread. The interaction with the CME most likely leaves the induced magnetosphere disturbed.
These values of the cone angle have to be compared with what would be expected for the undisturbed IMF. This can be done by calculating the angle of the Parker spiral at the location of comet 67P/CG. Parker (1958) gave the angle ΨP as
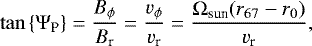 (2)
(2)
where Ωsun = 2.98 × 10−6 rad s−1 is the angular velocity of the Sun, r67 = 2.69 AU is the distance Sun-comet 67P/CG, r0 ≈ 0 is the location of the surface of the Sun, and vr = 400 km s−1 is the nominal radial solar wind velocity. For these nominal values, the Parker spiral angle is ΨP ≈ 71°, represented by the two green horizontal lines in Fig. 4A. It is clear that the cone angles of the magnetic field are well away from these two lines, at lower or higher values, indicating that the field is more toward radially from the Sun, and thereby showing draping characteristics.
4 Magnetic field strength
A piled-up solar wind magnetic field around the nucleus of comet 67P/CG leads to a higher magnetic field strength than the original solar wind field strength of ~3 nT. Figure 4D shows two-dimensional histograms of the magnetic field strength as a function of radial distance.
During the outbound leg Fig. 4D-left, the magnetic field remains rather constant near 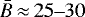 nT, with a slight increase between 800 ≤ R ≤ 1200 km. However, during the inbound leg, Fig. 4D-right, after starting off at the same level as the outbound leg, the field strength increases strongly after Rosetta reaches R ≈ 1100 km, to a value of
nT, with a slight increase between 800 ≤ R ≤ 1200 km. However, during the inbound leg, Fig. 4D-right, after starting off at the same level as the outbound leg, the field strength increases strongly after Rosetta reaches R ≈ 1100 km, to a value of 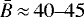 nT, with an extreme of B ≈ 71 nT just around the interaction with the CME. After the CME there is a large spread in field strengths centered around an average field of
nT, with an extreme of B ≈ 71 nT just around the interaction with the CME. After the CME there is a large spread in field strengths centered around an average field of 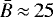 nT. Because of the data handling described above, the maximum field strength mentioned here is much lower than what was presented by Edberg et al. (2016), who showed a maximum value of ~ 200 nT.
nT. Because of the data handling described above, the maximum field strength mentioned here is much lower than what was presented by Edberg et al. (2016), who showed a maximum value of ~ 200 nT.
The boundary at R ≈ 700 km, where the magnetic field reaches its maximum, appears both in the outbound and inbound leg of the dayside excursion, slightly less pronounced in the former. Investigating the plasma properties during the dayside excursion, Mandt et al. (2016) calculated the location of the ion-neutral collisionopause (i.e., where ion-neutral collisions dominate the plasma dynamics, Mendis et al. 1986, 1989) based on measured outgassing rates of the nucleus by MIRO (Gulkis et al. 2007) and a range of collisional cross sections of 2− 8 × 10−15 cm2 (Mendis et al. 1986). The boundary was estimated to be between 143 and 615 km from the nucleus. The observed boundary appeared to be between 540 and 760 km from the nucleus.
This means that while it approaches the comet, the mass-loaded magnetic field increasingly interacts with the neutrals coming from the nucleus. This increased friction between the two species leads to an additional deceleration of the solar wind, similar to the diamagnetic cavity formation, thereby piling up the magnetic field at the collisionopause (see, e.g., Flammer & Mendis 1993).
 |
Fig. 2 A–D: components and total magnetic field strength. E: radial distance of Rosetta from comet 67P/CG. F: ICA ion bulkvelocity assuming all ions are H2O. G: ICA ion (Ni, blue) and MIP electron (Ne, red) density. H and I: IES electron and ion energy-time spectrogram. J and K: solar wind magnetic field and velocity components shifted by six days. L: cone angle of the RPC-MAG data and of the time-shifted solar wind magnetic field. The black vertical line shows the time of apoapsis of the dayside excursion. The two red vertical lines show the time interval during which the interaction with a CME took place. |
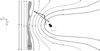 |
Fig. 3 Magnetic field line draping around an active cometary nucleus. The IMF, with changing field direction, is transported toward the comet, where it crosses a possible bow shock, becomes mass loaded, and creates nested draping around the nucleus. The figure is adapted from Volwerk et al. (2017) and is not to scale. The orbit of the dayside excursion is shown above the nucleus. |
5 Clock versus cone angle
The magnetic field is not only described by the cone angle, θco, but also by a clock angle, defined as
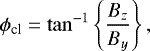 (3)
(3)
where ϕcl = 0°∕180° means the field directed in the ± Y -direction in the Y Z-plane, whereas ϕcl = 90°∕270° means the field directed in the ± Z-direction.
A two-dimensional histogram of the distribution of cone and clock angle is shown in Fig. 4C. There appears to be a structure in the distribution, with different populations for sunward-directed magnetic field and for the antisunward field. For cone angles within 0° ≤ θco ≤ 40° and 140° ≤ θco ≤ 180°, the clock angle is in the interval |ϕcl| ≥ 100°, whereas for 40° ≤ θco ≤ 140°, the clock angle is |ϕcl | ≤ 100°. This also holds for the short interval in the inbound leg at R ≈ 1100 km, where the cone angle changes from ~140° to ~ 50° and the clock angle changes to ~0°, as well as just before the CME.
To show the relation between the cone and clock angle more clearly, Fig. 5 presents the two-dimensional histogram of these two angles. Clearly, there is a pattern that was dimly visible in Fig. 4. The relationship between the two angles is obvious, and it seems to be almost repeated in the outbound and inbound leg of the excursion.
Naturally, the behavior of the cone angle in Fig. 4A, for instance, needs to be taken into account in an interpretation of this structure. It is not a continuous curve in θcl, there are clear jumps, for example, in the outbound leg from the small cloud in the bottom left at θcl ~ 30° to the small cloud in the top right at θcl ~ 140°, and then back again to the large cloud at θcl ~ 60°. Similarly, jumps can be identified in the inbound leg. Nevertheless, there seems to be an ordered distribution of the draped magnetic field cone and clock angles.
When we compare this to the angle distribution of the propagated solar wind, Fig. 6, the solar wind also shows a pattern, if not as narrow as in the Rosetta data. The resolution of the OMNI data is lower (1 min) than the RPC-MAG data in this paper. There is a clear bidirectional structure in the solar wind, considering that the y-axis with the clock angle “wraps around”. One cloud is centered on θco ~ 130° and ϕcl ~ 0°, and another cloud on θco ~ 50° and ϕcl ~ 180°. This just signifies different solar wind sectors with the magnetic field either pointing sunward (θco ~ 50°) or antisunward (θco ~ 130°) with the field in the equatorial plane (ϕcl ~ 0°∕180°, and is basically the Parker spiral angle near Earth of θParker ≈ 45°.
This Parker spiral field becomes draped around the outgassing comet, and the two main clock angles indeed reappear in Fig. 5. It is clear, however, that the layering and compression of the magnetic field in front of the comet reduces the spread of angles, which creates more order in the field.
6 Magnetic field and plasma bulk velocity
Based on observations made with RPC-ICA, the ion (H2O+) density and bulk velocity was determined (Behar 2018). They are shown in Fig. 2, panels F and G. ICA can be operated in two ways, either a full energy and angular scan, or a reduced-energy scan of two-dimensional data with high time-resolution. Only the former is suitable for the moment calculations we used. The resulting moment estimates shown in Figs. 2F, G and 4B are thus produced using only the full energy and angular scan data. For consistency, the magnetic field strength was resampled at the same time-stamps as the ICA data.
During the outbound leg the ion velocity slowly increased from ~ 15 km s−1 to values up to ~ 40 km s−1. During the inbound leg the ions increased in velocity with values up to ~ 60 km s−1, with even higher values for the CME interval. The ion density is strongly variable with a median value of Ni ≈ 12 cm−3, but values of more than 200 cm−3 are also observed.
Figure 2G shows two important things: first, there is a discrepancy between the ICA ion density (blue) and the LAP-MIP electron density (red). When the spacecraft did not have a very negative potential and the ions were at quite low energy, ICA saw only a small fraction of all ions. For quite high ion energies, when the spacecraft was far out during the excursion, ICA ion fluxes covered a significant part of the total ion fluxes. In the middle of the panel, around the vertical black line defining apoapsis, Ni and Ne are indeed much closer together than at the sides of the box, closer to the comet. Second, the density fluctuates more strongly closer in to the comet, for R ≤ 700 km.
One of the most striking features of Fig. 4B is the very good correlation between the top two panels showing Bm and Vi. Figure 7 shows a plot of B versus Vi, with color-coding for the different intervals as given in the legend. A linear fit is made through the cloud of points, assuming that there are errors in both variables (see, e.g., Isobe et al. 1990), which is shown in Fig. 7 as a magenta line with a slope 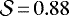 nT/(km s) that has a regression coefficient
nT/(km s) that has a regression coefficient 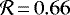 .
.
In order to check the temporal relationship between B and V, the data areplotted again in Fig. 8, where the top panel shows the magnetic field strength in blue and the ion velocity in green.
The two bottom panels show the smoothed data (magnetic field over 60 points, ion velocity over 5 points), normalized to the maximum of the data during the interval. Again it is clear that B and V follow each other very well, but it is difficult to deduce the temporal relationship between the two. At point 1, the field strength peaks after the velocity has reached maximum, but at point 2, the velocity increases while the field strength decreases, and then again at point 3, the velocity peaks well before the magnetic field. In the right panel, which contains the CME interaction, we show that B and V peak at the same time at point 4 (where shortly after a data gap appears between the two dashed lines), and at point 5, the magnetic field peaks between two velocity peaks. A possible explanation for this behavior is given in the discussion section below.
 |
Fig. 4 A: two-dimensional histograms of the cone angle of the magnetic field along the Rosetta orbit for the outbound (left) and inbound (right) leg. B: magnetic field, ICA ion velocity, IES ion energy-time spectrogram, and propagated solar wind. The magnetometer data are only shown when simultaneous ICA data are available. The red points are for simultaneous MAG-ICA-MIP data. C: two-dimensional histograms of the clock angle of the magnetic field along the Rosetta orbit. D: two-dimensional histograms of the magnetic field strength along the Rosetta orbit. The two vertical white (red) lines in the inbound column show where the interaction with the CME took place. Between the vertical green and red line is the interval where small CMEs may have interacted with the comet (see Edberg et al. 2016). |
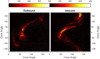 |
Fig. 5 Two-dimensional histogram of the clock vs. cone angle of the RPC-MAG data, clearly showing a structure in the draped magnetic field of directions that are visited. |
 |
Fig. 6 Two-dimensional histogram of the clock and cone angle for the propagated OMNI solar wind magnetic field data. The solar wind also shows a structure, related to the different sectors of the IMF; it switches direction from sunward (θc ≈ 45°) to antisunward (θcl ≈ 145°). |
7 Magnetic field and electron density
The electron density from LAP-MIP is again at a different cadence than the magnetometer data used in this paper. Therefore, the magnetic field data were downsampled to the time tags of the electron density. In Fig. 9 the full-resolution data are show in the top panel, where there seems to be an indication of an anticorrelation between the two quantities. In the middle panel the data are smoothed over 30 data points, taking out the high-frequency signals, and the anticorrelation is better visible. This also means that the electron density is anticorrelated with the ion velocity.
8 Discussion
The Rosettadayside excursion from 22 September until 10 October 2015 is a unique data set, the like of which is not available from any previous missions. It provided a radial cut through the cometary coma and magnetic pile-up region of a comet. It gives the first actual evidence for dynamic field line draping around an active comet, whereas before, only snapshots were obtained of the draping patterns. For example, nested field line draping at the upstream side of comet 1P/Halley with VEGA (Riedler et al. 1986) and Giotto (Raeder et al. 1987) were observed, as well as a bilobal tail structure at comet 21P/Giacobini-Zinner with ICE (Slavin et al. 1986a). Moreover, during the so-called pyramidal orbits of Rosetta around comet 67P/CG, Volwerk et al. (2017) found possible evidence of nested field line draping, where the crossing time of magnetic field in one direction could be as short as about one hour, which at a spacecraft velocity of about 1 m s−1 translates into a length scale of about 4 km or much larger if the magnetic field is frozen into the ion fluid. In this case, however, Rosetta did not venture farther than about 150 km from the comet. This means that because of the slow speed of the spacecraft, this nesting has to be interpreted with caution.
When the low-pass filtered magnetic field data are combined with the plasma data, we receive information about the large-scale structures in the upstream-induced magnetosphere and their dynamics, unlike previous studies such as that by Mandt et al. (2016), who concentrated on plasma boundaries based on the ion collisionopause, or Edberg et al. (2016), who concentrated on the interaction of a CME with the induced magnetosphere and flux ropes.
 |
Fig. 7 Scatter plot of magnetic field strength vs. ICA ion velocity. The colored dots show the different periods of the dayside excursion (black: all data; red: outbound leg; green: inbound leg; and blue: CME interval). The magenta line is a fit to the scatter cloud, with the assumption that both variables have errors in their measurements (Isobe et al. 1990), with a slope
|
 |
Fig. 8 Top panel: MAG Bm and ICA Vi plotted together. Bottom panels: zoom-in onto two short intervals that show no clear leading of one of the two variables. |
 |
Fig. 9 Top panel: downsampled magnetic field (black, to LAP-MIP resolution) and full-resolution LAP-MIP electron density (green, values divided by 10). Middle panel: smoothed data over 30 data points. A signature of an anticorrelation between B and Ne is discernable. Bottom panel: scatter plot of magnetic field strength vs. electron density. The red points show the mean of the magnetic field with error bars for consecutive intervals of Ne of 10 cm−3 width. |
8.1 Draping
The magnetic field line draping during the dayside excursion shows evidence for dynamic draping, that is, consecutive regions of differently directed magnetic field. Close to the comet, R ≤ 600 km, the magnetic field strength was found to be rather constant around 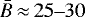 nT. However, at farther distances, there was an increase between 600 ≤ R ≤ 1100 km, and during the interaction with a CME. For this study the magnetic field data were boxcar-averaged over intervals of 512 s shifted by 30 s. This means that the maximum field strength claimed here is lower than that of the full-resolution study performed, for example, in Mandt et al. (2016) and Edberg et al. (2016). However, the main emphasis lies on the large-scale structure of the upstream magnetic field, and not the small-scale details.
nT. However, at farther distances, there was an increase between 600 ≤ R ≤ 1100 km, and during the interaction with a CME. For this study the magnetic field data were boxcar-averaged over intervals of 512 s shifted by 30 s. This means that the maximum field strength claimed here is lower than that of the full-resolution study performed, for example, in Mandt et al. (2016) and Edberg et al. (2016). However, the main emphasis lies on the large-scale structure of the upstream magnetic field, and not the small-scale details.
During the outbound leg, Rosetta crossed from sunward (θco < 90°) to tailward (θco > 90°) to sunward-directed magnetic field. After the turning point, at the start of the inbound leg, there was still sunward-directed field, and then Rosetta entered a region of tailward-directed field near R ≈ 1300 km, which did not exist during the outbound leg. With a radial velocity of ~ 2 m s−1, Rosetta moved much slower than the solar wind magnetic field.
An estimate of the velocity of the magnetic field cannot be obtained by studying the ion velocity from ICA because it can be assumed that the magnetic field is no longer frozen into the ion fluid, as the ions are assumed to be unmagnetized. When a regular solar wind is assumed upstream of the comet, and with the MIP/LAP plasma densities, an estimate can be made of the slowing-down of the solar wind, based on momentum conservation. With vsw ~ 400 km s−1 and ρsw ~ 5mp cm−3 and 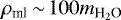 cm−3, the resulting slowed-down magnetic field velocity would be vslow ~ 1 km s−1, which is rather slow, but also a very simplified estimate.
cm−3, the resulting slowed-down magnetic field velocity would be vslow ~ 1 km s−1, which is rather slow, but also a very simplified estimate.
This means that Rosetta did not move into a region of tailward-directed field, but that a region of tailward-directed field was overtaking Rosetta. This again means that the later crossing, after the CME interaction, can be into the now compressed sunward-directed field region of the outbound leg. Thus, the buildup of the nested draped field region could be observed here. This draping also agrees well with the observations by Goetz et al. (2017). In this paper, mainly the large, long-time directions of the magnetic field are discussed, but as noted above, there are short rotations of the magnetic field from the observed field, which show themselves as not very pronounced vertical stripes in Fig. 4A (near R ≈ 700, 1300, 1100, 800 km).
Although we showed that differently directed magnetic field regions are transported toward comet 67P/CG, it cannot be claimed that nested draping is observed, as this can only be by a lateral crossing of the coma at fast speed (compared to the plasma flow velocity), as in the case of comet 1P/Halley. Therefore, the question can be asked if indeed different layers can be stacked and held wrapped around the nucleus of comet 67P/CG. For this to be happening, the diffusion time of the magnetic field from upstream to downstream of the nucleus has to be longer than the upstream loading time. This question is related tothe existence of the diamagnetic cavity, where, since observations at comet 1P/Halley (Neubauer et al. 1986; Neubauer 1988), the ion-neutral collisions are assumed to keep the magnetic field from approaching the nucleus.
However, Goetz et al. (2016a,b) showed that the ion-neutral friction was too small to keep off the boundary of the cavity at the large distances it was observed. The electron-neutral collisions are probably more likely to play a major role as the boundary of the diamagnetic cavity seems to be well correlated to the location of the electron collisionopause (see, e.g., Henri et al. 2017). It could therefore be posited that if a diamagnetic cavity exists (as was the case at comet 1P/Halley Neubauer et al. 1986; Neubauer 1987), nested field line draping can occur because the magnetic field is effectively stopped by the collisional friction upstream of the nucleus.
The behavior of the clock angle during the dayside excursion shows some interesting features in Fig. 4C. Close to the comet, at R ≤ 600 km in the outbound panel, ϕcl ~ ±120°, which means that the magnetic vector is pointing northward or southward, instead of being in the equatorial plane. This shows the deflection of the magnetic field through pickup of newly formed ions and was described by Broiles et al. (2015) and Koenders et al. (2016). Farther away from the comet with less pickup, the clock angle moves toward increasingly smaller angles. At larger distances, R ≥ 1400 km, the clock angle seems to increase again to values ϕcl ~ 120°, which mightjust be a variation in the solar wind IMF because shortly thereafter, the cone angle changes again from sunward to antisunward.
During the inbound leg the clock angles moved to large angles |ϕcl | ≥ 150, indicating mostly horizontal field directions, until the spacecraft reaches R ≤ 700. Then a broad swath of clock angle values from horizontal ϕcl = 0° to almost vertical ϕcl = ±90° was visible.
Figure 5 shows that only a small region in the cone clock angle space becomes populated during the dayside excursion. This might be considered a compressed version of the solar wind distribution as shown in Fig. 6, especially for the inbound leg. Interestingly, this Fig. 5 is reminiscent of Fig. 4 in Brain et al. (2006), where the elevation and azimuth angles of the draped magnetic field around Mars as measured by the Mars Global Surveyor (MGS) are shown to be mainly limited to a small area in this angular space, much more confined than the undisturbed solar wind, for which it was often used as a proxy. Nilsson et al. (2010) showed that the distribution of the draped magnetic field as measured by the MGS does not directly reflect the IMF clock angle.
The question now is how these results may be interpreted in view of other measurements of draped magnetic fields as presented in Volwerk et al. (2016, 2018). The answer is difficult because the activity of the comet was rather different during the various observations. For the dayside excursion, the outgassing rate of comet 67P/CG was Q ≈ 2–3 × 1028 s−1 (Hansen et al. 2016), whereas during the nightside excursion, it was Q ≈ 1 × 1026 s−1 and during the pyramidal orbits in May–July 2015, it was Q ≈ 4–6 × 1027 s−1, thus there are differences of some orders of magnitude between these papers. This means that the interaction of the solar wind and the comet is rather different for all three situations and cannot be compared directly. However, close to the comet during the tail excursion, the draping pattern was similar to what is observed upstream of the comet in this paper.
8.2 Magnetic field strength
The magnetic field strength over a distance of about 1500 km seems to be rather constant near 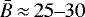 nT, which is in agreement with a model for magnetic pile-up (Goetz et al. 2017) including charge-exchange cooling (Galeev et al. 1985). In the region between 600 ≤ R ≤ 1100 km, however, the average field strength increases, slightly in the outbound leg and more prominently in the inbound leg. This could be related to the location of the collisionopause, which was found to be located between 540 and 760 km from the comet (Mandt et al. 2016). Here the friction of the ions through collisions with the neutrals will be higher, leading to a deceleration and thereby a pile-up of the magnetic field. There can also be another effect, during the inbound leg, related to the CME interaction, for the stronger increase in the magnetic field strength. Images from the Solar and Heliospheric Observatory (SOHO)2 showed five CMEs on 30 September, which were predicted to arrive at comet 67P/CG around 4–5 October 2015 (for a full discussion see Edberg et al. 2016). The angular widths of the CMEs are not large enough for them to be observed by Earth L1 solar wind monitors. Therefore, it is not possible to check whether the dynamic pressure of the solar wind increased before the CME arrived at comet 67P/CG by using propagated OMNI data3. Edberg et al. (2016) speculated that before the CME interacted with the coma of comet 67P/CG, there may have been three earlier smaller CMEs, the first of which would occur near R ≈ 1100 km, which agrees well with the increase in field strength in Fig. 4A-right. The interaction could also cause the enhanced acceleration of the ions.
nT, which is in agreement with a model for magnetic pile-up (Goetz et al. 2017) including charge-exchange cooling (Galeev et al. 1985). In the region between 600 ≤ R ≤ 1100 km, however, the average field strength increases, slightly in the outbound leg and more prominently in the inbound leg. This could be related to the location of the collisionopause, which was found to be located between 540 and 760 km from the comet (Mandt et al. 2016). Here the friction of the ions through collisions with the neutrals will be higher, leading to a deceleration and thereby a pile-up of the magnetic field. There can also be another effect, during the inbound leg, related to the CME interaction, for the stronger increase in the magnetic field strength. Images from the Solar and Heliospheric Observatory (SOHO)2 showed five CMEs on 30 September, which were predicted to arrive at comet 67P/CG around 4–5 October 2015 (for a full discussion see Edberg et al. 2016). The angular widths of the CMEs are not large enough for them to be observed by Earth L1 solar wind monitors. Therefore, it is not possible to check whether the dynamic pressure of the solar wind increased before the CME arrived at comet 67P/CG by using propagated OMNI data3. Edberg et al. (2016) speculated that before the CME interacted with the coma of comet 67P/CG, there may have been three earlier smaller CMEs, the first of which would occur near R ≈ 1100 km, which agrees well with the increase in field strength in Fig. 4A-right. The interaction could also cause the enhanced acceleration of the ions.
8.3 Coordinate system
It can be argued that the CSEQ coordinate system is not appropriate for this study, as the solar wind will be surely aberrated. Unfortunately, only during a very short interval, 6 October 0000–0400 UT, was the ICA (Nilsson et al. 2007) able to measure solar wind ions (Edberg et al. 2016). However, artificially aberrating the solar wind direction by up to 20° (which highly overestimates the real abberation) does not significantly change the results presented in this paper. A similar calculation can indeed also be performed by relating the data to the Parker spiral direction (for lack of real-time upstream solar wind data). This shows similar patterns as in the figures above, but with different values of the cone angles, which are then defined through the cone around the Parker spiral.
8.4 Magnetic field strength, ion velocity, and electron density
The correlation between the ion velocity as measured by RPC-ICA and the magnetic field strength is clear, as shown in Figs. 7 and 8. As stated above, there is no clear indication that either B or Vi is leading, but it is clear that they change in unison.
The gyro radii of the ions vary greatly in the coma of comet 67P/CG if the ions are picked up in the undisturbed solar wind. Upstream of the comet, the gyro radius is ρ ~ 10 000 km. However, ions that are picked up in the slowed-down solar wind closer to the comet, at higher magnetic field strength, will have smaller gyro radii. When the measured ion velocity Vi ≥ 20 km s−1 is used with a B ≥ 20 nT, for instance, then the H2O+ gyro radius is on the order of ρ ~ 200 km. When we also consider that the diamagnetic cavity boundary strongly correlates with the electron collisionopause, it can well be expected that the magnetic field is no longer frozen into the ion fluid, but is more likely frozen into the electron fluid, as shown by Deca et al. (2017). Nilsson et al. (2015b, 2017, 2018b) discussed the general antisunward motion of the ions and how this may be related to unmagnetized ions and magnetized electrons.
When we assume that the ions are not magnetized, a process is sought by which the magnetic field and ion velocity can change in unison. The ions are most likely accelerated by the convection electric field in the coma. This electric field will increase or decrease depending on the changes in the magnetic field strength and convecting velocity. These variations in the coma can be generated by variations in the solar wind.
Figure 9 showed a possible anticorrelation between the magnetic field strength and the electron density, although the scatter in the electron density is rather large. An explanation for this behavior would be that when the magnetic field is frozen into the electron fluid and the electrons are in a ring-beam distribution, they can be forced out of the region of increased magnetic field by mirroring.
9 Conclusions
Comet 67P/Churyumov-Gerasimenko shows dynamic magnetic field line draping during the dayside excursion. The fast (incomparison to the velocity of Rosetta) magnetic field, moving toward the nucleus, shows draping signatures, with the cone angle being well away from the Parker spiral angle in a more radial direction from the Sun.
Becauseof the slow velocity of Rosetta, no statement can be made about the presence of the so-called nested draping as this can only be observed by a snapshot of the whole coma with a fast spacecraft.
The strong correlation between the velocity of the unmagnetized ions and the magnetic field strength is most likely caused by variations inthe convection electric field in the cometary coma, which is driven by variations in the undisturbed external solar wind.
Acknowledgements
The RPC-MAG and ICA data are available through ESA’s Plaetary Science Archive (PSA) and NASA’s Planetary Data System (PDS). Rosetta is an ESA mission with contributions from its Member States and NASA. We acknowledgethe staff of CDDP and IC for the use of AMDA and the RPC Quicklook database (provided by a collaboration between the Centre de Données de la Physique des Plasmas, supported by CNRS, CNES, Observatoire de Paris, and Université Paul Sabatier, Toulouse, and Imperial College London, supported by the UK Science and Technology Facilities Council). The work on RPC-MAG was financially supported by the German Ministerium für Wirtschaft und Energie and the Deutsches Zentrum für Luft- und Raumfahrt under contract 50QP 1401. We are indebted to the whole of the Rosetta Mission Team, SGS, and RMOC for their outstanding efforts in making this mission possible.
References
- Acton, H. C. 1996, Planet. Space Sci., 44, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Alfvén, H. 1957, Tellus, 9, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E. 2018, PhD Thesis, Luleå University of Technology, Sweden [Google Scholar]
- Behar, E., Nilsson, H., Henri, P., et al. 2018, A&A, 616, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biermann, L. 1951, Z. Astrophys., 29, 274 [NASA ADS] [Google Scholar]
- Brain, D. A., Mitchell, D. L., & Halekas, J. 2006, Icarus, 182, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Breuillard, H., Henri, P., Bucciantini, L., et al. 2019, A&A, 630, A39 (Rosetta 2 SI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Broiles, T. W., Burch, J. L., Clark, G., et al. 2015, A&A, 583, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burch, J. L., Goldstein, R., Cravens, T. E., et al. 2006, Space Sci. Rev., 128, 697 [Google Scholar]
- Carr, C., Cupido, E., Lee, C. G. Y., et al. 2007, Space Sci. Rev., 128, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, S. W. H. 1987, Phil. Trans. R. Soc. Lond., 323, 405 [Google Scholar]
- Deca, J., Divin, A., Henri, P., et al. 2017, Phys. Rev. Lett., 118, 205101 [NASA ADS] [CrossRef] [Google Scholar]
- Edberg, N. J. T., Alho, M., André, M., et al. 2016, MNRAS, 462, S45 [CrossRef] [Google Scholar]
- Eriksson, A. I., Boström, R., Gill, R., et al. 2006, Space Sci. Rev., 128, 729 [Google Scholar]
- Flammer, K. R., & Mendis, D. A. 1993, J. Geophys. Res., 98, 21003 [NASA ADS] [CrossRef] [Google Scholar]
- Galeev, A. A., Cravens, T. E., & Gombosi, T. I. 1985, ApJ, 289, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Glassmeier, K.-H. 2017, Phil. Trans. R. Soc. A., 375, 20160256 [NASA ADS] [CrossRef] [Google Scholar]
- Glassmeier, K.-H., Boehnhardt, H., Koschny, D., Kührt, E., & Richter, I. 2007a, Space Sci. Rev., 128, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Glassmeier, K.-H., Richter, I., Diedrich, A., et al. 2007b, Space Sci. Rev., 128, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, C., Koenders, C., Richter, I., et al. 2016a, A&A, 588, A24 [Google Scholar]
- Goetz, C., Koenders, C., Hansen, K. C., et al. 2016b, MNRAS, 462, S459 [Google Scholar]
- Goetz, C., Volwerk, M., Richter, I., & Glassmeier, K.-H. 2017, MNRAS, 469, S268 [CrossRef] [Google Scholar]
- Gulkis, S., Frerking, M., Crovisier, J., et al. 2007, Space Sci. Rev., 128, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Gunell, H., Goetz, C., Simon Wedlund, C., et al. 2018, A&A, 619, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hansen, K. C., Altwegg, K., Berthelier, J.-J., et al. 2016, MNRAS, 462, S491 [Google Scholar]
- Henri, P., Vallières, X., Hajra, R., et al. 2017, MNRAS, 469, S372 [Google Scholar]
- Heritier, K. L., Henri, P., Vallières, X., et al. 2017, MNRAS, 469, S118 [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. T. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koenders, C., Glassmeier, K.-H., Richter, I., Motschmann, U., & Rubin, M. 2013, Planet. Space Sci., 87, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Koenders, C., Götz, C., Richter, I., Motschmann, U., & Glassmeier, K.-H. 2016, MNRAS, 462, S235 [CrossRef] [Google Scholar]
- Mandt, K. E., Eriksson, A., Edberg, N. J. T., et al. 2016, MNRAS, 462, S9 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Gosling, J. T., Bame, S. J., et al. 1987a, J. Geophys. Res., 92, 1139 [NASA ADS] [CrossRef] [Google Scholar]
- McComas, D. J., Gosling, J. T., Russell, C. T., & Slavin, J. A. 1987b, J. Geophys. Res., 92, 10111 [NASA ADS] [CrossRef] [Google Scholar]
- Mendis, D. A., Smith, E. J., Tsurutani, B. T., et al. 1986, Geophys. Res. Lett., 13, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Mendis, D. A., Flammer, K. R., Rème, H., Sauvaud, J. A., & D’Uston, C. 1989, Ann. Geophys., 7, 99 [NASA ADS] [Google Scholar]
- Neubauer, F. M. 1987, A&A, 187, 73 [NASA ADS] [Google Scholar]
- Neubauer, F. M. 1988, J. Geophys. Res., 93, 7272 [NASA ADS] [CrossRef] [Google Scholar]
- Neubauer, F. M., Glassmeier, K. H., Pohl, M., et al. 1986, Nature, 321, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Lundin, R., Lundin, K., et al. 2007, Space Sci. Rev., 128, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Carlsson, E., Brain, D. A., et al. 2010, Icarus, 206, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2015a, Science, 347, aaa0571 [NASA ADS] [CrossRef] [Google Scholar]
- Nilsson, H., Wieser, G. S., Behar, E., et al. 2015b, A&A, 583, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2017, MNRAS, 469, S252 [CrossRef] [Google Scholar]
- Nilsson, H., Gunell, H., Karlsson, T., et al. 2018a, A&A, 616, A50 [Google Scholar]
- Nilsson, H., Stenberg Wieser, G., Behar, E., et al. 2018b, MNRAS, 469, S804 [CrossRef] [Google Scholar]
- Opitz, A., Karrer, R., Wurz, P., et al. 2009, Sol. Phys., 256, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Opitz, A., Fedorov, A., Wurz, P., et al. 2010, Sol. Phys., 264, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Perez-de-Tejada, H. 1990, J. Geophys. Res., 95, 10711 [NASA ADS] [CrossRef] [Google Scholar]
- Raeder, J., Neubauer, F. M., Ness, N. F., & Burlaga, L. F. 1987, A&A, 187, 61 [NASA ADS] [Google Scholar]
- Riedler, W., Schwingenschuh, K., Yeroshenko, Y. E., Styashkin, V. A., & Russell, C. T. 1986, Nature, 321, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Simon Wedlund, C., Alho, M., Gronoff, G., et al. 2017, A&A, 604, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slavin, J. A., Smith, E. J., Tsurutani, B. T., et al. 1986a, Geophys. Res. Lett., 13, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Slavin, J. A., Golberg, B. A., Smith, E. J., et al. 1986b, Geophys. Res. Lett., 13, 1085 [NASA ADS] [CrossRef] [Google Scholar]
- Trotignon, J. G., Michau, J. L., Lagoutte, D., et al. 2006, Space Sci. Rev., 128, 713 [Google Scholar]
- Volwerk, M., Richter, I., Tsurutani, B., et al. 2016, Ann. Geophys., 34, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Volwerk, M., Jones, G. H., Broiles, T., et al. 2017, J. Geophys. Res., 122, 3308 [Google Scholar]
- Volwerk, M., Goetz, C., Richter, I., et al. 2018, A&A, 614, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Original definition from the SPICE kernel: +X-axis is the position of the Sun relative to the body; it is the primary vector and points from the body to the Sun; +Z-axis is the component toward the north pole of the Sun of date orthogonal to the +X-axis; +Y -axis completes the right-handed reference frame; the origin of this frame is the center of mass of the body (Acton 1996).
All Figures
 |
Fig. 1 Three-dimensional view of the dayside excursion. In blue we show the orbit of Rosetta, with hourly magnetic field vectors in green. In black we show the orbit projected on the three orthogonal planes. The projections show that the orbit was inclined by ~ 45° in each plane, making it very useful for the investigation of nested draped magnetic fields. |
| In the text | |
 |
Fig. 2 A–D: components and total magnetic field strength. E: radial distance of Rosetta from comet 67P/CG. F: ICA ion bulkvelocity assuming all ions are H2O. G: ICA ion (Ni, blue) and MIP electron (Ne, red) density. H and I: IES electron and ion energy-time spectrogram. J and K: solar wind magnetic field and velocity components shifted by six days. L: cone angle of the RPC-MAG data and of the time-shifted solar wind magnetic field. The black vertical line shows the time of apoapsis of the dayside excursion. The two red vertical lines show the time interval during which the interaction with a CME took place. |
| In the text | |
 |
Fig. 3 Magnetic field line draping around an active cometary nucleus. The IMF, with changing field direction, is transported toward the comet, where it crosses a possible bow shock, becomes mass loaded, and creates nested draping around the nucleus. The figure is adapted from Volwerk et al. (2017) and is not to scale. The orbit of the dayside excursion is shown above the nucleus. |
| In the text | |
 |
Fig. 4 A: two-dimensional histograms of the cone angle of the magnetic field along the Rosetta orbit for the outbound (left) and inbound (right) leg. B: magnetic field, ICA ion velocity, IES ion energy-time spectrogram, and propagated solar wind. The magnetometer data are only shown when simultaneous ICA data are available. The red points are for simultaneous MAG-ICA-MIP data. C: two-dimensional histograms of the clock angle of the magnetic field along the Rosetta orbit. D: two-dimensional histograms of the magnetic field strength along the Rosetta orbit. The two vertical white (red) lines in the inbound column show where the interaction with the CME took place. Between the vertical green and red line is the interval where small CMEs may have interacted with the comet (see Edberg et al. 2016). |
| In the text | |
 |
Fig. 5 Two-dimensional histogram of the clock vs. cone angle of the RPC-MAG data, clearly showing a structure in the draped magnetic field of directions that are visited. |
| In the text | |
 |
Fig. 6 Two-dimensional histogram of the clock and cone angle for the propagated OMNI solar wind magnetic field data. The solar wind also shows a structure, related to the different sectors of the IMF; it switches direction from sunward (θc ≈ 45°) to antisunward (θcl ≈ 145°). |
| In the text | |
 |
Fig. 7 Scatter plot of magnetic field strength vs. ICA ion velocity. The colored dots show the different periods of the dayside excursion (black: all data; red: outbound leg; green: inbound leg; and blue: CME interval). The magenta line is a fit to the scatter cloud, with the assumption that both variables have errors in their measurements (Isobe et al. 1990), with a slope
|
| In the text | |
 |
Fig. 8 Top panel: MAG Bm and ICA Vi plotted together. Bottom panels: zoom-in onto two short intervals that show no clear leading of one of the two variables. |
| In the text | |
 |
Fig. 9 Top panel: downsampled magnetic field (black, to LAP-MIP resolution) and full-resolution LAP-MIP electron density (green, values divided by 10). Middle panel: smoothed data over 30 data points. A signature of an anticorrelation between B and Ne is discernable. Bottom panel: scatter plot of magnetic field strength vs. electron density. The red points show the mean of the magnetic field with error bars for consecutive intervals of Ne of 10 cm−3 width. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.