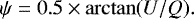| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 18 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201935072 | |
| Published online | 23 September 2019 | |
The geometry of the magnetic field in the central molecular zone measured by PILOT
1
IRAP, Université de Toulouse, CNRS, CNES, UPS, Toulouse,
France
e-mail: anna.mangilli@irap.omp.eu
2
Dipartimento di Fisica, Università di Roma “Tor Vergata”,
via della Ricerca Scientifica 1,
00133
Roma,
Italy
3
Institut d’Astrophysique de Paris, Université Pierre et Marie Curie (UPMC), Sorbonne Université, CNRS (UMR 7095),
75014 Paris,
France
4
Department of Physics and Astrophysics, PO Box 913, Cardiff University,
5 the Parade,
Cardiff,
UK
5
Department of Physics, School of Science and Technology, Nazarbayev University,
Astana
010000,
Kazakhstan
6
Dipartimento di Fisica, Università degli studi di Roma “La Sapienza”,
P.le A. Moro, 2,
00185
Roma,
Italia
7
Instituto de Astronomia, Geofísica e Ciências Atmosféricas – Universidade de São Paulo (IAG-USP),
Rua do Matão,
São Paulo
05508-090, Brazil
8
Institut d’Astrophysique Spatiale (IAS), Bât 131, Université Paris XI, Orsay, France
9
Laboratoire Univers et Particules de Montpellier, Université de Montpellier, CNRS/IN2P3,
CC 72, Place Eugène Bataillon,
34095 Montpellier Cedex 5, France
10
Scientific Support Office, SRE-S, ESTEC,
PO Box 299
2200AG Noordwijk, The Netherlands
11
Centre National des Etudes Spatiales, DCT/BL/NB,
18 Av. E. Belin,
31401
Toulouse,
France
12
Thales Services, Toulouse,
France
13
CEA/Saclay, 91191 Gif-sur-Yvette Cedex,
France
14
Department of Physics, Stanford University,
Stanford,
California
94305,
USA
15
University College London Observatory, University College London
Gower Street -
WC1E 6BT,
London, UK
Received:
16
January
2019
Accepted:
17
June
2019
We present the first far infrared (FIR) dust emission polarization map covering the full extent of Milky Way’s central molecular zone (CMZ). The data, obtained with the PILOT balloon-borne experiment, covers the Galactic center region − 2° < ℓ < 2°, − 4° < b < 3° at a wavelength of 240 μm and an angular resolution of 2.2′. From our measured dust polarization angles, we infer a magnetic field orientation projected onto the plane of the sky (POS) that is remarkably ordered over the full extent of the CMZ, with an average tilt angle of ≃22° clockwise with respect to the Galactic plane. Our results confirm previous claims that the field traced by dust polarized emission is oriented nearly orthogonally to the field traced by GHz radio synchrotron emission in the Galactic center region. The observed field structure is globally compatible with the latest Planck polarization data at 353 and 217 GHz. Upon subtraction of the extended emission in our data, the mean field orientation that we obtain shows good agreement with the mean field orientation measured at higher angular resolution by the JCMT within the 20 and 50 km s−1 molecular clouds. We find no evidence that the magnetic field orientation is related to the 100 pc twisted ring structure within the CMZ. The low polarization fraction in the Galactic center region measured with Planck at 353 GHz combined with a highly ordered projected field orientation is unusual. This feature actually extends to the whole inner Galactic plane. We propose that it could be caused by the increased number of turbulent cells for the long lines of sight towards the inner Galactic plane or to dust properties specific to the inner regions of the Galaxy. Assuming equipartition between magnetic pressure and ram pressure, we obtain magnetic field strength estimates of the order of 1 mG for several CMZ molecular clouds.
Key words: Galaxy: center / polarization / magnetic fields / balloons / methods: data analysis / dust, extinction
© A. Mangilli et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The interstellar medium (ISM) near the Galactic center (GC) is dominated by the central molecular zone (CMZ), a large reservoir of dense molecular gas with a total mass of ~107 M⊙ and typical gas densities of a few times 104 cm−2 (e.g, Ferrière et al. 2007). The CMZ is structured into a thin, elliptical sheet of gas that is oriented roughly parallel to the Galactic plane. In the plane of the sky, it extends out to r ~ 250 pc at positive longitudes and to r ~ 150 pc at negative longitudes, with a full width at half maximum (FWHM) thickness ~30 pc (e.g. Heiligman 1987; Bally et al. 1988)1. The CMZ itself contains a ring-like feature with mean radius ~180 pc, and, deeper inside, a population of dense molecular clouds (e.g. Bally et al. 1988; Sofue 1995a,b). These clouds appear to be arranged along a twisted elliptical ring (Molinari et al. 2011).
The first observational clues to the orientation of the interstellar magnetic field in the CMZ date back to the 1980s, when radio astronomers discovered systems of radio continuum filaments running nearly perpendicular to the Galactic plane (Yusef-Zadeh et al. 1984; Liszt 1985). As summarized by Morris (1996), these filaments are typically a few to a few tens of parsecs longand a fraction of a parsec wide. They appear straight or mildly curved along their entire length. Their radio continuum emission is linearly polarized and has a spectral index consistent with synchrotron radiation, leading to their denomination as non-thermal radio filaments (NRFs).
The long and thin shape of NRFs strongly suggests that they follow magnetic field lines. This suggested alignment is confirmed by the measured radio polarization angles (corrected for Faraday rotation), which indicate that, in the plane of the sky, the magnetic field inside NRFs is indeed oriented along their long axes (e.g. Tsuboi et al. 1985, 1986; Reich 1994; Lang et al. 1999). From this, it has been concluded that the magnetic field in the CMZ is approximately vertical, that is, perpendicular to the Galactic plane, at least close to the plane. At larger distances from the plane, the orientation of NRFs tends to lean outwards (i.e. away from the vertical), consistent with the magnetic field having an overall poloidal geometry (Morris 1990).
Following the initial discovery of the NRF phenomenon, many new NRFs have been identified in the CMZ. By plotting the sky distribution of all the (confirmed and likely candidate) NRFs detected at 20 cm, Yusef-Zadeh et al. (2004) observed that only the longer NRFs are nearly straight and aligned with the vertical; the shorter NRFs exhibit a broad range of orientations, with only a loose trend toward the vertical. This could indicate that the magnetic field in the CMZ is not as ordered as initially claimed, and that it has a significant fluctuating component.
Faraday rotation measurements (RMs) toward NRFs provide valuable information on the magnetic field in the diffuse ionized medium near the GC. Novak et al. (2003) collected all the available RMs toward NRFs within 1° (≃ 150 pc) of Sgr A* and, by doing so, they showed that there is a clear pattern in the sign of RMs, such that RM > 0 in the northeast and southwest quadrants and RM < 0 in the northwest and southeast quadrants. These authors argued that the observed RM pattern could be explained by the model of Uchida et al. (1985), in which an initially vertical magnetic field is sheared out in the azimuthal direction by the differential rotation of the dense clouds present near the Galactic plane.
A different RM pattern was obtained by Roy et al. (2005), who measured the RMs of 60 background extragalactic sources through a 12° × 4° window centered on Sgr A* and found mostly positive values, with no evidence for a sign reversal either across the rotation axis or across the midplane. Roy et al. (2008) pointed out that this RM distribution is consistent with either the large-scale Galactic magnetic field having a bisymmetric spiral configuration or the magnetic field in the central region of the Galaxy being oriented along the Galactic bar.
More relevant to the present paper, far-infrared (FIR) and submillimeter (submm) polarization studies of dust thermal emission make it possible to probe the orientation in the plane of the sky of the magnetic field inside dense molecular clouds.
FIR polarimetry of the innermost (~3 pc diameter) GC region was first performed by Werner et al. (1988), who detected linear polarization of 100 μm emission from three locations in the inner circumnuclear ring (CNR). At each location, they measured polarization angles ≃ 90°−100°, implying a mean magnetic field oriented at ≃0°−10° east of north, meaning within ≃10°−20° of the plane of the CNR. Since the CNR is thought to be in differential rotation, they concluded that its mean magnetic field must be predominantly azimuthal (with respect to its rotation axis). Finally, from the measured polarization fractions, they inferred that the magnetic field has a turbulent component comparable to the mean azimuthal field.
As a follow-up to the work of Werner et al. (1988), Hildebrand et al. (1990) measured the linear polarization of the 100 μm emission at six positions in the CNR, along the main FIR emission ridge, and they confirmed that the mean magnetic field is approximately parallel to the plane of the CNR. Hildebrand et al. (1993) then expanded the set of 100 μm polarization measurements, to cover not only the main FIR emission ridge, but the whole area of the CNR. A few of their observed positions happen to fall inside the area of the northern streamer. By analyzing the corresponding polarization measurements, Hildebrand & Davidson (1994) found that the magnetic field runs parallel to the axis of the streamer along its entire length, that is, out to a projected distance ≃ 4 pc from Sgr A*.
The first submm polarimetric observations of the GC region were carried out by Novak et al. (2000). They targeted three separate 5 pc × 5 pc areas, centered on the CNR and on the peaks of the M−0.02−0.07 and M−0.13−0.08 molecular clouds, respectively, and in each area they detected linear polarization of the 350 μm emission. For the CNR, they inferred a mean magnetic field orientation that is approximately north-south, in good overall agreement with the FIR results. In M−0.02−0.07, the field appears to have two distinct behaviors: upstream of the Sgr A East shock, it runs nearly perpendicular to the Galacticplane, while downstream it closely follows the curved ridge of shock-compressed material. In M−0.13−0.08, the field is on average parallel to the long axis of the cloud, with a spiky structure toward the CNR, which suggests that the field has been stretched out by the tidal forces that gave the cloud its elongated shape.
Novak et al. (2003) observed a much larger, 170 pc × 30 pc, area around Sgr A*. Their 450 μm polarization map clearly shows that the magnetic field threading molecular clouds is, on the whole, approximately parallel to the Galactic plane. To reconcile the horizontal field measured in molecular clouds with the poloidal field traced by the NRFs, Novak et al. (2003) proposed that the large-scale magnetic field in the GC region is predominantly poloidal in the diffuse ISM and predominantly toroidal in dense regions along the Galactic plane, where it was sheared out in the azimuthal direction by the differential rotation of the dense gas.
Chuss et al. (2003) performed additional 350 μm polarimetric observations toward eight selected areas within the central 50 pc. These measurements, combined with those of Novak et al. (2000), offer a broader and more complete view of the magnetic field morphology in the GC region, which conveys the general impression that the field is globally organized on scales much larger than the typical sizes of molecular clouds, while also being subject to strong local distortions by environmental forces such as shock compression and tidal shearing. Chuss et al. (2003) also found that the measured magnetic field orientation depends on the molecular gas density, being generally parallel to the Galactic plane in high-density regions and generally perpendicular to it in low-density regions.
Near-infrared (NIR) polarization observations of starlight extinction by dust also offer a promising tool to trace the magnetic field orientation in dense regions near the GC. Nishiyama et al. (2009) obtained a NIR polarization map of a 50 pc × 50 pc area centered on Sgr A*. Compared to earlier NIR polarimetric observations toward the GC (e.g. Eckart et al. 1995; Ott et al. 1999), they were able, for the first time, to separate out the contribution from foreground dust and to isolate the polarization arising within ~ (1−2) kpc of Sgr A*. They inferred that the distribution of polarization angles exhibits a strong peak in a direction nearly parallel to the Galactic plane, in good agreement with the results of FIR/submm polarimetry. However, in contrast to Chuss et al. (2003), Nishiyama et al. (2009) found no indication that the magnetic field orientation depends on gas density – the field appears to be everywhere horizontal, including in the diffuse ISM.
All sky maps of the thermal dust and synchrotron polarized emission have been obtained with the Planck satellite at wavelengths above 850 μm (353 GHz) and angular resolution above 5′. These maps obviously include the Galactic center region, but no specific study of this region was discussed in the literature. The analysis of the all-sky map of thermal dust polarization at 850 μm (Planck Collaboration Int. XIX 2015) has clearly shown the existence of large variations of the polarization fraction from unexpectedly large values (up to pmax ≃ 22%) occurring essentially in the diffuse ISM, down to very low values occurring mostly on line-of-sights (LOS) with larger column densities. Over most of the sky included in the analysis, which avoided the Galactic plane (usually |b | < 5°), the variations of p appeared tightly anti-correlated with the polarization angle dispersion function (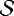 ) which measures the rotation of the observed field around a given sky location. This indicates that the intrinsically large dust polarization fraction is efficiently modulated by the B-field twisted geometry resulting in efficient depolarization of the signal both in the beam and along the LOS. Planck Collaboration Int. XX (2015) showed that this behaviour is expected from MHD simulations of the ISM. These properties were confirmed in the latest analysis of the all-sky Planck data at 353 GHz based on the latest Planck data release in Planck Collaboration XII (2019), which also studied departures from the
) which measures the rotation of the observed field around a given sky location. This indicates that the intrinsically large dust polarization fraction is efficiently modulated by the B-field twisted geometry resulting in efficient depolarization of the signal both in the beam and along the LOS. Planck Collaboration Int. XX (2015) showed that this behaviour is expected from MHD simulations of the ISM. These properties were confirmed in the latest analysis of the all-sky Planck data at 353 GHz based on the latest Planck data release in Planck Collaboration XII (2019), which also studied departures from the  anti-correlation in details. They showed that the departures are unlikely to reflect large variations of the dust alignment efficiency up to a column density of NH = 2 × 1022 cm−2. However, this analysis excluded regions near the Galactic plane (|b| < 2°), and therefore the Galactic center discussed here. The main reason for avoiding the Galactic plane and in particular the inner Galactic regions was to avoid very long LOS through the plane were many B-field reversal are likely to happen, which could have affected the trend with column density. An additional difficulty comes from specific systematic effects which could be affecting data near the plane, such as band-pass mismatch and/or contamination by molecular lines (such as the CO lines) in the Planck photometric bands.
anti-correlation in details. They showed that the departures are unlikely to reflect large variations of the dust alignment efficiency up to a column density of NH = 2 × 1022 cm−2. However, this analysis excluded regions near the Galactic plane (|b| < 2°), and therefore the Galactic center discussed here. The main reason for avoiding the Galactic plane and in particular the inner Galactic regions was to avoid very long LOS through the plane were many B-field reversal are likely to happen, which could have affected the trend with column density. An additional difficulty comes from specific systematic effects which could be affecting data near the plane, such as band-pass mismatch and/or contamination by molecular lines (such as the CO lines) in the Planck photometric bands.
In this context, the PILOT data bring useful information regarding both the structure of the magnetic field and the physics of dust. First, the angular resolution of the instrument (2.2′) is higher than that of the Planck data, which helps following the field structure into small and/or distant objects, while the large instantaneous field-of-view of the instrument allows mapping large regions, allowing to bridge high resolution ground-based observation which often suffer from a limited sky coverage. Second, the data obtained with the PILOT instrument operating at 240 μm will allow, in conjunction with polarization data obtained at longer wavelength, to constrain the polarization SED of thermal dust with a large lever arm, which is an important constraint for dust models. Finally, the systematic effects affecting the PILOT data are likely to be of a different nature than that relevant for other instruments, which will help the analysis and interpretation of the polarized signals when co-analysis is possible.
In this paper, we present the map of polarized dust emission in the CMZ obtained at 240 μm by the PILOT balloon-borne experiment. The PILOT observations cover a 4° × 6° field centered at (ℓ, b) = (0, 0) (we refer to this observed field as “L0” in the rest of the article), a much wider field than all previous observations of polarized FIR emission in the GC region. The PILOT maps reveal the projected magnetic field structure across the whole CMZ with an angular resolution of 2.2′, that is with 2.3 times better linear resolution or 5 times more spatial information than the 353 GHz polarization data obtained by Planck.
The paper is organized as follows. In Sect. 2, we describe the observing strategy. The PILOT data processing is described in Sect. 3, including an overview of how we construct Stokes I, Q and U maps by using two map-making software packages (ROMA and SCANAMORPHOS) in Sect. 3.5. In Sect. 4 we present the polarization results focusing on the polarization angles, we discuss the polarization maps in Sect. 4.1, in Sect. 4.2, we validate them by comparing the results of the two independent map-making procedures and in Sect. 4.3 we compare our measurements with the ones obtained with the Planck satellite. We discuss the results in Sect. 5, focusing on the relevance of the CMZ in Sect. 5.1, on the magnetic field orientation in Sect. 5.2 and on the magnetic field strength in Sect. 5.3. We investigate the relationship between the magnetic field structure in the CMZ measured by PILOT and recently proposed models for gas orbits in the Galactic center in Sect. 5.4, using a model for the Milky Way’s magnetic field that we describe in Appendix A. We discuss the comparison of our results with previous ground measurements in Sect. 5.5. We summarize our conclusions in Sect. 6.
To aid discussion, a schematic diagram identifying key features of the CMZ that we refer to in this paper, overlaid on a map of the PILOT 240 μm intensity, is presented in Fig. 1. Throughout the paper, we quote polarization angles in the GAL-COSMO convention (i.e., clockwise from Galactic north when looking at the source). We employ the acronym POS to describe quantities and structures that are projected onto the plane of the sky (e.g. the orientation of the magnetic field that is accessible via dust polarization measurements, which elsewhere in the literature is sometimes denoted as ⟨B⊥⟩), and the common acronym LOS to mean line-of-sight.
2 PILOT observations
PILOT observations of the GC region were obtained during the second flight of the PILOT balloon experiment, which took place from Alice Springs, Australia, as part of the 2017 French Space Agency (CNES) balloon campaign. A complete description of the PILOT instrument is presented in Bernard et al. (2016), while the performance of the PILOT instrument during the Alice Springs flight is described in Mangilli et al. (2018).
The data presented in this paper were obtained during four consecutive observing tiles2 while the target field was at elevationsbetween 16.5° and 56°. The total duration of the observations was ≃32 min, including time for slewing and calibrations at the end of individual scans. The temperatures of the TRANS and REFLEX focal planes during the observationswere stable, 304.96 ± 0.04 mK and 309.07 ± 0.03 mK respectively.The median balloon altitude was 39.8 km, with peak-to-peak variation between 39.7 and 39.9 km. The four observing tiles used four distinct positions of the half wave-plate (HWP) in order to uniformly sample polarization analysis directions as projected on the sky. Each of the observing tiles was configured to scan the target region at a different angle, with a median scan speed of 11.8′ /s and a median scan leg duration of 13 s.
These scan directions were chosen to be preferentially perpendicular to the Galactic plane, while at the same time providing sufficiently varied directions for efficient destriping during map-making (see Sect. 3.5). The consequence of this observing strategy is that the elevation varies during scans, which causes variations of the signal due to emission from the residual atmosphere (see Sect. 3.4). In Sect. 3.3, we describe how we use the elevation-dependent variations across the whole flight to obtain a focal plane map of the individual detector responses.
3 Data processing
3.1 Time constant correction
The procedure that we used to estimate the time constants of the bolometers is described in Mangilli et al. (2018). In summary, we used a combination of in-flight measurements of the internal calibration source (ICS) and of strong glitches detected throughout the flight to derive the time constants of both the ICS and of individual bolometers, which we assumed to be constant throughout the flight. The timeline of each bolometer was then deconvolved from the corresponding time constant in Fourier space. The bolometer time constants are at most ~ 1 sample (= 25 ms) and we estimate our knowledge of their value to be accurate within ≃2 msec.
 |
Fig. 1 Top panel: map of the Galactic central molecular zone obtained with the PILOT experiment at 240 μm. The color scale shows the total intensity in log scale. The overlaid texture based on the line integral convolution (Cabral & Leedom 2000) shows the orientation of the magnetic field projected on the plane, inferred from the measured dust polarization. Bottom panel: intensity as above, overlaid with total intensity contours at 0.1, 0.2, 0.5, and 1 × 105 MJy sr−1. The circles show the location of the 100-pc twisted ring as defined in Molinari et al. (2011). The filled symbols are discussed in Sect. 5.4. The names of key molecular regions are overlaid. |
3.2 Pointing reconstruction
The pointing of each detector can be computed given the Estadius stellar sensor information, the offset between the Estadius and PILOT optical axes and a description of the PILOT focal plane geometry.
The Estadius stellar sensor (Montel et al. 2015) data provides the pointing quaternion at a frequency of 4 Hz with an accuracy of ≃ 5 arcsec in both directions and ≃15 arcsec in field rotation. During the observations of the CMZ region presented here, the performances of the Estadius sensor were optimal. The offset between the Estadius and the PILOT optical axes was found to vary during flight, due to thermal and mechanical deformation of the instrument. This offset was monitored during the whole flight using bright sources. For that purpose, we used total intensity maps of individual observing tiles of the PILOT data obtained using the SCANAMORPHOS map-making algorithm (see Sect. 3.5). These maps were obtained using coordinates computed with preliminary Estadius offsets derived during the flight from planet observations. These maps were correlated with Herschel maps of the same sky region at 250 μm for different assumed values of the Estadius offset. The best Estadius offset for each observing tile was derived as the one providing the best Pearson correlation coefficient between the PILOT and Herschel data. We note that three different bright sources were used in the L0 observations to derive Estadius offsets.
Preliminary version of the PILOT focal plane geometry was obtained during ground calibration of the instrument (Bernard et al. 2016). Here, we used all parameters of this determination including the pixel size and array rotation values. However, we refined the detector array position offsets with respect to the PILOT focal plane center using in-flight measurements. For that purpose, we used a similar procedure as for deriving Estadius offsets but applied to maps obtained with data from individual arrays. The offset difference between the individual offsets and the Estadius offsets was adopted as the refined arrays offsets of the focal plane geometry.
The bolometer coordinates used here were derived combining the three quaternions describing the Estadius pointing, the Estadius offset with respect to the PILOT focal plane center and each bolometer location in the focal plane. The Estadius quaternions were interpolated in time to the time corresponding to each data sample, taking into account the time shift between individual detectors within one array caused by the time-multiplexing readout electronics. For a given observing tile, the Estadius offsets were assumed constant. The focal plane geometry was assumed invariant over all observations.
We estimate that the accuracy of the pointing from the differences between pointing reconstruction solutions obtained with different Estadius offsets computed on the various sources used in L0 is ≃ 15 arcsec.
 |
Fig. 2 Calibrated PILOT data for one observing tile during L0 observations. Top panel: data before atmospheric signal removal. Bottom panel: data with the atmospheric signal removed as described in Sect. 3.4. In each panel, we show the array-averaged signal in V as a function of time on the TRANS array #6 and REFLEX array #7, from top to bottom. Vertical lines show the extent of individual scans. The modulated signal during calibration sequences on the ICS at some ends of scans is clearly seen. |
3.3 Gain calibration
The gain calibration was performed as described in Mangilli et al. (2018). The raw data for each individual bolometer located by its position in the focal plane (x, y), for each observing tile (observed at a time ttile), were dividedby a response R(x, y, ttile), computed as:
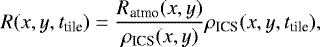 (1)
(1)
where Ratmo(x, y) is a normalized map of the relative response between all detectors, derived from the atmospheric signal averaged over the whole flight, ρICS is the ICS signal averaged over the whole flight and ρICS(x, y, ttile) is the ICS signal averaged over the observing tile. R(x, y, ttile) is allowed tovary during the flight but is assumed to be constant within a given observing tile. This gain calibration strategy assumes that the ICS signal is intrinsically unpolarized.
From the all-flight time statistics on R, we estimate that detectors gain inter-calibration is accurate at the percent level Mangilli et al. (2018). The absolute calibration of the data was obtained from the correlation between total intensity maps of L0 with Herschel maps.
3.4 Atmospheric signal subtraction
In order to isolate the astronomical signal from the residual atmospheric emission, we correlate the observed signal of each pixel with the pointing elevation consistent with the pointing solution described in Sect. 3.2. The slope of the correlation is averaged over each observing tile, and the correlated component of the signal is subtracted from the data. The top panel of Fig. 2 shows the time evolution of the average signal measured on the five PILOT arrays for one observing tile before subtraction of the residual atmospheric emission for an observing tile scanned with decreasing elevations. We can see that the timeline signal increases as the elevation decreases. In the bottom panel of Fig. 2, the atmospheric signal has been cleaned and the timeline shows a flat baseline.
3.5 Map-making
3.5.1 PILOT measurements
The PILOT signal can be expressed as described in Mangilli et al. (2018) for a given bolometer at a position (x, y) in the focal plane:
![\begin{equation*} m = R_{xy} T_{xy} \times [I \pm Q \cos(2\theta) \pm U \sin(2\theta)]+O_{xy},\end{equation*}](/articles/aa/full_html/2019/10/aa35072-19/aa35072-19-eq4.png) (2)
(2)
where Rxy and Txy are the system response and optical transmissionrespectively, and Oxy is an arbitrary electronics offset. For the configuration of the HWP and analyzer in the PILOT instrument, the ± sign is + and − for the REFLEX and TRANS arrays respectively (see Bernard et al. 2016). θ = 2 × ω + ϕ is the analysis angle. ω is the angle between the HWP fast axis direction as projected on the sky and the horizontal direction measured counter-clockwise as seen from the instrument. In practice, the same patch of sky is observed at different times with at least two values of the analysis angle. ϕ is the time varying parallactic angle measured counterclockwise from equatorial North to Zenith for the time and direction of the current observation. The precise positioning of the HWP fast axis was measured from ground calibration measurements obtained in front of a polarized signal of known polarization direction. From the variations between various calibration sequences, we estimate that ω is known to an accuracy of ≃1°.
The light polarization fraction p and polarization orientation angle ψ are then defined as:
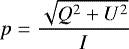 (3)
(3)
The magnetic field orientation is defined by ψ rotated by 90°. The Q and U in Eq. (2), and therefore ψ are in the IAU convention, that is, positive counterclockwise on the sky, and measured with respect to Equatorial north (corresponding to ψ = 0 °). Comparison to data taken in different convention, such as the Planck data, which are delivered in the COSMO convention with respect to Galactic North, require changing the angle convention (which can be done simply as QC = QI) and UC = −1 × UI) and the appropriate coordinate rotation of Q and U. In this paper, since we study the orientation of the magnetic field in the Galactic plane, we discuss values of the polarization angles in Galactic coordinates and in the COSMO convention (as defined in the HEALPIX software packages Górski et al. 2005). In this paper, we also refer to the angle dispersion function 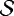 which quantifies the regularity of the B orientation measured defined as: (Planck Collaboration Int. XIX 2015, see) as
which quantifies the regularity of the B orientation measured defined as: (Planck Collaboration Int. XIX 2015, see) as
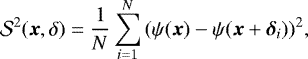 (5)
(5)
where x represents the central pixel, and ψ(x +δi) the polarization angle at a sky position displaced from the center by the displacement vector δi. The average in Eq. (5) is taken over an annulus of radius δ = |δ| (the “lag”) and width Δδ around the central pixel and containing N pixels. 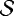 can be computed at varying angular resolution of the data and with a lag usually ranging from half the data FWHM to arbitrarily large scale, and
can be computed at varying angular resolution of the data and with a lag usually ranging from half the data FWHM to arbitrarily large scale, and 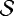 increases with δ as the field structure decorelates with increasing scale.
increases with δ as the field structure decorelates with increasing scale.
Inversion of the observed signals to derive sky maps of I, Q and U was done through polarization map-making algorithms. We used two different map-making algorithms, SCANAMORPHOS and ROMA, which are described in Sects. 3.5.2 and 3.5.3 respectively. We checked that the two algorithms give consistent results, and used the SCANAMORPHOS maps for the data analysis, which appeared of better quality at the current stage of the processing.
3.5.2 SCANAMORPHOS
The SCANAMORPHOS software was initially developed to process on-the-fly data from the PACS and SPIRE bolometer arrays on-board Herschel (Roussel 2013). The software has subsequently been refined to cope with the dominant atmosphericemission in ground-based observations for different instrument architectures, such as ArTéMiS on APEX (Roussel 2018) and NIKA2 on the IRAM 30-m telescope. It has also been adapted to process the polarization data of PILOT as outlined below. Its core principle is to exploit all the available redundancy in the observations, assuming only that the sky brightness is invariant in time and that the component of the low-frequency noise that is uncorrelated (termed individual drifts or flicker noise in the documents describing the code) has a symmetric probability distribution around zero, without necessarily being Gaussian. The full processing comprises the following tasks, most of them iterative: (1) slicing of scans into distinct scan legs, allowing for a large variability of the scanning speed inherent to balloon observations; (2) baseline subtraction using robust linear fits to the time series of the whole observing tiles, blocks of 4 scan legs, and individual scan legs, over a source mask that is automatically built and updated; (3) destriping using baseline subtraction in which the fits are constrained by the data redundancy, in order to provide acoherent solution for all scan legs and all detectors; (4) masking of glitches detected exploiting the redundancy to avoid masking true sources; (5) subtraction of the average drift on small timescales, that is, the common mode of both the residual low-frequency noise and the residual atmospheric signal; (6) subtraction of the individual drifts on successively smaller timescales; (7) projection of the corrected data. The definition of the time and space grids used by these tasks and the algorithm are described in the companion paper of the code developed for Herschel.
In order to deal with polarization data, ideally three time series corresponding to the I, Q and U Stokes parameters should be considered in the modules subtracting the drifts, instead of a single brightness time series. Even in the absence of noise, the recorded signal at a given location varies as a function of time and detector, due changes in the HWP position, focal plane position and parallactic angle as given in Eq. (2). However, the noise-free I, Q and U series should be invariant. The Stokes parameters are recomputed at each iterative step following the formalism of Eq. (2). The measured signal at a given time and for a given detector can then in principle be compared to the signal predicted from I, Q and U series computed from all the available data. But the signal depends on Q and U through sinusoidal terms, whose argument depends on time and detector. To avoid modulating the errors on Q and U when computing signal averages or differences, we proceed in a slightly different way, by subtracting the simulated Q and U terms from the measured signal to generate a “noised intensity” time series, that can be directly compared to the simulated intensity. In case where there is not enough redundancy in the analysis angles for a given pixel, that is, when these are distributed over fewer than 4 separate groups, Q and U are not computed and the total intensity is equated to twice the average signal. This occurs only on the edges of the maps. In practice, the initial data are too noisy to allow meaningful estimates of the Stokes parameters, leading us to perform the first few drift subtraction steps as if the data were not polarized (i.e., assuming Q = U = 0). It is only when the major part of the average drift has been subtracted that we take polarization into account.
For the observations discussed here, the data was taken in a way such that three observing tiles out of four were taken with roughly the same scan direction, the fourth tile being taken roughly in the orthogonal direction. We have explored the possibility of modifying the reference I, Q, U maps in the SCANAMORPHOS destriping module. These are normally computed from the whole data at the previous iteration of the destriping, but it is possible to lower the weight of some tiles, or to provide independent maps from simulations, for example. We have not used this option for the present work. Given the median scan speed and the sampling rate of the data, the fiducial value of the noise stability length is 1.5 times the beam FWHM, and we have set it to twice the FWHM to increase sample statistics.
The timelines described in Sect. 3.4 were provided to the code, without glitch masking, since glitches are identified internally to SCANAMORPHOS. We provided timelines with the atmospheric contribution removed, but checked that maps computed without this initial correction are compatible with the ones presented here, thanks to the ability of SCANAMORPHOS to subtract common modes. The resulting I, Q, U maps obtained over the extent of the whole region mapped are shown in Fig. 3. The structure of the magnetic field inferred is shown in Fig. 5. The uncertainty on the polarization angle are also shown in Fig. 5. These maps are discussed in Sect. 4.
 |
Fig. 3 PILOT maps of the I, Q, U parameters obtained towards the galactic center region, processed using the SCANAMORPHOS software. The maps are shown at the full resolution of the instrument of 2.2′. The maps are in units of 103 MJy sr−1. |
3.5.3 ROMA
The ROMA code, described in de Gasperis et al. (2016), was developed for cosmology experiments aiming at measuring the polarization of the Cosmic Microwave Background (CMB). For this reason it is optimized for noise dominated timelines. The code assumes stationnarity of the noise statistical properties, which is reasonably the case for the data of PILOT flight#2 (see Mangilli et al. 2018). Under the assumption of a Gaussian and stationary noise, the ROMA code adopts a Fourier-based, preconditioned conjugate gradient iterative method to solve for the maximum-likelihood signal map yield by the Generalized Least Square (GLS) approach (see de Gasperis et al. 2016, for details). In particular, given the pointing matrix A and the timeline vector D, the optimal GLS solution for the signal estimate 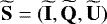 is:
is:
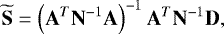 (6)
(6)
where 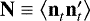 is the noise covariance matrix in the time domain (nt indicates the instrumental noise at time t). It should be noted that the matrix N is block diagonal only in case of no noise cross-correlation.
is the noise covariance matrix in the time domain (nt indicates the instrumental noise at time t). It should be noted that the matrix N is block diagonal only in case of no noise cross-correlation.
The PILOT timelines of the four galactic center region observations are provided to the code after gap-filling of calibration sequences at the ends of scans using a white noise realization with the white noise level of each detector. The glitches are also masked and the atmospheric contribution is removed as described in Sect. 3.4.
In order to ensure that the signal is noise dominated, we subtracted from the observed timeline a simulated timeline based on the Planck 353 GHz total intensity map extrapolated to the PILOT frequency. The subtracted component is assumed unpolarized and is therefore equal on the TRANS and REFLEX detectors apart for possible pointing mismatch. The difference timeline is processed through ROMA with 100 iterations that are enough to ensure a good convergence. The map used for the signal subtraction is added back to the resulting total intensity map. The noise covariance matrix provided to the ROMA code was determined from the PILOT observations of the BICEP field obtained during the same flight (Mangilli et al. 2018), treated in the same way as the L0 data. The map resolution is set to Nside = 2048 (1.7′). The code also provides maps of the variances on the Stokes parameters as well as a map of the inverse conditioning matrix allowing to assess if a sufficient number of data taken at different HWP angles are available for a given pixel. The pixel inverse condition number (ICN) is defined as the ratio of the absolute values of the smallest and largest eigenvalue of the preconditioning matrix, and provides a good tracer of the errors in the map due to a non ideal angle coverage on the given pixel (a value of ICN = 0.5 means uniform angle coverage). In our case, pixels with ICN ≤ 10−2 are removed from the analysis.
The I, Q, U maps obtained are shown in Fig. 6. Due to the difficulty of accurately modeling the noise covariance matrix, in particular the off-diagonal terms that are not included in the analysis, the quality of the ROMA polarization maps is degraded and residuals stripes are still present, in particular in the Q map. For this reason we will not use the ROMA maps as the baseline for the analysis. Still, the ROMA maps allow for validation tests of the baseline results, as discussed in Sect. 4.2
 |
Fig. 4 PILOT maps of, from top to bottom, the total intensity I, the polarized intensity P, the Stokes Q and U parameters, zoomed on the CMZ region and processed using the SCANAMORPHOS software. The maps are shown at the full resolution of the instrument of 2.2′. The intensity map is shown in log scale. The maps of P, Q and U are in units of 103 MJy sr−1. |
4 Polarization results
4.1 Polarization maps
The final maps of Stokes I, Q and U parameters across the full Galactic center field observed by PILOT are shown in Fig. 3. In this paper, we focus on the polarization results for the ~ 3.1° × 0.9° CMZ region, for which we show zoomed maps of I, Q and U in Fig. 4. The corresponding map of the polarization angle ψ, calculated according to Eq. (4) is shown as an overlay in Fig. 5.
A common issue for the interpretation of polarization observations is how the observed polarization angles (and inferred magnetic field structure) projected onto the plane of the sky correspond to emission regions situated along the LOS. This is especially of concern for observations in the Galactic Plane. In Appendix A, we present a simple model that we have developed to quantify LOS depth through the Galactic Plane that is probed by our observations. From this model, we conclude that the CMZ makes the dominant contribution to our observed polarization signal towards the Galactic center. This is qualitatively confirmed by Fig. 4, where it is evident that the structure in the PILOT Q and U maps (as well as I) is dominated by well-known emission features of the CMZ, for instance, Sgr B2, the Brick and the 20 km s−1 cloud (Fig. 1) (e.g. Kauffmann et al. 2017, and references therein).
What is most striking about the PILOT polarization data for the CMZ is that the polarization angle is relatively uniform across the entire region shown in Fig. 5, with a dominant orientation of approximately + 22°. This corresponds to a dominant POS magnetic field orientation of approximately + 22° with respect to the Galactic Plane. Close inspection of the polarization vectors in Fig. 5 suggests that the polarization angle diverges from this overall mean orientation in regions of high brightness, for instance, near the Sgr B2, 20 and 50 km s−1 clouds. We quantify this in Fig. 7, where we show the distribution of polarization angles within regions of increasing 240 μm intensity in the I map. Polarization angle measurements with high uncertainty (σ(ψ) > 8°) are excluded from the analysis. The peak of the polarization angle distribution measured for high brightness regions (shown as blue histograms in the top panel) is clearly shifted towards lower values compared to the polarization angles measured in regions of lower intensity. We discuss possible explanation for this trend in Sect. 5.2, where we make a preliminary estimate for the average magnetic field strength in the CMZ based on the POS field structure that we infer from the PILOT dust polarization measurements.
 |
Fig. 5 Top panel: map of the B-field orientation as derived from the PILOT data using the SCANAMORPHOS software. The total intensity is shown as the color map, in log scale. The B-field orientation is shown as constant length segments orthogonal to the polarization orientation, where σψ < 8°. Bottom panel: map of the polarization angle uncertainty per beam, in degrees. |
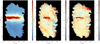 |
Fig. 6 PILOT large scale maps of the I, Q and U Stokes parameters obtained with the ROMA software. The maps are in units of 103 MJy sr−1. |
 |
Fig. 7 Dust polarization angles measured in the CMZ as a function of 240 μm intensity. Top panel: polarization angle distributions plotted separately for intervals of increasing 240 μm intensity in the PILOT I map. The characteristic 240 μm brightness is indicated using colour, and ranges from 103.5 (red) to 105.1 MJy sr−1 (blue). Bottom panel: mean and mode of the polarization angle distributions directly as a function of the 240 μm intensity. |
4.2 Comparison between map-making methods
We take advantage of having two independent map-making methods to compare the polarization angles results obtained with the two pipelines.
Figure 8 shows the ψ map pixel histograms obtained with the SCANAMORPHOS software and the ROMA software in the signal dominated region defined by − 1.4° < ℓ < 1.8° and − 0.1° < b < 0.4°. The two histograms peak at angle values that are similar (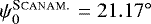 ,
,  ), however the ROMA histogram shows a larger dispersion which is due to the poorer quality of the ROMA polarization maps that show residual stripes, in particular inthe Q map. As mentioned in Sect. 3.5.3, this is due to the fact that the ROMA map-making strongly depends on the accurate modeling of the detector noise and the noise covariance matrix for the moment does not include the off-diagonal terms linked to the correlated noise between the detectors.
), however the ROMA histogram shows a larger dispersion which is due to the poorer quality of the ROMA polarization maps that show residual stripes, in particular inthe Q map. As mentioned in Sect. 3.5.3, this is due to the fact that the ROMA map-making strongly depends on the accurate modeling of the detector noise and the noise covariance matrix for the moment does not include the off-diagonal terms linked to the correlated noise between the detectors.
The very good agreement of the polarization angles obtained with two pipelines that rely on very different assumptions and are implemented independently shows the robustness of the results and it is an important test of the quality of the data.
 |
Fig. 8 Normalized histograms of the PILOT polarization angles obtained by analyzing the polarization angles map generated with the ROMA map making (black) and with the SCANAMORPHOS map making (red). |
4.3 Comparison with Planck
The Planck satellite experiment observed the whole sky with two instruments, the Low Frequency Instrument (LFI) from 30 to 70 GHz and the High Frequency Instrument (HFI) from 100 to 857 GHz. Among the nine observing bands, seven channels between 30 and 353 GHz measured polarization in addition to intensity with spatial resolutions ranging from 30′ to 5′ (Planck Collaboration I 2018). In this paper, we make use of the publicly available Planck 2018 release LFI and HFI maps, described in Planck Collaboration II (2019) and Planck Collaboration III (2019). Planck polarization maps adopt the HEALPIX projection scheme (Górski et al. 2005), in Galactic coordinates, and use the COSMO convention for the definition of the polarization angles. Polarization angles for Planck data are computed from the Q and U maps according to Eq. (4).
Given that dust emission is optically thin at Planck frequencies as well as 240 μm, even towards the inner regions of the Galactic plane and that the same population of dust grains is expected to dominate the emission in both wavelength regimes, it is expected that the orientation of the polarization detected with Planck and PILOT should be similar. Different emerging polarization angles could result from emission by specific dust populations with different alignment properties or spatial distribution and varying B-field orientation along the LOS. More probably however, differences would result from remaining systematic effects in the PILOT or Planck data. Comparing apparent polarization directions is therefore an important test of the data quality.
Figure 9 compares the B-field orientation measured with PILOT at 240 μm and Planck at 353 GHz. We can see, despite the different resolutions (5′ for Planck 353 GHz and 2′ for PILOT),that there is an overall agreement between the measured polarization directions. It can be noticed on this figure that the Planck polarization angle directions are less homogeneous than the directions measured by PILOT. The difference map of the polarization angle between Planck and PILOT (bottom panel) shows some excursions as large as 45° for some pixels, but are spread around zero, especially along the Galactic plane. We can see on this difference map obvious imprint of the low Nside HEALPIX pixels that can be seen in the Planck 353 GHz polarization angle map (and can not come from PILOT maps as they are not projected using HEALPIX). Since dust emission is in principle optically thin at the PILOT and Planck frequencies even towards the CMZ region, and the observed orientation differences do not increase with column density, we do not think that they are due to the data at the different frequencies sampling B at different distances along the LOS. We consider it more likely that the observed differences reflect uncertainties in the bandpass mismatch corrections applied to the Planck data (see, e.g. Planck Collaboration IX 2014; Planck Collaboration III 2019) or spatial filtering of the PILOT data. As a consequence, the magnetic field orientation inferred from either experiment in those areas shouldbe taken with caution.
Figure 10 shows the histograms of the polarization orientation observed with PILOT (degraded to a resolution of 5′, to match Planck highest frequencies) and Planck (70, 100, 143, 217 and 353 GHz). Histograms are computed from the polarization maps inside a box having − 1.3° < ℓ < 1.8° and − 0.4° < b < 0.1°, corresponding roughly to where the intensity measured by PILOT at 240 μm is larger than 500 MJy sr−1. The histogram of the PILOT polarization angle peaks at a value (the Gaussian best fit of the histogram has ψ0 = 24.1°, σ =5.9°) very similar to where Planck 217 and 353 GHz histograms peak (ψ0 = 21.3°, σ =11.3° and ψ0 = 24.9°, σ =12.3°, respectively), showing that PILOT sees the same dust as Planck at 217 and 353 GHz. The PILOT histogram is narrower than the Planck ones (when PILOT data resolution is degraded to 5′), highlighting the more homogeneous polarization directions already observed in Fig. 9.
The Planck 100 GHz channel is expected to have an important CO-line contribution towards the Galactic center region and therefore a strong spurious polarization due to spectral mismatch between bolometers. This spurious polarization was corrected for in the Planck 2018 maps, but the correction is known to be inaccurate in this region were the matter velocity can shift the CO-line significantly with respect to other regions of the sky, where the 100 GHz bolometer response to the CO-line was calibrated for spurious polarization correction (Planck Collaboration III 2019). We interpret the mean value of the angle at 100 GHz of approximately − 50° to be partially due to this residual spurious polarization. At the other Planck frequencies (70 and 143 GHz), the histograms peak around 0° (ψ0 = −3.6°, σ =15.2° and ψ0 = 1.5°, σ =12.8°, respectively).
In Fig. 11, we look at the Galactic longitude profile of the PILOT and Planck polarization angles, computed in boxes of size Δℓ = 0.15° and Δb = 0.3° on either side of the Galactic plane, ranging from ℓ = −7.5° to ℓ = 7.5°. We can see that the PILOT data polarization angle profile follows fairly that of Planck 217 and 353 GHz and that the discrepancies between PILOT and Planck 217 and 353 GHz is of the same order than that of the discrepancies between those two Planck channels. The global dust polarization profile, traced by PILOT and Planck 217 and 353 GHz, shows a polarization angle close to zero (magnetic field projection on the sky along the Galacitc plane) from ℓ = −7.5° to ℓ = 7.5°, except for a region corresponding to the extent of the CMZ (from − 1° to 1.5° Molinari et al. 2011) where the measured angles range from 20° to 30°. At 143 GHz, the polarization angle follows that of the dust outside the CMZ (ℓ < −1° and ℓ > 1.5°) but shows completely different behaviour inside, being much closer to zero (as noticed in Fig. 10). This is the hint for another component than dust – presumably synchrotron – dominating the emission in the CMZ at frequencies under 143 GHz.
 |
Fig. 9 Top panel: comparison between the B-field orientation as derived from the PILOT 240 μm (red) and Planck 353 GHz (green) dust polarization measurements. The B-field orientationis shown as constant length line segments. The background image is the PILOT Stokes I map shown in log scale. Bottom panel: map of the angle difference (in degrees) between Planck 353 GHz and PILOT 240 μm. |
 |
Fig. 10 Histogram of the PILOT polarization angles (black) on the Galactic center region compared to Planck observations at 70, 100, 143, 217 and 353 GHz (blue, green, yellow, orange and red, respectively). We overplot the Gaussian fits of these histograms as thicker lines to guide the eye. |
 |
Fig. 11 Polarization angle profile as a function of Galactic longitude. The mean polarization angle is computed from longitudes between −7.5° and 7.5° and latitudes between −0.15° and 0.15° in 100 boxes of size 0.15° in longitude. The longitude profiles are shown for the Planck 143, 217 and 353 GHz channels (blue, orange and red, respectively) and PILOT (black). The error bars represent the standard deviation of the angle in each boxes. |
5 Discussion
5.1 Do PILOT polarization measurements probe the field structure in the CMZ?
Analysis of the Planck satellite dust polarization data has shown that depolarization due to the complex nature of the field structure is omnipresent (see e.g. Planck Collaboration Int. XIX 2015). This is especially true towards the Galactic plane where the magnetic field is likely to rotate significantly along the LOS and within the instrument beam as result of variations of the ordered field and turbulence. Even if dust emission is optically thin at the observed frequencies, it is thus not necessarily the case that polarization measurements are sensitive to the emission along the whole LOS, as the signal may suffer significant depolarization.
Here we verify that when observing towards the Galactic center with PILOT, the polarized signal is indeed dominated by the CMZ region. For this, we use a simplified model of the ordered and turbulent distribution of the magnetic field in the Galactic disk. For the dust density distribution, we assume that the Milky Way has a four-armed spiral structure, superimposed on an axisymmetric exponential profile. The model, which is described in Appendix A, is constrained using the observed polarization fraction profile along the Galactic plane obtained from the Planck RC4 data. We use this model to estimate the relative contribution of structures in the Galactic disk along the LOS of sight towards the region observed with PILOT. We explore three representative regimes: no turbulent field, equipartition between the ordered and turbulent fields, and a turbulent field that is three times stronger than the ordered field. In all cases, turbulence in the disk along the LOS towards the Galactic center is insufficient to depolarize the dust emission to the low values (pobs ~ 1 to 2%) that are observed. We conclude that the observed polarization properties are due to emission that is intrinsic to the CMZ. This is qualitatively confirmed by the good correspondence between emission structures in the PILOT total intensity map and the Q, U and polarized intensity (P) maps of the CMZ (see Fig. 4).
5.2 Uniform orientation of the POS B-field
The orientation of POS magnetic field inferred from the polarization direction measured by PILOT is surprisingly uniform across the 3.1° × 0.9° field presented in this paper (see Sect. 4). In this subsection, we quantify the regularity of the field on linear (and not just angular) scales in the CMZ via a comparison with the dispersion in the dust polarization angles in the local ISM measured by Planck. We then consider how the observed regularity of the field can be reconciled with the low fraction of dust polarization that is observed towards this region by Planck, and what we can infer about the large-scale geometry of the field in the Galacticcenter region.
The polarization angle dispersion function 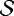 quantifies how polarization angles decorrelate with increasing angular scale (see Eq. (5)). In Planck Collaboration Int. XIX (2015), the large scale distribution of
quantifies how polarization angles decorrelate with increasing angular scale (see Eq. (5)). In Planck Collaboration Int. XIX (2015), the large scale distribution of 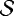 was studied at an angular resolution of 1° and associated lag of 30′, since these parameter values mitigate noise bias for an intermediate latitude study.
was studied at an angular resolution of 1° and associated lag of 30′, since these parameter values mitigate noise bias for an intermediate latitude study.
Using the same Planck data product, working resolution and lag as in Planck Collaboration Int. XIX (2015), we find a median value of 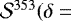 30′)=3.2° in the region covered in Fig. 4. This value is close to the median value of
30′)=3.2° in the region covered in Fig. 4. This value is close to the median value of 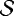 measured over the entire mid-latitude sky by Planck Collaboration Int. XIX (2015). We emphasize, however, that this apparent agreement does not mean that the field in the Galactic center and local ISM have similar structural properties. The dust emission measured by Planck at intermediate latitudes is produced in the relatively nearby ISM (within ~ 1 kpc). An angular scale measured at intermediate latitude therefore corresponds to a spatial scale that is ~ 8 times smaller than the spatial scale corresponding to the same angular scale measured at the Galactic center. Expressed otherwise, our measurement of
measured over the entire mid-latitude sky by Planck Collaboration Int. XIX (2015). We emphasize, however, that this apparent agreement does not mean that the field in the Galactic center and local ISM have similar structural properties. The dust emission measured by Planck at intermediate latitudes is produced in the relatively nearby ISM (within ~ 1 kpc). An angular scale measured at intermediate latitude therefore corresponds to a spatial scale that is ~ 8 times smaller than the spatial scale corresponding to the same angular scale measured at the Galactic center. Expressed otherwise, our measurement of 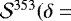 30′)=3.2° in the Galactic center indicates that the POS field structure remains homogeneous over a ~ 8 times larger length scale than in the local ISM.
30′)=3.2° in the Galactic center indicates that the POS field structure remains homogeneous over a ~ 8 times larger length scale than in the local ISM.
We constructed a map of 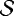 from the PILOT data itself. After degrading the resolution of the PILOT data to 5′ to mitigate noise bias, we obtain a median value of
from the PILOT data itself. After degrading the resolution of the PILOT data to 5′ to mitigate noise bias, we obtain a median value of 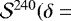 2.5′) = 2.5°. This value is consistent with the median
2.5′) = 2.5°. This value is consistent with the median 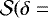 30′) from Planck, considering that it is measured at a smaller lag. We conclude that the POS magnetic field orientation in the GC region is intrinsically more regular than in the nearby ISM.
30′) from Planck, considering that it is measured at a smaller lag. We conclude that the POS magnetic field orientation in the GC region is intrinsically more regular than in the nearby ISM.
The analysis of the Planck data demonstrated that there is an anti-correlation between 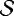 and dust polarization fraction p (see Fig. 23 of Planck Collaboration Int. XIX 2015), a relation that can be used to infer the characteristic value of p that would be expected for a given value of
and dust polarization fraction p (see Fig. 23 of Planck Collaboration Int. XIX 2015), a relation that can be used to infer the characteristic value of p that would be expected for a given value of 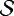 . For
. For 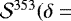 30′) = 3.2°, the
30′) = 3.2°, the 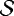 -p anti-correlation would predict pref ≃ 6%. The largest possible p values compatible with this
-p anti-correlation would predict pref ≃ 6%. The largest possible p values compatible with this 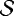 value – corresponding to an orientation of the ordered B-field that is maximally in the plane of the sky – would be very close to pref = pmax ≃ 22%, the maximumvalue observed on the sky in the Planck data at 353 GHz (Planck Collaboration Int. XIX 2015; Planck Collaboration XII 2019). However, the polarization fraction at 353 GHz that is actually measured by Planck in the Galactic center region is pobs = 1.6% only. This leads to a value for theproduct
value – corresponding to an orientation of the ordered B-field that is maximally in the plane of the sky – would be very close to pref = pmax ≃ 22%, the maximumvalue observed on the sky in the Planck data at 353 GHz (Planck Collaboration Int. XIX 2015; Planck Collaboration XII 2019). However, the polarization fraction at 353 GHz that is actually measured by Planck in the Galactic center region is pobs = 1.6% only. This leads to a value for theproduct 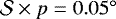 , much smaller than observed values in the Planck data at latitudes |b | > 2°, including towards regions with columndensities up to NH = 2 1023 H/cm2 at 10′ resolution similar to those of the CMZ (see in Planck Collaboration XII 2019). Inspection of the Planck maps of p and
, much smaller than observed values in the Planck data at latitudes |b | > 2°, including towards regions with columndensities up to NH = 2 1023 H/cm2 at 10′ resolution similar to those of the CMZ (see in Planck Collaboration XII 2019). Inspection of the Planck maps of p and 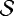 at 353 GHz shows that low values of
at 353 GHz shows that low values of 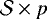 are not specific to the CMZ region discussed here, but actually extend to the whole inner Galactic plane, over a region covering − 60° < ℓ < +60°. In principle, this discrepancy could be dueto lower values of either p or
are not specific to the CMZ region discussed here, but actually extend to the whole inner Galactic plane, over a region covering − 60° < ℓ < +60°. In principle, this discrepancy could be dueto lower values of either p or 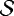 . We explore each of these two possibilities below.
. We explore each of these two possibilities below.
Lower values of p in the inner MW could be due to an additional, unpolarized emission such as free–free or spinning dust emission. To explore this possibility, we compared the Planck Sky Model intensity maps of the thermal dust and the free–free emission at 353 and 217 GHz, using the templates described in Planck Collaboration X (2016). We computed the ratio of the thermal dust and the free–free emissions as a function of the longitude in the Galactic plane. We found that the contribution of the free–free emission in the Galactic plane is at least two orders of magnitude lower than the thermal dust, both at 217 and 353 GHz. In the Galactic center region the ratio between the thermal dust and the free–free component is ≃ 150. Adding the free–free contribution to the total intensity would therefore lower the polarization fraction by at most 0.06%. We also considered the Anomalous Microwave Emission (AME) using the same procedure and found that this contribution is negligible, whichever realistic model is used for SED extrapolation. These additional components are therefore insufficient to explain the low polarization fraction observed in the Galactic plane.
From now on, we consider that the observed polarized emission is entirely due to thermal dust emission. Because this emission occurs in the Rayleigh regime where the dust grain size is much smaller than the emission wavelength, p can be written as
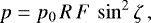 (7)
(7)
where 0 ≤ R ≤ 1 is the Rayleigh reduction factor expressing the degree of grain alignment (Greenberg 1968), 0 ≤ F ≤ 1 is the depolarization factor due to magnetic turbulence along the LOS (Lee & Draine 1985), and p0 is the intrinsic dust polarization fraction that would be observed if all other parameters were unity. Within this framework, an observed decrease of p can be attributed to a decrease of p0, R, F or sin2ζ or to a combination. We now examine the effect of each parameter in turn.
Dust grains in the inner regions of the Galaxy could have different properties than in the diffuse ISM, for instance, due to an evolution of the grain shape and/or composition, which would cause them to be either less polarizing (lower p0) or less efficiently aligned with the magnetic field (lower R). Although there is currently no independent observational evidence to support this hypothesis, we note that the spectral index of thermal dust emission β in the Planck frequency is observed to change from values typical of the diffuse ISM (β ≃ 1.6) in the outer Galactic plane to significantly larger values (β > 2) on LOS towards the inner Galactic plane in the Planck data (Planck Collaboration XI 2014b; Planck Collaboration Int. XLVIII 2016). The origin of these variations is currently not understood. The potential relationship between the low polarization fraction and high spectral index observed toward the inner Galactic plane would deserve further investigation.
Turning to the parameter F, we consider the possibility that magnetic turbulence is stronger, and hence more depolarizing (lower F), toward the inner Galactic plane. The general expression of F is 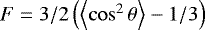 (Lee & Draine 1985), where θ is the angle between the local magnetic field and the ordered field, and the average is taken along the LOS. F should decrease with increasing level of magnetic turbulence, from F = 1 for a perfectly ordered field to F → 0 for a fully random field. For the long LOS toward the inner Galactic plane, which presumably encounter a large number of turbulent cells, F should tend toward a limiting value, F0, that reflects the typical ratio of the ordered field to the total (ordered + turbulent) field.
(Lee & Draine 1985), where θ is the angle between the local magnetic field and the ordered field, and the average is taken along the LOS. F should decrease with increasing level of magnetic turbulence, from F = 1 for a perfectly ordered field to F → 0 for a fully random field. For the long LOS toward the inner Galactic plane, which presumably encounter a large number of turbulent cells, F should tend toward a limiting value, F0, that reflects the typical ratio of the ordered field to the total (ordered + turbulent) field.
To closethe discussion on Eq. (7), we consider the possibility that the magnetic field could be oriented close to the LOS (low sin2ζ). The values of the dust polarization fraction discussed above (6% < pref < pmax) would imply 15° < ζ < 30°. If the distribution around the Planck 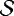 -p anti-correlation at constant
-p anti-correlation at constant 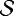 is mostly due to variations in ζ along any LOS, then we would favour ζ ~ 15° for the GC, corresponding to a dust polarization fraction close to the maximum value observed with Planck of pmax ≃ 22%. A mean magnetic field that is weakly inclined to the LOS in the GC region could possibly be explained by the geometry of the large-scale Galactic magnetic field, for instance, if the large-scale field is bi-symmetric and follows the Galactic bar, which is now believed to be inclined by ~ 30° with respect to the LOS (Bland-Hawthorn & Gerhard 2016). Such a simple geometric explanation for the low
is mostly due to variations in ζ along any LOS, then we would favour ζ ~ 15° for the GC, corresponding to a dust polarization fraction close to the maximum value observed with Planck of pmax ≃ 22%. A mean magnetic field that is weakly inclined to the LOS in the GC region could possibly be explained by the geometry of the large-scale Galactic magnetic field, for instance, if the large-scale field is bi-symmetric and follows the Galactic bar, which is now believed to be inclined by ~ 30° with respect to the LOS (Bland-Hawthorn & Gerhard 2016). Such a simple geometric explanation for the low 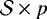 values based on a specific value of ζ would be likely if the low values were restricted to the CMZ region, but it can probably not explain the low values observed over the whole inner Galactic plane.
values based on a specific value of ζ would be likely if the low values were restricted to the CMZ region, but it can probably not explain the low values observed over the whole inner Galactic plane.
We finally turn to the polarization angle dispersion function, 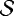 , which could also possibly explain the low observed values of
, which could also possibly explain the low observed values of 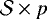 . As a reminder,
. As a reminder, 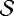 measures the local POS variations of the polarization angle, ψ, and reflects the independent changes of ψ between neighbouring LOS. As such,
measures the local POS variations of the polarization angle, ψ, and reflects the independent changes of ψ between neighbouring LOS. As such, 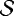 is sensitive to the differential effect of turbulent cells between those LOS. As we argued in our discussion of F, the long LOS toward the inner Galactic plane must encounter a large number N of turbulent cells. Therefore, we expect ψ for each LOS to tend toward a limiting value, ψ0, representative of the average magnetic field along that LOS, with the deviation from ψ0 decreasing as N−1∕2. Accordingly, we expect
is sensitive to the differential effect of turbulent cells between those LOS. As we argued in our discussion of F, the long LOS toward the inner Galactic plane must encounter a large number N of turbulent cells. Therefore, we expect ψ for each LOS to tend toward a limiting value, ψ0, representative of the average magnetic field along that LOS, with the deviation from ψ0 decreasing as N−1∕2. Accordingly, we expect 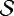 computed at small lags to converge towards 0°, following
computed at small lags to converge towards 0°, following 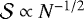 , as shown at constant p in Planck Collaboration XII (2019).
, as shown at constant p in Planck Collaboration XII (2019).
To conclude on the low observed values of 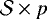 , we favor interpretations invoking the large number of turbulent cells along the long LOS towards the inner Galactic plane, which affects both p and
, we favor interpretations invoking the large number of turbulent cells along the long LOS towards the inner Galactic plane, which affects both p and 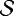 . We exclude the possibility that additional unpolarized emission such as free–free or AME could explain the observations, but cannot rule out dust properties specific to the inner regions of the Galaxy. An exhaustive analysis of this effect will require realistic simulations of the magnetic field and density distribution in the MW, which is beyond the scope of this paper.
. We exclude the possibility that additional unpolarized emission such as free–free or AME could explain the observations, but cannot rule out dust properties specific to the inner regions of the Galaxy. An exhaustive analysis of this effect will require realistic simulations of the magnetic field and density distribution in the MW, which is beyond the scope of this paper.
The POS magnetic field in the GC region is found to be tilted clockwise to the trace of the Galactic plane by ≃ + 22° on average. Figure 11 shows the polarization angle profile as a function of Galactic longitude for the Planck 143, 217 and 353 GHz channels (blue, orange and red, respectively) and PILOT (black). The mean polarization angle is computed from longitudes between −7.5° and 7.5° and latitudes between − 0.15° and 0.15° in 100 boxes of size 0.15° in longitude. The error bars represent the standard deviation of the angle in each box. The comparison with larger-scale Planck maps indicates that the + 22° tilt angle is actually restricted to the longitude range − 1.5° < ℓ < +1.5°. Outside thisrange, the tilt angle approaches zero, that is, the POS magnetic field becomes approximately parallel to the Galactic plane.
The measured tilt angle ≃+22° is not easilyunderstood. There is no obvious gaseous structure that fills the GC region and has a + 22° clockwise tilt to the Galactic plane. The CMZ spans roughly the above longitude range, but it is much less extended in latitude, and only a relatively small portion of it (the western part of the twisted ring; see Sect. 5.4) was observed to have a clockwise tilt compatible with + 22°.
5.3 Characteristic magnetic field strength in the CMZ
The regularity of the POS magnetic field orientation in the L0 region suggests that the magnetic field there is very strong, that is, strong enough for magnetic pressure, Pmag, to withstand the ram pressure from ambient interstellar clouds, Pram. Using a conservative estimate for Pram in the Galactic center region, Yusef-Zadeh & Morris (1987) previously showed that the condition Pmag ≳ Pram is roughly equivalent to B ≳ 1 mG.
Here, we employ similar reasoning in an effort to estimate the magnetic field strength using the observed structure of the POS magnetic field in the CMZ region. As described in Sect. 4.1, we observe that the POS magnetic field orientation tends to become more parallel to the Galactic Plane in regions of high brightness. This is especially evident for the high-brightness structure in our total intensity map corresponding to Sgr B2, the 20 and 50 km s−1 clouds and the Brick, which exhibit significant departures from the mean POS magnetic field orientation ≃ + 22°. We can thus reasonably imagine that these clouds have a ram pressure perpendicular to the magnetic field that is comparable to the local magnetic pressure: Pram,⊥~ Pmag, where 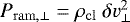 , ρcl is the mean mass density of the cloud, and δv⊥ is the relative cloud velocity (with respect to its surroundings) perpendicular to the magnetic field.
, ρcl is the mean mass density of the cloud, and δv⊥ is the relative cloud velocity (with respect to its surroundings) perpendicular to the magnetic field.
For the characteristic gas densities in these regions ρcl, we adopt values obtained from HC3N excitation studies by Mills et al. (2018) and Morris et al. (1976). For the LOS velocity of a cloud δvLOS relative to its surroundings, we use the kinematic structure of the CMZ region presented by Henshaw et al. (2016). The values that we adopt for each cloud are listed in Table 1. To obtain the corresponding real space (i.e., 3D) relative velocities, we assume that the clouds as well as their surroundings follow the orbital trajectory proposed by Kruijssen et al. (2015) and we assign each cloud to the orbital velocity at its nearest projected point on the trajectory. Finally, we project the 3D relative velocities onto the plane perpendicular to the mean magnetic field, which we take to be inclined by ζ to the LOS and to have a POS orientation angle of + 22° (see Sect. 5.2). Table 1 shows the range of magnetic field strength estimates Bequ for ζ varying in the allowed range 0° < ζ < 90°.
Our four magnetic field strength estimates are reasonably close to each other. The spread by a factor ~ 3 can be attributed to differences in the estimated ram pressures of the four clouds. As expected, clouds with larger ram pressures tend to cause stronger perturbations in the magnetic field. Our field strength estimates are also very high by interstellar standards. Indeed, B is typically ~ a few μG in the Galactic disk and almost certainly stronger in the Galactic center region, with estimates ranging from ~ 10 μG (LaRosa et al. 2005)to B ≳ 1 mG (Yusef-Zadeh & Morris 1987) (see Ferrière 2009 for a review).
5.4 Coincidence with the 100-pc ring
The molecular cloud at the center of the CMZ is likely to orbit around the Galactic center following well defined trajectories, as described in Molinari et al. (2011) and Kruijssen et al. (2015). A legitimate question is to ask if the magnetic field as traced by dust associated to those clouds follows these structures even partly, or if the field lines are affected by the gas motion along those trajectories. If the field lines are significantly dragged by the gas motion, we would expect the B-field orientation to be somewhat parallel to the trajectories. We would also expect the polarization fraction to lower at the tangent point of the trajectories, where the B-field orientation would be essentially along the LOS. We used the analytical description of the trajectory proposed in Molinari et al. (2011) and the tabulated orbital values in Kruijssen et al. (2015) to construct the sky projected trajectory track on the plane of the sky. This track is overlaid for the Molinari et al. (2011) 100-pc ring on Fig. 1. We then compute the tangent direction to the track at each location along the trajectory. We finally compute the angle difference between this direction and the B-field orientation as measured by our polarization data, at each location along the track.
Figure 12 shows the angle difference between the B-field orientation as measured with PILOT and the tangent to the 100-pc ring. There is a very decent match between the B-field direction and the tangent to the trajectories of the Molinari 100-pc ring over half of the trajectory spanning negative longitudes. Over this section of the track, the B-field follows the tangent to the track to better than 8°. Those locations are indicated in Fig. 1. Along the location at positive longitudes however, the match is poor, with angle differences approaching≃45°. Using the physically motivated trajectories from Kruijssen et al. (2015) does not lead to a better overall match. In both cases, we looked but did not find any clear evidence for a trend for a decrease polarization fraction at the tangent points of the trajectories. These analyses confirm the visual impression when comparing the field orientation of Fig. 5 and the trajectories in Fig. 1 that the magnetic field orientation is very homogeneous over the whole region, as described inSect. 5.2, and shows very little direction change at the location of the trajectories. Therefore, the match in direction over half the 100-pc ring as described in Molinari et al. (2011) could also be purely fortuitous.
5.5 Comparison with previous ground measurements
In principle, the B-field orientation inferred from our data could be compared to that derived from similar FIR/submm data obtained from ground observations, as long as these observations are dominated by polarized emission from large dust grains. In practice, however, the comparison is complicated by several limitations. First, ground data are often obtained at high angular resolution, but cover very small sky regions. As a consequence, the data tabulated in the literature is often too scarce to fill-up one the PILOT beam, preventing the comparison. Second, the data processing of ground data is likely to filter large scale emission. A fair comparison would require filtering the PILOT data using the transfer function of the data processing applied to the ground data, but this is usually not feasible, since the information about the processing is often incomplete and the processing software is not readily available.
Out of the FIR/submm polarization data available described in Sect. 1, we selected the JCMT data of Matthews et al. (2009) obtained at 450 μm as the one with spatial coverage and completeness best matching that of our data. This data covers most of the extent of the 50 km s−1 molecular cloud highlighted in Fig. 1. Figure 13 shows the comparison between the JCMT data and the PILOT data. In order to perform the comparison, we transformed the JCMT data provided under the form of polarization fraction and angle into Stokes parameters and we computed the total intensity weighted average of the JCMT Stokes parameters falling in each pixel of our map. Those values were sky rotated to the same angle convention and coordinate system as the PILOT data. We then computed the corresponding angle orientation ψJCMT. In a simplified attempt to reproduce the low spatial frequency filtering of the signal in the JCMT data, we subtracted from the PILOT Q and U maps the average values measured in the region of Fig. 13 covered by our data but not observed in the JCMT data. The background subtracted map was used to compute ψ. The top panel of Fig. 13 shows the B-field orientation of JCMT and PILOT, overlaid to the PILOT intensity map, within the cloud 50 km s−1 region covered by the JCMT data. The bottom panel of Fig. 13 shows the histogram of the angles obtained from the two datasets. Although there is a significant dispersion and the statistics are low, the average of the angles are 17.05° and 16.72° for the PILOT and JCMT data respectively, and the corresponding average angle difference between the two datasets is 0.54°. If no background subtraction is applied to the PILOT data, the histogram is significantly skewed towards a non-zero angle difference value. This indicates that the somewhat large dispersion is unlikely to be due to noise in the PILOT or JCMT data,but is more probably due to inadequate filtering of the PILOT data. A more accurate comparison would require processing the PILOT data through the JCMT pipeline used by Matthews et al. (2009), which is beyond the scope of this study.
The reasonable agreement between the observed B-field angles between the two experiments at different FIR frequency confirms that the main orientation of the B-field observed on large scales with PILOT persist with a very similar orientation within the 50 km s−1 molecular cloud.
 |
Fig. 12 Angle difference between the B-field orientation and the tangent to the 100 pc ring as defined in Molinari et al. (2011) as a function of the phase angle along the ring (black dots). The red and blue profiles show the corresponding 240 μm intensity and polarization fraction profiles in arbitrary units. The horizontal lines show the range ± 20°. The verticalboxes show the tangent point of the ring. |
 |
Fig. 13 Top panel: B-field vector of the averaged JCMT data (blue) and PILOT background subtracted data (red) over the extent of cloud 50 km s−1 covered by the JCMT data, overlaid on the PILOT intensity image. Bottom panel: histogram of the JCMT (blue) and PILOT (red) B-field orientation. The vertical lines show the mean (solid) and median (dashed) angle values of each distributions. |
6 Summary and conclusions
In this paper, we have presented new measurements of the polarized dust emission at 240 μm in the Galactic center region. The data were obtained during ≃30 min of observations during the second flight of the PILOT balloon-borne experiment, which was launched from Alice Springs, Australia in April 2017. The observed region covers a wide field (− 2° < ℓ < 2°, − 4° < b < 3°) at an angular resolution of 2.2′. This paper is the first PILOT paper to present scientific analysis of polarization measurements towards astronomical targets. To validate these measurements and assess the overall quality of our data processing pipeline, we present polarization maps from the PILOT data using two independent map-making methods (SCANAMORPHOS and ROMA). The two pipelines generate similar I, Q and U maps, and yield a similar distribution of polarization angles across our observed field. The SCANAMORPHOS maps of I, Q and U used for the analysis in this paper are publicly available through the Centre d’Analyse des Données Étendues (CADE3).
The key results of our analysis are:
-
We obtain a clear detection of polarized thermal dust emission from the Milky Way’s central molecular zone (CMZ). This is obvious from the observed structure of emission features in the PILOT I, Q and U maps (Fig. 4). We develop a Galactic model with ordered and turbulent magnetic field components and a realistic density distribution to demonstrate quantitatively that the observed polarization properties cannot be explained by the magnetic field of the Galactic disk along the line-of-sight to the Galactic center region.
-
The PILOT polarization angle measurements show that the structure of the magnetic field in the plane of the sky is remarkably uniform over the full extent of our mapped region. The observed distribution of polarization angles indicatesthat the POS B-field in the CMZ has a dominant orientation of ≃22° measured clockwise with respect to the Galactic plane (Fig. 5). There are no obvious structures in the PILOT total intensity maps that correspond to this characteristic orientation.
-
Within our observed field, the POS magnetic field structure tends to become more parallel to the Galactic Plane in regions with high 240 μm brightness, such as the well-known Sgr B2, 20 and 50 km s−1 clouds (Fig. 7).
-
The polarization angles measured by PILOT are in good agreement with the polarization angles measured by Planck at 217 and 353 GHz over the extent of the CMZ. Larger differences are observed away from the Galactic plane which could be due to imperfect bandpass mismatch correction in the Planck data or filtering in the PILOT data. At lower frequencies (at 70, 100 and 143 GHz), the PILOT data shows poorer agreement with the distribution of polarization angles measured by Planck, which is likely due to the impact of contamination by the CO line and synchrotron emissionin those channels.
-
The combination of a low polarization fraction and a very regular POS magnetic field orientation observed towards the CMZ lead to unusually low values of
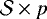 , which are only observed towards the inner Galactic plane in the data. We propose that this could be explained by the increased number of turbulent cells for the long LOS towards those regions and the overall alignment of
B
with the Galactic plane producing lower values of
, which are only observed towards the inner Galactic plane in the data. We propose that this could be explained by the increased number of turbulent cells for the long LOS towards those regions and the overall alignment of
B
with the Galactic plane producing lower values of  . We exclude that unpolarized free–free or anomalous microwave emission could explain low p
values, but cannot exclude that dust properties specific to the inner regions of the Galaxy could explain the observations.
. We exclude that unpolarized free–free or anomalous microwave emission could explain low p
values, but cannot exclude that dust properties specific to the inner regions of the Galaxy could explain the observations. -
Assuming equipartition between the magnetic pressure and ram pressure, we obtain magnetic field strengths estimates of the order of 1 mG for several CMZ molecular clouds (see Table 1).
-
We find no evidence for a connection between the orientation of the POS magnetic field structure inferred from the PILOT observations and the twisted ring structure identified in the CMZ by Molinari et al. (2011).
-
We find broadly good agreement between the POS magnetic field orientations observed by PILOT at 240 μm and by SCUBAPOL on the JCMT at 450 μm for a subfield centered on the 50 km s−1 molecular cloud. This suggests that the homogeneity of the POS magnetic field persists to smaller scales within the 50 km s−1 molecular cloud region.
Acknowledgements
This work benefited from the continuous financial and logistic support of the CNES balloon division during the development, the integration and the test phases of the PILOT instrument and the flight operations. This work was supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES.
Appendix A: Simplified Galactic model
We model the Galactic plane as follows, inspired from models such as that of Jaffe et al. (2013). The dust density distribution is composed of an axisymmetric exponential profile, plus four spiral arms with Gaussian profiles in their cross sections. The magnetic field is the sum of an ordered component and a turbulent part, with amplitude proportional to the square root of the dust density (Crutcher et al. 2010; Crutcher 2012). The ordered part is spiral and the turbulent one is modeled as a Gaussian random field, isotropic and homogeneous, with its three components not correlated among them. Thus, all components have the same power spectrum, taken to be a power law with spectral index α in the range [kmin, kmax] and zero otherwise. A typical coherence length for this turbulent part is obtained by taking kmin = 10 kpc−1 (cf. Haverkorn & Spangler (2013) and references therein). The precise value of the dissipation scale does not matter for our purpose as long as it is small enough, and we choose kmax = 1000 kpc−1. As for the index, we consider a Kolmogorov-like turbulence for which α = −11∕3. We generatethe turbulent magnetic field along a given LOS as three independent Gaussian realizations (one for each component), while the values of that field along the adjacent LOS are constrained by the fact that the total 3D field has to be divertgentless. In practice, we do not need to explicit the precise values along these adjacent LOS since the following calculation is performed one LOS at a time, but we note here that we indeed have enough freedom left in the construction of our field for it to be physical (i.e., divertgentless).
We compute the polarization fraction p as follows. In principle it may be obtained using the expressions (5) to (7) of Planck Collaboration Int. XX (2015). However, for the purpose of this simple estimate, we note that to a first approximation we may neglect the optical depth effects and take eτν = 1 in the I, Q and U integrals for the frequency of interest (Boulanger et al. 1996), and that the source function Sν and p0 are constant along the LOS. Therefore we have
![\begin{equation*} {\footnotesize p(s) = p_0 \frac{\sqrt{\left(\int_0^s n_{\textrm{d}} \cos (2 \phi) \cos^2 {\gamma} {\textrm{d}}s'\right)^2 + \left(\int_0^s n_{\textrm{d}} \sin (2 \phi) \cos^2 {\gamma} {\textrm{d}}s'\right)^2}}{\int_0^s n_{\textrm{d}} \left[1 - p_0 \left(\cos^2 {\gamma} - \frac{2}{3}\right)\right] \textrm{d}s'}, } \end{equation*}](/articles/aa/full_html/2019/10/aa35072-19/aa35072-19-eq49.png) (A.1)
(A.1)
where we use the same notations as in the aforementioned Planck paper, with nd the dust density and ϕ the local polarization angle in the HEALPIX convention, γ is the angle between the B and the POS (γ = π∕2 − ζ), s is the distance along the LOS, with origin at the Sun, and we take p0 = 0.2. With this definition p can be greater than p0.
We proceed in two steps. First, we consider the longitudes beyond the central region (ℓ ∈ [−180°, −20°] ∪ [20°, 180°]) in order to evaluate how turbulent the magnetic field is, inside and between the spiral arms. In the top of Fig. A.1 we show how inour model the polarization fraction depends on the longitude for three limiting cases: the blue curve corresponds to a switched off turbulence, orange corresponds to equipartition between the ordered and turbulent parts, and in red the root mean square of the turbulent part is three times larger than the ordered part. Comparing these results to the observed signal (bottom of that same figure) indicates that the turbulent component is important, with a typical root mean square of 2 to 3 μG. Secondly, we focus on the longitudes ℓ ∈ [−20°, 20°], and estimate thecontribution to p of everything along these LOS, except the bulge and the CMZ. To do so, we take a vanishing dust density inside the molecular ring, and compute p using the estimated properties of turbulence in the disk from the first step. The results are plotted in Fig. A.1. Naturally, the stronger the turbulence, the lower p is. But p does not reach values as low as the measured ones. Indeed, the polarization fraction p observed by Planck is of typically 1% throughout that central region, while even in the case of a strong turbulence (red curve) p is around 4%. Therefore the central part has a non negligible contribution to the observed signal.
 |
Fig. A.1 Top panel: polarization fraction as a function of longitude in our model. The curves correspond to single realizations of the turbulent field, but are representative of the typical behaviour. Bottom panel: measured values with Planck, using the modified asymptotic estimator (Plaszczynski et al. 2014) at a resolution of 15′. |
References
- Bally, J., Stark, A. A., Wilson, R. W., & Henkel, C. 1988, ApJ, 324, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, J. P., Ade, P., André, Y., et al. 2016, Exp. Astron., 42, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J. P., et al. 1996, A&A, 312, 256 [Google Scholar]
- Cabral, B., & Leedom, L. 2000, Proceedings of the 20th annual conference on Computer graphics and interactive techniques, 128, 263 [Google Scholar]
- Chuss, D. T., Davidson, J. A., Dotson, J. L., et al. 2003, ApJ, 599, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M. 2012, ARA&A, 50, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperis, G., Buzzelli, A., Cabella, P., de Bernardis, P., & Vittorio, N. 2016, A&A, 593, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eckart, A., Genzel, R., Hofmann, R., Sams, B. J., & Tacconi-Garman, L. E. 1995, ApJ, 445, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. 2009, A&A, 505, 1183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrière, K., Gillard, W., & Jean, P. 2007, A&A, 467, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M. 1968, Interstellar Grains, eds. B. M. Middlehurst & L. H. Aller (Chicago: University of Chicago Press), 221 [Google Scholar]
- Haverkorn, M., & Spangler, S. R. 2013, Space Sci. Rev., 178, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Heiligman, G. M. 1987, ApJ, 314, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Henshaw, J. D., Longmore, S. N., Kruijssen, J. M. D., et al. 2016, MNRAS, 457, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H., & Davidson, J. A. 1994, in NATO ASIC Proc. 445: The Nuclei of Normal Galaxies: Lessons from the Galactic center, eds. R. Genzel & A. I. Harris, 199 [Google Scholar]
- Hildebrand, R. H., Gonatas, D. P., Platt, S. R., et al. 1990, ApJ, 362, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H., Davidson, J. A., Dotson, J., et al. 1993, ApJ, 417, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Jaffe, T. R., Ferrière, K. M., Banday, A. J., et al. 2013, MNRAS, 431, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., Zhang, Q., et al. 2017, A&A, 603, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kruijssen, J. M. D., Dale, J. E., & Longmore, S. N. 2015, MNRAS, 447, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, C. C., Anantharamaiah, K. R., Kassim, N. E., & Lazio, T. J. W. 1999, ApJ, 521, L41 [NASA ADS] [CrossRef] [Google Scholar]
- LaRosa, T. N., Brogan, C. L., Shore, S. N., et al. 2005, ApJ, 626, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H. M., & Draine, B. T. 1985, ApJ, 290, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Liszt, H. S. 1985, ApJ, 293, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Mangilli, A., Foënard, G., Aumont, J., et al. 2018, ArXiv e-prints [arXiv:1804.05645] [Google Scholar]
- Matthews, B. C., McPhee, C. A., Fissel, L. M., & Curran, R. L. 2009, ApJS, 182, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, E. A. C., Ginsburg, A., Immer, K., et al. 2018, ApJ, 868, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Bally, J., Noriega-Crespo, A., et al. 2011, ApJ, 735, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Montel, J., Andre, Y., Mirc, F., et al. 2015, in 22nd ESA Symposium on European Rocket and Balloon Programmes and Related Research, ed. L. Ouwehand, ESA SP, 730, 509 [NASA ADS] [Google Scholar]
- Morris, M. 1990, in Galactic and Intergalactic Magnetic Fields, eds. R. Beck, P. P. Kronberg & R. Wielebinski, IAU Symp., 140, 361 [NASA ADS] [Google Scholar]
- Morris, M. 1996, in Unsolved Problems of the Milky Way, eds. L. Blitz & P. J. Teuben, IAU Symp., 169, 247 [NASA ADS] [Google Scholar]
- Morris, M., Turner, B. E., Palmer, P., & Zuckerman, B. 1976, ApJ, 205, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Nishiyama, S., Tamura, M., Hatano, H., et al. 2009, ApJ, 690, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, G., Dotson, J. L., Dowell, C. D., et al. 2000, ApJ, 529, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, G., Chuss, D. T., Renbarger, T., et al. 2003, ApJ, 583, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, T., Eckart, A., & Genzel, R. 1999, ApJ, 523, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, 571, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2018, A&A, submitted [arXiv:1807.06205] [Google Scholar]
- Planck Collaboration II. 2019, A&A, in press, https://doi.org/10.1051/xs0004-6361/201833293 [Google Scholar]
- Planck Collaboration III. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201832909 [Google Scholar]
- Planck Collaboration XII. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201833885 [Google Scholar]
- Planck Collaboration Int. XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XX. 2015, A&A, 576, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVIII. 2016, A&A, 596, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plaszczynski, S., Montier, L., Levrier, F., & Tristram, M. 2014, MNRAS, 439, 4048 [NASA ADS] [CrossRef] [Google Scholar]
- Reich, W. 1994, in NATO Advanced Science Institutes (ASI) Series C, NATO Advanced Science Institutes (ASI) Series C, eds. R. Genzel & A. I. Harris, 445, 55 [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roussel, H. 2018, ArXiv e-prints [arXiv:1803.04264] [Google Scholar]
- Roy, S., Rao, A. P., & Subrahmanyan, R. 2005, MNRAS, 360, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, S., Pramesh Rao, A., & Subrahmanyan, R. 2008, A&A, 478, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofue, Y. 1995a, PASJ, 47, 527 [NASA ADS] [Google Scholar]
- Sofue, Y. 1995b, PASJ, 47, 551 [NASA ADS] [Google Scholar]
- Tsuboi, M., Inoue, M., Handa, T., Tabara, H., & Kato, T. 1985, PASJ, 37, 359 [Google Scholar]
- Tsuboi, M., Inoue, M., Handa, T., et al. 1986, AJ, 92, 818 [NASA ADS] [CrossRef] [Google Scholar]
- Uchida, Y., Shibata, K., & Sofue, Y. 1985, Nature, 317, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Davidson, J. A., Morris, M., et al. 1988, ApJ, 333, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., & Morris, M. 1987, ApJ, 322, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Morris, M., & Chance, D. 1984, Nature, 310, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Yusef-Zadeh, F., Hewitt, J. W., & Cotton, W. 2004, ApJS, 155, 421 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top panel: map of the Galactic central molecular zone obtained with the PILOT experiment at 240 μm. The color scale shows the total intensity in log scale. The overlaid texture based on the line integral convolution (Cabral & Leedom 2000) shows the orientation of the magnetic field projected on the plane, inferred from the measured dust polarization. Bottom panel: intensity as above, overlaid with total intensity contours at 0.1, 0.2, 0.5, and 1 × 105 MJy sr−1. The circles show the location of the 100-pc twisted ring as defined in Molinari et al. (2011). The filled symbols are discussed in Sect. 5.4. The names of key molecular regions are overlaid. |
| In the text | |
 |
Fig. 2 Calibrated PILOT data for one observing tile during L0 observations. Top panel: data before atmospheric signal removal. Bottom panel: data with the atmospheric signal removed as described in Sect. 3.4. In each panel, we show the array-averaged signal in V as a function of time on the TRANS array #6 and REFLEX array #7, from top to bottom. Vertical lines show the extent of individual scans. The modulated signal during calibration sequences on the ICS at some ends of scans is clearly seen. |
| In the text | |
 |
Fig. 3 PILOT maps of the I, Q, U parameters obtained towards the galactic center region, processed using the SCANAMORPHOS software. The maps are shown at the full resolution of the instrument of 2.2′. The maps are in units of 103 MJy sr−1. |
| In the text | |
 |
Fig. 4 PILOT maps of, from top to bottom, the total intensity I, the polarized intensity P, the Stokes Q and U parameters, zoomed on the CMZ region and processed using the SCANAMORPHOS software. The maps are shown at the full resolution of the instrument of 2.2′. The intensity map is shown in log scale. The maps of P, Q and U are in units of 103 MJy sr−1. |
| In the text | |
 |
Fig. 5 Top panel: map of the B-field orientation as derived from the PILOT data using the SCANAMORPHOS software. The total intensity is shown as the color map, in log scale. The B-field orientation is shown as constant length segments orthogonal to the polarization orientation, where σψ < 8°. Bottom panel: map of the polarization angle uncertainty per beam, in degrees. |
| In the text | |
 |
Fig. 6 PILOT large scale maps of the I, Q and U Stokes parameters obtained with the ROMA software. The maps are in units of 103 MJy sr−1. |
| In the text | |
 |
Fig. 7 Dust polarization angles measured in the CMZ as a function of 240 μm intensity. Top panel: polarization angle distributions plotted separately for intervals of increasing 240 μm intensity in the PILOT I map. The characteristic 240 μm brightness is indicated using colour, and ranges from 103.5 (red) to 105.1 MJy sr−1 (blue). Bottom panel: mean and mode of the polarization angle distributions directly as a function of the 240 μm intensity. |
| In the text | |
 |
Fig. 8 Normalized histograms of the PILOT polarization angles obtained by analyzing the polarization angles map generated with the ROMA map making (black) and with the SCANAMORPHOS map making (red). |
| In the text | |
 |
Fig. 9 Top panel: comparison between the B-field orientation as derived from the PILOT 240 μm (red) and Planck 353 GHz (green) dust polarization measurements. The B-field orientationis shown as constant length line segments. The background image is the PILOT Stokes I map shown in log scale. Bottom panel: map of the angle difference (in degrees) between Planck 353 GHz and PILOT 240 μm. |
| In the text | |
 |
Fig. 10 Histogram of the PILOT polarization angles (black) on the Galactic center region compared to Planck observations at 70, 100, 143, 217 and 353 GHz (blue, green, yellow, orange and red, respectively). We overplot the Gaussian fits of these histograms as thicker lines to guide the eye. |
| In the text | |
 |
Fig. 11 Polarization angle profile as a function of Galactic longitude. The mean polarization angle is computed from longitudes between −7.5° and 7.5° and latitudes between −0.15° and 0.15° in 100 boxes of size 0.15° in longitude. The longitude profiles are shown for the Planck 143, 217 and 353 GHz channels (blue, orange and red, respectively) and PILOT (black). The error bars represent the standard deviation of the angle in each boxes. |
| In the text | |
 |
Fig. 12 Angle difference between the B-field orientation and the tangent to the 100 pc ring as defined in Molinari et al. (2011) as a function of the phase angle along the ring (black dots). The red and blue profiles show the corresponding 240 μm intensity and polarization fraction profiles in arbitrary units. The horizontal lines show the range ± 20°. The verticalboxes show the tangent point of the ring. |
| In the text | |
 |
Fig. 13 Top panel: B-field vector of the averaged JCMT data (blue) and PILOT background subtracted data (red) over the extent of cloud 50 km s−1 covered by the JCMT data, overlaid on the PILOT intensity image. Bottom panel: histogram of the JCMT (blue) and PILOT (red) B-field orientation. The vertical lines show the mean (solid) and median (dashed) angle values of each distributions. |
| In the text | |
 |
Fig. A.1 Top panel: polarization fraction as a function of longitude in our model. The curves correspond to single realizations of the turbulent field, but are representative of the typical behaviour. Bottom panel: measured values with Planck, using the modified asymptotic estimator (Plaszczynski et al. 2014) at a resolution of 15′. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.