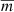| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 6 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201935502 | |
| Published online | 25 June 2019 | |
Praesepe (NGC 2632) and its tidal tails⋆
Zentrum für Astronomie der Universität Heidelberg, Astronomisches Rechen-Institut, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
e-mail: roeser@ari.uni-heidelberg.de, elena@ari.uni-heidelberg.de
Received:
20
March
2019
Accepted:
16
April
2019
Aims. Within a 400 pc sphere around the Sun, we search for Praesepe’s tidal tails in the Gaia Data Release 2 (DR2) data set.
Methods. We used a modified convergent-point method to find stars with space velocities close to the space velocity of the Praesepe cluster.
Results. We find a clear indication for the existence of Praesepe’s tidal tails, both extending up to 165 pc from the centre of the cluster. A total of 1393 stars populate the cluster and its tails, giving a total mass of 794 M⊙. We determined a tidal radius of 10.77 pc for the cluster and a tidal mass of 483 M⊙. The corresponding half-mass radius is 4.8 pc. We also found a clear indication for mass segregation in the cluster. The tidal tails outside 2 tidal radii are populated by 389 stars. The total contamination of our sample by field stars lies between 50 and 100 stars or 3.6–7.2%. We used an astrometrically and photometrically clean subsample of Gaia DR2, which makes our Praesepe sample incomplete beyond MG ≈ 12.0 mag; this corresponds to about 0.25 M⊙. A comparison with an N-body model of the cluster and its tails shows remarkably good coincidence. Three new white dwarfs are found in the tails.
Key words: open clusters and associations / individual: Praesepe
Data of stars shown in Figs. 2 and 3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/627/A4
© ESO 2019
1. Introduction
Tidal tails around open clusters have been predicted about a decade ago by, for example Kharchenko et al. (2009) and Ernst et al. (2011). An introduction to this topic was given in our previous paper (Röser et al. 2019), hereafter called Paper I, and is not repeated in this work. The first detection of tidal tails of open clusters using the data from Gaia Data Release 2 (DR2; Gaia Collaboration 2018b) were reported at the end of 2018 by Röser et al. (2019) and Meingast & Alves (2019) who revealed the tidal tails of the Hyades. This was followed by a number of publications in which tidal tails have now been found around other open clusters. Tang et al. (2019) and Fürnkranz et al. (2019) recently reported on the detection of tidal tails of the Coma Berenices (Melotte 111) open cluster, and Yeh et al. (2019) found hints of tidal tails from the very old, logt = 9.33 (MWSC; Kharchenko et al. 2013), open cluster Ruprecht 147. So, tidal tails now seem to be a common feature of older open clusters and are revealed thanks to the high data quality of Gaia DR2.
NGC 2632 (Praesepe) is an old open cluster, logt = 8.92 in MWSC, logt = 8.85 according to Gaia Collaboration (2018a). The latest major review of the stellar content of Praesepe (Kraus & Hillenbrand 2007) dates back more than one decade. Over an area of 300 deg2 on the sky, Kraus & Hillenbrand found 1010 candidate members in Praesepe and also estimated the total mass to be 550 ± 40 M⊙ and a tidal radius of 11.5 ± 0.3 pc. Khalaj & Baumgardt (2013) used photometry from the Two Micron All Sky Survey (2MASS) and from the Sloan Digital Sky Survey (SDSS) as well as proper motions from the PPMXL catalogue to determine the stellar content of Praesepe. These authors found a total cluster mass of about 630 M⊙ and a 2D half-mass radius of 3.90 pc. Using Gaia DR2 data, Gaia Collaboration (2018a) and Cantat-Gaudin et al. (2018) published membership lists of stars for several hundred of open clusters in the solar neighbourhood, including Praesepe. Gaia Collaboration (2018a) found 938 candidate members, and they also determined a mean parallax, mean proper motions, and age of, and reddening towards, NGC 2632. For Praesepe, Cantat-Gaudin et al. (2018) gave membership probabilities for 719 stars as well as mean parallax and mean proper motions.
This paper is primarily aimed at the detection of the tidal tails of Praesepe, if they existed, but we also publish some characteristic astrophysical data of the cluster itself. The paper is structured as follows: in Sect. 2 we describe the steps we took to find Praesepe’s tidal tails. Section 2 is divided into subsections describing the cuts to obtain an astrometrically and photometrically clean sample, the separation of over-densities in position and velocity space from the Galactic background, the identification of Praesepe and its tails, and the estimation of contamination and completeness. In Sect. 3 we discuss the cluster and its tails and present some characteristic astrophysical parameters. A summary concludes the paper.
2. Finding Praesepe’s tidal tails
The N-body simulations of the dynamical evolution of a Galactic open cluster (Kharchenko et al. 2009; Ernst et al. 2011) literally were tailored to model the case of the Hyades cluster at an age of logt = 8.8 (Martín et al. 2018; Gossage et al. 2018) and at about the galacto-centric distance of the Sun. As the galacto-centric distance and age of Praesepe are comparable to those of the Hyades, and as the clusters are also similar with regard to their stellar content, it is justified that we use the data set of the model from Kharchenko et al. (2009) as our model cluster to compare with the observations of Praesepe.
As a starting point we determined the 6D phase space coordinates of the centre of Praesepe on the basis of positions, proper motions, parallaxes, and radial velocities from Gaia DR2 and we got information on membership from Gaia Collaboration (2018a). The coordinates are given in the solar system barycentric Galactic Cartesian coordinate system where the X-axis points to the Galactic centre, the Y-axis in the direction of Galactic rotation, and Z-axis to the Galactic north pole. The corresponding velocity coordinates are U, V, W. We found mean values
These mean values are based upon 136 stars from Gaia Collaboration (2018a) with measured radial velocities. The standard errors of the mean in a position coordinate are 0.25 pc, and those of a velocity coordinate are 0.08 km s−1.
2.1. Preparatory work
From the Gaia DR2 data set (Gaia Collaboration 2018b) we extracted all entries with a parallax greater than 2.4 mas, which gave 43 038 142 objects. To obtain a stellar sample cleaned from possible artefacts we followed the procedures described in Sect. 4.3 and Appendix C, Figs. C.1, and C.2 of Lindegren et al. (2018) with one small, important change.
Instead of the “unit weight error”-cut (UWE; cf. Eq. (C.1) in Lindegren et al. 2018) we followed the new approach presented by Lindegren in the document GAIA-C3-TN-LU-LL-124-01, which can be found on ESA’s webpage1. In this concept UWE is scaled by a factor depending on the magnitude and colour of the source. The result is a renormalised UWE, or RUWE, which needs only a single threshold of 1.4. Values for RUWE can be found at the service2 in table gaiaDR2light. All the other cuts are the same as in Paper I. We obtained an astrometrically and photometrically clean sample of 8 131 092 stars out of the original 43 million objects. The price for this cleaning is an incompleteness at the faint end of the magnitude distribution near G = 18 mag and also near the parallax limit of 2.4 mas.
2.2. Constraining the range in space and velocity
In general, a cluster and its possible tidal tails reveal themselves as an over-density in position and velocity space. In the ideal case, we need observed space velocities for each star in a sample to identify stars co-moving with the Praesepe cluster. However, accurate radial velocities are lacking for the vast majority of stars. Therefore we had to rely on criteria that are solely based on their tangential velocities. This implies that we may detect stars that are highly probable to be co-moving, although when the radial velocities are measured they will need final confirmation. We followed the formalism of the convergent-point (CP) method as described in van Leeuwen (2009), for instance, and transformed the Cartesian velocity vector of the cluster motion Vc from Eq. (1) to give predicted velocities V∥pred and V⊥pred parallel and perpendicular to the direction to the CP for each star depending on its position on the sky. We note that V⊥pred ≡ 0. Also following van Leeuwen (2009), we similarly transformed the measured (observed) tangential velocities for each star, i.e. κ μα*/ϖ and κ μδ/ϖ into V∥obs and V⊥obs. In this case ϖ is the measured trigonometric parallax in Gaia DR2 and κ = 4.74047 is the transformation factor from 1 mas yr−1 at 1 kpc to 1 km s−1. We set in the following ΔV∥ = V∥obs − V∥pred and ΔV⊥ = V⊥obs − V⊥pred. We note that the differences between the predicted and observed velocities (ΔV∥, ΔV⊥) are equal to (0,0), when the space velocity of a star is identical to Vc in Eq. (1). We also determined the covariance matrix for the velocities V∥obs and V⊥obs via error propagation from the covariance matrix of the μα*, μδ, and ϖ.
For further analysis we did not use the full sphere with ϖ ≤ 2.4 mas, but constrained the volume around Praesepe by a cut in the z-plane as |Z − Zc| ≤ 50 pc, where Zc is given in Eq. (1). This gives a volume of 4.867 × 107 pc3. We also introduced a restriction in the tangential velocity plane by requiring |ΔV∥| ≤ 7 km s−1 and |ΔV⊥| ≤ 7 km s−1, a total area of 196 (km s−1)2. These cuts are ample compared to the predicted extent of the model tails, and they reduced our selection to a subsample containing 78 163 stars which populate this search volume.
As we are interested in Praesepe and its possible tails, we also transform the spacial coordinates X, Y, Z to a coordinate system XP, YP, ZP (the subscript P refers to Praesepe) with origin at the centre of the Praesepe cluster, where the XP-axis points to the Galactic centre, YP-axis to the direction of Galactic rotation, and the ZP-axis to the Galactic north pole. To achieve this we first went from the solar system barycentric Galactic Cartesian coordinates X, Y, Z to the Galactocentric cylindrical coordinate system R, θ, Z with R⊙ = 8300 pc (Gillessen et al. 2013). Then we transformed back into the cluster-centric Galactic Cartesian system XP, YP, Z, and finally ZP = Z − Zc. We note that this transformation is not necessary for the way we determine over-densities, it only puts Praesepe into the centre of the volume we consider.
2.3. Method to find over-densities
In Paper I we cut a small rectangle in the tangential velocity plane where we suspected the signature of the tails, and then looked for over-densities in 3D space. In this work we follow a different, more general approach: we search simultaneously for over-densities in 5D space. The main purpose is to separate the over-densities such as clusters or moving groups (signal) from the local Galactic background (noise). In other words, for each star in the subsample of 78 163 stars we want to decide, if it belongs to the general Galactic field, or to an over-density significantly above the general background. We make the decision by counting neighbours of this star in a 5D neighbourhood and compare this with the expected background counts where the background is modelled by a Poisson distribution. We make the following neighbourhood definition: a star j with 5D coordinates (XPj, YPj, ZPj, ΔV∥j, ΔV⊥j) is a neighbour to star i with coordinates (XPi, YPi, ZPi, ΔV∥i, ΔV⊥i) if
and
The free parameters a, b, and rlim can be specified according to the goal of the study. We chose an elliptical shape for the velocity condition since the error ellipses in the tangential velocity plane can be eccentric. Indeed, in the case of the Praesepe subsample, σV∥obs, and σV⊥obs are very different; the mean σV∥obs is 0.79 km s−1, and the mean σV⊥obs is 0.12 km s−1. Considering an intrinsic velocity dispersion in the cluster and tails as well, we chose 1.2 km s−1 as the semi-major axis a of our selection ellipse and 0.5 km s−1 as the semi-minor axis b. With these velocity conditions we found, on average, 1.6 × 10−5 stars for each velocity ellipse and per 1 pc−3. Further we chose rlim = 15 pc to get, on average, 0.2 stars per 5D neighbourhood volume. We can only determine the neighbourhood for those stars, where the volumes specified for neighbourhood are fully contained in the subset given in Sect. 2.2. This holds for the 54 652 stars we call the BS.
When a star i is surrounded by k neighbours, we call this case a “k-neighbourhood”. In the BS we found a total of 41 586 zero-neighbourhoods and 9952 one-neighbourhoods, i.e. the vast majority of stars (94.3%) has less than 2 neighbours in the BS. There is a high probability that these are Galactic field stars (background noise). To determine an upper limit for the average density of the neighbours in the background we tentatively allowed all cases with up to 5 neighbours to be considered as background. These contain 97.9 per cent of the stars in the basic sample, which on the other hand means that only the remaining about 2.1 per cent are signal. The average number of neighbours in the BS is 0.273 stars. So, the distribution of neighbours in the background should follow a Poisson distribution with the mean λ = 0.273. We then calculated the quantity Nexp(k) = Pλ(k)×NBS, where Pλ(k) is the probability mass function of the Poisson distribution representing the background. We give Pλ(k) in the second and Nexp(k) in the third column of Table 1 for all k ≤ 7. The fourth column in Table 1 gives the observed number of k-neighbourhoods Nobs(k) in the BS. Comparing Cols. 3 and 4 we found that Nobs(k) follows Nexp(k) very well for cases k = 0, 1, 2. For increasing k the number of observed k-neighbourhoods Nobs(k) rapidly exceeds the prediction Nexp(k). If the case k = 5 belonged to the background, the expected number of cases would be less than 1; the observed number is 36. So, we certainly did not underestimate the mean density λ for the background distribution. In the case of Praesepe the highest value of k is 405. The ratio pcont = Nexp(k)/Nobs(k) given in Col. 5 of Table 1 is the probability that a star in a k-neighbourhood belongs to the background distribution. Hence, for each star, we can interpret pcont as the degree of how much it is contaminated by background. According to the construction of these k-neighbourhoods a particular star from the BS can be found in the k-neighbourhood of several other stars, and we give it the contamination pcont of the neighbourhood with the highest k, where this star is found. In Fig. 1 we show the distribution of all stars from the BS coded by their individual pcont. The left panel shows the distribution in the ΔV∥, ΔV⊥-plane, in the right panel we present the same set of stars, but in the XP, YP-plane. The background is filled by the vast majority (97.2%) of stars from the BS having pcont ≈ 1 (cases k = 0, 1, 2 in Table 1), which cover the whole area. Stars with intermediate contamination (cases k = 3, 4) are clearly identifiable by their colour, and the remaining stars with pcont ≈ 0 are shown in black. The huge signal centred at ΔV∥, ΔV⊥ = (0, 0) in the left panel and XP, YP = (0, 0) in the right panel represents Praesepe and its tails. A minor over-density at about ΔV∥, ΔV⊥ = (2.5, 6.3) and XP,YP = (445, 220) is the open cluster Collinder 350 and has nothing to do with Praesepe. In the following we considered only cases with k ≥ 3, which we regard as a signal. This yields 1543 stars or 2.8% of the BS.
Distribution of the k-neighbourhoods of stars in the BS.
 |
Fig. 1. Left: distribution of the stars from the BS in the tangential velocity plane ΔV∥, ΔV⊥ (see text for further explanation). The zero point is the predicted value derived from the space motion of Praesepe. The ΔV∥-axis points in the direction of the CP. Stars are colour coded by their individual probability of contamination pcont. Right: distribution of the same stars in the YP, XP-plane. In this figure we use a Galactic Cartesian coordinate system with origin in the centre of the Praesepe cluster and not, as usual, in the barycentre of the solar system. Praesepe and its tails are represented by the large dark structure at XP, YP = (0, 0). The over-density at XP, YP = (445 pc, 220 pc) is the open cluster Collinder 350. |
The selection of the parameters (a, b) = (1.2 km s−1, 0.5 km s−1) in velocity space and rlim = 15 pc in positional space turned out to be a reasonable compromise to obtain a significant signal for Praesepe and its tails on one hand and a relatively small noise in the background on the other hand (see Fig. 1). We tentatively kept a and b constant and increased rlim up to 25 pc. This resulted in a slight increase of the length of the tails together with a raise of spurious over-densities in the surrounding background created at velocities inconsistent with that of Praesepe. A similar effect occurred when we kept rlim constant at 15 pc and increased (a, b) to (1.5 km s−1, 0.7 km s−1).
We used TOPCAT3 (Taylor 2005) to extract the stars belonging to Praesepe and its tails out of the 1543 stars with k ≥ 3. Three manual cuts, first in the XP, YP-plane, next in the ΔV∥, ΔV⊥-plane, and last in the XP, ZP-plane, were necessary to give the final number (1393) of members (candidates) for Praesepe and its tails. Henceforth we call this set of 1393 stars the Praesepe sample (PrS). By adding pcont of the stars from the PrS we found a total contamination of 47 stars, 40 of which come from the stars in a 3-neighbourhood alone.
In Fig. 2 we show the 1393 stars from Praesepe and its tails in the (YP, XP)-plane and the (YP, ZP)-plane. Stars coded in grey are 1266 stars with pcont < 0.015, in orange 53 stars with pcont ≈ 0.1 and in light green 74 stars with pcont ≈ 0.5. The tails extend up to 165 pc from the cluster centre. For comparison we also present the result of the N-body calculation for the Hyades cluster by Kharchenko et al. (2009), which we also transformed into the XP, YP, ZP coordinate system of Praesepe. The model stars are shown as a beige density plot in the background. The coincidence between observations and model is remarkable, especially in the (YP, XP)-plane. Such a good coincidence we already found in Paper I in the case of the Hyades. The present result could have been expected since the Hyades and Praesepe are very similar in age and in stellar content. Among the stars in Fig. 2 which are slightly inconsistent with the model, we find that a majority have higher contamination (green and orange dots). A more rigorous cut in TOPCAT would have eliminated these stars, but it serves as an illustration of how well our general selection method using the k-neighbourhood works. On the other hand, there are 5 stars with higher contamination in the trailing tail in Fig. 2 that are consistent with the model (left panel) and they are those farthest away from the cluster centre. At the same time these stars are most distant from the Sun (up to 300 pc). The restrictions from Sect. 2.1 applied to the full Gaia DR2 data set to get an astrometrically and photometrically clean sample creates some incompleteness, especially at the faint end of the stellar sample. We note that incompleteness in signal leads to higher contamination by noise.
The internal contamination by field stars is given by summing up the values of pcont. We sub-divided the PrS stars into three subgroups: (a) 725 stars within the tidal radius rt of 10.77 pc which is derived below, (b) 279 stars between 1 and 2 tidal radii, and (c) 389 stars outside 2rt and in the tails. For these groups we found contamination of 0.83 stars (group a), 0.69 stars (group b), and 46.1 stars or 11.8% (group c). These values refer only to the contamination within our 5D approach. At this stage it is also appropriate to estimate the possible field star contamination that comes from the fact that we did not consider radial velocities for estimating membership, since radial velocity data are only measured for a small subset of stars in the BS. Nevertheless, for 245 stars in the PrS radial velocities are available in Gaia DR2. Only eight of them (3.3%) have radial velocities inconsistent with Praesepe’s space velocity. The contamination increases from 1.2% within the tidal radius to 10% outside 2rt. By combining these two kinds of contamination, we expect a total contamination between about 50 and 100 stars for our PrS.
3. Astrophysical properties of Praesepe
In Fig. 3 we show the colour-absolute–magnitude diagram (CAMD) MG vs. GBP − GRP of the 1393 stars of the PrS. The stars are colour coded according to their contamination value pcont. We also present a PARSEC (version 1.2S) isochrone (Chen et al. 2014) with Z = 0.02 and logt = 8.85, and E(B − V) = 0.027 mag (Gaia Collaboration 2018a). We used the Gaia passbands from Maíz Apellániz & Weiler (2018); we also applied the corrections to the GaiaG-magnitudes given in the same paper. We note that the tails are spread over a wide part of space and, hence, the assumption of a unique reddening is not fully appropriate for tail stars. Nevertheless, over a wide range of GBP − GRP, the isochrone gives a reasonable fit to the observations except for the low-mass stars redder than about GP − GRP = 2.8 mag. Anyway, we used the isochrone shown in Fig. 3 to estimate individual masses roughly via a mass–luminosity relation in the three Gaia photometric bands, neglecting binary issues. The incompleteness of our sample beyond G ≈ 18 mag (see Sect. 2.1) creates incompleteness at MG ≈ 11.8 mag near the cluster centre, and brighter or fainter in the tails, depending on the individual parallax of the stars. Via our mass–luminosity relation this transfers to about 0.25 M⊙.
 |
Fig. 2. Praesepe cluster and its tidal tails shown in the YP, Xp-plane (left) and the YP, Zp-plane (right). Stars selected in Gaia DR2 are shown as dots colour coded by their pcont-values (pcont < 0.015 in grey, pcont ≈ 0.1 in orange and pcont ≈ 0.5 in light green). The location of the simulated tidal tails from the model by Kharchenko et al. (2009) is indicated as beige-coloured structures. |
 |
Fig. 3. Colour-absolute–magnitude diagram (CAMD) MG vs. GBP − GRP of the 1393 stars of Praesepe and its tails. Stars are colour coded by their pcont. In addition we plot a PARSEC isochrone (Z = 0.02) with logt = 8.85, and E(B − V) = 0.027 mag. |
The total mass of all stars from the PrS amounts to 794 M⊙. We followed the recipes in Röser et al. (2011) and used the individual masses to estimate the tidal radius of the Praesepe cluster. In the galactic disc the sphere of influence of a cluster is given by
where xL is the distance of the Lagrangian points from the centre, Mt is the total mass inside a distance xL from the centre, 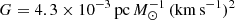 is the gravitational constant, and A and B are Oort’s constants at the position of the Sun. We use A (15.3 km s−1 kpc−1) and B (−11.9 km s−1 kpc−1) from Bovy (2017). The distance xL is often referred to as the tidal radius rt of a cluster. The tidal radius rt separates, in general, stars gravitationally bound to a cluster from those that are unbound. Adding up the individual masses from the centre outwards we found rt = 10.77 pc; 725 stars are within rt and give a tidal mass Mt = 483 M⊙ for Praesepe. Considering our incompleteness at about 0.25 M⊙, this tidal radius is a lower bound. But, even if a total of 100 M⊙ in low-mass stars with m < 0.25 M⊙ were contained in the inner part of the cluster, the tidal radius would only rise to 11.5 pc. In models of star clusters the Lagrangian radius for 50% of the cluster mass plays an important role and is called half-mass radius rh. Estimated from a tidal mass of 483 M⊙, the half-mass radius rh is 4.8 pc at the present state of evolution of Praesepe.
is the gravitational constant, and A and B are Oort’s constants at the position of the Sun. We use A (15.3 km s−1 kpc−1) and B (−11.9 km s−1 kpc−1) from Bovy (2017). The distance xL is often referred to as the tidal radius rt of a cluster. The tidal radius rt separates, in general, stars gravitationally bound to a cluster from those that are unbound. Adding up the individual masses from the centre outwards we found rt = 10.77 pc; 725 stars are within rt and give a tidal mass Mt = 483 M⊙ for Praesepe. Considering our incompleteness at about 0.25 M⊙, this tidal radius is a lower bound. But, even if a total of 100 M⊙ in low-mass stars with m < 0.25 M⊙ were contained in the inner part of the cluster, the tidal radius would only rise to 11.5 pc. In models of star clusters the Lagrangian radius for 50% of the cluster mass plays an important role and is called half-mass radius rh. Estimated from a tidal mass of 483 M⊙, the half-mass radius rh is 4.8 pc at the present state of evolution of Praesepe.
Kraus & Hillenbrand (2007) made an inventory of the Praesepe cluster about a decade ago. They used data from the SDSS, 2MASS, USNOB1.0, and UCAC-2.0 surveys and analysed proper motions and photometry over 300 deg2 on the sky. They found 1010 stars in Praesepe being candidate members with probability > 80%. These authors also estimated the total mass of the cluster to be 550 ± 40 M⊙ and a tidal radius of 11.5 ± 0.3 pc. The small disagreement between our tidal radius and that from Kraus & Hillenbrand (2007) comes partly from their assumed values of A = 14.4 km s−1 kpc−1 and B = −12.0 km s−1 kpc−1. With the values from Bovy (2017) and Kraus & Hillenbrand (2007) would have obtained rt = 11.25 pc given that their derived total mass of 550 M⊙ was inside 11.25 pc. Considering the fact that Kraus & Hillenbrand (2007) did not have accurately measured trigonometric parallaxes available, the coincidence of their tidal radius with ours is satisfactory. From their 1010 members with probability 80% we found 785 among our 1393 stars. From the remaining 225, only 77 passed the cuts in Sect. 2.1, but were not selected as members when using our criteria.
Using the individual masses we determine the radial density and mass profiles of the cluster. In Fig. 4 we present the number density D, the mass density ρ, and the average mass per star as a function of the distance from the centre rc. The bottom panel of Fig. 4 reveals the mass segregation in Praesepe; the average mass per star (ρ/D) decreases from 1.17 M⊙ close to the centre to about 0.46 M⊙ at the tidal radius rt. Again the apparent increase of the average mass per star towards larger distances from the centre is attributed to incompleteness at the low-mass end. The mass density of Praesepe, shown in the middle part of Fig. 4, is fitted to a Plummer model (Plummer 1915), where the mass density follows the equation
 |
Fig. 4. Number density D, mass density ρ, and average mass per star |
In this equation rco is the so-called core radius of a cluster. Using the tidal mass of Mt = 483 M⊙ the best fit to the observed density distribution (blue line) in Fig. 4 is obtained with a core radius rco of 3.7 pc. In the two top panels of Fig. 4 the core radius is seen as the distance at which the slope in the density and mass distributions changes. The corresponding Plummer model (dashed line in Fig. 4) shows good agreement with observations. The ratio of the half-mass radius rh to rco in Praesepe is 1.297, which is in remarkable coincidence with the theoretical ratio of 1.305 for a Plummer model (see Spitzer & Shull 1975).
Figure 3 shows the presence of white dwarfs (WDs) in Praesepe and its tails. In total, we find 13 WDs, 9 of which are inside the tidal radius of 10.77 pc. We disregard the two objects with MG ≈ 14 mag and GBP − GRP near 1. Twelve out of 13 objects are known in SIMBAD (Wenger et al. 2000) as WDs or blue proper motion stars. One star Gaia DR2 62998983199228032 is not known as a WD in SIMBAD, but it fits perfectly to the loci of the other WDs and has recently been rated as a member of Praesepe by Salaris & Bedin (2019). All WDs by Salaris & Bedin (2019) are confirmed by us with the exception of WD 0840+205, which did not pass the quality cuts in Sect. 2.1. Three WDs, US 2088, SDSS J092713.51+475659.6, and LAMOST J081656.19+204946.4 in the tidal tails, have not been mentioned before as being related to Praesepe, but now we can confirm their provenance from Praesepe.
In Fig. 5 we show the location on the sky of Praesepe (yellow pluses) and the Hyades (cyan pluses) as well as the tidal tails of both clusters. The background is the greyscale density map of Gaia DR2 (©ESA/Gaia/DPAC). This composite image has been produced using the facilities of Aladin Desktop4.
 |
Fig. 5. Tidal tails of Praesepe (yellow) and the Hyades (cyan) over-plotted to the Gaia DR2 sky using TOPCAT and Aladin facilities. |
A comparison with a theoretical model from N-body calculations (Kharchenko et al. 2009) for an 650 Myr old cluster (Hyades) also showed very good coincidence with regard to the location of the tidal tails of Praesepe. After the findings in Paper I, this is another very satisfactory confirmation for both theory and observations, in general. In detail, we observe for both clusters that the preceding tail is more pronounced than the trailing tail, although we have good reasons to suspect that this is due to different causes. In the case of Praesepe the trailing tail stretches to larger distances from the Sun and probably suffers from the incompleteness of our sample at fainter stars. Both Hyades tails are located at about the same distance from the Sun but the trailing tail of the Hyades shows an inhomogeneous structure and may have been shredded by shocks or collisions in the past. Moreover, the proportion N2rt/Npt of stars within the central part of the cluster, inside 2rt (N2rt), to stars in the preceding tail (Npt) is considerably higher for Praesepe than for the Hyades, namely 5 and 2, respectively. This may indicate a later stage of dynamical evolution of the Hyades. They may be closer to dissolution than is Praesepe. However, this hypothesis must be supported by future investigations, for example N-body simulations.
4. Summary
Using the data from Gaia DR2, we searched for the presence of Praesepe’s (NGC 2632) tidal tails in a sphere of some 400 pc radius around the Sun. First, the Gaia DR2 data were cleaned according to the recipes given in Lindegren et al. (2018) and described in Sect. 2.1 to obtain an astrometrically and photometrically clean sample. Within this volume we cut a slice of ±50 pc around the Zc coordinate of Praesepe and a primary window of 7 km s−1 by 7 km s−1 in velocity space around the expected tangential velocity of Praesepe members predicted by the CP method. We developed a method to find over-densities in a 5D phase space with three spatial coordinates and two in velocity space. By modelling the Galactic background distribution via a Poisson distribution we were able to distinguish between over-densities and background noise. The over-density related to Praesepe is populated by 1393 stars. The background contamination in 5D phase space amounts to 47 stars, and the estimate of contamination due to unknown discordant radial velocities gives about the same number. So the total contamination is estimated to lie between 50 and 100 stars or between 3.6 and 7.2% of the PrS. We used a 3D (MG, MGBP, MGRP) mass–luminosity relation to obtain individual masses for the stars from the PrS and found a total mass of 794 M⊙. We determined the tidal radius rt of 10.77 pc and a tidal mass Mt = 483 M⊙ for Praesepe that is a lower limit since our sample gets incomplete at masses below 0.25 M⊙. The half-mass radius rh is 4.8 pc. The shape of the cluster can be represented by a Plummer model with core radius rco = 3.7 pc. We observe a clear mass segregation of the cluster inside the tidal radius. The average mass per star drops from 1.17 M⊙ in the centre to about 0.46 M⊙ at the distance of the tidal radius rt. We found 725 cluster members within one tidal radius and a total of 1004 within two tidal radii. The remaining 389 stars from the PrS populate two tidal tails. The tails extend up to about 165 pc on both sides along the Y-axis of Galactic rotation at the position of Praesepe.
The locations of the tidal tails of Praesepe in 3D space are in very good coincidence with a theoretical model for tidal tails (Kharchenko et al. 2009) tailored to fit the 650 Myr old Hyades cluster. In detail, however, the ratio of the number of stars inside two tidal radii to outside (in the preceding tail) is much higher for Praesepe (factor 5) than for the Hyades (factor 2). This is a hint that the Hyades may already be in a later stage of evolution than Praesepe.
We found 13 WDs in our PrS, 9 within one tidal radius and 4 outside. Three WDs in the tail have not been assigned to Praesepe before, but this paper now identifies them as of Praesepe origin. We publish the data of all 1393 stars of the PrS at the CDS.
Acknowledgments
We thank the referee, Carme Jordi, for her very constructive and useful comments that helped to improve the paper. This study was supported by Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject B5) of the German Deutsche Forschungsgemeinschaft, DFG. This research has made use of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
References
- Bovy, J. 2017, MNRAS, 468, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [NASA ADS] [CrossRef] [Google Scholar]
- Ernst, A., Just, A., Berczik, P., & Olczak, C. 2011, A&A, 536, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fürnkranz, V., Meingast, S., & Alves, J. 2019, A&A, 624, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018a, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018b, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Fritz, T. K., et al. 2013, in Advancing the Physics of Cosmic Distances, ed. R. de Grijs, IAU Symp., 289, 29 [NASA ADS] [Google Scholar]
- Gossage, S., Conroy, C., Dotter, A., et al. 2018, ApJ, 863, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Khalaj, P., & Baumgardt, H. 2013, MNRAS, 434, 3236 [NASA ADS] [CrossRef] [Google Scholar]
- Kharchenko, N. V., Berczik, P., Petrov, M. I., et al. 2009, A&A, 495, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R.-D. 2013, A&A, 558, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., & Hillenbrand, L. A. 2007, AJ, 134, 2340 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., & Weiler, M. 2018, A&A, 619, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín, E. L., Lodieu, N., Pavlenko, Y., & Béjar, V. J. S. 2018, ApJ, 856, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Meingast, S., & Alves, J. 2019, A&A, 621, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1915, MNRAS, 76, 107 [NASA ADS] [Google Scholar]
- Röser, S., Schilbach, E., Piskunov, A. E., Kharchenko, N. V., & Scholz, R.-D. 2011, A&A, 531, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röser, S., Schilbach, E., & Goldman, B. 2019, A&A, 621, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., & Bedin, L. R. 2019, MNRAS, 483, 3098 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, Jr., L., & Shull, J. M. 1975, ApJ, 200, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, S. Y., Pang, X., Yuan, Z., et al. 2019, ApJ, 877, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
- van Leeuwen, F. 2009, A&A, 497, 209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yeh, F.-C., Carraro, G., Montalto, M., & Seleznev, A. F. 2019, AJ, 157, 115 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Left: distribution of the stars from the BS in the tangential velocity plane ΔV∥, ΔV⊥ (see text for further explanation). The zero point is the predicted value derived from the space motion of Praesepe. The ΔV∥-axis points in the direction of the CP. Stars are colour coded by their individual probability of contamination pcont. Right: distribution of the same stars in the YP, XP-plane. In this figure we use a Galactic Cartesian coordinate system with origin in the centre of the Praesepe cluster and not, as usual, in the barycentre of the solar system. Praesepe and its tails are represented by the large dark structure at XP, YP = (0, 0). The over-density at XP, YP = (445 pc, 220 pc) is the open cluster Collinder 350. |
| In the text | |
 |
Fig. 2. Praesepe cluster and its tidal tails shown in the YP, Xp-plane (left) and the YP, Zp-plane (right). Stars selected in Gaia DR2 are shown as dots colour coded by their pcont-values (pcont < 0.015 in grey, pcont ≈ 0.1 in orange and pcont ≈ 0.5 in light green). The location of the simulated tidal tails from the model by Kharchenko et al. (2009) is indicated as beige-coloured structures. |
| In the text | |
 |
Fig. 3. Colour-absolute–magnitude diagram (CAMD) MG vs. GBP − GRP of the 1393 stars of Praesepe and its tails. Stars are colour coded by their pcont. In addition we plot a PARSEC isochrone (Z = 0.02) with logt = 8.85, and E(B − V) = 0.027 mag. |
| In the text | |
 |
Fig. 4. Number density D, mass density ρ, and average mass per star |
| In the text | |
 |
Fig. 5. Tidal tails of Praesepe (yellow) and the Hyades (cyan) over-plotted to the Gaia DR2 sky using TOPCAT and Aladin facilities. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



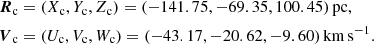
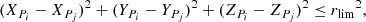
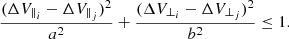
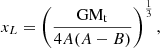
![$$ \begin{aligned} \rho ({r_{\rm c}}) = \frac{3M_{\rm t}}{4\pi {r_{\rm co}}^3}\frac{1}{[1+(r_{\rm c}/{r_{\rm co}})^2]^{5/2}}\cdot \end{aligned} $$](/articles/aa/full_html/2019/07/aa35502-19/aa35502-19-eq6.gif)