| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A69 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201935485 | |
| Published online | 02 July 2019 | |
XMM-Newton observations of PSR J0726−2612, a radio-loud XDINS
1
INAF, Istituto di Astrofisica Spaziale e Fisica Cosmica Milano, Via A. Corti 12, 20133 Milano, Italy
2
Dipartimento di Fisica G. Occhialini, Università degli Studi di Milano Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
e-mail: m.rigoselli@campus.unimib.it
3
Institut fur Astronomie und Astrophysik, Sand 1, 72076 Tubingen, Germany
4
Kazan (Volga region) Federal University, Kremlevskaja str., 18, Kazan 420008, Russia
5
Space Research Institute of the Russian Academy of Sciences, Profsoyuznaya Str. 84/32, Moscow 117997, Russia
6
Ioffe Institute, Politekhnicheskaya 26, 194021 Saint Petersburg, Russia
7
Dipartimento di Fisica e Astronomia, Università di Padova, Via F. Marzolo 8, 35131 Padova, Italy
8
MSSL-UCL, Holmbury St. Mary, Dorking, Surrey RH5 6NT, UK
9
Dipartimento di Matematica e Fisica, Università di Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy
Received:
18
March
2019
Accepted:
4
June
2019
We present the results of an XMM-Newton observation of the slowly rotating (P = 3.4 s), highly magnetized (B ≈ 3 × 1013 G) radio pulsar PSR J0726–2612. A previous X-ray observation with the Chandra satellite showed that some of the properties of PSR J0726–2612 are similar to those of the X-ray-dim isolated neutron stars (XDINSs), a small class of nearby slow pulsars characterized by purely thermal X-ray spectra and undetected in the radio band. We confirm the thermal nature of the X-ray emission of PSR J0726–2612, which can be fitted by the sum of two blackbodies with temperatures kT1=0.074+0.006-0.011 keV and kT2=0.14+0.004-0.002 keV and emitting radii R1=10.4+10.8-2.8 km and R2=0.5+0.9-0.3 km, respectively (assuming a distance of 1 kpc). A broad absorption line modeled with a Gaussian profile centered at 0.39+0.02-0.03 keV is required in the fit. The pulse profile of PSR J0726–2612 is characterized by two peaks with similar intensity separated by two unequal minima, a shape and pulsed fraction that cannot be reproduced without invoking magnetic beaming of the X-ray emission. The presence of a single radio pulse suggests that in PSR J0726–2612 the angles that the dipole axis and the line of sight make with the rotation axis, ξ and χ, respectively, are similar. This geometry differs from that of the two radio-silent XDINSs with double-peaked pulse profiles similar to that of PSR J0726–2612, for which ξ ∼ 90° and χ ∼ 45° have recently been estimated. These results strengthen the similarity between PSR J0726–2612 and the XDINSs and support the possibility that the lack of radio emission from the latter might simply be due to an unfavorable viewing geometry.
Key words: pulsars: general / pulsars: individual: PSR J0726−2612 / stars: neutron / X-rays: stars
© ESO 2019
1. Introduction
Observations with the ROSAT satellite in the mid-1990s led to the discovery of a small group of isolated neutron stars characterized by thermal emission at soft X-rays, now known as XDINSs (X-ray-dim isolated neutron stars; see Haberl 2007; Turolla 2009 for reviews). The XDINSs have spin periods in the range P ∼ 3−17 s and period derivatives of a few 10−14 s s−1, which result in characteristic ages of τc = P/2Ṗ ∼ 1−4 Myr. With the usual assumption that the spin-down is due to magnetic dipole braking, these timing parameters imply magnetic fields of the order of a few 1013 G.
The XDINSs are at distances of only a few hundred parsecs and for two of them the parallax of the optical counterpart has been measured (Walter et al. 2010; Tetzlaff et al. 2011). The XDINSs have X-ray luminosities of 1031−1032 erg s−1, higher than their spin-down power. Their X-ray spectra are very soft, with blackbody temperatures of kT ∼ 45−110 eV, often showing the presence of broad absorption lines. If these lines are interpreted as proton cyclotron features or atomic transitions (see, e.g., Kaplan et al. 2008), the magnetic fields estimated from their energies are of the same order as those derived from the spin-down rate assuming magnetic dipole braking. The X-ray emission of XDINSs, consisting only of thermal components, is believed to come directly from the star surface and, given the small distance of these sources, it is little affected by photoelectric absorption in the interstellar medium. The discovery of XDINS caused some excitement since they appeared as optimal targets to test neutron star surface emission models without being affected by the presence of nonthermal emission. However, the ultimate goal of constraining the star radius and hence the equation of state with these studies is still hampered by our poor knowledge of the composition and magnetization of the surface layers of neutron stars.
The attempt to explain the different manifestations of neutron stars (e.g., Mereghetti 2011) in the context of a unified evolutionary picture is one of the current challenges in the study of neutron stars (Kaspi 2010; Igoshev et al. 2014). In the P−Ṗ diagram, shown in Fig. 1, XDINSs are located in the region below that occupied by the magnetars, a group of isolated neutron stars powered mainly by magnetic energy (see, e.g. Mereghetti et al. 2015; Turolla et al. 2015; Kaspi & Beloborodov 2017). This has led to the suggestion that the XDINSs might be the descendants of magnetars (Heyl & Kulkarni 1998; Colpi et al. 2000). The strong internal field of magnetars (B ≳ 1015 G) significantly affects their thermal evolution (Viganò et al. 2013), resulting in luminosities higher than those predicted for normal pulsars of a similar age.
 |
Fig. 1. P−Ṗ diagram of rotation-powered pulsars (black dots) and other classes of isolated pulsars (colored symbols). Lines of equal characteristic age (dotted, 104−1010 yr) and equal dipole magnetic field (dashed, 1012−1016 G) are indicated. The radio pulsar death line B/P2 = 1.7 × 1011 G s−2 (Bhattacharya et al. 1992) is also shown. The data are taken from the ATNF Pulsar Catalogue (Manchester et al. 2005). |
A distinctive property of the XDINSs is that they are not detected in the radio band1 (Kondratiev et al. 2009). The reason for the lack of radio emission is still uncertain. One possibility is that this is due to their old age and long spin period (Baring & Harding 1998, 2001). However, a few radio pulsars with periods ≳10 s have recently been discovered: PSR J0250+5854 with P = 23.5 s (Tan et al. 2018), and a second one with P = 12.1 s (Morello et al., in prep). Another explanation might be related to the geometrical configuration of their magnetosphere, that, especially if they are old magnetars, might be strongly nondipolar (Turolla et al. 2015). Finally, it cannot be excluded that (at least some of) the XDINSs are simply ordinary radio pulsars with radio beams unfavorably aligned with respect to the Earth. In this respect, it is interesting to investigate radio-loud pulsars with X-ray properties and/or timing parameters similar to those of the XDINSs, such as the long-period (greater than a few seconds) and high-B (>1013 G) pulsars.
Among these, here we focus on PSR J0726–2612, a radio pulsar with spin period P = 3.44 s and characteristic age of 200 kyr that was discovered in the Parkes High-Latitude Survey (Burgay et al. 2006). Its timing parameters (Table 1) are in the range of those of the XDINSs. The similarity with the XDINSs was reinforced by X-ray observations with the Chandra satellite (Speagle et al. 2011), that revealed a soft thermal spectrum with blackbody temperature kT ≈ 87 eV, and pulsations with a sinusoidal, double-peaked profile. The distance of PSR J0726–2612 is unknown. Its dispersion measure DM = 69.4 ± 0.4 cm−3 pc (Burgay et al. 2006) implies a distance d = 2.9 kpc, assuming the Galactic electrons distribution of Yao et al. (2017). However, there are a few facts suggesting that this is probably an overestimate. For example, such a large value for d would give a distance of 230 pc from the Galactic plane, implying that if PSR J0726–2612 was born close to the plane and its true age were similar to τc, its velocity would be of the order of a thousand kilometers per second. This value is not impossible, but it would be at the far end of the pulsar velocity distribution (Hobbs et al. 2005). More importantly, for such a large d, one would expect an X-ray absorption corresponding to a sizeable fraction of the total Galactic H I column density, which in this direction is ∼5 × 1021 cm−1 (Kalberla et al. 2005), while the observed value is a factor ten smaller. Finally, the line of sight toward PSR J0726–2612 crosses the Gould belt, which is not included in the electron distribution model of Yao et al. (2017). This could explain the large distance inferred from the DM. This local structure (d ∼ 200−400 pc) comprises several OB associations that have been proposed as the birthplace of the XDINSs (Popov et al. 2003, 2005). Speagle et al. (2011) suggested that PSR J0726–2612 could also be associated with the Gould belt and hence be closer than ∼1 kpc.
Observed and derived parameters for PSR J0726–2612.
Here we report the results of XMM-Newton observations which show other similarities between PSR J0726–2612 and the XDINSs. In the following we scale all the distance-dependent quantities to dkpc = 1 kpc and adopt representative values of mass and radius of 1.2 M⊙ and 12 km, respectively.
2. Observations and data reduction
PSR J0726–2612 was observed with the European Photon Imaging Cameras (EPIC) instrument on board XMM-Newton with a single pointing lasting 108 ks on 2013 April 8. The three cameras of EPIC (0.1–12 keV), the pn (Strüder et al. 2001), and the two MOS (Turner 2001), were operated in Full Frame mode with the thin optical filter. While the EPIC-pn time resolution (73.4 ms) is adequate to reveal the pulsations of the source, this is impossible for the EPIC-MOS given its resolution time of 2.6 s.
The data reduction was performed using the EPPROC and EMPROC pipelines of version 15 of the Science Analysis System (SAS)2. We selected single- and multiple-pixel events (PATTERN ≤ 4 and PATTERN ≤ 12) for both the EPIC-pn and -MOS. We then removed time intervals of high background using the SAS program ESPFILT with standard parameters. The source was detected by EPIC at coordinates 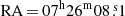 , Dec = −26° 12′38″, fully consistent with the radio position (Table 1). The source events were selected from a circle of radius 40″ centered at the radio position, while the background was extracted from a nearby circular region of radius 60″. The resulting net exposure times and source events are listed in Table 2. At the corresponding count rates pile-up effects are not relevant.
, Dec = −26° 12′38″, fully consistent with the radio position (Table 1). The source events were selected from a circle of radius 40″ centered at the radio position, while the background was extracted from a nearby circular region of radius 60″. The resulting net exposure times and source events are listed in Table 2. At the corresponding count rates pile-up effects are not relevant.
Exposure times and source counts for PSR J0726–2612 in the three EPIC cameras.
3. Results
3.1. Timing analysis
PSR J0726–2612 is barely detected above 1.5 keV, therefore we limited our timing analysis to the energy band 0.15–1.5 keV. The times of arrival were converted to the barycenter of the solar system with the task BARYCEN. An epoch folding search of the EPIC-pn data gave a best period of P = 3.442396(1) s, which is consistent within 0.7σ with the value expected at the XMM-Newton observation epoch (56 390 MJD) using the ATNF ephemeris reported in Table 1. The background-subtracted light curve in the energy band 0.15–1.5 keV is shown in Fig. 2. The position of the radio pulse is indicated, with its 1σ uncertainty, as a vertical red line.
 |
Fig. 2. Pulse profile of PSR J0726–2612 in the energy range 0.15–1.5 keV obtained by folding the EPIC-pn data in 20 phase bins at the period derived from the radio ephemeris (Table 1). The vertical red line represents the location of the radio pulse (derived from Speagle et al. 2011), with its uncertainty (1σ). The colored bands indicate the intervals used for the phase-resolved spectroscopy. |
The EPIC-pn pulse profile shows two peaks with the same intensity (net count rate of max1 = 0.62 ± 0.02 cts s−1 and max2 = 0.64 ± 0.02 cts s−1), separated by about 0.5 cycles. The two minima of the pulse profile are instead significantly different: min1 = 0.34 ± 0.01 cts s−1 and min2 = 0.39 ± 0.01 cts s−1. The pulse profile is symmetric in phase with respect to any of the two minima, but a fit with a constant plus a sine function at half of the spin period is not acceptable (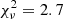 for 17 d.o.f.). The pulsed fraction3 is 30 ± 2%.
for 17 d.o.f.). The pulsed fraction3 is 30 ± 2%.
Figure 3 shows that the soft (0.15−0.4 keV) and hard energy ranges (0.4−1.5 keV) have slightly different pulsed fractions: 26 ± 3% and 37 ± 3%, respectively. Moreover, the positions of the first minimum and of the second maximum are shifted of about 1 bin between the two energy ranges, but the symmetry around the minima is preserved in both bands. Fits with a constant plus sine function give 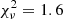 and
and 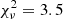 for the soft and hard profiles, respectively. The hardness ratio4, shown in the lower panel of the same figure clearly indicates the presence of phase-dependent spectral variations: the source is softer during the minima and harder during the maxima.
for the soft and hard profiles, respectively. The hardness ratio4, shown in the lower panel of the same figure clearly indicates the presence of phase-dependent spectral variations: the source is softer during the minima and harder during the maxima.
 |
Fig. 3. EPIC-pn light curve of PSR J0726–2612 (20 phase bins) in the energy ranges 0.15−0.4−1.5 keV together with the corresponding hardness ratio. |
3.2. Spectral analysis
The spectral analysis was performed using XSPEC (version 12.8.2). The spectra were rebinned using the GRPPHA tool with a minimum of 50 counts per bin. The spectra of the three cameras were fitted simultaneously, including a renormalization factor to account for possible cross-calibration uncertainties. Errors on the spectral parameters are at 1σ confidence level.
We used the photoelectric absorption model TBABS, with cross sections and abundances from Wilms et al. (2000). Both a single power law and a blackbody did not provide acceptable fits, giving 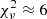 and
and 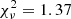 for 213 d.o.f. (null-hypothesis probability, nhp, of 3 × 10−4), respectively. We then attempted a fit with magnetized hydrogen atmosphere models (NSA and NSMAXG in XSPEC, Pavlov et al. 1995; Ho et al. 2008, 2014). However, neither of the two sets of available models (the first with a single surface B and Teff, the second with B and Teff varying across the surface according to the magnetic dipole model) gave an acceptable fit (
for 213 d.o.f. (null-hypothesis probability, nhp, of 3 × 10−4), respectively. We then attempted a fit with magnetized hydrogen atmosphere models (NSA and NSMAXG in XSPEC, Pavlov et al. 1995; Ho et al. 2008, 2014). However, neither of the two sets of available models (the first with a single surface B and Teff, the second with B and Teff varying across the surface according to the magnetic dipole model) gave an acceptable fit (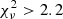 for 213 d.o.f.). In conclusion, we could not find a good fit with single-component models.
for 213 d.o.f.). In conclusion, we could not find a good fit with single-component models.
Furthermore, modeling the spectra with a blackbody plus power law or with the sum of two blackbodies was unsatisfactory. With the former we obtained a negative photon index for the power law, while with the latter, the second thermal component had a negligible flux, and did not improve the quality of the fit with respect to that of a single blackbody (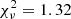 for 211 d.o.f., nhp = 10−3).
for 211 d.o.f., nhp = 10−3).
A real improvement in the fit was obtained by adding to the blackbody a broad absorption line modeled with a Gaussian (GBB) centered at E = 1.09 ± 0.09 keV and width σ = 0.28 ± 0.08 keV (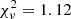 for 210 d.o.f.). Following the recent results of Yoneyama et al. (2019), we explored the possibility of adopting a two-blackbody component model plus a Gaussian line in absorption (G2BB). With this model we found a good fit with the line placed at
for 210 d.o.f.). Following the recent results of Yoneyama et al. (2019), we explored the possibility of adopting a two-blackbody component model plus a Gaussian line in absorption (G2BB). With this model we found a good fit with the line placed at 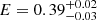 keV and with a broadening of
keV and with a broadening of 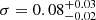 keV (
keV (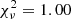 for 208 d.o.f.). The addition of the line yields an improvement of the χ2 of
for 208 d.o.f.). The addition of the line yields an improvement of the χ2 of 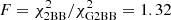 . To assess the statistical significance of the line, we estimated through Monte Carlo simulations the probability of obtaining by chance an equal (or better) fit improvement: we estimate a probability of ∼10−5 of having F ≥ 1.32, corresponding to a ∼4.4σ significance of the line. The cold blackbody (kT1 ≈ 0.074 keV) has an emitting radius
. To assess the statistical significance of the line, we estimated through Monte Carlo simulations the probability of obtaining by chance an equal (or better) fit improvement: we estimate a probability of ∼10−5 of having F ≥ 1.32, corresponding to a ∼4.4σ significance of the line. The cold blackbody (kT1 ≈ 0.074 keV) has an emitting radius 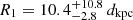 km, compatible with emission from the whole neutron star, while the hot blackbody has kT2 ≈ 0.14 keV and
km, compatible with emission from the whole neutron star, while the hot blackbody has kT2 ≈ 0.14 keV and 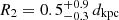 km.
km.
A good fit was also found with the magnetized atmosphere models with a dipole distribution of the surface magnetic field (B = 1013 G at the poles) plus a Gaussian line in absorption. With the NSA model, we found an effective temperature Teff = 0.40 ± 0.08 MK (corresponding to an observed temperature kT = 0.029 ± 0.001 keV), 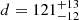 pc, and
pc, and 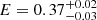 keV,
keV, 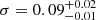 keV for the Gaussian line (
keV for the Gaussian line (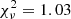 for 210 d.o.f.). With the NSMAXG model, for an impact parameter (that is the angle between the line of sight and the dipole axis) η = 90°, the model parameters are Teff = 0.39 ± 0.02 MK (kT = 0.028 ± 0.001 keV),
for 210 d.o.f.). With the NSMAXG model, for an impact parameter (that is the angle between the line of sight and the dipole axis) η = 90°, the model parameters are Teff = 0.39 ± 0.02 MK (kT = 0.028 ± 0.001 keV), 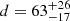 pc and E = 0.28 ± 0.09 keV,
pc and E = 0.28 ± 0.09 keV, 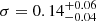 keV for the Gaussian line (
keV for the Gaussian line (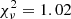 for 210 d.o.f.). Using instead the same model with η = 0°, the fit was not acceptable (
for 210 d.o.f.). Using instead the same model with η = 0°, the fit was not acceptable (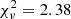 for 210 d.o.f.).
for 210 d.o.f.).
The spectral results are summarized in Table 3, while in Fig. 4 the best blackbody fits are shown.
Results for the phase-averaged and phase-resolved spectra of PSR J0726–2612.
 |
Fig. 4. EPIC-pn (black), -MOS1 (red) and -MOS2 (green) phase-averaged spectra of PSR J0726–2612. Top panel: best fit using a Gaussian absorption feature at E = 0.39 keV and two blackbodies (G2BB). Lower panels: residuals of the best fit (G2BB), of a Gaussian absorption feature at E = 1.09 keV and one blackbody (GBB), and of a single blackbody (BB) in units of σ. Data have been rebinned for display purposes only. |
The light curves and hardness ratio shown in Fig. 3 indicate that a spectral variation occurs as a function of the rotation phase. Therefore, we extracted the EPIC-pn spectra of the phase intervals corresponding to the two minima and the two maxima of the pulse profile, as shown in Fig. 2 (the number of source events in each spectrum is listed in Table 2). In order to illustrate the spectral variations, we fitted the spectra with the G2BB model, fixing all of the parameters at the best fit values of the phase-averaged spectrum, except for an overall normalization. The residuals shown in the two lower panels of Fig. 5 indicate that the spectra of the two maxima are similar and significantly harder than those of the minima. Their normalization factors with respect to the phase-averaged spectrum are consistent (Nmax1 = 1.16 ± 0.02 and Nmax2 = 1.14 ± 0.02), while those of the two minima are different (Nmin1 = 0.85 ± 0.01 and Nmin2 = 0.80 ± 0.01).
 |
Fig. 5. EPIC-pn phase-resolved spectra fitted with the G2BB model used for the phase-averaged spectra (the color code is the same as in Fig. 2). The overall normalization is the only free parameter. The residuals of the spectra at maxima and minima, in units of σ, are shown in the lower panels. Data have been rebinned for display purposes only. |
We then fitted the four spectra separately, keeping only the interstellar absorption and the parameters of the cold blackbody fixed, because we do not expect them to vary during a stellar rotation. The results are given in Table 3. The absorption line is at the same energy in the four spectra, but it has different widths and normalizations. The hot blackbody temperature is lower (kT ≈ 0.11 keV) and its emission radius is larger (R ≈ 1.5 dkpc km) at the two maximum phases than at the first minimum (kT ≈ 0.17 keV and R ≈ 0.20 dkpc km), while these parameters are poorly constrained at the second minimum. We also tried other fits allowing more parameters to vary, but the results were inconclusive due to the strong parameter degeneracy.
4. Discussion
Our XMM-Newton results for PSR J0726–2612 are consistent with those previously obtained with Chandra (Speagle et al. 2011), but thanks to a significant detection with good statistics over a broader energy range, they provide more information on the spectrum and pulse profile of this pulsar.
4.1. The X-ray spectrum
We found that the spectrum of PSR J0726–2612 is more complex than the single blackbody that was adequate to fit the Chandra data. The single blackbody fit requires the addition of a broad absorption line at E ≈ 1.09 keV. A better fit was obtained with two blackbody components, but also in this case a line at E ≈ 0.39 keV is required. The colder blackbody component has an emitting area consistent with a large fraction of the star surface (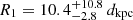 km), while the hotter one can be attributed to a small hot spot (
km), while the hotter one can be attributed to a small hot spot (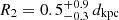 km), likely located at the magnetic pole.
km), likely located at the magnetic pole.
Our results confirm that the interstellar absorption is about a factor of ten smaller than the value (NH = 2.1 × 1021 cm−2) inferred from the dispersion measure and the usual assumption of a 10% ionization of the interstellar medium (He et al. 2013). This might be due to the line of sight crossing the Gould belt.
An equally good fit was obtained with a magnetized hydrogen atmosphere covering the whole surface of the star, but also in this case the presence of an absorption line at E ≈ 0.37 keV (NSA model) or E ≈ 0.28 keV (NSMAXG model) is required. We note that the constant (polar) value of the magnetic field in the NSA (NSMAXG) model is fixed in the fits at B = 1013 G, and that the NSA model assumes a uniform distribution of the temperature. The NSMAXG model is more realistic, but it assumes that the dipole axis is orthogonal to the line of sight, which is not necessarily true for the case of PSR J0726–2612. Moreover, the inferred distance of ≈63 pc seems unrealistically small.
The absorption lines we found in the spectra can be interpreted as proton cyclotron features at Ecyc = 0.063 B13 × (1 + z) keV, where z is the gravitational redshift and B13 the magnetic field in units of 1013 G. In the case of G2BB model, for Ecyc = 0.39 keV and z ≈ 0.2, we get B ≈ 5 × 1013 G, in good agreement with the dipole magnetic field evaluated at the poles (Bp ≈ 6 × 1013 G). However, we caution that other explanations cannot be ruled out, including the possibility that the lines are simply an artefact resulting from an oversimplified modeling of the continuum emission. In fact, Viganò et al. (2014) showed that nonhomogeneus temperature distributions on a neutron star surface can in some cases lead to the appearance of broad features when the spectra are fitted with simple blackbody models.
4.2. The X-ray pulse profile
Contrary to the previous Chandra results, we also found that the double-peaked pulse profile of PSR J0726–2612 is not well described by a sinusoid, owing to the significant difference in the flux of the two minima. Remarkably, the pulse profile is symmetric for phase reflection around any of the two minima. Within the limits due to their lower statistics, these properties seem to hold also for the profiles in the soft and hard X-ray bands. The pulse profiles are moderately energy-dependent, with evidence for a harder emission in correspondence of the two peaks.
Although a detailed modeling of the light curves of PSR J0726–2612 is beyond the scope of the present work, we explored whether or not a simple model based on blackbody emission components with parameters consistent with the spectral results could reproduce the pulse profile. We assumed that the hotter blackbody comes from two antipodal magnetic polar caps with opening angle θc, 1 = 3°, while the colder one from two annuli extending between θc, 1 and θc, 2 = 36°. The temperatures of the emitting regions were set to the values derived from the spectral analysis (model G2BB, kT1 = 0.074 keV, kT2 = 0.14 keV) and the angular apertures were chosen in such a way as to reproduce the emitting radii derived from the fit for a NS radius of 12 km. We also added interstellar absorption and a Gaussian absorption line, with parameters fixed to those of the phase averaged spectrum. Synthetic light curves were computed using the method by Turolla & Nobili (2013) and account for general-relativistic effects. We convolved the obtained light curves with the EPIC-pn instrumental response and evaluated the pulsed fraction in the energy range 0.15–1.5 keV. The results depend on the angles χ and ξ that the rotation axis makes with the line of sight and the magnetic axis, respectively. As shown in Fig. 6, this simple model is unable to yield the observed pulsed fraction even for the most favorable geometry (PF ≈ 21% for ξ ≈ χ ≳ 35°). This is also true if only two antipodal point-like polar caps are considered, which is the configuration yielding the maximum pulsed fraction using isotropic emission (see e.g., Turolla & Nobili 2013). Another problem is that, owing to the intrinsic symmetry of the model, the resulting light curves cannot exhibit different minima, as observed in PSR J0726–2612.
 |
Fig. 6. Pulsed fraction for the G2BB model, where the blackbody emission comes from two, antipodal “cap+ring” spots centered on the magnetic poles. The aperture of the hot cap (kT = 0.14 keV) is θc, 1 = 3°, while the colder (kT = 0.074 keV) ring extends from θc, 1 to θc, 2 = 36°. The considered energy range is 0.15–1.5 keV, and a compactness of M/R = 0.1 M⊙ km−1 has been assumed. |
Indeed, this model is oversimplified and unlikely to apply to the real case. Whatever the mechanism responsible for the surface emission, the presence of a strong magnetic field results in some degree of anisotropy in the emitted radiation. In the case of a magnetized atmosphere, more complicated energy-dependent beaming patterns are produced; they consist of a relatively narrow pencil-beam aligned with the magnetic field, surrounded by a broader fan-beam at intermediate angles and account for most of the escaping radiation (see e.g., Pavlov et al. 1994). The angular pattern of the emerging intensity depends also on the local surface temperature and magnetic field, meaning that the morphology of the pulse profiles can be extremely variegated. Using a partially ionized hydrogen atmosphere model (Suleimanov et al. 2009) with improved opacities from Potekhin et al. (2014), we computed the expected pulse profiles, as described in Rigoselli et al. (2019). The best match with the data was obtained assuming emission from two antipodal hot spots with an effective temperature of 0.5 MK, and ξ = 30°, χ = 35°. In Fig. 7 we show two examples with representative values of the magnetic field, B = 4 × 1013 G and B = 6 × 1013 G. Although these pulse profiles qualitatively resemble that observed in PSR J0726–2612, we note that they have been computed considering only the X-ray emission from the polar caps. The addition of a contribution from an extended part of the star surface would reduce the pulsed fractions of the light curves shown in Fig. 7.
 |
Fig. 7. Pulse profiles in the 0.15–1.5 keV range in the case of emission from a hydrogen atmosphere model at two point-like polar caps with Teff = 0.5 MK and B = 4 × 1013 G (upper panel), and B = 6 × 1013 G (lower panel). We assumed ξ = 30°, χ = 35° and a compactness M/R = 0.1 M⊙ km−1. The vertical red line shows the phase expected for the radio peak. |
4.3. Connections with the XDINSs
Our spectral results, and in particular the presence of a broad absorption line, strengthen the similarity between PSR J0726–2612 and the XDINSs, for which similar spectral features have been reported (see Table 4). As illustrated in Fig. 8, not only the line properties, but also the best fit parameters of the continuum model are very similar to those recently reported in a systematic analysis of all the XDINS spectra with the G2BB model (Yoneyama et al. 2019).
Comparison between PSR J0726–2612 and the XDINSs.
 |
Fig. 8. Comparison of the spectral parameters of the XDINSs (from Yoneyama et al. 2019) and PSR J0726–2612 (red cross) obtained with two blackbodies and a Gaussian absorption line model (G2BB). Upper panel: blackbody radii (black: cold; green: hot) for the XDINSs and for PSR J0726–2612 (red cross). Lower panel: line width vs. line centroid energy (black dots are for XDINSs and the red cross for PSR J0726–2612). |
The age–luminosity diagram shown in Fig. 9 gives even more strength to this analogy. The figure represents the bolometric luminosity of thermally emitting neutron stars as a function of their ages, characteristic or kinematic. The luminosity of PSR J0726–2612 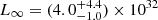 erg s−1 corresponds to the cold component of the G2BB fit to the phase-averaged spectrum (for d = 1 kpc). This component is in fact representative of the cooling emission from the entire star surface (the inclusion of the hot component would not significantly change the result, adding only about 3% to the total luminosity, well within the uncertainties). The observational data for other neutron stars are displayed in Fig. 9 as in Potekhin & Chabrier (2018); most of them are taken from Viganò et al. (2013), with some updates and additions. The horizontal error bars show the uncertainties of kinematic ages, when available; otherwise the bars are replaced by arrows.
erg s−1 corresponds to the cold component of the G2BB fit to the phase-averaged spectrum (for d = 1 kpc). This component is in fact representative of the cooling emission from the entire star surface (the inclusion of the hot component would not significantly change the result, adding only about 3% to the total luminosity, well within the uncertainties). The observational data for other neutron stars are displayed in Fig. 9 as in Potekhin & Chabrier (2018); most of them are taken from Viganò et al. (2013), with some updates and additions. The horizontal error bars show the uncertainties of kinematic ages, when available; otherwise the bars are replaced by arrows.
 |
Fig. 9. Thermal luminosities vs. ages of isolated neutron stars. The same color coding as in Fig. 1 is used (in addition to PSR J0726–2612, the three High-B pulsars are J1119−6127, J1718−3718 and J1819−1458). The solid and dashed lines are the theoretical cooling curves of a neutron star with mass M = 1.2 M⊙ and the dipole magnetic field of PSR J0726–2612 (Bp = 6 × 1013 G), with the heat blanketing outer envelope composed either of iron (solid line) or of accreted light elements (dashed line). |
The position of PSR J0726–2612 in this diagram is indeed close to the group of XDINSs. Its place can be considered as intermediate between the regions occupied by ordinary neutron stars, which have either smaller luminosities or smaller ages, magnetars, which generally have larger luminosities, and XDINSs, which have somewhat smaller luminosities and larger ages. For comparison we plot two cooling curves, with heavy (nonaccreted) and light (accreted) chemical elements in the outer heat-blanketing envelope. The cooling curves are calculated for a neutron star of mass M = 1.2 M⊙ and the dipole magnetic field inferred for PSR J0726–2612 (Bp = 6 × 1013 G) using the code of Potekhin & Chabrier (2018) with the equation of state BSk24 (Pearson et al. 2018), and singlet pairing-type superfluidity of neutrons and protons (according to Margueron et al. 2008 and Baldo & Schulze 2007, respectively, both in the parametrized form of Ho et al. 2015). The triplet pairing-type superfluidity of neutrons is not included, because it is strongly suppressed by many-particle correlations, according to recent results of Ding et al. (2016). The latter suppression delays the onset of the Cooper pair breaking-formation mechanism of neutrino emission in the core of the neutron star and thus slows down the cooling, making the theoretical cooling curves compatible with the XDINS observations even without additional internal heating, which otherwise would be needed (e.g., Viganò et al. 2013).
While most of the XDINSs have single-peaked pulse profiles, two of them (RX J1308.6+2127, Hambaryan et al. 2011, and RX J0720.4−3125, Hambaryan et al. 2017) show double-peaked profiles similar to PSR J0726–2612, although with smaller pulsed fractions (18% and 11%, respectively). The remarkable difference between PSR J0726–2612 and these two XDINSs is the presence of radio emission in the former. Here we discuss the possibility that this is due to an unfavorable orientation of their radio beam. Based on the radio beaming fraction of long-period pulsars, Kondratiev et al. (2009) estimated that a much larger number of XDINSs (∼40) would need to be observed to detect one with the radio beam crossing our line of sight.
We marked in Fig. 10 the values of the angles ξ and χ estimated for RX J1308.6+2127 and RX J0720.4−3125 by Hambaryan et al. (2011, 2017). They imply that these two pulsars are nearly orthogonal rotators (ξ ≈ 90°) seen with a large impact parameter η = |χ − ξ| ≈ 45°. With the usual assumption that the radio beam coincides with, or is close to, the magnetic dipole axis, such a large impact parameter can naturally account for the fact that their radio emission is not visible from the Earth. As an example, the dashed lines in Fig. 10 indicate the region where ξ ≈ χ for which a radio beam with an aperture of ∼8° would be visible. Contrary to the two XDINSs, PSR J0726–2612 should lie inside this region. Our atmosphere model used to compute the pulse profiles of Fig. 7 predicts that the radio pulse appearing when the magnetic axis is in the plane defined by the line of sight and rotation axis is in phase with one of the two minima of the X-ray profile. Considering the current relative error in the radio and X-ray phase alignment (see Fig. 2), this possibility cannot be excluded.
 |
Fig. 10. Visibility of a radio beam with aperture of ∼8° as a function of the ξ and χ angles. The estimated positions for RX J1308.6+2127 [ blue dot]ham11 and RX J0720.4−3125 [ red dot]ham17 are shown. |
5. Conclusions
Our analysis of XMM-Newton data of the slow, highly magnetized radio pulsar PSR J0726–2612 reveals the presence of a broad absorption line in its soft thermal spectrum, with parameters similar to those of the lines seen in most of the XDINSs. The X-ray pulse profile of PSR J0726–2612 is double-peaked and moderately energy-dependent. These findings reinforce the similarity between this radio pulsar and the XDINSs. Assuming a distance of 1 kpc, the luminosity of PSR J0726–2612 is 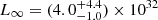 erg s−1. This is greater than its spin-down luminosity, as for the XDINSs (see Table 4), but is in reasonable agreement with the expected thermal luminosity of a ∼200 kyr-old pulsar (see Fig. 9).
erg s−1. This is greater than its spin-down luminosity, as for the XDINSs (see Table 4), but is in reasonable agreement with the expected thermal luminosity of a ∼200 kyr-old pulsar (see Fig. 9).
More observations are needed to reduce the uncertainty in the radio and X-ray phase alignment and better constrain the geometry of PSR J0726–2612. This could help to decipher whether or not the detection of radio emission in this pulsar, and not in the XDINSs with a similar double-peaked X-ray pulse profile, is due only to orientation effects.
The possible detection of pulsed emission from two XDINSs at very low frequencies (Malofeev et al. 2005, 2006) is so far unconfirmed.
Acknowledgments
We are grateful to an anonymous referee for constructive suggestions. We acknowledge financial contribution from the agreement ASI-INAF n.2017-14-H.0. Part of this work has been funded using resources from the research grant “iPeska” (P.I. Andrea Possenti) funded under the INAF national call Prin-SKA/CTA approved with the Presidential Decree 70/2016. This work is based on observations obtained with XMM-Newton, an European Space Agency (ESA) science mission with instruments and contributions directly funded by ESA Member States and NASA. The work of A.Y.P. was supported by DFG and RFBR within the research project 19-52-12013. The work of V.S. was supported by Deutsche Forschungsgemeinschaft (DFG, (grant WE 1312/51-1)) and by the subsidy allocated to Kazan Federal University for the state assignment in the sphere of scientific activities (3.9780.2017/8.9).
References
- Baldo, M., & Schulze, H.-J. 2007, Phys. Rev. C, 75, 025802 [NASA ADS] [CrossRef] [Google Scholar]
- Baring, M. G., & Harding, A. K. 1998, ApJ, 507, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Baring, M. G., & Harding, A. K. 2001, ApJ, 547, 929 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, D., Wijers, R. A. M. J., Hartman, J. W., & Verbunt, F. 1992, A&A, 254, 198 [NASA ADS] [Google Scholar]
- Burgay, M., Joshi, B. C., D’Amico, N., et al. 2006, MNRAS, 368, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Geppert, U., & Page, D. 2000, ApJ, 529, L29 [Google Scholar]
- Ding, D., Rios, A., Dussan, H., et al. 2016, Phys. Rev. C, 94, 025802 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F. 2007, Ap&SS, 308, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Haberl, F., Motch, C., Zavlin, V. E., et al. 2004, A&A, 424, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hambaryan, V., Suleimanov, V., Schwope, A. D., et al. 2011, A&A, 534, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hambaryan, V., Suleimanov, V., Haberl, F., et al. 2017, A&A, 601, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- He, C., Ng, C.-Y., & Kaspi, V. M. 2013, ApJ, 768, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Heyl, J. S., & Kulkarni, S. R. 1998, ApJ, 506, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G. 2014, IAU Symp., 302, 435 [NASA ADS] [Google Scholar]
- Ho, W. C. G., Potekhin, A. Y., & Chabrier, G. 2008, ApJS, 178, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, W. C. G., Elshamouty, K. G., Heinke, C. O., & Potekhin, A. Y. 2015, Phys. Rev. C, 91, 015806 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, G., Lorimer, D. R., Lyne, A. G., & Kramer, M. 2005, MNRAS, 360, 974 [NASA ADS] [CrossRef] [Google Scholar]
- Igoshev, A. P., Popov, S. B., & Turolla, R. 2014, Astron. Nachr., 335, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaplan, D. L. 2008, AIP Conf. Ser., 968, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M. 2010, Proc. Natl. Acad. Sci., 107, 7147 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, V. M., & Beloborodov, A. M. 2017, ARA&A, 55, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Kondratiev, V. I., McLaughlin, M. A., Lorimer, D. R., et al. 2009, ApJ, 702, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Malofeev, V. M., Malov, O. I., Teplykh, D. A., Tyul’Bashev, S. A., & Tyul’Basheva, G. E. 2005, Astron. Rep., 49, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Malofeev, V. M., Malov, O. I., Teplykh, D. A., et al. 2006, ATel, 798 [Google Scholar]
- Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, VizieR Online Data Catalog, VII/7245 [Google Scholar]
- Margueron, J., Sagawa, H., & Hagino, K. 2008, Phys. Rev. C, 77, 054309 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S. 2011, Astrophys. Space Sci. Proc., 21, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Mereghetti, S., Pons, J. A., & Melatos, A. 2015, Space Sci. Rev., 191, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Mignani, R. P., Zane, S., Turolla, R., et al. 2011, A&A, 530, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlov, G. G., Shibanov, Y. A., Ventura, J., & Zavlin, V. E. 1994, A&A, 289, 837 [NASA ADS] [Google Scholar]
- Pavlov, G. G., Shibanov, Y. A., Zavlin, V. E., & Meyer, R. D. 1995, in NATO Advanced Science Institutes (ASI) Series C, eds. M. A. Alpar, U. Kiziloglu, & J. van Paradijs, 450, 71 [Google Scholar]
- Pearson, J. M., Chamel, N., Potekhin, A. Y., et al. 2018, MNRAS, 481, 2994 [NASA ADS] [Google Scholar]
- Pires, A. M., Schwope, A. D., Haberl, F., et al. 2019, A&A, 623, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popov, S. B., Colpi, M., Prokhorov, M. E., Treves, A., & Turolla, R. 2003, A&A, 406, 111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popov, S. B., Turolla, R., Prokhorov, M. E., Colpi, M., & Treves, A. 2005, Ap&SS, 299, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., & Chabrier, G. 2018, A&A, 609, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Ho, W. C. G. 2014, A&A, 572, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigoselli, M., Mereghetti, S., Turolla, R., et al. 2019, ApJ, 872, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Kaplan, D. L., & van Kerkwijk, M. H. 2011, ApJ, 743, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suleimanov, V., Potekhin, A. Y., & Werner, K. 2009, A&A, 500, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tan, C. M., Bassa, C. G., Cooper, S., et al. 2018, ApJ, 866, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Tetzlaff, N., Eisenbeiss, T., Neuhäuser, R., & Hohle, M. M. 2011, MNRAS, 417, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Tiengo, A., & Mereghetti, S. 2007, ApJ, 657, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turolla, R. 2009, W. Becker, 357, 141 [Google Scholar]
- Turolla, R., & Nobili, L. 2013, ApJ, 768, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Turolla, R., Zane, S., & Watts, A. L. 2015, Rep. Prog. Phys., 78, 116901 [Google Scholar]
- Viganò, D., Rea, N., Pons, J. A., et al. 2013, MNRAS, 434, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Viganò, D., Perna, R., Rea, N., & Pons, J. A. 2014, MNRAS, 443, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F. M., Eisenbeiß, T., Lattimer, J. M., et al. 2010, ApJ, 724, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Yoneyama, T., Hayashida, K., Nakajima, H., & Matsumoto, H. 2019, PASJ, 71, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zane, S., Cropper, M., Turolla, R., et al. 2005, ApJ, 627, 397 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. P−Ṗ diagram of rotation-powered pulsars (black dots) and other classes of isolated pulsars (colored symbols). Lines of equal characteristic age (dotted, 104−1010 yr) and equal dipole magnetic field (dashed, 1012−1016 G) are indicated. The radio pulsar death line B/P2 = 1.7 × 1011 G s−2 (Bhattacharya et al. 1992) is also shown. The data are taken from the ATNF Pulsar Catalogue (Manchester et al. 2005). |
| In the text | |
 |
Fig. 2. Pulse profile of PSR J0726–2612 in the energy range 0.15–1.5 keV obtained by folding the EPIC-pn data in 20 phase bins at the period derived from the radio ephemeris (Table 1). The vertical red line represents the location of the radio pulse (derived from Speagle et al. 2011), with its uncertainty (1σ). The colored bands indicate the intervals used for the phase-resolved spectroscopy. |
| In the text | |
 |
Fig. 3. EPIC-pn light curve of PSR J0726–2612 (20 phase bins) in the energy ranges 0.15−0.4−1.5 keV together with the corresponding hardness ratio. |
| In the text | |
 |
Fig. 4. EPIC-pn (black), -MOS1 (red) and -MOS2 (green) phase-averaged spectra of PSR J0726–2612. Top panel: best fit using a Gaussian absorption feature at E = 0.39 keV and two blackbodies (G2BB). Lower panels: residuals of the best fit (G2BB), of a Gaussian absorption feature at E = 1.09 keV and one blackbody (GBB), and of a single blackbody (BB) in units of σ. Data have been rebinned for display purposes only. |
| In the text | |
 |
Fig. 5. EPIC-pn phase-resolved spectra fitted with the G2BB model used for the phase-averaged spectra (the color code is the same as in Fig. 2). The overall normalization is the only free parameter. The residuals of the spectra at maxima and minima, in units of σ, are shown in the lower panels. Data have been rebinned for display purposes only. |
| In the text | |
 |
Fig. 6. Pulsed fraction for the G2BB model, where the blackbody emission comes from two, antipodal “cap+ring” spots centered on the magnetic poles. The aperture of the hot cap (kT = 0.14 keV) is θc, 1 = 3°, while the colder (kT = 0.074 keV) ring extends from θc, 1 to θc, 2 = 36°. The considered energy range is 0.15–1.5 keV, and a compactness of M/R = 0.1 M⊙ km−1 has been assumed. |
| In the text | |
 |
Fig. 7. Pulse profiles in the 0.15–1.5 keV range in the case of emission from a hydrogen atmosphere model at two point-like polar caps with Teff = 0.5 MK and B = 4 × 1013 G (upper panel), and B = 6 × 1013 G (lower panel). We assumed ξ = 30°, χ = 35° and a compactness M/R = 0.1 M⊙ km−1. The vertical red line shows the phase expected for the radio peak. |
| In the text | |
 |
Fig. 8. Comparison of the spectral parameters of the XDINSs (from Yoneyama et al. 2019) and PSR J0726–2612 (red cross) obtained with two blackbodies and a Gaussian absorption line model (G2BB). Upper panel: blackbody radii (black: cold; green: hot) for the XDINSs and for PSR J0726–2612 (red cross). Lower panel: line width vs. line centroid energy (black dots are for XDINSs and the red cross for PSR J0726–2612). |
| In the text | |
 |
Fig. 9. Thermal luminosities vs. ages of isolated neutron stars. The same color coding as in Fig. 1 is used (in addition to PSR J0726–2612, the three High-B pulsars are J1119−6127, J1718−3718 and J1819−1458). The solid and dashed lines are the theoretical cooling curves of a neutron star with mass M = 1.2 M⊙ and the dipole magnetic field of PSR J0726–2612 (Bp = 6 × 1013 G), with the heat blanketing outer envelope composed either of iron (solid line) or of accreted light elements (dashed line). |
| In the text | |
 |
Fig. 10. Visibility of a radio beam with aperture of ∼8° as a function of the ξ and χ angles. The estimated positions for RX J1308.6+2127 [ blue dot]ham11 and RX J0720.4−3125 [ red dot]ham17 are shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


