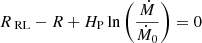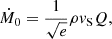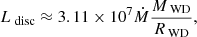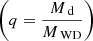| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 27 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201935322 | |
| Published online | 25 June 2019 | |
Evolution of helium star plus carbon-oxygen white dwarf binary systems and implications for diverse stellar transients and hypervelocity stars
1
Argelander Institut für Astronomy (AIfA), University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: neunteufel@astro.uni-bonn.de
2
Department of Physics and Astronomy, Seoul National University, 599 Gwanak-ro, Gwanak-gu, Seoul 151-742, Korea
Received:
20
February
2019
Accepted:
28
April
2019
Context. Helium accretion induced explosions in CO white dwarfs (WDs) are considered promising candidates for a number of observed types of stellar transients, including supernovae (SNe) of Type Ia and Type Iax. However, a clear favorite outcome has not yet emerged.
Aims. We explore the conditions of helium ignition in the WD and the final fates of helium star-WD binaries as functions of their initial orbital periods and component masses.
Methods. We computed 274 model binary systems with the Binary Evolution Code, in which both components are fully resolved. Both stellar and orbital evolution were computed including mass and angular momentum transfer, tides, gravitational wave emission, differential rotation, and internal hydrodynamic and magnetic angular momentum transport. We worked out the parts of the parameter space leading to detonations of the accreted helium layer on the WD, likely resulting in the complete disruption of the WD to deflagrations, where the CO core of the WD may remain intact and where helium ignition in the WD is avoided.
Results. We find that helium detonations are expected only in systems with the shortest initial orbital periods, and for initially massive WDs (MWD ≥ 1.0 M⊙) and lower mass donors (Mdonor ≤ 0.8 M⊙), which have accumulated helium layers mostly exceeding 0.1 M⊙. Upon detonation, these systems would release the donor as a hypervelocity pre-WD runaway star, for which we predict the expected range of kinematic and stellar properties. Systems with more massive donors or initial periods exceeding 1.5 h likely undergo helium deflagrations after accumulating 0.1 − 0.001 M⊙ of helium. Helium ignition in the WD is avoided in systems with helium donor stars below ∼0.6 M⊙, and leads to three distinctly different groups of double WD systems.
Conclusions. The size of the parameter space open to helium detonation corresponds to only about 3% of the galactic SN Ia rate and to 10% of the SN Iax rate, while the predicted large amounts of helium (0.1 M⊙) in progenitors cannot easily be reconciled with observations of archetypical SN Ia. However, the transients emerging from these systems may contribute significantly to massive helium novae, calcium-rich SNe Ib, and, potentially, very close double degenerate systems that may eventually produce either ordinary or peculiar SNe Ia, or, for the smallest considered masses, R Coronae Borealis stars.
Key words: accretion / accretion disks / binaries: close / novae / cataclysmic variables / white dwarfs / supernovae: general
© ESO 2019
1. Introduction
The study of binary star systems containing at least one white dwarf (WD) has long been considered a promising approach to identifying a number of astrophysical transient phenomena. Undoubtedly the most observationally important of these phenomena, owing their use as “standard candles” in cosmological distance measurements (Perlmutter et al. 1999; Riess et al. 1998; Schmidt et al. 1998), are Ia Type supernovae (SNe Ia) and, owing to their relatively high event rate, classical novae (Gallagher & Starrfield 1978). While SNe Ia and classical novae provided the impetus for the attempt to link explosive transients to binaries, a number of additional classes and subclasses of transients have been either theoretically proposed or observationally confirmed. Among these are SNe Iax (Li et al. 2003; Foley et al. 2013), the (theoretical) subluminous Type “.Ia” (Bildsten et al. 2007; Kilic et al. 2014), AM Canum-Venaticorum (AM CVn) systems (Iben & Tutukov 1987; Warner 1995; Nelemans 2005), and other “peculiar” transients (Woosley & Kasen 2011). Somewhat recently, a connection between interacting WDs and observationally identified fast-faint Ca-enhanced SNe Ib (Perets et al. 2010) was proposed by Waldman et al. (2011). Given the importance of these transients and of classical SNe Ia in particular, the comparative lack of understanding concerning the progenitors, their evolution, and their relation to each other needs to be addressed.
While the progenitors of cataclysmic variables are adequately well characterized observationally, the others still lack definitive observational evidence. Despite decades of intensive observational searches, SNe Ia still need to be connected to a prototype progenitor, although a number of nondetections (see Kelly et al. 2014; Nelemans et al. 2008; Maoz & Mannucci 2008; Schaefer & Pagnotta 2012; Li et al. 2011) have considerably limited the available parameter space for candidate systems.
McCully et al. (2014) succeeded in identifying a possible progenitor of SN 2012Z as a luminous blue source, interpreted as a massive main sequence (MS) star, blue supergiant, or a helium giant of ∼2.0 M⊙. However, a nondetection by Foley et al. (2015) of the progenitor of SN 2014dt excluded some of the interpretations of the former study. Therefore, in spite of the arguably better observational groundwork, the identity of the prototype progenitor of SNe Iax is only marginally better known than that of SNe Ia. Furthermore, the findings of Foley et al. (2015) imply that SNe Iax are products of several dissimilar progenitor systems.
In any case, it is thought that both SNe Ia and Iax potentially occur in binary systems consisting of a WD and a nondegenerate companion of some description. This scenario, as first proposed for SNe Ia (Whelan & Iben 1973), has become known as the single degenerate (SD scenario) scenario, which is in contrast to the double degenerate (DD scenario) scenario. The DD scenario assumes, again specifically in the context of SNe Ia, a system consisting of two interacting WDs that result in a thermonuclear explosion (Iben & Tutukov 1984; Webbink 1984). In the context of cataclysmic variables, the SD scenario is usually linked to classical novae and the DD scenario to AM CVn systems. The question of the role of DD systems as the possible progenitor of R Coronae Borealis (RCB) stars has also raised significant interest in the scientific community (Webbink 1984; Saio & Jeffery 2002; van Kerkwijk et al. 2010).
An important aspect in observations of SNe Ia and Iax progenitors is that He stars are generally not excluded as mass donors. This is notwithstanding that Li et al. (2011), failing to identify the progenitor of the SN Ia 2011fe, excluded a large part of the available parameter space for most types of He donor stars, leaving only a small margin for low mass helium giant as donors for this particular event.
Recently, a number of authors (Shen et al. 2010; Bildsten et al. 2007; Shen & Bildsten 2009) proposed a possible connection between the theoretically predicted SNe .Ia and AM CVn systems. Further studies by Shen & Moore (2014) suggested a continuum of He-accretion-induced transients defined by the nature of the donor star, the orbital period of the system and the associated mass transfer rate.
Considerable effort has been expended on the question of whether SD systems can provide the conditions necessary to allow the core of a CO WD to grow to the Chandrasekhar mass (e.g., Han & Podsiadlowski 2004; Brooks et al. 2016). This is usually accomplished by providing mass transfer rates high enough for steady processing of helium into carbon and oxygen to take place, requiring a donor star with an extended envelope, i.e., a helium giant or subgiant (Yoon & Langer 2003; Wang et al. 2009). The possibility of this type of system leading to a core collapse to form a neutron star, requiring some of the carbon to be processed into neon, forming a neon-oxygen WD, before collapse can take place, has also been investigated (Brooks et al. 2017; Wang et al. 2017).
In the 1980s, the possibility of mass accretion precipitating an ignition and subsequent detonation of the accumulated He shell on a sub-Chandrasekhar mass WD was first seriously explored (Taam 1980a,b; Nomoto 1980, 1982a,b). The required mass-accretion rates would have to be low enough (∼10−8 M⊙ yr−1) to preclude premature ignition of the accumulated material, which would result in a cataclysmic variable star instead of a detonation. Working from the required criterion for the mass transfer rate, Ergma & Fedorova (1990) investigated the ability of binaries containing a CO WD and a He-rich star to induce He detonation. While some of these detonations were predicted to leave the carbon-oxygen (CO) core of the WD intact, a clear possibility that the developing shock in the He envelope could induce a subsequent detonation of the core became apparent. This detonation would result in the complete destruction of the star and, hence, a supernova (SN) as bright as an ordinary SN Ia. This mechanism became known as the double detonation mechanism (hereafter, DDet). Later 1D and multidimensional studies (Livne 1990, 1997; Livne & Glasner 1990, 1991; Livne & Arnett 1995; Benz 1997; Fink et al. 2007, 2010; Sim et al. 2010; Kromer et al. 2010; Woosley & Kasen 2011) established He accretion as a promising avenue in the search for progenitors of explosive transients such as SNe Ia. However, synthetic spectra (Woosley & Kasen 2011; Sim et al. 2010; Kromer et al. 2010; Höflich et al. 1998) suggest that lower amounts of He generally lead to better agreement with the spectra of regular SNe Ia.
Further refinement in the understanding of the ignition conditions in accreting WDs was obtained through the inclusion of the effects of rotation and rotational instabilities (Yoon & Langer 2004a,b) and magnetic torques (Neunteufel et al. 2017), showing that these effects cannot be neglected in the study of accreting WDs. All these studies showed a higher probability for deflagrations instead of detonations as a result of He accretion at a rate of ∼10−8 M⊙ yr−1. Neunteufel et al. (2017) also predicted a large increase in the amount of helium required to induce detonation.
However, many of the aforementioned studies assume a constant accretion rate onto a single model WD. This assumption, while facilitating the creation of physically plausible ignition conditions, is of limited predictive power when applied to naturally occurring He star plus WD binaries. The problem with assumed constant accretion rates is twofold: on the one hand, the implicitly assumed infinite supply of accretable helium neglects the evolution of the donor star and its ability to provide material to the accretor during different phases of its evolution and, on the other hand, the assumption of constant accretion itself neglects possible effects arising from the variation of the mass transfer rate in natural systems (see also Wang et al. 2013; Neunteufel et al. 2016).
In this study we investigate the evolution of a grid of fully resolved CO-WD plus He star systems. As such, this is the first study to include rotational effects and magnetic torques in a comprehensive exploration of the parameter space of SD helium star progenitors of thermonuclear transients. This paper is organized as follows: in Sect. 2 we discuss the computational framework, physical assumptions, and describe the nature of our chosen initial stellar and binary models. In Sect. 3 we discuss the bulk properties of our simulated system. We comment on the evolution of the accretor and the donor star, discuss the expected outcomes in different parts of the parameter space, and define the limiting effects in each of the cases (Sect. 4). We also comment on some of the expected observable features of each system during different phases of its evolution (Sect. 5). In Sect. 7 we discuss our findings in the context of previous results and address expected uncertainties. In Sect. 8 we summarize our work and highlight the most important conclusions.
2. Methods and physical assumptions
2.1. Numerical methods
The Binary Evolution Code (BEC) is a well-established computational framework capable of performing detailed one-dimensional numerical experiments of single or binary star systems (Langer et al. 2000; Yoon & Langer 2004b). This code is capable of performing simulations of rotating and degenerate systems, including mass transfer and accretion (Braun 1998; Heger et al. 2000; Heger & Langer 2000).
We made use of the full treatment of rotational instabilities currently available in BEC, namely the Solberg-Hoiland instability, secular shear instability, dynamical shear instability, and Eddington-Sweet circulation. We further included magnetic torques in the form of the Tayler–Spruit (hereafter: ST) dynamo (Spruit 2002; Heger et al. 2005), implemented as described in Neunteufel et al. (2017). In WD models, a proper description of dynamical angular momentum redistribution due to, for example, the dynamical shear instability, requires a dedicated numerical solver (Yoon & Langer 2004b). The same is true for the treatment of the ST dynamo, as implemented by Neunteufel et al. (2017) in an attempt to study accreting, rotating WDs under the influence of magnetic torques (hereafter, magnetic WDs).
The computational approach utilized in this study is the following. Instead of computing the evolution of both the donor and the accretor at the same time, we adopted a sequential approach. We first calculated the evolution of the donor and a point mass of the mass of the intended WD mass. Then we carried out a second simulation, in which only the evolution of a single WD model of the appropriate mass, reacting to the time-dependent accretion rate obtained in the first run. This approach, chosen for numerical convenience, is largely equivalent to concurrent calculation of binary systems. We are, however, limited to the assumption of conservative mass transfer.
The BEC calculates the mass transfer rate by implicitly solving
according to the prescription by Ritter (1988) and Kolb & Ritter (1990). In this case, HP is the photospheric pressure scale height, R the stellar radius as defined by the photosphere, and RRL the Roche lobe radius. The value RRL is calculated following the widely used prescription by Eggleton (1983). Further,
where vS is the speed of sound in a plasma as defined by 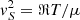 , where ℜ is the ideal gas constant, T the plasma temperature, μ the mean molecular weight, and Q is the effective stream cross section calculated as prescribed by Meyer & Meyer-Hofmeister (1983).
, where ℜ is the ideal gas constant, T the plasma temperature, μ the mean molecular weight, and Q is the effective stream cross section calculated as prescribed by Meyer & Meyer-Hofmeister (1983).
Angular momentum loss due to gravitational radiation (GWR) has a significant impact on the evolution of close binary systems. The BEC incorporates this following the canonical description (see, for example Landau & Livshitz 1975).
Prior to impacting the accretor, the material transferred from the donor is expected to form a Keplerian accretion disk (Paczynski 1991; Popham & Narayan 1991), carrying with it a specific angular momentum as defined by 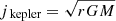 , where r is the distance from the center of force (which equals the radius of the star in this case). Within the context of the BEC framework, the amount of specific angular momentum (jacc) carried by accreted matter is manually controlled by the choice of facc in the expression jacc = facc ⋅ jkepler. Neunteufel et al. (2017) showed that the choice of facc has a significant impact on the outcome of the accreting evolution of the WD if constant accretion is assumed. However, in the absence of observational evidence to the contrary, the most natural choice of facc = 1.0 is the value adopted for the purposes of this study.
, where r is the distance from the center of force (which equals the radius of the star in this case). Within the context of the BEC framework, the amount of specific angular momentum (jacc) carried by accreted matter is manually controlled by the choice of facc in the expression jacc = facc ⋅ jkepler. Neunteufel et al. (2017) showed that the choice of facc has a significant impact on the outcome of the accreting evolution of the WD if constant accretion is assumed. However, in the absence of observational evidence to the contrary, the most natural choice of facc = 1.0 is the value adopted for the purposes of this study.
Super-critical rotation of the accretor is avoided by imposing facc = 0 if further accretion would lead to super-critical rotation. The excess angular momentum is assumed to be transported outward in the accretion disk (Paczynski 1991; Popham & Narayan 1991).
The treatment of angular momentum transport within the accretor is subject to some numerical uncertainty. This uncertainty stems from the implementation of centrifugal effects via the prescriptions of Endal & Sofia (1978), which, while generally consistent with the stellar structure equations, tends to underestimate the centrifugal force in cases in which the local shellular tangential velocity v fulfills v/vK > 0.6, where vK is the Keplerian velocity (see Neunteufel et al. 2017, Sect. 2.1.2, for a more detailed discussion).
2.2. Initial models
We investigated binary systems consisting of one CO WD and one nondegenerate He star as a mass donor.
2.2.1. Formation of He star plus CO WD systems
The progenitor system of a CO WD plus He star system starts out a binary that is composed of two low- to intermediate mass (Mi = 2.0 − 8.0 M⊙) hydrogen-rich stars. He star plus CO WD binaries may be produced from this kind of MS binaries through one of three main channels (see Wang & Han 2012, for a more detailed discussion):
-
The primary fills its Roche lobe when entering the Hertzsprung gap (HG) or its first giant branch (FGB), filling its Roche lobe and losing its envelope, becoming a He star. Subsequently, the primary evolves a CO core, filling its Roche lobe once more, and losing the remainder of its helium-rich envelope to the secondary, becoming a CO WD. The secondary then evolves, filling its Roche lobe during the HG or FGB stage. If the thus initiated mass transfer is unstable, a common envelope (CE) phase may be initiated, which leads to significant orbital decay. If the CE is ejected (the alternative being an immediate merger), the result is a CO WD and a He star in a close orbit.
-
If the primary is in the early asymptotic giant branch, when first filling its Roche lobe mass loss may be dynamically unstable, leading to a CE phase at the end of which the primary is left as a helium red giant. Further Roche lobe overflow (RLOF) may proceed in a stable manner, removing the remaining He envelope. The secondary may then, as in Scenario 1, initiate a CE, leaving a CO WD and a He star in a close orbit.
-
If the primary reaches the thermally pulsating AGB stage while the secondary is in the core helium burning stage, the resulting unstable RLOF and CE may strip the remaining envelopes of both stars simultaneously, leaving once more a He star plus CO WD binary in a close orbit.
The viability of these progenitor channels depends, in large part, on the exact disposition of both binary components in the aftermath of at least one or possibly more CE phases. The mechanisms governing CE evolution have been investigated over the last few decades (Paczynski 1976; Livio & Soker 1988). However, given the highly dynamic nature and (on an astronomical timescale) short duration of a common stellar envelope, predictions regarding its exact effect on the components of a binary are still of inadequate reliability (see Ivanova et al. 2013, for a review). For the purposes of this study, the orbital separation of the components at the time of envelope ejection and the thermal disposition of the degenerate component would be of the greatest importance. Lack of reliable predictions in this area limits us to making some general assumptions in the selection of appropriate WD models, as discussed in Sect. 2.2.2.
2.2.2. Selection of WD models
One of the main aims of this study is the characterization of the ignition of sub-Chandrasekhar mass WDs in binary systems evolving under the influence of magnetic angular momentum diffusion with an emphasis on helium detonations. Previously obtained results in this area govern our choice of the parameter space for the WD component. According to Woosley & Weaver (1994) and Woosley & Kasen (2011), helium detonation is favored by high ignition densities (> 1 × 106 g cm−3). Neunteufel et al. (2017) showed that in rotating, magnetic systems such as those under consideration in this work, high ignition densities are expected to be correlated with high (> 0.1 M⊙) helium shell masses. Further, the amount of helium needed to induce detonation is inversely correlated with the initial mass of the CO WD. The lower limit of our range of accretor masses should therefore be high enough that helium ignition can be induced with the amount of helium available for transfer in the donor. The upper limit on the other hand is determined by stellar evolution because CO cores more massive than 1.10 M⊙ in intermediate mass stars would undergo carbon burning to become ONeMg cores.
We therefore confine ourselves to a range of WD masses of 0.54 M⊙ ≤ MWD ≤ 1.10 M⊙. Table 1 provides an overview of the initial states of the WD models used in this study. These WD models were created by evolving pure helium star models up to the point of core helium exhaustion and then removing the remaining helium envelope, although the MWD = 0.82 M⊙ and the MWD = 1.00 M⊙ models retain a small ∼0.01 M⊙ helium layer.
Physical parameters of the initial WD models.
The proper choice for the initial luminosity of a WD for this kind of study is not straightforward; uncertainties persist, as mentioned above, as to the effects of a CE on the engulfed component, the state of the accretor immediately prior to the CE phase, and the orbital evolution during the CE phase. This study would benefit from more detailed knowledge of the effects on the thermal state of the accretor. Previous studies (e.g., Ricker & Taam 2008) have suggested that the amount of material accreted by a compact object (including WDs) during a CE should be around 10−4 M⊙. This would suggest that the inner layers of the WD would not be markedly affected by the accreted mass, but the increased temperature (compared to an isolated, cooling, WD) of the outer layer would affect the ignition behavior if helium accretion were to begin within a short time after the completion of the most recent CE phase. Significant uncertainty is introduced by the fact that these systems may be produced through three distinct channels with different delay times leading to different thermal states of the accretor at the onset of the most recent CE phase.
As shown by Neunteufel et al. (2017), the amount of helium required to ignite helium burning is affected by the temperature of the accretor at the onset on mass accretion, with the required amount decreasing with an increase in temperature. However, the aforementioned study also showed that this effect is correlated with the expected rate of mass accretion. The lower the mass accretion rate, the smaller the difference between the amounts of helium required to initiate helium burning at different initial temperatures. As we show in what follows, helium detonation is expected to occur at very low accretion rates. This means that systems experiencing helium ignition leading to an outcome other than detonation are most affected by the uncertainty in the initial thermal state of the accretor.
Further uncertainty is introduced by the lack of reliable predictions as to the effects of the CE on the orbital parameters of the binary. The three different progenitor channels detailed above are, with respect to the beginning of the CE phase(s), mainly distinguished by the zero age MS masses of the progenitors, their evolutionary stage, and their orbital separation, which would impact the state of the prospective accretor at the beginning of the most recent CE phase and, hence, its state at its conclusion. It therefore would be somewhat speculative, for the purposes of this study, to assign a unique, reliable thermal state the accretor in given accretor-donor pair. Previous studies (e.g., Yoon & Langer 2003, 2004b; Piersanti et al. 2015; Neunteufel et al. 2017) tackle this problem by simulating a set of initial luminosities. However, while the initially assumed luminosity of the accretor exerts significant influence on the prevailing conditions at the point of helium ignition, namely lowering the accreted helium shell mass and ignition density, Neunteufel et al. (2017) have suggested that this effect diminishes as enough angular momentum is accumulated for the accretor to approach critical rotation. This study assumes a given luminosity of the accretor (log Li/L⊙ ≈ −1) at the beginning of the mass transfer episode.
Computational treatment of rotation for the WD includes the full set of prescriptions available in the BEC code, including viscous heating (Yoon & Langer 2004b), as discussed in Sect. 2. The accretors are assumed to be initially rotating with a rotational velocity of vsurf ≃ 10 km s−1, which is commensurate with rotational velocities of observed isolated WDs (Heber et al. 1997; Koester et al. 1998; Kawaler 2003; Suijs et al. 2008; Mosser et al. 2012). The most recent CE phase is not expected to impact the rotational velocity of the WD significantly, as the engulfed object is assumed to be co-orbiting with the CE material. However, since accretion from the donor in a binary system imparts angular momentum on the accretor, as we show, the angular velocity of the WD is expected to increase significantly prior to helium ignition. Hence, the WD models used in this study can be thought of as initially nonrotating.
2.2.3. Selection of He-star models
Since we are interested in the role of the evolution of the donor star in the mass transfer history of our systems, the helium star is modeled from the end of the most recent CE phase of the system. We assume this point to coincide with the helium ignition of the He star. We note that this assumption may be at odds with progenitor channel 3 discussed in Sect. 2.2.1. The initial masses of our donor stars cover a range of 0.4 M⊙ ≤ Mdonor ≤ 1.0 M⊙. The upper mass limit was chosen such that the nuclear timescale of the most massive donors would still be long enough to expect mass transfer rates commensurate with steady helium accretion in Case BA systems1. The lower limit was chosen such that the helium supply of the least massive donors would be large enough to expect helium detonation on the accretor before the mass loss would quench core helium burning in the donor. He stars lose their ability to maintain core helium burning once their mass decreases below ∼0.3 M⊙, leading to a convenient choice of Md,i = 0.4 M⊙ as the lower limit for the initial donor star mass range in our calculations. See Table 2 for a comprehensive list of the most important initial parameters of the donor stars.
Physical parameters of the initial donor star models.
Our donor models start out as chemically homogeneous helium stars at solar metallicity that are left to attain thermal equilibrium before being implanted into a suitable binary model. Rotation in the donor models and wind mass loss is neglected.
2.2.4. Detonation conditions
In the case of helium ignition in the accreting WD, we distinguish cases leading to a helium detonation and a helium deflagration. A detonation implies the formation of a supersonic burning front, while in a deflagration, the burning front proceeds subsonically. Ignition of a detonation is assumed to proceed via the Zel’Dovich effect (Zel’Dovich et al. 1970; Blinnikov & Khokhlov 1987). Ignition via the Zel’dovich effect is predicated on the existence of a shallow temperature gradient in the vicinity of the point of ignition. Our models, in agreement with Neunteufel et al. (2017), invariably show the development of a thin convective layer around the ignition point prior to (within ≤1 kyr of) the thermonuclear runaway. This convective layer, in tandem with increasing degeneracy of the medium, provides for a sufficiently shallow temperature gradient.
We follow the evolution of our WD models until the onset of unstable helium ignition, if ignition occurs at all, or until the donor star becomes unable to sustain helium core burning. Our code is unable to follow through the aftermath of unstable helium ignition, which we define as the point at which the helium burning timescale becomes comparable to the star’s dynamical timescale (i.e., τnuc,He ≈ τdyn). We follow the criterion laid out by Woosley & Weaver (1994) to distinguish between deflagration and detonation. We assume that all thermonuclear runaways with an ignition density ρign = ρ(Tmax)|th. runaway ≥ 106 g cm−3 result in a detonation. We would like to emphasize that ρ(Tmax)|th. runaway is defined at the time of the start of the thermal runaway only. As found by Neunteufel et al. (2017), helium burning tends to start at somewhat lower densities. The value ρ(Tmax) then increases until τnuc,He ≈ τdyn is reached.
As we show in the following sections, the majority helium ignitions classified as detonations occur at ignition densities ρign ≫ 106 g cm−3, while the majority of all other types of ignition occur at ρign ≪ 106 g cm−3. Our results are therefore relatively insensitive to the exact value of the critical density.
We further adopt the findings of Woosley & Kasen (2011) by assuming that all detonations in the He shell lead to a double detonation. The question whether quasi-rigid rotation, as seen in our models, in accreting WDs inhibits their ability to undergo double detonations was addressed by García-Senz et al. (2018). It was found that quasi-rigid rotation is no hindrance to double detonations.
3. Bulk behavior of close He star plus CO WD systems
In this section we summarize the results of our simulation runs. In Sect. 3.1 we broadly outline the possible outcomes of the investigated binary systems, their classification, and their location in the investigated parameter space.
3.1. Possible outcomes from our models
As explained in Sect. 2, all systems were evolved until either unstable helium ignition in the accreted helium envelope, or the evident formation of a DD system. Figure 1 shows the entirety of the investigated parameter space, giving the amount of helium at the end of the simulation (where applicable) and encoding the expected outcomes of the model sequence. The possible outcomes can broadly be categorized into two groups: systems undergoing helium ignition and systems forming a DD binary. The first group can be subdivided into two further cases:
-
Helium deflagration (HeDef). This case is characterized by unstable helium ignition (as defined in Sect. 2) occurring at densities lower than the critical value of ρign = 106 g cm−3. This precludes the formation of a burning shock necessary for an ignition of the CO core. Systems like this are unlikely to immediately form SN via the DDet.
-
Helium detonation (HeDet). Systems falling in this category have built up a substantial helium envelope, the base of which is sufficiently dense as to allow for the formation of a shock in the aftermath of unstable helium ignition according to the above-mentioned density criterion. The formation of a shock (also: supersonic burn) allows for the propagation of nuclear burning into the CO core, providing the necessary preconditions for the DDet to act (see Sect. 2.2.4).
The second group can be subdivided into three further cases:
-
Double degenerate binary after Case BA mass transfer (DD I). In systems falling into this category, RLOF and mass transfer are initiated and a substantial amount of mass is transferred, but the transferred amount is insufficient for the accretor to undergo helium ignition. Instead, the donor loses enough mass to compromise its ability to sustain core helium burning before consuming its entire core helium supply. The (former) helium star then contracts to become a WD while retaining a substantial amount of helium, mixed with its dominant burning products, carbon and oxygen, in its core as well as a significant envelope of unprocessed helium (i.e., a “hybrid HeCO WD”). The expected state of the donor star at the end of helium burning is discussed in some detail in Sect. 3.3. This path results in a system composed of a CO WD with a significant (> 0.1 M⊙) helium envelope (the former accretor) and an hybrid HeCO WD (the former donor star), which also has a significant helium envelope.
-
Double degenerate binary after Case BAB mass transfer (DD II). As in the other two subcategories of this group, helium ignition is not initiated on the accretor. Unlike DD III, RLOF is initiated, but, unlike DD I, concludes after the donor star has exhausted its core helium supply. A substantial amount of helium is still transferred to the accretor. This leaves the system a DD binary, which is composed of one relatively massive CO WD with a substantial (∼0.1 M⊙) helium envelope (the former accretor) and a less massive CO WD with a less massive (∼0.03 M⊙) He envelope (the former donor star).
-
Double degenerate without mass transfer (DD III). These systems do not initiate RLOF while the helium star is on its helium MS. This is possible only in systems with a comparatively low mass (Md ≤ 0.6 M⊙) helium stars; once the helium star exhausts its core helium supply, the star contracts to become a WD itself.
 |
Fig. 1. Simulated systems shown in the Mdonor − Pinit plane. The color bar shows the mass of the helium transferred to the accretor at the end of the simulation run. Systems denoted with a filled circle undergo unstable helium ignition at the end of their evolution (HeDef). Filled circles with a black border indicate helium detonation (HeDet). In systems denoted with a square, helium burning in the donor star ends before helium ignition on the accretor (DD I). Upward pointing triangles indicate a CO WD with a He envelope with a second CO WD (DD II) and downward pointing triangles a system composed of two bare CO WDs (DD III). Systems denoted with a black x could not be resolved because of numerical issues related to the utilized opacity tables. Empty circles denote the occurrence of mass transfer rates exceeding 106 M⊙ yr−1, leading to numerical instabilities. |
As can be see in Fig. 1, HeDets are most prevalent in systems with MWD,i = 1.10 M⊙, their occurrence decreasing with MWD,i. Since we did not find any detonations in the exploratory grid with MWD,i = 0.54 M⊙, we did not increase its resolution further. The HeDets are bounded toward lower initial orbital periods by the demand that neither component fills its Roche lobe at the end of the most recent CE phase and bounded toward higher initial orbital periods by the core helium burning lifetime of the donor star. Toward higher donor star masses, the detonation zone is bounded by the nuclear timescale of the donor star (see Sect. 3.2.2).
3.2. Systems undergoing helium ignition
This section discusses the various outcome scenarios in greater detail, focusing on the physical parameters and differentiating these parameters from each other. We focus on the conditions inside the WD, as relevant to the different scenarios undergoing helium ignition, in Sect. 3.4. Table 3 gives a brief overview of the expected outcomes and the chosen terminology.
Summary of possible model end state characteristics.
As outlined in Sect. 2, our code is unable to follow the evolution of the WD model much past the point of helium ignition, restricting us to using the ignition density, defined as ρign = ρ(Tmax)|ign, the density of the stellar material at the point of the highest temperature at the time of unstable helium ignition, as a yardstick for predicting the final fate of the model. Neunteufel et al. (2017) showed that high ignition densities are correlated with low constant mass accretion rates, with a steep increase in ignition densities between high (Ṁ ≤ 3 × 10−8 M⊙ yr−1) and low (Ṁ ≤ 2 × 10−8 M⊙ yr−1). This increase resulted from centrifugal forces reducing the density of the helium shell layers most affected by compressional heating, which is correlated with the mass accretion rate, and viscous heating induced in the outermost (< 0.01 M⊙) layers. In binary systems, the mass transfer rate depends on the current orbital separation, in which smaller values incurring higher mass transfer rates owing to the effects of angular momentum loss as a consequence of GWR, and the current state of evolution of the donor star. This translates into a nontrivial correspondence of the expected mass transfer rate on the initial orbital period of the system.
Figure 2 shows the evolution of the donor star radius (Rd), the donor star’s Roche lobe radius (RRL,d) and the associated mass transfer rate (Ṁ) for two sets of representative model sequences. A binary system enters a mass transfer phase when Rd = RRL,d. The minimum in the evolution of the donor star radius indicates the end of core helium burning in the donor (see also Figs. 3 and 5) and subsequent RLOF proceeds on the thermal timescale of the donor star (Case BB instead of type BA mass transfer). As can be seen in Fig. 2, the expected mass transfer rate fluctuates over the duration of the mass transfer phase. In Case BA systems, the mass transfer rate initially decreases, then increases as the system approaches helium ignition on the accretor. The explanation for this behavior can be found through an investigation into which physical process dominates the mass transfer rate of the system. At low initial periods, the orbital separation of the components is short and the mass transfer rate is dominated by the shrinking of the orbit as demanded by the effects of GWR. As the initial orbital period increases, the orbital separation of the system at the time of RLOF increases concurrently, and the mass transfer proceeds on the nuclear timescale. As the mass of the donor decreases, the nuclear reaction rate decreases faster than the mass of the helium it contains, leading to an increase of the nuclear timescale. This increase in turn leads to a decrease of the mass transfer rate. As mass transfer continues, the orbital separation of the system starts to gradually decrease owing to GWR2.
 |
Fig. 2. Evolution of essential binary interaction parameters for two sets of representative model sequences. Color indicates the initial orbital period (Pinit) of the system. Lines of the same color are valid for the same initial orbital period. RRL,d, represented by the bold lines, is the radius of the donor star’s Roche lobe. Ṁ is the mass transfer rate, represented by the thin dash-dotted lines. The radius of the donor star, Rd, is represented by the thick black line. Each plot shows all model sequences obtained for the entire range of initial orbital periods for a single pair of initial donor star (Md,i) and WD (MWD,i) masses. The parameters chosen for panel (A) are Md,i = 0.55 M⊙ and MWD,i = 1.10 M⊙ and for panel (B)Md,i = 0.65 M⊙ and MWD,i = 1.10 M⊙. Obtained outcomes are indicated by the rectangles. We note that in graph (B), the systems with Pinit = 0.06 d (see Fig. 3) and Pinit = 0.065 d (see Fig. 5), have been left out for clarity. |
 |
Fig. 3. Evolution of the donor star’s stellar radius Rdon, Roche lobe radius RRL, and the associated mass transfer rate Ṁ over time for the intermittently accreting system 110650060, an archetypical BABDef system. The dashed green line indicates the mass transfer rate during the Case BA mass transfer episode of the system and the dashed red line denotes the mass transfer rate during the (comparatively short) Case BB mass transfer episode. Labels indicate the point at which the donor leaves the He MS (i.e., the end of its core helium burning phase) and the extent of the gap between the two mass transfer episodes (accretion gap). |
 |
Fig. 4. Isotope abundance profiles of two representative donor star models after the quenching of helium burning in DD I systems. Abundances are given in units of Misotope,shell/Mshell over the mass coordinate. Panel (A): model sequence 11050045, with an initial WD mass of MWD,i = 1.10 M⊙, an initial donor star mass of Md,i = 0.50 M⊙, and an initial orbital period of Pinit = 0.045 d. Panel (B): model sequence 11050075, with an initial WD mass of MWD,i = 1.10 M⊙, an initial donor star mass of Md,i = 0.50 M⊙, and an initial orbital period of Pinit = 0.075 d. |
 |
Fig. 5. Orbital parameters of a representative DD II case system (110650065). The value RRL is the radius of the donor star Roche lobe, Rd the radius of the donor star, and Ṁ the mass transfer rate. |
3.2.1. Detonations
The outcome of Case BA mass transfer is either a helium ignition, most likely a detonation, if the helium supply of the donor star is sufficient, or a DD I, if it is not. If RLOF happens less than about a thermal timescale before the end of core helium burning on the donor star, the system detaches. Mass transfer then resumes after the donor initiates helium shell burning (BABDef system). Our model sequences invariably show that Case BA mass transfer initiated earlier than within the described time window proceeds as Case BA until either helium ignition in the accretor or cessation of helium burning in the donor star is reached.
Detailed population synthesis calculations are beyond the scope of this work, but as we are concerned with the same parameter space that Wang et al. (2013) studied, we are able to make some predictions concerning occurrence rates using their numbers. This is accomplished in the following way. Wang et al. (2013) estimated a relative event rate of the systems leading to detonation from their grid of helium star plus CO WD binary star models. Since the entirety of our parameter space resulting in the same outcome is covered by the parameter space discussed by Wang et al. (2013) and the composition of our initial models is essentially identical, their mass and initial period-dependent relative event rates can be summed up to include all of our HeDet systems. As the sum of all relative event rates predicted by Wang et al. (2013) represents an absolute SN Ia and SN Iax rate, the relative event rate for our systems is a fraction of this absolute rate. The predictions for the formation rates of systems with the same binary parameters as our detonating systems presented in Fig. 1 allow us to roughly estimate occurrence rates depending on the CE ejection parameter αCE. We estimate occurrence rates for helium detonations to be lower by a factor of 10 than the SN Ia occurrence rates calculated by Wang et al. (2013) if αCE = 1.5, giving a rate of ∼1.5 × 10−4 yr−1 and lower by a factor of 20 if αCE = 0.5, giving a rate of ∼2 × 10−5 yr−1. This corresponds to ∼3% of the inferred galactic SN Ia rate in the high estimate and ∼0.2% in the low estimate. The observationally inferred SN Iax rate is about one-third of the SN Ia rate (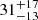 per 100 SNe Ia in a given volume; Foley et al. 2013), of which our model would predict ∼10% in the high estimate and ∼0.6% in the low estimate to result from double detonations in He star plus CO WD binaries.
per 100 SNe Ia in a given volume; Foley et al. 2013), of which our model would predict ∼10% in the high estimate and ∼0.6% in the low estimate to result from double detonations in He star plus CO WD binaries.
We conclude from this estimate, independent from the lack of helium in the observed spectra, that double detonations in He star plus CO WD binaries are not the dominant progenitor of either SN Ia or SN Iax. See Table A.2 for a list of representative model parameters of all systems in our sample undergoing helium detonation.
3.2.2. Deflagrations in case BB systems
Case BB mass transfer leads to thermal timescale mass transfer rates. Our model sequences suggest two distinct possible outcomes for Case BB systems: either the high mass accretion rates trigger helium ignition in the surface layers of the accretor after a comparatively small amount (< 0.01 M⊙) of helium has been accreted or the system forms a DD. This kind of ignition invariably occurs at ignition densities too low for helium detonation. The resulting observable would likely resemble a massive helium nova. We end our calculations at the point of the first unstable helium ignition. A deflagration is very likely to leave the core of the WD mostly intact. Depending on the mass retention rate η (i.e., the ratio of the mass of helium envelope retained after helium ignition to the helium envelope prior to ignition, effective values of which are still a subject of debate), this core may gain mass and eventually reach the Chandrasekhar mass. An estimate shows that under ideal conditions (i.e., fully conservative mass transfer), η ≥ 0.46 would be required in the systems under consideration in this study. According to Kato & Hachisu (2004), mass retention rates of this magnitude are expected for CO WDs with M ≥ 0.7 M⊙ and mass accretion rates ≥6.3 × 10−8 M⊙ yr−1. This suggests that at least some of the accretors under consideration reach the Chandrasekhar mass. The WD would have been spun up comparatively little at the point of helium ignition. The remaining core retains some of the angular momentum imparted on it before the first deflagration. Depending on the helium budget of the donor, the system may then experience a number of subsequent mass transfer phases akin to the first, but with a slightly faster rotating accretor.
We speculate that the expected outcome for this system would be a detached DDS akin to the DD II scenario discussed in Sect. 3.3, albeit with a faster rotating accretor. If these deflagratory outbursts exhibit the required mass retention rates, the WD may eventually reach the Chandrasekhar mass. However, since the accretor is also rotating rapidly at that point, reaching the Chandrasekhar mass may not necessarily lead to an explosion. It has been shown in the past that strong differential rotation can stabilize WDs against gravitational collapse. This effect is diminished if the WD is rotating quasi-rigidly, as in our case, but some increase to the maximum WD mass is still to be expected (see, e.g., Yoon & Langer 2005; Chen & Li 2009; Hachisu et al. 2012). See Table A.3 for a complete list of systems resulting in this outcome.
3.2.3. Deflagrations in case BAB systems
System 110650060 (orbital parameter evolution plotted in Figs. 2B and 3) is a representative example of deflagration in a Case BAB (BABDef) system. These BABDef systems exhibit relatively large variations in their mass transfer rates. These systems combine some aspects of both archetypical HeDet systems, in that their accreted helium shell mass is higher than comparable HeDef systems, and archetypical HeDefs, in that their ignition densities are relatively low. The variation in question is brought about if the system enters Case BA mass transfer late during the core helium burning phase of the donor star (roughly within a thermal timescale to the end of core helium burning). As seen in Fig. 3, helium stars in the mass range under consideration tend to contract by a few percent of their radius prior to the end of their He MS lifetime. This contraction usually proceeds faster than the decrease in orbital separation brought about by angular momentum loss due to GWR and angular momentum transfer, leading to detachment of the system and independent evolution of the two components for a certain period of time (∼0.81 Myr in the case of 110650060). During this “accretion gap”, the donor star ends its helium MS phase, begins helium shell burning and expands, leading to renewed RLOF. This renewed mass transfer proceeds on the thermal timescale and is confronted with a potentially massive helium envelope already in place on the accretor from the first mass transfer episode. This leads to an ignition, but the amount of helium would be higher by 0.1 − 0.25 M⊙ than in comparable deflagration systems via Case BA mass transfer. Depending on how this ignition proceeds, this either leads to a bright outburst as the accumulated helium ignites in a deflagration, or if steady burning is achieved the WD becomes a reignited red giant that quickly fills its own Roche lobe, leading to a CE.
3.3. Double degenerate systems
The second major group of expected outcome scenarios, apart from the occurrence of a explosive helium ignition in accreting CO WDs, is the formation of a DDS. Double degenerate systems, as mentioned in Sect. 3.1, are created in three different end states, each requiring the cessation of helium burning in the donor star. The difference in the state of the resulting DDSs is determined by the state of the donor and the cause of the end of helium burning. Most of these systems are expected to merge within Hubble time (see Sect. 6.2).
3.3.1. Double degenerate systems after Case BA mass transfer (DD I)
The reason for the emergence of a DD I system is the quenching of core helium burning (as opposed to helium shell burning in the DD II scenario) in the donor star, precipitated by mass loss during Case BA mass transfer. The ability of a helium-rich star to sustain core helium burning diminishes as its mass decreases toward 0.30 M⊙. We evolve our models until helium core burning stops in the donor star. The initial conditions for DD I scenario (i.e., stable Case BA mass transfer, with RLOF starting well before the end of core helium burning in the donor) are the same as those for the detonation scenario. The only difference is the insufficient helium budget provided by the donor star. Insofar, the DD I scenario could be viewed as a failed HeDet.
While the mechanism for the DD I outcome is the same for all such systems, the disposition of the accretor only varies with respect to the mass of its accreted helium envelope. The remnant of the donor star (i.e., the donor star at the point of the end of core helium burning) is subject to greater variation. Figure 4 shows the most significant isotope profiles of two example donor remnants. Helium stars of this mass range usually contain significant convective cores, and convection produces flat isotope profiles in the deeper regions of the star. Outside the convective cores, the pristine helium remains unmixed. This behavior is responsible for the discontinuity in the isotope profiles evident in both models depicted in Fig. 4. As core helium burning decreases as a consquence of mass loss, the convective core of the donor recedes3. If the recession of the convective zone proceeds slowly, predicated by a low mass transfer rate, a shallow isotope gradient is induced (as in Fig. 4B).
In DD I systems the donor remnant would contract to become a WD on its thermal timescale. Concurrently, the orbit of the two WDs would shrink owing to angular momentum loss to GWR. The evolution of the systems during the contraction phase of the former donor star is beyond the scope of this study (see, alternatively, Ergma & Fedorova 1990; Yungelson 2008), but it is possible to make a number of conditional statements. If the donor contracts to become a WD, implying that the system detaches during the contraction phase, GWR likely leads to another mass transfer episode. Given high or unstable mass transfer rates (> 10−7 M⊙ yr−1) and the presence of a degenerate helium envelope on the accretor, this may lead to explosive nuclear burning of the helium envelope on the former accretor (Shen et al. 2018). Otherwise, the system may merge. In the meantime, the system would consist of a rather massive (≥1.2 M⊙) CO WD with a thick (≥0.2 M⊙) helium envelope (the former accretor) and a relatively low mass (≤0.36 M⊙) hybrid WD with a strongly mixed He CO core and a significant (up to 0.15 M⊙) helium envelope (the former donor).
If the system does not detach during the contraction phase, as is indicated by the observation that the gravitational merger timescale of these systems at the end of core helium burning in the donor is usually shorter than the Kelvin–Helmholtz timescale of the donor, helium ignition may still ensue. See Table A.1 for a list of representative model parameters of all systems in our sample resulting in the DD I scenario.
3.3.2. Double degenerate systems after Case BAB mass transfer (DD II)
If the system initiates Case BB mass transfer, the high mass loss rate strips the envelope of the donor star quickly enough to stop helium shell burning, leading to the donor star contracting to become a WD. This sequence constitutes the DD II scenario. In Fig. 2B, the donor star model can be seen to rapidly expand after the end of core helium burning. This rapid expansion pauses after a few million years, and then gradually resumes. Mass transfer rates are correlated with the rate of expansion. Our models show that the lower rates of mass transfer during this “expansion gap” are sufficient to delay helium ignition on the accretor long enough for a quenching of helium shell burning to take place. If mass transfer is initiated outside the expansion gap, the most likely outcome is a helium deflagration. If RLOF occurs within the expansion gap, a DD II is the expected outcome. The amount of helium transferred during this phase can still be substantial (≲0.15 M⊙). At this point we note that this mechanism practically encompasses the WD plus He subgiant scenario discussed by, for example, Ruiter et al. (2013). However, the window in initial orbital periods leading to RLOF during the expansion gap is comparatively small. We therefore expect the relative occurrence rate of this outcome (the relative number of resulting systems for each case in our sample notwithstanding), compared to both the DD I and the DD III to be small.
3.3.3. Double degenerate systems without mass transfer (DD III)
The possibility of no interaction as an evolutionary path has to be studied separately in all discussions of scenarios in binary evolution. This path is represented in our sample by the DD III archetype. In this scenario, the donor evolves through its helium MS (i.e., core helium burning phase), during which the convective core of the star is converted to carbon and oxygen, enters a helium shell burning phase, and contracts to form a WD without ever experiencing RLOF. We find that all donor stars in our sample that are more massive than 0.6 M⊙ fill their Roche lobe at some point during their evolution; therefore, in our sample, only stars with M ≤ 0.6 M⊙ are light enough to potentially result in a DD III. Since introducing an upper limit to the initial orbital period limits the maximum extent of the Roche lobe of the donor star, this outcome lies outside our parameter space for the more massive donors4. In any case, all DD III systems result in a close binary composed of two CO WDs, both of which retain a thin (< 0.03 M⊙) helium envelope.
3.4. Ignition conditions
This section focuses on the conditions present in the WD at the point of helium ignition in HeDef and HeDet systems, their relation to the WD’s rotational state, and the effect of time-dependent mass transfer.
The influence of variability of the mass transfer rate on the ignition density of a WD is easily seen in Fig. 6. Generally, this plot confirms the findings of Neunteufel et al. (2017) in that the final helium shell mass in an igniting system is correlated with the ignition density. That is, the higher the final helium shell mass, the higher the ignition density. We can further confirm the findings of that paper that the increase in final helium shell mass is not continuous between deflagrations and detonations. This is exemplified in Fig. 6 by the “gap” between MHe = 0.04 M⊙ and MHe = 0.23 M⊙ (for systems with MWD,init = 1.10 M⊙) containing no blue data points (except for the system marked 1104005). This behavior indicates that an accreting system that results in a helium ignition either ignites after only a small amount of helium has been accreted, or continues on to form a detonation once a much larger amount of helium has been accreted. In both these cases, the final helium shell mass and the ignition density are correlated. The mechanism responsible for this “jump” was discussed at some length by Neunteufel et al. (2017). Only system 1104005 (with MWD,i = 1.10 M⊙, Md,i = 0.40 M⊙, and Pinit = 0.05 d, indicated by the red arrow in Fig. 6A) falls into this gap. However, the existence and attributes of 1104005 make it clear that the gap is not a physically forbidden region, but that systems inhabiting it have to be fine-tuned. There is a third system apart from the two distinct groups created by this mechanism: systems that result in a deflagration, often with very low ignition densities (ρi ≪ 106 g cm−3), but exhibit high final helium shell mass (≥0.05 M⊙). This group (the yellow squares in Fig. 6) can be identified with BABDef systems. As discussed in Sect. 3.4, the window for BABDef systems is very small, so we expect this behavior to be the exception rather than the norm. While HeDet and HeDef systems largely adhere to the expectations set by models calculated with constant accretion, the occurrence of BABDef systems, i.e., systems that result in helium ignition in massive (MHe > 0.1 M⊙) accreted He envelopes not resulting in a detonation, is a direct consequence of the time-dependence of the mass transfer rate. It is further evident that, as expected, the amount of helium needed to induce a detonation is inversely correlated with the initial mass of the WD. Systems with MWD,i = 0.54 M⊙ have proven unable to produce a detonation, at least within the confines of our parameter space, but are capable of accreting up to 0.1 M⊙ prior to a deflagration.
 |
Fig. 6. Ignition densities (ρign) plotted against final He shell masses (MHe). Each subplot contains data from a single initial WD mass (MWD,i). BABDef systems are depicted by a yellow square. Only systems experiencing helium ignition are included (i.e., only detonations and deflagrations). The black dashed line indicates the border between detonations and deflagrations. The red arrow in subfigure (A) indicates system 1104005. |
Figure 7 shows that, except for BABDef systems (hollow circles), ignition density is correlated with final surface rotation, with higher ignition densities coinciding with higher surface rotation. The expectation that detonating WDs with higher initial masses rotate faster at ignition than lower mass WDs at the same ignition densities is explained by the overall ignition mass (i.e., MWD,i + MHe) being correlated with the initial mass in the case of detonation and the associated higher critical rotational velocity. As explained in Sect. 2, our models stop accreting angular momentum if the resulting surface rotational velocity would be super-critical. The rotational velocity of a WD at detonation could be an indicator of the mass of the WD at the beginning of the mass transfer phase in naturally occurring systems. Conservation of angular momentum coupled with an inverse mass-radius relationship in WDs explains why less massive WDs exhibit relatively higher surface rotation at the same ignition densities than higher mass WDs. This behavior is seen in Fig. 7 with models with MWD,i = 0.54 M⊙ exhibiting ignition densities of 104 − 105 g cm−3 at surface rotational velocities of vsurf = 1000 − 2000 km s−1 compared to vsurf < 1000 km s−1 in models with initial masses MWD,i ≥ 0.82 M⊙ (excluding BABDef systems) in the same range of ignition densities.
 |
Fig. 7. Ignition density ρign plotted against the final surface rotational velocity vsurf,f. This figure only includes systems experiencing helium ignition (i.e., systems resulting in a merger candidate are excluded). The black line indicates the threshold density for helium detonation. Color indicates the initial mass of the degenerate component (MWD,i). Hollow circles indicate BABDef systems. |
The DDet scenario (in 1D) distinguishes two distinct ignition mechanisms, the “edge-lit” mechanism and the “ignition-at-altitude” mechanism (see Woosley & Kasen 2011). Both cases require the burning front to proceed supersonically. In the edge-lit scenario, helium ignition occurs directly at the interface between helium shell and CO core, simultaneously setting off an outward moving detonation of the helium shell and an inward moving detonation of the underlying carbon and oxygen, destroying the WD. In the ignition-at-altitude scenario, helium ignition occurs some distance above the shell-core interface inside the helium shell. In this case, helium ignition produces two shock fronts in the helium shell: one moving outward and the other moving inward. The inward moving shock front propagates into the core as a pressure wave, igniting the carbon and oxygen in the center of the WD. The thus created carbon detonation moves outward, unbinding the star in the process.
It should be mentioned that numerical predictions on the exact mechanism of this process depend significantly on the dimensionality of the utilized simulation environment. The 1D simulations necessarily assume ignition of a spherically symmetric layer. The 2D and 3D simulations are less constrained. Assuming asymmetrical ignition in a single point in the helium shell, two induced shock fronts travel laterally through the envelope, converging on the other side of the CO core to set off a carbon detonation in a single point at the core-shell interface (Sim et al. 2010; Kromer et al. 2010; García-Senz et al. 2018). As we are working within the confines of a 1D code, our results are valid for the case of spherical ignition only.
Figure 8 shows the relative mass coordinate of the ignition point in the He shell with respect to the mass of the accreted helium shell. Detonations clearly favor ignition at the base of the helium shell, and the only outlier is model sequence 1104005. Therefore, we expect systems within this sample to favor edge-lit detonations. For deflagrations, the χ-parameter (i.e., depth of the helium envelope below the ignition point) is correlated with the accreted helium shell mass. In particular only BABDef systems exhibit χ-factors > 0.07. This, again is a result of increased compressional heating as the system initiates Case BAB mass transfer.
 |
Fig. 8. Relative location of helium ignition within the accreted helium envelope (MHe) in relation to the mass of the helium envelope. The relative location is given by the dimensionless variable χ = (m(Tmax)−MWD,i)/MHe. The green points indicate that the WD experiences helium deflagration; blue points indicate helium detonation. The hollow circles indicate BABDef systems. Groups resulting from different initial WD masses (MWD,i) are indicated. The dashed line indicates χ = 0. |
4. Detailed description of the grid
In this section, we provide a more detailed discussion of the effects and outcomes seen in the different parts of the parameter space ordered by the initial mass of the WD. Before we discuss each group of systems in detail, we point out a few general tendencies present in all groups.
-
Detonations are correlated with high helium shell masses and high rotational velocities close to critical. This behavior is concordant with the findings of Neunteufel et al. (2017).
-
The final rotational velocity is correlated with the accreted helium shell mass. This behavior is expected from considering angular momentum conservation of the accreted material.
-
The final rotational velocity is correlated with the ignition density only in BABDef systems.
-
The shift from Case BA to Case BAB mass transfer in BABDef systems appears as a discontinuous jump, as opposed to a gradual shift, in the accreted helium shell mass. This behavior is, as explained in Sect. 3.2, a result of the contraction of the donor star at core helium exhaustion.
-
The amount of helium required to initiate helium detonation (detonating systems only) is correlated with the initial orbital period Pinit. The reason for this behavior lies in the relation between mass transfer rate and the evolutionary state of the donor, as discussed in Sect. 3.4.
4.1. Systems with MWD, i = 1.10 M⊙
Figure 9 shows the final states of the accretor in all systems with MWD,i = 1.10 M⊙. The upper group of subplots shows final helium shell masses, independent of which outcome is reached, and ignition densities (for systems undergoing either detonation or deflagration). To each mass-density subplot there is a corresponding subplot detailing the rotational state of the accretor (lower group, same label). The rotational state is given in two different parameters, namely the final surface rotational velocity vsurf,f, which is the surface rotational velocity at the end of the simulation run (i.e., the point of helium ignition, the end of donor core helium burning in DD I systems, or renewed RLOF otherwise), and the maximum surface rotational velocity vsurf,max, which is the maximum value of the surface rotational velocity during the entirety of the mass accretion phase. The distinction is necessary since, although the WD is in quasi-solid body rotation for most of the mass accretion phase, the onset of helium ignition, prior to the thermonuclear runaway, leads to some expansion of the envelope, wherein conservation of angular momentum forces a decrease in surface rotational velocity and reintroduces some measure of differential rotation. Therefore, in systems where vsurf,f ≠ vsurf,max, vsurf,max is a more accurate reflection of the state of the accretor just prior to the onset of helium ignition than vsurf,f. We have vsurf,f = vsurf,max for DD I systems.
 |
Fig. 9. Final helium shell masses (MHe) of all simulated systems and, for igniting systems, the ignition density (ρign) in the upper group of plots. Masses are plotted on the left-hand y-axis, densities on the right hand y-axis. The lower group shows final and maximum rotational velocities. All systems contain a WD of MWD,i = 1.10 M⊙. Point styles indicate the expected outcomes; the nomenclature is the same as in Fig. 1. The x-axis represents initial orbital periods (Pinit). Each subplot shows results obtained for a single initial donor star mass (MHe). BABDef systems are indicated by a blue ring in the MHe plot. |
In the following, “group” refers to a single pair of subplots in Figs. 9–12 denoted by the same label. Each group5 depicts systems with the same MWD,i and Md,i but different Pinit.
Group (A) shows systems with Md = 0.4 M⊙. This group is split between HeDef systems at initial orbital periods < 0.05 d and DD I-type systems at initial orbital periods > 0.05 d with one detonating system in between. The donor stars in these systems are only able to lose a little more than 0.10 M⊙ of material before becoming unable to sustain helium core burning. Furthermore, the long nuclear timescale of helium stars of this mass produces low mass transfer rates, even aided by angular momentum transfer to the heavier partner, a process that tends to widen orbital radii, precluding the quick formation of a helium flame on the accretor. Therefore, the DD I outcome would be expected. This outcome, however, is only realized at long initial orbital periods in this group. The driving force behind the deflagrations at short Pinit is angular momentum loss due to GWR leading to increased mass transfer through a decrease of orbital separation. This also explains the increase of the mass of the accreted helium shell with the initial orbital period, which remains inversely correlated with the mass transfer rate. The single detonating system (model number 1104005) seems to be fine-tuned (see Sect. 3.4), with mass transfer rates just high enough to lead to helium ignition before the donor becomes unable to supply any more helium, yet low enough to allow for the ignition densities required for detonation. While the helium shell masses of this system are more in line with the values obtained for nonrotating models, its value as a specific progenitor model for detonating transients is doubtful because of the inherent inaccuracy of our assumed initial conditions.
Group (B) only contains DD I-type systems. This is a consequence of angular momentum loss as a consequence of GWR being diminished as dictated by the smaller mass ratio of these systems compared to group (A).
Group (C) includes DD I type systems at initial orbital periods < 0.08 d and one deflagrating system at Pinit = 0.08 d. The limiting factor for the DD I scenario is the border between Case BA and Case BB lying between Pinit = 0.075 d and Pinit = 0.08 d. As can be seen, the spin-up of the WD is significantly lower in deflagrating systems compared to DD I systems.
Systems in group (D) result in detonations at Pinit ≤ 0.045 d, DD I if 0.045 d < Pinit ≤ 0.065 d, a deflagration if Pinit = 0.07 d, a DD II if Pinit = 0.075 d, and a DD III system at Pinit = 0.08 d. The reason for the occurrence of DD I systems at higher Pinit than detonation lies in the mass transfer rate decreasing, as discussed in Sect. 3.4, toward the end of the helium MS of the donor star.
Group (E) contains detonating systems at Pinit ≤ 0.06 d. The shift toward Case BB systems is marked by a system with strongly variable mass transfer at Pinit = 0.065 d. This system, again exhibits exceptionally low ignition densities for its igniting helium mass, leading to a deflagration. However, the rotational velocity is high compared to non-BABDef systems. The system at Pinit = 0.07 d initiated RLOF during the expansion gap of the donor, leading to a DD II. The system with Pinit = 0.075 d reaches RLOF after the expansion gap and results in a HeDef. The result at Pinit = 0.08 d is a DD III.
Groups (F) through (H) largely follow the same pattern as group (E). However, group (H) contains two gaps, at Pinit = 0.045 d and Pinit = 0.055 d, where the evolution of the accretor could not satisfactorily be followed up to the point of helium ignition owing to constraints on the utilized opacity tables and had to be discarded.
Group (I) shows HeDet systems at Pinit ≤ 0.045 d and a BABDef system at Pinit = 0.05 d. The increase in helium shell masses at Pinit = 0.065 d is due to RLOF during the expansion gap. In systems with lower mass donors, RLOF during the expansion gap would have resulted in a DD II. However, more massive donors, such as used in this group (Md = 0.8 M⊙) do not experience a quenching of helium shell burning, which is the primary reason for the contraction an subsequent formation of a degenerate in the DD II scenario seen with lower mass donors. The ignition mass decreases above Pinit = 0.065 d as the mass transfer rate increases with the evolution of the donor during helium shell burning.
Group (J) includes only deflagrations. However, the switch from case BA to Case BAB mass transfer is still noticeable, with an BABDef system at Pinit = 0.05 d. The system with Pinit = 0.045 d had to be discarded owing to limitations with the utilized opacity tables.
Group (K) contains only deflagrating systems. However, the BABDef marking the switch from Case BA to Case BAB in this group at Pinit = 0.05 d exemplifies the reducing mass transfer rates as the donor approaches the end of its helium MS with ignition masses about ten times that of the Case BA deflagrations at Pinit < 0.05 d. Again, the local maximum of ignition masses at Pinit = 0.065 d is caused by RLOF being initiated during the expansion gap.
4.2. Systems with MWD, i = 1.00 M⊙
Figure 10 is analogous to Fig. 9 but for systems with an initial WD mass of MWD,i = 1.00 M⊙. Since the amount of helium required to induce helium ignition was expected to rise, compared to systems with MWD,i = 1.10 M⊙, only donor star masses Md,i ≥ 0.5 M⊙ were considered.
Group (N) consists of DD I systems at Pinit < 0.08 d and one BABDef system at Pinit = 0.08 d. Group (O) contains DD I systems at Pinit ≤ 0.065 d, one BABDef system at Pinit = 0.07 d, one DD II system at Pinit = 0.075 d, and a DD IIIsystem at Pinit = 0.08 d. The fact that this group, as opposed to group (N), includes a DD III system can be traced back to the shorter MS lifetime (by about 30 Myr) of a helium star with a mass of 0.55 M⊙ compared to one with 0.5 M⊙.
Group (P) shows HeDets at Pinit ≤ 0.045 d, a DD I at 0.045 d < Pinit < 0.065 d, then the familiar sequence of deflagration, DD II (owing to RLOF being initiated during the expansion gap), and DD III systems. Higher initial periods are expected to result in DD III systems.
Group (Q) is remarkable because of the presence of a single DD I system at Pinit = 0.05 d in a sequence of HeDet systems. At this initial period, the mass transfer rate is just high enough to quench helium core burning in the donor earlier than at Pinit ≤ 0.07 d, but too low to lead to a HeDet. It is suspected that an even slightly larger helium budget would facilitate a detonation in this system. This group also contains three systems at Pinit ≥ 0.07 d, which could not be followed through to helium ignition owing to the mass transfer rate becoming high enough (exceeding Ṁ = 5 × 10−6 M⊙ yr−1) to cause numerical issues with the donor star model. However, since high mass transfer rates generally lead to helium ignition after a short while, these systems are expected to undergo helium ignition which, in these cases, do not lead to a detonation, but may lead to stable helium burning.
Group (R) once again contains a system that could not be satisfactorily be brought to the point of helium ignition because of constraints in the utilized opacity tables at Pinit ≤ 0.055 d. Group (S) largely conforms to the pattern of the preceding groups. However, the BABDef system at Pinit = 0.05 d accretes enough material to be spun up to critical rotation, as does the DD II system at Pinit = 0.06 d.
The BABDef system in group (T) at Pinit = 0.045 d can be described as a “failed detonation”. Case BA mass transfer stopped just short of the required amount for detonation. Once mass transfer resumes in Case BAB, a deflagration ensues, even though the helium shell is actually more massive than in the lower period systems that resulted in a detonation. Evidently the occurrence of detonations diminishes with smaller initial WD masses, as seen in Fig. 1 as well.
4.3. Systems with MWD, i = 0.82 M⊙
Figure 11 details ignition masses, ignition densities, and surface rotation for systems with MWD,i = 0.82 M⊙. A major physical difference between this system and the previous systems is that, at donor masses Md ≥ 0.85 M⊙, the donor star is initially the more massive component. Angular momentum transfer from the heavier to the lighter partner acts to decrease the orbital radius of a binary system and enhances the mass transfer rate if RLOF occurs.
Group (Y) generally follows the pattern for systems with donor stars unable to provide sufficient helium to induce a detonation with DD I being the outcome of systems with Pinit ≤ 0.07 d. The He core burning phase of the donor star from this group is followed by a short helium shell burning phase, leading to the BABDef system at Pinit = 0.075 d, and a DD III system at Pinit = 0.08 d.
Group (Z) was run with a coarser grid (ΔPinit = 0.01 d), but is otherwise similar to the example provided by the previous group. Group (AA) generally follows the pattern of the previous group, but features a DD II type systems at Pinit ≥ 0.06 d.
Groups (AC) through (AD) follow the pattern of group (Y) as well. Group (AC) was calculated with a coarser grid above Pinit = 0.065 d. The system at Pinit ≤ 0.04 d in group (AD) had to be discarded because of issues with the utilized opacity tables. The effects of the donor initially being the more massive component becomes apparent in group (AD) with the final helium shell mass decreasing with the initial orbital period in Case BA systems. This decrease is an effect of the higher mass transfer rate in systems with q > 1 compared to systems with q < 1.
In group (AE), RLOF happens close enough to the end of the helium MS of the donor in the systems with Pinit ≤ 0.04 d and 0.045 d to lead to DD II. The border between Case BA and Case BB mass transfer lies between Pinit = 0.045 d and 0.05 d.
Group (AF) while again containing a detonation at Pinit = 0.035 d, more closely follows the pattern for high mass donor systems with q > 1, as the accreted helium shell mass decreases with Pinit in Case BA systems due to the increase in mass transfer rates. This leads to a deflagration with a comparatively large helium shell mass at Pinit = 0.04 d. The border between Case BA and Case BB mass transfer lies between Pinit = 0.05 d and 0.055 d.
Group (AG) only contains deflagrating systems. The dependence of MHe on Pinit is similar to groups (X) and (M), but we note the lack of decrease in the final helium shell mass in Case BA systems (Pinit ≤ 0.045 d. The donor in the system occupying Pinit = 0.035 d would fill its Roche lobe at the beginning of the simulation and was omitted.
4.4. Systems with MWD, i = 0.54 M⊙
Figure 12 shows ignition densities, final helium shell masses, and surface rotational velocities for systems with MWD,i = 0.54 M⊙. Since no detonations were expected in this part of the parameter space, only a cursory grid was simulated to search for interesting outcomes. The amount of helium required to induce detonation is expected to be exceptionally large (MHe > 0.5 M⊙) with WDs of this relatively low mass 9as found by Neunteufel et al. 2017), therefore no donor stars less massive than Md = 0.8 M⊙ were considered. All of the systems were found to result ultimately in deflagrations during Case BA mass transfer. These closer orbits result in more efficient angular momentum loss due to GWR prior to RLOF, which in turn results in an enlarged parameter space for Case BA mass transfer. Further, with q > 1, the mass transfer rate is enhanced owing to angular momentum transfer from the donor to the accretor and angular momentum loss, again, to GWR. The thus increased mass transfer rate (∼10−7 M⊙ yr−1) increases the likelihood of a deflagration.
5. Observability of He-detonation progenitors
Figure 13 shows the number density in the Hertzsprung–Russel (HR) diagram of all simulated systems resulting in a helium detonation, reconstituted as a model population. In this case, the initial mass function was not taken into consideration; each combination of initial parameters (Md, Macc, Pinit) was assumed to occur with the same probability. As seen in Fig. 13A, accretors in this population are most likely to exhibit a temperature of ∼85 000 K and a luminosity of ∼3 L⊙. We note that the accreted matter in these systems is expected to form an accretion disk, which will increase the overall luminosity of the accretor (e.g., Iben 1982; Faulkner et al. 1983). Iben (1982) estimated the luminosity of the accretion disk forming around an accreting WD as
 |
Fig. 13. Number density plot of all HR tracks across the entire investigated parameter space leading to helium detonation. Main panel (A): number density, where shading indicates the normalized number density of tracks crossing the associated area at any one time, normalized to unity. This means that the lower the number density at any one point, the lower the probability to find a system at that point and vice versa. Parts of the diagram containing donor star tracks are indicated. The side panels show observational probabilities across the temperature (panel B) and luminosity (panel C) axes. Here color indicates time since the end of the most recent CE phase. |
where Ṁ is the mass accretion rate. This suggests that disk luminosities attained in our models lie in the range 300 L⊙ > Ldisc > 1 L⊙. Panels (B) and (C) show histograms of the set of stars of the same age (isochrone populations, as measured from the initial t = 0) of the population depicted in panel (A). In the youngest isochrone population, the effective temperature of the accretors range between 160 000 K and 70 000 K with maximum probability at 115 000 K. In the isochrone population at 4.4 Myr the mass transfer rate is expected to be lower than in younger systems, the effective temperature of the population is expected to be lower than in the initial isochrone population. We expect a maximum rate at ∼75 000 K. As the systems continue to evolve, some of the systems, namely those with the highest MWD,i undergo helium detonation, leading to a depletion of the older isochrone populations. This depletion raises the expected temperature maximum in the oldest population (t = 6.6 Myr) to ∼90 000 K.
The accretor population initially exhibits luminosities centered around ∼9 L⊙ in a wide distribution, decreasing to ∼2 L⊙ in a narrow distribution after 4.4 Myr and gradually increasing to ∼3 L⊙ thereafter. The donor star population is expected to outshine the accretor population during the majority of the accretion phase with the initial luminosity of the population falling into the range 10 L⊙ ≤ Ldonor ≤ 200 L⊙ centered around ∼70 L⊙. As the donors lose mass, the average luminosity of the isochrone population is expected to decrease to around ∼4 L⊙, remaining brighter than the associated isochrone accretor population.
The effective temperature of the donor population is expected to be initially centered around ∼40 000 K, gradually decreasing to ∼30 000 K, centering their emission spectrum in the ultraviolet.
We conclude that these systems would be difficult to observe in the optical. However, the donor star, because it is consistently brighter than the accretor, discounting accretion disks, would be the more favorable target. Including accretion disks, in systems experiencing high mass transfer rates (Ṁ ≈ 10−7 M⊙) the accretor (or, more precisely, its accretion disk) would be the brighter component. In systems resulting in a detonation, because of their mass transfer rates that are constantly lower (Ṁ ≤ 5 × 10−8 M⊙), the associated accretion disk is unlikely to outshine the donor star. Further, the fact that both components diminish in brightness as the system approaches an explosion due to helium ignition in the accreting WD indicates a higher likelihood of detection while the system is in the early stages of mass transfer with the expected explosion still on the order of millions of years in the future.
Because of the very similar mass transfer rates involved in the creation of DD I systems and a HeDet systems, we speculate that, without accurate measurements of the mass of the donor, predicting the further evolution of any such system, if one were discovered, would not be straightforward.
6. Further evolution of the remnants
6.1. Fate of DD I type systems
Figure 14 shows a comparison of the initial and final state of systems resulting in the DD I scenario. We show the positions of these systems in the mass ratio6-orbital period plane. The maximum mass ratio for systems resulting in a DD I is q = 0.91. The minimum mass ratio present in our grid is q ≃ 0.37. We note, however, that this lower limit is a result of our choice of the lower limit of included donor star masses. Donor stars could conceivably be as light as 0.3 M⊙, which would decrease initial the mass ratio to q ≃ 0.27.
 |
Fig. 14. Mass ratio |
As seen in Fig. 14 (B), all DD I systems evolve toward low mass ratios of 0.18 < q < 0.38 and low orbital periods of 0.005 d < Porb < 0.02 d, irrespective of initial parameters. The mass transfer from the lower mass component to the higher mass component acts to widen a binary. But this effect, owing to the low mass transfer rates present in the systems under consideration in this work, is too small to counteract angular momentum loss due to GWR. This explains the overall evolution toward shorter orbital periods seen in this work. The evolution toward smaller mass ratios is readily explained by conservative mass transfer (see Sect. 2) and entirely expected. The range of resulting mass ratios is explained by core helium burning becoming uniformly unsustainable at ≈0.3 M⊙ in low mass helium stars, which also marks the end point of our calculations.
The question regarding whether the system detaches subsequent to the end of core helium burning in the donor star is determined by the contraction timescale of the burnt out helium star compared to the timescale of the decrease of the orbital separation due to GWR. The contraction timescale in this case is equal to the Kelvin-Helmholtz timescale of the star, which has expected values on the order of 107 yr. This would indicate that some, if not all, systems would not detach subsequent to the end of core helium burning in the donor star. Mass transfer in this case is expected to continue, but rates would steadily increase toward Ṁ ≃ 10−7 M⊙ yr−1 as the donor contracts (Yungelson 2008). In this case, compressional heating drives a helium ignition at low densities, resulting in a transient similar to BABDef systems.
If the system detaches and mass transfer in renewed interaction proceeds dynamically, a merger can be expected. Merging DD systems (more precisely: He WD plus CO WD systems) have been put forward as potential progenitors for RCB type stars (Webbink 1984; Saio & Jeffery 2002; van Kerkwijk et al. 2010). Further study would be required to ascertain whether DD I systems as presented in this work would be viable progenitors for these stars. The total final mass (Md,f + Macc,f) of the least massive of our models resulting in a DD I outcome is 1.34 M⊙, higher than expected for RCB stars. If DD I systems were to result in an RCB-like object, this discrepancy would have to be accounted for. Further, the composition of the less massive components in our systems may present a challenge to this idea. Our models suggest a large amount of oxygen and carbon being present in the core of the former and future donor star, while observational spectra of RCB stars suggest an overabundance of carbon and nitrogen, but not oxygen (e.g., Clayton 1996; Jeffery et al. 2011).
Discounting an RCB object as an outcome of a merger of DD I type systems, another possibility would be a thermonuclear SN according to the archetypical DD scenario, which may lead to a SN Ia or Iax. These systems would contain significantly more helium than is conventionally expected for CO WD binaries. In a merger event this helium may increase the likelihood of a prompt detonation (i.e., a detonation during the ongoing merger process; Guillochon et al. 2010; Röpke et al. 2012; Pakmor et al. 2012; Moll et al. 2014).
It should be mentioned that direct collapse of the WD into a neutron star is inhibited by the presence of a substantial helium envelope. It is considered necessary to convert the core of a CO WD into oxygen and neon (ONe) for a WD to collapse to form a neutron star (compare, e.g., Brooks et al. 2017). With a substantial helium envelope present on the accretor, any helium ignition would either lead to a detonation, which in turn would lead to a thermonuclear SN, a helium deflagration, which is likely eject the envelope, or a weak ignition, which is expected to produce a reignited helium giant and lead to a CE phase.
6.2. Fate of DD II and DD III type systems
As described in Sect. 3, we follow both DD II and DD III type systems to the point of the donor star, having evolved to become degenerate, fills its Roche lobe once again (i.e., RLOF in a DD system; DD RLOF). Figure 15 shows the chemical composition of all DD II and DD III type systems included in our sample. In both cases, the donor star has a distinct CO core with a thin, but non-negligible (∼0.03 M⊙) He envelope. The two main differences between the two outcomes are the mass of the helium layer present on the accretor at the point of DD RLOF and the rotational state of the accretor. Accretors in DD III type systems have accreted no additional helium during the CO WD plus He star phase. They are furthermore not expected to have accumulated any additional angular momentum through accretion, and therefore, neglecting tidal effects, the accretors would be rotating with their initial rotational velocity. Once DD RLOF happens in these systems, the outcome is either a merger or stable RLOF with mass transfer rates higher than ∼10−7 M⊙ yr−1. In the latter case, the transferred material would initially still be He rich, leading to low mass helium ignitions. Once the remaining helium on the donor is depleted, the system is left as a CO WD binary.
 |
Fig. 15. Combined chemical structure of pre-DD RLOF components of DD II and DD III type systems. Indicated are the masses of He-rich (MHe,acc, MHe,d) and CO-rich (MCO,acc, MCO,d) layers of both the accretor and the donor star for both DD II and DD III type systems. The horizontal black line indicates the Chandrasekhar-mass. We note that only masses higher than 0.6 M⊙ are shown for legibility. |
Accretors in DD II type systems have a substantial (≲0.15 M⊙) envelope of unburnt helium. These would further rotate rapidly (see Figs. 9–11). Once DD RLOF occurs, the outcome is again either a merger or stable mass transfer. In the latter case, mass transfer rates would again exceed ∼10−7 M⊙ yr−1 and the helium layer on the WD is expected to ignite. If helium ignition leads to a deflagration, the accretor would then be left as a pure CO WD. Mass transfer would then continue until the remaining helium of the donor star is depleted and the system is left as a binary CO WD. A helium ignition leading to stable helium shell burning would likely produce a reignited helium giant, leading to unstable RLOF and thus a CE phase. Once the remaining helium is removed from the system, the transferred material consists of carbon and oxygen that is directly deposited on the CO core of the accretor. As shown in Fig. 15, most DD III and all DD II systems contain sufficient CO to allow the accretor to reach the Chandrasekhar mass. We note that for DD systems with q ≳ 0.63 (Eggleton et al. 2006; Dan et al. 2012; Sato et al. 2016), mass transfer is expected to be unstable. Mass ratios of the remnants of DD II and DD III systems (as can be derived from Fig. 15) range from q ∼ 0.76 on the high end, and q ∼ 0.43. This indicates that systems undergoing stable mass transfer and systems undergoing mergers are both present in our sample. As shown in Fig. 15, the majority of both DD II and DD III type systems in our sample would contain a combined CO mass exceeding the Chandrasekhar mass. The question whether these systems would be promising SN progenitors under the DD channel is beyond the scope of this study. However, as in the DD I case DD II systems retain a substantial He envelope, which may play a role in prompt detonation scenarios (Guillochon et al. 2010; Röpke et al. 2012; Pakmor et al. 2012; Moll et al. 2014). Therefore systems of this case could be an attractive subject for subsequent hydrodynamical simulations.
6.3. Runaway stars
In case of a helium detonation, the accreting WD is expected to be completely destroyed in the ensuing explosion. The former donor star, which is expected to survive (Marietta et al. 2000; Shappee et al. 2013), moves away from the former location of the binary with a velocity equal to its former orbital velocity relative to the center of mass of the system, which is is augmented by the momentum imparted by the impacting SN ejecta. Previous studies (e.g. Liu et al. 2013) have shown this impact to contribute ≤ 100 km s−1 on helium companions of 1.0 − 1.2 M⊙. The impact momentum vector is oriented roughly perpendicular to the circularized orbital velocity vector of the donor star and in the systems in question has a second-order effect. In the absence of kick velocities directly applicable to our models, we follow precedent (e.g., Justham et al. 2009) by approximating the ejection velocity as the barycentric velocity of the donor star at the point of explosion.
As seen in Fig. 16, we expect a strong inverse correlation between ejection velocity and donor star mass with velocities in the range of 620 km s−1 ≤ vrem ≤ 1040 km s−1. The ejection velocity of any former donor star from a binary is defined by the mass-radius relationship of that star and the condition that the star fills its own Roche lobe at the time of the ejection event.
 |
Fig. 16. Expected runaway velocities (vrem) of the surviving donor star plotted over the mass of the survivor (Mrem). Color indicates the time since the end of the most recent CE phase. The solid black line and red shading indicate the observed velocity and associated error bars of the hypervelocity hot subdwarf US 708 (Geier et al. 2015). The dashed black line and green areas indicates the galactic escape velocity (Piffl et al. 2014), including error bars; Macc is the mass of the accreting WD at helium ignition. |
There is a diversity among the types of currently observed hypervelocity stars. Brown et al. (2006) discussed five individual objects (HVS1 to HVS5), of these, HVS1, HVS4 and HVS5 have been classified as late B stars with a high likelihood of having been ejected through interaction with a massive black hole in the galactic center. HVS3 (hereafter, after its catalog ID, US 708) has been classified as a hot subdwarf (SdO/B, Geier et al. 2015) and its most likely origin has been traced back to the galactic disk. Further, Shen et al. (2018) identified three more candidates classified as helium-poor remnants of DD SNe.
Systems depicted in Fig. 16 represent the entire set of helium detonations obtained in our sample. Considering a galactic escape velocity of 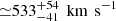 (Piffl et al. 2014), all of the systems undergoing helium detonation in our sample should produce a hypervelocity hot subdwarf with, at least superficially, US 708-like properties.
(Piffl et al. 2014), all of the systems undergoing helium detonation in our sample should produce a hypervelocity hot subdwarf with, at least superficially, US 708-like properties.
Figure 16 also shows the inferred ejection velocity of the observed hypervelocity subdwarf US 708, which, including error bars, lies at the upper end of our expected velocity range. US 708 was found to have crossed the plane of the galactic disk well away from the galactic core, which disfavours but does not disprove dynamical gravitational interaction with other stellar bodies as an acceleration mechanism. The mass of US 708 is insufficiently constrained at the time of writing, but if it is the survivor of a He star plus CO WD double detonation, we expect its mass to be close to 0.3 M⊙.
We note that Fig. 16 is bounded toward lower masses by our condition that, if core helium burning is extinguished by mass loss in the donor star, the system is classified as a DD I system and therefore not included in this figure. Consideration of orbital mechanics suggests that if helium detonation were to occur at lower donor star masses, then these donors would be ejected at higher velocities than shown in Fig. 16. It is likely, however, that ejection velocities cannot be arbitrarily high. This is due to the effects of angular momentum transport in binary systems with highly disparate masses and the response of the donor star to mass loss, but a detailed discussion of this topic is beyond the scope of this paper. Discovery of further such objects could, if more of their stellar parameters can be observed, constitute a convenient observational test of the parameters of the progenitor system.
7. Discussion
We find that our results regarding the ignition conditions on the accreting WD generally agree well with those obtained in simulations assuming the same angular momentum dissipation physics, but constant accretion rates (Neunteufel et al. 2017). We find, however, that inclusion of rotation, magnetic torques and time-dependent mass transfer rates in the low mass accretion regime (Ṁ ≲ 10−7 M⊙ yr−1) is capable of resolving evolutionary outcomes inaccessible to calculations neglecting either of these effects both individually and collectively. As such, prior studies of helium accretion onto WDs neglecting rotation (Taam 1980a,b; Woosley et al. 1986; Woosley & Weaver 1994; Woosley & Kasen 2011; Bauer et al. 2017) generally underestimated the amount of helium required for ignition and greatly underestimated the amount of helium required to induce a detonation. Studies that take rotational effects into account but neglect magnetic effects (Yoon & Langer 2004a,b) generally predict no helium detonations and greatly underestimate the amount of helium required to induce ignition.
Neglecting the evolutionary behavior of the donor star and the binary as a whole, potentially resulting in both time-dependence of the mass transfer rate and interruptions of the mass transfer phase, leads to certain evolutionary outcomes, such as deflagrations in massive (MHe > 0.1 M⊙) helium envelopes, not being predicted at all. We find that, in general, the parameter space available for detonations, underestimation of the required helium mass, and consequent mischaracterization of the binary at the point of ignition notwithstanding, is generally well resolved by studies including evolution of the binary parameters (Wang et al. 2013; Neunteufel et al. 2016), but that part of the detonations predicted by these studies rather result in a WD plus proto-WD binary.
Assuming the applicability of the Tayler–Spruit mechanism, the results of this work suggest that future studies on helium accretion onto WDs should lightheartedly waive neither the simulation of the full binary model nor angular momentum redistribution, including magnetic torques.
However, because the Tayler–Spruit effect is dependent on a stably stratified environment, we do not expect our results to immediately challenge the viability of calculations performed in regimes of steady burning of the accreted helium into carbon and oxygen (e.g. Brooks et al. 2016, 2017), which is expected to induce a zone of convection in the burning region.
Uncertainties in this study persist in a number of areas, most notably the efficiency and applicability of the Tayler–Spruit mechanism (Maeder & Meynet 2004; Denissenkov & Pinsonneault 2007) and the efficiency of angular momentum accretion in an accretion disk (Paczynski 1991; Popham & Narayan 1991). If either of these mechanisms are less efficient than assumed in this case, ignition masses and rotational velocities are lowered.
The treatment of centrifugal forces as an accreting star approaches critical rotation (Endal & Sofia 1976) requires revision. We thus likely underestimate ignition masses.
The proper treatment of mass loss and mass transfer is still a topic of discussion and, as suggested by Neunteufel et al. (2017), the ignition behavior of WDs with rotation and magnetic torques is as sensitive to the accretion rate as in cases where these effects are neglected (e.g., Woosley & Kasen 2011). If realistic mass transfer rates turn out to be lower than calculated in this work, the parameter space of detonations is shifted toward higher donor star masses and toward lower donor masses if it is higher.
The thermal reaction of a WD undergoing CE evolution is still insufficiently well understood (Ivanova et al. 2013). If accretors can be expected to be generally hotter than assumed at the beginning of the mass transfer phase, fewer detonations are produced. Further, owing to the strong dependence of the outcome on the mass of the donor star and the initial orbital separation, corrections to the CE prescriptions used by Wang et al. (2013) strongly impacts our occurrence rate estimates.
A major uncertainty in this study is the border of the detonation regime toward lower mass donors. Since we stop our calculations at the end of helium burning in the donor star, we are unable to resolve detonations that may arise after continued mass transfer once the donor has become a proto-WD. If these systems do not detach (as suggested by Ergma & Fedorova 1990; Yungelson 2008), depending on the amount of helium present at the point of the donor becoming a proto-WD, they may still produce a helium detonation or alternatively, if mass transfer rates increase during contraction, a massive helium deflagration.
Our results allow us to comment on the evolution of a number of observed close binaries containing a WD. CD-30 has been argued to contain a WD with a mass of 0.75 − 0.77 M⊙ and a hot subdwarf (sdB) of 0.44 − 0.48 M⊙ in a detached configuration with a period of P = 0.04897906 ± 0.00000004 d (Vennes et al. 2012). Allowing for some decrease of the orbital period of the system since the end of the most recent CE phase, systems of this configuration are expected to result in a DD I, according to our classification. KPD 1930–2752 is assumed to consist of a sdB of 0.5 M⊙ and a WD of 0.97 ± 0.01 M⊙ with a period of P ∼ 0.095 d (Maxted et al. 2000), which puts it slightly outside of our considered parameter space. However allowing for some decrease in orbital separation since the most recent CE phase, it is likely that this system will not undergo RLOF and result in the DD III scenario. V445 Pup is a nova-like variable that erupted in late 2000 and was argued to represent a helium nova event (Ashok & Banerjee 2003) on a massive 1.35 M⊙ WD (Kato et al. 2008) with a relatively massive 1.2 − 1.3 M⊙ helium star companion (Woudt et al. 2009). While outside the parameter space explicitly under consideration in this study, the high mass transfer rates associated with helium donors of this mass disfavor double detonations. If steady burning can be avoided, a massive helium nova akin to our HeDef systems is the expected outcome. It is reasonable to assume that such a system would undergo similar outbursts in the future.
8. Conclusions
We conducted 274 detailed stellar evolution calculations of resolved He star plus CO WD binary models, including the effects of rotation and magnetic torques. We investigated the state of the system and the accretor at the point of either the first unstable helium ignition in the accreting WD or the end of helium burning in the donor star.
In line with previous results that include the effects of rotation and magnetic torques in helium accretion on WDs, but not the effects of binary evolution, we expect that induction of a helium detonation on the accretor requires the accumulation of a significant (≥0.1 M⊙) helium envelope from the helium-rich companion.
The highest donor star mass capable of providing the low mass transfer rates required for detonation is inversely correlated with the initial WD mass with Mdonor = 0.95 M⊙ at MWD = 0.82 M⊙, Mdonor = 0.85 M⊙ at MWD = 1.00 M⊙, and Mdonor = 0.8 M⊙ at MWD = 1.10 M⊙. We further find that the increased amount of helium required to induce helium detonation with rotation and magnetic torques as found by Neunteufel et al. (2017) does not fully inhibit the ability of He star plus CO WD binaries to produce helium detonations, and, consequently, double detonations. The large amount of helium present on the accretors at the point of helium detonation, however, seems to disfavor their viability as progenitors of both SNe Ia and Iax (see, e.g., Shen et al. 2010; Woosley & Kasen 2011; Foley et al. 2013). We find that, at the point of helium detonation, in line with past studies, the accreting WD is rotating close to breakup velocity.
More work, specifically hydrodynamic simulations, would be needed to confirm what the observational counterpart of a helium detonation in our systems would be. However, we reiterate the conclusion of Neunteufel et al. (2017) that the large amount of helium (≥0.1 M⊙) necessary to induce helium ignition in rotating CO WDs under the influence of magnetic torques seems to align with the ignition conditions found for calcium-rich Type Ib SNe, as argued by Waldman et al. (2011).
Our simulation s cover the entirety of the parameter space expected to lead to helium detonations without prior formation of a DD binary, or the donor star becoming unable to continue He core burning, for the considered range of initial WD masses. This allows us to estimate the expected occurrence rates of these events. Assuming that these systems would result in SNe Ia or Iax, the occurrence rate of helium detonations would only be able to account for 0.2 − 3% of the observationally inferred SN Ia rate or 0.6 − 10% of the SN Iax rate taking into account Wang et al. (2013) and Foley et al. (2013).
Systems undergoing helium detonation eject the donor stars at velocities higher than the galactic escape velocity. We find that helium detonations in this kind of system are able to produce runaway subdwarfs with velocities of 600 km s−1 < vrem < 1050 km s−1. The inferred ejection velocity of the observed hypervelocity subdwarf US 708 (Geier et al. 2015) is at the upper end of the predicted velocity range. Considering the estimated low occurrence rate of helium detonations under investigation in this work, the apparent scarcity of hypervelocity runaway hot subwarfs does not contradict the He star plus CO WD binary channel as the production mechanism of US 708.
We also find a relatively large parameter space where helium detonation is inhibited by the high mass transfer rates expected with the onset of mass transfer after the donor star initiates shell helium burning. Instead of a detonation, these systems are expected to experience a weaker, subsonic helium ignition. These ignitions are not expected to be able to ignite the CO core of the WD and would thus be unable to produce a bright SN. Instead, an ignition like this is expected to result in a massive helium nova or a .Ia SN (Bildsten et al. 2007; Kilic et al. 2014), with accreted helium envelopes of MHe ≃ 0.01 M⊙ (compared to envelope masses of ≃10−5 − 10−3 M⊙ in cataclysmic variables, e.g., Townsley & Bildsten 2004). While the exact observational attributes of a transient like this would have to be studied in greater detail, we can state that because of quasi-rigid rotation imposed on the accretor by the active magnetic torques, the surviving object would maintain the same angular velocity as before the outburst, assuming additional torques induced by the deflagration event can be neglected. Subsequent accretion episodes further increases the rotational velocity of the WD. Depending on the mass retention efficiency during these outbursts, the accretor may reach the Chandrasekhar mass at some point. Alternatively, the system might become a DD binary with a comparatively long orbital period.
Apart from sy stems resulting in helium detonations and deflagrations at MHe ≃ 0.01 M⊙, we find that the time-dependence of the mass transfer rate in physical binaries should lead to systems igniting only after MHe ≥ 0.1 M⊙ has been accreted, but has not undergone detonation. Ignition in these objects tends to take place close to the outer surface of the envelope. These objects are not expected to produce a bright SN. Further studies of the ignition process would be needed to ascertain whether they would lead to a massive transient or form a reignited helium giant.
The parameter space available to helium detonations is further constrained by the limited supply of helium provided by low mass donor star (Mdonor ≤ 0.75 M⊙ at MWD = 0.82 M⊙, Mdonor ≤ 0.6 M⊙ at MWD = 1.00 M⊙, and Mdonor ≤ 0.55 M⊙ at MWD = 1.10 M⊙). Systems containing donor stars unable to provide sufficient helium to induce ignition on the accretor ends up as binaries composed of a CO WD and a contracting proto-WD with comparatively short (0.02 d ≤ Porb ≤ 0.04 d) orbits and gravitational merger timescales of 0.6 Myr < τGR < 54 Myr. If contraction of the former donor causes the system to detach, the former becomes a hybrid HeCO WD, i.e., a CO WD with a comparatively massive ≥0.1 M⊙ remaining helium envelope and a strongly mixed core consisting of carbon, oxygen, and unprocessed helium. The former accretor retains the preexisting CO core inside a helium envelope with a mass ≥0.1 M⊙ and is rotating rapidly. These systems may be of interest either as SN progenitors in the DD scenario or progenitors of RCB stars.
In summary, it can be stated that the differences between the inferred progenitors of observed SNe Ia and Iax and our predictions, especially concerning the expected mass of the helium envelope and formation rates, cannot easily be reconciled. This represents a more serious challenge to the concept of helium induced double detonations as a viable scenario for ordinary Type Ia SNe. We conclude that He star plus CO WD systems are not a major channel for SNe Ia and Iax, if helium detonation is assumed to occur during the core helium burning phase of the donor star. However, CO plus hybrid HeCO systems formed in this scenario may contribute to the SN Ia and Iax rate through the DD channel. Further study into these systems, apart from their possible role as SN Ia progenitors, is merited as the massive helium novae predicted by our models should have high occurrence rates and may be identified optically. These transients would need to be characterized through hydrodynamical simulations. Helium detonations occurring in these systems should also be taken into account as possible origins of hypervelocity runaway stars and calcium-rich SNe Ib. Further, more detailed investigation of the possible connection between DD systems resulting from these progenitors and RCB stars would be worthwhile.
Systems in which RLOF-induced mass transfer starts before the core hydrogen supply of the donor is exhausted are generally referred to as “Case A” systems, and “Case B” after. Analogously for systems containing a helium burning star, systems where RLOF begins before the core helium supply of the star is exhausted are called “Case BA” systems and “Case BB” after. “Case BAB” systems undergo one Case BA mass transfer phase, followed by another mass transfer phase during the post core He burning stages. (see Eggleton et al. 2006).
Acknowledgments
This research was supported by the Korea Astronomy and Space Science Institute under the R&D program (Project No. 3348-20160002) supervised by the Ministry of Science, ICT and Future Planning. Support by the Deutsche Forschungsgemeinschaft (DFG), Grant No. Yo 194/1-1, is gratefully acknowledged. P.N. would like to thank Phillip Podsiadlowski and Stephan Geier for useful discussions.
References
- Ashok, N. M., & Banerjee, D. P. K. 2003, A&A, 409, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, E. B., Schwab, J., & Bildsten, L. 2017, ApJ, 845, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W. 1997, in NATO Advanced Science Institutes (ASI) Series C, eds. P. Ruiz-Lapuente, R. Canal, & J. Isern, 486, 457 [Google Scholar]
- Bildsten, L., Shen, K. J., Weinberg, N. N., & Nelemans, G. 2007, ApJ, 662, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Blinnikov, S. I., & Khokhlov, A. M. 1987, Sov. Astron. Lett., 13, 364 [NASA ADS] [Google Scholar]
- Braun, A. 1998, PhD Thesis, University of Basel [Google Scholar]
- Brooks, J., Bildsten, L., Schwab, J., & Paxton, B. 2016, ApJ, 821, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, J., Schwab, J., Bildsten, L., Quataert, E., & Paxton, B. 2017, ApJ, 843, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, W. R., Geller, M. J., Kenyon, S. J., & Kurtz, M. J. 2006, ApJ, 640, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, W.-C., & Li, X.-D. 2009, ApJ, 702, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, G. C. 1996, PASP, 108, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Dan, M., Rosswog, S., Guillochon, J., & Ramirez-Ruiz, E. 2012, MNRAS, 422, 2417 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., & Pinsonneault, M. 2007, ApJ, 655, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P., King, A., Lin, D., et al. 2006, Evolutionary Processes in Binary and Multiple Stars (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Endal, A. S., & Sofia, S. 1976, ApJ, 210, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Ergma, E. V., & Fedorova, A. V. 1990, Ap&SS, 163, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Faulkner, J., Lin, D. N. C., & Papaloizou, J. 1983, MNRAS, 205, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Fink, M., Hillebrandt, W., & Röpke, F. K. 2007, A&A, 476, 1133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fink, M., Röpke, F. K., Hillebrandt, W., et al. 2010, A&A, 514, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foley, R. J., Challis, P. J., Chornock, R., et al. 2013, ApJ, 767, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Van Dyk, S. D., Jha, S. W., et al. 2015, ApJ, 798, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. S., & Starrfield, S. 1978, ARA&A, 16, 171 [NASA ADS] [CrossRef] [Google Scholar]
- García-Senz, D., Cabezón, R. M., & Domínguez, I. 2018, ApJ, 862, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Geier, S., Fürst, F., Ziegerer, E., et al. 2015, Science, 347, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Guillochon, J., Dan, M., Ramirez-Ruiz, E., & Rosswog, S. 2010, ApJ, 709, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., Saio, H., & Nomoto, K. 2012, ApJ, 744, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, P. 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U., Napiwotzki, R., & Reid, I. N. 1997, A&A, 323, 819 [NASA ADS] [Google Scholar]
- Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Wheeler, J. C., & Thielemann, F. K. 1998, ApJ, 495, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I. 1982, ApJ, 259, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1987, ApJ, 313, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Jeffery, C. S., Karakas, A. I., & Saio, H. 2011, MNRAS, 414, 3599 [NASA ADS] [CrossRef] [Google Scholar]
- Justham, S., Wolf, C., Podsiadlowski, P., & Han, Z. 2009, A&A, 493, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., Hachisu, I., & Kiyota, S. 2008, in Hydrogen-Deficient Stars, eds. A. Werner, & T. Rauch, ASP Conf. Ser., 391, 267 [NASA ADS] [Google Scholar]
- Kawaler, S. D. 2003, ArXiv e-prints [arXiv:astro-ph/0301539] [Google Scholar]
- Kelly, P. L., Fox, O. D., Filippenko, A. V., et al. 2014, ApJ, 790, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Hermes, J. J., Gianninas, A., et al. 2014, MNRAS, 438, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, D., Dreizler, S., Weidemann, V., & Allard, N. F. 1998, A&A, 338, 612 [NASA ADS] [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Kromer, M., Sim, S. A., Fink, M., et al. 2010, ApJ, 719, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L., & Livshitz, E. 1975, The Classical Theory of Fields, Course of Theoretical Physics (Oxford: Butterworth Heinemann) [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Li, W., Filippenko, A. V., Chornock, R., et al. 2003, PASP, 115, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Bloom, J. S., Podsiadlowski, P., et al. 2011, Nature, 480, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z.-W., Pakmor, R., Seitenzahl, I. R., et al. 2013, ApJ, 774, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 1988, ApJ, 329, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Livne, E. 1990, ApJ, 354, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Livne, E. 1997, in NATO Advanced Science Institutes (ASI) Series C, eds. P. Ruiz-Lapuente, R. Canal, & J. Isern, 486, 425 [Google Scholar]
- Livne, E., & Arnett, D. 1995, ApJ, 452, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Livne, E., & Glasner, A. S. 1990, ApJ, 361, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Livne, E., & Glasner, A. S. 1991, ApJ, 370, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2004, A&A, 422, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maoz, D., & Mannucci, F. 2008, MNRAS, 388, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Marsh, T. R., & North, R. C. 2000, MNRAS, 317, L41 [NASA ADS] [CrossRef] [Google Scholar]
- McCully, C., Jha, S. W., Foley, R. J., et al. 2014, Nature, 512, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1983, A&A, 128, 420 [NASA ADS] [Google Scholar]
- Moll, R., Raskin, C., Kasen, D., & Woosley, S. E. 2014, ApJ, 785, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G. 2005, in The Astrophysics of Cataclysmic Variables and Related Objects, eds. J. M. Hameury, & J. P. Lasota, ASP Conf. Ser., 330, 27 [NASA ADS] [Google Scholar]
- Nelemans, G., Voss, R., Roelofs, G., & Bassa, C. 2008, MNRAS, 388, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Neunteufel, P., Yoon, S.-C., & Langer, N. 2016, A&A, 589, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neunteufel, P., Yoon, S.-C., & Langer, N. 2017, A&A, 602, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K. 1980, J. C. Wheeler, 164 [Google Scholar]
- Nomoto, K. 1982a, ApJ, 257, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K. 1982b, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1976, in Structure and Evolution of Close Binary Systems, eds. P. Eggleton, S. Mitton, & J. Whelan, IAU Symp., 73, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paczynski, B. 1991, ApJ, 370, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Perets, H. B., Gal-Yam, A., Mazzali, P. A., et al. 2010, Nature, 465, 322 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Yungelson, L. R., & Tornambé, A. 2015, MNRAS, 452, 2897 [NASA ADS] [CrossRef] [Google Scholar]
- Piffl, T., Scannapieco, C., Binney, J., et al. 2014, A&A, 562, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popham, R., & Narayan, R. 1991, ApJ, 370, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, P. M., & Taam, R. E. 2008, ApJ, 672, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H. 1988, A&A, 202, 93 [NASA ADS] [Google Scholar]
- Röpke, F. K., Kromer, M., Seitenzahl, I. R., et al. 2012, ApJ, 750, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Sim, S. A., Pakmor, R., et al. 2013, MNRAS, 429, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Saio, H., & Jeffery, C. S. 2002, MNRAS, 333, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, Y., Nakasato, N., Tanikawa, A., et al. 2016, ApJ, 821, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E., & Pagnotta, A. 2012, Nature, 481, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. P., Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Kochanek, C. S., & Stanek, K. Z. 2013, ApJ, 765, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Bildsten, L. 2009, ApJ, 699, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., & Moore, K. 2014, ApJ, 797, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Kasen, D., Weinberg, N. N., Bildsten, L., & Scannapieco, E. 2010, ApJ, 715, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Boubert, D., Gänsicke, B. T., et al. 2018, ApJ, 865, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Sim, S. A., Röpke, F. K., Hillebrandt, W., et al. 2010, ApJ, 714, L52 [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suijs, M. P. L., Langer, N., Poelarends, A.-J., et al. 2008, A&A, 481, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taam, R. E. 1980a, ApJ, 237, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E. 1980b, ApJ, 242, 749 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Townsley, D. M., & Bildsten, L. 2004, ApJ, 600, 390 [NASA ADS] [CrossRef] [Google Scholar]
- van Kerkwijk, M. H., Chang, P., & Justham, S. 2010, ApJ, 722, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Vennes, S., Kawka, A., O’Toole, S. J., Németh, P., & Burton, D. 2012, ApJ, 759, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Waldman, R., Sauer, D., Livne, E., et al. 2011, ApJ, 738, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., & Han, Z. 2012, New Astron. Rev., 56, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Justham, S., & Han, Z. 2013, A&A, 559, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, B., Podsiadlowski, P., & Han, Z. 2017, MNRAS, 472, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1995, Ap&SS, 225, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, Jr., I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Kasen, D. 2011, ApJ, 734, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1994, ApJ, 423, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., Taam, R. E., & Weaver, T. A. 1986, ApJ, 301, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Steeghs, D., Karovska, M., et al. 2009, ApJ, 706, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2003, A&A, 412, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004a, A&A, 419, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2004b, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., & Langer, N. 2005, A&A, 435, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yungelson, L. R. 2008, Astron. Lett., 34, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Zel’Dovich, Y. B., Librovich, V. B., Makhviladze, G. M., & Sivashinskil, G. I. 1970, J. Appl. Mech. Tech. Phys., 11, 264 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional tables
Initial and final model parameters for DD I systems.
Initial and final model parameters for HeDet systems.
Initial and final model parameters for HeDef and BABDef systems.
All Tables
All Figures
 |
Fig. 1. Simulated systems shown in the Mdonor − Pinit plane. The color bar shows the mass of the helium transferred to the accretor at the end of the simulation run. Systems denoted with a filled circle undergo unstable helium ignition at the end of their evolution (HeDef). Filled circles with a black border indicate helium detonation (HeDet). In systems denoted with a square, helium burning in the donor star ends before helium ignition on the accretor (DD I). Upward pointing triangles indicate a CO WD with a He envelope with a second CO WD (DD II) and downward pointing triangles a system composed of two bare CO WDs (DD III). Systems denoted with a black x could not be resolved because of numerical issues related to the utilized opacity tables. Empty circles denote the occurrence of mass transfer rates exceeding 106 M⊙ yr−1, leading to numerical instabilities. |
| In the text | |
 |
Fig. 2. Evolution of essential binary interaction parameters for two sets of representative model sequences. Color indicates the initial orbital period (Pinit) of the system. Lines of the same color are valid for the same initial orbital period. RRL,d, represented by the bold lines, is the radius of the donor star’s Roche lobe. Ṁ is the mass transfer rate, represented by the thin dash-dotted lines. The radius of the donor star, Rd, is represented by the thick black line. Each plot shows all model sequences obtained for the entire range of initial orbital periods for a single pair of initial donor star (Md,i) and WD (MWD,i) masses. The parameters chosen for panel (A) are Md,i = 0.55 M⊙ and MWD,i = 1.10 M⊙ and for panel (B)Md,i = 0.65 M⊙ and MWD,i = 1.10 M⊙. Obtained outcomes are indicated by the rectangles. We note that in graph (B), the systems with Pinit = 0.06 d (see Fig. 3) and Pinit = 0.065 d (see Fig. 5), have been left out for clarity. |
| In the text | |
 |
Fig. 3. Evolution of the donor star’s stellar radius Rdon, Roche lobe radius RRL, and the associated mass transfer rate Ṁ over time for the intermittently accreting system 110650060, an archetypical BABDef system. The dashed green line indicates the mass transfer rate during the Case BA mass transfer episode of the system and the dashed red line denotes the mass transfer rate during the (comparatively short) Case BB mass transfer episode. Labels indicate the point at which the donor leaves the He MS (i.e., the end of its core helium burning phase) and the extent of the gap between the two mass transfer episodes (accretion gap). |
| In the text | |
 |
Fig. 4. Isotope abundance profiles of two representative donor star models after the quenching of helium burning in DD I systems. Abundances are given in units of Misotope,shell/Mshell over the mass coordinate. Panel (A): model sequence 11050045, with an initial WD mass of MWD,i = 1.10 M⊙, an initial donor star mass of Md,i = 0.50 M⊙, and an initial orbital period of Pinit = 0.045 d. Panel (B): model sequence 11050075, with an initial WD mass of MWD,i = 1.10 M⊙, an initial donor star mass of Md,i = 0.50 M⊙, and an initial orbital period of Pinit = 0.075 d. |
| In the text | |
 |
Fig. 5. Orbital parameters of a representative DD II case system (110650065). The value RRL is the radius of the donor star Roche lobe, Rd the radius of the donor star, and Ṁ the mass transfer rate. |
| In the text | |
 |
Fig. 6. Ignition densities (ρign) plotted against final He shell masses (MHe). Each subplot contains data from a single initial WD mass (MWD,i). BABDef systems are depicted by a yellow square. Only systems experiencing helium ignition are included (i.e., only detonations and deflagrations). The black dashed line indicates the border between detonations and deflagrations. The red arrow in subfigure (A) indicates system 1104005. |
| In the text | |
 |
Fig. 7. Ignition density ρign plotted against the final surface rotational velocity vsurf,f. This figure only includes systems experiencing helium ignition (i.e., systems resulting in a merger candidate are excluded). The black line indicates the threshold density for helium detonation. Color indicates the initial mass of the degenerate component (MWD,i). Hollow circles indicate BABDef systems. |
| In the text | |
 |
Fig. 8. Relative location of helium ignition within the accreted helium envelope (MHe) in relation to the mass of the helium envelope. The relative location is given by the dimensionless variable χ = (m(Tmax)−MWD,i)/MHe. The green points indicate that the WD experiences helium deflagration; blue points indicate helium detonation. The hollow circles indicate BABDef systems. Groups resulting from different initial WD masses (MWD,i) are indicated. The dashed line indicates χ = 0. |
| In the text | |
 |
Fig. 9. Final helium shell masses (MHe) of all simulated systems and, for igniting systems, the ignition density (ρign) in the upper group of plots. Masses are plotted on the left-hand y-axis, densities on the right hand y-axis. The lower group shows final and maximum rotational velocities. All systems contain a WD of MWD,i = 1.10 M⊙. Point styles indicate the expected outcomes; the nomenclature is the same as in Fig. 1. The x-axis represents initial orbital periods (Pinit). Each subplot shows results obtained for a single initial donor star mass (MHe). BABDef systems are indicated by a blue ring in the MHe plot. |
| In the text | |
 |
Fig. 10. Same as Fig. 9 but for WD,i = 1.00 M⊙. |
| In the text | |
 |
Fig. 11. Same as Fig. 9 but for WD,i = 0.82 M⊙. |
| In the text | |
 |
Fig. 12. Same as Fig. 9 but for WD,i = 0.54 M⊙. |
| In the text | |
 |
Fig. 13. Number density plot of all HR tracks across the entire investigated parameter space leading to helium detonation. Main panel (A): number density, where shading indicates the normalized number density of tracks crossing the associated area at any one time, normalized to unity. This means that the lower the number density at any one point, the lower the probability to find a system at that point and vice versa. Parts of the diagram containing donor star tracks are indicated. The side panels show observational probabilities across the temperature (panel B) and luminosity (panel C) axes. Here color indicates time since the end of the most recent CE phase. |
| In the text | |
 |
Fig. 14. Mass ratio |
| In the text | |
 |
Fig. 15. Combined chemical structure of pre-DD RLOF components of DD II and DD III type systems. Indicated are the masses of He-rich (MHe,acc, MHe,d) and CO-rich (MCO,acc, MCO,d) layers of both the accretor and the donor star for both DD II and DD III type systems. The horizontal black line indicates the Chandrasekhar-mass. We note that only masses higher than 0.6 M⊙ are shown for legibility. |
| In the text | |
 |
Fig. 16. Expected runaway velocities (vrem) of the surviving donor star plotted over the mass of the survivor (Mrem). Color indicates the time since the end of the most recent CE phase. The solid black line and red shading indicate the observed velocity and associated error bars of the hypervelocity hot subdwarf US 708 (Geier et al. 2015). The dashed black line and green areas indicates the galactic escape velocity (Piffl et al. 2014), including error bars; Macc is the mass of the accreting WD at helium ignition. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.