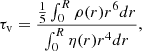| Issue |
A&A
Volume 689, September 2024
|
|
|---|---|---|
| Article Number | A287 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/202450008 | |
| Published online | 20 September 2024 | |
Expected evolution of the binary system PTF J2238+743015.1
1
INAF – Osservatorio Astronomico d’Abruzzo, Via Mentore Maggini, snc, 64100 Teramo, Italy
2
INFN – Sezione di Perugia, Via Pascoli, 123, 06123 Perugia, Italy
3
Institute of Astronomy of the Russian Academy of Sciences, 48 Pyatnitskaya Str, 119017 Moscow, Russia
e-mail: lev.yungelson@gmail.com
4
Departamento de Física Teórica y del Cosmos, Universidad de Granada, 18071 Granada, Spain
e-mail: eduardo.bravo@ugr.es
Received:
17
March
2024
Accepted:
27
May
2024
Context. Binary systems harboring a low-mass CO WD and a He-rich donor are considered to be the possible progenitors of explosive events via He detonation, producing low-luminosity thermonuclear supernovae with a peculiar nucleosynthetic pattern. Recently, the binary system PTF J223857.11+743015.1 was proposed as a candidate for this kind of stars.
Aims. We investigate the evolution of the PTF J223857.11+743015.1 system, which is composed of a 0.75 M⊙ CO WD and a 0.390 M⊙ subdwarf. We consider the rotation of the WD component.
Methods. Using the FuNS code, we computed the evolution of the two stars simultaneously, taking into account the possible evolution of the orbital parameters, as determined by mass transfer between the components and by mass ejection from the system during episodes of Roche lobe overflow. We consider that the WD gains angular momentum due to accretion and we followed the evolution of the angular velocity profile as determined by angular momentum transport via convection and rotation-induced instabilities.
Results. As the donor H-rich envelope is transferred, the WD experiences recurrent very strong H-flashes triggering Roche lobe overflow episodes during which the entirety of the accreted matter is lost from the system. Due to mixing of chemicals by rotation-induced instabilities during the accretion phase, H-flashes occur inside the original WD. Hence, pulse by pulse, the mass of the accretor is reduced down to 0.7453 M⊙. Afterwards, when He-rich matter is transferred, He detonation does not occur in the rotating WD, which undergoes six very strong He-flashes and subsequent mass-loss episodes. Also in this case, due to rotation-induced mixing of the accreted layers with the underlying core, the WD is eroded. Later, as the mass-transfer rate from the donor decreases, a massive He buffer is piled up onto the accretor, which ends its life as a cooling WD.
Conclusions. The binary system PTF J2238+743015.1 and all other binary systems with components of similar masses and similar orbital parameters are not good candidates as thermonuclear explosion progenitors.
Key words: accretion, accretion disks / nuclear reactions / nucleosynthesis / abundances / binaries: general / stars: individual: PTF J2238+743015.1 / stars: rotation / supernovae: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
This paper is the continuation of a series of studies (Piersanti et al. 2014, 2015, 2019) devoted to investigating the consequences of the accretion of He-rich matter onto carbon–oxygen white dwarfs (CO WDs), which may occur in close interacting binaries harboring either a CO WD and a He WD or a CO WD and a nondegenerate He companion (a hot subdwarf (sdB)).
As first recognized by Taam (1980) and Nomoto (1980), in CO WDs in close binaries, within certain ranges of mass and combined with certain accretion rates of helium, accretion may produce an off-center detonation of the accumulated He layer, which in turn may trigger detonation of carbon and result in a Type Ia supernova (SN Ia). For a certain time, this mechanism did not attract much attention, as the dominating paradigm was the close-to-Chandrasekhar-mass SN Ia due to the merger of two CO WDs. However, accretion-induced detonation garnered a second wave of popularity when after Livne (1990), Livne & Glasner (1991), and other authors demonstrated that He detonation at the surface of a sub-Chandrasekhar WD may trigger converging shock waves which, in principle, are able to initiate detonation of the underlying WD. The latest studies (e.g., Boos et al. 2021; Shen et al. 2021; Wong & Bildsten 2023) show that accretion of ≲0.03 M⊙ of He onto a sufficiently massive CO WD (MWD ≥ 0.9 M⊙) is sufficient to initiate a double detonation and produce the light curves and spectra of most nonpeculiar SN Ia. Detonations in more massive shells may result in peculiar SNe Ia. A comprehensive list of studies of the “double-detonation (DD) scenario” and a discussion of their results may be found, for example, in Wong & Bildsten (2023). These latter authors also demonstrated that, in binary systems with a degenerate He-rich donor, the larger the entropy of the accreted matter the lower the maximum attained mass-transfer rate and therefore the more likely the explosion of the CO WD.
The overwhelming majority of works devoted to studying the accretion of He-rich material onto CO WDs neglect the effects of rotation on the thermal evolution of the accretor. However, Yoon & Langer (2004a) considered that the accreted matter could deposit angular momentum, influencing the WD spin-up, and investigated the effects of rotation-induced mixing and energy dissipation via viscous friction. Their results demonstrated that differential rotation results in heating of the accreted layers and a lower degree of degeneracy of the matter at the epoch of He-ignition, which occurs sooner than in models accreting at the same rate Ṁ but without rotation. This may prevent He detonation, forcing He burning to occur through a series of “helium novae”. The outburst of V445 Puppis (Ashok & Banerjee 2003) may be a manifestation of such an event. It should be noted that, having in mind suspected rather high masses of the components of V445 Puppis (Kato et al. 2008; Woudt et al. 2009), implying also high Ṁ, mass transfer in this system should not lead to a detonation, even if the WD was non rotating
Additionally, Yoon & Langer (2004a) suggested that, for low values of the accretion rate, mass loss from the system may occur during outbursts. This could result in the detachment of the two components, which would nevertheless be brought back into contact thanks to orbital angular momentum loss (AML) via gravitational wave radiation (GWR). Further, Neunteufel et al. (2017) accounted for the possible generation of a magnetic field due to the spin-up produced by angular-momentum deposition and included magnetically induced instabilities in their simulation.
The studies of the influence of rotation on the outcomes of He accretion pursued by Yoon, Langer, and their collaborators came to a climax in Neunteufel et al. (2019), who computed a grid of almost 300 model binaries with masses of WDs of between 0.54 and 1.1 M⊙ and masses of nondegenerate He donors from 0.4 to 1.0 M⊙, accounting for the effects of rotation and magnetic torques, and with both components fully resolved. The grid was parameterized by initial orbital periods of the binaries, resulting in Roche lobe overflow (RLOF) by the model donors when helium in their cores was exhausted to different extents. Such He-burning models of mass-transferring stars typically have Ṁ ≈ 10−8 − 10−7 M⊙ yr−1 (Yungelson 2008). Evolution was traced up to the moment when the He-burning timescale became comparable to the dynamical timescale of the WDs. The main results of Neunteufel et al. (2019) may be roughly summarized as follows: (1) At least 0.1 M⊙ of He must be accreted in order to trigger a detonation; (2) He detonation does not occur if MWD ≲ 0.8 M⊙; (3) the masses of the donors that provide sufficiently low mass-transfer rates to initiate a detonation are inversely correlated with initial WD mass and span from 0.95 M⊙ for MWD = 0.82 M⊙ to 0.8 M⊙ for MWD = 1.1 M⊙; (4) the range of initial orbital periods allowing detonation to occur in such binaries is rather narrow, from ≲0.04 day for the less massive pairs to ≲0.06 day for the most massive ones. In other systems, either a He deflagration occurs or He burning in the donor ceases before a He buffer massive enough to trigger He-ignition is accumulated onto the WD. In the latter case, two CO WDs form.
Verification of the theoretical modeling described above has been hampered by the absence of observations of sufficiently close sdB+WD systems with well-established parameters. However, a very close sdB+WD system was recently discovered and thoroughly studied by Kupfer et al. (2022): PTF J223857.11+743015.1 (henceforth, PTF J2238). Another system, CD-30°11223 (CD-30 hereafter) was discovered more than a decade ago (Vennes et al. 2012), but the ambiguity in the determination of its parameters was resolved only recently (see Deshmukh et al. 2024, and references therein). For PTF J2238, it is expected that the subdwarf will overflow its Roche lobe in ≈6 Myr. CD-30 is expected to become semidetached in ≈40 Myr.
Following Tutukov & Yungelson (1990) and Ruiter et al. (2010), Kupfer et al. (2022) assumed that the subdwarf was formed first as a result of the stable loss of most of the H-rich envelope of a (2−5) M⊙ star with a nondegenerate He core via RLOF in the hydrogen-shell-burning stage, while the CO WD formed via subsequent CE during the AGB phase. Components of the binary are currently brought into contact due to AML via GWR. To satisfy log g and Teff of the sdB, Kupfer et al. (2022) assumed that the He core of the donor has a 10−3 M⊙ hydrogen envelope1.
Kupfer et al. (2022) used the code MESA (Paxton et al. 2011, and subsequent papers) to model the evolution of PTF J2238, approximating it by a binary system with MWD = 0.75 M⊙ and MsdB = 0.41 M⊙. Possible rotation of the WD was not considered. Following Woosley & Kasen (2011), Bauer et al. (2017), and Kupfer et al. (2022) predict that, after loss of the H/He envelope of the donor via accretion onto the WD, accompanied by a series of H-burning outbursts, accumulation of a ΔM = 0.17 M⊙ He layer on the WD surface should result in a thermonuclear runaway likely to destroy the WD in a “peculiar thermonuclear SN”.
In the present study, we compare the evolution of PTF J2238 assuming a nonrotating and a rotating WD, by closely following both phases of mass transfer, one H-rich and the other He-rich. The paper is structured as follows. In Section 2 we describe the adopted input physics and the evolutionary code we use. In Section 3 the properties of the binary system after the formation of the compact configuration are described, while in Sections 4 and 5 the results of our computations for the nonrotating and rotating models of the WD in PTF J2238 are presented, respectively. In Section 6 we investigate the possible outcome of the evolution of PTF J2238. In Section 7 we discuss the uncertainties associated with the computation of the rotating model. Finally, in Section 8 we draw our conclusions.
Estimated properties of the binary system PTF J2238 at the current epoch.
2. Input Physics and Numerics
All our models were computed with an updated version of the hydrostatic 1D Lagrangian code FuNS (Straniero et al. 2006; Cristallo et al. 2009; Piersanti et al. 2013). With respect to the previous version, we added the possibility of following the evolution of both components in a binary system simultaneously in order to evaluate the mass-transfer rate and the corresponding evolution of the orbital parameters self-consistently. In this regard, we assume that if the accretor fills its Roche lobe during a mass-transfer episode, the matter is lost from the system with the specific angular momentum of the accretor (Piersanti et al. 2015, 2019). Here, we consider models with initial solar metallicity, adopting the solar mixture as derived in Piersanti et al. (2007) for the compilation of solar abundances provided by Grevesse & Sauval (1998). We adopt the equation of state provided by Straniero (1988) and successive upgrades (Prada Moroni & Straniero 2002) for temperatures greater than 3 × 106 K, while for lower temperature, the tables of thermodynamic variables EOS_2005 are used (Rogers et al. 1996). Radiative opacities for temperatures lower than 5 × 108 K were obtained via the web facility provided by the OPAL group (Iglesias & Rogers 1996), while at larger temperature we make use of the LANL OPLIB tables (Colgan et al. 2018)2. Conductive opacities are included according to the prescription in Cassisi et al. (2021)3. As in Piersanti et al. (2014), the adopted nuclear network includes elements from H to Fe, linked by α-, p-, and n-capture reactions as well as β± decays. To take into account the energy contribution due to n-captures on isotopes heavier than 56Fe, we introduced a fictitious neutron sink following the prescription by Jorissen & Arnould (1989). At variance with our previous works on CO WDs accreting matter from He-rich companions, we include the NCO chain by adopting the weak rates for e-capture on 14N and β-decay of 14C provided by G. Martínez-Pinedo (priv. comm.), while the reaction rate for 14C(α,γ)18O process is derived from Johnson et al. (2009).
In the computation of rotating models, the effects of rotation are accounted for as in Piersanti et al. (2013) (see their Section 2), by assuming that the transport of angular momentum can be represented as a pure diffusive process. We consider convection to be responsible for angular momentum transport (which is assumed to enforce rigid rotation in convectively unstable regions), as well as rotation-induced circulations, such as Eddington-Sweet (ES), Goldreich-Schubert-Fricke (GSF), Solberg-Höilland (SH), and shear (both dynamical and secular, abbreviated here as DS and SS, respectively) instabilities. Hence, the total diffusion coefficient for the transport of angular momentum Dj is given by
where Dconv, DES, DGSF, DSH, and DDS are computed as described in detail in Piersanti et al. (2013) (see also Endal & Sofia 1978; Heger et al. 2000), while DSS is computed according to Zahn (1992), as implemented by Yoon & Langer (2004b; see their Eq. (13)). We evaluate the electron viscosity –which is necessary to define the onset of secular shear instability– according to Itoh et al. (1987, and references therein). We treat the presence of μ-barriers by defining an equivalent μ-current opposing the rotation-induced circulation. Following Heger et al. (2000), the μ-gradient ∇μ in all the quantities defining the diffusion coefficients above is replaced by fμ∇μ, where fμ is a free parameter in the range [0, 1] describing the sensitivity of rotation-induced instabilities to chemical gradients. Modifications of the local chemical composition due to both convection and rotation instabilities are described by adopting a diffusive scheme. The corresponding total diffusion coefficient DM now becomes:
where fc is a parameter in the range [0, 1] describing the mixing efficiency of rotation-induced instabilities. At variance with Piersanti et al. (2013), we set fc = 0.04, as derived by Pinsonneault et al. (1989) to reproduce the surface abundance of lithium in the Sun, and fμ = 0.05, as derived by Heger et al. (2000) to reproduce the nitrogen surface abundance in massive stars.
Following Kippenhahn & Thomas (1978), we include in the energy conservation equation the dissipation of rotational energy via the friction term εdiss. Following Yoon (2004) and Paxton et al. (2013, see their Appendix B.6), the finite difference equations describing the transport of angular momentum are solved implicitly using multiple sub-time-steps δti smaller than the time-step Δt used to integrate the other stellar equations. The exact values of δti are fixed so that they appear smaller than the minimum local diffusion timescale related to the angular momentum transport. Such a procedure is adopted to improve the accuracy of our evaluation of the angular velocity profile.
In the present work, we assume that H and He are ignited when the energy released per unit time by the CNO cycle and the 3α-reactions, respectively, first becomes higher than the surface luminosity by a factor 100. Consistently, we define the H- and He-ignition point as the mass coordinate where H- and He burning have a maximum at the ignition epoch.
3. The initial system
Basing on the analysis and results of Kupfer et al. (2022), we modeled the current epoch PTF J2238 as a binary harboring a CO WD of 0.75 M⊙ and an sdB companion of 0.390 M⊙ with an orbital period of P = 76.4 min. Following (Kupfer et al. 2022), we also assume that the compact binary formed 172 Myr ago with an orbital period of P0 = 122.7 min and has a He-burning core of 0.3879 M⊙ and an H-rich outer layer of 2.1 × 10−3 M⊙.
The initial CO WD model for our computations was constructed by accreting He-rich matter onto the “heated” model M070 from Piersanti et al. (2014) at Ṁ = 3 × 10−7 M⊙ yr−1 to simulate the evolution in the AGB phase. With this choice of parameters, we find that, at the current epoch, the PTF J2238 system has the properties presented in Table 1, in agreement with those derived observationally by Kupfer et al. (2022). By computing the expected further evolution of this system, we find that the sdB component will fill its Roche lobe in 13.08 Myr.
4. Non-rotating model
First, we computed the evolution of the PTF J2238 system neglecting the effects of rotation. This model is used as a reference for our analysis of the rotating model (see the following section). The upper panel of Fig. 1 shows the history of the mass transfer from the sdB component onto the CO WD, while the lower panel shows the hydrogen (solid black line) and helium (dashed red line) abundances (by mass fraction) as tracers of the chemical composition of the accreted matter. Figure 2 reports several physical properties of the accreting WD for the phase of H-rich matter accretion. During this phase, the CO WD experiences 11 H-flashes followed by a Roche lobe overflow. The mass-transfer rate is very low, and so H-flashes are very strong and all the matter accreted onto the WD is lost from the system4.
 |
Fig. 1. Time evolution of the mass-transfer rate (upper panel) and of the H- and He abundances in the transferred matter (lower panel) for the nonrotating model. The origin of the x-axis is fixed at the epoch when the sdB component filled its Roche lobe (Age0 = 185.08 Myr). |
 |
Fig. 2. Evolution of selected physical properties of the nonrotating CO WD during the accretion phase of H-rich material. From top to bottom, we report: the luminosity of the H-burning shell (LH in solar units); the variation in the CO WD total mass defined as |
Closer inspection of Fig. 2 reveals that, for the first eight H-flashes, the amount of mass to be accreted to trigger the flash episode slightly increases pulse by pulse, because the mass-transfer rate decreases (see the upper panel in Fig. 1). After that, Ṁ starts to increase, because the H abundance in the accreted matter starts to decline. This results in a decrease in the interpulse period.
The 12th and last H-flash at ≃50.4 Myr after the onset of mass transfer is peculiar in many ways. Compared to the previous flash, the average mass-transfer rate is about two orders of magnitude higher (2 × 10−9 vs. 2 × 10−11 M⊙ yr−1), while the amount of mass that is accreted and triggers the flash also almost doubles (4.35 × 10−4 vs. 2.64 × 10−4 M⊙), meaning that the density at the base of the H-shell at the onset of the thermonuclear runaway is also higher (8.92 × 103 vs. 4.94 × 103 g cm−3). Notwithstanding, the maximum luminosity (i.e., the maximum value of the total nuclear energy released per unit time via H-burning) during the two flashes is almost the same, at LH ≃ 1010 L⊙, and, most importantly, the mass lost during the Roche lobe triggered by the 12th flash is only 2.6 × 10−5 M⊙ (not visible in the plot). The above outcomes are due to the fact that during the 12th accretion cycle of H-rich matter, the H abundance is very low, as shown in Fig. 3, where we report the chemical stratification of the accreted layer at the onset of the 11th and 12th H-flashes. This implies that during the very last H-flash, the amount of energy per unit mass injected into the accreted layers is small and therefore the external layers of the accreting WD need only inflate by a relatively small amount and the equilibrium configuration is restored.
 |
Fig. 3. Comparison of the abundances of selected isotopes involved in the CNO cycle for the nonrotating model at the onset of the H-flash in the 11th (solid line) and 12th (dashed line) cycles, respectively. |
After the H-rich layer of the sdB component has been completely lost, He-rich material is accreted onto the WD (see Fig. 1). We find that when the total mass of the WD becomes MWD = 0.888 M⊙, that is, after a He buffer as massive as 0.138 M⊙ has been accumulated, a He-flash will be ignited at the mass coordinate 0.8 M⊙, where the density at the ignition epoch is 8 × 105 g cm−3. As the FuNS code is a hydrostatic one, we check the possibility that this model could produce a successful explosion using the 1D SN Ia explosion code Thermonuclear SUpernova Hydrodynamics and Nucleosynthesis (TSUHN – Bravo et al. 2018). We find that the entire WD is destroyed, the kinetic energy of the ejecta being 1.07 foe. As a consequence of the explosion, 0.295 M⊙ of 56Ni is produced, with 0.260 M⊙ coming from the CO core and the remaining 0.035 M⊙ from the He-rich mantle. Among intermediate-mass elements, we find that the produced total amount of sulfur and calcium are 0.122 M⊙ and 0.04 M⊙, respectively, while the mass of ejected manganese is 0.00187 M⊙. The chemical composition of the ejecta is peculiar, as the abundances relative to 56Fe of 78Kr, 80Kr, 44Ca, 48Ti, 74Se, and 51V are more than ten times larger than the solar values.
Due to the explosion, it is expected that the remnant of the donor in PTF J2238, having a final mass of MsdB = 0.2496 M⊙, is kicked off with an escape velocity equal to its orbital velocity of vsdB = 867 km s−1.
The amount of accreted He-rich matter and the WD mass at detonation are commensurate with the values obtained for the nonrotating model of PTF J2238 by Kupfer et al. (2022), of namely ΔMHe = 0.17 M⊙ and MWD = 0.92 M⊙, respectively. Furthermore, these values are in reasonable agreement with the data of Neunteufel et al. (2016), who found that for a (0.8−1.0) M⊙ WD, on average, 0.163 M⊙ of He should be accumulated for detonation.
We remark that the occurrence of He detonation is related to the mass-transfer history in the stage of He-rich matter accretion, which in turn depends on the adopted binary parameters for PTF J2238 at the current epoch. In particular, for a different set of donor and/or accretor masses, and for a different separation, Ṁ may increase with time more rapidly than reported in Fig. 1. Helium would then be ignited via a very strong nondynamical flash. In this case, the binary would survive and the accreting WD would experience several He-flashes, during which all the accreted matter would be ejected from the system via RLOF. In this case, the fate of the WD would likely be a CO core surrounded by an extended He buffer (see the discussion in Piersanti et al. 2015; Brooks et al. 2015).
5. Rotating model
According to the observations of a sample of DA WDs (Berger et al. 2005), the rotation velocity of compact degenerate stellar remnants is very low (ω ≤ 10−2 rad s−1), clearly suggesting that in stars that left main-sequence angular momentum has been subtracted from the radiative core. This conclusion is confirmed by the rotational curve derived from the data obtained by the Kepler mission for a sample of red giant branch (RGB) stars (Mosser et al. 2012), showing that the ratio of the angular velocity in the radiative core and the convective envelope is in the range of 5−10 (see, e.g., the discussion in Eggenberger et al. 2012; Marques et al. 2013). Hence, we can safely assume that both compact objects in PTF J2238 are initially almost at rest. Moreover, by assuming that, after the formation of the compact binary system, the synchronization of the orbits occurs on a very short timescale and remembering that the orbital period of the system under study in the course of further evolution will be in the range of 10−70 min, we find that the angular velocity of both components before RLOF by the subdwarf will always remain lower that 0.01 rad s−1, meaning that the correction to the local gravity, which is proportional to (ωWD/ωc)2, is lower than 1% (see also the discussion in Sect. 5 of Bauer & Kupfer 2021). According to these considerations, we can safely assume that the evolution of the sdB is not affected by rotation. On the other hand, during the mass-transfer process, the accreted matter is expected to supply angular momentum to the CO WD, which would very quickly become a fast rotator, at least in the external zone. Therefore, in our calculation of the evolution of PTF J2238, we include the effects of rotation only in the computation of the accretor.
For the mass ratio of donor and accretor in the model studied here, mass transfer is stable (Marsh et al. 2004) and the material transferred from the donor forms a thin Keplerian accretion disk around the accretor. Matter deposited onto the WD surface carries an amount of angular momentum almost equal to the Keplerian value at the equator. This implies that very soon after the onset of mass transfer, the CO WD surface attains the critical rotation rate and therefore, in principle, no more matter can be added. Paczynski (1991) and Popham & Narayan (1991) demonstrated that, under these conditions, mass continues to be accreted onto the WD, which maintains its angular velocity close to the break-up value and transfers the angular momentum excess back to the disk. Hence, following Yoon & Langer (2004b), we assume that the accreted matter does not deposit angular momentum if the rotation velocity on the WD surface is equal to its Keplerian value:
where vWD is the surface equatorial velocity of the accreting WD, 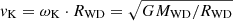 is the Keplerian velocity at the WD equator, jacc is the specific angular momentum of the accreted matter, and
is the Keplerian velocity at the WD equator, jacc is the specific angular momentum of the accreted matter, and 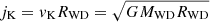 is the specific angular momentum at the WD equator. In our computation, we fix the factor fj in Eq. (3) to 1.
is the specific angular momentum at the WD equator. In our computation, we fix the factor fj in Eq. (3) to 1.
5.1. Evolution during the H-rich matter accretion phase
Figure 4 shows the time evolution of the H-burning luminosity during the first H-rich matter accretion episode for the rotating model (solid black line); for comparison we also report the same quantity for the nonrotating model discussed in Sect. 4 (red dashed line). As the mass-transfer history is the same for the two models, we find that in the rotating model the first H-flash is ignited when a smaller amount of mass has been accreted (ΔMacc = 1.27 × 10−4 M⊙ and 1.74 × 10−4 M⊙ for the rotating and nonrotating models respectively). This is somewhat expected and is related to the heating induced by the rotational energy dissipation due to the transport of angular momentum via rotation-induced instabilities (see the discussion in Yoon & Langer 2004a). Figure 4 also shows that the H-flash is stronger in the rotating model (the maximum LH value is larger than that in the nonrotating model). Further analysis reveals that the density at the H-ignition point in the rotating model is 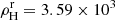 g cm−3, a factor almost 2 higher than in the nonrotating model (
g cm−3, a factor almost 2 higher than in the nonrotating model (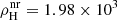 g cm−3).
g cm−3).
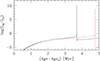 |
Fig. 4. Time evolution of the H-burning shell luminosity during the first H-flash for the nonrotating and rotating models (red dashed and black solid lines, respectively). |
 |
Fig. 5. Profiles of hydrogen abundance X(H) (upper panel) and angular velocity (lower panel) at various epochs during the first mass-transfer episode in the rotating model. The time after the onset of mass transfer corresponding to each line is reported in the plot. The x-axis is defined in such a way that the original WD surface (M = 0.75 M⊙) coincides with the origin. Lines a to e correspond to the evolution before the onset of the H-flash; line f corresponds to the epoch when flash-driven convection sets in; line g corresponds to the epoch when flash-driven convection attains its maximum extension. Dots connected by the heavy dashed line mark the position of the H-burning shell. |
In the nonrotating model, H-flash occurs at the surface of the original CO WD. As rotation reduces the density of the external layers of the accreting WD, in the rotating model the first H-flash occurs well below the surface of the original WD. Such an occurrence is due to the mixing induced by rotation-driven instability (mainly shear) of the accreted layer with the most external zone of the original WD. This is clearly illustrated in Fig. 5, where we report the H abundance X(H) as a tracer of the accreted matter (upper panel), and the angular velocity ω (lower panel) as a function of the WD mass, for various epochs during the first mass-transfer episode of H-rich material. Here, we note that, during the H-flash, the H-rich zone –that is, the zone of the WD where X(H) > 0.1– is a factor 2.2 more massive than the accreted one (orange solid line, labeled g), which is due to rotation-induced mixing. Further inspection of Fig. 5 discloses that, at the epoch of maximum extension of the flash-driven convective shell, the zone below the H-burning shell has a flat distribution of chemicals (see line g), which is a peculiarity as compared to flashes occurring in nonrotating models. Moreover, after the onset of convection, shear instability transports angular momentum inward and efficiently mixes the zone above the H-burning shell with the underlying zones. As a consequence, these inner layers also become unstable for convection. As the flash proceeds, the local increase in temperature due to the H-flash splits the convective shell so that matter is no longer carried efficiently through the burning shell. To investigate this issue further, we recomputed the first H-flash episode by setting fj = 0.6 in Eq. (3), that is, by assuming that the accreted matter has a specific angular momentum equal to 60% of the equatorial Keplerian value. We find that, with respect to the rotating model described above, at the H-ignition (which occurs at M = 0.7499 M⊙) the angular velocity at the H-burning shell decreases by 25% (from 8.75 to 6.62 × 10−2 rad s−1), the mass accreted increases by 13% (from 1.27 to 1.46 × 10−4 M⊙), the ignition density decreases by 12%, and the maximum value of LH decreases by 30%. Moreover, at the epoch of the maximum extension of the flash-driven convective shell, the H-rich zone is a factor 1.8 more massive than the accreted matter. These results demonstrate that the physical conditions at the H-ignition point (mainly density), and hence the strength of the resulting H-flash, depend on the rotation rate of the accreted layers.
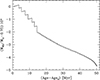 |
Fig. 6. Time evolution of the WD total mass during the phase of H-rich mass accretion for the rotating model. Age0 is the epoch of RLOF by the sdB star. |
As in the nonrotating model, due to the H-flash, the rotating WD expands and fills its Roche lobe, giving rise to mass loss from the binary system. As illustrated in Fig. 6, where we report the evolution of the total mass of the accreting WD, all the matter accreted before the H-flash, as well as the most external layers of the original WD, are lost via Roche-lobe overflow, resulting in the reduction of the WD mass. Figure 6 also reveals that the entire phase of H-rich matter accretion is characterized by a secular reduction of the initial WD mass. Nevertheless, the evolution of the mass-transfer rate with time during the H-rich mass-transfer phase for the rotating model is very similar to that of the nonrotating WD shown in Fig. 1. Moreover, even if in the rotating model the WD mass is reduced, its variation is small, meaning that the effect on the binary separation is almost negligible.
Further inspection of Fig. 6 reveals that the evolution of the WD total mass is very irregular. For instance, the amount of mass lost by the WD is at maximum during the Roche lobe episode triggered by the seventh H-flash. This occurs because, during the previous six flash episodes, the most external zones of the original WD were removed, meaning that during the seventh episode the accreted matter began to be mixed via rotation-induced instabilities with layers enriched in 12C (X(12C) > 0.1) produced during the evolution of the CO WD progenitor in He-shell burning. This occurs when the H-flash is on the verge of being ignited, and very closely resembles the “mixing during thermonuclear runaway” invoked by Starrfield et al. (2020) to explain nova outbursts (see also Casanova et al. 2011; José et al. 2020). As a consequence, the H-flash becomes stronger and the burning extends inward, engulfing a larger zone of the WD, which is subsequently involved in the mass loss via Roche-lobe overflow.
 |
Fig. 7. Time-dependence of the He-burning luminosity (top panel), WD total mass (middle panel), and mass-transfer rate (lower panel, left y-scale) during the stage of He-rich-matter accretion. The two leftmost spikes in the upper panel show, for comparison, the He-burning luminosity during the last two (61th and 62nd) H-burning outbursts. The lower panel also presents the evolution of the abundances of 4He (solid cyan line), 12C (long dashed red line), and 16O (dashed blue line) as tracers of the chemical composition of the accreted matter (right y-scale). |
In the following H-rich mass-transfer episodes, the accreted matter is mixed with C-enriched material during the entire accretion phase, meaning that a smaller amount of accreted mass is sufficient to trigger the H-flash. This situation is quite similar to what occurs in nonrotating models accreting H-rich matter with increased CNO abundance. Finally, we note that for (Age-Age0) > 43 Myr, when the hydrogen abundance in the accreted matter drops below 0.5 (see Fig. 1), the mass-transfer rate from the donor rapidly increases so that the compressional heating produced on the WD surface is larger, and hence a smaller amount of accreted mass is needed to trigger H-flashes (see Fig. 1). Overall, we find that, due to the accretion of H-rich mass, the CO WD experiences 62 flashes (compared to 12 in nonrotating model) and its total mass reduces to MWD = 0.7453 M⊙.
5.2. Evolution during the phase of He-rich-matter accretion
When the H-rich mantle of the sdB has been completely transferred, He-rich matter starts to be accreted and the corresponding Ṁ rapidly increases above ∼10−8 M⊙ yr−1 (see lower panel in Fig. 7). We find that our model experiences a strong, nondynamical He-flash after 1.29 × 10−2 M⊙ of He-rich matter has been accreted. However, as shown in Table 2, where we report several physical properties of the accreting WD during the phase of He-flashes, due to rotation-induced mixing the mass of the He-rich zone, that is, the zone with a He abundance greater than 0.1 (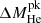 in Table 2), is almost two times larger than the mass of the accreted matter ΔMacc. As a consequence, during the RLOF episode triggered by the He-flash, all the accreted matter as well as the most external zone of the WD are lost from the binary system, meaning that the retention efficiency, defined as the percentage of transferred mass effectively retained by the accretor (
in Table 2), is almost two times larger than the mass of the accreted matter ΔMacc. As a consequence, during the RLOF episode triggered by the He-flash, all the accreted matter as well as the most external zone of the WD are lost from the binary system, meaning that the retention efficiency, defined as the percentage of transferred mass effectively retained by the accretor (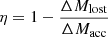 ), is negative. By computing the long-term evolution of this model, we find that the CO WD in the PTF J2238 binary experiences six He-flashes, as illustrated in Fig. 7.
), is negative. By computing the long-term evolution of this model, we find that the CO WD in the PTF J2238 binary experiences six He-flashes, as illustrated in Fig. 7.
Selected properties of the accreting WD during the evolution throughout recurrent He-flashes of the rotating model.
Further inspection of both Fig. 7 and Table 2 reveals that the physical properties of the He-flashes do not exhibit a well-defined regular behavior as a consequence of the variation in the mass-accretion rate, the chemical composition of the accreted matter, that of the matter in the external layers of the WD, the efficiency of the angular momentum transport, and the temperature profile in the outermost zone of the WD.
In particular, the amount of accreted mass triggering the first He-flash was lower than the amount that triggered the second outburst. The first flash is less energetic than the second one, despite the fact that in both cases Ṁ was comparable immediately prior to the flash (see Fig. 7). In fact, the He abundance at the surface of the WD at the onset of the first He-rich mass-transfer episode was 0.33, while at the onset of the second one it was only 0.14. During the last ≃55 H-flashes, angular momentum remained stored in the most external layers of the WD because of the very short recurrence time of flashes, which hampers its efficient inward transport. During the He-accretion phase, interpulse periods increase and angular momentum is transferred inward at a higher rate. For instance, at the onset of He accretion, the angular momentum was concentrated in the outermost 2.7 × 10−3 M⊙ of the WD, while at the onset of accretion before the second flash, this zone was more than ten times more massive (3.9 × 10−2 M⊙). This affected the strength of the flashes, because angular momentum (and hence angular velocity) distribution defines the lifting effect of rotation, as well as the mixing efficiency. Finally, the temperature profile in the external layers of the WD before He accretion started was almost flat, with a very low peak of the order of 40 MK, while at the onset of the second mass-transfer episode, the outermost 9 × 10−3 M⊙ had a large thermal content with a peak temperature of almost 300 MK.
In summary, the structure of the outer layers of the WD at the beginning of the first He-flash was different from that at the beginning of the second He-flash, and this produced differences in the properties of the flashes. From the second to the sixth He-flash, the physical conditions in the outermost layers of the WD at the repeated onset of mass accretion after RLOF episodes were quite similar and the differences in the properties of the flashes depend on the mass-transfer rate and/or the chemical composition of the accreted matter.
The third He-flash episode is characterized by a larger mass-transfer rate as compared to the previous one, meaning that less mass is accreted before the onset of the flash and therefore that the resulting flash is less strong. On the other hand, during the fourth episode of He-rich matter accretion, a larger amount of mass is accreted as compared to the third one, even if Ṁ increased to 5.7 × 10−8 M⊙ yr−1, while the strength of the flash is comparable. During this accretion cycle, the zones of the donor partially involved in central He burning start to be transferred onto the WD and the He abundance in the accreted matter decreases to 0.715. As a consequence, a larger mass has to be accreted to trigger the He-flash, as reduced X(4He) limits the rate of the 3α reaction and prevents a stronger flash.
During the fifth He-accretion cycle, the mass-transfer rate attains a maximum (Ṁ ≃ 10−7 M⊙ yr−1). The He abundance in the accreted matter decreases to 0.38, but unlike the previous flash episode, the increase in Ṁ is now the leading parameter, resulting in a sizable reduction in the accreted mass. Finally, during the sixth accretion episode, the mass-transfer rate decreases to 4.5 × 10−8 M⊙ yr−1, resulting in an increase in the amount of matter that needs to be accreted in order to trigger the He-flash, which is ignited at higher density, thus producing a definitively larger maximum temperature in the He-rich buffer. As the amount of available fuel above the He-burning shell is lower6, the energy injected into the He-rich envelope is lower and, as a consequence, during the following Roche lobe episode a small amount of the accreted matter is retained by the accreting WD. Overall, we find that during the six He-flashes, the binary system loses about 0.2869 M⊙ and the mass of the donor reduces to 0.1416 M⊙.
 |
Fig. 8. Selected properties of the last computed structure in the rotating model. We report the abundance of 4He, 12C, and 16O in the upper panel (solid lines) and the ω and ωcr profiles in the lower panel (solid and dashed lines, respectively). For comparison, in the upper panel we report the abundances of the same isotopes in the initial 0.75 M⊙ WD model (dashed lines). |
After the sixth He-flash, when mass transfer from the donor resumes, the orbital period of the system is 10.16 min. The subsequent evolution of the system is similar to that of AM CVn stars with strongly evolved nonrotating He-star donors at the beginning of RLOF (see, e.g., Yungelson 2008; Nelemans et al. 2010). The system reaches the minimum of the periods at ≈8.27 min and then evolves to longer ones. Mass-transfer rate continuously decreases and hence the amount of matter to be accreted to trigger a new flash becomes larger and larger and, as a matter of fact, is never attained. We stop computations when the mass of the donor reduces to 0.018 M⊙ because the adopted equation of state does not provide thermodynamic quantities for extremely cool objects. At that epoch, the orbital period is ≈34.47 min, and the donor, corresponding to the homogeneous former core of a He-burning star, consists of a C/O mixture with traces of He. The accreting WD now has a mass of MWD = 0.8274 M⊙, while the mass-transfer rate is Ṁ = 2.17 × 10−11 M⊙ yr−1. In Fig. 8 we report, for the last computed structure of the accretor, the profile of the most abundant isotopes (upper panel) and that of ω and ωcr (lower panel).
5.3. Nucleosynthesis during He-flashes
During the phase of He-rich matter accretion, the resulting six flashes are very strong, meaning that the temperature in the He-burning shell exceeds 4 × 108 K (see Table 2). The 22Ne(α, n)25Mg reaction is then fully efficient and therefore n-capture nucleosynthesis is expected to occur. We note that the 22Ne abundance is almost the same as the original CNO abundance in the progenitor of the sdB in PTF J2238. Isotope 22Ne in the WD appears as a result of nitrogen burning in the accreted matter via the reaction chain 14N(α, γ)18F(β+)18O(α, γ)22Ne during the initial phases of the He-flash. To characterize the chemical composition of the matter ejected by the system during the six RLOF episodes, we considered the third He-flash episode as representative of the whole phase and repeated the computation by adopting a full nuclear network up to 210Po, as in Piersanti et al. (2019). The results are displayed in Fig. 9, where we report the abundance of isotopes produced during the He-flash episode relative to their solar value. As can be seen, the most overproduced isotopes are 40K, 46Ca, 21Ne, 22Ne, and 58Fe, whose abundances are larger than the solar ones by factors of 314, 356, 138, 103, and 97, respectively. Isotopes with atomic numbers 26 < Z ≤ 32 are overproduced by factors exceeding 10, while the abundances of isotopes from Br to Sm are increased by factors of a few. Finally, isotopes with Z > 62 do not exhibit any particular trend. On the other hand, we find that the abundances of 210Pb, 210Bi, and 210Po, the endpoints of the adopted nuclear network, are 1.2 × 10−11, 1.7 × 10−13, and 2.6 × 10−11, respectively, clearly indicating that the nucleosynthesis during the He-flash should also produce heavier isotopes and eventually also actinides. This topic is far beyond the scope of the present work and will be addressed in a forthcoming paper devoted to studying the nucleosynthesis in interacing binaries.
 |
Fig. 9. Abundances of isotopes up to samarium produced during the third He-flash episode in the rotating model relative to their solar value. The unstable isotopes have been allowed to decay to their stable isobars. |
6. The destiny of the PTF J2238 system
In our model of PTF J2238, when we stop the accretion of He-rich matter, the WD is stable because its angular velocity profile has attained an equilibrium configuration, meaning that the fate of this rather massive WD is to cool down. However, if angular momentum is removed from the star, then the WD can undergo a contraction, which leads to compressional heating of the inner zones, thus potentially triggering the ignition of the 3α reaction. Chandrasekhar (1970) and Friedman & Schutz (1978) suggested that rapidly rotating compact stars can emit gravitational waves, thus becoming unstable for nonaxysimmetric perturbations. Currently, two different modes are considered as responsible for these instabilities, namely the f-mode and the r-mode with nodal numbers of spherical harmonics l = m = 2. In general, Andersson & Kokkotas (2001) suggested that gravitational instabilities are strongly suppressed in the presence of large turbulence-driven viscosity. Therefore, it is usually assumed that no GWR emission can occur at all during the mass accretion. In this regard, it should be noted that, according to Imamura et al. (1995), the secularly unstable modes can also survive in the presence of shear instability.
As shown in many works (e.g., see Ostriker & Tassoul 1969; Durisen 1975; Durisen & Imamura 1981), the f-mode instability in a rapidly rotating object can occur only if the ratio of the rotational to gravitational energy Θ = Erot/|W| becomes larger than a critical value, which is fixed to 0.14 for a wide range of angular velocity profiles, even if Imamura et al. (1995) have shown that this limit can be as low as 0.09 for strongly differentially rotating objects. Our massive WD at the end of the mass-transfer process has Θ = 0.044, and so we can exclude that this instability could affect the evolution of the WD angular momentum at all. On the other hand, r-modes are always unstable in rotating inviscid stars (Andersson 1998) and their growth timescale can be estimated according to Lindblom (1999) as
where ρ(r) and ω(r) represent the density and angular velocity profile of the equilibrium configuration. Such a timescale has to be compared to the viscous timescale τv defined as
where η(r) represents the shear viscosity profile (Lindblom 1999). We find that, after the sixth He-flash, when the mass-transfer rate in our model of PTF J2238 drops below ∼3.3 × 10−8 M⊙ yr−1, that is, when the WD total mass grows above 0.71 M⊙, τv becomes larger than 109 yr and rapidly increases above 1010 yr. For the final structure we computed, we obtain τr = 2.36 × 109 yr, an order of magnitude smaller than the viscous timescale. We note that this value is nevertheless definitively longer than the one derived by Yoon & Langer (2004b) for a 1.5 M⊙ WD (see their Fig. 14), mainly because the average angular velocity in the structure studied by these authors is a factor 5 larger than in our case.
We compute the further evolution of the rotating WD by subtracting, at each time step δt, an amount of angular momentum equal to δj = JWD ⋅ exp(−δt/τr), where JWD is the actual value of the WD total angular momentum. We find that, as angular momentum is subtracted from the surface, a local gradient of the angular velocity forms, thus determining the onset of shear instabilities in the outermost zones of the WD. As the braking process goes on, shear instability affects increasingly internal zones, meaning that the whole structure progressively reduces its angular velocity; at the same time, rotation-driven mixing also resumes, and He-rich material is mixed downward at a higher level. In any case, as the braking timescale is very long, the WD does not heat up to any significant level and therefore He burning cannot be ignited at all (see also the discussion in Yoon & Langer 2004b).
With the aim of determining under which physical conditions He burning could be eventually ignited in the accretor of PTF J2238, we computed exploratory models by adopting a definitively shorter braking timescale τb than the τr above, even if no physical mechanisms responsible for such a fast deacceleration have been identified or even proposed so far. We find that for τb = 2 × 107 yr, a very strong He-flash occurs at the mass coordinate 0.743 M⊙, with the maximum attained temperature being of the order of 6 × 108 K. For longer braking timescales, the thermal energy delivered by the induced compression is transferred inward, without producing an increase in temperature in the He-rich layer of sufficient size to trigger He-ignition. On the other hand, if τb is reduced, He burning is ignited in progressively more external zones. Moreover, He detonation does not occur at all, as expected given the fact that the He buffer is not massive enough (ΔMHe ≃ 0.12 M⊙), and in addition, the He abundance there is as low as 0.13 (see the lower panel in Fig. 8).
7. Discussion
Our results show that, due to the combined effect of rotation-induced lifting, shear dissipation heating, and chemical mixing, the accreting WD in PTF J2238 will never attain physical conditions suitable for a detonation and will end its life as a CO core capped by a massive He buffer. Moreover, we find that during the mass-transfer phase of both H-rich and He-rich material, the WD experiences recurrent strong nova-like flashes that trigger Roche-lobe overflow episodes, during which all the accreted matter as well as a part of the underlying zones are lost from the system. As far as we know, such an occurrence has never been reported before in the literature, even if Yoon & Langer (2004a) suggested that it could happen for low Ṁ values. Moreover, this is the first time that a series of H- and He-flashes have been computed for a rotating WD accreting at low Ṁ so that during each runaway the accretor overfills its Roche lobe. The explanation of the secular reduction of the accretor mass pulse-by-pulse should be sought in the mixing of the accreted layers with the underlying WD as determined by rotation-induced instabilities. Thus, the zone involved in the flash is larger as compared to the that in the nonrotating model and hence the amount of mass that has to be lost during the Roche lobe overflow episode is larger.
Selected properties of models computed by varying the values of the parameters affecting the mixing efficiency of rotation-induced instabilities (fμ, fc – models T1 and T2, respectively), the amount of angular momentum deposited by the accreted matter (fj model T3), and by assuming very high efficiency for the angular momentum transport (model T4).
This is unavoidable as it is a direct consequence of rotation, even if, on general grounds, the exact amount of matter lost during each flash episode depends on the assumed amount of angular momentum deposited onto the WD, as well as on the assumed efficiency of angular momentum transport and rotation-induced mixing. To investigate this issue, we repeated the computation of the third He-accretion cycle by varying the following scaling parameters: fj in Eq. (3), which determines the amount of angular momentum accreted onto the WD; fμ, which defines the efficiency of “μ-current” opposing the rotation-induced circulation (see Section 2), and fc, which affects the efficiency of chemical mixing by rotation-induced instabilities (see Eq. 2). The results are reported in Table 3.
As can be seen, a reduction of the μ-barrier to rotation instabilities (model T1) produces only minor differences in the properties of the flashing structure. On the other hand, an increase in the mixing efficiency due to rotation-induced instabilities (model T2) causes a more rapid smearing of chemical gradient, meaning that angular momentum is transferred inward more efficiently, determining a reduction of the lifting effects due to rotation in the accreted He-rich buffer and hence a definitively larger inward extension of the He-rich zone. As a consequence, a larger amount of matter has to be accreted to trigger the flash, which also becomes stronger. Thus, the mass lost during the following Roche lobe episode is larger, even if the original WD is eroded by almost the same amount.
Finally, the reduction of angular momentum deposited by the accreted matter (model T3) results in a lower rotation velocity in the accreted layers (see e.g., the discussion in Yoon & Langer 2004a), meaning that a definitively more massive He buffer is required to trigger the He-flash. Moreover, as the angular momentum gained by the accretor is lower as compared to the STD case, the effects of rotation are also weaker, meaning that the He-flash is definitively stronger even if the original WD is eroded to a lesser extent.
In the present work, we do not account for the transport of angular momentum via magnetic instabilities. In general, a reliable physical theory describing the separate evolution of the poloidal and radial components of magnetic field is still missing. Therefore, in 1D, the computation of the torque exerted in differentially rotating stars is also particularly complex and largely uncertain. In a differentially rotating body, the onset of magnetic field is expected, and its amplification could occur if the velocity field due to convection were to generate a dynamo. However, Spruit (2002) demonstrated that, in differentially rotating stars, the magnetic field is amplified by an instability in the toroidal field –most probably the Tayler instability–, which could also occur in radiative regions. However, the applicability of the so-called “Tayler-Spruit” mechanism, as well as the derived efficiency of angular momentum transport, have been questioned by some authors (see, e.g., Maeder & Meynet 2004; Denissenkov & Pinsonneault 2007). Recently, Fuller et al. (2019) suggested that the dissipation of unstable magnetic field perturbations determines the saturation of the Tayler instability, which means that a smaller amount of energy is dissipated and the resulting magnetic field on average attains larger amplitudes. As a consequence, the corresponding angular momentum transport is definitively more efficient than that derived by Spruit (2002).
This issue, as well as the effects of magnetic fields on the evolution of interacting binary systems experiencing recurrent mass-transfer episodes, will be addressed in detail in a forthcoming paper. Here we limit our study to the computation of an additional test model (model T4 in Table 3), in which we assume that angular momentum transport due to magnetic instabilities is efficient enough to enforce rigid rotation along the whole accreting WD. We find that the mass to be accreted to trigger the He-flash is more than doubled with respect to the standard case, in agreement with Neunteufel et al. (2017) (see their Figure 7). Moreover, due to the very efficient angular momentum transport, the amount of angular momentum stored in the accreted layers largely decreases and, in addition, the angular velocity gradient (the so-called “shear factor”) rapidly goes to zero. As a result, viscous shear and GSF instability are suppressed, meaning that the mixing of the accreted matter with the original WD material is avoided (we note that 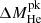 is only 4% larger than ΔMacc in model T4). In addition, the heating of the accreted layers via dissipation of rotational energy also does not occur. Finally, since angular momentum does not remain stored in the accreted layers, the ω value at the WD surface does not attain its critical value and hence a larger amount of angular momentum could be acquired by the accreting WD. As a consequence, the only effect of rotation is the reduction of the local gravity along the whole WD (lifting), and hence the amount of accreted matter needed to trigger a flash becomes larger as compared to the STD model. Due to the large increase in the mass of the accreted matter, He-ignition occurs at a higher density, and so the resulting He-flash is definitively stronger even if it does not turn into a detonation. We stop our computation when the WD fills its Roche lobe. It must be noted that, according to the extant formulations, magnetic instabilities can operate only if the shear factor is larger than a critical value. This implies that a small gradient in the ω profile survives, thus triggering both the release of thermal energy via viscous dissipation and a partial chemical mixing. Both these effects result in a slight reduction of the amount of mass to be accreted for the ignition of the He-flash, which should be less energetic. These considerations seem to suggest that, after also including the effects of magnetic instabilities, the model of the accretor in PTF J2238 will not experience a detonation, even if the physical properties of the accreting WD –in particular the exact value of the retention efficiency during subsequent RLOF episodes– could be significantly different.
is only 4% larger than ΔMacc in model T4). In addition, the heating of the accreted layers via dissipation of rotational energy also does not occur. Finally, since angular momentum does not remain stored in the accreted layers, the ω value at the WD surface does not attain its critical value and hence a larger amount of angular momentum could be acquired by the accreting WD. As a consequence, the only effect of rotation is the reduction of the local gravity along the whole WD (lifting), and hence the amount of accreted matter needed to trigger a flash becomes larger as compared to the STD model. Due to the large increase in the mass of the accreted matter, He-ignition occurs at a higher density, and so the resulting He-flash is definitively stronger even if it does not turn into a detonation. We stop our computation when the WD fills its Roche lobe. It must be noted that, according to the extant formulations, magnetic instabilities can operate only if the shear factor is larger than a critical value. This implies that a small gradient in the ω profile survives, thus triggering both the release of thermal energy via viscous dissipation and a partial chemical mixing. Both these effects result in a slight reduction of the amount of mass to be accreted for the ignition of the He-flash, which should be less energetic. These considerations seem to suggest that, after also including the effects of magnetic instabilities, the model of the accretor in PTF J2238 will not experience a detonation, even if the physical properties of the accreting WD –in particular the exact value of the retention efficiency during subsequent RLOF episodes– could be significantly different.
8. Conclusions
We investigated the evolution of the binary system PTF J2238, which harbors a CO WD with an sdB companion. This object (Kupfer et al. 2022), as well as similar ones (e.g., CD-30 – Deshmukh et al. 2024), have been addressed as progenitors of double detonation events, leading to low-luminosity peculiar-nucleosynthesis type Ia supernovae. At variance with previous studies, we considered the fact that, due to mass accretion from the companion, the WD acquires angular momentum, and we followed the evolution of the rotation velocity in the accretor interior, as determined by convection and rotation-induced instabilities.
Due to the combined effect of rotation-induced lifting, shear dissipation heating, and chemical mixing, the WD in PTF J2238 will never develop the physical conditions for a detonation during the accretion stage and will become a CO core capped by a massive He buffer. Furthermore, detonation will not happen during subsequent evolution driven by angular momentum losses from the WD.
This conclusion also applies to all those binary systems with a He-rich component and a mass-transfer history similar to that described for our case study. In particular, in CD-30, the rate of mass transfer from the donor is expected to quite closely resemble that of our case study (compare our Fig. 1 with Figure 7 in Deshmukh et al. 2024), meaning that, similarly, we suspect that the system will end its evolution without producing an explosion of supernova proportion.
We note that mass loss via RLOF from the progenitor of an MsdB ≃ 0.4 M⊙ He star in a close binary terminates when the donor still has an ≈0.05 M⊙ homogeneous H/He envelope and a “transition” zone of about the same mass, where hydrogen abundance declines from its initial value to zero. The mass-loss rate from hot subdwarfs (Krtička et al. 2016) is not sufficient to remove the H/He envelope in 170 Myr, the estimated age of PTF J2238. One must consider the possibility of an unknown process capable of efficiently removing mass while the presubdwarf crosses the HR diagram, changing chemical abundance profile.
Though outbursts are strong, we do not expect them to have the scale of a nova, as to get a nova it is necessary to largely increase the CNO abundance at the base of the H-burning shell. The only possible way is mixing with the underlying WD, but the CO core is capped by a He buffer whose outermost zone has an 14N abundance equal to that of the initial CNO abundance, and this is insufficient to trigger a nova.
We reiterate the fact that very soon after RLOF by low-mass He stars, nuclear burning in their interiors quenches and the chemical composition of the transferred matter is defined by the extent of the sdB evolution prior to RLOF and the abundances profile formed while nuclear burning extinguishes (Yungelson 2008).
Acknowledgments
We thanks the anonymous referee for useful comments and suggestions. We are grateful to S.-C. Yoon and N. Langer for helpful discussions. L.P. and L.R. Y. acknowledge partial financial support from the INAF Minigrant 2023 Self-consistent Modeling of Interacting Binary Systems. L.P. acknowledges partial financial support from the Italian MUR project 2022RJLWHN: Understanding R-process & Kilonovae Aspects (URKA). E.B. acknowledges partial support from the Spanish grant PID2021-123110NB-100 funded by MICIU/AEI/10.13039/501100011033 and by FEDER, UE.
References
- Andersson, N. 1998, ApJ, 502, 708 [CrossRef] [Google Scholar]
- Andersson, N., & Kokkotas, K. D. 2001, Int. J. Mod. Phys. D, 10, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Ashok, N. M., & Banerjee, D. P. K. 2003, A&A, 409, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, E. B., & Kupfer, T. 2021, ApJ, 922, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, E. B., Schwab, J., & Bildsten, L. 2017, ApJ, 845, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, L., Koester, D., Napiwotzki, R., Reid, I. N., & Zuckerman, B. 2005, A&A, 444, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boos, S. J., Townsley, D. M., Shen, K. J., Caldwell, S., & Miles, B. J. 2021, ApJ, 919, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Bravo, E., Badenes, C., & Martínez-Rodríguez, H. 2018, MNRAS, 482, 4346 [Google Scholar]
- Brooks, J., Bildsten, L., Marchant, P., & Paxton, B. 2015, ApJ, 807, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Casanova, J., José, J., García-Berro, E., Shore, S. N., & Calder, A. C. 2011, Nature, 478, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Salaris, M., & Pietrinferni, A. 2021, A&A, 654, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1970, Phys. Rev. Lett., 24, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Colgan, J., Kilcrease, D. P., Magee, N. H., et al. 2018, ASP Conf. Ser., 515, 55 [NASA ADS] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A., & Pinsonneault, M. 2007, ApJ, 655, 1157 [Google Scholar]
- Deshmukh, K., Bauer, E. B., Kupfer, T., & Dorsch, M. 2024, MNRAS, 527, 2072 [Google Scholar]
- Durisen, R. H. 1975, ApJ, 195, 483 [CrossRef] [Google Scholar]
- Durisen, R. H., & Imamura, J. N. 1981, ApJ, 243, 612 [CrossRef] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, J. L., & Schutz, B. F. 1978, ApJ, 222, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Fuller, J., Piro, A. L., & Jermyn, A. S. 2019, MNRAS, 485, 3661 [NASA ADS] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [Google Scholar]
- Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Imamura, J. N., Toman, J., Durisen, R. H., Pickett, B. K., & Yang, S. 1995, ApJ, 444, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Kohyama, Y., & Takeuchi, H. 1987, ApJ, 317, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, E. D., Rogachev, G. V., Mitchell, J., Miller, L., & Kemper, K. W. 2009, Phys. Rev. C, 80, 045805 [NASA ADS] [CrossRef] [Google Scholar]
- Jorissen, A., & Arnould, M. 1989, A&A, 221, 161 [Google Scholar]
- José, J., Shore, S. N., & Casanova, J. 2020, A&A, 634, A5 [EDP Sciences] [Google Scholar]
- Kato, M., Hachisu, I., Kiyota, S., & Saio, H. 2008, ApJ, 684, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Thomas, H. C. 1978, A&A, 63, 265 [NASA ADS] [Google Scholar]
- Krtička, J., Kubát, J., & Krtičková, I. 2016, A&A, 593, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupfer, T., Bauer, E. B., van Roestel, J., et al. 2022, ApJ, 925, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblom, L. 1999, Phys. Rev. D, 60, 064007 [NASA ADS] [CrossRef] [Google Scholar]
- Livne, E. 1990, ApJ, 354, L53 [Google Scholar]
- Livne, E., & Glasner, A. S. 1991, ApJ, 370, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A., & Meynet, G. 2004, A&A, 422, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsh, T. R., Nelemans, G., & Steeghs, D. 2004, MNRAS, 350, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelemans, G., Yungelson, L. R., van der Sluys, M. V., & Tout, C. A. 2010, MNRAS, 401, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Neunteufel, P., Yoon, S. C., & Langer, N. 2016, A&A, 589, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neunteufel, P., Yoon, S. C., & Langer, N. 2017, A&A, 602, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neunteufel, P., Yoon, S. C., & Langer, N. 2019, A&A, 627, A14 [EDP Sciences] [Google Scholar]
- Nomoto, K. 1980, Space Sci. Rev., 27, 563 [CrossRef] [Google Scholar]
- Ostriker, J. P., & Tassoul, J. L. 1969, ApJ, 155, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1991, ApJ, 370, 597 [Google Scholar]
- Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
- Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
- Piersanti, L., Straniero, O., & Cristallo, S. 2007, A&A, 462, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piersanti, L., Cristallo, S., & Straniero, O. 2013, ApJ, 774, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Tornambé, A., & Yungelson, L. R. 2014, MNRAS, 445, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Yungelson, L. R., & Tornambé, A. 2015, MNRAS, 452, 2897 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Yungelson, L. R., Cristallo, S., & Tornambé, A. 2019, MNRAS, 484, 950 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [Google Scholar]
- Popham, R., & Narayan, R. 1991, ApJ, 370, 604 [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [CrossRef] [Google Scholar]
- Rogers, F. J., Swenson, F. J., & Iglesias, C. A. 1996, ApJ, 456, 902 [Google Scholar]
- Ruiter, A. J., Belczynski, K., Benacquista, M., Larson, S. L., & Williams, G. 2010, ApJ, 717, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K. J., Boos, S. J., Townsley, D. M., & Kasen, D. 2021, ApJ, 922, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
- Starrfield, S., Bose, M., Iliadis, C., et al. 2020, ApJ, 895, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O. 1988, A&AS, 76, 157 [NASA ADS] [Google Scholar]
- Straniero, O., Gallino, R., & Cristallo, S. 2006, Nucl. Phys. A, 777, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E. 1980, ApJ, 237, 142 [CrossRef] [Google Scholar]
- Tutukov, A. V., & Yungelson, L. R. 1990, Soviet Astron., 34, 57 [Google Scholar]
- Vennes, S., Kawka, A., O’Toole, S. J., Németh, P., & Burton, D. 2012, ApJ, 759, L25 [Google Scholar]
- Wong, T. L. S., & Bildsten, L. 2023, ApJ, 951, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Kasen, D. 2011, ApJ, 734, 38 [Google Scholar]
- Woudt, P. A., Steeghs, D., Karovska, M., et al. 2009, ApJ, 706, 738 [Google Scholar]
- Yoon, S. C. 2004, Ph.D. Thesis, Sterrenkundig Insituut, Univsersiteit Utrecht, The Netherlands [Google Scholar]
- Yoon, S. C., & Langer, N. 2004a, A&A, 419, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S. C., & Langer, N. 2004b, A&A, 419, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yungelson, L. R. 2008, Astron. Lett., 34, 620 [Google Scholar]
- Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Tables
Selected properties of the accreting WD during the evolution throughout recurrent He-flashes of the rotating model.
Selected properties of models computed by varying the values of the parameters affecting the mixing efficiency of rotation-induced instabilities (fμ, fc – models T1 and T2, respectively), the amount of angular momentum deposited by the accreted matter (fj model T3), and by assuming very high efficiency for the angular momentum transport (model T4).
All Figures
 |
Fig. 1. Time evolution of the mass-transfer rate (upper panel) and of the H- and He abundances in the transferred matter (lower panel) for the nonrotating model. The origin of the x-axis is fixed at the epoch when the sdB component filled its Roche lobe (Age0 = 185.08 Myr). |
| In the text | |
 |
Fig. 2. Evolution of selected physical properties of the nonrotating CO WD during the accretion phase of H-rich material. From top to bottom, we report: the luminosity of the H-burning shell (LH in solar units); the variation in the CO WD total mass defined as |
| In the text | |
 |
Fig. 3. Comparison of the abundances of selected isotopes involved in the CNO cycle for the nonrotating model at the onset of the H-flash in the 11th (solid line) and 12th (dashed line) cycles, respectively. |
| In the text | |
 |
Fig. 4. Time evolution of the H-burning shell luminosity during the first H-flash for the nonrotating and rotating models (red dashed and black solid lines, respectively). |
| In the text | |
 |
Fig. 5. Profiles of hydrogen abundance X(H) (upper panel) and angular velocity (lower panel) at various epochs during the first mass-transfer episode in the rotating model. The time after the onset of mass transfer corresponding to each line is reported in the plot. The x-axis is defined in such a way that the original WD surface (M = 0.75 M⊙) coincides with the origin. Lines a to e correspond to the evolution before the onset of the H-flash; line f corresponds to the epoch when flash-driven convection sets in; line g corresponds to the epoch when flash-driven convection attains its maximum extension. Dots connected by the heavy dashed line mark the position of the H-burning shell. |
| In the text | |
 |
Fig. 6. Time evolution of the WD total mass during the phase of H-rich mass accretion for the rotating model. Age0 is the epoch of RLOF by the sdB star. |
| In the text | |
 |
Fig. 7. Time-dependence of the He-burning luminosity (top panel), WD total mass (middle panel), and mass-transfer rate (lower panel, left y-scale) during the stage of He-rich-matter accretion. The two leftmost spikes in the upper panel show, for comparison, the He-burning luminosity during the last two (61th and 62nd) H-burning outbursts. The lower panel also presents the evolution of the abundances of 4He (solid cyan line), 12C (long dashed red line), and 16O (dashed blue line) as tracers of the chemical composition of the accreted matter (right y-scale). |
| In the text | |
 |
Fig. 8. Selected properties of the last computed structure in the rotating model. We report the abundance of 4He, 12C, and 16O in the upper panel (solid lines) and the ω and ωcr profiles in the lower panel (solid and dashed lines, respectively). For comparison, in the upper panel we report the abundances of the same isotopes in the initial 0.75 M⊙ WD model (dashed lines). |
| In the text | |
 |
Fig. 9. Abundances of isotopes up to samarium produced during the third He-flash episode in the rotating model relative to their solar value. The unstable isotopes have been allowed to decay to their stable isobars. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



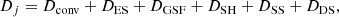
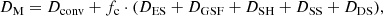
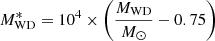
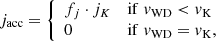
![$$ \begin{aligned} \tau _{\rm r}=\left[{\frac{2\pi }{25}\left(\frac{4}{3}\right)^8 \frac{G}{c}} \int _0^R \rho (r)\left(\frac{r\omega (r)}{c}\right)^6 dr\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2024/09/aa50008-24/aa50008-24-eq19.gif)