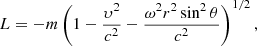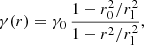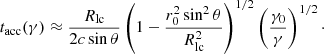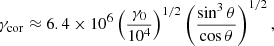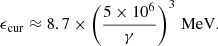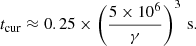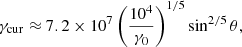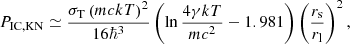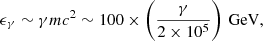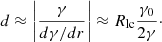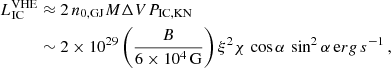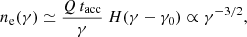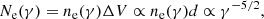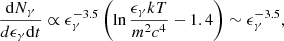EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 627 (July 2019) A&A, 627 (2019) A22 Full HTML
Free Access
Issue
A&A
Volume 627, July 2019
Article Number A22
Number of page(s) 5
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201935030
Published online 26 June 2019

© ESO 2019

1. Introduction

One of the most enigmatic high-energy astrophysical objects is the Vela pulsar (PSR B0833−45). Located at a distance of dl ≃ 300 pc (Caraveo et al. 2001) the Vela pulsar is a young pulsar with a period of rotation of P = 89 ms, an estimated age of t = P/(2Ṗ) ≃ 1.1 × 104 yr (Reichley et al. 1970), and a spin-down luminosity of the order of Ė ≃ 1037 erg s−1 (Manchester et al. 2005; Mignani et al. 2017).

Pulsed gamma-ray emission from the MeV to GeV domain has been reported by a variety of instruments early on, from SAS-2 and COS B to CGRO, AGILE, and Fermi-LAT (Thompson et al. 1975, 1977; Kanbach 1980; Kanbach et al. 1994; Pellizzoni 2009; Abdo et al. 2009). At high γ-ray energies its light curve is found to exhibit two prominent peaks, P1 and P2, which are separated in phase by 0.43 and connected by a so-called P3 bridge.

In particular, while Fermi-LAT initially detected high-energy (HE; > 100 MeV) emission from the Vela pulsar up to ∼10 GeV, further observations have increased this to 20 GeV (Abdo et al. 2010) and 50 GeV (Leung et al. 2014), respectively. At very high energies (VHE; > 100 GeV) on the other hand, the Vela pulsar has not been seen in early H.E.S.S. observations with an energy threshold of 170 GeV, imposing constraints on a possible inverse Compton (IC) contribution from outer gap models (Aharonian et al. 2007). New results based on H.E.S.S. II (CT5-only) observations in the sub-20 GeV to 100 GeV range have recently been reported (Abdalla et al. 2018), with pulsed γ-rays from the strong P2 peak (phase interval 0.5−0.6) detected at a significance level of 15σ. The results for P2 confirm the sub-exponential cutoff shape found at lower energies with Fermi-LAT and support the presence of emission above 100 GeV. Perhaps most intriguingly, there are converging indications for the emergence of a hard spectral component above 50 GeV in the leading wing of the second peak, LW2 (phase interval 0.45−0.5), which possibly extends beyond 100 GeV. A simple power law fit of the H.E.S.S. II data for LW2 with two different energy thresholds, CI and CII, yields comparable photon indices of Γ = 3.72 ± 0.51 (CI) and Γ = 3.48 ± 0.21 (CII), respectively (Abdalla et al. 2018). Here CI and CII refer to different analysis cuts optimized so as to yield a large effective area in the 10−20 GeV range, with the threshold for CI approaching 5−10 GeV depending on zenith angles, and the threshold being approximately two times higher for CII. If the inferred hardening were to be confirmed by further observations it would point to the presence of a second and new emission component.

Motivated by these indications we study the possible generation of high- and very-high-energy gamma-rays in the context of magneto-centrifugal acceleration (e.g., Machabeli & Rogava 1994; Gangadhara 1996; Osmanov & Rieger 2009, 2017; Bogovalov 2014). As the magnetic field in the magnetospheres of pulsars is extremely high, charged particles will quickly transit to the ground Landau level and start sliding along the magnetic field lines. Since the field is co-rotating with the star, the particle dynamics is likely to be highly influenced by the effects of centrifugal acceleration. This particularly applies for particles approaching the light cylinder (LC) surface.

The possible relevance of this for the origin of the emission in the Crab pulsar was studied early on by Gold (1969), who suggested that this could facilitate an efficient energy transfer from the rotator into the kinetic energy of plasma particles. Using an idealized model for centrifugal acceleration, Machabeli & Rogava (1994) later showed that incorporation of (special) relativistic effects can lead to a radial deceleration of the particle motion, resembling features known from general relativity (Abramowicz & Prasanna 1990).

As a convenient analogy, centrifugal particle acceleration has since been studied in a variety of contexts, for example for predicting the location, for frequency mapping in pulsars (Gangadhara 1996; Thomas & Gangadhara 2007), or for investigating the origin of the gamma-ray emission from the rotating jet base in active galactic nuclei (AGNs; e.g., Gangadhara & Lesch 1997; Rieger & Mannheim 2000; Xu 2002; Osmanov et al. 2007, 2014; Ghisellini et al. 2009). In particular, by applying magneto-centrifugal acceleration to Crab-like pulsars it was found that on approaching the LC area, electrons could achieve Lorentz factors up to γ ∼ 107 (Osmanov & Rieger 2009; Bogovalov 2014), suggesting that IC scattering in the magnetosphere of the Crab Pulsar could generate detectable pulsed VHE emission in the TeV band. A subsequent evaluation of the spectral characteristics (Osmanov & Rieger 2017) showed that they are in good agreement with the observational data.

The present paper focuses on an application to the Vela pulsar, assessing the potential of magneto-centrifugal acceleration to generate detectable VHE gamma-ray emission. As we show in Sect. 2, IC up-scattering of thermal soft photons can indeed facilitate the production of pulsed VHE emission at levels compatible with current experimental findings. This provides interesting insight into pulsar physics.

2. Rotationally driven γ-ray emission

For simplicity we consider a single particle approach and assume that the magnetospheric electrons follow the co-rotating magnetic field lines. In particular, the Vela pulsar is characterized by P = 0.089 s and dP/dt ≈ 1.25 × 10−13 s−1. This leads to a strong magnetic induction close to the surface of the star of 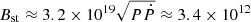B st ≈ 3.2 × 10 19 P P ˙ ≈ 3.4 × 10 12 $ B_{\mathrm{st}}\approx 3.2\times 10^{19} \sqrt{P\dot{P}} \approx 3.4\times 10^{12} $ Gauss. Therefore, plasma particles will follow the field lines, accelerating along them. For a single relativistic massive particle one can define the Lagrangian

L = − m ( 1 − υ 2 c 2 − ω 2 r 2 sin 2 θ c 2 ) 1 / 2 , $$ \begin{aligned} L = -m\left(1-\frac{\upsilon ^2}{c^2}-\frac{\omega ^2r^2\sin ^2\theta }{c^2}\right)^{1/2}, \end{aligned} $$(1)

where m is the rest mass of the particle, υ = ṙ, r, which is the radial coordinate along the straight magnetic field line inclined by θ with respect to the rotation axis, and ω = 2π/P, which is the angular velocity of rotation. Since L does not depend explicitly on time, the corresponding Hamiltonian, 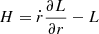H = r ˙ ∂ L ∂ r − L $ H = \dot{r}\frac{\partial L}{\partial r}-L $, is a constant of motion, resulting in the following expression for the particle Lorentz factor (Osmanov & Rieger 2017)

γ ( r ) = γ 0 1 − r 0 2 / r l 2 1 − r 2 / r l 2 , $$ \begin{aligned} \gamma (r) = \gamma _0\,\frac{1-r_0^2/r_{\rm l}^2}{1-r^2/r_{\rm l}^2}, \end{aligned} $$(2)

where r0 and γ0 denote the initial radial coordinate and Lorentz factor, respectively, rl = Rlc/sinθ, and Rlc = c/ω = 4.25 × 108 cm, which is the LC radius. As evident from Eq. (2), on approaching the LC area the Lorentz factor asymptotically increases, leading to a very efficient acceleration process. Close to the LC zone the corresponding acceleration timescale, 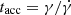t acc = γ / γ ˙ $ t_{\mathrm{acc}}=\gamma/\dot{\gamma} $, behaves as (Osmanov & Rieger 2017)

t acc ( γ ) ≈ R lc 2 c sin θ ( 1 − r 0 2 sin 2 θ R lc 2 ) 1 / 2 ( γ 0 γ ) 1 / 2 · $$ \begin{aligned} t_{\rm acc}(\gamma )\approx \frac{R_{\rm lc}}{2c\sin \theta }\left(1-\frac{r_0^2\sin ^2\theta }{R_{\rm lc}^2}\right)^{1/2} \left(\frac{\gamma _0}{\gamma }\right)^{1/2}\cdot \end{aligned} $$(3)

This timescale is a continuously decreasing function of γ, and since the latter formally tends to infinity on the LC, tacc tends to zero, indicating an extremely efficient process.

It is clear that acceleration cannot be a continuous process and must be terminated. As already mentioned, centrifugal acceleration is provided by the frozen-in condition of magnetospheric plasma particles. This condition will only last until the plasma energy density, nGJ(r)γmc2, becomes comparable to the energy density in the magnetic field B2/8π, where nGJ(r) = ω ⋅ B M(2πec)−1 = M n0, GJ, which is the Goldreich-Julian particle number density (Goldreich & Julian 1969), taking account of the multiplicity factor, 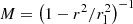M= ( 1− r 2 / r l 2 ) −1 $ M = {\left( {1 - {r^2}/r_{\rm{l}}^2} \right)^{ - 1}} $. Assuming a dipolar magnetic field structure, B(rl)≃Bst × (rs/rl)3, with rs = 11.5 km (e.g., Li et al. 2016), the co-rotation condition imposes a constraint on the maximum attainable electron Lorentz factor of

γ cor ≈ 6.4 × 10 6 ( γ 0 10 4 ) 1 / 2 ( sin 3 θ cos θ ) 1 / 2 , $$ \begin{aligned} \gamma _{\rm cor}\approx 6.4\times 10^6\left(\frac{\gamma _0}{10^4}\right)^{1/2}\left(\frac{\sin ^3\theta }{\cos \theta }\right)^{1/2}, \end{aligned} $$(4)

taking Lorentz factors γ0 ∼ 104 for the secondaries (Daugherty 1982) as reference value. Similar to the emission model proposed by Gold (1969) electrons close to the LC area co-rotate with almost Rlc, suggesting that curvature γ-ray emission might be of significance. The corresponding curvature photon energy 3hcγ3/(4πRlc) is in the range

ϵ cur ≈ 8.7 × ( 5 × 10 6 γ ) 3 MeV . $$ \begin{aligned} \epsilon _{\rm cur}\approx 8.7\times \left(\frac{5\times 10^6}{\gamma }\right)^3\,\mathrm{MeV} . \end{aligned} $$(5)

Curvature emission could therefore in principle lead to a pulsed γ-ray contribution in the COMPTEL (1−10) MeV regime. It is clear that curvature emission also introduces some constraints on the maximum attainable energies. The cooling timescale due to curvature emission, tcur = γmc2/Pcur where 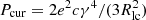P cur =2 e 2 c γ 4 /(3 R lc 2 ) $ {P_{{\rm{cur}}}} = 2{e^2}c{\gamma ^4}/(3R_{{\rm{lc}}}^2) $ is the single particle power (Ochelkov & Usov 1980), becomes

t cur ≈ 0.25 × ( 5 × 10 6 γ ) 3 s . $$ \begin{aligned} t_{\rm cur}\approx 0.25\times \left(\frac{5\times 10^6}{\gamma }\right)^3\,\mathrm{s} . \end{aligned} $$(6)

Acceleration would therefore formally be balanced by curvature cooling at

γ cur ≈ 7.2 × 10 7 ( 10 4 γ 0 ) 1 / 5 sin 2 / 5 θ , $$ \begin{aligned} \gamma _{\rm cur}\approx 7.2\times 10^7\left(\frac{10^4}{\gamma _0}\right)^{1/5}\sin ^{2/5}\theta , \end{aligned} $$(7)

assuming r0 ≪ Rlc. Hence the co-rotation limit (see Eq. (4)) is generally expected to impose the most stringent constraints; see also Fig. 1 for illustration.

thumbnail Fig. 1.

Characteristic timescales for the Vela pulsar as a function of particle Lorentz factor: centrifugal acceleration timescale (pink), curvature cooling timescale (green), and IC cooling timescale (blue). The red vertical line represents the upper limit imposed by γcor. Acceleration here is essentially limited by γcor. The set of parameters employed is γ0 = 104, γcor = 6 × 106 and sinθ ∼ 1.

The above analysis suggests that rotationally driven curvature emission could lead to a non-negligible γ-ray contribution at ∼(1−10) MeV energies that could help to alleviate tensions in for example outer-gap spectral energy distribution (SED) modeling of the Vela pulsar (e.g., Takata et al. 2004). One can roughly estimate the possible curvature megaelectronvolt contribution from Lcur ≃ 2 n0, GJMΔVPcur (see also Eqs. (10) and (11)), yielding Lcur ∼ 1031 (B/6 × 104G) (γ/4 × 106)4 ξ2χ cosα erg s−1. In the COMPTEL regime the flux is of the order of FCOM ∼ 10−10 erg s−1 cm−2 (Bennett 1993), translating into an isotropic-equivalent luminosity 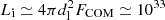L i ≃4π d l 2 F COM ≃ 10 33 $ {L_{\rm{i}}} \simeq 4\pi d_{\rm{l}}^2{F_{{\rm{COM}}}} \simeq {10^{33}} $ erg s−1. If one assumes that focusing in this energy band is of the same order as in the teraelectronvolt regime, 0.25 sr (see the estimates below), the inferred luminosity L ∼ Li(0.25/4π) ∼ 1031 erg s−1 would be very close to Lcur derived above.

On the other hand, as shown below, rotationally driven IC scattering of thermal soft photons from the surface of the neutron star can lead to a VHE contribution in the ∼(0.1−1) TeV regime. This is different from typical outer gap models, which would predict a rising IC contribution peaking at ∼10 TeV (e.g., Aharonian & Bogovalov 2003; Takata et al. 2006).

The surface temperature of the Vela pulsar is below the standard cooling curve and probably in the range T ≃ (6−8) × 105 K (Page et al. 1996; Mori et al. 2004; Weisskopf et al. 2011). We take T = 7 × 105 K as a reference value in the following. The thermal photons thus have characteristic peak energies of the order of ϵph ≈ 2.8 kT ∼ 0.2 keV, where k is the Boltzmann constant. If these photons encounter centrifugally accelerated electrons, the former will inevitably gain energy. Since the ratio γϵph/(mc2) exceeds unity for electron Lorentz factors exceeding γ ≈ 2.3 × 103, IC up-scattering to the VHE regime essentially occurs in the Klein-Nishina (KN) regime where the corresponding single-particle IC power can be suitably approximated by (e.g., Blumenthal & Gould 1970)

P IC , KN ≃ σ T ( m c k T ) 2 16 ħ 3 ( ln 4 γ k T m c 2 − 1.981 ) ( r s r l ) 2 , $$ \begin{aligned} P_{\rm IC,KN}\simeq \frac{\sigma _{\rm T}\left(mckT\right)^2}{16\hbar ^3}\left(\ln \frac{4\gamma kT}{mc^2}-1.981\right)\left(\frac{r_{\rm s}}{r_{\rm l}}\right)^2, \end{aligned} $$(8)

with σT being the Thomson cross section and ℏ the Planck constant. We use the general expression for the electron-loss rate derived in Aharonian & Atoyan (1981) to evaluate the corresponding IC cooling timescale tIC = γmc2/PIC. The result is shown in Fig. 1 together with the timescales for curvature losses tcurv and particle acceleration tacc.

As evident from this figure, IC scattering does not impose any constraints on the maximum attainable energies of electrons, the latter essentially being determined by the co-rotation limit.

Despite the negligible role of IC in limiting maximum attainable energies, up-scattering of thermal photons could lead to detectable γ-ray emission in the VHE energy regime (cf. Bogovalov & Kotov 1992). Scattered (KN) photon energies,

ϵ γ ∼ γ m c 2 ∼ 100 × ( γ 2 × 10 5 ) GeV , $$ \begin{aligned} \epsilon _{\gamma } \sim \gamma mc^2\sim 100\times \left(\frac{\gamma }{2\times 10^5}\right)\, \mathrm{GeV} , \end{aligned} $$(9)

may in principle extend into the teraelectronvolt regime (for γ ≤ γcor), though expected teraelectronvolt flux levels could be too low to allow for a significant detection. The latest H.E.S.S. observations of the Vela pulsar in fact provide indications for γ-ray emission above 100 GeV (Abdalla et al. 2018). For an order-of-magnitude estimate of the intrinsic rotationally driven IC-VHE (100 GeV) luminosity we take into account the fact that the process of efficient acceleration and radiation production occurs in a thin shell close to the LC (Osmanov & Rieger 2009) whose characteristic width is given by

d ≈ | γ d γ / d r | ≈ R lc γ 0 2 γ · $$ \begin{aligned} d\approx \left|\frac{\gamma }{d\gamma /dr}\right| \approx R_{\rm lc}\frac{\gamma _0}{2\gamma }\cdot \end{aligned} $$(10)

Multiplying the corresponding particle number with the single IC power PIC, KN, Eq. (8), one obtains

L IC VHE ≈ 2 n 0 , GJ M Δ V P IC , KN ∼ 2 × 10 29 ( B 6 × 10 4 G ) ξ 2 χ cos α sin 2 α e r g s − 1 , $$ \begin{aligned} L_{\rm IC}^\mathrm{VHE}&\approx 2\, n_{\rm 0,GJ} M \Delta V P_{\rm IC, KN}\nonumber \\ &\sim 2 \times 10^{29} \left(\frac{B}{6 \times 10^4\,\mathrm{G} }\right) \xi ^2 \chi \,\cos \alpha \,\sin ^2\alpha \,\mathrm erg\,s^{-1} \,, \nonumber \\ \end{aligned} $$(11)

using M ∼ γcor/γ0 and γcor/γ = 30, and using ΔV ≈ χ(δl)2 d to denote the corresponding volume; χ ≲ 1 is a dimensionless factor depending on the topology of magnetic field lines, δl ∼ Rlcθ is the azimuthal length scale involved in this process, and θ ∼ ΩP (ξ/10) = 2π (ξ/10) is the corresponding angle, where (ξ/10)P is an approximate value for the pulse duration (ξ ≤ 10). Obviously, 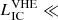L IC VHE ≪ $ L_{\mathrm{IC}}^{\mathrm{VHE}} \ll $ the spin-down luminosity Ė.

A rough estimate for the corresponding power in electrons, Ėe, can be obtained from Ėe = ṄICγICmec2. Here, ṄIC is the total rate of IC emitting electrons, 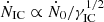N ˙ IC ∝ N ˙ 0 / γ IC 1 / 2 $ \dot{N}_{\mathrm{IC}} \propto \dot{N}_0/\gamma_{\mathrm{IC}}^{1/2} $ (cf. Eq. (12)), and Ṅ0 = n0,GJ M dA ṙ where 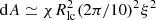dA≃χ R lc 2 (2π/10) 2 ξ 2 $ {\rm{d}}A \simeq \chi {\mkern 1mu} R_{{\rm{lc}}}^2{\mkern 1mu} {(2\pi /10)^2}{\mkern 1mu} {\xi ^2} $ using the notation above. Assuming M ≃ γcor/γ0 one finds Ėe ∼ 1032 erg s−1, again much below the spin-down luminosity Ė ≃ 1037 erg s−1 of the Vela pulsar. In principle, polar cap heating by secondary particles flowing back to the neutron star could lead to some excess thermal emission and thereby modify the IC emission. As shown by Harding & Muslimov (2001) however, this effects is expected to be negligible for Vela-type pulsars.

The recent H.E.S.S. analysis suggests isotropic-equivalent VHE (100 GeV) flux levels of the order of Li ∼ 1031 erg s−1. This would indicate that the VHE emission of the Vela pulsar is collimated with corresponding emission cones confined to solid-angle areas of 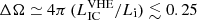Δ Ω ≃ 4 π ( L IC VHE / L i ) ≲ 0.25 $ \Delta\Omega \simeq 4\pi \, (L_{\mathrm{IC}}^{\mathrm{VHE}}/L_{\mathrm{i}}) \lesssim 0.25 $ sr.

The indications for the emergence of a hard spectral component above 50 GeV in LW2 are particularly interesting, alluding to the possibility that VHE emission well beyond 100 GeV may be present in the Vela pulsar. To investigate the spectral characteristics of rotationally driven VHE in more detail, we follow the description developed in Rieger & Aharonian (2008). Accordingly, assuming electrons are injected at a constant rate, Q, into the region of centrifugal acceleration, the differential particle density distribution along the magnetic field lines can be written as

n e ( γ ) ≃ Q t acc γ H ( γ − γ 0 ) ∝ γ − 3 / 2 , $$ \begin{aligned} n_{\rm e}(\gamma ) \simeq \frac{Q\,t_{\rm acc}}{\gamma }~ H(\gamma -\gamma _0) \propto \gamma ^{-3/2}, \end{aligned} $$(12)

where the behavior tacc ≃ γ−1/2 (see Eq. (3)) has been used. The (effective) differential number of electrons, 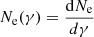N e ( γ ) = d N e d γ $ N_{\mathrm{e}}(\gamma) = \frac{\mathrm{d}N_{\mathrm{e}}}{d\gamma} $, then becomes (Osmanov & Rieger 2017)

N e ( γ ) = n e ( γ ) Δ V ∝ n e ( γ ) d ∝ γ − 5 / 2 , $$ \begin{aligned} N_{\rm e}(\gamma ) = n_{\rm e}(\gamma )\Delta V\propto n_{\rm e}(\gamma )d\propto \gamma ^{-5/2}, \end{aligned} $$(13)

taking into account that higher-energy particles accumulate in a narrower region close to the LC, with width scaling as d ∝ 1/γ, Eq. (10). Inverse Compton up-scattering of thermal soft photons in the KN regime then produces a photon spectrum (Blumenthal & Gould 1970)

d N γ d ϵ γ d t ∝ ϵ γ − 3.5 ( ln ϵ γ k T m 2 c 4 − 1.4 ) ∼ ϵ γ − 3.5 , $$ \begin{aligned} \frac{\mathrm{d}N_{\gamma }}{d\epsilon _{\gamma } \mathrm{d}t} \propto \epsilon _{\gamma }^{-3.5} \left(\ln \frac{\epsilon _{\gamma } kT}{m^2c^4}-1.4\right) \sim \epsilon _\gamma ^{-3.5} ,\end{aligned} $$(14)

with a VHE photon index compatible with the ones inferred for LW2, that is, Γ = 3.72 ± 0.51 (CI) and Γ = 3.48 ± 0.21 (CII).

Figure 2 shows the γ-ray SED for the Vela pulsar along with a characteristic model calculation of the expected IC γ-ray contribution using NAIMA (Zabalza 2015). The calculations assume (quasi-isotropic) up-scattering of thermal photons (T = 7 × 105 K) close to LC by an exponential cut-off power-law electron distribution, n(γ)∝γ−2.5 exp(−[γ/γc]2), with γc = 6 × 106 and γ0 ≃ 104. The Fermi-LAT data for P2 and LW2 are illustrated by their best-fit (exponential cutoff power-law model) representations (green and red curve, respectively), as detailed in Abdalla et al. (2018).

thumbnail Fig. 2.

SED representation with best fits to the phase-resolved spectra based on ∼8 years of Fermi-LAT data (green and red lines) (Abdalla et al. 2018), along with a characteristic model calculation for the rotationally driven thermal IC contribution at VHE energies (black curve). The blue-shaded area represents results from power-law fits of recent H.E.S.S. II data in the range 10−110 GeV for P2 (Abdalla et al. 2018). Orange-shaded area indicates the range of H.E.S.S. II power-law indices inferred for LW2 (CII cuts). Blue upper limits denote early H.E.S.S. I constraints above 170 GeV (Aharonian et al. 2007). In this case rotationally driven IC γ-ray emission below 100 GeV may become detectable for LW2 but not P2.

In a similar way to in other LC models (e.g., Cheng et al. 1986; Bogovalov & Kotov 1992) we assume that particles leaving the acceleration zone no longer make a significant contribution to the pulsed VHE emission. This could be related to electrons quickly cooling out of the VHE window due to increased synchro-curvature losses in bent fields, along with a reduced focusing of the resultant emission. In particular, particle escaping from the acceleration zone and experiencing non-zero pitch angles (e.g., due to excitation of instabilities close to LC; Machabeli & Osmanov 2010) would immediately cool down on characteristic length scales 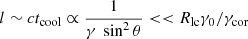l ∼ c t cool ∝ 1 γ sin 2 θ < < R lc γ 0 / γ cor $ l \sim c t_{\mathrm{cool}} \propto \frac{1}{\gamma~\sin^2\theta} < < R_{\mathrm{lc}} \gamma_0/\gamma_{\mathrm{cor}} $ for a wide range of angles. In the present model one can roughly estimate the possible synchrotron contribution below a few gigaelectronvolts via Lsyn(γ)∼NPsyn ∼ 2 N [γ2σTc (B2/8π)sin2 θ], where N ∼ ṄIC tcool, yielding Lsyn ∼ 1032 erg s−1. On the other hand, for a more detailed spectral modeling, quasi-linear diffusion and the maintenance of pitch angles would have to be incorporated (Machabeli & Osmanov 2010); this is however beyond the scope of the current paper.

As can be seen in Fig. 2, rotationally driven IC γ-ray emission may reach into the teraelectronvolt regime, but become apparent below ∼100 GeV only for LW2. These results motivate detailed VHE studies with higher sensitivity, as will become possible with CTA South (Burtovoi et al. 2017), in order to better characterize the γ-ray emission above ∼100 GeV. If confirmed by further observations, this would highlight the relevance of incorporating rotationally driven effects for our understanding of the γ-ray emission in young pulsars.

Taking account of the angular dependency in Eq. (4) suggests that rotationally driven IC emission could well yield VHE emission up to several teraelectronvolts. When compared to the Crab pulsar, where rotationally driven curvature emission can lead to a detectable gigaelectronvolt contribution (Osmanov & Rieger 2017), supporting a smoother GeV-VHE connection, as indeed observed (Ansoldi et al. 2016), rotationally driven curvature emission in the Vela pulsar peaks at megaelectronvolt energies only (Eq. (5)); rotationally driven IC VHE component in the Vela pulsar thus appears as a separate, second and new component.

We note that rotational acceleration in principle predicts a decrease in individual pulse width with increasing energy. Neglecting local changes in the field topology, the observed pulse duration is roughly proportional to 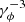γ ϕ − 3 $ \gamma_{\phi}^{-3} $ (Rybicki & Lightman 2007), where 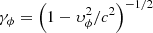γ ϕ = ( 1− υ ϕ 2 / c 2 ) −1/2 $ {\gamma _\phi } = {\left( {1 - \upsilon _\phi ^2/{c^2}} \right)^{ - 1/2}} $ is the azimuthal Lorentz factor. Taking into account Eq. (2) we approximately have γϕ ≃ (γ/γ0)1/2. Hence, for VHE emission with γ ∼ 106 and γ0 ∼ 104 for example, the characteristic observed pulse width could be as small as ∼10−3. This seems interesting when compared with the inferred Gaussian width of ∼0.002 for the additional γ-ray (phasogram) component in the range (10−80) GeV around P2 (Abdalla et al. 2018).

3. Conclusion

The generation of VHE γ-rays in fast pulsars is still an open issue (e.g., Bednarek 2012; Mochol & Pétri 2015; Hirotani 2015; Osmanov & Rieger 2017; Harding et al. 2018). The latest H.E.S.S. observations of the Vela pulsar in the sub-20 GeV to 100 GeV regime have now revealed pulsed γ-rays from its P2 peak at high significance, and together with an updated analysis of Fermi-LAT data suggest the emergence of a second, new hard VHE component above 50 GeV in the leading wing (LW2) of P2 (Abdalla et al. 2018).

Motivated by this, we analyzed the potential role of centrifugal acceleration in the generation of pulsed VHE emission in the magnetosphere of the Vela pulsar. Our results show that IC up-scattering of thermal photons by rotationally accelerated electrons close to the light cylinder could lead to a hard (yet falling) power-law-like VHE contribution that reaches into the teraelectronvolt regime and in the case of LW2 could become apparent above ∼50 GeV. Future observations with increased sensitivity will be important to better probe its spectral characteristics and to eventually allow a clear identification. Along with the Crab pulsar (Osmanov & Rieger 2017), this could be the second case where rotationally driven γ-ray emission turns out to be important to fully understand the VHE emission in young pulsars.

Acknowledgments

Useful comments by the referee are gratefully acknowledged. We also thank S. Bogovalov and D. Khangulyan for discussions. The research of ZO was supported by a German DAAD scholarship within the program Research Stays for University Academics and Scientists, 2018, and was partially supported by Shota Rustaveli National Science Foundation Grant NFR17-587. ZO also acknowledges hospitality of the MPIK and the group of F. Aharonian during his visit in 2018. FRM acknowledges financial support by a DFG Heisenberg Fellowship under RI 1187/6-1.

References

  1. Abdalla, H., Aharonian, F., Ait Benkhali, F., et al. 2018, A&A, 620, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 696, 1084 [NASA ADS] [CrossRef] [Google Scholar]
  3. Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJ, 713, 154 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abramowicz, M. A., & Prasanna, A. R. 1990, MNRAS, 245, 729 [NASA ADS] [Google Scholar]
  5. Aharonian, F. A., & Atoyan, A. M. 1981, Ap&SS, 79, 321 [NASA ADS] [Google Scholar]
  6. Aharonian, F. A., & Bogovalov, S. V. 2003, Nature, 8, 85 [Google Scholar]
  7. Aharonian, F., Akhperjanian, A. G., Bazer-Bachi, A. R., et al. 2007, A&A, 466, 543 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Ansoldi, S., et al. (MAGIC Collaboration) 2016, A&A, 585, 133 [Google Scholar]
  9. Bednarek, W. 2012, MNRAS, 424, 2079 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bennett, K., et al. 1993, A&AS, 97, 317 [NASA ADS] [Google Scholar]
  11. Bhat, P. N., et al. 1980, A&A, 81, 3 [NASA ADS] [Google Scholar]
  12. Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bogovalov, S. V. 2014, MNRAS, 443, 2197 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bogovalov, S. V., & Kotov, I. D. 1992, MNRAS, 257, 537 [NASA ADS] [CrossRef] [Google Scholar]
  15. Burtovoi, A., Saito, T. Y., Zampieri, L., & Hassan, T. 2017, MNRAS, 471, 431 [NASA ADS] [CrossRef] [Google Scholar]
  16. Caraveo, P. A., De Luca, A., Mignani, R. P., & Bignami, G. F. 2001, ApJ, 561, 930 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cheng, K. S., Ho, C., & Ruderman, M. 1986, ApJ, 300, 522 [NASA ADS] [CrossRef] [Google Scholar]
  18. Daugherty, J. K., & Harding, A. K. 1982, ApJ, 252, 337 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gangadhara, R. T. 1996, A&A, 314, 853 [NASA ADS] [Google Scholar]
  20. Gangadhara, R. T., & Lesch, H. 1997, A&A, 323, L45 [NASA ADS] [Google Scholar]
  21. Ghisellini, G., Tavecchio, F., Bodo, G., & Celotti, A. 2009, MNRAS, 393, L16 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gold, T. 1969, Nature, 221, 25 [NASA ADS] [CrossRef] [Google Scholar]
  23. Goldreich, P., & Julian, W. H. 1969, ApJ, 157, 869 [NASA ADS] [CrossRef] [Google Scholar]
  24. Harding, A. K., & Muslimov, A. G. 2001, ApJ, 556, 987 [NASA ADS] [CrossRef] [Google Scholar]
  25. Harding, A. K., Kalapotharakos, C., Barnard, M., & Venter, C. 2018, ApJ, 869, L18 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hirotani, K. 2015, ApJ, 798, L40 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kanbach, G., Arzoumanian, Z., Bertsch, D. L., et al. 1994, A&A, 289, 855 [NASA ADS] [Google Scholar]
  28. Kanbach, G., et al. 1980, A&A, 90, 163 [NASA ADS] [Google Scholar]
  29. Leung, G. C. K., Takata, J., Ng, C. W., et al. 2014, ApJ, 797, L13 [NASA ADS] [CrossRef] [Google Scholar]
  30. Li, A., Dong, J. M., Wang, J. B., & Xu, R. X. 2016, ApJS, 223, 16 [NASA ADS] [CrossRef] [Google Scholar]
  31. Machabeli, G. Z., & Rogava, A. D. 1994, Phys. Rev. A, 50, 98 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  32. Machabeli, G., & Osmanov, Z. 2010, ApJ, 709, 547 [NASA ADS] [CrossRef] [Google Scholar]
  33. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mignani, R. P., Paladino, R., Rudak, B., et al. 2017, ApJ, 851, L10 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mori, K., Hailey, C. J., Paerels, F., & Zane, S. 2004, Adv. Space Res., 33, 503 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mochol, I., & Pétri, J. 2015, MNRAS, 449, L51 [NASA ADS] [CrossRef] [Google Scholar]
  37. Ochelkov, Yu P., & Usov, V. V. 1980, Ap&SS, 69, 439 [NASA ADS] [CrossRef] [Google Scholar]
  38. Osmanov, Z., & Rieger, F. M. 2009, A&A, 502, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Osmanov, Z., & Rieger, F. M. 2017, MNRAS, 464, 1347 [NASA ADS] [CrossRef] [Google Scholar]
  40. Osmanov, Z., Rogava, A. S., & Bodo, G. 2007, A&A, 470, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Osmanov, Z., Mahajan, S., Machabeli, G., & Chkheidze, N. 2014, MNRAS, 445, 4155 [NASA ADS] [CrossRef] [Google Scholar]
  42. Page, D., Shibanov, Y. A., & Zavlin, V. E. 1996, Roentgenstrahlung from the Universe, 173 [Google Scholar]
  43. Pellizzoni, A., et al. 2009, ApJ, 691, 1618 [NASA ADS] [CrossRef] [Google Scholar]
  44. Reichley, P. E., Downs, G. S., & Morris, G. A. 1970, ApJ, 159, L35 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rieger, F. M., & Mannheim, K. 2000, A&A, 353, 473 [NASA ADS] [Google Scholar]
  46. Rieger, F. M., & Aharonian, F. 2008, A&A, 479, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Rybicki, G. B., & Lightman, A. P. 2007, Radiative Processes in Astrophysics (Weinheim: Wiley-VCH) [Google Scholar]
  48. Takata, J., Shibata, S., & Hirotani, K. 2004, MNRAS, 348, 241 [NASA ADS] [CrossRef] [Google Scholar]
  49. Takata, J., Shibata, S., Hirotani, K., & Chang, H.-K. 2006, MNRAS, 366, 1310 [NASA ADS] [CrossRef] [Google Scholar]
  50. Thomas, R. M. C., & Gangadhara, R. T. 2007, A&A, 467, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Thompson, D. J., Fichtel, C. E., Kniffen, P. A., et al. 1975, ApJ, 200, L79 [NASA ADS] [CrossRef] [Google Scholar]
  52. Thompson, D. J., Fichtel, C. E., Kniien, D. A., et al. 1977, ApJ, 214, L17 [NASA ADS] [CrossRef] [Google Scholar]
  53. Weisskopf, M. C., Tennant, A. F., Yakovlev, D. G., et al. 2011, ApJ, 743, 139 [NASA ADS] [CrossRef] [Google Scholar]
  54. Xu, Y. D. 2002, A&A, 381, 357 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Zabalza, V. 2015, 34th Int. Cosmic Ray Conf. (ICRC2015), 34, 922 [Google Scholar]

All Figures

thumbnail Fig. 1.

Characteristic timescales for the Vela pulsar as a function of particle Lorentz factor: centrifugal acceleration timescale (pink), curvature cooling timescale (green), and IC cooling timescale (blue). The red vertical line represents the upper limit imposed by γcor. Acceleration here is essentially limited by γcor. The set of parameters employed is γ0 = 104, γcor = 6 × 106 and sinθ ∼ 1.
In the text
thumbnail Fig. 2.

SED representation with best fits to the phase-resolved spectra based on ∼8 years of Fermi-LAT data (green and red lines) (Abdalla et al. 2018), along with a characteristic model calculation for the rotationally driven thermal IC contribution at VHE energies (black curve). The blue-shaded area represents results from power-law fits of recent H.E.S.S. II data in the range 10−110 GeV for P2 (Abdalla et al. 2018). Orange-shaded area indicates the range of H.E.S.S. II power-law indices inferred for LW2 (CII cuts). Blue upper limits denote early H.E.S.S. I constraints above 170 GeV (Aharonian et al. 2007). In this case rotationally driven IC γ-ray emission below 100 GeV may become detectable for LW2 but not P2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.