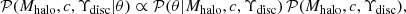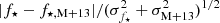| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A56 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935553 | |
| Published online | 12 June 2019 | |
Peak star formation efficiency and no missing baryons in massive spirals
1
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
2
Université de Strasbourg, CNRS UMR 7550, Observatoire astronomique de Strasbourg, 11 rue de l’Université, 67000 Strasbourg, France
e-mail: lorenzo.posti@astro.unistra.fr
3
ASTRON, Netherlands Institute for Radio Astronomy, Oude Hoogeveensedijk 4, 7991 PD Dwingeloo, The Netherlands
Received:
26
March
2019
Accepted:
30
April
2019
It is commonly believed that galaxies use, throughout Hubble time, a very small fraction of the baryons associated with their dark matter halos to form stars. This so-called low star formation efficiency f⋆ ≡ M⋆/fbMhalo, where fb ≡ Ωb/Ωc is the cosmological baryon fraction, is expected to reach its peak at nearly L* (at efficiency ≈20%) and decline steeply at lower and higher masses. We have tested this using a sample of nearby star-forming galaxies, from dwarfs (M⋆ ≃ 107 M⊙) to high-mass spirals (M⋆ ≃ 1011 M⊙) with HI rotation curves and 3.6 μm photometry. We fit the observed rotation curves with a Bayesian approach by varying three parameters, stellar mass-to-light ratio Υ⋆, halo concentration c, and mass Mhalo. We found two surprising results: (1) the star formation efficiency is a monotonically increasing function of M⋆ with no sign of a decline at high masses, and (2) the most massive spirals (M⋆ ≃ 1−3 × 1011 M⊙) have f⋆ ≈ 0.3−1, i.e. they have turned nearly all the baryons associated with their halos into stars. These results imply that the most efficient galaxies at forming stars are massive spirals (not L* galaxies); they reach nearly 100% efficiency, and thus once both their cold and hot gas is considered in the baryon budget, they have virtually no missing baryons. Moreover, there is no evidence of mass quenching of the star formation occurring in galaxies up to halo masses of a few × 1012 M⊙.
Key words: galaxies: kinematics and dynamics / galaxies: spiral / galaxies: structure / galaxies: formation
© L. Posti et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In our Universe, only about one-sixth of the total matter is baryonic, while the rest is widely thought to be in form of non-baryonic, collisionless, non-relativistic dark matter (e.g. Planck Collaboration VI 2018). In the so-called standard Λ cold dark matter (ΛCDM) paradigm, galaxies form within extended halos of dark matter that were able to grow enough to become gravitationally bound (e.g. White & Rees 1978). In this scenario it is then reasonable to expect that the amount of baryons present in galaxies today is roughly a fraction fb ≡ Ωb/Ωc = 0.188 (the cosmological baryon fraction; e.g. Planck Collaboration VI 2018) of the mass in dark matter. However, it was realised that the total amount of baryons that we can directly observe in galaxies (stars, gas, dust, etc.) is instead at most only about 20% of the cosmological value (e.g. Persic & Salucci 1992; Fukugita et al. 1998). This became known as the missing baryons problem and has prompted the search for large resevoirs of baryons within the diffuse, multi-phase circumgalactic medium of galaxies (Bregman 2007; Tumlinson et al. 2017).
Arguably the most important indicator of this issue is the stellar-to-halo mass relation, which connects the stellar mass M⋆ of a galaxy to its dark matter halo of mass Mhalo (see Wechsler & Tinker 2018, for a recent review). This relation can be probed observationally through many different techniques, e.g. galaxy abundance as a function of stellar mass (e.g. Vale & Ostriker 2004; Behroozi et al. 2010; Moster et al. 2013), galaxy clustering (e.g. Kravtsov et al. 2004; Zheng et al. 2007), group catalogues (e.g. Yang et al. 2008), weak galaxy-galaxy lensing (e.g. Mandelbaum et al. 2006; Leauthaud et al. 2012), satellite kinematics (e.g. van den Bosch et al. 2004; More et al. 2011; Wojtak & Mamon 2013), and internal galaxy dynamics (e.g. Persic et al. 1996; McConnachie 2012; Cappellari et al. 2013; Desmond & Wechsler 2015; Read et al. 2017; Katz et al. 2017; hereafter K17). Amongst all these determinations there is wide consensus on the overall shape of the relation and, in particular, on the fact that the ratio of stellar-to-halo mass f⋆ = M⋆/fbMhalo (sometimes called star formation efficiency), is a non-monotonic function of mass with a peak (f⋆ ≈ 0.2) at Mhalo ≈ 1012 M⊙ (roughly the mass of the Milky Way). One interpretation is that galaxies of this characteristic mass have been, during the course of their lives, the most efficient at turning gas into stars. Even so, efficiencies of the order of 20% are still relatively low, implying that most baryons are still undetected even in these systems1.
Several works have suggested that the exact shape of the stellar-to-halo mass relation depends on galaxy morphology (e.g. Mandelbaum et al. 2006; Conroy et al. 2007; Dutton et al. 2010; More et al. 2011; Rodríguez-Puebla et al. 2015; Lange et al. 2018), especially on the high-mass side (log M⋆/M⊙ ≳ 10) where red, passive early-type systems appear to reside in more massive halos with respect to blue, star-forming, late-type galaxies. This is intriguing since it suggests that galaxies with different morphologies likely followed different evolutionary pathways that led the late-type ones, at a given M⋆, to live in lighter halos and to have a somewhat smaller fraction of missing baryons with respect to early-type systems2. However, one of the main difficulties associated with these measurements is the scarcity of high-mass galaxies in the nearby Universe (e.g. Kelvin et al. 2014), given that most of the above-mentioned observational probes use statistical estimates based on large galaxy samples.
In this paper we use another, complementary approach to estimate the stellar-to-halo mass relation through accurate modelling of the gas dynamics within spiral galaxies. We use the observed HI rotation curves of a sample of regularly rotating, nearby disc galaxies to fit mass models comprising a baryonic plus a dark matter component. We then extrapolate the dark matter profile to the virial radius, with cosmologically motivated assumptions, to yield the halo mass. A considerable advantage of this method is that each system can be studied individually and halo masses, along with their associated uncertainties, can be determined in great detail for each object. We show that this approach leads to a coherent picture of the relation between stellar and halo mass in late-type galaxies, which in turn profoundly affects our perspective on the star formation efficiency in the high-mass regime.
The paper is organised as follows: we present our sample and methodology to derive stellar and halo masses in Sect. 2; we describe our results in Sect. 3; and we discuss the results in detail in Sect. 4.
2. Method
Here we describe the data and methodology of our analysis. We adopt a standard ΛCDM cosmology with parameters estimated by the Planck Collaboration VI (2018). In particular, we use a Hubble constant of H0 = 67.66 km s−1 Mpc−1 and a cosmological baryon fraction of fb ≡ Ωb/Ωc = 0.188.
2.1. Data
We use the sample of 175 disc galaxies with near-infrared photometry and HI rotation curves (SPARC) collected by Lelli et al. (2016a; hereafter LMS16). This sample of spirals in the nearby Universe spans more than 4 orders of magnitude in luminosity at 3.6 μm and all morphological types, from irregulars to lenticulars. The galaxies were selected to have extended, regular, high-quality HI rotation curves and measured near-infrared photometry; thus, it is not volume limited. Nevertheless, it still provides a fair representation of the population of (regularly rotating) spirals at z = 0 and most importantly is best suited for our dynamical study.
The HI rotation curves are used as tracers of the circular velocity of the galaxies, while the individual contributions of the atomic gas (Vgas) and stars (V⋆) to the circular velocity are derived from the HI and 3.6 μm total intensity maps, respectively (see LMS16, for further details). The velocity Vgas traces the distribution of atomic hydrogen, corrected for the presence of helium, while the near-infrared surface brightness is decomposed into an exponential disc (Vdisc) and a spherical bulge (Vbulge). The contribution of the stars to the circular velocity is then  , given stellar mass-to-light ratios of the disc (Υdisc) and bulge populations (Υbulge).
, given stellar mass-to-light ratios of the disc (Υdisc) and bulge populations (Υbulge).
2.2. Model
We model the observed rotation curve as
Here VDM is the dark matter contribution to the circular velocity; for simplicity, we have assumed that Υbulge = 1.4Υdisc, as suggested by stellar population synthesis models (e.g. Schombert & McGaugh 2014), thus 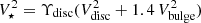 . In Appendix A we explore the effect of fixing different mass-to-light ratios Υdisc and Υbulge for disc and bulge, respectively: our findings on the stellar-to-halo mass relation do not change significantly if we assume Υdisc = 0.5 and Υbulge = 0.7, for which the scatter of the baryonic Tully–Fisher relation is minimised (Lelli et al. 2016b).
. In Appendix A we explore the effect of fixing different mass-to-light ratios Υdisc and Υbulge for disc and bulge, respectively: our findings on the stellar-to-halo mass relation do not change significantly if we assume Υdisc = 0.5 and Υbulge = 0.7, for which the scatter of the baryonic Tully–Fisher relation is minimised (Lelli et al. 2016b).
The dark matter distribution is modelled as a Navarro et al. (1996; hereafter NFW) spherical halo, which is characterised by a dimensionless concentration parameter (c) and the halo mass (Mhalo), which we take as that within a radius enclosing 200 times the critical density of the Universe. Thus, our rotation curve model has three free parameters: Mhalo, c, and Υ⋆.
We compute the posterior distributions of these parameters with a Bayesian approach. We define a standard χ2 likelihood 𝒫, given the data θ, as
where Vobs, i is the ith point of the observed rotation curve at radius Ri and σVobs, i is its observed uncertainty. The posterior distribution of the three parameters is then given by the Bayes theorem
where 𝒫(Mhalo, c, Υdisc) is the prior. We sample the posterior with an affine-invariant Markov chain Monte Carlo method (MCMC, in particular, we use the python implementation by Foreman-Mackey et al. 2013).
We use a flat prior on the stellar mass-to-light ratio Υdisc limited to a reasonable range, 0.01 ≲ Υdisc ≲ 1.2, which encompasses estimates obtained with stellar population models (Meidt et al. 2014; McGaugh & Schombert 2014). In a ΛCDM Universe the halo mass and concentration are well known to be anti-correlated. Thus, in order to test whether standard ΛCDM halos can be used to fit galaxy rotation curves and then yield a stellar-to-halo mass relation, for the halo concentration we assume a prior that follows the c − Mhalo relation as estimated in N-body cosmological simulations (e.g. Dutton & Macciò 2014; hereafter DM14): for each Mhalo, the prior on c is lognormal with mean and uncertainty given by the c = c(Mhalo) of DM14 (their Eq. (8)). The prior on the dark matter halo mass Mhalo is, instead, flat over a wide range: 6 ≤ log Mhalo/M⊙ ≤ 15.
A non-uniform prior on the halo concentration is needed to infer reasonable constraints on the halo parameters (see e.g. K17). The reason for this is that the HI rotation curves do not typically extend enough to probe the region where the NFW density profile steepens, thus yielding only a weak inference on c. The ΛCDM-motivated prior on the c − Mhalo relation proves to be enough to constrain all the model parameters. Furthermore, we note that the DM14 c − Mhalo relation does not distinguish between halos hosting late-type or early-type galaxies, so we use it under the assumption that it provides a reasonable description of the correlation for the halos where late-type galaxies form. We summarise our choice of priors in Table 1.
3. Results
We modelled the rotation curves and we measured the posterior distributions of Υdisc, Mhalo, and c for all the 158 SPARC galaxies with inclination on the sky higher than 30° (for nearly face-on systems the rotation curves are very uncertain). For each parameter, we define the best value to be the median of the posterior distribution and its uncertainty as the 16th–84th percentiles. In Appendix A we provide all the measurements and uncertainties, together with the value of the likelihood associated with the best model (see Table A.1). We also present the full rotation curve decomposition for one case as an example (NGC 3992, Fig. A.1), while we make available the plots of all the other galaxies online3.
Unsurprisingly, we find that our model typically does not give very stringent constraints on the stellar mass-to-light ratio, with only 84 (68) galaxies having an uncertainty on Υ⋆ lower than 50% (30%). In these cases, which are mostly for M⋆ > 1010 M⊙ where the signal-to-noise ratio is high, the Vobs and V⋆ profiles are similar enough to yield good constraints on Υdisc. We find that these galaxies are not all maximal discs, as their Υdisc is homogeneously distributed in the range allowed by our prior. We find the highest mass spirals (M⋆ ≳ 1011 M⊙) to have much better fits with a slightly higher mass-to-light ratio (Υdisc ∼ 0.7) than the mean of our prior (Υdisc = 0.6), consistently with previous works who found that high-mass discs are close to maximum (e.g. Lapi et al. 2018; Starkman et al. 2018; Li et al. 2018). Smaller systems, instead, typically have a poorer inference on the mass-to-light ratio, with about ∼50 cases in which the posterior on Υdisc is quite flat. Even in these extreme cases it is still useful to let the MCMC explore the full range of possible mass-to-light ratios (0.01 ≤ Υdisc ≤ 1.2) as opposed to just fixing a value for Υdisc because it provides a more realistic estimate of the uncertainty on the other parameters of the dark matter halo. In other words, when the inference on Υdisc is poor, it may be thought of as a nuisance parameter over which the posterior distributions of the other two more interesting halo parameters are marginalised.
For 137 galaxies (out of 158) we obtained a unimodal posterior distribution for the halo mass, thus we were able to associate a measurement and an uncertainty with Mhalo; instead, the remaining 21 galaxies had either a multi-modal or a flat posterior on the halo mass and thus we discarded them. These 21 galaxies are mostly low-mass systems (M⋆ ≲ 2 × 109 M⊙) and their removal does not alter in any way the high-mass end of the population, which is the main focus of our work. For some of the remaining 137 galaxies, we find that the NFW halo model provides a poor fit to the observed rotation curve, as their best-fit χ2 value is high. This is not surprising, since it is well known that low-mass discs in particular tend to have slowly rising rotation curves, which makes them more compatible with having centrally cored halos (e.g. de Blok et al. 2001; K17). Indeed, by re-fitting all rotation curves with a cored halo model from Burkert (1995), we have found 27 mostly low-mass (M⋆ ≲ 1010 M⊙) systems for which a similar cored profile is preferred to the NFW at a 3-σ confidence level. For consistency we decided to remove these 27 systems from our sample, but in Appendix A we demonstrate that their stellar and halo masses, derived by extrapolating the Burkert profile to the virial radius, are perfectly consistent with the picture that we present below.
In Fig. 1 we plot the M⋆ − Mhalo relation for the 110 SPARC galaxies in our final sample. Points are the median of the posterior distributions of Mhalo and M⋆; the 16th–84th percentiles of the Mhalo distribution define the error bar, while the uncertainty on the stellar mass is calculated as in Lelli et al. (2016b, their Eq. (5)), where the uncertainty on Υdisc is given by the 16th–84th percentiles of its posterior. For comparison we also plot the M⋆ − Mhalo relation estimated by Moster et al. (2013) using abundance matching. In general we find that the abundance matching model is in good agreement with our measurements for M⋆ ≲ 5 × 1010 M⊙, even though our points have a large scatter especially at the lowest masses. The agreement is instead much poorer at high stellar masses, where the Moster et al. (2013) model predicts significantly higher halo masses with respect to our estimates. Our measurements indicate that there is no sign of a break in the stellar-to-halo mass relation of spirals and that it is consistent with being an increasing function of mass with roughly the same slope at all masses.
 |
Fig. 1. Stellar-to-halo mass relation for 110 galaxies in the SPARC sample. The points are colour-coded by the ratio of HI-to-stellar mass. The stellar-to-halo mass relation estimated by Moster et al. (2013) using abundance matching is shown as a black dashed curve; the scatter of the relation is shown shaded in grey. Galaxies that have converted all the available baryons in the halo into stars would lie on the long-dashed line, whose thickness encompasses uncertainties on fb. For reference, we also show the location of the Milky Way (cross) and of the Andromeda galaxy (plus) on the plot, as given by the modelling by Posti & Helmi (2019) and Corbelli et al. (2010), respectively. |
The tension at the high-mass end between our measurements and the abundance matching model is much clearer if we plot the stellar fraction, i.e. f⋆ ≡ M⋆/fbMhalo, also sometimes called star formation efficiency, as a function of the stellar mass: we show this in Fig. 2. This plot highlights the two main findings of our work, the first being that f⋆ appears to increase monotonically with galaxy stellar mass with no indication of a peak in the range 10 ≤ log M⋆/M⊙ ≤ 11, where most abundance matching models find a maximum star formation efficiency. For instance, a galaxy with M⋆ = 2 × 1011 M⊙ has f⋆ ≃ 0.04 in the Moster et al. (2013) model, while we find f⋆ ≃ 0.5. By computing the difference between the measured f⋆ and that expected in the Moster et al. (2013) model, normalised by the sum in quadrature of the measured uncertainty on f⋆ and of the intrinsic scatter of the model, we find the measurement for the high-mass systems to be inconsistent at 2−3σ with the model (see the coloured points in Fig. 2). This discrepancy is very robust and holds for all the tests we have run (see the f⋆ − M⋆ diagram in all these cases, Fig. A.2):
 |
Fig. 2. Stellar fraction as a function of stellar mass for 110 galaxies in the SPARC sample. Top panel (in log-scale): individual measurements with their uncertainties. Bottom panel (in linear-scale): f⋆ (orange dashed line) and fbaryons = f⋆ + 1.4fHI + fH2 (blue dot-dashed line; see text for details) in bins of log M⋆ (shaded areas are the 1σ uncertainties). In both panels, the stellar-to-halo mass relation estimated by Moster et al. (2013) using abundance matching is shown as a black curve, with a shaded area representing its scatter. Points in the top panel are colour-coded by how many standard deviations away the galaxy is from the Moster et al. (2013) relation, i.e. |
-
we fit the rotation curves assuming a cored (Burkert 1995) instead of a cuspy (NFW) profile. In general, this yields better fits for many low-mass systems, slightly higher stellar masses, and lower halo virial masses for all galaxies;
-
we used the fits recently obtained by Ghari et al. (2019), who used Einasto (1965) halo profiles (and distances and mass-to-light ratios from Li et al. 2018). In general, we typically find slightly lower halo virial masses, but broadly consistent with our estimates with NFW profiles;
-
we fixed the mass-to-light ratio of the bulge and disc components to reasonable values suggested by stellar population synthesis models (Υdisc = 0.5, Υbulge = 0.7, see e.g. Meidt et al. 2014; Schombert & McGaugh 2014);
-
we tried allowing both Υdisc and Υbulge to vary in our fits, with the additional constraint of Υdisc ≤ Υbulge. This had an effect only on the 28 galaxies (out of 110) in our final sample that have non-negligible bulges. We find the resulting uncertainties on Υdisc to be significantly larger in this case, but never dramatically so.
In all these cases the final result is that the f⋆ − M⋆ diagram is not significantly different from that presented in Fig. 2. Additionally, as shown by Katz et al. (2014, see their Figs. 20 and 23), the effect of adiabatic contraction of the dark matter halos due to the formation of stellar discs has a negligible impact on f⋆ for galaxies in the interested mass regime.
The other main finding highlighted by Fig. 2 is even more surprising: we find that all spirals with M⋆ ≳ 1011 M⊙ have a stellar fraction very close to unity, in the range f⋆ ≈ 0.3−1; a handful of them are consistent with f⋆ = 1 within the uncertainties. This implies that these galaxies were extremely efficient at turning gas into stars and that the amount of mass collapsed in stars is a considerable portion of the total amount of baryons expected to be associated with their halos. In fact, if we also include the contribution of atomic and molecular hydrogen (the latter estimated through the MHI − MH2 relation given by Catinella et al. 2018), spirals with M⋆ ≥ 1011 M⊙ are found to be consistent with a cold baryon budget of fbaryons = f⋆ + 1.4fHI + fH2 ≈ 1 within the uncertainties (where the factor 1.4 accounts for helium, e.g. Lelli et al. 2016a), with a mean value of ∼0.6 and uncertainties of [ − 0.3, +0.5]. Moreover, considering that galaxies are known to be surrounded by massive, hot coronae, which are detected in X-rays and with the Sunyaev–Zeldovich effect, and account for about 0.1−0.3fbMhalo (typically estimated statistically by stacking over many galaxies with a given stellar mass, e.g. Planck Collaboration Int. XI 2013; Bregman et al. 2018, and references therein), the total (cold+hot) baryon budget is easily compatible with unity at the high-mass end, with very little room for other baryonic components. In other words, we have found that the most massive, regularly rotating spirals in the nearby Universe have virtually no missing baryons.
4. Discussion
Our analysis provided us with a robust and unbiased estimate of the halo virial mass for a sample of 108 spiral galaxies in the nearby Universe using their high-quality HI rotation curves. While we find good agreement with previous determinations of the stellar-to-halo mass relation for galaxies roughly up to the mass of the Milky Way (M⋆ = 5 × 1010 M⊙), we also find systematically lower halo masses (factor ∼10), corresponding to higher stellar-to-halo mass ratios, for the most massive spirals with respect to expectations from most up-to-date abundance matching models (e.g. Wechsler & Tinker 2018).
A possible explanation for this discrepancy is that while the high-mass end (M⋆ ≳ 1011 M⊙) of the galaxy stellar mass function is vastly dominated by passive early-type galaxies that occupy massive (Mhalo ≳ 5 × 1012 M⊙) dark matter halos, there still exists a population of star-forming spirals that inhabit halos of lower masses. The presence of this second population – which is not well represented by current abundance matching models – implies the existence of different evolutionary pathways for building galaxies of a given stellar mass. This suggests, for example, that a massive system that has evolved in isolation may have had the chance to sustain star formation unimpeded for its entire life, potentially converting most of its available baryons into stars. While this is certainly not the case for high-mass early-types galaxies, which tend to live in high-density environments, it may well be the pathway taken by the high-mass population of spirals studied in this work. McGaugh et al. (2010), by simply analysing the Tully–Fisher relation of a similar sample of spirals, also concluded that f⋆ does not turn over at the highest masses.
A discrepancy between the expected halo mass for a typical passive (red) 1011 M⊙ galaxy and an active (blue) galaxy of the same stellar mass, was also noted by other authors using various probes, such as satellite kinematics (e.g. Conroy et al. 2007; More et al. 2011; Wojtak & Mamon 2013), galaxy–galaxy weak lensing (e.g. Mandelbaum et al. 2006, 2016; Reyes et al. 2012), abundance matching (e.g. Rodríguez-Puebla et al. 2015), or combinations (e.g. Dutton et al. 2010). The works most similar to ours are those of K17 and Lapi et al. (2018). We use the same galaxy sample as in K17 (SPARC) and we perform an analysis that is similar to theirs, but with the crucial difference that we do not impose a prior on halo mass that follows an M⋆ − Mhalo relation from abundance matching, which slightly biases some of the high-mass galaxies towards higher halo masses4. Lapi et al. (2018), on the other hand, have a much larger sample of spirals than ours, but they rely on stacked rotation curves for their mass decompositions, i.e. they stack individual curves of galaxies in bins of absolute magnitude, whereas we focus on individual, well-studied systems. Finally, we note that, amongst the detailed studies of individual systems, Corbelli et al. (2010) measured the dynamical mass of M31 by decomposing its HI rotation curve, to find a surprisingly high f⋆ ≃ 0.6, and Martinsson et al. (2013) decomposed the HI rotation curves of a small sample of 30 spirals from the DiskMass Survey to find the highest star formation efficiencies f⋆ ≳ 0.3 for their three most massive galaxies (logM⋆/M⊙ ≳ 10.9). While our results align with these previous works, to our knowledge we are the first to focus specifically on the f⋆ − M⋆ relation and to highlight the fact that (i) the highest mass spirals are the most efficient galaxies at turning gas into stars, (ii) f⋆ increases monotonically with stellar mass for regularly rotating nearby discs, and (iii) virtually all high-mass discs have ≳30% of the total baryons within their halos in stars.
Our analysis establishes that the most efficient galaxies at forming stars are not L* galaxies, as previously thought (e.g. Wechsler & Tinker 2018), but much more massive systems, some of the most massive spiral galaxies in the nearby Universe (M⋆ ≳ 1011 M⊙). Not only does the galactic star-formation efficiency peak at much higher masses than we knew before, but we also showed that several massive discs have efficiencies f⋆ of the order unity. This result alone is of key importance since it demonstrates that there is no universal physical mechanism that sets the maximum star formation efficiency to 20−30%.
Furthermore, the fact that some massive galaxies with high f⋆ exist has fundamental implications for star formation quenching. Since these galaxies live in halos with Mhalo ∼ 2−5 × 1012 M⊙, if mass is the main driver of quenching and if a critical mass for quenching exists (e.g. as expected in scenarios where virial shock heating of the circumgalactic medium is the key process, see Birnboim & Dekel 2003; Dekel & Birnboim 2008), then it follows that this critical mass cannot be lower than ∼5 × 1012 M⊙, which is almost an order of magnitude higher than previously thought (e.g. Dekel & Birnboim 2006). Interestingly, such a high threshold is instead expected in scenarios where the accretion of cool gas is hampered (“starvation”), for example by the high virial temperature of the circumgalactic gas in a galactic fountain cycle (e.g. Armillotta et al. 2016) or by the complex interplay of radiative cooling and feedback in the smooth gas accretion from cold filaments (e.g. van de Voort et al. 2011).
Even if we have measured high f⋆ for some massive spirals, the vast majority of galaxies living in Mhalo > 1012 M⊙ halos still have f⋆ ≪ 1, which means that they managed to efficiently quench their star formation. Our results imply that since mass cannot be the major player in quenching galaxies, at least for Mhalo ≲ 5 × 1012 M⊙, some other mechanism must play a fundamental role in the transition from active to passive star formation. One of the main suspects is environment, since gas removal happens more frequently and also gas accretion is more difficult in high-density environments (e.g. Peng et al. 2010; van de Voort et al. 2017). Another is the powerful feedback from the active galactic nucleus (AGN), which can episodically suppress any gas condensation throughout the galaxy (e.g. Croton et al. 2006; Fabian 2012). Finally, another key process is the interaction with other galaxies, with passive galaxies being hosted in halos with an active merger history, which can result in bursty star formation histories and subsequent suppressive stellar/AGN feedback (e.g. Cox et al. 2006a; Gabor et al. 2010). This scenario also naturally accounts for the morphological transformation of disc galaxies, living in halos with quiet merger histories, to spheroids, which are the dominant galaxy population at the high-mass end, where mergers are also more frequent (e.g. Cox et al. 2006b). This scenario is, in principle, testable with current cosmological simulations and with a new abundance matching model that depends on secondary halo parameters, such as merger history or formation time, and it is able to predict not only stellar masses but also other galaxy properties, such as morphology or colour.
Blue galaxies typically also have larger reservoirs of cold gas with respect to red ones. However, on average, the amount cold gas is sub-dominant with respect to stars for M⋆ > 1010 M⊙. (e.g. Papastergis et al. 2012).
Taking into account this difference in the priors used, our results are very well compatible with theirs: our conclusions sit in the middle between their case with uniform priors (their Fig. 3) and that in which they impose a prior following the Moster et al. (2013)M⋆ − Mhalo relation (their Fig. 5).
Acknowledgments
We thank E. Corbelli, B. Famaey, A. Lapi, F. Lelli, A. Robertson, J. Sellwood, and F. van den Bosch for the useful discussions and A. Ghari for making the Einasto fits available to us. LP acknowledges financial support from a VICI grant from the Netherlands Organisation for Scientific Research (NWO) and from the Centre National d’Etudes Spatiales (CNES).
References
- Armillotta, L., Fraternali, F., & Marinacci, F. 2016, MNRAS, 462, 4157 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P. S., Conroy, C., & Wechsler, R. H. 2010, ApJ, 717, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Birnboim, Y., & Dekel, A. 2003, MNRAS, 345, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, J. N. 2007, ARA&A, 45, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Bregman, J. N., Anderson, M. E., Miller, M. J., et al. 2018, ApJ, 862, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Burkert, A. 1995, ApJ, 447, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Saintonge, A., Janowiecki, S., et al. 2018, MNRAS, 476, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., Prada, F., Newman, J. A., et al. 2007, ApJ, 654, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Corbelli, E., Lorenzoni, S., Walterbos, R., Braun, R., & Thilker, D. 2010, A&A, 511, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, T. J., Jonsson, P., Primack, J. R., & Somerville, R. S. 2006a, MNRAS, 373, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, T. J., Dutta, S. N., Di Matteo, T., et al. 2006b, ApJ, 650, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- de Blok, W. J. G., McGaugh, S. S., Bosma, A., & Rubin, V. C. 2001, ApJ, 552, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2008, MNRAS, 383, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Desmond, H., & Wechsler, R. H. 2015, MNRAS, 454, 322 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., Conroy, C., van den Bosch, F. C., Prada, F., & More, S. 2010, MNRAS, 407, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J. 1965, Trudy Astrofizicheskogo Instituta Alma-Ata, 5, 87 [NASA ADS] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fukugita, M., Hogan, C. J., & Peebles, P. J. E. 1998, ApJ, 503, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Gabor, J. M., Davé, R., Finlator, K., & Oppenheimer, B. D. 2010, MNRAS, 407, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Ghari, A., Famaey, B., Laporte, C., & Haghi, H. 2019, A&A, 623, A123 [Google Scholar]
- Katz, H., McGaugh, S. S., Sellwood, J. A., & de Blok, W. J. G. 2014, MNRAS, 439, 1897 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., Lelli, F., McGaugh, S. S., et al. 2017, MNRAS, 466, 1648 [NASA ADS] [CrossRef] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2014, MNRAS, 444, 1647 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Berlind, A. A., Wechsler, R. H., et al. 2004, ApJ, 609, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Lange, J. U., van den Bosch, F. C., Zentner, A. R., Wang, K., & Villarreal, A. S. 2018, MNRAS, submitted [arXiv:1811.03596] [Google Scholar]
- Lapi, A., Salucci, P., & Danese, L. 2018, ApJ, 859, 2 [Google Scholar]
- Leauthaud, A., Tinker, J., Bundy, K., et al. 2012, ApJ, 744, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016a, AJ, 152, 157 [Google Scholar]
- Lelli, F., McGaugh, S. S., & Schombert, J. M. 2016b, ApJ, 816, L14 [Google Scholar]
- Li, P., Lelli, F., McGaugh, S., & Schombert, J. 2018, A&A, 615, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelbaum, R., Seljak, U., Kauffmann, G., Hirata, C. M., & Brinkmann, J. 2006, MNRAS, 368, 715 [Google Scholar]
- Mandelbaum, R., Wang, W., Zu, Y., et al. 2016, MNRAS, 457, 3200 [NASA ADS] [CrossRef] [Google Scholar]
- Martinsson, T. P. K., Verheijen, M. A. W., Westfall, K. B., et al. 2013, A&A, 557, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McConnachie, A. W. 2012, AJ, 144, 4 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., Schombert, J. M., de Blok, W. J. G., & Zagursky, M. J. 2010, ApJ, 708, L14 [Google Scholar]
- Meidt, S. E., Schinnerer, E., van de Ven, G., et al. 2014, ApJ, 788, 144 [NASA ADS] [CrossRef] [Google Scholar]
- More, S., van den Bosch, F. C., Cacciato, M., et al. 2011, MNRAS, 410, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Papastergis, E., Cattaneo, A., Huang, S., Giovanelli, R., & Haynes, M. P. 2012, ApJ, 759, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., & Salucci, P. 1992, MNRAS, 258, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Persic, M., Salucci, P., & Stel, F. 1996, MNRAS, 281, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2018, A&A, submitted [arXiv:1807.06209] [Google Scholar]
- Planck Collaboration Int. XI. 2013, A&A, 557, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Posti, L., & Helmi, A. 2019, A&A, 621, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, J. I., Iorio, G., Agertz, O., & Fraternali, F. 2017, MNRAS, 467, 2019 [NASA ADS] [Google Scholar]
- Reyes, R., Mandelbaum, R., Gunn, J. E., et al. 2012, MNRAS, 425, 2610 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Puebla, A., Avila-Reese, V., Yang, X., et al. 2015, ApJ, 799, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Salucci, P., & Burkert, A. 2000, ApJ, 537, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Schombert, J., & McGaugh, S. 2014, PASA, 31, e036 [NASA ADS] [CrossRef] [Google Scholar]
- Starkman, N., Lelli, F., McGaugh, S., & Schombert, J. 2018, MNRAS, 480, 2292 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Vale, A., & Ostriker, J. P. 2004, MNRAS, 353, 189 [Google Scholar]
- van den Bosch, F. C., Norberg, P., Mo, H. J., & Yang, X. 2004, MNRAS, 352, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- van de Voort, F., Schaye, J., Booth, C. M., Haas, M. R., & Dalla Vecchia, C. 2011, MNRAS, 414, 2458 [NASA ADS] [CrossRef] [Google Scholar]
- van de Voort, F., Bahé, Y. M., Bower, R. G., et al. 2017, MNRAS, 466, 3460 [NASA ADS] [CrossRef] [Google Scholar]
- Wechsler, R. H., & Tinker, J. L. 2018, ARA&A, 56, 435 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Wojtak, R., & Mamon, G. A. 2013, MNRAS, 428, 2407 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., Mo, H. J., & van den Bosch, F. C. 2008, ApJ, 676, 248 [Google Scholar]
- Zheng, Z., Coil, A. L., & Zehavi, I. 2007, ApJ, 667, 760 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Supplementary material
Results of the fits for individual galaxies.
 |
Fig. A.1. Example of rotation curve decomposition for NGC 3992. Left panel: observed rotation curve (black points) with our best model (red solid curve), decomposed into the contributions from stars (gold dashed curve), gas (blue dotted curve), and dark matter (purple dot-dashed curve). Right panel: posterior distributions of the three parameters of the model: halo mass, halo concentration, and mass-to-light ratio of the stellar disc. Similar plots for all the other galaxies in our sample can be found online at http://astro.u-strasbg.fr/~posti/PFM19_fiducial_fits/. |
 |
Fig. A.2. Resulting f⋆ − M⋆ relation when varying the assumptions on the fit of the galaxy rotation curves. In the top row the dark matter halo model was varied: NFW (left), Burkert (centre), or Einasto (right). In the first two cases, the rotation curves were fit with a uniform prior on Υdisc, assuming Υbulge = 1.4Υdisc and with a prior on the concentration-mass relation for the NFW profile (from Dutton & Macciò 2014) and one on the core radius-core mass relation for the Burkert profile (from Salucci & Burkert 2000). Instead, the fits in the Einasto case were obtained by Ghari et al. (2019), who used the mass-to-light ratios derived by Li et al. (2018). In the bottom row, an NFW halo was used, but the assumptions on the mass-to-light ratios were varied: either fixed (left) or both left free to vary with the condition Υdisc ≤ Υbulge (right). In all panels the colouring of the points, the dashed horizontal line, and the abundance matching predictions (dashed curve with grey band) are as in Fig. 2. |
All Tables
All Figures
 |
Fig. 1. Stellar-to-halo mass relation for 110 galaxies in the SPARC sample. The points are colour-coded by the ratio of HI-to-stellar mass. The stellar-to-halo mass relation estimated by Moster et al. (2013) using abundance matching is shown as a black dashed curve; the scatter of the relation is shown shaded in grey. Galaxies that have converted all the available baryons in the halo into stars would lie on the long-dashed line, whose thickness encompasses uncertainties on fb. For reference, we also show the location of the Milky Way (cross) and of the Andromeda galaxy (plus) on the plot, as given by the modelling by Posti & Helmi (2019) and Corbelli et al. (2010), respectively. |
| In the text | |
 |
Fig. 2. Stellar fraction as a function of stellar mass for 110 galaxies in the SPARC sample. Top panel (in log-scale): individual measurements with their uncertainties. Bottom panel (in linear-scale): f⋆ (orange dashed line) and fbaryons = f⋆ + 1.4fHI + fH2 (blue dot-dashed line; see text for details) in bins of log M⋆ (shaded areas are the 1σ uncertainties). In both panels, the stellar-to-halo mass relation estimated by Moster et al. (2013) using abundance matching is shown as a black curve, with a shaded area representing its scatter. Points in the top panel are colour-coded by how many standard deviations away the galaxy is from the Moster et al. (2013) relation, i.e. |
| In the text | |
 |
Fig. A.1. Example of rotation curve decomposition for NGC 3992. Left panel: observed rotation curve (black points) with our best model (red solid curve), decomposed into the contributions from stars (gold dashed curve), gas (blue dotted curve), and dark matter (purple dot-dashed curve). Right panel: posterior distributions of the three parameters of the model: halo mass, halo concentration, and mass-to-light ratio of the stellar disc. Similar plots for all the other galaxies in our sample can be found online at http://astro.u-strasbg.fr/~posti/PFM19_fiducial_fits/. |
| In the text | |
 |
Fig. A.2. Resulting f⋆ − M⋆ relation when varying the assumptions on the fit of the galaxy rotation curves. In the top row the dark matter halo model was varied: NFW (left), Burkert (centre), or Einasto (right). In the first two cases, the rotation curves were fit with a uniform prior on Υdisc, assuming Υbulge = 1.4Υdisc and with a prior on the concentration-mass relation for the NFW profile (from Dutton & Macciò 2014) and one on the core radius-core mass relation for the Burkert profile (from Salucci & Burkert 2000). Instead, the fits in the Einasto case were obtained by Ghari et al. (2019), who used the mass-to-light ratios derived by Li et al. (2018). In the bottom row, an NFW halo was used, but the assumptions on the mass-to-light ratios were varied: either fixed (left) or both left free to vary with the condition Υdisc ≤ Υbulge (right). In all panels the colouring of the points, the dashed horizontal line, and the abundance matching predictions (dashed curve with grey band) are as in Fig. 2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



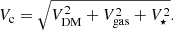
![$$ \begin{aligned} \chi ^2&= -\ln {\mathcal{P} (\theta |M_{\mathrm{halo}},c,\Upsilon _{\mathrm{disc}})} \nonumber \\&= \sum _{i=0}^{N} \frac{1}{2}\left[\frac{V_{\mathrm{obs},i}- V_{\mathrm{c}}(R_i|M_{\mathrm{halo}},c,\Upsilon _{\mathrm{disc}})}{\sigma _{V_{\mathrm{obs},i}}}\right]^2 , \end{aligned} $$](/articles/aa/full_html/2019/06/aa35553-19/aa35553-19-eq4.gif)