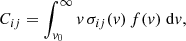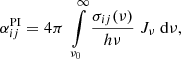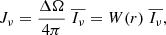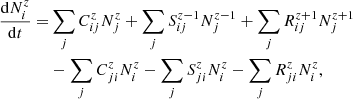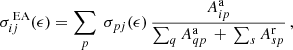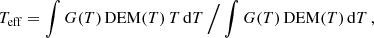| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 13 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201935133 | |
| Published online | 21 June 2019 | |
Modelling ion populations in astrophysical plasmas: carbon in the solar transition region⋆
DAMTP, Univerity of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
e-mail: rpd21@cam.ac.uk
Received:
25
January
2019
Accepted:
28
April
2019
The aim of this work is to improve the modelling of ion populations in higher density, lower temperature astrophysical plasmas, of the type commonly found in lower solar and stellar atmospheres. Ion population models for these regions frequently employ the coronal approximation, which assumes conditions more suitable to the upper solar atmosphere, where high temperatures and lower densities prevail. The assumed conditions include all ions being in the ground state and steady-state equilibrium, where there is sufficient time for ionisation and recombination to take place. Using the coronal approximation for modelling the solar transition region gives theoretical lines intensities for the Li-like and Na-like isoelectronic sequences which are often factors of two to five times lower than observed. The works of Burgess & Summers (1969, ApJ, 157, 1007) and Nussbaumer & Storey (1975, A&A, 44, 321) show the important part ions in excited levels play when included in the modelling. As density increases metastable levels become populated and ionisation rates increase, whereas dielectronic recombination through highly excited levels is suppressed. Photo-ionisation is also shown by Nussbaumer & Storey to have an effect on the charge-state distribution of carbon in these regions. Their models, however, use approximations for the atomic rates to determine the ion balance. Presented here is the first stage in updating these earlier models of carbon by using rates from up-to-date atomic calculations and more recent photo-ionising radiances. Where atomic rates were not readily available, in the case of electron impact direct ionisation and excitation–auto-ionisation, new calculations were made using the Flexible Atomic Code and Autostructure, and compared to theoretical and experimental studies. The effects each atomic process has on the ion populations as density changes is illustrated, and final results from the modelling are compared to the earlier works. Lastly, the new results for ion populations were used to predict line intensities for the solar transition region in the quiet Sun. In comparison to coronal approximation modelling the new results show significantly improved agreement with observations.
Key words: Sun: transition region / atomic data / atomic processes
Rate coefficients for direct ionisation and excitation–auto-ionisation by electron impact are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/626/A123
© ESO 2019
1. Introduction
This paper is the first in a series of studies in which the aim is to improve the modelling of the transition region (TR) lines, that is, those lines emitted by the thin layer between the chromosphere and corona (Mariska 1992). One long standing issue regards the strongest lines in the UV and extreme ultraviolet (EUV) from the Li- and Na-like ions, which are significantly enhanced by factors ranging from two to five compared to their predicted values, as obtained using lines from other ions. Notable examples are the C IV and Si IV lines, the latter being routinely observed by the IRIS satellite (De Pontieu et al. 2014). This characteristic behaviour of these ions was first noted by Burton et al. (1971), although even earlier observations present the same problem (see the Solar Living Review by Del Zanna & Mason 2018). Del Zanna et al. (2002) showed for the first time that the same problem occurs in stellar transition regions. Consequently, this is an important issue for astrophysics, not just for solar physics.
Non-equilibrium effects have long been thought to be the most likely cause. For example, departures from ionisation equilibrium can enhance significantly some of the ions that have long ionisation and recombination times, as shown in Bradshaw et al. (2004) for example, or in the case of IRIS lines by Olluri et al. (2013) and Martínez-Sykora et al. (2016) for instance. Non-Maxwellian electron distributions tend to shift the formation temperature of the TR lines towards lower values (see the review of non-equilibrium processes by Dudík et al. 2017), leading to an enhancement in predicted intensities, as shown for the Si IV case by Dudík et al. (2014).
However, there are several other physical processes which could affect the modelling of these ions and which are usually not taken into account in the literature (see the review by Del Zanna & Mason 2018). The main ones discussed in the present paper are density effects on the charge-state distribution through electron impact ionisation and dielectronic recombination. The rôle of photo-ionisation is also explored.
Burgess & Summers (1969) were the first to point out density effects on the ion balance, principally through the suppression of dielectronic recombination. This was followed by Nussbaumer & Storey (1975), who incorporated the effects of both density and photo-ionisation in a collisional-radiative (CR) model for carbon. The important part metastable levels play in the ionisation balance was expanded by McWhirter & Summers (1984). It was succeeded by a CR modelling suite made available to the Atomic Data and Analysis Structure (ADAS) consortium, (later described in Summers et al. 2006 for example). Some density effects were included approximately in modelling by Vernazza & Raymond (1979), and in modelling solar irradiance measurements by Judge et al. (1995). The latter conclude that density effects alone could not account for the large discrepancies in the intensities of Li-like and Na-like ions. More accurate modelling of the density effects used the ADAS rates, (see e.g. Doyle et al. 2005). However, in most atomic databases (e.g. Chianti1, Dere et al. 1997; Del Zanna et al. 2015) and literature, density effects and photo-ionisation are usually neglected. Charge-state distributions are used for a wide range of diagnostics. Thus, it is important that ion populations derived from density dependent modelling are used when interpreting lines from the TR, such as for the measurements of densities (see e.g. Polito et al. 2016) or chemical abundances (as discussed e.g. by Young 2018).
The aim here is to build a database of new atomic data and codes to take into account these and other effects which are not normally included in modelling. The ultimate goal is to study all the main effects in a self-consistent way through several steps. To begin with, carbon is discussed in this paper, as all the main physical processes were included by Nussbaumer & Storey (1975). In most cases the atomic rates available at the time were very approximate; more accurate rates for most of the relevant processes have been published since their work. The principal exception is collisional ionisation by electron impact, especially from excited states, which is the main focus of this paper, along with building the first stages of a CR model. In addition, the effect of photo-ionisation is explored, since this is shown by Nussbaumer & Storey to be an important process for carbon in the lower TR, although it is noted that other effects, such as opacity, are at play. There is currently a renewed interest in modelling the low charge-states of carbon, such as singly-ionised C II (see e.g. Rathore & Carlsson 2015), as spectral lines are routinely observed by IRIS and used to study this part of the solar atmosphere.
The next section presents an overview of the relevant atomic processes applicable to this region, and the processes for which new calculations have been made. It also includes a discussion about how ion populations are calculated. The results of both the atomic calculations and ion population modelling are presented in Sect. 3, as well as a comparison with the earlier works. The impact the results have on the predicted line intensities and how they compare to observations of the quiet Sun are demonstrated in Sect. 4. Brief conclusions and the outlook for further work are given in the final section.
2. Methods
As mentioned above, for solar TR densities of Ne ≈ 1010 cm−3 there are two atomic processes which are particularly important in shifting the formation temperature of an ion when compared to low densities. The first one is electron impact ionisation from excited levels of the lower ionisation stages, and the second is suppression of the dielectronic recombination rates.
In plasmas with TR densities, ions are collisionally excited and a significant proportion occupy metastable levels just above the ground. The levels last sufficiently long that ionisation can occur from these levels, (see for instance Mariska 1992). Ionisation rates from those levels are faster than from the ground, and the ensuing result will be greater populations in the next higher charge state compared to when metastable levels are not present in the modelling.
Dielectronic recombination (DR) is shown by Burgess (1964, 1965) and Seaton (1964) to be the main recombination process for the solar TR and corona. Recombination at these temperatures for this process takes place into highly excited levels. Recombined ions in these states will be rapidly re-ionised by electron collisions, again causing larger populations to exist in an higher charge state than would be present when high n levels are not included. Following the discovery of the importance of DR in the solar atmosphere and the first ionisation-equilibrium calculations to include it (Burgess & Seaton 1964), many calculations have been published over the years (e.g. Arnaud & Rothenflug 1985; Mazzotta et al. 1998). The vast majority, however, are based on calculations at zero electron density. Indeed, even at the lower density of the quiet solar corona (Ne = 108 cm−3) some density effects can be present.
Many codes and CR models have been developed for atomic fission or fusion, but are not publicly available. The original CR model of Burgess & Summers (1969) was developed further by Summers (1972, 1974) and then implemented within ADAS. In most cases, the ion models are simplified by bundling levels into either LS terms, configurations or quantum number n. The results of the CR modelling have been recently made available as effective ionisation and recombination rates via OPEN-ADAS2. Several inconsistencies in the OPEN-ADAS rates have been noted (Del Zanna 2019). The reasons for the inconsistencies are difficult to ascertain, as details of the basic atomic rates used for the modelling are not available.
The objective, then, is to build a CR model based on up-to-date, level-resolved rates, where available. The main atomic processes necessary to model the plasma conditions of the solar TR are: ionisation by electron impact, photo-ionisation, radiative and dielectronic recombination, collisional excitation by electron and proton impact, and radiative decay. Because a full CR model including all the highly excited states is quite complex on its own, the first stage has been primarily to assess the effect of collisional ionisation from the metastable levels and the suppression of DR on the ionisation balance. In the future, work will include the full modelling, which takes into account the high n levels, as well as other processes which influence the charge-state distribution in the TR to a lesser extent: auto-ionisation, photo-excitation, charge exchange and three body recombination. The following section describes the sources used for the atomic rates incorporated into the model and Sect. 2.2 discusses the steps taken to build the CR model itself.
2.1. Atomic processes
2.1.1. Collisional ionisation
Direct ionisation (DI) by electron impact is the main ionisation process, although, as Goldberg et al. (1965) note for some isoelectronic sequences, additional, non-negligible ionisation can occur via inner-shell excitation into a state above the ionisation threshold which spontaneously ionises (excitation–auto-ionisation, EA). EA has been confirmed with experiments, (see e.g. Crandall et al. 1979).
Many theoretical and experimental studies of DI have been published over the years. The majority of studies have focussed on cross sections from the ground level, except for Be-like ions, where ions in metastable levels are often present. For example, Bell et al. (1983) presents a widely used review of calculated and measured cross sections between ground states of the main ions relevant for astrophysics (it is noted that their Eq. (8) is incorrect). Dere (2007) used the Flexible Atomic Code (FAC, Gu 2008) to calculate DI and EA cross sections for electron impact ionisation, but only between ground states. Some of the calculated rates were also adjusted to agree with laboratory data. Together with the improved DR rates from the DR project, these rates formed a new, reference ionisation equilibrium, which was released for Chianti v.6 (Dere et al. 2009).
Therefore, since rates were required for each level included in the model, it was resolved to calculate the DI cross sections for the ground and excited states using FAC. The approach differed with Dere (2007) in that the rate coefficients were not adjusted to agree with experiment, particularly since ions in excited states may have been present in the experiments, affecting the cross sections measured. In fact, a large scatter (often beyond the quoted experimental uncertainties) in the laboratory measurements can be present. This scatter and differences with calculated values can be used as a measure of the uncertainty in the cross sections; this will be used in a follow-up paper to provide uncertainties in the charge-state distribution.
It has been noticed that, where the threshold for EA is close to that of DI, the EA rates can have an observable effect on ion populations. Consequently, level-resolved EA cross sections were calculated for the ground and excited states, this time using Autostructure (AS, Badnell 2011). For each ion, the calculations were benchmarked with available theoretical and experimental studies.
For the modelling, the rate coefficient for a collisional process taking place from an initial level j to a final level i is related to the cross section σij(v) by:
where v is the velocity of the impacting partcile, f(v) is the velocity distribution of these particles, and the limits of the integral are from the ionisation threshold velocity to infinity. The velocity distribution will be Maxwellian in thermal equilibrium. The rate coefficient is multiplied by the number density of free particles involved in the collision to give the rate at which transitions from j to i take place.
2.1.2. Recombination
For radiative recombination (RR) rate coefficients calculated by Badnell (2006) were used. For the DR rate coefficients at zero density the values calculated by the DR project, led by N.R. Badnell (see Badnell et al. 2003), were used. They are significantly different than the rate coefficients used in the original CR modelling by Burgess & Summers (1969).
Since this is the first stage in the modelling and highly excited levels were not included, the total RR and DR rates from each of the ground and metastable levels of the recombining ion were used. Total recombination rates from an initial level in the recombining ion are the sum of recombination rates from that initial level to every possible level in the recombined ion. In this model, the total recombination rates were applied to the ground level in the recombined ion. Although this may appear to overstate populations in the ground state, collisional excitations and radiative decays are orders of magnitude faster than ionisation and recombination rates. Consequently, level populations in the recombined ions rapidly reach their equilibrium values before further ionisation or recombination takes place. Testing this method against using partial recombination rates into individual levels of the recombined ion showed in the case of RR from C IV into C III, for example, a difference of 0.2% in the ion populations.
In order to assess the suppression of DR when density increases, Nikolić et al. (2013) suggest an empirical formula to reproduce the DR suppression which has been demonstrated by Summers (1974). This is used to “correct” the new DR rates at zero density to indicate when a CR model including density effects is required. The main assumptions of this method are that: (a) the effective recombination rates which have been provided by Summers (1974) are only due to the DR process; and, (b) the behaviour with density would be the same with the new DR rates. The approach applies, however, only to total recombination rates and not to level resolved rates. It is noted that Young (2018) used the DR project rates in combination with this approximate estimate of their suppression, employing a revised version of the Nikolić et al. (2013) approach published shortly afterwards (Nikolić et al. 2018).
The effect of density on DR was approximated here by following a similar approach to Nikolić et al. (2013, 2018). Unlike Nikolić et al. (2013), the DR suppression was estimated directly from the Summers (1974) rates, rather than using analytical formulæ. This was carried out for every ion by calculating at each temperature point the ratio of the effective recombination rate at the particular density of interest to the effective recombination rate at the lowest density in the tables, Ne = 104 cm−3. The total DR rates of Badnell et al. (2003) at each temperature point were multiplied by this ratio to estimate the suppressed DR rate for the density in hand.
2.1.3. Collisional excitation and radiative rates
For most ions, atomic data from Chianti v.8 (Del Zanna et al. 2015) for collisional excitation (by electron and proton impact) and radiative decay were used. For C III, the improved collisional excitation calculations from Fernández-Menchero et al. (2014) were incorporated.
2.1.4. Photo-ionisation
Photo-ionisation can also be important in the lower TR, as shown by Nussbaumer & Storey (1975). Estimating the photo-ionising radiation is not a trivial issue. Observations on the disc in the UV and EUV are strongly affected by solar variation. Irradiance measurements are in principle better but include limb-brightening effects. Variations of the radiances with the solar cycle can be significant, also (Andretta & Del Zanna 2014; Del Zanna & Andretta 2015).
The photo-ionising radiation used in the present model was derived from the quiet Sun irradiances observed by the Solar Dynamics Observatory EVE instrument in the EUV, as reported by Woods et al. (2009). This set of data has a wide spectral range, which covers the appropriate wavelengths for all ion stages of carbon. The irradiances were cross checked with the higher resolution radiances which have been given by Curdt et al. (2001), as observed by the Solar Heliospheric Observatory SUMER instrument. Its narrow range meant it was not suitable to be used for the rates, but comparisons showed good overall agreement with the radiances derived from Woods et al. (2009).
The solar radiation adopted by Nussbaumer & Storey (1975) was taken from a variety of sources. The main source was Malinkovsky et al. (1973) for the EUV. It is noted that these are irradiance observations obtained when the Sun was very active (see Del Zanna 2019); it is not straightforward to convert irradiances to radiances in this case. In fact, even for normal, quiet Sun conditions different spectral lines have a different limb brightening, which has been discussed by Andretta & Del Zanna (2014). In some cases, radiances turn out to be incorrect by factors of about two, (see Del Zanna & Andretta 2015, and references therein).
The analytical fits to the Opacity Project, R-Matrix cross section backgrounds derived by Verner et al. (1996), widely used in the literature for modelling, are not suitable for the level resolved picture since they give total rates only from the ground level. In this CR model it would not take into account photo-ionisation of ions in excited levels nor the differing ionisation rates of those levels. Consequently, level resolved cross sections were used, as calculated by Badnell (2006) and made available on the APAP Network website3. These were checked by comparing the total rates of the ground level with the Verner et al. fits and found to be in very good agreement.
The rate coefficient for photo-ionisation by an incident photon of frequency ν from a bound level j to a final level i in the next higher charge state is given by:
where ν0 is the threshold frequency below which the bound-free cross section σij(ν) for the process is zero.
where Ω is solid angle, W(r) is the dilution factor of the radiation, that is, the geometrical factor which accounts for the weakening of the radiation field at a distance r from the Sun, and 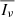 is the average disc radiance at frequency ν.
is the average disc radiance at frequency ν.
2.2. Collisional-radiative modelling
The population 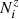 (for each temperature) of an ion with charge z+ in a level i can be obtained from:
(for each temperature) of an ion with charge z+ in a level i can be obtained from:
where 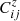 represents the collisional-radiative matrix element for processes within an ion from level j to level i;
represents the collisional-radiative matrix element for processes within an ion from level j to level i; 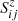 is the matrix element for ionisation processes from level j of charge state z+ into level i of the next higher charge state; and,
is the matrix element for ionisation processes from level j of charge state z+ into level i of the next higher charge state; and, 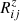 is the element for recombination processes out of level j in charge state z+ into level i of the next lower charge state. In addition, there is the normalisation condition that the total ion populations should be equal to the elemental abundance: N(X) = ∑zNz. In ionisation equilibrium,
is the element for recombination processes out of level j in charge state z+ into level i of the next lower charge state. In addition, there is the normalisation condition that the total ion populations should be equal to the elemental abundance: N(X) = ∑zNz. In ionisation equilibrium, 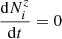 .
.
The usual method to calculate ion charge states at zero density (as in e.g. the Chianti database) is to consider the total ionisation and recombination rates between successive charge states considering only the ground states. The relative population of two ions is then obtained directly from the ratio of the total ionisation and recombination rates at each temperature. To take into account density, a level resolved model was developed in which all the main fine structure levels for the carbon ions were included. Matrices which included all the rates were built for each ion. The matrix elements for the processes occurring within one ion were obtained in the same way as in the Chianti package; they included collisional excitation and de-excitation by electron and proton impact, photo-excitation and -de-excitation, plus radiative decay. The other elements of the matrices, for transitions between ions, were populated using the ionisation and recombination rates for the ground and metastable levels which were described earlier. The populations of all the levels for all ions were solved at once. This was a novel approach; it used a significant modification of the Chianti codes, and was written in IDL. Part of these codes have been included in v.9 of Chianti (Dere et al. 2019), where a matrix for two ions at once is solved to calculate the intensities of the satellite lines.
3. Results
3.1. Atomic data
3.1.1. Direct ionisation
Level resolved DI cross sections for each charge state of carbon, up to C V, were computed using the semi-relativistic, distorted wave (DW) method as implemented in FAC. The rate coefficients for the ground and metastable levels have been made available at the CDS. Comparisons were made with available experiments and theoretical calculations in order to validate the results. Experiments where ions in metastable levels were present provided a valuable way of validating cross sections for both ground and metastable levels at the same time, so long as the populations of ions in metastable levels were known within a reasonable degree of accuracy.
To model the C II populations effectively, C I ionisation rates were required. Abdel-Naby et al. (2013) carried out theoretical cross section computations, utilising DW, R-Matrix and time dependent, close coupling (TDCC) methods. However, they do not give a sufficiently high energy range to be able to use the results for ionisation rates. Calculations of ionisation cross sections were made with FAC, whilst bearing in mind the known shortcomings of the DW approximation for nearly neutral charge states. The main experiment used for comparison has been Brook et al. (1978), which Bell et al. (1983) and Suno & Kato (2007) used for their recommended data.
For the ground state the non-perturbative R-Matrix and TDCC calculations of Abdel-Naby et al. (2013) lie very close to the experimental data. Their DW result lies 18% above the other results at the peak. For the same level, the configuration-average FAC cross section is almost 30% above the recommended data, as shown in Fig. 1. For the first excited configuration, 2s 2p3, the DW calculations from FAC and Abdel-Naby et al. lie 39% and 24% respectively above TDCC values. For ionisation from the 2s 2p2 3l configurations FAC is equal to the TDCC calculations, while their DW results diverge.
 |
Fig. 1. Configuration-average DI cross section for C I ground state; blue solid line – this work, green dash-dotted – Bell et al. (1983), purple dashed – Abdel-Naby et al. (2013) TDCC, red dotted – Abdel-Naby et al. (2013) DW. |
For rate coefficients, accuracy in the cross section near the threshold is important, which can be another shortcoming of the DW approach. A simple reduction of the FAC cross sections by 30% did not resolve the situation. To solve the problem and provide rates for the model, the recommended data of Bell et al. (1983) was adjusted in height based on the ratio of the excited level to the ground level cross sections from FAC. The scaled energies of Bell et al. were converted to incident energies by using the FAC ionisation threshold energies for each level, which were in good agreement with Abdel-Naby et al..
For C II, Bell et al. (1983) follows the experiment of Aitken et al. (1971) for their recommended data because Hamdan et al. (1978) has noticeable values below threshold. A later experiment by Yamada et al. (1989) has no below-threshold behaviour and lies a few per cent below Aitken et al.. Figure 2 shows that the FAC ground level cross section follows a very similar energy distribution and peaks just a few per cent above Bell et al.. Chianti uses the ground level cross section of Dere (2007), who also used FAC. The rate coefficient in Chianti is 10% lower than in this work. The R-Matrix result of Ludlow et al. (2008) is very close to the Yamada et al. experiment. The only available comparison for the metastable term is with the work of Ludlow et al.. Their configuration average, DW cross section is 5% higher than this work, but their term resolved, R-Matrix cross section is 25% higher. However, the R-Matrix result includes EA, (see Sect. 3.1.2).
 |
Fig. 2. DI cross section from C II ground level; solid blue line – this work, red dotted – Chianti v.8, green dashed – Bell et al. (1983), orange circles – Yamada et al. (1989). |
For C III the FAC cross section for the ground state lies close to the DW work of Younger (1981) and 10% above the R-Matrix values of Fogle et al. (2008), which are shown in Fig. 3. Chianti is a further 10% higher. The cross section of the excited term 2s 2p 3P in the current work is very close to the earlier DW calculation of Younger (1981) and less than 10% higher than the R-Matrix approach. The Fogle et al. (2008) experiment was able to determine the proportion of metastable ions in the beam more accurately, but they have fewer energy points and a larger scatter than Woodruff et al. (1978). Woodruff et al. also have more energy points close to threshold, which is useful for comparing with the EA calculations discussed in Sect. 3.1.2. Falk et al. (1983) estimate the Woodruff et al. metastable fraction to be 40%, and comparison with the R-Matrix cross sections combined according to those populations suggests this is reasonable (Fig. 4). An estimated uncertainty of 20% in the metastable population (cf. the 15% uncertainty in the Fogle et al. experiment) is shown by the dashed lines either side of the combined DI cross sections from this work. It is seen that the theoretical cross sections are almost entirely within the experimental uncertainties. The rate coefficients calculated using the FAC cross sections and a Maxwellian electron distribution are all within 10% of the Fogle et al. R-Matrix rate coefficients for this ion.
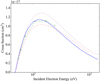 |
Fig. 3. DI cross section for C III ground level; blue solid line – this work, green dashed – Younger (1981), red dash-dotted – Fogle et al. (2008) R-Matrix, purple dotted - Chianti v.8. |
 |
Fig. 4. Combined DI cross section for C III with 40% metastable population; blue solid line – this work, blue dashed – difference in cross section owing to metastable population uncertainty, green dotted – Younger (1981), red dash-dotted – Fogle et al. (2008) R-Matrix, orange circles – Woodruff et al. (1978) experiment. |
Bell et al. (1983) consider the C IV values of the Crandall et al. (1979) experiment to be too low and recommend the theoretical results of Jakubowicz & Moores (1981) Coulomb-Born-Exchange approximation. The Dere (2007) cross section is close to the Knopp et al. (2001) experimental values. Calculations from FAC lie less than 10% below Bell et al. Similarly, for C V the ground state cross sections are close to Bell et al. (1983), who believe the Crandall et al. (1979) experimental technique produced inherently high values for this ion. The cross sections from Dere (2007) are close to Crandall et al..
3.1.2. Excitation–auto-ionisation data
To calculate the cross sections for EA requires data from several processes: collisional excitation, auto-ionisation and radiative decay. A bound electron is collisionally excited to an auto-ionising state above the threshold, and then it may either spontaneously ionise or decay. Calculating EA cross sections involves multiplying the excitation cross section to a level by the auto-ionisation branching ratio from that level, and summing over all levels which lie above the ionisation threshold. The auto-ionisation branching ratio is the probability that auto-ionisation takes place instead of decay. The EA cross section for an ion in an initial level j to ionise to a final level i in the next higher charge-state, through a collision with a free electron with energy ϵ, is given by:
where σpj(ϵ) is the electron-impact excitation cross section to an auto-ionising level p, Aa is the auto-ionisation rate and Ar is the radiative decay rate. The sum over p is for excitations to all levels within the ion over the ionisation limit, the sum over q is for all final levels in the next higher charge-state to which the ion may spontaneously ionise, and the sum over s is for all levels to which radiative decay may take place within the existing ion. Autostructure was used to obtain data for the required processes, which were then combined to create level resolved rate coefficients for ground and metastable levels, which have been made available online. Only excitations to energy levels shown by NIST4 (Kramida et al. 2018) to be above the ionisation limit were included.
As mentioned in Sect. 3.1.1, the DW method is less reliable for neutral or nearly neutral charge states. This was observed when computing EA cross sections for C II, which showed variations of factors of two to three in the cross section depending on the structure of the ion. To resolve this, the structure used by Liang et al. (2012) for carbon was utilised. This produced a total EA cross section for the ground term, 2s2 2p 2P, which has a peak of 1.2 × 10−17 cm−3 at 55 eV, (cf. the DI cross section in Fig. 2). At the same energy, the Ludlow et al. (2008) DW, total EA cross section is 20% higher. Their R-Matrix cross sections include both DI and EA. Compared to that result, the total DI and EA cross section from this work is 26% higher at the peak. This accords with the conclusion of Ludlow et al., who state how electron coupling effects, inherently included in R-Matrix calculations, can reduce total cross sections by 15–35%. For the metastable term, 2s 2p2 4P, the total DI and EA cross section at the peak is 8% below their R-Matrix cross section (Fig. 5).
 |
Fig. 5. Total collisonal ionisation cross section for C II metastable term, 2s 2p2 4P; blue solid line – this work, blue dotted – this work (DI only), red dashed – Ludlow et al. (2008) R-Matrix. |
The uncertainty observed in the cross sections, which arose from differences in structure, was also seen in the rate coefficients. Because of this variability, the EA rate coefficients were computed using the R-Matrix, thermally averaged collision strengths from Liang et al. (2012) in combination with AS auto-ionisation data, which was calculated using an identical structure. Since the R-Matrix collision strengths only include outer shell excitations, inner shell EA has been added to the rate coefficients by using AS DW excitation and auto-ionisation data with the same structure. Inner shell EA contributes significantly less to the total EA over most of the temperature range for this ion. As an example of the contribution made by EA for this ion, at 40 000 K the ground level EA rate coefficient is one-third of the ground level DI value. Because of the uncertainty found with the DW approximation for C II and the absence of similar R-Matrix excitation data for C I, no attempt has been made to produce EA rate coefficients for C I at this stage.
For C III EA from the ground and metastable levels is possible through excitations of the 2s2 and 2s 2p electrons to the 2p 4d 3D term and above followed by auto-ionisation to the ground level of C IV (cf. Loch et al. 2005). This is seen in the cross section shown in Fig. 6. The inner shell cross section of this work is within 5% of Chianti, which does not have outer shell excitations. The main contributions for the ground level come from weaker two-electron transitions, whereas for the metastable, 2s 2p 3P, term the dominant contributions come from one-electron excitations. Consequently, the metastable term EA cross section is an order of magnitude higher, which is in agreement with the value given by Loch et al. (2005), that is, about 10% of the DI value. For EA from ground and metastable levels to final levels in C IV above the ground the only contribution to EA is from K-shell excitations.
 |
Fig. 6. Total EA cross section for C III ground level; blue solid line – this work, green dashed – Chianti v.8. |
Cross sections were much less prone to variations caused by the structure than for C II; differences in structure altered the results by 10% at the most. However, owing to sensitivity of the collision strengths to the mixing coefficients and weak, two-electron excitations from the ground, EA rate coefficients were affected by which approximation was used for the scattering computation. Consequently, EA rate coefficients were computed using R-Matrix collision strengths and AS auto-ionisation data, in the same way as for C II. This time, the excitation data were from Fernández-Menchero et al. (2014). Using the R-Matrix data also had the advantage of including the resonance contributions. Since only L-shell excitations are available for C III in Fernández-Menchero et al., to these were added unitarised DW, K-shell contributions, employing the same structure as the R-Matrix data. Inner shell EA becomes important in the rate coefficients for temperatures above 106 K when calculated with a Maxwellian electron distribution.
A comparison close to the threshold of the total, collisional ionisation cross section of C III with the experiment of Woodruff et al. (1978) is shown in Fig. 7. It may be possible to observe some peaks close to the relevant thresholds, but, given that the combined uncertainties in the metastable population and cross section measurements are greater than the EA contribution, these may simply be scatter in the results.
 |
Fig. 7. Combined total collisional ionisation cross section for C III with 40% metastable population; blue solid line – this work, blue dashed – difference in cross section owing to metastable population uncertainty, green dotted – Younger (1981) (DI only), red dash-dotted – Fogle et al. (2008) R-Matrix, orange circles – Woodruff et al. (1978) experiment. |
For C IVK-shell excitations provide the only possibility for EA to take place. The cross section for the ground level is within 10% of Chianti. Teng et al. (2000) estimate the uncertainty in their experimental values to be 20–30%, which encompasses both of the cross sections shown here (Fig. 8). The DW rate coefficients agree with the R-Matrix rate coefficients produced from the thermally averaged collision strengths calculated by Liang & Badnell (2011) to within 5%, but the R-Matrix ones are made available here for the sake of completeness.
 |
Fig. 8. Total EA cross section for C IV ground level; blue solid line – this work, green dashed – Chianti v.8, red dash-dotted – Teng et al. (2000) experiment. |
3.1.3. Multiple ionisation cross sections
Hahn et al. (2017) compile a set of experimental, multiple ionisation cross sections for a wide range of astrophysically relevant ions. From these, they provide geometrical fitting formulæ to reproduce the cross sections. The formulæ they provide were used to calculate rates, which were included in the CR model.
Double, direct ionisation produces cross sections which are between 0.5% and 4% of single DI values. Ionisation followed by auto-ionisation is about an order of magnitude lower than double DI, except in the case of C II, where it is comparable, but at an higher threshold. Triple DI is two orders of magnitude less than double DI, and was not included in the modelling. Another factor to bear in mind for the CR model is that the threshold for double ionisation is much higher, and so, compared to single ionisation, the rates will be significantly lower. The rates may be more significant with non-Maxwellian electron distributions which have an enhanced population at high energies.
3.2. Collisional-radiative model
As described in Sect. 2.2, the rates available in Chianti were imported into the model, followed by the collisional ionisation and photo-ionisation rates calculated in this work. The effect of each process was determined by first running the model in the coronal approximation, that is, ions in a single, ground level with total rates connecting neighbouring charge states. This assisted identifying the primary effect each process has on the charge-state distribution. Thereafter, the model was switched to modelling resolved by levels for each atomic process to determine the effect on ion populations. From Chianti, data were imported from 42 levels of C I, 204 levels of C II, 238 of C III and 331 of C IV. The remaining charge states were each modelled as a single level. These ion models are valid for solar densities, up to flare densities of Ne = 1013 cm−3.
3.2.1. CR model with collisional ionisation from metastables
It is densities which redistribute ion populations to terms above the ground term that produce the first noticeable effects of shifting the temperature formation of ions in the level resolved model, compared to the single level model. For C I, the term above the ground is populated at a density of 104 cm−3. Therefore, the difference in C I populations at this density between the single level model, which is used by Chianti, and the level resolved model of this work is owing to ionisation occurring from the metastable levels (Fig. 9). For C II and C III, however, the term above the ground is not appreciably populated until the density reaches 108−1010 cm−3. Consequently, the difference between the populations of the single level and level resolved models for those ions at densities lower than 108 cm−3 arises from the differing ionisation rates for the ground term being used by the models. At 1010−1012 cm−3 the metastable populations have reached statistical balance in these ions, and so above these densities the effect collisional ionisation plays through metastable levels reaches saturation. To illustrate these effects, at 40 000 K the total C II population is 47% with a density of 104 cm−3, 45% at 108 cm−3, 34% at 1010 cm−3 and 31% at 1012 cm−3.
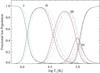 |
Fig. 9. Effect with density of level-resolved, collisional ionisation on the CR model; blue dotted line – Chianti v.8, green dash-dotted – this work at 104 cm−3 density, red dash-dot-dotted – 108 cm−3, purple dashed – 1010 cm−3, black solid – 1012 cm−3. |
The changes in the ionisation balance also affect the temperature at which ions peak in their abundance. At a density of 1012 cm−3 C II now forms its peak at 21 000 K instead of 24 000 K at zero density; for C III it is now at 56 000 K from 76 000 K, and forms 92% of the population at the peak, instead of 87%. C IV witnesses a 55% increase in abundance at its peak, from a fractional population of 0.29 to 0.45. Since it has no metastable levels, the ionisation rates of C IV do not change with density, and so the increased populations seen in both C IV and C V are attributable to the formation of C III at lower temperatures in the level resolved model.
Many CR models only include K-shell EA, (see e.g. Arnaud & Rothenflug 1985; Avrett & Loeser 2008). However, the threshold energy is far above the formation temperatures of the ions, and EA makes negligible changes to the ion populations. It is L-shell EA that is making an equal contribution to DI in the shift in ion formation (Fig. 10). Goldberg et al. (1965) indicate that EA would make an important contribution to ion populations for B-like O IV, but not for Be-like O V. With carbon EA is seen to be important for both B-like and Be-like ions. Since the ionisation potential of C I is small, there would be many excited configurations which would contribute to EA of this ion, and so it is reasonable to expect its formation temperature to be lowered further. It would broaden the temperature range over which C II forms, increasing its contribution to emission. Multiple ionisation has no noticeable influence on the charge-state distribution in these conditions.
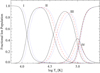 |
Fig. 10. Changes in the effect of level-resolved, collisional ionisation on the CR model at 1010 cm−3 density when EA is excluded; black solid line – this work with EA, red dashed – this work without EA, blue dotted – Chianti v.8. |
3.2.2. CR model with DR suppression
Although DR suppression is approximated here, it gives clues to the behaviour seen in full CR models, in which high n levels are included. Looking at the impact of DR suppression on the single level, coronal approximation model first, in order to separate this phenomenon from the effect of collisional ionisation, the only noticeable effect on C I is in the reduction of populations at the higher temperature end of its formation, above log Te(K) = 4.1 (Fig. 11). This can be accounted for in the DR rates of C II, which are at their weakest in the range 2000–15 000 K. Suppressing these rates will have little impact on the charge-state distribution.
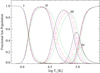 |
Fig. 11. Effect with density of DR suppression on the ground-to-ground CR model; blue dotted line – Chianti v.8, green dash-dotted – this work at 104 cm−3 density, red dash-dot-dotted – 108 cm−3, purple dashed – 1010 cm−3, black solid – 1012 cm−3. |
The DR rates for C III are strong in the region of log Te(K) = 4.6–5.9, explaining the greater effect DR suppression has on the populations of C II and C III at temperatures above log Te(K) = 4.5. The suppression causes a shift in the peak abundance of C III from 76 000 K to 55 000 K and the peak population from 0.87 to 0.93 at a density of 1012 cm−3 compared to zero density modelling. This is similar to the effect level resolved, collisional ionisation has on the model. The consequent effect of lowering the formation temperature of C III is, again, to substantially increase abundance of C IV. This time, the peak abundance of C IV increases from 0.29 at density 104 cm−3 to 0.56 at 1012 cm−3, a rise of 93%, more significant than the rise seen with collisional ionisation.
The behaviour seen in C IV through density suppression of DR is explained by two factors. Firstly, the DR rate from C IV is much larger than radiative recombination at its formation temperature. Thus, suppressing the DR rate causes more ions to remain in this ionisation stage, and reducing the populations in C III. Secondly, it is explained by a relatively small change in the population of C V. Physically, this is based on the closed shell nature of C V. The ions will be almost completely in the ground level, which requires free electrons to have high energies in order to excite bound, K-shell electrons to the next, L-shell level in order for DR to occur. Thus, the C V DR rates are not significant until temperatures rise above 106 K, far higher than where C IV forms. These ions are being formed by the interplay of collisional ionisation of C IV and radiative recombination from C V, processes which have significantly lower thresholds.
3.2.3. CR model with both metastable ionisation and DR suppression
Considering the combination of level resolved, collisional ionisation and dielectronic recombination suppression (Fig. 12), the change with density between C I and C II comes through ionisation of the metastable levels in C I. Between C II and C III, the individual effects of collisional ionisation and DR suppression are comparable and both contribute to lowering the peak formation temperatures. Level resolved ionisation from C III has a lesser impact on the population of C IV, and so it is the DR suppression of C IV that is influencing its increase in population the most. Since there are no metastable levels in C IV, the only increase in formation of C V at a lower temperature is owing to the increased population of C IV.
 |
Fig. 12. Combined effect with density of level-resolved, collisional ionisation and DR suppression on the CR model; blue dotted line – Chianti v.8, green dash-dotted – this work at 104 cm−3 density, red dash-dot-dotted – 108 cm−3, purple dashed – 1010 cm−3, black solid – 1012 cm−3. |
Looking at the charge-state distribution as a whole, the reduction in temperature at which C I ionises combined with almost no change in the formation temperature of C V means there is a wider range over which the intervening ions may form. There is a consequent shift towards lower temperatures and higher peak populations.
3.2.4. Effect of photo-ionisation on ion populations
PI rates become weaker with increasing charge state, such that C V and C VI are unaffected by this process; collisional processes are dominating the higher density plasma conditions typical of the solar and stellar atmospheres which are being modelled here. Since the PI rates are independent of temperature and density, in conditions of higher density the collisional rates will dominate. So, based on the quiet Sun radiances used in this model, at densities above 1012 cm−3 the charge-state distribution is unaffected by PI. At lower densities, such as TR densities of around 1010 cm−3, the usual formation curves of C III and C IV exist, but a small population of C III (12%) is present at lower temperatures, which arises from PI of C II (Fig. 13).
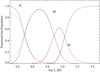 |
Fig. 13. Effect of photo-ionisation on the level-resolved CR model at 1010 cm−3 density; black solid line – this work without PI, red dashed – this work with PI. |
Since the PI rates depend on the particular radiances present for each of the transitions, it is difficult to determine systematic differences when switching between the coronal approximation and level resolved models. In the particular scenario simulated here, in the ground-to-ground model where total rates are used for all the processes the C III population is 7% at 20 000 K, instead of 12%. The scenario demonstrates, as with collisional ionisation, level resolved photo-ionisation produces greater populations in the next higher charge states because of the faster ionisation rates from metastable levels. Stronger radiances in other conditions, when active regions are present or during flares, for instance, should result in greater population shifts towards higher charge states.
3.2.5. Comparisons with other CR models
Now that the basic model has been built, it is possible to compare it with the results of earlier works (Fig. 14). Although there are many processes at play in a full model, it may be possible to explain several of the differences between the two models. The C II ionisation cross section used by Nussbaumer & Storey (1975) was the approximation of Lotz (1968), which is noticeably below experiment for this particular ion. As noted in Sect. 3.1.2, the total collisional ionisation rate for the ground term of C II is noticeably higher than the R-Matrix results, further enhancing the ionisation rates in this work by comparison. Nussbaumer & Storey also included fewer excitations to auto-ionising states above the threshold, leading to further differences in the ionisation rates of C II and C III. Their ion populations could also be different with these ions and for C IV because they used the general formula of Burgess & Summers (1969) for DR.
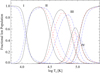 |
Fig. 14. Comparison of the CR model with other works at 1010 cm−3 density; black solid line – this work, red dashed – Nussbaumer & Storey (1975), blue dash-dotted – Summers (1974). |
Density effects on the population of C IV can certainly be seen in the work of Summers (1974), but it is being formed at an obviously higher temperature. It suggests the model may have used either slower ionisation or faster recombination rates, or a combination of both. Comparison with the later ADAS modelling, which updates the work of Summers (1974) and used both the DR rates and modelling described in Badnell et al. (2003), shows similar results to the current work.
Comparing the case with photo-ionisation included (Fig. 15), differences in radiation field and PI cross sections can reasonably be expected to produce variations between the two models; Nussbaumer & Storey (1975) used radiances from a quiet Sun where some active regions were present. Allowing for this, the similarities in the overall charge-state distribution are recognised, especially with the difference in collisional ionisation rates taken into consideration, which was noted in the case without PI.
 |
Fig. 15. Comparison of the CR model and other work at 1010 cm−3 density when photo-ionisation is included; black solid line – this work, red dashed – Nussbaumer & Storey (1975). |
4. Modelling the quiet Sun transition region
In order to test how much the present ion populations could affect plasma diagnostics, a means of comparing the results with observations is now discussed. A diagnostic technique which uses ion populations involves predicting line intensities from a given set of ion populations and comparing the results with observed intensities. This provides a way of determining the plasma conditions which produced the observed emission. Since the conditions to which this CR model most applies is the solar TR tests against the line emission from this region will be made.
The technique used to calculate the theoretical line intensities is known as differential emission measure (DEM) modelling, (as described e.g. by Del Zanna & Mason 2018). It uses the observed line intensities to estimate the amount of plasma present along the line of sight and its density distribution. The technique can be used in situations where the temperature distribution of the plasma varies smoothly along the field of view, which is a reasonable assumption for these solar conditions. It uses ion and level populations from the modelling, radiative decay rates and solar elemental abundances, along with the plasma density distribution with height, in order to calculate the expected intensity of each line. The DEM technique is also used for other purposes, such as determining elemental abundances, for instance.
The DEM modelling is dependent on ion populations, which is the very quantity being tested here. As a result, ion populations which have been previously published should be used to calculate the density distribution of the plasma with height. Once the density distribution has been established, the predicted intensities can be calculated using carbon ion populations from different sources and compared with observations.
4.1. Method to compare the CR model with observations
The modelling of the quiet Sun TR observed on the disc was considered. The analysis differs from that of Del Zanna (2019), who uses the EUV irradiances in the 60–1040 Å range. It also differs from the analysis which has been presented in Parenti et al. (2019), since they utilise the narrower UV range obtained by the Solar Ultraviolet Measurement of Emitted Radiation (SUMER) instrument on the Solar and Heliospheric Observatory. The radiances used to calculate the photo-ionisation rates in Sect. 2.1.4 were not used for the DEM because they do not extend to wavelengths which are important for line emission from carbon in the TR.
As a baseline, the quiet Sun UV and EUV radiances obtained with the Skylab SO55 Harvard instrument by Vernazza & Reeves (1978) were used because of the more extended spectral range. The 35% radiometric uncertainty and spectral resolution of about 1.6 Å of the instrument are noted. Only a few, relatively unblended, strong lines were selected, formed at temperatures close to those of C II–C IV. Much better spectra in the UV (in terms of spectral resolution and radiometric calibration) were obtained by SUMER. However, as has been pointed out by Wilhelm et al. (1998), very good agreement between the SUMER and Skylab SO55 quiet Sun radiances is present when lines relatively bright and isolated were considered. The Skylab radiances were therefore supplemented with a few among those which have been reported by Wilhelm et al. (1998) for the quiet Sun during the 1996 solar minimum. Often, good agreement is found with the quiet Sun radiances which have been obtained by OSO-4 (Dupree 1972). As shown by Andretta & Del Zanna (2014) and Del Zanna & Andretta (2015), solar cycle variations of quiet Sun radiances and irradiances for TR lines are smaller than the calibration uncertainties. For weaker or unresolved lines the quiet Sun, SUMER radiances of Parenti et al. (2005) were considered, although it has been seen that some noticeable differences with both the Skylab SO55 and SUMER radiances of Wilhelm et al. (1998) are present.
Chianti v.8 atomic data (Del Zanna et al. 2015) were used and the Asplund et al. (2009) photospheric abundances. The DEM modelling was carried out with the improved version released in Chianti v.9 (Dere et al. 2019). It uses MPFIT to find the best solution, assuming the DEM is a spline distribution.
The intensity of the vast majority of the strongest spectral lines is largely independent of density. However, some TR lines are sensitive to the varying density in the lower part of this region. It is customary to model TR lines with constant pressure, and the value selected for this work was 3 × 1014 cm−3 K−1, obtained from the model atmosphere given by Avrett & Loeser (2008). The effective temperature of a line is given by:
which is an average temperature more indicative of where a line is formed. As the DEM increases exponentially towards lower temperatures, Teff is normally much lower than Tmax, the temperature where the contribution function G(T) of a line has a maximum. In turn, Tmax is normally higher than the temperature of maximum ion population in equilibrium.
4.2. Results of the DEM modelling
As a baseline, the charge-state distributions at zero density from Chianti were used for all ions in order to determine the DEM from the observed lines. Carbon lines were excluded from this process so that the results for carbon from zero density modelling and this work were treated equally; it also prevented the zero density modelling of Li-like C IV adversely affecting the DEM. Once the DEM was determined, the ratios of predicted to observed intensities for all of the lines were calculated. The ratios using the Chianti ion populations are shown in column R1 of Table 1. The ratios using the ion populations from this work are given in column R2.
Comparison of predicted and observed quiet-Sun UV and EUV radiances.
Regarding the results of Chianti in column R1, clearly there are some issues at lower temperatures, particularly with N II and N III, where the ratios of predicted to observed intensities for lines emitted within the same ion are not comparable with each other. Since both pairs of lines from these nitrogen ions are largely independent of density, it suggests the cause is more likely to be related to the formation temperatures of the lines. Based on the evidence of modelling carbon, it is reasonable to infer that modelling which is dependent on density would show shifts in the formation temperatures of the nitrogen ions and provide improved theoretical values. It is also noted that the N II measurements do not come from the same observations, although this does not apply to the N III measurements, which show the same discrepancy. Although for the O III lines the predicted intensities are lower than observations, both ratios are similar. For the lines which are formed at higher temperatures, the modelling at zero density clearly provides better results than when it is used for lower temperatures, confirming the discussion in Sect. 1.
Looking at the carbon ions, C II is particularly interesting. Some opacity effects are present as both ratios of the strong multiplets around 1036 Å and 1335 Å deviate from the theoretical ones in the optically thin approximation. However, the deviations are not large and are similar. For example, the ratio of the 1335.7 Å (self-blend) and 1334.5 Å radiances is about 1.4 as measured by SUMER (cf. Judge et al. 2003) or 1.3 as measured by HRTS (Sandlin et al. 1986) compared to a theoretical ratio of nearly two. The ratio of the 1037 Å and 1036.3 Å doublet is about 1.3 as measured on the disc by SUMER (Wilhelm et al. 1998) compared to the optically thin ratio of two. The C II lines are nearly Gaussian in the middle of the disc, but become increasingly broad and affected by opacity towards the solar limb.
The ratio of the line with lower oscillator strengths, at 1036.3 Å, with the 1335.7 Å self-blend is strongly temperature sensitive. With an isothermal approximation, the observed radiances indicate a temperature of log T[K] = 4.23, that is, lower than the temperature of line formation in equilibrium with Chianti, log T[K] = 4.45, and with this work, log T[K] = 4.40. Indeed, there is a significant discrepancy in this ratio of 2.1 as predicted using the Chianti tables. Using the ion fractions from the level resolved modelling reduces the ratio to 1.8.
Considering C III, as described for example in Del Zanna & Mason (2018), the ratio of the resonance line at 977 Å with any line within the 1175 Å multiplet is both density and temperature sensitive. With the results both from this work and Chianti, the ratios of the lines within the ion are close to one another, suggesting the pressure selected for the modelling was a good reflection of actual conditions. However, with the Chianti results there is obviously a discrepancy between predicted intensities and observations. In contrast, very good agreement with observation was obtained when using the ion populations modelled in this work.
The combined effect of lowering the formation temperature and increasing the peak abundance of Li-like C IV increases its predicted line intensity by more than a factor of two compared to the zero density modelling. This significantly reduces the discrepancy between predicted and observed intensities in the quiet Sun. The DEM was established using ion populations from modelling at zero density and, as discussed earlier, does not fully reflect the conditions of higher density, lower temperature plasmas. This could, therefore, have affected determining the DEM properly. Once ion populations for other elements have been modelled in the way described here it may produce improvements in the DEM modelling and further agreement with observations for this ion.
5. Conclusions
This study has again highlighted, for carbon, in astrophysical plasmas of higher density, the importance of electron impact ionisation from metastable levels and the suppression of dielectronic recombination in establishing the ion populations. The effect of ionisation from metastable levels reaches saturation once the level populations reach statistical equilibrium at high enough densities, whereas DR suppression makes an increasing contribution as density rises. Outer shell excitation–auto-ionisation for C II and C III was shown to contribute significantly to the shift with density in the formation temperatures of C III and C IV.
Suppression of dielectronic recombination was approximated as a way of determining its influence on the charge-state distribution. As Nikolić et al. (2013, 2018) state, the method is to be used only as a guide to determine whether full modelling is required. The work carried out here shows that, in these plasma conditions, building the full CR model is not only warranted, but necessary in order to effectively model the ion populations. The focus of the work will now be to build a full model by the inclusion of highly excited levels. Initial indications show that photo-ionisation could also be important for the low charge states of carbon, but the true extent of this will not be known until radiative transfer effects have been included.
Modelling with the new atomic rates has noticeably improved predictions for the carbon charge states observed in the quiet Sun, and in particular for Li-like C IV. The results of the modelling are particularly relevant for understanding the formation of the carbon TR lines observed by instruments like IRIS, and SPICE on the forthcoming Solar Orbiter mission. It has been demonstrated that diagnostics derived from such instruments which are dependent on ion populations require level resolved, charge-state distributions to correctly infer the plasma conditions.
Acknowledgments
Support by STFC (UK) via the consolidated grant of the DAMTP astrophysics group at the University of Cambridge is acknowledged, and the support of a University of Cambridge Isaac Newton Studentship. The authors would like to thank the anonymous reviewer for highlighting areas where explanations could be clarified and the focus of the paper improved. Most of the atomic rates used in the present study were produced by the UK APAP network, funded by STFC via several grants to the University of Strathclyde. Acknowledgment is made of the use of the OPEN-ADAS database, maintained by the University of Strathclyde. Chianti is a collaborative project involving George Mason University, the University of Michigan, the NASA Goddard Space Flight Centre (USA) and the University of Cambridge (UK).
References
- Abdel-Naby, S. A., Ballance, C. P., Lee, T. G., Loch, S. D., & Pindzola, M. S. 2013, Phys. Rev. A, 87, 022708 [NASA ADS] [CrossRef] [Google Scholar]
- Aitken, K. L., Harrison, M. F. A., & Rundel, R. D. 1971, J. Phys. B At. Mol. Phys., 4, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Andretta, V., & Del Zanna, G. 2014, A&A, 563, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., & Rothenflug, R. 1985, A&AS, 60, 425 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Avrett, E. H., & Loeser, R. 2008, ApJS, 175, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2006, ApJS, 167, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R. 2011, Comput. Phys. Commun., 182, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., O’Mullane, M. G., Summers, H. P., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, K. L., Gilbody, H. B., Hughes, J. G., Kingston, A. E., & Smith, F. J. 1983, J. Phys. Chem. Ref. Data, 12, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Bradshaw, S. J., Del Zanna, G., & Mason, H. E. 2004, A&A, 425, 287 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brook, E., Smith, A. C. H., & Harrison, M. F. A. 1978, J. Phys. B At. Mol. Phys., 11, 3115 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A. 1964, ApJ, 139, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A. 1965, ApJ, 141, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., & Seaton, M. J. 1964, MNRAS, 127, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., & Summers, H. P. 1969, ApJ, 157, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, W. M., Jordan, C., Ridgeley, A., & Wilson, R. 1971, Phil. Trans. R. Soc. London Ser. A, 270, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Crandall, D. H., Phaneuf, R. A., Hasselquist, B. E., & Gregory, D. C. 1979, J. Phys. B At. Mol. Phys., 12, L249 [CrossRef] [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phy., 289, 2733 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G. 2019, A&A, 624, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., & Andretta, V. 2015, A&A, 584, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., & Mason, H. E. 2018, Liv. Rev. Sol. Phys., 15 [Google Scholar]
- Del Zanna, G., Landini, M., & Mason, H. E. 2002, A&A, 385, 968 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P. 2007, A&A, 466, 771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Young, P. R., et al. 2009, A&A, 498, 915 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Del Zanna, G., Young, P. R., Landi, E., & Sutherland, R. S. 2019, ApJS, 241, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, J. G., Summers, H. P., & Bryans, P. 2005, A&A, 430, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dudík, J., Del Zanna, G., Dzifčáková, E., Mason, H. E., & Golub, L. 2014, ApJ, 780, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Dudík, J., Dzifčáková, E., Meyer-Vernet, N., et al. 2017, Sol. Phys., 292, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Dupree, A. K. 1972, ApJ, 178, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Falk, R. A., Stefani, G., Camilloni, R., et al. 1983, Phys. Rev. A, 28, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Menchero, L., Del Zanna, G., & Badnell, N. R. 2014, A&A, 566, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fogle, M., Bahati, E. M., Bannister, M. E., et al. 2008, ApJS, 175, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, L., Dupree, A. K., & Allen, J. W. 1965, Ann. d’Astrophys., 28, 589 [NASA ADS] [Google Scholar]
- Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, M., Müller, A., & Savin, D. W. 2017, ApJ, 850, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Hamdan, M., Birkinshaw, K., & Hasted, J. B. 1978, J. Phys. B At. Mol. Phys., 11, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Jakubowicz, H., & Moores, D. L. 1981, J. Phys. B At. Mol. Phys., 14, 3733 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. G., Woods, T. N., Brekke, P., & Rottman, G. J. 1995, ApJ, 455, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Judge, P. G., Carlsson, M., & Stein, R. F. 2003, ApJ, 597, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Knopp, H., Teng, H., Ricz, S., Schippers, S., & Müller, A. 2001, Phys. Scr. Vol. T, 92, 379 [NASA ADS] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team 2018, NIST Atomic Spectra Database (ver. 5.6.1.) [Google Scholar]
- Liang, G. Y., & Badnell, N. R. 2011, A&A, 528, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, G. Y., Badnell, N. R., & Zhao, G. 2012, A&A, 547, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loch, S. D., Witthoeft, M., Pindzola, M. S., et al. 2005, Phys. Rev. A, 71, 012716 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, W. 1968, Z. Phys., 216, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, J. A., Loch, S. D., Pindzola, M. S., et al. 2008, Phys. Rev. A, 78, 052708 [NASA ADS] [CrossRef] [Google Scholar]
- Malinkovsky, M., Heroux, L., & Sahal-Brechot, S. 1973, A&A, 23, 291 [NASA ADS] [Google Scholar]
- Mariska, J. T. 1992, The Solar Transition Region (Cambridge: Cambridge University Press), 290 [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., Hansteen, V. H., & Gudiksen, B. 2016, ApJ, 817, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Mazzitelli, G., Colafrancesco, S., & Vittorio, N. 1998, A&AS, 133, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McWhirter, R. W. P., & Summers, H. P. 1984, in Applied Atomic Collision Physics Volume 2: Plasmas, eds. C. F. Barnett, & M. F. A. Harrison, 52 [Google Scholar]
- Nikolić, D., Gorczyca, T. W., Korista, K. T., Ferland, G. J., & Badnell, N. R. 2013, ApJ, 768, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolić, D., Gorczyca, T. W., Korista, K. T., et al. 2018, ApJS, 237, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Nussbaumer, H., & Storey, P. J. 1975, A&A, 44, 321 [NASA ADS] [Google Scholar]
- Olluri, K., Gudiksen, B. V., & Hansteen, V. H. 2013, ApJ, 767, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Parenti, S., Vial, J.-C., & Lemaire, P. 2005, A&A, 443, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parenti, S., Del Zanna, G., & Vial, J. 2019, A&A, 625, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polito, V., Del Zanna, G., Dudík, J., et al. 2016, A&A, 594, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rathore, B., & Carlsson, M. 2015, ApJ, 811, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Sandlin, G. D., Bartoe, J.-D. F., Brueckner, G. E., Tousey, R., & Vanhoosier, M. E. 1986, ApJS, 61, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1964, Planet. Space Sci., 12, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, H. P. 1972, MNRAS, 158, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, H. P. 1974, MNRAS, 169, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Summers, H. P., Dickson, W. J., O’Mullane, M. G., et al. 2006, Plasma Phys. Control. Fusion, 48, 263 [CrossRef] [Google Scholar]
- Suno, H., & Kato, T. 2007, J. Phys. Conf. Ser., 72, 012018 [CrossRef] [Google Scholar]
- Teng, H., Knopp, H., Ricz, S., et al. 2000, Phys. Rev. A, 61, 060704 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., & Raymond, J. C. 1979, ApJ, 228, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., & Reeves, E. M. 1978, ApJS, 37, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhelm, K., Lemaire, P., Dammasch, I. E., et al. 1998, A&A, 334, 685 [NASA ADS] [Google Scholar]
- Woodruff, P. R., Hublet, M.-C., Harrison, M. F. A., & Brook, E. 1978, J. Phys. B At. Mol. Phys., 11, L679 [CrossRef] [Google Scholar]
- Woods, T. N., Chamberlin, P. C., Harder, J. W., et al. 2009, Geophys. Res. Lett., 36, L01101 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, I., Danjo, A., Hirayama, T., et al. 1989, J. Phys. Soc. Jpn., 58, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R. 2018, ApJ, 855, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Younger, S. M. 1981, Phys. Rev. A, 24, 1278 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Configuration-average DI cross section for C I ground state; blue solid line – this work, green dash-dotted – Bell et al. (1983), purple dashed – Abdel-Naby et al. (2013) TDCC, red dotted – Abdel-Naby et al. (2013) DW. |
| In the text | |
 |
Fig. 2. DI cross section from C II ground level; solid blue line – this work, red dotted – Chianti v.8, green dashed – Bell et al. (1983), orange circles – Yamada et al. (1989). |
| In the text | |
 |
Fig. 3. DI cross section for C III ground level; blue solid line – this work, green dashed – Younger (1981), red dash-dotted – Fogle et al. (2008) R-Matrix, purple dotted - Chianti v.8. |
| In the text | |
 |
Fig. 4. Combined DI cross section for C III with 40% metastable population; blue solid line – this work, blue dashed – difference in cross section owing to metastable population uncertainty, green dotted – Younger (1981), red dash-dotted – Fogle et al. (2008) R-Matrix, orange circles – Woodruff et al. (1978) experiment. |
| In the text | |
 |
Fig. 5. Total collisonal ionisation cross section for C II metastable term, 2s 2p2 4P; blue solid line – this work, blue dotted – this work (DI only), red dashed – Ludlow et al. (2008) R-Matrix. |
| In the text | |
 |
Fig. 6. Total EA cross section for C III ground level; blue solid line – this work, green dashed – Chianti v.8. |
| In the text | |
 |
Fig. 7. Combined total collisional ionisation cross section for C III with 40% metastable population; blue solid line – this work, blue dashed – difference in cross section owing to metastable population uncertainty, green dotted – Younger (1981) (DI only), red dash-dotted – Fogle et al. (2008) R-Matrix, orange circles – Woodruff et al. (1978) experiment. |
| In the text | |
 |
Fig. 8. Total EA cross section for C IV ground level; blue solid line – this work, green dashed – Chianti v.8, red dash-dotted – Teng et al. (2000) experiment. |
| In the text | |
 |
Fig. 9. Effect with density of level-resolved, collisional ionisation on the CR model; blue dotted line – Chianti v.8, green dash-dotted – this work at 104 cm−3 density, red dash-dot-dotted – 108 cm−3, purple dashed – 1010 cm−3, black solid – 1012 cm−3. |
| In the text | |
 |
Fig. 10. Changes in the effect of level-resolved, collisional ionisation on the CR model at 1010 cm−3 density when EA is excluded; black solid line – this work with EA, red dashed – this work without EA, blue dotted – Chianti v.8. |
| In the text | |
 |
Fig. 11. Effect with density of DR suppression on the ground-to-ground CR model; blue dotted line – Chianti v.8, green dash-dotted – this work at 104 cm−3 density, red dash-dot-dotted – 108 cm−3, purple dashed – 1010 cm−3, black solid – 1012 cm−3. |
| In the text | |
 |
Fig. 12. Combined effect with density of level-resolved, collisional ionisation and DR suppression on the CR model; blue dotted line – Chianti v.8, green dash-dotted – this work at 104 cm−3 density, red dash-dot-dotted – 108 cm−3, purple dashed – 1010 cm−3, black solid – 1012 cm−3. |
| In the text | |
 |
Fig. 13. Effect of photo-ionisation on the level-resolved CR model at 1010 cm−3 density; black solid line – this work without PI, red dashed – this work with PI. |
| In the text | |
 |
Fig. 14. Comparison of the CR model with other works at 1010 cm−3 density; black solid line – this work, red dashed – Nussbaumer & Storey (1975), blue dash-dotted – Summers (1974). |
| In the text | |
 |
Fig. 15. Comparison of the CR model and other work at 1010 cm−3 density when photo-ionisation is included; black solid line – this work, red dashed – Nussbaumer & Storey (1975). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.