| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A40 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201935286 | |
| Published online | 07 May 2019 | |
Additional fluorine abundance determinations in evolved stars
1
Departamento Física Teórica y del Cosmos, Universidad de Granada,
18071
Granada,
Spain
e-mail: cabia@ugr.es
2
Istituto Nazionale di Astrofisica – Osservatorio Astronomico d’Abruzzo,
Via Maggini snc,
64100,
Teramo,
Italy
3
INFN – Sezione di Perugia,
Via A. Pascoli,
Perugia, Italy
4
Observatório Nacional, Rua General José Cristino,
77,
20921-400
São Critovão, Rio de Janeiro,
RJ, Brazil
5
University of Arizona,
Tucson,
AZ
85719, USA
6
Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS,
Laboratoire Lagrange, France
7
National Optical Astronomy Observatories,
Tucson,
AZ
85719, USA
Received:
15
February
2019
Accepted:
22
March
2019
We present new fluorine abundance measurements for a sample of carbon-rich asymptotic giant branch (AGB) stars and two other metal-poor evolved stars of Ba/CH types. The abundances are derived from IR, K-band, high-resolution spectra obtained using GEMINI-S/Phoenix and TNG/Giano-b. Our sample includes an extragalactic AGB carbon star belonging to the Sagittarius dSph galaxy. The metallicity of our stars ranges from [Fe/H] = 0.0 down to − 1.4 dex. The new measurements, together with those previously derived in similar stars, show that normal (N-type) and SC-type AGB carbon stars of near solar metallicity present similar F enhancements, discarding previous hints that suggested that SC-type stars have larger enhancements. These mild F enhancements are compatible with current chemical-evolution models pointing out that AGB stars, although relevant, are not the main sources of this element in the solar neighbourhood. Larger [F/Fe] ratios are found for lower-metallicity stars. This is confirmed by theory. We highlight a tight relation between the [F/⟨s⟩] ratio and the average s-element enhancement [⟨s⟩/Fe] for stars with [Fe/H] > −0.5, which can be explained by the current state-of-the-art low-mass AGB models assuming an extended 13C pocket. For stars with [Fe/H] < −0.5, discrepancies between observations and model predictions still exist. We conclude that the mechanism of F production in AGB stars needs further scrutiny and that simultaneous F and s-element measurements in a larger number of metal-poor AGB stars are needed to better constrain the models.
Key words: stars: AGB and post-AGB / stars: abundances / stars: carbon / nuclear reactions, nucleosynthesis, abundances
© ESO 2019
1 Introduction
Jorissen et al. (1992) were the first to establish firm observational evidence suggesting that the fragile element fluorine (19F) can be produced in asymptotic giant branch (AGB) stars during the thermally pulsing (TP) phase. These authors found F enhancements up to a factor fifty times solar in galactic AGB stars (both oxygen and carbon-rich) of near solar metallicity and concluded that these objects might be one of the main sources of this element in the Galaxy. However, subsequent and more ample studies of galactic AGB carbon stars (Uttenthaler et al. 2008; Abia et al. 2009, 2010, 2015), despite confirming the existence of F enhancements in AGB stars, systematically revised downward the enhancements found by Jorissen et al. (1992) up to a factor of six in some stars. Part of such a discrepancy is ascribed to the presence of molecular blends not properly accounted for by Jorissen et al. (1992) in the analysis of the HF lines in the near infrared (~2.3 μm). Moreover, these authors used line excitation energies that were inconsistent with how the excitation potentials were used in the calculation of the partition function and dissociation energy of the HF molecule (see Jönsson et al. 2014a, for a detailed explanation of this long-standing confusion). This downward revision of the F abundances has cast some doubt about the real contribution of AGB stars to the total budget of fluorine in the Galaxy.
As a matter of fact, the evolution of fluorine has recently attracted considerable attention (Renda et al. 2004; Kobayashi et al. 2011; Jönsson et al. 2017). The observed [F/Fe] and [F/O] ratios obtained in unevolved disc stars (Recio-Blanco et al. 2012; Nault & Pilachowski 2013; Pilachowski & Pace 2015; Jönsson et al. 2014a, 2017) and bulge stars (Cunha et al. 2008; Jönsson et al. 2014b) suggest a secondary behaviour of F against O for stars with [O/H] > −0.51, which may also exist against Fe. This secondary-like behaviour in unevolved stars with metallicities close to solar, if confirmed, would be compatible with that expected if low- and intermediate-mass stars (i.e. AGB stars) were found to be significant F contributors at these metallicities (Prantzos et al. 2018), although Wolf-Rayet stars may be an alternative explanation (Spitoni et al. 2018).
Future F abundance determinations in unevolved stars in a wider range of metallicities will certainly clarify the behaviour of this element with metallicity. Meanwhile, an accurate evaluation of the contribution of AGB stars to the total F budget requires a full comprehension of how F is produced in these stars. To achieve this goal, additional determinations of F abundances in AGB stars of different metallicities and their comparison with theoretical nucleosynthesis predictions are needed. In previous studies (see references above) we showed that F abundances in AGB carbon stars and the current theoretical models of F production in these stars agree within the observational uncertainties. However, two issues remained open that need further investigation: (i) the first concerns AGB carbon stars of spectral type SC, which on average show larger F overabundances than the normal (N-type) carbon stars (see e.g. Abia et al. 2015). We note that the SC-type stars are carbon stars with a C/O ≈ 1 in the envelope within a fewhundredths of a dex. Therefore, it is accepted that they are simply in the preceding evolutionary stage to that of N-type stars, which clearly showC/O > 1. The carbon enhancement of the envelope is due to the operation of third dredge-up (TDU) events after each TP, whereby the convective envelope penetrates the interior, carrying out to the surface material which has undergone He burning2. The recurrent action of TDU episodes can transform an initially O-rich (C/O < 1) AGB star into carbon rich, which dramatically alters the spectrum of the star, leading to a sequence of spectral types M-MS-S-SC-C(N-type) during the AGB phase. This spectral sequence is believed to also be a chemical one. Since F is also transported into the envelope by the TDU episodes, SC-type stars should be on average less (or similarly) enriched in this element than the normal (N-type) carbon stars. Thus, the observational fact that SC-type carbon stars appear more enriched in F than the N-type seems controversial. (ii) The second open issue concerns heavy-element nucleosynthesis. In fact, a correlation is also expected between F and the s-element enhancement in AGB stars, due to the fact that the 19F production path requires the presence of neutrons. The latter are efficiently released by the 13C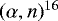 O reaction in a tiny 13C enriched layer named the 13C-pocket, which is themain neutron source of the s-process in low-mass AGB stars (e.g. Straniero et al. 1995; Gallino et al. 1998; Forestini et al. 1992). This correlation is indeed observed in near-solar-metallicity AGB carbon stars, showing a notable agreement with theoretical predictions. However, at lower metallicities, observations and models partially disagree, with models showing an F overproduction with respect to s-elements. Even so, it should be stressed that the number of available observationsat those metallicities is very small (see Abia et al. 2011). In Cristallo et al. (2014) and Abia et al. (2015) we discussed the possible nuclear and stellar model solutions to this problem, respectively. Unfortunately, a definitive answer has not yet been found.
O reaction in a tiny 13C enriched layer named the 13C-pocket, which is themain neutron source of the s-process in low-mass AGB stars (e.g. Straniero et al. 1995; Gallino et al. 1998; Forestini et al. 1992). This correlation is indeed observed in near-solar-metallicity AGB carbon stars, showing a notable agreement with theoretical predictions. However, at lower metallicities, observations and models partially disagree, with models showing an F overproduction with respect to s-elements. Even so, it should be stressed that the number of available observationsat those metallicities is very small (see Abia et al. 2011). In Cristallo et al. (2014) and Abia et al. (2015) we discussed the possible nuclear and stellar model solutions to this problem, respectively. Unfortunately, a definitive answer has not yet been found.
To shed light on the above-mentioned issues, further F determinations in SC-type and metal-poor AGB stars are necessary. This is the goal of the present study. Here we present abundance determinations of fluorine and s-process elements in ten new AGB carbon stars (five of SC-type and five of N-type) including a new extragalactic metal-deficient carbon star belonging to the Sagittarius Dwarf galaxy (Sgr 9). Furthermore, due to the difficulty of finding metal-poor AGB stars in the Galaxy, we also reanalyse two extrinsic stars (a Ba- and a CH-type star) to increase the number of metal-poor evolved stars with available F abundance. The structure of the paper is as follows. In Sect. 2 we describe the observations and the main properties of the sample stars. Section 3 contains the abundance analysis and Sect. 4 discusses the results in the framework of the most recent nucleosynthesis models for AGB stars. Finally in the last section we summarise our main conclusions.
2 Observations and analysis
Table 1 shows the astronomical facilities (telescope and instrument) used in the observations presented here, namely the 8.1 m Gemini-South (GEMINI-S) telescope with the Phoenix spectrograph (Hinkle et al. 1998) at a resolving power of R ~ 50 000 centred at 23 350 Å, to include the HF(1—0) R9 line, which is known to be the most reliable line for F abundance determinations in cool stars (Abia et al. 2009); the 3.58 m Telescope Nationale Galileo (TNG) with the Giano-b (Origlia et al. 2014) echelle spectrograph with a similar spectral resolution in the range 0.96–2.45 μm, which allows for the inclusion of several secondary HF(1-0) lines other than the R9; and the 3.5 m CAHA telescope with the two-channel spectrograph Carmenes (Quirrenbach et al. 2012) covering the wavelength ranges from 0.52 to 0.96 μm and from 0.96 to 1.71 μm with spectral resolutions R = 80, 000–100, 000. The spectrum acquired with Carmenes was used to derive s-element abundances in the star IY Hya from a few lines in the J- and H-bands (see below). Data reduction was performed using the corresponding pipelines for Giano and Carmenes spectrographs or following the procedure detailed in Smith et al. (2002) in the case of the Phoenix spectrograph. All spectra were corrected for telluric absorptions dividing by the spectrum of a hot, rapidly rotating star observed at similar air-mass to the target star using the telluric task within the IRAF package. The S/Ns achieved in the final spectra at the location of the R9 HF line (λλ 2.33583 μm) are quoted in Table 1. All ratios exceeded S∕N ~ 100 except for the faint extra-galactic AGB carbon star, Sgr 9. In the case of the star HD 123396, we reanalysed the spectrum acquired by Alves-Brito et al. (2011)3 at Gemini-Swith Phoenix, available in the Gemini archive.
The bolometric magnitudes (luminosities) of the stars (see Table 1) were obtained using Gaia DR2 parallaxes and distances according to Bailer-Jones et al. (2018), except for Sgr 9, for which we used the distance estimated by Lagadec et al. (2009) from the period-luminosity relation of Feast et al. (2006). Bolometric corrections were calculated using the calibration with the (J–K) index by Kerschbaum et al. (2010) for oxygen and carbon-rich objects after correction from interstellar extinction according to the galactic model by Arenou et al. (1992). The typical uncertainty in the estimated Mbol values is ± 0.2 mag, mainly coming from the uncertainty in the parallax (≤ 10%) and the dispersion in the calibration of the bolometric corrections with the (J–K) index. The range of luminosities derived (see Table 1) is the one theoretically expected for carbon-rich stars of ~ 1.5–2 M⊙ with near solar metallicity on the AGB phase, and agrees with previous estimates (e.g. Guandalini & Cristallo 2013) within the uncertainty. Nevertheless, for the extremely red object IY Hya, we obtain a very high luminosity, Mbol ~−6.90. The large uncertainty (~ 30%) in the parallax of this star, together with its very high (J–K) index (at thelimit of the calibration validity, 1.0 ≤ (J–K) ≤ 4.4), may explain this unrealistic luminosity for a typical AGB carbon star of 1.5–3 M⊙. However, we note that more massive (>3 M⊙) and thus more luminous stars may also become carbon stars for a short period of time at the end of the AGB phase when, due to the exhaustion of the hot bottom envelope burning, the C/O ratio may exceed unity at the surface (see e.g. Karakas & Lattanzio 2014; Ventura et al. 2015). We note also that the range of Mbol values derived here for normal and SC-type AGB carbon stars shows apparently no difference. A full Gaia DR2 luminosity analysis for a larger sample of AGB carbon stars is deferred to a forthcoming paper. On the other hand, the luminosity derived for the star HD 121477 agrees with that expected for a mildly metal-poor Ba star of ~ 2–3 M⊙ in the RGB phase. The much lower luminosity obtained for the other Ba/CH star, HD 123396, would indicate instead a lower mass (~1 M⊙; see e.g. Escorza et al. 2017). These stars are O-rich and were analysed here to extend the number of evolved metal-poor stars with F abundance determination and comparison purposes.
Effective temperatures were derived from infrared (IR) photometry calibrations by Bergeat et al. (2001). For the other parameters (gravity, metallicity, microturbulence, and the CNO abundances), the values derived by Lambert et al. (1986), Abia & Wallerstein (1998), and/or Abia et al. (2002) were used. These stellar parameters were considered nevertheless as a starting point; the final adopted values (Table 2) were obtained through an iterative process by comparing the observed spectra with the theoretical ones. A value of gravity log g = 0.0 was adopted for all AGB stars since this is the average value for the typical values of mass, effective temperature, and luminosity of AGB carbon stars (see e.g. Lambert et al. 1986). In any case, we verified that the chemical analysis is not very sensitive to the values of log g within ± 0.5 dex. For the stars observed with GEMINI-S/Phoenix, we verified that such initial metallicity values are compatible (within the uncertainty) with the metallicity derived from a Fe I line at λλ ~ 2.3308 μm and a Na I line at λλ ~ 2.3348 μm, present in the spectral region of the HF(1-0) R9 line. However, for those observed with TNG/Giano-b we were able to estimate the metallicity using several lines in the 2.0 μm spectral region, namely Fe I at λλ2.1096 and 2.2619 μm, Ca I at 2.2607, 2.2624, and 2.2651 μm and Ti I at 2.2621 and 2.2632 μm, respectively. The metallicity values ([M/H]4) quoted in Table 2 therefore refer to the average quantity derived from all these metallic lines. These metallicities agree with previous estimates within the uncertainty (± 0.3 dex). Unfortunately, for the star Sgr 9, we estimated the metallicity from only the Na I line mentioned above. Therefore, the metallicity for this star has to be considered rather uncertain. In fact, the derived value is significantly lower than the average metalliciy in the main stellar population of the Sagittarius dSph galaxy ([Fe/H] = −0.4 to − 0.7, Bellazzini et al. 2006). Finally, for the CH/Ba stars HD 121477 and HD 123396 we used the stellar parameters obtained by Merle et al. (2016) and Allen & Barbuy (2006), respectively. We also adopted a solar F abundance of 4.43 (Abia et al. 2015).
The chemical analysis was made using the spectral synthesis method in LTE using the version v15.1 of the Turbospectrum code (Plez 2012). To take the instrumental profile and other broadening effects (e.g. macroturbulence) into account, the raw spectra were convolved with Gaussian functions with the corresponding FWHM depending on the instrumental setup used and the spectral region studied. The fluorine analysis is based mainly on the HF(1-0) R9 line but, for the stars observed with Giano-b at the TNG, we also used other secondary HF lines available in the spectral region covered (see Abia et al. 2010 for details and Table 2). For these stars we further derived the 12C/13C ratio using 13CO lines in the 2.347 μm region (see Fig. 1), and when possible the 16O/17O ratio was also determined from C17O lines in the same spectral region. Details on this later analysis and the specific C17O lines used can be seen in Abia et al. (2017). Unfortunately our instrumental setup did not include reliable C18O lines needed to derive the 16O/18O ratio. The interplay between fluorine abundances and carbon and oxygen isotopic ratios may provide valuable information on the existence of envelope burning and/or non-standard mixing processes in evolved stars (see e.g. Busso et al. 2010; Abia et al. 2017). On the other hand, for the stars observed with Giano-b at the TNG, the s-element abundances were determined using a Sr I line at λλ1.0327 μm, two Y I lines at λλ1.0332 and λλ1.0333 μm, and several lines of Ce II and Nd II present in the H-band region (see Hasselquist et al. 2016; Cunha et al. 2017). The remaining stars, abundances were taken from the literature: Abia & Wallerstein (1998) and Abia et al. (2002) for the AGB stars, or Merle et al. (2016) and Allen & Barbuy (2006) for the two Ba/CH stars. The [⟨s⟩/Fe] values quoted in Table 2 are the average s-element abundance ratios derived from these lines or the literature, respectively. Further details on the atomic and molecular line lists used for the spectral synthesis can be found in Abia et al. (2002, 2015, 2017), and references therein. Theoretical spectra were computed using unpublished (kindly provided by K. Eriksson) spherical atmosphere models for cool carbon-rich stars with the corresponding stellar parameters. In the case of the stars R Gem, HD 121477, and HD 123396, that is, stars with C/O < 1, we instead used atmosphere models from Van Eck et al. (2017; R Gem) and Gustafsson et al. (2008), respectively.
Figures 1 and 2 show examples of theoretical fits to the observed spectra in the R9 HF line region of the SC-type and the extragalactic (normal) AGB carbon stars R Cmi and Sgr 9, respectively. The star Sgr 9 is added to the small number of extragalactic AGB carbon stars where the fluorine abundance has been derived (see Abia et al. 2011, 2015). In these figures, the red line shows the theoretical best fit to the R9 line (we note that in some stars, other secondary HF lines were used; see Table 2). In Fig. 1 we indicate the position of the Na I line and two C17O features used to estimate the average metallicity and the 16O/17O ratio, respectively. The start of the 13CO-band from which we derive the 12C/13C ratio in some stars is also indicated. Similar-quality fits were obtained for all the stars except for IY Hya. Our analysis of the spectrum of this star in the 2.3 μm region revealed the difficulty to fit the global spectrum with a single set of stellar parameters. Indeed, apparently the IR spectrum of IY Hya seems to be the mixing of two different components: one corresponding to a warm atmosphere (Teff > 4000 K), which accounts for the weak high-excitation CO lines and other weak molecular features (mainly CN), and another very cool atmosphere (Teff < 2000 K) responsible of the strong low-excitation CO lines. Furthermore, all these strong CO-lines appeared blue-shifted by ~ 7 kms−1 with respect to the rest-frame of the warm-component spectrum. This suggests that the cool component may form in an expanding envelope perhaps produced by a recent strong mass-loss episode5. The expansion velocity that we estimated is similar to the values observed in many AGB stars showing strong mass-loss rates and extended circumstellar envelopes (see e.g. Baud & Habing 1983; Jiménez-Esteban et al. 2005). Expansion velocities of this order are typically measured in AGB stars (OH/IR sources) associated with a stellar population with larger masses than that of the normal AGB carbon stars. This might be compatible with the high luminosity that we derived for this star. The R9 HF line in IY Hya is indeed present and intense, and can be accounted for by the warm atmosphere component giving a large overabundance ([F/Fe] > 0.5). However, because of the complexity of the IR spectrum, we consider it safer to exclude this star from the analysis. Also, the star HD 123396 deserves special attention. As mentioned above, we reanalysed the original spectrum in Alves-Brito et al. (2011); however, we derive a significantly lower fluorine abundance than these authors (log ɛ(F) = 3.6 instead of 4.1; see Table 2). Nevertheless, this difference is entirely due to the inconsistent excitation energy of the R9 line used by these authors: χ = 0.48 eV instead of the correct one (0.227 eV) used here (see Jönsson et al. 2014a).
Table 2 lists the final F abundance and s-element enhancement derived in each star. For some stars, several HF lines were used. The agreement between the different HF lines is in general good with a typical mean dispersion of ± 0.08 dex. The formal error in the F abundance due to uncertainties in the stellar parameters ranges from 0.20 to 0.30 dex, depending on the particular HF line. Considering the abundance dispersion and the uncertainty in the continuum position as additional sources of error, we estimate a total uncertainty of ± 0.30–0.35 dex in the [F/H] ratio (see Abia et al. 2010, for details on the estimation of the errors). However, the abundance ratio between F and any other element typically has a smaller error since some of the above uncertainties cancel out when deriving the abundance ratio: for the [F/Fe] ratio, we estimate a total uncertainty in the range ± 0.25–0.30 dex. On the other hand, the typical uncertainty for the average s-element abundance is ± 0.3 dex (see Abia et al. 2002), and slightly lower in the warmer stars HD 123396 and HD 121477 (see Allen & Barbuy 2006; Merle et al. 2016).
Spectral types, photometry, and luminosities for the stars studied.
Stellar parameters and abundances.
 |
Fig. 1 Comparison between observed (thick black line) and theoretical spectra for the SC-type star R Cmi around the spectral region of the R9(1-0) HF line. Top panel: continuous red line corresponds to the best fit (log ɛ(F) = 4.9) and black dashed lines are synthetic spectra computed with no F and log ɛ(F) = 4.2, respectively. The R9 HF, Na I and C17O lines at ~2.3358, 2.3380 and 2.3395 μm, respectively are marked. Note that the R9 line is blended to the left with a C17O line (not marked in the figure). Bottom panel: the same as in top panel showing another C17O feature used (among others) to derived the 16O/17O ratio, and the head of the 13CO molecular band from which the 12C/13C ratio was derived in some stars (see text). |
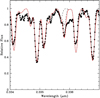 |
Fig. 2 Similar to Fig. 1 but in a narrower wavelength range around the R9 HF line for the extragalactic AGB carbon star Sgr 9 (black line with dots). The red line corresponds to the best fit (log ɛ(F) = 3.75) and black dashed lines are theoretical spectra computed with no F or log ɛ(F) = 3.0, respectively. |
3 Results and discussion
Hereafter, we discuss the comparison between the available data in the literature and our theoretical AGB models. Starting from the seminal paper by Forestini et al. (1992), the theoretical study of fluorine nucleosynthesis in AGB stars has been widely explored. Some papers were entirely devoted to the nuclear physics aspect (see e.g. Lugaro et al. 2004; Cristallo et al. 2014), while others concentrated on the stellar sites able to reproduce the observed galactic fluorine trend (see e.g. Renda et al. 2004; Lugaro et al. 2008; Lucatello et al. 2011; D’Orazi et al. 2013; Abia et al. 2015). We refer to those papers for detailed descriptions of 19F theory and for comparisons with observations made using different sets of models. Here, we concentrate exclusively on FRUITY models (Cristallo et al. 2011). In Abia et al. (2015) we already highlighted that standard FRUITY models are not able to properly fit observations, particularly for low-metallicity AGB stars. At that time, we suggested that models with an extended 13C pocket (we named them “TAIL” models; see Cristallo et al. 2015) could provide a better match. This agrees well with theoretical studies aiming at fitting isotopic composition of pre-solar SiC grains (e.g. Liu et al. 2018). Here we have expanded the set of theoretical models and have compared them to the newly available observations. In FRUITY models, convective velocities are calculated in the framework of the mixing length theory. As a consequence, during a TDU, the velocity at the inner border of the convective envelope may be large. This is ascribed to the opacity difference between the envelope (H-rich, andthus opaque) and the underlying layers (He-rich, and thus transparent to radiation). As a consequence, such a border would be unstable. We treat this radiative/convective interface by applying an exponentially decreasing profile of convective velocities (see Cristallo et al. 2009, for the calibration of the algorithm). In TAIL models we allow protons to penetrate down to the layer whose convective velocity is a factor 10−11 lower than the last convective mesh, as defined by the Schwarzschild criterion. TAIL models generally show larger 13C pockets and larger surface s-process enrichments as a consequence.
Figure 3 shows the [F/Fe] ratios derived in our new sample stars versus the stellar metallicity together with those obtained in previous studies in intrinsic AGB carbon stars (Abia et al. 2010, 2011, 2015) and extrinsic CH stars (Lucatello et al. 2011). The different colours refer to the different spectral types of carbon enhanced stars as indicated in the caption. We note that to compare with theoretical models, we have to consider the [F/Fe] ratios obtained in these Ba/CH stars as lower limits due to their extrinsic nature: these stars have accreted s-process-enriched material from a former AGB star (now seen as a white dwarf) in a binary system, and therefore the original material has been diluted with the envelope of the secondary star that we actually observe. From Fig. 3 and considering the observational uncertainties, we can make the following three conclusions. (a) SC-type AGB carbon stars, contrary to what we suggested in previous studies, show on average similar F enhancements to N-type stars of solar metallicity, namely: [F/Fe] = 0.23 ± 0.12 for SC-type and [F/Fe] = 0.17 ± 0.18 for N-type stars. The spectroscopic errors do not allow us to distinguish between the two classes. Therefore, concerning fluorine abundances, SC-type stars are compatible with the accepted spectral evolution M-MS-S-SC-C(N) along the AGB phase (which is thought to be a consequence of the progressive carbon enrichment of the stellar envelope because of TDU episodes). If this spectral sequence is also accepted as a chemical evolution sequence, SC- and N-type starsshould therefore show a similar chemical composition, which indeed seems to be the case (see e.g. Abia & Wallerstein 1998; Abia et al. 2002). There is only a small appreciable difference, with SC-type stars showing on average lower 16O/17O ratios (670 ± 130) than normal carbon stars (990 ± 300; from Abia et al. 2017 and this study). Since this ratio is barely altered during the AGB phase, this observational figure may suggest thatSC-type stars typically have larger masses than normal N-type stars. Indeed, for low-mass stars (1–3 M⊙), starting from a solar 16O/17O ratio on the main sequence (~2700), the higher the initial mass, the lower the expected oxygen isotopic ratio in the envelope after the first dredge-up (Lebzelter et al. 2015; Hinkle et al. 2016; Straniero et al. 2017; Abia et al. 2017). However, we note that the preliminary estimation of the luminosity function of these two spectral types of AGB carbon stars from Gaia DR2 distances and parallaxes apparently shows no differences (Abia et al., in prep.). (b) Stars with lower [Fe/H] than solar present larger [F/Fe] ratios with respect to their solar-metallicity counterparts. This trend is confirmed in the metal-poor galactic carbon star ZZ Gem (filled black circle; close to [Fe/H] ~ −1.0), the new extragalactic AGB carbon star Sgr 9 (filled blue circle), and the two metal-poor Ba stars (filled magenta circles) studied here, which show a markedly larger fluorine overabundance. The lower limits set in the two CH stars of Lucatello et al. (2011) are also compatible with this trend, thus confirming the result in previous studies. Dashed lines in Fig. 3 are the predicted [F/Fe] ratios as a function of the metallicity for a typical non-rotating 2 M⊙ (for [Fe/H] > −0.5) and 1.5 M⊙ (for [Fe/H] < −0.5) AGB star at different TPs (as labelled). We compare the observational data with stellar models of 2 M⊙ and 1.5 M⊙, depending of the metallicity, because the 1.5 M⊙ models of solar-like metallicities may not reach the C-rich phase due to the already large oxygen pristine abundance. It can be seen that the observed and predicted [F/Fe] ratios agree well within observational errors. Briefly, we reconfirm the predicted dependence of the F production on metallicity (e.g. Lugaro et al. 2004; Fishlock et al. 2014; Cristallo et al. 2015). Finally, (c) the new fluorine determinations confirm that this element is indeed produced in AGB stars. However, observational evidence has gradually shown that the fluorine enhancement in these stars is much lower than previously thought, particularly in AGB stars of near-solar metallicity. This agrees with the conclusion from recent chemical evolution studies that AGB stars, although relevant, may not be the main sources of fluorine in the Galaxy, and that other contributing sources are required: rotating massive stars (Prantzos et al. 2018) or WR stars (Jönsson et al. 2017; Spitoni et al. 2018).
Next, we address the problem of the fluorine and s-process element enhancements. Considering the paucity of observations with a fluorine detection at low metallicity, we repeat our comparison with theory for two different metallicity sets, that is, stars with Z ≥ 4 × 10−3 ([Fe/H] ≥ −0.5) and stars with Z < 4 × 10−3 ([Fe/H] < −0.5). In Fig. 4 we report the high-metallicity set. We prefer to compare with the [F/⟨s⟩] ratio rather than the [F/Fe] one (as made in previous studies) because in this case we can safely compare models with fluorine enhancements found in the extrinsic stars (magenta symbols in Fig. 4), since in this case this ratio is without the problems related to dilution. Observations and models show a very similar behaviour, with the [F/⟨s⟩] ratio showing an almost linear decreasing trend with increasing s-process surface enrichment. We note how close this observational relationship is considering the large observational uncertainty. We also note that this observational trend seems to be almost independent of the stellar metallicity for stars with [Fe/H] > −0.5, in close agreement with theoretical predictions: in fact, the few sub-solar metallicty stars in our sample are placed in the range − 1.0 ≤ [F/⟨s⟩] ≤ −0.6 in Fig. 4. This fact is fully supported by theoretical FRUITY TAIL models and confirms our findings from previous studies (see e.g. Abia et al. 2015, and references therein).
The same comparison at lower metallicities is less trivial. First of all, considering that a homogeneous sample of stars with a consistent number of s-process elements is not available, we compared model predictions to Ba only (thus, we assume that this element is representative of the average s-element enhancement; see Fig. 5). This element is in fact the only one measured in the stars HD 5523 and HE1152-0355 (open magenta circles). We further split observations into two panels: stars with [Fe/H] ~ −1 (upper panel) and stars with [Fe/H] ~ −2 (lower panel). Two of the three stars with Z ~ 10−3 (or [Fe/H] ~ −1.0, ZZ Gem and HD 123396) are well reproduced by the model with the corresponding metallicity. The extragalactic star SMC BMB-30 (open blue dot) instead shows a lower [F/Ba] ratio than the theoretical expectation (Fig. 5 top panel). Things get worse at lower metallicities (lower panel in Fig. 5). In fact, for metallicities lower than [Fe/H] ~ −1.3 (i.e. the one of the two CH stars HE1152-0355 and HD 5523 from Lucatello et al. 2011 and the two extragalactic AGB stars in Carina, ALW6 and ALW7, Abia et al. 2008, 2011), theoretical models (continuous lines) systematically overproduce fluorine with respect to Ba. While two stars agree with theoretical expectations within errors, two stars show definitively lower values (with a difference between a factor of five and ten). Even considering the fact that Ba lines may be partially saturated in those stars, we cannot conclude that models and observations agree. Certainly, more determinations of fluorine abundance in evolved metal-poor stars at very low metallicities are needed to confirm our statement. A reduction of fluorine production would definitely improve the match to spectroscopic data. As previously shown, in AGB stars 19F is mainly synthesised through a nuclear chain starting from 13C seeds. Part of this 13C lies in the 13C-pocket, while part isleft in the H-burning ashes and is burnt convectively during TPs. The latter depends on the TDU efficiency. Any decrease of the TDU efficiency would also affect s-process elements, while we are interested in a process decreasing the 19F production only. Therefore, it is worthless to explore this hypothesis. Nuclear reaction rates have been widely explored as a potential source for uncertainty in galactic fluorine production (Cristallo et al. 2014; see also the most recent D’Agata et al. 2018). However, to date no study has clearly demonstrated that a single reaction is able to significantly modify 19F nucleosynthesis, provided that reaction rates are varied within estimated uncertainties. The only viable alternative is to produce less 19F during the radiative burning of the convective envelope. This can be fulfilled by decreasing the amount of 14N in the 13C pocket. We note, in fact, that the nuclear chain synthesising 19F requires the presence of 14N, which captures neutrons emitting protons via the resonant 14N(n,p)14C reaction. Recently, a series of publications (Trippella et al. 2014, 2016; Palmerini et al. 2018) identified magnetic buoyancy as a viable mechanism to obtain the formation of the 13C pocket. Such a mechanism leads to extended 13C pockets (similar to the ones we obtain in the TAIL models), but with a smaller amount of 14N. This is linked to the different mixing efficiency below the formal border of the 13C pocket. We therefore suppose that magnetic buoyancy could (at least partially) alleviate the disagreement between observations and models concerning the production of 19F in very metal-poor AGB stars. Such a statement however has to be still clearly demonstrated in the future.
 |
Fig. 3 [F/Fe] vs. [Fe/H] in the stars analysed here (filled circles) and in previous studies (open circles, see text). Colour code: black, normal (N-type) Galactic carbon stars; green, SC-type stars; blue, extragalactic carbon stars; magenta, extrinsic Ba/CH stars. Dashed lines represent theoretical predictions for a non-rotating 2 M⊙ (for [Fe/H] > −0.5) and 1.5 M⊙ (for [Fe/H] < −0.5) AGB star at different TPs, according to Cristallo et al. (2015). A typical error bar is indicated. |
 |
Fig. 4 [F/⟨s⟩] vs. [⟨s ⟩/Fe] in the sample stars with [Fe/H] > −0.5. As in Fig. 1, filled symbols correspond to the stars analysed here while open symbols are stars previously studied (see text). Colour code: black, normal C-stars; green, SC-stars; magenta, CH/Ba stars. Lines are theoretical predictions for a non-rotating 2.0 M⊙ TP-AGB star at different metallicities (quoted in the figure), according to Cristallo et al. (2015). The continuous part of the lines indicates the theoretical C-rich phase while the dashed part shows the O-rich phase. We note that at these metallicities, theoretically, stars become C-rich during the AGB phase after several TPs. The middle continuous line corresponds to the model with Z = Z⊙ but the label has been omitted for clarity. |
 |
Fig. 5 [F/Ba] vs. [Ba/Fe] in the sample stars with [Fe/H] ~ −1.0 (top) and ~ −2.0 (bottom). Symbols as Fig. 1; colour code: black, normal galactic C-stars; blue, extragalactic C-stars; magenta, CH/Ba stars (see text). Continuous lines are theoretical predictions for a non-rotating 1.5 M⊙ TP-AGB star with metallicity Z ~ 10−3 and 10−4 in the top and bottom panels, as labelled respectively, according to Cristallo et al. (2015). We note that for these low metallicities, theoretically AGB stars become carbon rich from the very first TPs. |
4 Conclusions
We obtained high-resolution IR observations in a sample of eleven AGB carbon stars: five SC-type and six normal N-type. The latter sample includes a new extragalactic AGB carbon star in the Sagittarius dwarf spheroidal galaxy. Additionally, two metal-poor CH/Ba stars were studied for comparison purposes. The aim was to measure 19F and s-element contents. F could be measured in all sample stars except in IY Hya, an AGB star which shows a rare IR spectrum probably as the consequence of a recent episode of strong mass loss. Together with the previous determinations of F in AGB carbon stars in the literature, we found that SC- and N-type stars of near solar metallicity show very similar F enrichments. In the full range of metallicity studied, the F overabundances are moderate, pointing out that AGB stars are not the main contributors of this element in the solar neighbourhood, in agreement with recent chemical evolution models. Nevertheless, the comparison, in an ample range of metallicities, of observations with theoretical models of low-mass AGB nucleosynthesis, which assume the formation of a different and more extended 13C pocket with respectto previous models, shows that models are able to reproduce the observed correlations, that is, [F/Fe] vs. [Fe/H] and [F/⟨s⟩] vs. [⟨s ⟩/Fe], for metallicities larger than about [Fe/H] > −0.5. At lower metallicities however, models and observations are still in conflict. In particular, models overproduce F with respect to s-elements especially for the most metal-poor objects. We briefly discuss the possible solutions to this problem.
Acknowledgements
This work was partially supported by the Spanish grant AYA2015-63588-P within the European Founds for Regional Development (FEDER). Based in part on observations made with the Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundacion Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. We thank Calar Alto Observatory for allocation of director’s discretionary time to this programme. Facility: Gemini:South (Phoenix).
References
- Abia, C., & Wallerstein, G. 1998, MNRAS, 293, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., Domínguez, I., Gallino, R., et al. 2002, ApJ, 579, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., de Laverny, P., & Wahlin, R. 2008, A&A, 481, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abia, C., Recio-Blanco, A., de Laverny, P., et al. 2009, ApJ, 694, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., Cunha, K., Cristallo, S., et al. 2010, ApJ, 715, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., Cunha, K., Cristallo, S., et al. 2011, ApJ, 737, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Abia, C., Cunha, K., Cristallo, S., & de Laverny, P. 2015, A&A, 581, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abia, C., Hedrosa, R. P., Domínguez, I., & Straniero, O. 2017, A&A, 599, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen, D. M., & Barbuy, B. 2006, A&A, 454, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves-Brito, A., Karakas, A. I., Yong, D., Meléndez, J., & Vásquez, S. 2011, A&A, 536, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenou, F., Grenon, M., & Gomez, A. 1992, A&A, 258, 104 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Baud, B., & Habing, H. J. 1983, A&A, 127, 73 [NASA ADS] [Google Scholar]
- Bellazzini, M., Newberg, H. J., Correnti, M., Ferraro, F. R., & Monaco, L. 2006, A&A, 457, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergeat, J., Knapik, A., & Rutily, B. 2001, A&A, 369, 178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Busso, M., Palmerini, S., Maiorca, E., et al. 2010, ApJ, 717, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Gallino, R., et al. 2009, ApJ, 696, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Di Leva, A., Imbriani, G., et al. 2014, A&A, 570, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Smith, V. V., & Gibson, B. K. 2008, ApJ, 679, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Cunha, K., Smith, V. V., Hasselquist, S., et al. 2017, ApJ, 844, 145 [NASA ADS] [CrossRef] [Google Scholar]
- D’Agata, G., Pizzone, R. G., La Cognata, M., et al. 2018, in Eur. Phys. J. Web Conf., 184, 02003 [CrossRef] [Google Scholar]
- D’Orazi, V., Lucatello, S., Lugaro, M., et al. 2013, ApJ, 763, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Escorza, A., Boffin, H. M. J., Jorissen, A., et al. 2017, A&A, 608, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feast, M. W., Whitelock, P. A., & Menzies, J. W. 2006, MNRAS, 369, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Fishlock, C. K., Karakas, A. I., Lugaro, M., & Yong, D. 2014, ApJ, 797, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Forestini, M., Goriely, S., Jorissen, A., & Arnould, M. 1992, A&A, 261, 157 [NASA ADS] [Google Scholar]
- Gallino, R., Arlandini, C., Busso, M., et al. 1998, ApJ, 497, 388 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guandalini, R., & Cristallo, S. 2013, A&A, 555, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasselquist, S., Shetrone, M., Cunha, K., et al. 2016, ApJ, 833, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Cuberly, R. W., Gaughan, N. A., et al. 1998, in Infrared Astronomical Instrumentation, ed. A. M. Fowler, Proc. SPIE, 3354, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K. H., Lebzelter, T., & Straniero, O. 2016, ApJ, 825, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Esteban, F. M., Agudo-Mérida, L., Engels, D., & García-Lario, P. 2005, A&A, 431, 779 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jönsson, H., Ryde, N., Harper, G. M., et al. 2014a, A&A, 564, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jönsson, H., Ryde, N., Harper, G. M., Richter, M. J., & Hinkle, K. H. 2014b, ApJ, 789, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Jönsson, H., Ryde, N., Spitoni, E., et al. 2017, ApJ, 835, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164 [NASA ADS] [Google Scholar]
- Karakas, A. I., & Lattanzio, J. C. 2014, PASA, 31, e030 [NASA ADS] [CrossRef] [Google Scholar]
- Kerschbaum, F., Lebzelter, T., & Mekul, L. 2010, A&A, 524, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, C., Izutani, N., Karakas, A. I., et al. 2011, ApJ, 739, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Lagadec, E., Zijlstra, A. A., Sloan, G. C., et al. 2009, MNRAS, 396, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Lambert, D. L., Gustafsson, B., Eriksson, K., & Hinkle, K. H. 1986, ApJS, 62, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lebzelter, T., Straniero, O., Hinkle, K. H., Nowotny, W., & Aringer, B. 2015, A&A, 578, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, N., Gallino, R., Cristallo, S., et al. 2018, ApJ, 865, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Lucatello, S., Masseron, T., Johnson, J. A., Pignatari, M., & Herwig, F. 2011, ApJ, 729, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Ugalde, C., Karakas, A. I., et al. 2004, ApJ, 615, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., de Mink, S. E., Izzard, R. G., et al. 2008, A&A, 484, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merle, T., Jorissen, A., Van Eck, S., Masseron, T., & Van Winckel, H. 2016, A&A, 586, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nault, K. A., & Pilachowski, C. A. 2013, AJ, 146, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Origlia, L., Oliva, E., Baffa, C., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471E [Google Scholar]
- Palmerini, S., Trippella, O., Busso, M., et al. 2018, Geochim. Cosmochim. Acta, 221, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pilachowski, C. A., & Pace, C. 2015, AJ, 150, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Plez, B. 2012, Astrophysics Source Code Library [recore ascl:1205.004] [Google Scholar]
- Prantzos, N., Abia, C., Limongi, M., Chieffi, A., & Cristallo, S. 2018, MNRAS, 476, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Seifert, W., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, Proc. SPIE, 8446,84460R [CrossRef] [Google Scholar]
- Recio-Blanco, A., de Laverny, P., Worley, C., et al. 2012, A&A, 538, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renda, A., Fenner, Y., Gibson, B. K., et al. 2004, MNRAS, 354, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, V. V., Hinkle, K. H., Cunha, K., et al. 2002, AJ, 124, 3241 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Matteucci, F., Jönsson, H., Ryde, N., & Romano, D. 2018, A&A, 612, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Straniero, O., Gallino, R., Busso, M., et al. 1995, ApJ, 440, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O., Bruno, C. G., Aliotta, M., et al. 2017, A&A, 598, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trippella, O., Busso, M., Maiorca, E., Käppeler, F., & Palmerini, S. 2014, ApJ, 787, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Trippella, O., Busso, M., Palmerini, S., Maiorca, E., & Nucci, M. C. 2016, ApJ, 818, 125 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Uttenthaler, S., Aringer, B., Lebzelter, T., et al. 2008, ApJ, 682, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Van Eck, S., Neyskens, P., Jorissen, A., et al. 2017, A&A, 601, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., Karakas, A. I., Dell’Agli, F., et al. 2015, MNRAS, 450, 3181 [NASA ADS] [CrossRef] [Google Scholar]
The lower mass limit to the occurrence of the TDU is believed to be ~ 1.5 M⊙ at solar-like metallicities, with this value decreasing with decreasing metallicity (see e.g. Karakas & Lattanzio 2014; Cristallo et al. 2015).
All Tables
All Figures
 |
Fig. 1 Comparison between observed (thick black line) and theoretical spectra for the SC-type star R Cmi around the spectral region of the R9(1-0) HF line. Top panel: continuous red line corresponds to the best fit (log ɛ(F) = 4.9) and black dashed lines are synthetic spectra computed with no F and log ɛ(F) = 4.2, respectively. The R9 HF, Na I and C17O lines at ~2.3358, 2.3380 and 2.3395 μm, respectively are marked. Note that the R9 line is blended to the left with a C17O line (not marked in the figure). Bottom panel: the same as in top panel showing another C17O feature used (among others) to derived the 16O/17O ratio, and the head of the 13CO molecular band from which the 12C/13C ratio was derived in some stars (see text). |
| In the text | |
 |
Fig. 2 Similar to Fig. 1 but in a narrower wavelength range around the R9 HF line for the extragalactic AGB carbon star Sgr 9 (black line with dots). The red line corresponds to the best fit (log ɛ(F) = 3.75) and black dashed lines are theoretical spectra computed with no F or log ɛ(F) = 3.0, respectively. |
| In the text | |
 |
Fig. 3 [F/Fe] vs. [Fe/H] in the stars analysed here (filled circles) and in previous studies (open circles, see text). Colour code: black, normal (N-type) Galactic carbon stars; green, SC-type stars; blue, extragalactic carbon stars; magenta, extrinsic Ba/CH stars. Dashed lines represent theoretical predictions for a non-rotating 2 M⊙ (for [Fe/H] > −0.5) and 1.5 M⊙ (for [Fe/H] < −0.5) AGB star at different TPs, according to Cristallo et al. (2015). A typical error bar is indicated. |
| In the text | |
 |
Fig. 4 [F/⟨s⟩] vs. [⟨s ⟩/Fe] in the sample stars with [Fe/H] > −0.5. As in Fig. 1, filled symbols correspond to the stars analysed here while open symbols are stars previously studied (see text). Colour code: black, normal C-stars; green, SC-stars; magenta, CH/Ba stars. Lines are theoretical predictions for a non-rotating 2.0 M⊙ TP-AGB star at different metallicities (quoted in the figure), according to Cristallo et al. (2015). The continuous part of the lines indicates the theoretical C-rich phase while the dashed part shows the O-rich phase. We note that at these metallicities, theoretically, stars become C-rich during the AGB phase after several TPs. The middle continuous line corresponds to the model with Z = Z⊙ but the label has been omitted for clarity. |
| In the text | |
 |
Fig. 5 [F/Ba] vs. [Ba/Fe] in the sample stars with [Fe/H] ~ −1.0 (top) and ~ −2.0 (bottom). Symbols as Fig. 1; colour code: black, normal galactic C-stars; blue, extragalactic C-stars; magenta, CH/Ba stars (see text). Continuous lines are theoretical predictions for a non-rotating 1.5 M⊙ TP-AGB star with metallicity Z ~ 10−3 and 10−4 in the top and bottom panels, as labelled respectively, according to Cristallo et al. (2015). We note that for these low metallicities, theoretically AGB stars become carbon rich from the very first TPs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


