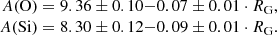| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 13 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201834554 | |
| Published online | 23 May 2019 | |
Radial abundance gradients in the outer Galactic disk as traced by main-sequence OB stars⋆
1
Observatório Nacional-MCTIC, Rua José Cristino, 77., 20921-400 Rio de Janeiro, RJ, Brazil
e-mail: daflon@on.br
2
Observatoire de la Côte d’Azur, 06304 Nice, France
3
Steward Observatory, University of Arizona, 933 N. Cherry Ave., Tucson, AZ 85721, USA
4
Lund Observatory, Department of Astronomy and Theoretical physics, Box 43, 221 00 Lund, Sweden
5
National Optical Astronomy Observatory, 950 N. Cherry Ave., Tucson, AZ 85719, USA
6
Department of Astronomy, University of Michigan, 311 West Hall, 1085 S. University Ave., Ann Arbor, MI 48109-1107, USA
Received:
1
November
2018
Accepted:
2
April
2019
Context. Elemental abundance gradients in galactic disks are important constraints for models of how spiral galaxies form and evolve. However, the abundance structure of the outer disk region of the Milky Way is poorly known, which hampers our understanding of the spiral galaxy that is closest to us and that can be studied in greatest detail. Young OB stars are good tracers of the present-day chemical abundance distribution of a stellar population and because of their high luminosities they can easily be observed at large distances, making them suitable to explore and map the abundance structure and gradients in the outer regions of the Galactic disk.
Aims. Using a sample of 31 main-sequence OB stars located between galactocentric distances 8.4−15.6 kpc, we aim to probe the present-day radial abundance gradients of the Galactic disk.
Methods. The analysis is based on high-resolution spectra obtained with the MIKE spectrograph on the Magellan Clay 6.5-m telescope on Las Campanas. We used a non-NLTE analysis in a self-consistent semi-automatic routine based on TLUSTY and SYNSPEC to determine atmospheric parameters and chemical abundances.
Results. Stellar parameters (effective temperature, surface gravity, projected rotational velocity, microturbulence, and macroturbulence) and silicon and oxygen abundances are presented for 28 stars located beyond 9 kpc from the Galactic center plus three stars in the solar neighborhood. The stars of our sample are mostly on the main-sequence, with effective temperatures between 20 800−31 300 K, and surface gravities between 3.23−4.45 dex. The radial oxygen and silicon abundance gradients are negative and have slopes of −0.07 dex kpc−1 and −0.09 dex kpc−1, respectively, in the region 8.4 ≤ RG ≤ 15.6 kpc.
Conclusions. The obtained gradients are compatible with the present-day oxygen and silicon abundances measured in the solar neighborhood and are consistent with radial metallicity gradients predicted by chemodynamical models of Galaxy Evolution for a subsample of young stars located close to the Galactic plane.
Key words: stars: abundances / stars: early-type
© ESO 2019
1. Introduction
To understand how large spiral galaxies like the Milky Way formed and evolved to their current state is a major goal in Galactic research. Observational results from analyses of the Galactic structure and chemical composition combined with modern models of Galactic chemical evolution are required to constrain how galaxies form and evolve (Maiolino & Mannucci 2019). However, the observational picture of the Milky Way is incomplete and still lacks some major pieces. In particular the outer disk is poorly mapped and poorly understood. This is unfortunate, as Galactic radial gradients of elemental abundances are important observational constraints for models of Galactic chemical evolution (Maiolino & Mannucci 2019; Wang et al. 2019). These gradients are influenced by the evolution of the Milky Way on the largest scales. Differences in the history of the halo evolution may affect the chemical distribution in the outer disk at galactocentric distances greater than 10 kpc, whereas the inner gradients remain unchanged (e.g., Chiappini et al. 2001).
Massive stars are considered the main drivers of the Galactic chemo-dynamical evolution (Crowther 2012; Matteucci 2014). They are the first stars to process hydrogen to heavier elements and to return these processed elements to the interstellar medium. Their strong winds and supernova explosions are important triggers of star formation (Crowther 2012). Also, due to their short lifetimes, OB stars are naturally bound to their place of birth in the Galactic plane (Schulz 2012). Thus they provide observational constraints on the present state of the Galaxy through detailed analyses of their photospheres. The abundance radial gradients derived from these objects can be used to infer the infall rate and mixing of the gas within the thin disk (Chiappini et al. 2001).
Massive stars have been studied for decades by several groups using photometric and spectroscopic tools (e.g., Rolleston et al. 2000; Daflon & Cunha 2004). However, the samples studied in previous works concentrate in the “local” disk and typically include less than about ten stars outside the solar circle.
In this work we present stellar parameters (effective temperature, surface gravity and v sin i, microturbulent and macroturbulent velocities) and oxygen and silicon abundances in non-LTE for a sample of 28 main-sequence OB stars located toward the Galactic anticenter, between galactocentric radii ∼9.5 and 15.6 kpc, plus three stars in the solar neighborhood. The sample analyzed here is part of the larger sample of 136 OB stars in the outer disk analyzed by Garmany et al. (2015), where multiplicity, photometric effective temperature, and projected rotational velocity (v sin i) were determined.
This paper is structured as follows: Section 2 describes the target selection and the observations; Sect. 3 explains the methodology used to analyse the stellar spectra and Sect. 4 explains how the distances of the stars were obtained. In Sect. 5 we discuss the radial distribution of the silicon and oxygen abundances; our conclusions are presented in Sect. 6.
2. Observations and sample selection
The target stars were selected from the catalogs by Reed (1998, 2003), using the reddening-free index Q to select stars with spectral types earlier than B2. Additional selection criteria include the stellar magnitudes (V > 10) and the location toward the outer edge of the Galactic disk in order to provide OB stars that are likely to be located at large galactocentric distances. A detailed description of the selection criteria of the sample stars is presented in Garmany et al. (2015).
High-resolution spectra were obtained over six nights (Dec. 29, 2007–Jan. 3, 2008) for 136 stars with the MIKE spectrograph (Bernstein et al. 2003) at the Magellan Clay 6.5 m telescope at Las Campanas Observatory in Chile. MIKE is a double echelle spectrograph that simultaneously records red (4900−9500 Å) and blue (3350−5000 Å) spectra. The observations were done with a 0.7 arcsec slit, providing spectra with nominal resolution of about R ≈ 53 000 with the blue arm, as measured in the Th-Ar calibration images. The exposure times were estimated to give spectra with S/N ∼ 100 per pixel for the stars that have V magnitudes in the range 10−14 mag.
At the time of the observing run, the blue CCD of the MIKE spectrograph was suffering from a serious disfiguring feature affecting a number of orders, and the CCD response function was changing with time (Ian Thompson, priv. comm.; the CCD was replaced in 2009). In addition, a strong contamination in the line profiles was introduced by the use of a B star as a milky flat. As a result, the spectra that were reduced using the standard pipeline displayed a relatively strong feature (about 20−30%) in the central regions (∼20 Å) on the orders 1–12 on the blue arm (i.e., 5000−4400 Å). Thus, the spectra had to be re-reduced using the data reduction packages written in Python and provided by Carnegie Observatories1. This resulted in better quality spectra (corrected for the blaze function and CCD defect) obtained through a careful flat-field selection, using quartz lamp spectra, as shown in Fig. 1 for the star ALS 14013, in the region 4680−4695 Å.
 |
Fig. 1. Example spectra in the region 4670−4720 Å for the star ALS 14013 reduced with the pipeline (gray line) and re-reduced (blue line). The feature introduced by the CCD defect in the region 4680−4695 Å has been adequately removed. |
Some intrinsic characteristics of early-type stars such as fast rotation, binarity, and stellar winds, can contribute to make the spectral analysis of massive OB stars challenging. Stellar rotation (v sin i) becomes a dominant broadening mechanism and affects in particular the weak metal lines present in the spectra of OB stars; these are smeared at v sin i ≈ 100 km s−1 or higher, preventing an accurate abundance analysis. In this study, we selected only those stars with sharp-lined spectra (with v sin i < 70 km s−1) in order to avoid any systematics and larger errors that could be introduced in our abundance results due to high stellar rotation. Recently, Cazorla et al. (2017) analyzed two fast-rotating stars (ALS 864 and ALS 18675) from our full sample.
A majority of massive stars are found in binary or multiple star systems (Sana et al. 2012, 2013) and some of them may present double (or even multiple) lines in their spectra (double-lined spectroscopic binaries, SB2). In such cases one has to disentangle the component spectra (e.g. Harmanec et al. 2004) and treat the resulting spectra individually. Massive stars with moderate to strong winds may also display emission lines in the center of the hydrogen lines. Depending on the intensity of the emission lines, the wings of hydrogen lines that are generally used to determine the surface gravity may be affected.
From the original sample of 136 stars described in Garmany et al. (2015), stars with broad line profiles (v sin i > 70 km s−1), strong emission profiles in the center of H lines, and clear double lines were eliminated for this study. One additional star (ALS 16807) was also discarded (see Sect. 3.2).
Single-epoch spectra like those analyzed in this paper are not adequate to identify and study binary systems. However, in order to discard potential single-lined binaries, we did a search in the literature for radial velocity measurements or any information on binarity. The results are the following:
-
For the stars ALS 45, ALS 404, ALS 428, ALS 9209, ALS 18679, and ALS 18681, we compared the observed spectra with previous data obtained with FEROS @ ESO 1.52 m by our group. Only ALS 428 shows significant variation of radial velocity, although no spectral line from a companion could be detected in the two spectra.
-
For the stars ALS 384, ALS 9209, and ALS 18714 we compared our measurements of radial velocity with previous values listed in the literature: the two sets of measurements are consistent within 10 km s−1.
-
The star ALS 17694 has been studied by Lester et al. (2016) as a possible member of an eclipsing binary and has been discarded as a component of the system.
-
For the remaining 19 stars, no measurement of radial velocity and no information on binarity are available in the literature. We thus adopted a simple approach based on visual inspection of single-epoch spectra searching for potential asymmetry in the line profiles or any other spectral signature from a companion. As no clear signature has been found in the observed spectra, we considered these stars as single and we proceeded the abundance analysis.
Our final sample contains 28 stars suitable for a detailed chemical abundance analysis. Figure 2 shows sample spectra in the region between 4660 Å and 4720 Å for six stars in our sample. The positions of all observed stars projected in the Galactic plane are shown in Fig. 3. Gray circles show the original sample of 136 stars and red circles show the subsample of 28 stars selected for the abundance analysis with revised heliocentric distances as described in Sect. 4.
 |
Fig. 2. Example spectra for six observed stars in the region 4660−4720 Å. The spectra are vertically shifted for better visualization. Some spectral lines are identified on the top. |
 |
Fig. 3. Positions of the all 136 observed stars (gray circles) projected onto the Galactic plane; the 28 stars selected for a detailed abundance analysis are presented (red circles) with reviewed distances (see Sect. 4). All stars are located in the third Galactic quadrant. |
3. Abundance analysis
3.1. Non-LTE analysis and atomic data
Atmospheric parameters and chemical abundances were determined using a grid of non-LTE line-blanketed model atmospheres calculated with TLUSTY (Hubeny 1988; Hubeny & Lanz 1995, 2017a) and the synthesis code SYNSPEC. The model atoms used to compute the original atmosphere grids OSTAR2002 (Lanz & Hubeny 2003) and BSTAR2006 (Lanz & Hubeny 2007) have been updated: in the place of superlevels previously adopted, the updated model atoms now explicitly include the higher energy levels. The updated models of C II, C III, and C IV have 60, 95, and 55 energy levels, respectively. The models of O I and O II have been updated to include 69 and 219 levels, respectively, while the updated models of Si II, Si III, and Si IV have 70, 122, and 53 levels, respectively. A new grid of model atmospheres was created with 20 values of effective temperatures in the range between 14 000 and 33 000 K, in steps of 1000 K, and 13 values of surface gravity in the range between 3.0 and 4.5 dex, in steps of 0.12 dex. All models have a microturbulent velocity of 2.0 km s−1.
Stellar parameters and abundances of oxygen and silicon were determined using the list of lines (O I, O II, Si II, Si III, and Si IV) presented in Table 1 with their respective log g f-values.
Line list and adopted values of oscillator strength (log g f).
3.2. Stellar atmospheric parameters
Spectral features are typically sensitive to more than one atmospheric parameter at the same time: most of the spectral lines show sensitivity to the effective temperature, log g, and microturbulence. For example, the broad wings of hydrogen lines in OB stars are mainly sensitive to the surface gravity but are also (although to a lesser degree) sensitive to the effective temperature. The intermediate and strong metal lines are, as expected, very sensitive to the microturbulent velocity (ξt), whilst the weak lines remain constant with respect to the ξt-value. The projected rotational velocity, v sin i, on the other hand, will affect the metal lines in a similar way but the weak lines will not be measurable. All these relations introduce an interdependency in the spectroscopic determination of the stellar parameters.
In our approach, the atmospheric parameters and elemental abundances for the sample stars were determined via an iterative scheme, inspired by the method described in Hunter et al. (2007). Effective temperatures (Teff), surface gravities (log g), projected rotational velocities (v sin i), macroturbulent velocities (ζmac), microturbulent velocities (ξt) and abundances of O and Si were determined in a self-consistent way, based on the non-LTE synthesis of line profiles, with the best fits to the observed spectra obtained using χ2 minimisation. The adopted methodology is illustrated by the flowchart in Fig. 4, with the following steps:
-
Initial estimates of Teff are based on the spectral types; the initial value of log g is 4.0 dex (a reasonable log g value for OB stars with luminosity class IV-V). The initial ξt value is set to 2 km s−1, the same value as adopted in the calculation of the model atmospheres with TLUSTY. The main role of ξt, however, is to promote the broadening of the line profiles but it doe not affect the model convergence (Hubeny & Lanz 2017b). For v sin i, the values listed in Garmany et al. (2015) were adopted as initial guesses.
-
Teff is obtained by requiring ionisation balance of the available species Si II/Si III/Si IV and O I/O II/O III. The new Teff is the average value weighted according to the number of species available in the observed stellar spectrum.
-
The fitting of all O and Si lines is repeated for the fixed Teff value in order to determine v sin i, which is the mean of a gaussian fit to the distribution of the v sin i values. Limb darkening coefficient is fixed as ϵ = 0.6, following Hubeny & Lanz (2017a).
-
A similar fitting procedure is repeated in order to obtain ζmac, adopting a radial-tangential approach (Hubeny & Lanz 2017a).
-
The surface gravity is determined by fitting the wings of Balmer lines, which are very sensitive to pressure broadening. Profiles of Hα, Hβ and Hγ are used whenever available, and the adopted value is the average from the values obtained from each of the hydrogen lines.
-
The determination of the microturbulent velocity, ξt, follows the classical approach of requiring the agreement between weak and strong lines. Equivalent widths of Si III and O II lines are used as indicators of the line strength. The adopted stellar microturbulence is the average of ξt-values obtained for Si and O, rounded to the nearest integer.
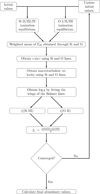 |
Fig. 4. Flowchart illustrating the iterative methodology to determine the stellar parameters and elemental abundances, based on the ionisation balance of O I/O II/O III and Si II/Si III/Si IV and χ2 minimisation. |
Once convergence between input and output values of all the stellar parameters is achieved, the adopted parameters are fixed and used to refit the spectral lines to derive the final elemental abundances. We note that for one star (ALS 18607) we were not able to obtain convergence using this methodology and this will be further explored in a future study. The stellar parameters and chemical abundances obtained for the 28 stars of our sample are given Table 2, in order of increasing ALS number. The abundances represent average values computed from the individual lines and the standard deviation.
Stellar parameters and elemental abundances for the sample stars.
3.3. Uncertainties
Uncertainties in the derived abundances were estimated by recomputing the elemental abundances after changing the stellar parameters (Teff, log g, v sin i, microturbulent and macroturbulent velocities), one at a time, by the uncertainty in the given parameter. The adopted uncertainties in stellar parameters are: ΔTeff = 1000 K, Δlog g = 0.15, Δv sin i = 15%, Δξt = 2 km s−1, and Δζmac = 15%; these represent the precision of the adopted methodology in obtaining each individual parameter. The total abundance error was computed by adding the individual abundance variations in quadrature. Typical abundance errors range from 0.01 dex to 0.13 dex, with a mean of 0.06 dex.
The stellar parameters that have the highest impact on the derived O and Si abundances are the microturbulent velocity and the effective temperature. In particular, the Si III lines analyzed are good indicators for deriving of the microturbulent velocity since the intermediate-to-strong Si III lines are mainly sensitive to the microturbulent velocity: a variation of 2 km s−1 in ξ results in a difference in average of 0.08 dex in the Si abundance. The O II lines, which are overall weaker than the Si III lines, are less sensitive to the microturbulent velocity: for oxygen, the same average difference is 0.05 dex. The adoption of ΔTeff = 1000 K results in a average variation of 0.11 and 0.06 for oxygen and silicon respectively, showing that O II lines are sensitive monitors of the effective temperature. For most of the stars studied, the total random errors in the elemental abundances are generally below 0.06 dex.
3.4. Consistency checks
We tested our methodology on three well-studied OB stars from the literature which are located closer to the Sun (compared to the outer disk sample): HD 61068, HD 63922 and HD 74575. We note that HD 63922 is a known binary, although we do not see any spectral signature from the secondary, as also observed by Nieva & Przybilla (2012). The analysis was based on high-quality spectra (S/N ≈ 400) obtained with the FEROS spectrograph (Kaufer et al. 1999) on the ESO/MPI 2.2 m telescope. The derived stellar parameters and oxygen and silicon abundances are listed in the bottom part of Table 2, and these three stars are referred to as “Local disk sample stars”.
In Table 3 we compare the results obtained for the Local disk sample stars in this work (US) and by Nieva & Przybilla (2007, 2012; NP). Generally, we find reasonable agreement with the results presented in this table, although with some differences: our values of Teff, log g, v sin i and ζmac tend to be slightly lower (<6.5%, <0.22 dex, 2−5 km s−1 and 0−10 km s−1, respectively), whilst our microturbulent velocities are usually higher (2−6 km s−1). The line broadening parameters seem to compensate each other so that the differences observed in the obtained parameters translate into abundance variations that are less than 0.04 dex for oxygen and less than 0.13 dex for silicon. The difference in the silicon abundance is probably due to our higher values of microturbulent velocity. Nonetheless, these abundance differences between the two sets of results can be explained in terms of the uncertainties in the abundance determinations (see Sect. 3.3). Our conclusion from this comparison is that our abundance results are consistent and in good agreement with those of Nieva & Przybilla (2007, 2012).
Comparison between stellar parameters and abundances from this work (US) and Nieva & Przybilla (2007, 2012; NP).
3.5. Comparisons with other studies
Several previous studies in the literature have measured the projected rotational velocities (v sin i) of Galactic OB stars. Daflon et al. (2007), Huang & Gies (2006), and Wolff et al. (2007) derived v sin i for large samples of OB stars from analyses of He I lines and in some cases also Mg II lines. Garmany et al. (2015) also presented v sin i values for the stars studied here based on measurements of full width at half maximum of three He I lines interpolated in a grid of synthetic widths provided by Daflon et al. (2007). Previous studies of chemical abundances of OB stars include the earlier study by Kaufer et al. (1994), which traced the radial abundance gradients based on LTE abundances for a sample of 16 OB stars located between 7 and 16 kpc from the Galactic center. Smartt et al. (1996a) analyzed six stars toward the Galactic anticenter using line-blanketed LTE model atmospheres and spectral synthesis, and added two stars in a subsequent study (Smartt et al. 1996b) based on a line-by-line differential abundance methodology. Smartt & Rolleston (1997) then compiled the abundance results of several previous works of their group, updated to account for non-LTE line formation calculations. Radial abundance gradients for seven elements have been studied in a sample of 69 OB stars by Daflon & Cunha (2004), based on non-LTE spectral synthesis.
A comparison of our results of Teff, log g, and v sin i for stars found to be in common with the studies mentioned above are found in Fig. 5. Our Teff-values show reasonable agreement to within ∼10% with respect those effective temperatures that are based on spectroscopy: the mean difference ⟨us − them⟩ = −320 ± 1290. Notable differences are found when comparing with the Teff values from Garmany et al. (2015), which are based on a photometric calibration for the reddening-free index Q and therefore are expected to be more uncertain. The log g values show differences of up to 0.4 dex (middle plot of Fig. 5), despite the fact that in all cited studies the gravities have been obtained by fitting the wings of H lines. The mean difference ⟨us − them⟩ = −0.10 ± 0.25. We note that this offset is the same uncertainty adopted for the log g (see Sect. 3.3) and has minimal impact on the final abundances. The projected rotational velocities obtained in this study are overall in good agreement with the literature values (right panel in Fig. 5), except for a slightly larger scatter for very sharp lined stars (v sin i ≲ 20 km s−1). The difference between our v sin i results and those listed in the sources presented in Fig. 5 is on average −3.5 ± 8.7 km s−1. The lower v sin i values we report may be the result of including the macroturbulent velocity as an extra parameter of line broadening in our spectrum synthesis analysis.
 |
Fig. 5. Comparison between effective temperature (left panel), surface gravity (middle panel), and projected rotational velocity (right panel) from Table 2 with values listed in previous studies in the literature, identified by different symbols. |
Comparisons between our derived abundances of oxygen and silicon and the literature values are shown in Fig. 6. We note, however, that for two stars (ALS 404 and ALS 428) there is a larger discrepancy in the two sets of results. The large discrepancy in the oxygen and silicon abundances for these two stars may be due to differences in the adopted line lists, Teff, and/or the microturbulence. In particular, the effective temperatures in Daflon & Cunha (2004) are photometric, based on a calibration for the reddening-free indice Q. The resolutions of the spectra analyzed in the two studies are comparable, although the data of the present study has higher signal-to-noise ratio (we used a larger telescope), the equivalent widths measured are consistent between the two studies.
 |
Fig. 6. Comparison between O and Si abundances (left and right panel, respectively), obtained in this work and in the literature for stars in common. |
3.6. Stellar parameters and abundance results
Figure 7 shows the studied sample of 28 early B-type outer disk stars, as well as the three solar neighborhood stars, in the Teff − log g plane, with evolutionary tracks from Ekström et al. (2012) calculated for non-rotating stars at Z = 0.014 and color-coded according to the initial mass, ranging from 7 to 20 M⊙. Almost all studied stars have masses in the range 7–15 M⊙ and fall between the zero-age main sequence (ZAMS) and the terminal-age main sequence. ALS 921 is the most evolved star of our sample, with log g = 3.23, M⋆ ∼ 20 M⊙ and a high microturbulence value of ξt = 10 km s−1.
 |
Fig. 7. The spectroscopic HR diagram for the sample stars: red circles represent the outer disk stars and the blue triangles represent the Local disk stars. Evolutionary tracks computed for masses 7, 9, 12, 15, and 20 M⊙ (solid lines, from yellow to orange, respectively) and for the Zero Age Main Sequence (ZAMS, dashed line) are also shown (Ekström et al. 2012). |
Our iterative procedure based on spectral synthesis treats the broadening mechanisms (projected rotational velocity v sin i, microturbulent velocity ξt, and radial-tangential macroturbulent velocity ζmac) as if they were independent. ξt-values for the studied stars span from 2 to 14 km s−1, with most of the stars (27 stars) with ξt ≤ 8 km s−1 and an average value of 4.6 ± 1.5 km s−1. Two stars with ξt = 9 and 10 km s−1 are the most evolved stars of our sample, respectively log g = 3.44 and 3.23, which is consistent with generally higher microturbulences associated with lower gravities. On the other hand, stars ALS 18020 and HD 63922 show ξt higher than expected for their log g values. We note, however, that lower ξt for these stars would produce exceptionally high abundances. As discussed in Sect. 3.4 for HD 63922, one of the stars used to test our methodology, the final abundances are consistent with previous values from the literature, despite of some differences in the line broadening parameters. The ζmac and v sin i parameters broaden spectral lines in very similar ways which makes it very difficult to disentangle the effects of these parameters in those spectra with low S/N ratios. The v sin i broadens the full profile as the equivalent width remains constant, while the macroturbulent velocity affects mainly the wings of the metallic lines. We note that for spectra with lower S/N ratios, when the line wings are not well defined, the ζmac-values tend to be less accurate. The ζmac values also tend to be lower than 20 km s−1, with only a few stars reaching values up to about 50 km s−1, which are typical values for massive OB stars (Simón-Díaz et al. 2017). We stress that the sample is biased to slow rotators by design, that is, most stars of our sample have v sin i < 50 km s−1 to allow for a proper detailed elemental abundance study.
The non-LTE abundances of O and Si as a function of the Teff are presented in Fig. 8. The dashed lines in both panels represent the solar abundances A(O) = 8.69 and A(Si) = 7.51 (Asplund et al. 2009). The outer disk stars are represented by circles, color-coded according to the distance. Figure 8 also includes the abundances derived for the three OB stars in the Solar neighborhood (shown as triangles). The three stars with lowest O and Si abundances and Teff around 28 000–30 000 K are located at larger distances, indicating that the slight, apparent trend is probably a consequence of the radial abundance gradient. The lack of a correlation between abundances and Teff suggests that the methodology is consistent throughout the entire effective temperature range.
 |
Fig. 8. Silicon and oxygen abundances as a function of Teff. Circles represent the stars of the outer disk sample, color-coded by distance; triangles represent the three nearby stars. The dashed lines in both panels represent the solar abundances A(O) = 8.69 and A(Si) = 7.51 (Asplund et al. 2009). A slight, apparent correlation between abundances and Teff is likely connected to the radial gradient. |
4. Distances
One of the goals in this work is to obtain the radial distribution of O and Si abundances in the Galactic disk. The heliocentric distances (d⊙), a key parameter for such an analysis, were unknown a priori for most of the sample stars, although the star’s location toward the outer Galactic disk was one important selection criterion of the observed sample (Sect. 2).
In Garmany et al. (2015), we obtained heliocentric distances for the full observed sample (including the 28 stars studied here) based on intrinsic colors and a calibration between absolute magnitude and spectral type. We estimated the uncertainties of these heliocentric distances assuming a typical error of ∼0.06 dex in the apparent magnitude (Col. 6 of Table 4). The second Data Release (Gaia Collaboration 2018) provides state-of-the-art measurements of parallaxes for 31 stars analyzed in this work, including the three stars to represent the Local disk. For our objects, the errors on the parallaxes are 21%, on average, with one star having a relative error of 103% (ALS 18681). Bailer-Jones et al. (2018), using Bayesian statistics and a pure geometric prior, estimated the distances for approx-imately 1.33 billion stars of the second Gaia Data Release, and we present their distances for the full sample stars in Col. 7 of Table 4.
Galactic coordinates and distances for the sample stars.
We can estimate the distances to these stars more precisely than using just the Gaia parallaxes (as done by Bailer-Jones et al. 2018) if we use further information about the star. The stellar parameters and apparent color of the star (in combination with theoretical models) tell us about the intrinsic luminosity of the star, and the extinction toward it. Comparing this to the apparent magnitude tells us the distance. Our approach incorporates all of this information (including the Gaia parallax) with the associated uncertainties in a Bayesian framework. For stars which have small relative errors on their Gaia parallax, our results are very similar to those from using the parallax alone. When the relative errors on the Gaia parallax are large, the additional information we use allow us to make much more accurate distance estimates.
Specifically, our estimates are derived in the manner described in McMillan et al. (2018), which follows the pioneering approach of Burnett & Binney (2010). This scheme uses a prior and the observational data for a star to estimate the probability density function in the parameters of initial mass ℳ, age τ, metallicity [M/H], distance s and line-of-sight extinction (parametrized as AV) for the star. Isochrones from Bressan et al. (2012) are used to give the expected observables for these parameters, and to give distance estimates we marginalize over all the other parameters.
In this case we use the “Density” prior described by McMillan et al. (2018), which uses a dust extinction prior based on that from Sharma et al. (2011), and a flat prior on metallicity and age. The observables we use are 2MASS J, H and Ks magnitudes, Teff, log g, and A(O) from this study (where we make the approximation A(O)−8.69 ≈ [M/H]), and Gaia DR2 parallaxes. We make an effort to correct the Gaia parallaxes for a zero-point offset and systematic uncertainties. We apply a global parallax zero-point correction of 29 μas, and we add an uncertainty of 43 μas in quadrature with the quoted errors, corresponding to the values estimated by Lindegren et al. (2018). The distances obtained are listed in Col. 8 of Table 4.
Figure 9 shows a comparison between the distances obtained in this work and the distances published by Garmany et al. (2015; blue circles) and by Bailer-Jones et al. (2018; yellow circles), and Fig. 10 shows an alternative view of this comparison between different distances for each star of our sample. Different points in each line of this figure represent the distinct distance values in the literature (gray squares) as well as the distance obtained in this work (red circles), by Garmany et al. (2015; blue squares) and by Bailer-Jones et al. (2018; yellow triangles). The stars are identified by the ALS number in the y-axis. From Figs. 9 and 10, we note that the distances we derived and those obtained by Bailer-Jones et al. (2018) are in good agreement, while the distances obtained by Garmany et al. (2015) purely from photometric parameter are overestimated for most of the stars.
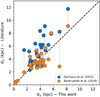 |
Fig. 9. Comparison between the heliocentric distances obtained in this work versus Garmany et al. (2015; blue circles) and Bailer-Jones et al. (2018; yellow circles). |
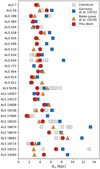 |
Fig. 10. Comparison of heliocentric distances star by star for results calculated in this work (red circles), Bailer-Jones et al. (2018; yellow triangles), by Garmany et al. (2015; blue squares) and obtained in the literature (gray squares). |
The Galactocentric distances projected onto the Galactic plane were computed using the Galactocentric distance of the Sun R⊙ = 8.33 ± 0.35 kpc from Gillessen et al. (2009). It was not possible to calculate the distance for ALS 18674 due to lack of 2MASS JHK photometry, hence we used the heliocentric distance calculated by Bailer-Jones et al. (2018) to obtain the Galactocentric distance. The calculated Galactocentric distances for the sample stars are listed in Col. 10 of Table 4.
5. Radial abundance gradients
Massive OB stars represent the present abundance distribution in the Galactic disk and radial abundance gradients traced by OB stars can help put observational constraints on Galactic chemical evolution models. Figure 11 shows the distribution of the oxygen (left panel) and silicon (right panel) abundances projected onto the Galactic plane. The abundances are color-coded from dark blue (highest abundances) to light yellow (lowest abundances). All stars of our sample are located in the third Galactic quadrant and the three stars near (0,0) in longitude and latitude represent the solar neighborhood stars HD 61068, HD 63922, and HD 74575. The Galactic spiral arms proposed by Carraro et al. (2015) are overplotted: the Perseus Arm (dashed curve), which is located near to the Sun and the stars that could be associated with this arm have heliocentric distances from 1 to 5 kpc, and the Outer Arm (dotted curve) which traverses the third quadrant have heliocentric distances from 6 to 10 kpc. From the figure, we note that a radial gradient does exist whereas the existence of an azimuthal gradient is not clear.
 |
Fig. 11. Distribution of chemical abundances of oxygen (left) and silicon (right) projected onto the Galactic plane. The location of the Perseus Arm (dashed curve) and the Outer Arm (dotted curve), from Carraro et al. (2015), is also shown. A radial gradient is visible on both plots while an azimuthal gradient is not so clear. |
The distribution of the stars’ abundances according to their projected Galactocentric distances is shown in Fig. 12, where the left and right panels show the results for oxygen and silicon, respectively, for the outer disk stars (red circles) and nearby stars (blue triangles). The Sun is represented in the figure with A(O) = 8.69 ± 0.05 and A(Si) = 7.51 ± 0.03 (Asplund et al. 2009) and RG = 8.33 kpc (Gillessen et al. 2009). On both panels, the distribution follows the usual pattern of a negative abundance gradient: as the Galactocentric distance increases, the abundance decreases (see Table 5).
 |
Fig. 12. Abundances of O and Si for the Outer disk sample stars (circles) and Local disk stars (triangles) as a function of the Galactocentric distance. The Sun (⊙) is represented at RG = 8.33 kpc for reference. A Markov chain Monte Carlo (MCMC) linear regression shows the abundance gradients for the distance covered by the sample stars. |
Radial gradient slopes.
To derive the radial abundance gradients for our sample, we used a Markov chain Monte Carlo (MCMC) linear regression algorithm that was built according to Foreman-Mackey et al. (2013), Hogg et al. (2010), and Vanderplas et al. (2012). The MCMC approach is more appropriate in this analysis because: (i) it is less sensitive to outliers when compared to the standard linear fitting method, (ii) it considers the errors on both variables, in this case abundances and distances, and (iii) it is suitable when the uncertainties may be high (which is the case of some of the distances). The radial abundance gradients obtained for 8.4 ≤ RG ≤ 15.6 kpc, are:
The sample of OB stars studied has been selected in order to cover the outer Galactic disk. The radial gradients we derived predict O and Si abundances at RG ∼ 8.5 kpc that are fully consistent with the abundances of the three nearby stars and the Sun that represent the abundances in the solar neighborhood.
In Table 5 we compile some results for the oxygen and silicon radial abundance gradients for young stellar populations in the Milky Way; for OB stars (Gummersbach et al. 1998; Rolleston et al. 2000; Daflon & Cunha 2004), Cepheids (Lemasle et al. 2013; Genovali et al. 2015; Luck 2018), and H II regions (Esteban et al. 2017; Fernández-Martín et al. 2017; Esteban & García-Rojas 2018).
The radial gradient obtained in this study for silicon of −0.09 dex kpc−1 is relatively steep. Overall, the silicon gradients in OB stars from the literature span a relatively large range of values from flat, −0.04 dex kpc−1, to quite steep, −0.11 dex kpc−1; this somewhat large variation in the slopes in the different studies may be due to the impact of the microturbulent velocity on the silicon abundance determinations, which, in general, are based on intermediate to strong Si III lines. The silicon results for the Cepheids in the three studies presented in Table 5 from Lemasle et al. (2013), Genovali et al. (2015), and Luck (2018) show more consistency and indicate a mean slope of −0.053 dex kpc−1.
The oxygen abundance gradients in the different OB star studies show a smaller variation in the derived slopes (from −0.03 to −0.07 dex kpc−1) when compared to silicon. The oxygen gradient obtained in this study for the OB stars of −0.07 dex kpc−1, as well as two earlier studies from the literature Gummersbach et al. (1998) and Rolleston et al. (2000), are steeper than those for Cepheids (Luck 2018) and for H II regions presented in the three studies in Table 5.
It is important to keep in mind, however, that the radial abundance gradients in the different studies were obtained for different galactocentric distance ranges and that the abundance gradients may not be uniform along the entire Galactic disk. Results for the galactic open clusters, for example, seem to indicate that there is a break in the metallicity slope at Rg ∼ 12 kpc with the gradient being flatter for RG > 12 kpc (Netopil et al. 2016; Reddy et al. 2016; Frinchaboy et al. 2013; Cunha et al. 2016).
The possibility of external flattening of the oxygen gradient has been discussed by Esteban et al. (2017). The authors divided their H II region sample into “inner” and “outer” disk samples (at RG = 11.5 kpc) and obtained oxygen gradients for the inner and outer disk that are equal within the uncertainties, finding no evidence of flattening of the radial gradient to within RG ≈ 17 kpc. More recently, Esteban & García-Rojas (2018) obtained a two-zone oxygen abundance gradient for his sample of H II regions finding that the oxygen slope is flatter in the inner disk, with a break at ∼8 kpc. Similarly, most of the OB stars (60 out of 69 stars) in the Daflon & Cunha (2004) sample are also within ∼9 kpc from the galactic center; the flatter gradients obtained in that study may be influenced by this selection.
Radial gradients traced by young massive B stars (age <20 Myr) are not affected by long-term processes such as radial migration (Magrini et al. 2017), for example. In Fig. 13 we compare the radial distributions of oxygen abundances obtained for different young objects of the Galaxy. Abundances of main-sequence OB stars are from this work (red circles) and from Daflon & Cunha (2004; blue squares). Average oxygen abundances derived by Luck (2018) based on a multiphase analysis for a large sample of Cepheids are represented by gray open circles. Nebular abundances of H II regions from Esteban et al. (2017) are represented by orange triangles. Oxygen abundances of young G- and K-type stars in star forming regions from Spina et al. (2017) are shown as green triangles (the oxygen abundances were estimated from their [Fe/H] values). It is clear from Fig. 13 that the oxygen abundance pattern for different types of young objects in the Galactic disk present an overall large spread. The results for Cepheids have significant scatter and overlap with the less scattered results for the OB stars derived in this study; the cepheids oxygen abundances, however, are offset from the results in Daflon & Cunha (2004) for Rg < ∼8 kpc. The H II region abundances have a smaller scatter but are systematically lower than the results for the OB stars and Cepheids. A comparison between oxygen abundances obtained for the Cocoon Nebula and its ionizing B stars by García-Rojas et al. (2014) shows a difference of ∼0.2 dex, the stellar abundances being higher than the nebular abundances considering corrections due to depletion onto dust. Similar discrepancy has been also discussed by Simón-Díaz & Stasińska (2011) for the Orion nebula. Such discrepancy in the star-gas abundances may be due to possible temperature fluctuations.
 |
Fig. 13. Radial gradient of oxygen abundance traced by young objects of the Galactic disk: OB stars from this work (red circles) and from Daflon & Cunha (2004; blue squares); cepheids from Luck (2018; open circles); SFR regions from Spina et al. (2017; green triangles); and H II regions from Esteban et al. (2017; orange triangles). |
The stars in star forming regions follow the trend in Daflon & Cunha (2004). Although with systematic differences between the probes, when considering all results for the OB stars and H II regions, there is evidence for a possible flattening in the inner disk (Rg < 8 kpc) and a steeper gradient between roughly Rg ∼ 8–16 kpc, as seen for the open clusters.
Chemical evolution models of the Galaxy by Chiappini et al. (2001) and Cescutti et al. (2007) considering two-infall episodes and inside-out formation of the Galactic disk predict negative radial abundance gradients. The halo surface mass density is the key parameter in their models that allows for the presence of gradients with different slopes: the adoption of a constant halo density within ∼8 kpc from the Galactic center, for example, produces flat gradients in the outer disk (Rg > ∼16 kpc). From our results, however, it is not possible to conclude if the gradients flatten in the outer disk, with a break in the metallicity slope at Rg ∼ 12 kpc. In a simple exercise, we split the sample stars in two groups, breaking at RG ∼ 12.5 kpc, and recomputed the gradients. The gradients in the two zones are consistent within the uncertainties to those obtained for the full sample. In addition, we note a larger abundance spread in the outermost zone, producing higher uncertainties in the recomputed slopes: the radial gradient of oxygen for RG < 12.5 kpc is −0.06 ± 0.02 dex kpc−1 whereas in the outer zone we obtained a gradient of −0.04 ± 0.04 dex kpc−1.
The more sophisticated chemodynamical models by Minchev et al. (2013, 2014) predict steeper radial metallicity gradient of −0.057 dex kpc−1 from a subsample of young (age <2 Gyr) stars located close to disk midplane (|z| < 0.25 kpc), while the radial gradient tends to flatten down to −0.020 dex kpc−1 for subsamples with increasing age and increasing distance to the plane. Our gradients obtained from abundances of young, massive B stars are consistent with these predictions of present-day radial metallicity gradient in the Galactic plane.
6. Conclusions
We present a detailed elemental abundance study of 28 main-sequence OB stars located toward the Galactic anticenter plus three stars in the solar neighborhood. We developed a robust and self-consistent methodology to analyze the spectra of these objects using a full Non-LTE approach, meaning that the stellar atmosphere models and synthetic spectra were both calculated in Non-LTE using the codes TLUSTY and SYNSPEC. The analytic tools used to compare the observed and synthetic spectra were built using IDL/GDL and Python technologies. The outputs of our iterative scheme are effective temperature, surface gravity, line broadening parameters (projected rotational velocity, macroturbulent and microturbulent velocities) as well as the abundances of oxygen and silicon. This methodology has been tested for three OB stars with abundance results previously presented in the literature and our present abundance results are consistent with the published values. The studied sample contains main-sequence OB stars with temperatures in the range 20 800–31 300 K. From the derived stellar parameters and evolutionary tracks, the masses of our target stars vary from 7 M⊙ to 20 M⊙, with most of the stars having masses between 9 and 15 M⊙.
With the derived elemental abundances from Table 2 and heliocentric distances from Table 4, we investigated the variation of oxygen and silicon abundances across the outer disk of the Milky Way. We found no evidence of an azimuthal gradient, although our sample is not suitable for such study, so further work is needed to confirm this. Regarding the radial gradient, we found slopes of −0.07 ± 0.01 and −0.09 ± 0.01 dex kpc−1 for oxygen and silicon, respectively, in the region of 8.4 < RG < 15.6 kpc. The negative slopes indicate the abundances systematically decrease from values roughly solar at the solar neighborhood to average values that are approximately 0.4−0.6 dex lower at RG ∼ 15 kpc. The gradients obtained present a general good agreement when compared to other results of the literature covering the outer disk. The slopes we obtained for our sample of Main Sequence OB stars are consistent with those predicted by chemodynamical models for a subsample of young stars located in the Galactic midplane.
The Carnegie Observatories CarPy python distribution is available for download at http://code.obs.carnegiescience.edu/carnegie-python distribution.
Acknowledgments
We thank the referee for a careful reading of the manuscript. G.A.B acknowledges financial support from CAPES (Ph.D. fellowship) and CNPq (post-doctoral fellowship), and the Observatoire de la Côte d’Azur for the warming hospitality. T.B. was funded by the project grant “The New Milky Way” from Knut and Alice Wallenberg Foundation. M.S.O and T.B. were supported by the US National Science Foundation, grant AST-0448900 to MSO. K.C. acknowledges funding from NSF grant AST-907873. This research has made use of NASA’s ADS Bibliographic Services, the SIMBAD database, operated by CDS, Strasbourg, Python, Astropy Astropy Collaboration (2013), IPython Pérez & Granger (2007), Matplotlib Hunter et al. (2007), NumPy van der Walt et al. (2011). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babu, G. S. D. 1983, A&A, 4, 235 [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 158, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, R., Shectman, S. A., Gunnels, S. M., Mochnacki, S., & Athey, A. E. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Bica, E., Bonatto, C., & Dutra, C. M. 2008, A&A, 489, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blitz, L., Fich, M., & Stark, A. A. 1982, ApJS, 49, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., & Bica, E. 2011, MNRAS, 414, 3769 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Burnett, B., & Binney, J. 2010, MNRAS, 407, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Carraro, G., Vázquez, R. A., Costa, E., Ahumada, J. A., & Giorgi, E. E. 2015, AJ, 149, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Cazorla, C., Morel, T., Nazé, Y., et al. 2017, A&A, 603, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cescutti, G., Matteucci, F., François, P., & Chiappini, C. 2007, A&A, 462, 943 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. 2012, Astron. Geophys., 53, 4.30 [CrossRef] [Google Scholar]
- Cunha, K., Frinchaboy, P. M., Souto, D., et al. 2016, Astron. Nachr., 337, 922 [NASA ADS] [CrossRef] [Google Scholar]
- Cunto, W., & Mendoza, C. 1992, Rev. Mex. Astron. Astrofis., 23, 107 [NASA ADS] [Google Scholar]
- Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Daflon, S., Cunha, K., de Araújo, F. X., Wolff, S., & Przybilla, N. 2007, AJ, 134, 1570 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esteban, C., & García-Rojas, J. 2018, MNRAS, 478, 2315 [NASA ADS] [CrossRef] [Google Scholar]
- Esteban, C., Fang, X., García-Rojas, J., & Toribio San Cipriano, L. 2017, MNRAS, 471, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Martín, A., Pérez-Montero, E., Vílchez, J. M., & Mampaso, A. 2017, A&A, 597, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fich, M., & Silkey, M. 1991, ApJ, 366, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzgerald, M. P., & Moffat, A. F. J. 1980, MNRAS, 193, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzgerald, M. P., Hurkens, R., & Moffat, A. F. J. 1976, A&A, 46, 287 [NASA ADS] [Google Scholar]
- Fitzsimmons, A. 1993, A&AS, 99, 15 [NASA ADS] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Frinchaboy, P. M., Thompson, B., Jackson, K. M., et al. 2013, ApJ, 777, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Froese Fischer, C., Tachiev, G., & Irimia, A. 2006, At. Data Nucl. Data Tables, 92, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Rojas, J., Simón-Díaz, S., & Esteban, C. 2014, A&A, 571, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garmany, C. D., Glaspey, J. W., Bragança, G. A., et al. 2015, AJ, 150, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Genovali, K., Lemasle, B., da Silva, R., et al. 2015, A&A, 580, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Gummersbach, C. A., Kaufer, A., Schaefer, D. R., Szeifert, T., & Wolf, B. 1998, A&A, 338, 881 [NASA ADS] [Google Scholar]
- Harmanec, P., Uytterhoeven, K., & Aerts, C. 2004, A&A, 422, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hensberge, H., Pavlovski, K., & Verschueren, W. 2000, A&A, 358, 553 [NASA ADS] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, ArXiv e-prints [arXiv:1008.4686] [Google Scholar]
- Huang, W., & Gies, D. R. 2006, ApJ, 648, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I. 1988, Comput. Phys. Commun., 52, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [Google Scholar]
- Hubeny, I., & Lanz, T. 2017a, ArXiv e-prints [arXiv:1706.01859] [Google Scholar]
- Hubeny, I., & Lanz, T. 2017b, ArXiv e-prints [arXiv:1706.01937] [Google Scholar]
- Hunter, I., Dufton, P. L., Smartt, S. J., et al. 2007, A&A, 466, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, P. D., Moffat, A. F. J., & Fitzgerald, M. P. 1977, A&A, 60, 417 [NASA ADS] [Google Scholar]
- Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
- Kaufer, A., Szeifert, T., Krenzin, R., Baschek, B., & Wolf, B. 1994, A&A, 289, 740 [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2005, A&A, 440, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kharchenko, N. V., Piskunov, A. E., Schilbach, E., Röser, S., & Scholz, R.-D. 2013, A&A, 558, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lahulla, J. F. 1987, AJ, 94, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Lemasle, B., François, P., Genovali, K., et al. 2013, A&A, 558, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lester, K. V., Gies, D. R., & Guo, Z. 2016, AJ, 152, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Hernandez, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luck, R. E. 2018, AJ, 156, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Lyubimkov, L. S., Lambert, D. L., Poklad, D. B., Rachkovskaya, T. M., & Rostopchin, S. I. 2013, MNRAS, 428, 3497 [NASA ADS] [Google Scholar]
- Magrini, L., Randich, S., Kordopatis, G., et al. 2017, A&A, 603, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 2014, The Origin of the Galaxy and Local Group, Saas-Fee Advanced Course (Berlin, Heidelberg: Springer-Verlag), 37, 145 [NASA ADS] [CrossRef] [Google Scholar]
- McMillan, P. J., Kordopatis, G., Kunder, A., et al. 2018, MNRAS, 477, 5279 [NASA ADS] [CrossRef] [Google Scholar]
- Mel’Nik, A. M., & Dambis, A. K. 2009, MNRAS, 400, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, A. F. J., & Vogt, N. 1975, A&AS, 20, 85 [NASA ADS] [Google Scholar]
- Moffat, A. F. J., Jackson, P. D., & Fitzgerald, M. P. 1979, A&AS, 38, 197 [NASA ADS] [Google Scholar]
- Moreno-Corral, M. A., Chavarría-K, C., & de Lara, E. 2002, Rev. Mex. Astron. Astrofis., 38, 141 [NASA ADS] [Google Scholar]
- Netopil, M., Paunzen, E., Heiter, U., & Soubiran, C. 2016, A&A, 585, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M. F., & Przybilla, N. 2007, A&A, 467, 295 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nieva, M.-F., & Przybilla, N. 2012, A&A, 539, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pandey, A. K., Sandhu, T. S., Sagar, R., & Battinelli, P. 2010, MNRAS, 403, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Park, B.-G., & Sung, H. 2002, AJ, 123, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Perren, G. I., Vázquez, R. A., & Piatti, A. E. 2015, A&A, 576, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Philip, A. G. D., Chromey, F. R., & Dubois, P. 1990, PASP, 102, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, A. B. S., Lambert, D. L., & Giridhar, S. 2016, MNRAS, 463, 4366 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B. C. 1998, ApJS, 115, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B. C. 2003, AJ, 125, 2531 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Rolleston, W. R. J., Dufton, P. L., & Fitzsimmons, A. 1994, A&A, 284, 72 [NASA ADS] [Google Scholar]
- Rolleston, W. R. J., Smartt, S. J., Dufton, P. L., & Ryans, R. S. I. 2000, A&A, 363, 537 [NASA ADS] [Google Scholar]
- Rudolph, A. L., Fich, M., Bell, G. R., et al. 2006, ApJS, 162, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Adami, C., & Georgelin, Y. M. 2007, A&A, 470, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schulz, N. 2012, The Formation and Early Evolution of Stars: From Dust to Stars and Planets, Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer) [Google Scholar]
- Sharma, S., Bland-Hawthorn, J., Johnston, K. V., & Binney, J. 2011, ApJ, 730, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., & Stasińska, G. 2011, A&A, 526, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., Godart, M., Castro, N., et al. 2017, A&A, 597, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smartt, S. J., Dufton, P. L., & Rolleston, W. R. J. 1996a, A&AS, 116, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smartt, S. J., Dufton, P. L., & Rolleston, W. R. J. 1996b, A&A, 310, 123 [NASA ADS] [Google Scholar]
- Smartt, S. J., & Rolleston, W. R. J. 1997, ApJ, 481, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Spina, L., Randich, S., Magrini, L., et al. 2017, A&A, 601, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turbide, L., & Moffat, A. F. J. 1993, AJ, 105, 1831 [NASA ADS] [CrossRef] [Google Scholar]
- van der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderplas, J., Connolly, A., Ivezić, Ž., & Gray, A. 2012, Conference on Intelligent Data Understanding (CIDU), 47 [CrossRef] [Google Scholar]
- Vázquez, R. A., Moitinho, A., Carraro, G., & Dias, W. S. 2010, A&A, 511, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, C., Liu, X. W., Xiang, M. S., et al. 2019, MNRAS, 482, 2189 [NASA ADS] [CrossRef] [Google Scholar]
- Wiese, W. L., Fuhr, J. R., & Deters, T. M. 1996, Atomic Transition Probabilities of Carbon, Nitrogen, and Oxygen: A Critical Data Compilation (Woodbury, NY: American Chemical Society) [Google Scholar]
- Wolff, S. C., Strom, S. E., Dror, D., & Venn, K. 2007, AJ, 133, 1092 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Comparison between stellar parameters and abundances from this work (US) and Nieva & Przybilla (2007, 2012; NP).
All Figures
 |
Fig. 1. Example spectra in the region 4670−4720 Å for the star ALS 14013 reduced with the pipeline (gray line) and re-reduced (blue line). The feature introduced by the CCD defect in the region 4680−4695 Å has been adequately removed. |
| In the text | |
 |
Fig. 2. Example spectra for six observed stars in the region 4660−4720 Å. The spectra are vertically shifted for better visualization. Some spectral lines are identified on the top. |
| In the text | |
 |
Fig. 3. Positions of the all 136 observed stars (gray circles) projected onto the Galactic plane; the 28 stars selected for a detailed abundance analysis are presented (red circles) with reviewed distances (see Sect. 4). All stars are located in the third Galactic quadrant. |
| In the text | |
 |
Fig. 4. Flowchart illustrating the iterative methodology to determine the stellar parameters and elemental abundances, based on the ionisation balance of O I/O II/O III and Si II/Si III/Si IV and χ2 minimisation. |
| In the text | |
 |
Fig. 5. Comparison between effective temperature (left panel), surface gravity (middle panel), and projected rotational velocity (right panel) from Table 2 with values listed in previous studies in the literature, identified by different symbols. |
| In the text | |
 |
Fig. 6. Comparison between O and Si abundances (left and right panel, respectively), obtained in this work and in the literature for stars in common. |
| In the text | |
 |
Fig. 7. The spectroscopic HR diagram for the sample stars: red circles represent the outer disk stars and the blue triangles represent the Local disk stars. Evolutionary tracks computed for masses 7, 9, 12, 15, and 20 M⊙ (solid lines, from yellow to orange, respectively) and for the Zero Age Main Sequence (ZAMS, dashed line) are also shown (Ekström et al. 2012). |
| In the text | |
 |
Fig. 8. Silicon and oxygen abundances as a function of Teff. Circles represent the stars of the outer disk sample, color-coded by distance; triangles represent the three nearby stars. The dashed lines in both panels represent the solar abundances A(O) = 8.69 and A(Si) = 7.51 (Asplund et al. 2009). A slight, apparent correlation between abundances and Teff is likely connected to the radial gradient. |
| In the text | |
 |
Fig. 9. Comparison between the heliocentric distances obtained in this work versus Garmany et al. (2015; blue circles) and Bailer-Jones et al. (2018; yellow circles). |
| In the text | |
 |
Fig. 10. Comparison of heliocentric distances star by star for results calculated in this work (red circles), Bailer-Jones et al. (2018; yellow triangles), by Garmany et al. (2015; blue squares) and obtained in the literature (gray squares). |
| In the text | |
 |
Fig. 11. Distribution of chemical abundances of oxygen (left) and silicon (right) projected onto the Galactic plane. The location of the Perseus Arm (dashed curve) and the Outer Arm (dotted curve), from Carraro et al. (2015), is also shown. A radial gradient is visible on both plots while an azimuthal gradient is not so clear. |
| In the text | |
 |
Fig. 12. Abundances of O and Si for the Outer disk sample stars (circles) and Local disk stars (triangles) as a function of the Galactocentric distance. The Sun (⊙) is represented at RG = 8.33 kpc for reference. A Markov chain Monte Carlo (MCMC) linear regression shows the abundance gradients for the distance covered by the sample stars. |
| In the text | |
 |
Fig. 13. Radial gradient of oxygen abundance traced by young objects of the Galactic disk: OB stars from this work (red circles) and from Daflon & Cunha (2004; blue squares); cepheids from Luck (2018; open circles); SFR regions from Spina et al. (2017; green triangles); and H II regions from Esteban et al. (2017; orange triangles). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.