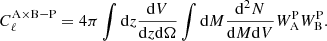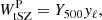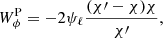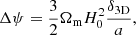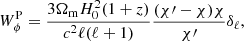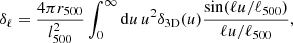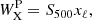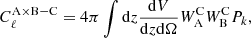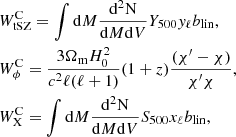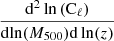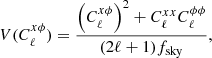| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | L4 | |
| Number of page(s) | 4 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201732071 | |
| Published online | 10 May 2019 | |
Letter to the Editor
First measurement of the cross-correlation between CMB weak lensing and X-ray emission
1
Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza de San Juan 1, planta 2, 44001 Teruel, Spain
e-mail: ghurier@ias.u-psud.fr, ghurier@cefca.es
2
Inter-University Centre for Astronomy and Astrophysics, Ganeshkhind, Post Bag 4, Pune 411007, India
Received:
10
October
2017
Accepted:
5
March
2019
Since the publication of the results of the Planck satellite mission in 2013, the local and early Universes have been considered to be in tension in respect of the determination of amplitude of the matter density spatial fluctuations (σ8) and the amount of matter present in the Universe (Ωm). This tension can be seen as a lack of massive galaxy clusters in the local Universe compared to the prediction inferred from Planck cosmic microwave background (CMB) best-fitting cosmology. In the present analysis we perform the first detection of the cross-correlation between X-rays and CMB weak lensing at 9.1σ. We next combine thermal Sunyaev–Zel’dovich effect, X-rays, and weak-lensing angular auto- and cross-correlation power spectra to determine the galaxy cluster hydrostatic mass bias. We derive (1 − bH) = 0.71 ± 0.07. Considering these constraints, we observe that estimations of σ8 in the local Universe are consistent with Planck CMB best-fitting cosmology. However, these results are in clear tension with the output of hydrodynamical simulations that favor (1 − bH)> 0.8.
Key words: cosmological parameters / large-scale structure of Universe / galaxies: clusters: general / galaxies: clusters: intracluster medium / cosmic background radiation
© ESO 2019
1. Introduction
Modern cosmology relies heavily on the observations and analysis of cosmic microwave background (CMB) data. If the standard six parameter Λ cold dark matter (ΛCDM) model provides a satisfying description of the outcome of the main cosmological probes (Planck Collaboration XIII 2016), the determination of its parameters appears to be in tension when separately considering the CMB angular power spectrum on the one hand, and the abundance of galaxy cluster in the local Universe (z < 1) on the other (see, e.g., Salvati et al. 2018, for a recent CMB-galaxy cluster joint analysis).
One current challenge of modern cosmology is thus related to the understanding of the origin of this apparent tension. This could be produced by our lack of knowledge regarding the galaxy cluster mass-observable relations, or by new physics beyond the standard ΛCDM model affecting the structure growth between the CMB last scattering surface and the local Universe (Salvati et al. 2018; Planck Collaboration XX 2014). In this context, several probes can be used to trace the large-scale distribution of matter in the Universe. During their propagation along the line of sight, the CMB photons are affected by several physical processes such as the inverse Compton scattering expressed by the thermal Sunyaev–Zel’dovich effect (Sunyaev & Zeldovich 1969, 1972; hereafter tSZ), and the CMB gravitational lensing (Blanchard & Schneider 1987) accounting for the deflections induced by the gravitational potential integrated along the line of sight, ϕ. The hot electrons causing the tSZ effect are also emitting in the X-ray domain through Bremsstrahlung radiation in such a way that the tSZ effect, X-ray emission, and gravitational lensing have been powerful sources of cosmological and astrophysical constraints (see, e.g., Planck Collaboration XX 2014; Planck Collaboration XVII 2014).
However, the use of galaxy clusters as cosmological probes often requires the determination of their total mass, a complicated step usually relying on the hydrostatic equilibrium hypothesis. While such mass estimates are known to be biased (Mhydro/Mtrue = 1 − bH), hydrodynamical simulations favor low values for this bias (bH < 0.2) (see, e.g., Lau et al. 2013; Biffi et al. 2016). At the same time, on the observational side a significant number of analyses combining X-ray, tSZ, and weak lensing observations have been conducted in the last five years, either based on an object-by-object approach or resorting to stacking algorithms (see, e.g., Hurier & Angulo 2018; Medezinski et al. 2018; Sereno et al. 2017; Jimeno et al. 2018; Parroni et al. 2017; Okabe & Smith 2016; Battaglia et al. 2016; Applegate et al. 2016; Smith et al. 2016; Hoekstra et al. 2015; Simet et al. 2015; Israel et al. 2015; von der Linden et al. 2014; Donahue et al. 2014; Gruen et al. 2014; Mahdavi et al. 2013). These analyses obtain a hydrostatic mass bias bH > 0.3, which seem to be compatible with the measurement obtained after combining CMB weak lensing and tSZ measurements towards SDSS DR8 redMaPPer (Rykoff et al. 2014) galaxy clusters: bH = 0.26 ± 0.07 (Hurier & Angulo 2018).
The statistical correlations of these tracers on the sky have also attracted a lot of attention. For instance, the correlation between tSZ–X and tSZ–ϕ cross-analyses have been used to set cosmological constraints (see, e.g., Hill & Spergel 2014; Hurier 2015; Hurier et al. 2015). These measurements present different sensitivities to cosmological parameters and mass-observable relations. Consequently, a coherent statistical analysis of ϕ, tSZ, and X-ray emission is a powerful tool for identifying the origin of the tension between the CMB and the low redshift Universe.
In the present paper we present the first measurement of the CMB weak lensing and X-ray emission cross-correlation power spectrum. We model this cross-correlation using a halo-model formalism to derive cosmological constraints. Finally, we combine this result with previous studies to derive constraints on the hydrostatic mass bias.
2. Modeling the tSZ, X-ray, and ϕ cross-correlations
We refer to Hurier (2015) for a detailed modeling of tSZ and ϕ cross-power spectra, and to Hurier et al. (2014) for the modeling of the X-ray emission. We relate cosmological parameters to the dark matter halo number per unit of mass and redshift 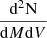 using the mass function from Tinker et al. (2008).
using the mass function from Tinker et al. (2008).
2.1. Poissonian term
Using the Limber approximation, we can write the one-halo term as
The tSZ contribution can be written as
where Y500 represents the tSZ flux of the clusters within a radius where the matter density equals 500 times the critical density at the clusters’ redshift, related to the mass contained in the same volume (M500) via the scaling law presented in Planck Collaboration XX (2014). In this same expression, yℓ represents the Fourier transform on the sphere of the cluster pressure profile per unit of tSZ flux from Planck Collaboration XX (2014). We consider a generalized Navarro–Frenk–White (GNFW) Universal pressure profile (Arnaud et al. 2010; Planck Collaboration Int. V 2013).
We model the lensing contribution as
with χ the comoving distance, χ′ the comoving distance to the surface of the last scattering of the CMB, and ψℓ the 3D lensing potential Fourier transform on the sky. We can express the potential ψ as a function of the density contrast,
with a the Universe scale factor and δ the density contrast. From this, the lensing contribution reads
where δℓ is the Fourier transform of the density contrast profile, δ3D(u), computed as
where u = r/r500 is the normalized radius of the profile, ℓ500 = DA/r500, DA is the angular diameter distance, and r500 is the radius within which the matter density is 500 times the critical density of the Universe.
Finally, the X-ray contribution can be written as
with 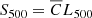 , the X-ray count-rate in the [0.5–2.0] keV energy band of the host halo, L500 the unabsorbed X-ray luminosity in the [0.1–2.4] keV energy range,
, the X-ray count-rate in the [0.5–2.0] keV energy band of the host halo, L500 the unabsorbed X-ray luminosity in the [0.1–2.4] keV energy range, 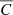 the average luminosity to count-rate conversion factor described in Hurier et al. (2014), and xℓ the Fourier transform of the X-ray number count profile. To model the L500 − M500 relation, we used the relation derived by Arnaud et al. (2010) from the REXCESS sample (Böhringer et al. 2007). We considered a polytropic equation of state with a polytropic index of 1.2 to compute the density and the temperature profiles from the pressure profile.
the average luminosity to count-rate conversion factor described in Hurier et al. (2014), and xℓ the Fourier transform of the X-ray number count profile. To model the L500 − M500 relation, we used the relation derived by Arnaud et al. (2010) from the REXCESS sample (Böhringer et al. 2007). We considered a polytropic equation of state with a polytropic index of 1.2 to compute the density and the temperature profiles from the pressure profile.
2.2. Large-scale correlation terms
We express the large-scale correlations, the two-halo term, contribution as
with Pk, the matter power-spectrum computed using CLASS (Lesgourgues 2011).
For the tSZ effect, the CMB weak lensing, and the X-ray count rate we can express the window functions as
where blin is the linear bias relating the halo distribution to the overdensity distribution. We considered the bias from Mo & White (1996), which is realistic on galaxy cluster scales.
We find that X-ray–lensing cross-correlation power spectra evolves as 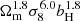 for ℓ = 200.
for ℓ = 200.
We present in Fig. 1 the power density distribution in the M500 − z plane for the X-ray, weak lensing, and tSZ auto- and cross-correlation power spectra at ℓ = 200. We observe that weak-lensing favors higher redshift objects compared to the tSZ effect and X-ray emission. The X-ray and tSZ are highly correlated (at ≃76%), while the tSZ effect and the weak lensing one-halo terms are moderately correlated (≃46%), and the X-ray emission and the weak lensing one halo-terms show a lower correlation at the level of ≃20%. We refer the reader to Hurier (2015) and Hurier et al. (2015) for a detailed description of the mass and redshift dependence of the CMB weak lensing and X-ray window functions. In the light of Fig. 1, it becomes clear that detecting the X-ray–lensing cross-correlation is particularly challenging, considering the high noise level of Planck CMB weak lensing maps, and the AGN-dominated X-ray sky.
 |
Fig. 1. Power density for power spectra |
3. First measurement of the cross-correlation between X-rays and weak-lensing
We use the ROSAT all-sky survey (RASS) public data1, which covers 99.8% of the sky, including 97% that has an exposure time longer than 100 s (Voges et al. 1999). A description of the reprojection of the RASS data on the Healpix full-sky map can be found in Hurier et al. (2015). We also use the Planck full-sky CMB weak lensing map (Planck Collaboration XVII 2014). We mask all regions with less than 100 s exposure time in RASS full-sky map, while using the mask associated with the Planck all-sky weak lensing map. This combination of masks results in an effective sky fraction of fsky ≃ 75% in the cross-correlation. We have also verified that using more aggressive galactic masks (down to a sky coverage of 50%) does not modify the results significantly.
We compute the uncertainty in the weakly non-Gaussian limit as
where 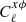 ,
, 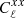 , and
, and 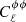 are the X-ray–lensing, X-ray, and weak lensing power spectra. We obtained a significance of 9.1σ for the X-ray-weak lensing cross-power spectrum in the range ℓ ∈ [10, 400].
are the X-ray–lensing, X-ray, and weak lensing power spectra. We obtained a significance of 9.1σ for the X-ray-weak lensing cross-power spectrum in the range ℓ ∈ [10, 400].
We verified that AGNs do not produce a significant contribution to the total signal by masking BOSS AGNs (Albareti et al. 2017) and performing our analysis on the BOSS footprint (fsky = 25%). We also masked NVSS bright sources, S > 0.03 Jy (Condon et al. 1998), and restrict our analysis to the NVSS footprint (δ > −40o). We do not observe any significant modification of our results when masking the BOSS AGNs or NVSS sources. We also modeled the AGN contribution following the AGN mass and luminosity functions from Hütsi et al. (2014) and Main et al. (2017). This contribution is about two orders of magnitude smaller than the X-ray–ϕ cross-correlation, as shown in Fig. 2 for the Hütsi et al. (2014) model. Consequently, the AGN impact on our results is small compared to the uncertainty level. We thus neglect the AGN contribution to the total X-ray–lensing cross-correlation.
 |
Fig. 2. X-ray–ϕ cross-correlation angular power spectrum, measured between Planck CMB lensing full-sky map and a RASS data reprojected on the full-sky (black sample); the same cross-spectra when masking NVSS sources is shown as grey samples. The red solid line shows the theoretical prediction assuming (σ8 = 0.8, Ωm = 0.3, bH = 0.2), the green dashed line shows the two-halo term contribution, and the blue dashed line the one-halo term contribution. The solid cyan line displays the contribution from AGN–ϕ cross-correlation. |
In Fig. 2, we present the derived angular cross-power spectrum, compared to our modeling for (σ8 = 0.8, Ωm = 0.3, bH = 0.2). We observe that the two-halo term dominates for ℓ < 100 and that the one-halo term dominates at higher multipoles. This illustrates how Planck weak lensing map contains a significant signal produced by compact objects like galaxy clusters. Assuming a Gaussian prior of bH = 0.20 ± 0.05, consistent with hydrodynamical simulations and marginalizing over other cosmological parameters according to Planck CMB best-fitting cosmology (Planck Collaboration XIII 2016), we derive Σ8 = σ8(Ωm/0.30)0.27 = 0.80 ± 0.03. We verified that masked galaxy clusters only marginally affect (< 1%) the constraints on σ8, which can thus be safely neglected.
4. Combined analysis of thermal Sunyaev–Zel’dovich effect, X-ray, and weak-lensing signals
We next combine our results with tSZ–ϕ, tSZ–tSZ, tSZ–X-ray, ϕ–ϕ, and CMB–CMB power spectra results. We assume that the CMB angular power spectrum is uncorrelated with all other probes2, so we compute the covariance between all large-scale structure tracers following the procedure described in Hurier & Lacasa (2017) accounting for non-Gaussian contributions to the uncertainties. We use the tSZ analysis from Hurier & Lacasa (2017), the tSZ–ϕ measurement corrected for cosmic infra-red background contamination from Hurier (2015), the tSZ–X-ray results from Hurier et al. (2015), the Planck weak lensing results from Planck Collaboration XVII (2014), and the Planck CMB results from Planck Collaboration XIII (2016).
We performed a join fit of these results to derived cosmological constraints on σ8 and Ωm and constraints on the hydrostatic mass bias bH. Both weak-lensing and CMB results are not sensitive to the hydrostatic mass bias. Consequently, weak lensing and CMB constraints set the cosmological parameters σ8 and Ωm, whereas the large-scale structure tracers, namely the tSZ effect and the X-ray emission, set the hydrostatic mass-bias value. From this combined analysis, we derived bH = 0.71 ± 0.07. We present the resultant likelihoods for tSZ, tSZ–X, tSZ–ϕ, X–ϕ, ϕ, and CMB analyses for bH = 0.71 ± 0.07 in Fig. 3. The X-ray auto-correlation power spectrum is not shown in this figure as it is particularly difficult to derive robust constraints from it, considering that the X-ray sky is dominated by AGN contribution. We observe that some tension remains, especially with tSZ derived constraints, but all large-scale structure analyses presented here are consistent within 2 σ with the Planck CMB results.
 |
Fig. 3. Likelihood function of Σ8 = σ8(Ωm/0.30)0.27 from different analyses: tSZ angular power spectrum, bispectrum, and number count (red, Hurier & Lacasa 2017); CMB weak lensing (dark blue, Planck Collaboration XVII 2014); CMB angular power spectrum (green, Planck Collaboration XIII 2016); tSZ–weak lensing cross correlation (cyan, Hurier 2015); tSZ–X-ray cross-correlation (orange, Hurier et al. 2015); and X-ray–ϕ cross-correlation (black, this work). |
5. Conclusion and discussion
We produced the first detection of the X-ray–ϕ cross-correlation angular power spectrum, with a significance of 9.1 σ. We established cosmological constraints on σ8 and Ωm from this cross-correlation, which we find consistent with previous large-scale structure (Hurier 2015; Hurier et al. 2015; Hurier & Lacasa 2017; Hurier & Angulo 2018) and CMB analyses (Planck Collaboration XIII 2016; Planck Collaboration XVII 2014). Similarly to the tSZ–X cross-correlation, the X–ϕ correlation favors values of the hydrostatic mass bias lower than those suggested in tSZ-CMB combined analyses (Salvati et al. 2018). It also favors a higher value for bH than most of the weak-lensing based analyses of the last four years (see, e.g., Medezinski et al. 2018; Sereno et al. 2017; Jimeno et al. 2018; Parroni et al. 2017; Okabe & Smith 2016; Battaglia et al. 2016; Applegate et al. 2016; Smith et al. 2016; Hoekstra et al. 2015; Simet et al. 2015; Israel et al. 2015; Donahue et al. 2014; Gruen et al. 2014; Mahdavi et al. 2013). These analyses prefer bH ≃ 0.20. With the constraint inferred here (bH = 0.29 ± 0.07), large-scale structure cosmological constraints from the local Universe on σ8 and Ωm now surround the CMB-based cosmological constraints. This result favors a high value of b compared to hydrodynamical simulations that prefer bH < 0.2. Additionally, under the assumption that these measurements are systematic-free, the significant difference between tSZ and X-ray based results may indicate that these two probes select significantly different populations of galaxy clusters in terms of hydrostatic mass bias.
This is a reasonable approximation provided the low level of correlation induced by the integrated Sachs–Wolfe effect, which is restricted to very low multipoles (ℓ < 50). We are also assuming that residual AGN and galaxy cluster tSZ residual contamination on the CMB should be of relevance at much higher multipoles than those considered here (ℓ > 1000).
Acknowledgments
We acknowledge the use of HEALPix (Górski et al. 2005).
References
- Albareti, F. D., Allende Prieto, C., Almeida, A., et al. 2017, ApJS, 233, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, D. E., Mantz, A., Allen, S. W., et al. 2016, MNRAS, 457, 1522 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, N., Leauthaud, A., Miyatake, H., et al. 2016, JCAP, 8, 013 [Google Scholar]
- Biffi, V., Borgani, S., Murante, G., et al. 2016, ApJ, 827, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Blanchard, A., & Schneider, J. 1987, A&A, 184, 1 [NASA ADS] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Donahue, M., Voit, G. M., Mahdavi, A., et al. 2014, ApJ, 794, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gruen, D., Seitz, S., Brimioulle, F., et al. 2014, MNRAS, 442, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, J. C., & Spergel, D. N. 2014, JCAP, 2, 030 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Hurier, G. 2015, A&A, 575, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., & Angulo, R. E. 2018, A&A, 610, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., & Lacasa, F. 2017, A&A, 604, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Aghanim, N., Douspis, M., & Pointecouteau, E. 2014, A&A, 561, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurier, G., Douspis, M., Aghanim, N., et al. 2015, A&A, 576, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hütsi, G., Gilfanov, M., & Sunyaev, R. 2014, A&A, 561, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Israel, H., Schellenberger, G., Nevalainen, J., Massey, R., & Reiprich, T. H. 2015, MNRAS, 448, 814 [NASA ADS] [CrossRef] [Google Scholar]
- Jimeno, P., Diego, J. M., Broadhurst, T., De Martino, I., & Lazkoz, R. 2018, MNRAS, 478, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Nagai, D., & Nelson, K. 2013, ApJ, 777, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Lesgourgues, J. 2011, ArXiv e-prints [arXiv:1104.2932] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., et al. 2013, ApJ, 767, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Main, R. A., McNamara, B. R., Nulsen, P. E. J., Russell, H. R., & Vantyghem, A. N. 2017, MNRAS, 464, 4360 [NASA ADS] [CrossRef] [Google Scholar]
- Medezinski, E., Battaglia, N., Umetsu, K., et al. 2018, PASJ, 70, S28 [NASA ADS] [Google Scholar]
- Mo, H. J., & White, S. D. M. 1996, MNRAS, 282, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., & Smith, G. P. 2016, MNRAS, 461, 3794 [NASA ADS] [CrossRef] [Google Scholar]
- Parroni, C., Mei, S., Erben, T., et al. 2017, ApJ, 848, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, 571, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rykoff, E. S., Rozo, E., Busha, M. T., et al. 2014, ApJ, 785, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Salvati, L., Douspis, M., & Aghanim, N. 2018, A&A, 614, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sereno, M., Covone, G., Izzo, L., et al. 2017, MNRAS, 472, 1946 [NASA ADS] [CrossRef] [Google Scholar]
- Simet, M., Battaglia, N., Mandelbaum, R., & Seljak, U. 2015, Am. Astron. Soc. Meet. Abstr., 225, 443.04 [NASA ADS] [Google Scholar]
- Smith, G. P., Mazzotta, P., Okabe, N., et al. 2016, MNRAS, 456, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1969, Nature, 223, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comments Astrophys. Space Phys., 4, 173 [NASA ADS] [EDP Sciences] [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Power density for power spectra |
| In the text | |
 |
Fig. 2. X-ray–ϕ cross-correlation angular power spectrum, measured between Planck CMB lensing full-sky map and a RASS data reprojected on the full-sky (black sample); the same cross-spectra when masking NVSS sources is shown as grey samples. The red solid line shows the theoretical prediction assuming (σ8 = 0.8, Ωm = 0.3, bH = 0.2), the green dashed line shows the two-halo term contribution, and the blue dashed line the one-halo term contribution. The solid cyan line displays the contribution from AGN–ϕ cross-correlation. |
| In the text | |
 |
Fig. 3. Likelihood function of Σ8 = σ8(Ωm/0.30)0.27 from different analyses: tSZ angular power spectrum, bispectrum, and number count (red, Hurier & Lacasa 2017); CMB weak lensing (dark blue, Planck Collaboration XVII 2014); CMB angular power spectrum (green, Planck Collaboration XIII 2016); tSZ–weak lensing cross correlation (cyan, Hurier 2015); tSZ–X-ray cross-correlation (orange, Hurier et al. 2015); and X-ray–ϕ cross-correlation (black, this work). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.