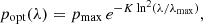| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201935266 | |
| Published online | 11 April 2019 | |
Letter to the Editor
Extreme starlight polarization in a region with highly polarized dust emission⋆
1
California Institute of Technology, MC249-17, 1200 East California Boulevard, Pasadena, CA 91125, USA
e-mail: panopg@caltech.edu
2
Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA
3
Department of Physics and ITCP, University of Crete, Voutes, 70013 Heraklion, Greece
4
Institute of Astrophysics, Foundation for Research and Technology-Hellas, Voutes, 70013 Heraklion, Greece
5
Astronomical Institute, St. Petersburg State University, Universitetsky pr. 28, Petrodvoretz, 198504 St. Petersburg, Russia
Received:
13
February
2019
Accepted:
23
March
2019
Context. Galactic dust emission is polarized at unexpectedly high levels, as revealed by Planck.
Aims. The origin of the observed ≃20% polarization fractions can be identified by characterizing the properties of optical starlight polarization in a region with maximally polarized dust emission.
Methods. We measure the R-band linear polarization of 22 stars in a region with a submillimeter polarization fraction of ≃20%. A subset of 6 stars is also measured in the B, V, and I bands to investigate the wavelength dependence of polarization.
Results. We find that starlight is polarized at correspondingly high levels. Through multiband polarimetry we find that the high polarization fractions are unlikely to arise from unusual dust properties, such as enhanced grain alignment. Instead, a favorable magnetic field geometry is the most likely explanation, and is supported by observational probes of the magnetic field morphology. The observed starlight polarization exceeds the classical upper limit of [pV/E(B−V)]max = 9% mag−1 and is at least as high as 13% mag−1, as inferred from a joint analysis of Planck data, starlight polarization, and reddening measurements. Thus, we confirm that the intrinsic polarizing ability of dust grains at optical wavelengths has long been underestimated.
Key words: polarization / ISM: magnetic fields / dust / extinction / submillimeter: ISM / local insterstellar matter
The polarization data in the R-band are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/624/L8
© ESO 2019
1. Introduction
Sensitive submillimeter observations from the Planck satellite revealed surprisingly high levels of polarized emission from Galactic dust (Planck Collaboration Int. XIX 2015). The observed polarization fractions in the Planck bands are higher than those anticipated by dust models consistent with starlight polarimetry (e.g., Draine & Fraisse 2009) and are challenging to reproduce with physical models (e.g., Guillet et al. 2018).
The same grains that radiate polarized emission in the infrared induce starlight polarization in the optical, and so the magnitudes of the two effects are tightly coupled. Indeed, the 353 GHz polarization fraction p353 and the V-band polarization per unit reddening pV/E(B − V) have a characteristic ratio of ≃1.5 mag (Planck Collaboration Int. XXI 2015; Planck Collaboration XII 2019). However, applying this relation to the highest observed values of p353 ≃ 20% implies starlight polarization far in excess of the classical upper limit of 9% mag−1 (Hiltner 1956; Serkowski et al. 1975). By performing stellar polarimetry in a region with p353 ≃ 20%, we seek to clarify the origin of the strong polarization.
If the derived p353 is truly reflective of Galactic dust polarization and not for example from over-subtraction of the cosmic infrared background or zodiacal light (Planck Collaboration X 2016; Planck Collaboration XII 2019), then stars in this region should be highly polarized. Strong dust emission and starlight polarization could be the result of dust with unusual polarization properties, such as enhanced grain alignment, or simply of a favorable magnetic field geometry, in which case the magnetic field is nearly in the plane of the sky and has a uniform orientation along the line of sight. To discriminate among these possibilities, we consider whether the wavelength dependence of the interstellar polarization conforms to a typical “Serkowski Law” (Serkowski et al. 1975) and whether the magnetic field orientation as probed by linear structures in HI emission (Clark 2018) is uniform along the line of sight.
In this Letter, we use RoboPol polarimetry of 22 stars within a small region to test whether stars in regions of high p353 have pV/E(B − V)≃13% mag−1, as inferred by the analysis of Planck Collaboration XII (2019). We compare the derived E(B − V) (Appendix A) to the observed optical fractional linear polarization (Sect. 3.1). We find that the optical polarization is in excess of the classical upper limit with pV/E(B − V) ≥ 13% mag−1. The six stars with multi-band polarimetry show typical wavelength dependence of the polarized extinction (Sect. 3.2), while starlight polarization angles and HI emission data suggest a highly uniform magnetic field orientation (Sect. 3.3). We therefore argue that the observed p353 ≃ 20% arises from favorable magnetic field geometry and that the classical upper limit of [pV/E(B−V)]max = 9% mag−1 underestimates the intrinsic polarizing efficiency of dust at optical wavelengths (Sect. 4).
2. Data
2.1. RoboPol observations and Gaia distances
Optical polarization observations were conducted using the RoboPol linear polarimeter (Ramaprakash et al. 2019). Stars were selected from the USNO-B1 catalog (Monet et al. 2003) within a 80′-wide region centered on (l, b) = 115°, −31° (circled region in Fig. 1). We selected 22 stars brighter than 14 mag in the R band with distances out to 1.5 kpc, based on the catalog of stellar distances derived from Gaia (Bailer-Jones et al. 2018). The measurements were made in the Johnsons-Cousins R band. To investigate the wavelength dependence of polarization in the region, we observed six of these stars in three additional bands (B, V, I). All sources were placed at the center of the RoboPol field of view, where the instrumental systematic uncertainty is lowest.
 |
Fig. 1. Left: map of fractional linear polarization of dust emission from Planck at 353 GHz at a resolution of 80′ (GNILC). Right: background image showing a map of E(B − V) from Planck Collaboration Int. XLVIII (2016; PG). The map has a pixel size of 1.7′. For stars with a significant detection of p̂R, we show segments that form an angle θ with the Galactic reference frame (according to the IAU convention). The length of each segment is proportional to the p̂R of the star (measured in the R band) and a line of p = 1% is shown on the bottom left for scale. In both panels the dashed circle marks the region in which we have measured stellar polarization. The locations of stars in the observed sample are shown with black dots. |
Observations were conducted over 8 nights in the autumn of 2018. The unpolarized standard stars HD 212311, BD +32 3739, HD 14069, and G191−B2B, as well as the polarized star BD +59 389 (Schmidt et al. 1992), were observed during the same nights for calibration. In total we obtained 22 measurements of standard stars in the R band and 10 measurements in each of the B, V, and I bands. We find systematic uncertainties on the fractional linear polarization of 0.16% in the R band, 0.23% in B, and 0.2% in V and I. We follow the data calibration and reduction methods described in Panopoulou et al. (2019).
The fractional linear polarization, p, and its uncertainty, σp, are calculated from the Stokes parameters q, u, taking into account both statistical and systematic uncertainties (as in Panopoulou et al. 2019). Throughout the paper we use the modified asymptotic estimator proposed by Plaszczynski et al. (2014) to correct for the noise bias on p. We refer to the noise-corrected p as the debiased fractional linear polarization, p̂, and use p̂B, p̂V, p̂R, p̂I for measurements in different bands.
The polarization angle measured with respect to the International Celestial Reference Frame (ICRS): ϕ = 0.5 arctan (u/q) is calculated using the two-argument arctangent function. The uncertainty in ϕ, σϕ, is found following Naghizadeh-Khouei & Clarke (1993). We convert ϕ to the polarization angle with respect to the Galactic reference frame, θ, following Panopoulou et al. (2016). Angles in the paper conform to the IAU convention.
2.2. Ancillary data
We use the Planck maps of Stokes I, Q, U at 353 GHz which have been processed with the Generalized Needlet Internal Linear Combination (GNILC) algorithm to filter out Cosmic Infrared Background anisotropies (Planck Collaboration IV 2019). We follow the procedures outlined in Planck Collaboration XII (2019) to construct maps of the fractional linear polarization p353 = P353/I, the polarized intensity 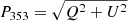 and the polarization angle χ353 = 0.5 arctan (−U/Q). The maps have a resolution (FWHM) of 80′ and are sampled using the Hierarchical Equal Area iso-Latitude Pixelization scheme (HEALPix, Górski et al. 2005) at a resolution nside 2048, which we downgrade to nside 128 to avoid oversampling.
and the polarization angle χ353 = 0.5 arctan (−U/Q). The maps have a resolution (FWHM) of 80′ and are sampled using the Hierarchical Equal Area iso-Latitude Pixelization scheme (HEALPix, Górski et al. 2005) at a resolution nside 2048, which we downgrade to nside 128 to avoid oversampling.
To estimate the reddening, E(B − V) and its uncertainty we make use of four different reddening maps:
-
The GNILC map of dust optical depth, τ353, Planck Collaboration Int. XLVIII (2016; PG). We adopt the conversion E(B − V) = (1.49 × 104 mag)⋅τ353 (Planck Collaboration XI 2014). The map beam size varies at high galactic latitude, but is generally ∼5′ at intermediate latitude.
-
The AV map from Planck Collaboration Int. XXIX (2016) (PDL), which was created by fitting the dust model of Draine & Li (2007) to dust emission and renormalized to match quasar extinctions. The beam size is 5′. To convert to reddening we assume a ratio of total to selective extinction RV = 3.1.
-
The reddening map of Schlegel et al. (1998, SFD), which is based primarily on 100 μm emission as measured by IRAS at 6′ resolution.
-
The line-of-sight integrated map of reddening from Green et al. (2018; G18)1, which is based on stellar photometry. In the selected region the resolution of this map is 7′.
Both the SFD and G18 maps are on the same reddening scale, which must be recalibrated to match E(B − V) from the other estimates. We follow Schlafly & Finkbeiner (2011) to find E(B − V) = E(B − V)SFD × 0.884. We note that reddening maps are constructed by making an assumption about the reddening law2. The uncertainty in the reddening law alone translates into a systematic uncertainty of ∼13% for all maps used here. Additional systematic uncertainties arising for example from the conversion from far-infrared opacity to extinction (see e.g., Fanciullo et al. 2015) affect maps based on far-infrared emission (PG, PDL, SFD).
Finally, we use data from the Galactic L-band Feed Array HI survey (GALFA-HI) Data release 2 (Peek et al. 2018) to obtain the HI column density and the orientation of linear structures seen in HI emission.
3. Results
We investigate the p353 in the selected area in Fig. 1 (left). The value of p353 in this region is 22%, equivalent to the 99.5 percentile of the distribution of p353 throughout the sky. The value of p353 ranges from 21 to 23% for the range of Galactic offset values used in Planck Collaboration XII (2019) (23−103 μKCMB).
Our observations in the R band yielded 17 significant detections of the fractional linear polarization (p̂R/σp ≥ 3) and five upper limits3. The mean S/N in p̂R is 7 with values ranging from 1.5 to 12. Figure 1 (right) shows the positions of the stars on the PG map of total reddening along the line of sight. The stars are located in areas with E(B − V) ranging from 0.065 ± 0.003 mag to 0.104 ± 0.005 mag. A segment at the position of each star shows the orientation of the measured linear polarization. The distribution of θ (including only significant detections) has a mean of 109° and a standard deviation of 5°.
In Appendix A, we examine the distribution of dust along the line of sight and find that the dominant contribution to the observed starlight polarization comes from a cloud located at 250 pc. In the following, we do not consider stars closer than 250 pc as they are foreground and have negligible polarization.
3.1. p/E(B–V)
The correlation of p̂R with E(B − V)PG for stars farther than 250 pc is shown in Fig. 2 (left). All of the measurements fall above the pR = 9% E(B − V) mag−1 limit, consistent with the prediction that high levels of p353 correspond to high levels of p/E(B − V). The best-fit line with zero intercept has a slope of 15.9 ± 0.4% mag−1. We note that pR and pV are expected to differ by only a few percent for typical Serkowski Law parameters (see Eq. (1)), and indeed pR and pV are consistent to within our measurement uncertainties for all stars with measurements of both (see Sect. 3.2). We therefore do not differentiate between pR/E(B − V) and pV/E(B − V).
 |
Fig. 2. Left: p̂R vs. the PG estimate of E(B − V) for stars farther than 250 pc (circles). Values of [pR/E(B − V)]max equal to 9% and 13% are indicated with black the solid and dashed lines, respectively. The linear fit to the data has a slope of 15.9 ± 0.4% mag−1 (orange line and 1σ uncertainty shown by shaded region). Each star is colored according to its distance (colorbar). Right: effect of uncertainty in E(B − V). A linear fit to the data from each reddening map (PG, orange, SFD, red, PDL, cyan, G18, green) is shown (shaded regions as in left panel). The weighted mean p̂R and E(B − V) is shown for the E(B − V) from PG (orange circle), SFD (red diamond), PDL (cyan square), and G18 (green triangle). |
The choice of reddening map has a significant impact on the best-fit slope (Fig. 2, right). We find values ranging from 13.6 ± 0.3% mag−1 (PDL) to 18.2 ± 0.5% mag−1 (SFD). This variation reflects the unaccounted-for systematic uncertainties in each of the reddening maps (see Sect. 2). Despite the uncertainties, all reddening estimates reject 9% mag−1 as an upper limit.
A potential systematic effect arises from the coarse angular resolution of each reddening map compared to the scales probed by stellar measurements. We could be underestimating the true reddening if clumpy regions of high reddening are smeared out by the beam (e.g., Pereyra & Magalhães 2007). To account for such an effect, we calculate the average E(B − V) in the observed 80′ region and compare it to the mean p̂R (found through the weighted mean q and u). The ratio of mean p̂R to mean E(B − V) is 15.7 ± 0.5% mag−1 (PG), 13.4 ± 1.8% mag−1 (PDL), 17.9 ± 0.5% mag−1 (SFD), and 14.6 ± 1.1% mag−1 (G18).
Our estimates of pV/E(B − V) appear to be higher than 13% mag−1, inferred by Planck Collaboration XII (2019). There are a few considerations that must be taken into account for a comparison to be made. First, the derivation of [pV/E(B−V)]max = 13% mag−1 was based on a slightly lower p353 (20%) than found in this region. This would allow for slightly higher values of pV/E(B − V). Second, since we do not subtract possible background reddening for stars that are closer than 600 pc (where the dust column saturates; see Appendix A), we are overestimating the reddening towards these stars and therefore our derivations of pV/E(B − V) are lower limits. By taking into account this fact, and the systematic uncertainty in the reddening law (Sect. 2), we can place a conservative lower limit on [pV/E(B−V)]max of 13% mag−1 (G18).
It is interesting to compare the average emission-to-extinction polarization ratios RP/p = P353/p̂R and RS/V = 3.1/1.086 p353/[pV/E(B − V)] in this region to those found over the larger sky area used in Planck Collaboration XII (2019). As we only have one independent measurement of P353 in the region, we calculate RP/p as the ratio of P353 to the mean p̂R (and similarly for RS/V). The value of RS/V inherits the large uncertainties from the determination of E(B − V). We find RS/V of 3.9 ± 0.1 (PG), 4.6 ± 0.6 (PDL), 3.4 ± 0.1 (SFD), and 4.2 ± 0.3 (G18). This is consistent with 4.2 ± 0.5 found in Planck Collaboration XII (2019). In contrast, we can place much stronger constraints on our estimate of RP/p. We find this ratio to be 4.1 ± 0.1 MJy sr−1, lower than that of ∼5.4 found in Planck Collaboration XII (2019) for the hydrogen column density in this region. Further investigation is required to understand the cause of this difference.
3.2. Wavelength dependence of polarization
The wavelength dependence of the optical polarized extinction popt is often parameterized as (Serkowski et al. 1975):
where popt has a maximum value of pmax at wavelength λmax and K is a parameter governing the width of the profile.
Figure 3 shows the measured fractional linear polarization as a function of wavelength for the six stars measured in the B, V, R, and I bands. Fixing K = 1.15 (Serkowski et al. 1975) and leaving λmax and pmax as free parameters, we fit the six polarization profiles to Eq. (1) using weighted least-squares.
 |
Fig. 3. Wavelength dependence of polarization for six of the stars in the R-band sample (USNO-B1 identifiers shown in the legend). Debiased fractional linear polarization (p̂) measured in the Johnsons-Cousins B, V, R, and I bands (horizontal axis shows effective wavelength). For each star, a line shows the best-fit Serkowski law (Eq. (1), with K set to 1.15). |
The fit λmax are in the range 580 ± 46 nm–643 ± 34 nm, while the fit pmax are in the range 0.9%−1.7%. Although limited by the uncertainties of the measurements, we find no evidence for substantial differences between the best-fit value of λmax in this sample compared to canonical values (Serkowski et al. 1975). If grain alignment were unusually efficient in this region with smaller grains able to be aligned, we might have expected a shift of λmax toward shorter wavelengths than the typical 550 nm (Martin et al. 1999). This is not observed.
3.3. Magnetic field morphology
If the magnetic field morphology is responsible for the high submillimeter polarization fractions, then any region with high p353 should have a magnetic field that lies mostly in the plane of the sky with no substantial change in orientation either along the line of sight or within the beam.
The orientation of the magnetic field as projected on the plane of the sky is probed by the optical polarization angle θR as well as the submillimeter polarization angle rotated by 90°. Within an 80′ beam centered on this region we find χ353 + 90° =112.8 ± 0.6°. The polarization angles inferred from stellar polarimery do not vary significantly across the region (Fig. 4, left). The standard deviation of the distribution of θR is consistent with it arising from measurement uncertainties, suggesting little beam depolarization.
 |
Fig. 4. Left: distribution of stellar polarization angles, θR for stars farther than 250 pc (solid line). The dashed vertical line shows the χ353+90° from Planck at 80′ resolution. Right: probability density functions of the orientation of linear HI structures (θRHT) for different velocity ranges (shown on the right). We only consider velocity ranges within the peak of the HI intensity spectrum. The filled circles in the bottom mark the mean value, ⟨θRHT⟩ for each velocity range. All angles are measured in the Galactic reference frame, according to the IAU convention. |
Linear structures seen in HI have also been shown to trace the interstellar magnetic field (Clark et al. 2014). Recently, Clark (2018) proposed that changes in the orientation of these structures in velocity space can be used to probe variations of the magnetic field orientation along the line of sight. By applying the Rolling Hough Transform (RHT) to maps of the HI emission as in Clark et al. (2014), and Peek et al. (2018) quantify the orientation of HI structures for different velocity channels for the entire GALFA-HI footprint. Figure 4 illustrates the probability density function of the orientation angle θRHT of linear HI structures in our selected region for different velocity channels. The mean θRHT cover a small range (99°–107°), as expected if the magnetic field exhibits minimal variation along the sightline.
4. Concluding remarks
We investigated the properties of starlight polarization in a region where p353 ≃ 20%, with the goal of understanding the origin of these high levels of polarization. We found that stars tracing the entire dust column show high pV/E(B − V), significantly exceeding the classical upper limit of 9% mag−1. The stellar polarimetry and the HI data suggest a well-ordered magnetic field both across the region and along the line of sight. The wavelength dependence of the optical polarization is consistent with a standard Serkowski Law with no shift in λmax to shorter wavelengths as might be expected if efficient grain alignment extended to unusually small grain sizes.
Although the studied region has unusually high p353, it appears typical in both the wavelength dependence of the optical polarization and in the ratio of polarized emission to polarized extinction. Therefore, there is no clear indication that the high polarization fractions are attributable to dust properties such as enhanced alignment or unusual composition. Rather, our analysis favors a scenario in which the observed high p353 and pV/E(B − V) arise simply from a favorable magnetic field geometry. This extends the conclusion of Planck Collaboration Int. XX (2015) that the magnetic field morphology can account for the observed polarized emission properties, even in the highest p353 regions of the sky.
Our findings show that the 13% mag−1 inferred by Planck Collaboration XII (2019) is likely a lower limit on the true [pV/E(B−V)]max, confirming that the classical upper limit of pV/E(B − V) ≤ 9% mag−1 should be revised. Further progress calls for more accurate determination of stellar E(B − V).
Finally, we note that the observed region is not unique in its unusually high pV/E(B − V), with other highly polarized sources reported elsewhere in the literature (e.g., Whittet et al. 1994; Leonard et al. 2002; Pereyra & Magalhães 2007; Andersson & Potter 2007; Frisch et al. 2015; Panopoulou et al. 2015, 2019; Skalidis et al. 2018; Planck Collaboration XII 2019). However, as discussed in Sect. 3.1, the determination of pV/E(B − V) is limited in large part by accurate determination of interstellar reddening. For instance, Gontcharov & Mosenkov (2019) find that the same sample of nearby stars may reject the classical [pV/E(B − V)]max limit or not, depending on the choice of reddening map. Through polarimetry of many stars in a single region of high submillimeter polarization, we have shown that the mean pV/E(B − V) in the region is inconsistent with an upper limit of 9% mag−1 regardless of which reddening map is used.
Acknowledgments
We thank V. Guillet for his insightful review, V. Pelgrims, for helpful comments, and P. Martin, S. Clark and the ESA/Cosmos helpdesk for advice on using Planck data. G. V. P. acknowledges support from the National Science Foundation, under grant number AST-1611547. R. S., D. B. and K. T. acknowledge support from the European Research Council under the European Union’s Horizon 2020 research and innovation program, under grant agreement No 771282. Based on observations obtained with Planck (http://www.esa.int/Planck), a European Space Agency (ESA) science mission. This work has made use of data from the ESA mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Based on Galactic ALFA HI (GALFA HI) survey data obtained with the Arecibo L-band Feed Array (ALFA) on the Arecibo 305m telescope. The Arecibo Observatory is a facility of the National Science Foundation (NSF) operated by SRI International in alliance with the Universities Space Research Association (USRA) and UMET under a cooperative agreement. The GALFA HI surveys are funded by the NSF through grants to Columbia University, the University of Wisconsin, and the University of California.
References
- Andersson, B.-G., & Potter, S. B. 2007, ApJ, 665, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E. 2018, ApJ, 857, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Fraisse, A. A. 2009, ApJ, 696, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Fanciullo, L., Guillet, V., Aniano, G., et al. 2015, A&A, 580, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, P. C., Berdyugin, A., Piirola, V., et al. 2015, ApJ, 814, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Gontcharov, G. A., & Mosenkov, A. V. 2019, MNRAS, 483, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Guillet, V., Fanciullo, L., Verstraete, L., et al. 2018, A&A, 610, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hiltner, W. A. 1956, ApJS, 2, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, D. C., Filippenko, A. V., Chornock, R., & Li, W. 2002, AJ, 124, 2506 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Clayton, G. C., & Wolff, M. J. 1999, ApJ, 510, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Monet, D. G., Levine, S. E., Canzian, B., et al. 2003, AJ, 125, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Naghizadeh-Khouei, J., & Clarke, D. 1993, A&A, 274, 968 [NASA ADS] [Google Scholar]
- Panopoulou, G., Tassis, K., Blinov, D., et al. 2015, MNRAS, 452, 715 [Google Scholar]
- Panopoulou, G., Tassis, K., Blinov, D., et al. 2016, MNRAS, 462, 2011 [NASA ADS] [CrossRef] [Google Scholar]
- Panopoulou, G. V., Tassis, K., Skalidis, R., et al. 2019, ApJ, 872, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Peek, J. E. G., Babler, B. L., Zheng, Y., et al. 2018, ApJS, 234, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Pereyra, A., & Magalhães, A. M. 2007, ApJ, 662, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IV. 2019, A&A, in press, DOI: 10.1051/0004-6361/201833881 [Google Scholar]
- Planck Collaboration XII. 2019, A&A, in press, DOI: 10.1051/0004-6361/201833885 [Google Scholar]
- Planck Collaboration Int. XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XX. 2015, A&A, 576, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXI. 2015, A&A, 576, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXIX. 2016, A&A, 586, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVIII. 2016, A&A, 596, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plaszczynski, S., Montier, L., Levrier, F., & Tristram, M. 2014, MNRAS, 439, 4048 [NASA ADS] [CrossRef] [Google Scholar]
- Ramaprakash, A. N., Rajarshi, C. V., Das, H. K., et al. 2019, MNRAS, 485, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, G. D., Elston, R., & Lupie, O. L. 1992, AJ, 104, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Serkowski, K., Mathewson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Skalidis, R., Panopoulou, G. V., Tassis, K., et al. 2018, A&A, 616, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. A., Carkner, A. L., et al. 1994, MNRAS, 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The distribution of dust along the line of sight
Figure A.1 shows the dependence of p̂R with distance. Polarization is very low for the nearest four stars in our sample. For all stars within 250 pc we have obtained only (2σ) upper limits on p̂R of 0.6% or lower. At distances farther than that of the fourth star (235 ± 3 pc) we find highly significant detections of p̂R with a mean of 1.3%. This abrupt change strongly suggests that there is a dust component (cloud) located at a distance between that of the fourth and fifth nearest star. If we take into account the distance of the fifth nearest star (263 ± 5 pc) we can place conservative limits on the cloud distance of 232−268 pc. We adopt 250 pc as our estimate of the distance to this cloud.
We note that in Fig. A.1 some stars at large distances are less polarized than nearby stars. This can appear as a reduction of p̂R with distance as might be caused by additional dust components with different polarization orientations. However, the stars at greater distances lie along sightlines with lower E(B − V) (colors in Fig. A.1), thus explaining the apparent trend.
 |
Fig. A.1. Debiased fractional linear polarization of stars measured in the R band (p̂R) vs. stellar distance. Points are colored according to the E(B − V) from PG at the position of the star. We only show 2σ upper limits on p̂R for stars with p̂R/σp < 3. |
We obtain a rough estimate of the distance at which the dust column ends from the 3D map of reddening of Green et al. (2018). For all sightlines, reddening saturates at a distance of ∼600 pc. This suggests that stars located farther than 600 pc are tracing the entire dust column. For these stars the E(B − V) from the maps presented in Sect. 2 will likely reflect their true reddening. For the six stars at distances between 250 and 600 pc, we do not correct for background reddening, which is within the G18 systematic uncertainty of 0.02 mag. Instead we assign the full line-of-sight reddening. This overestimates their reddening, meaning that our estimates of p/E(B − V) (Sect. 3.1) are conservative lower limits.
All Figures
 |
Fig. 1. Left: map of fractional linear polarization of dust emission from Planck at 353 GHz at a resolution of 80′ (GNILC). Right: background image showing a map of E(B − V) from Planck Collaboration Int. XLVIII (2016; PG). The map has a pixel size of 1.7′. For stars with a significant detection of p̂R, we show segments that form an angle θ with the Galactic reference frame (according to the IAU convention). The length of each segment is proportional to the p̂R of the star (measured in the R band) and a line of p = 1% is shown on the bottom left for scale. In both panels the dashed circle marks the region in which we have measured stellar polarization. The locations of stars in the observed sample are shown with black dots. |
| In the text | |
 |
Fig. 2. Left: p̂R vs. the PG estimate of E(B − V) for stars farther than 250 pc (circles). Values of [pR/E(B − V)]max equal to 9% and 13% are indicated with black the solid and dashed lines, respectively. The linear fit to the data has a slope of 15.9 ± 0.4% mag−1 (orange line and 1σ uncertainty shown by shaded region). Each star is colored according to its distance (colorbar). Right: effect of uncertainty in E(B − V). A linear fit to the data from each reddening map (PG, orange, SFD, red, PDL, cyan, G18, green) is shown (shaded regions as in left panel). The weighted mean p̂R and E(B − V) is shown for the E(B − V) from PG (orange circle), SFD (red diamond), PDL (cyan square), and G18 (green triangle). |
| In the text | |
 |
Fig. 3. Wavelength dependence of polarization for six of the stars in the R-band sample (USNO-B1 identifiers shown in the legend). Debiased fractional linear polarization (p̂) measured in the Johnsons-Cousins B, V, R, and I bands (horizontal axis shows effective wavelength). For each star, a line shows the best-fit Serkowski law (Eq. (1), with K set to 1.15). |
| In the text | |
 |
Fig. 4. Left: distribution of stellar polarization angles, θR for stars farther than 250 pc (solid line). The dashed vertical line shows the χ353+90° from Planck at 80′ resolution. Right: probability density functions of the orientation of linear HI structures (θRHT) for different velocity ranges (shown on the right). We only consider velocity ranges within the peak of the HI intensity spectrum. The filled circles in the bottom mark the mean value, ⟨θRHT⟩ for each velocity range. All angles are measured in the Galactic reference frame, according to the IAU convention. |
| In the text | |
 |
Fig. A.1. Debiased fractional linear polarization of stars measured in the R band (p̂R) vs. stellar distance. Points are colored according to the E(B − V) from PG at the position of the star. We only show 2σ upper limits on p̂R for stars with p̂R/σp < 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.