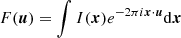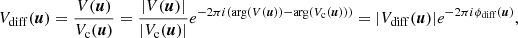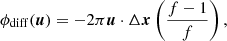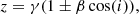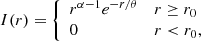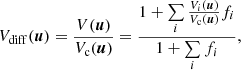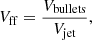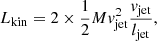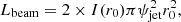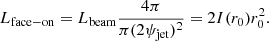| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834747 | |
| Published online | 24 April 2019 | |
Collimated radiation in SS 433⋆
Constraints from spatially resolved optical jets and Cloudy modeling of the optical bullets
1
Max Planck Institute for extraterrestrial Physics, Giessenbachstr., 85748 Garching, Germany
e-mail: idelw@mpe.mpg.de
2
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
Received:
29
November
2018
Accepted:
1
March
2019
Context. The microquasar SS 433 is well known for its precessing, relativistic, and highly collimated baryonic jets, which manifest in its optical spectrum as pairs of hydrogen and helium emission lines moving with large Doppler shifts. Depending on their heating mechanism, the optical jet bullets may serve as a probe of the collimated radiation coming from the inner region close to the compact object, and which is not directly visible to observers on Earth.
Aims. We aim to better understand the baryonic jet phenomenon in SS 433, in particular the properties of the optical bullets and their interaction with the ionizing collimated radiation.
Methods. The optical interferometer VLTI/GRAVITY has allowed us to spatially resolve the optical jets in SS 433 for the first time. We present here the second such observation taken over three nights in July 2017. In addition, we used the X-shooter spectrograph at VLT to study the optical bullets in SS 433 in detail. Over the full wavelength range 0.3−2.5 μm, we identified up to twenty pairs of jet lines observed simultaneously, which we modeled with the spectral synthesis code Cloudy.
Results. GRAVITY reveals elongated exponential-like radial spatial profiles for the optical jets on scales ≲1−10 mas, suggestive of a heating mechanism acting throughout a long portion of the jet and naturally explained by photoionization by the collimated radiation. We also spatially resolve the movement of the optical bullets for the first time, detecting more extended jet components corresponding to previous ejections. Cloudy photoionization models can explain the spatial intensity profiles measured with GRAVITY and the emission line ratios from X-shooter, and constrain the properties of the optical bullets and the ionizing radiation. We find that the latter must peak in the UV with an isotropic luminosity (as inferred by a face-on observer) ∼1041 erg s−1. Provided that the X-ray spectral energy distribution is sufficiently hard, the collimated X-ray luminosity could still be high enough so that the face-on observer would see SS 433 as ultraluminous X-ray source and it would still be compatible with the H/He/He+ ionization balance of the optical bullets. The kinetic power in the optical jets is constrained to 2−20 × 1038 erg s−1, and the extinction in the optical jets to AV = 6.7 ± 0.1. We suggest there may be substantial AV ≳ 1 and structured circumstellar extinction in SS 433, likely arising from dust formed in equatorial outflows.
Key words: techniques: interferometric / line: formation / binaries: close / stars: jets / stars: individual: SS 433
© I. Waisberg et al. 2019
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
More than forty years after its discovery, SS 433 (Stephenson & Sanduleak 1977; Clark & Murdin 1978) remains a unique object primarily due to its relativistic, precessing baryonic jets. They were first discovered through broad emission lines of hydrogen and helium moving across its optical spectrum with extreme Doppler shifts (Margon et al. 1979). Their blueshifts and redshifts follow a kinematic precession model (Fabian & Rees 1979; Margon 1984), according to which the jets precess over a period ≈163 days, following a cone of half opening angle ≈21° and a precessional axis that is inclined ≈78° relative to the line of sight, with jet material moving at a very stable speed of ≈0.26c along radial ballistic trajectories (Eikenberry et al. 2001). From the width of the emission lines and assuming a conical geometry, the optical jets are very collimated, with a half opening angle θ ≲ 1° (Borisov & Fabrika 1987). The jet precession is thought to be driven by gravitational torques by the compact object on the donor star (slaved disk model: Roberts 1974; van den Heuvel et al. 1980), whose spin axis is misaligned with the orbital plane presumably due to the supernova explosion that gave rise to the compact object ≲105 years ago (Zealey et al. 1980; Lockman et al. 2007), and whose remnant W50 is still observable today (e.g., Dubner et al. 1998). SS 433 is also an eclipsing binary, and the behavior of the X-ray and optical eclipses together with radial velocities of the emission lines reveal that the supercritical disk and its outflows dominate the continuum and line radiation at all wavelengths (for a review of the properties of SS 433 see, e.g., Fabrika 2004).
The jets in SS 433 were soon also detected in radio (Hjellming & Johnston 1981), confirming the kinematic precession model derived from the optical lines and establishing the position angle of the precessional axis on sky 98.2° (Stirling et al. 2002). Very Long Baseline Interferometry (VLBI) radio observations have regularly imaged the movement of individual jet knots (e.g., Vermeulen et al. 1993; Paragi et al. 1999), and larger scale images of the corkscrew structure created by the precessing jets have established a precise distance of d = 5.5 ± 0.2 kpc from the aberration induced by the light travel time effect between the two jets (Blundell & Bowler 2004). Later the jets were detected in X-rays (Watson et al. 1986), where they are seen as emission lines from highly ionized metals (e.g., Fe, Ni, S, Si) that follow the same kinematic precession model as the optical jets and have a similarly small opening angle (e.g., Kotani et al. 1996; Marshall et al. 2002). They have been modeled with multi-temperature, optically thin collisional ionization models to estimate properties such as temperature, density, and kinetic power. Because the X-ray jets are continuous, emission-line diagnostics depend on the assumptions on the geometry of the outflow, usually taken to be a radially outflowing cone, and may also be affected by photoionization from putative collimated radiation (Brinkmann & Kawai 2000). The behavior of the X-ray jets during eclipse constrains their length to ≳1012 cm (Marshall et al. 2013).
Because of its edge-on orientation, little is known about the radiation in the beam containing the optical jets, nor about the radiation from the inner parts of the accretion flow in general. The supercritical, geometrically and optically thick disk is thought to reprocess the latter to a large radius (∼Rsp, the spherization radius within which radiation pressure leads to a thick disk, Shakura & Sunyaev 1973), thermally downgrading it to the observed blackbody temperature T ∼ 30 000−100 000 K (Fabrika 2004). As a result, SS 433 is a relatively faint X-ray source, LX ∼ 1035−1036 erg s−1 to observers on Earth, with most of the received X-ray flux below 10 keV originating from thermal Bremststrahlung from the X-ray jets, without any apparent X-ray accretion disk (Watson et al. 1986). It has been proposed that, if viewed face on so that the inner portions of the accretion disk/jet funnel were directly visible, SS 433 would appear as an extremely bright X-ray source such as an ultraluminous X-ray source (ULX; Fabrika 2004; Begelman et al. 2006). Recent optical spectroscopy of ULX counterparts have shown strong emission lines akin to those seen in SS 433 and likely associated with supercritical disks (Fabrika et al. 2015), as well as the discovery of an ultraluminous supersoft source (ULS) containing a baryonic relativistic jet seen in a moving Hα line (Liu et al. 2015), so far the only other known object to show such a feature. Recently, Middleton et al. (2018) showed through time-resolved X-ray spectroscopy that the hard part of the X-ray spectrum in SS 433 is a reflection component of the wind-cone, and estimated an intrinsic X-ray luminosity of ∼1038 erg s−1. The corresponding face-on luminosity, LX ≳ 1039 erg s−1, suggests that SS 433 could be interpreted as an ULX for an observer with a favorable view towards the jets.
The optical bullets that make up the optical jets are thought to form from the collapse of gas from the continuous X-ray jet through a thermal instability as the jet expands and cools (Davidson & McCray 1980; Brinkmann et al. 1988). If the optical bullets are heated mainly by photoionization by collimated radiation (Bodo et al. 1985; Fabrika & Borisov 1987; Panferov & Fabrika 1993), they can serve as a probe of the latter. On the other hand, their heating has generally been ascribed to external processes related to interaction with the ambient gas, either by direct collisions (Davidson & McCray 1980; Brown et al. 1991) or through photoionization by extreme ultraviolet and X-ray photons produced in shocks and subsequent collisional ionization and excitation by suprathermal electrons (Begelman et al. 1980). Spatially resolving the optical jets could reveal the dominant heating process; however, they have been associated with scales ∼1014−1015 cm ↔ 1−10 mas (e.g., Borisov & Fabrika 1987; Marshall et al. 2013), beyond the reach of current diffraction-limited large telescopes.
The only way to spatially resolve the optical jets of SS 433 is through interferometry. In Gravity Collaboration (2017a; Paper I) we presented the first such observations taken during commissioning of the GRAVITY instrument (Gravity Collaboration 2017b) in July 2016 at the Very Large Telescope Interferometer (VLTI), which works in the near-infrared K band. These observations revealed that the optical jets peak very close to the binary and follow an extended exponential radial emission profile with decay constant ≈2 mas, suggestive of a continuous heating process throughout the jet. Here, we present a second set of three GRAVITY observations of SS 433 taken over four nights in July 2017 in which we could observe the change in spatial emission profiles of the jets as the emission lines brighten and fade. We also present the first X-shooter observations of SS 433, where we use up to twenty pairs of jet lines to constrain the properties of the bullets and the ionizing collimated radiation under the assumption of heating by photoionization suggested by the GRAVITY data.
This paper is organized as follows. In Sect. 2, we summarize the observations and data reduction. The GRAVITY and X-shooter data analysis are presented in Sects. 3 and 4, respectively. Finally, Sect. 5 contains the conclusions.
We often quote the results in mas since that is the actual measured unit in interferometry. For convenience, we quote 1mas ↔ 8.2 × 1013 cm = 1180 R⊙ = 5.5 AU, assuming a distance d = 5.5(±0.2) kpc (Blundell & Bowler 2004). The GAIA DR2 distance 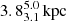 (68% limits; Luri et al. 2018; Bailer-Jones et al. 2018) is roughly consistent with this value but significantly more uncertain.
(68% limits; Luri et al. 2018; Bailer-Jones et al. 2018) is roughly consistent with this value but significantly more uncertain.
2. Observations and data reduction
2.1. GRAVITY
The microquasar SS 433 (K ≈ 8) was observed with GRAVITY (Gravity Collaboration 2017b) with the Unit Telescopes (UT) on VLTI on three nights over a period of four days in July 2017. Half of the K band light of SS 433 itself was directed to the fringe tracker (FT), which operates at > 1000 Hz to stabilize the fringes in the science channel (SC), allowing coherent integration over detector integration times of 10s in high spectral resolution (R ≈ 4000). The FT operates in low resolution (R ≈ 20) with five channels over the K band. The data were obtained in split polarization mode. The adaptive optics (AO) was performed at visual wavelength using SS 433 itself as the AO guide star (V ≈ 14).
Table 1 shows the precessional ϕprec and orbital ϕorb phases of each observation based on the ephemerides in Eikenberry et al. (2001) and Goranskij (2011), respectively. For more details on the observations and data reduction, including the uv coverage of the observations, we refer to the companion paper on the equatorial outflows (Waisberg et al. 2019). In light of a slightly improved jet model, we also reanalyze the 2016 observation (Paper I), which is included in Table 1.
Summary of observations.
2.2. X-shooter
SS 433 was observed five times between May and July of 2017 with the X-shooter échelle spectrograph (Vernet et al. 2011) mounted on the Very Large Telescope (VLT). The exposure times per epoch were 1240s, 1260s, and 1248s for the UVB (0.3−0.55 μm), VIS (0.55−1.0 μm) and NIR (1.0−2.5 μm) arms. The slit dimensions were 1.3″ × 11″, 0.9″ × 11″, and 0.4″ × 11″ for each arm, corresponding to spectral resolutions 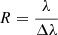 of 4100, 8900, and 11 600. The observations were made in nodding pattern for sky subtraction. Table 1 shows the precessional ϕprec and orbital ϕorb phases of each observation.
of 4100, 8900, and 11 600. The observations were made in nodding pattern for sky subtraction. Table 1 shows the precessional ϕprec and orbital ϕorb phases of each observation.
The data were reduced with the standard ESO X-shooter pipeline (version 2.9.0), which includes de-biasing, flat-fielding, wavelength calibration, sky subtraction, order merging, and flux calibration, the latter based on nightly response curves from flux standard stars. The line-modeling software Molecfit (Smette et al. 2015; Kausch et al. 2015) was used to correct for telluric absorption in the VIS and NIR arms. The performance of Molecfit was found to be at least as good as using a telluric calibrator star, with the additional benefit that manual removal of the many H I, He I, and additional lines of a telluric calibrator is not needed.
Although our observations were not designed for precise flux calibration, the latter has to be taken into account when comparing emission line strengths across a large wavelength range since SS 433 has a complex and variable continuum. Because the slit widths used are smaller than the seeing, it is necessary to correct for the wavelength-dependent slit losses. We have done this by assuming the typical wavelength dependence for seeing s ∝ λ−0.2, and using the overlapping regions between the spectral arms to fit for the average seeing, which is in good agreement with the estimated seeing value from the acquisition image at the start of each observation.
3. GRAVITY data analysis
3.1. K band spectrum
Figure 1 shows the GRAVITY spectra of SS 433 for the 2017 observations. There are stationary emission lines (Brγ, He I 2.06 μm, He I 2.11 μm, and high order (upper levels 19–24) Pfund lines) as well as emission lines from the baryonic jets. For the analysis of the stationary Brγ line, we refer to the companion paper on the equatorial outflows (Waisberg et al. 2019). In this paper, we focus on the jets. In the 2016 observation (Paper I), the precessional phase was such (ϕprec ≈ 0.7) that jet lines from Brγ, Brδ, and He I 2.06 μm fell into the K band spectrum (see Fig. A.1). In the 2017 observations presented here, the precessional phase was significantly different (ϕprec ≈ 0.9) so that other jet lines were observed: Brβ from the approaching jet and Paα from the receding jet (as well as very weak Brδ and Brϵ lines from the receding jet). Another difference in the latter observations is that there are often two components (knots) to the jet lines. The set of three observations over four nights allows us to follow the spatial evolution of the jets; while the knots in Epoch 1 had faded by Epoch 2, the knots in Epochs 2 and 3 partially overlap. The jet redshifts were such that the Paα jets are partially blended with the Brγ stationary line and the Brβ jets with stationary Pfund lines.
 |
Fig. 1. K band spectra for the three GRAVITY observations in 2017. The strongest jet emission lines are Paα and Brβ for the receding and approaching jets, respectively (the former is blended with the Brγ stationary line, the latter with stationary Pfund lines). The brightening and fading of different jet knots are visible over the three observations. Stationary emission lines are labeled in green, but are not the subject of this paper. |
Figure 2 shows the measured jet redshifts along with the kinematic precession model using the parameters from Eikenberry et al. (2001). They agree within the perturbations caused by nutational motion and random jitter (Fabrika 2004).
 |
Fig. 2. Jet redshifts (mostly approaching (eastern) jet in blue; mostly receding (western) jet in red) and position angle on sky (green) of the optical jets for each observation as a function of precessional phase. The curves were made using the kinematic model parameters in Eikenberry et al. (2001) and the precessional axis position angle in Stirling et al. (2002). The PA of the optical jets as derived from the GRAVITY data agrees well with the prediction from the radio jets. We plot both the 2016 (ϕprec ≈ 0.7) as well as the 2017 (ϕprec ≈ 0.9) GRAVITY observations. |
3.2. Optical jet interferometric model
The van-Cittert–Zernike theorem relates the spatial structure of the image on the sky plane I(x) to the coherent flux F(u) measured by an interferometer (e.g., Glindemann 2011),
where 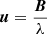 is the uv coordinate and B is the projected baseline on sky. GRAVITY measures the complex visibility
is the uv coordinate and B is the projected baseline on sky. GRAVITY measures the complex visibility 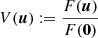 (i.e., normalized coherent flux) for a given set of uv coordinates. In single-field mode (i.e., without a phase-reference source), GRAVITY provides visibility amplitudes |V(u)| and closure phases (i.e., the sum of the visibility phases across closed triangles of telescopes), because the individual visibility phases are corrupted by the atmosphere. If enough uv coverage is obtained, an inverse image reconstruction process can be performed to obtain I(x); otherwise, model fitting to the available Fourier transform samples has to be done. The imaging resolution of the interferometric array is
(i.e., normalized coherent flux) for a given set of uv coordinates. In single-field mode (i.e., without a phase-reference source), GRAVITY provides visibility amplitudes |V(u)| and closure phases (i.e., the sum of the visibility phases across closed triangles of telescopes), because the individual visibility phases are corrupted by the atmosphere. If enough uv coverage is obtained, an inverse image reconstruction process can be performed to obtain I(x); otherwise, model fitting to the available Fourier transform samples has to be done. The imaging resolution of the interferometric array is 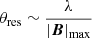 , which for GRAVITY (λ ∼ 2 μm; |B|max ∼ 100 m) corresponds to ∼3 mas.
, which for GRAVITY (λ ∼ 2 μm; |B|max ∼ 100 m) corresponds to ∼3 mas.
In addition, in the case of spectrally resolved interferometric observations, the differential complex visibility between the continuum and a spectral line are obtained as
where Vc(u) is the continuum visibility, |Vdiff(u)| is the differential visibility amplitude, and ϕdiff(u) the differential visibility phase. Because of their differential nature, these quantities are very robust and precise, allowing us to obtain spatial information on scales much smaller than the formal resolution of the telescope (i.e., sub-milliarcsecond or even microarcsecond). Additionally, in the marginally resolved limit (i.e., when the sizes of the structures are ≲θres), the differential phases ϕdiff can be converted to centroid offsets Δx between the line and the continuum (e.g., Waisberg et al. 2017):
where f is the line flux in continuum-normalized units. Therefore, the differential phases give information on the location of the line-emitting structure relative to the continuum. The differential visibility amplitudes, on the other hand, give information on the size of the line-emitting region relative to the continuum: in the marginally resolved limit, decaying or rising differential visibility amplitudes across a spectral line indicate that the line-emitting region is more or less extended than the continuum-emitting region, respectively.
Figure 3 shows the differential visibility amplitudes and phases for Epoch 3 of the 2017 observations. The only strong jet lines present in the GRAVITY spectrum are Paα for the receding jet and Brβ for the approaching jet. As in Paper I, the jets’ line emitting regions are more extended than the region emitting the near-infrared continuum as shown by the decrease of the differential visibility amplitude across the lines. In addition, the receding and approaching jets have differential visibility phases of opposite sign, which according to Eq. (3) means that they are located on opposite sides relative to the continuum, as expected for a jet.
 |
Fig. 3. Data and best-fit jet model for the 2017 Epoch 3 GRAVITY observation. Compact (recent) and extended (older) jet knots are shown in the spectrum as full and dashed lines, respectively. Stationary lines are labeled in green. There is substantial blending of the Paα lines from the receding jet with the stationary Brγ line, which also has differential visibility signatures across it. The fits are done to all lines simultaneously, but we plot only the model for jet lines for clarity. The baseline projected lengths and position angles on sky are indicated in the labels. |
We fit the spectrum and differential visibilities simultaneously. For the spectrum, we fit the jet knots as Gaussians. The model parameters are:
-
The jet inclination i, which determines the redshift via
where β = 0.26 is the jet speed in units of c and
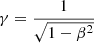 . Because we can measure the redshift very precisely for each jet line, we allow for different inclinations of the receding and approaching jets, as well as for the different components. We assume a constant velocity since it is very stable (Eikenberry et al. 2001), and the possible small variations in velocity are absorbed in the inclination.
. Because we can measure the redshift very precisely for each jet line, we allow for different inclinations of the receding and approaching jets, as well as for the different components. We assume a constant velocity since it is very stable (Eikenberry et al. 2001), and the possible small variations in velocity are absorbed in the inclination. -
The FWHM in kilometers per second, which is assumed to be the same for all the jet lines for all components;
-
The strength of each jet line relative to the normalized continuum.
To fit the visibilities, we model the jets as a 1D structure with a radial emission profile, since they are very collimated (opening angle ≲1°) from the width of the optical emission lines (Borisov & Fabrika 1987). The model parameters are:
-
The position angle (PA) of the jet on the sky plane. It is assumed to be the same for all the jet components in a given epoch because it cannot be measured nearly as precisely as the inclination (the typical error is a few degrees);
-
The radial emission profile is controlled by the three parameters θ, α, and r0,
where r is the distance from the center. This model is similar to the one used in Paper I, except for the additional parameter α, which allows for more general shapes besides an exponential (α = 1), from Gaussian-like (α > 1) to steeper profiles (α < 1). The parameters θ (which together with α control the shape of the profile) and r0 (the inner edge where the emission starts) are also debiased from the projection effect, that is, they are already divided by sin(i). Figure 4 shows representative jet radial emission profiles that can be produced with the model detailed above, and the corresponding differential visibility amplitudes and phases as a function of projected baselines in the direction of the jet. The continuum is modeled as an unresolved point source, the flux ratio between the jet and continuum is 0.5, and the wavelength is 2 μm. At the spatial scales probed by GRAVITY, more compact profiles (red) have smoother visibility curves, whereas more extended profiles (blue) have significant substructure that is not present in the data (e.g., different signs of differential visibility phases for different baselines). The profiles show that the expected longitudinal scale for the jet emission is ∼1−10 mas.

Fig. 4. Example jet radial emission profiles (left) that can be created by the model, and corresponding differential visibility amplitudes and phases (middle, right) as a function of projected baseline length in the jet direction. The continuum is modeled as an unresolved point source, the flux ratio between the jet and the continuum is 0.5, and the wavelength is 2 μm. At the spatial scales probed by GRAVITY, more compact profiles (red) have smoother visibility curves, whereas more extended profiles (blue) show more significant substructure in the visibilities.
The errors are estimated from the scatter in line-free regions. We fit for the spectrum and the differential visibilities simultaneously; however, because the former is sensitive to telluric correction and has very small statistical errorbars, we increase the flux errorbars by a factor of two. We found that this scaling led to a comparable reduced χ2 between flux and visibilities in all observations. Moreover, because of the blending with the Brγ stationary emission line, which also produces differential visibility signatures, it is necessary to perform simultaneous fits for the Brγ line and the jets. For the model and results for the Brγ stationary line we refer to the companion paper on the equatorial outflows (Waisberg et al. 2019). The results presented here correspond to the “outflow” model in the companion paper (which we favor over the “disk” model). The differential visibilities are computed with respect to the best-fit continuum model (also determined in the companion paper; Waisberg et al. 2019). The total differential visibility at a given spectral channel is then
where Vc is the continuum visibility, and fi and Vi are the flux ratios relative to the continuum and visibilities for each component i (different jet knots, Brγ stationary line). The fits are done through non-linear least squares minimization with the Levenberg–Marquardt method through the python package LMFIT1. The quoted errors correspond to the 1σ errors from the least squares fit, that is, the estimated derivatives around the optimal solution (scaled by
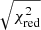 ). We caution, however, that true uncertainties are dominated by (i) degeneracies between the many parameters, which create a complicated multidimensional χ2 map; (ii) systematic errors from the continuum model; (iii) the assumption of our simple “geometric” models, which cannot capture all the complexities involved in this object. We note, in addition, that in Epoch 1 there is very severe spectral blending of the Paα jet lines with the stationary Brγ line, so that its results are less robust.
). We caution, however, that true uncertainties are dominated by (i) degeneracies between the many parameters, which create a complicated multidimensional χ2 map; (ii) systematic errors from the continuum model; (iii) the assumption of our simple “geometric” models, which cannot capture all the complexities involved in this object. We note, in addition, that in Epoch 1 there is very severe spectral blending of the Paα jet lines with the stationary Brγ line, so that its results are less robust.
3.3. Results
Table 2 shows the model fit results for the jet emission lines in all epochs. The data and best fits are shown in Fig. 3 for Epoch 3 of the 2017 observations and in Appendix A for all other observations. The measured position angle of the jets agrees well with that expected from the kinematic model and radio observations (Fig. 2). The results for the 2016 observation are mostly in agreement with Paper I, but the more general model emission profile allows us to better constrain r0 = 0.16 ± 0.02 mas. Because of the multiple jet components, the blending with stationary lines, and the smaller number of jet lines, the observations in 2017 are not nearly as constraining as the 2016 observation, and often only an upper limit on r0 can be estimated.
GRAVITY jets model fit results.
As noted before, there are often two components (“knots”) in the jet lines in the 2017 observations. The need for two components in 2017 is clear from:
-
the spectrum, as two Gaussian components are needed for an acceptable fit;
-
the interferometric quantities, as the peaks of the differential visibility amplitudes and phases are often not aligned with the peak flux of the line in the spectrum, which points to substructure within the line, that is, different components with different spatial structure.
In contrast, in the 2016 observation (Paper I), only one jet component is needed as the emission lines are well fit by a single Gaussian and the spectrum and interferometric quantities are perfectly aligned (see Fig. A.1).
Two components are clearly distinguishable in all epochs for the Paα line from the receding jet but only on Epoch 3 for the Brβ line from the approaching jet. One of the components is compact (emission centroid ≲2 mas), with an emission profile similar to the one in the 2016 observation, and associated with the most recent or current jet ejection. The other component is significantly more extended (emission centroid ≳6 mas), associated with a previous jet ejection. This interpretation agrees with the corresponding redshifts from the precession model in Epochs 1 and 2. Figure 5 shows the collection of radial emission profiles of the optical jets for all observations. The compact knots have an exponential-like profile, whereas the extended knots have more rotund shapes. We note that the plotted best-fit emission profiles are only approximate, in particular for the extended components, for which only an upper limit on r0 can usually be determined (we have used such an upper limit in the plots). Much more robust are the centroids of the emission profiles (last row in Table 2), which show a clear difference between compact and extended components, that is, a significant spatial structure to the combined emission.
 |
Fig. 5. Top: collection of optical jet radial emission profiles for all GRAVITY observations. These were derived from the available jet emission lines in the K band spectrum (Brγ, Brδ, and He I 2.06 μm in the 2016 observation, and Paα and Brβ in the 2017 observations). There are two classes of profiles: compact (solid lines), associated with recent or current knots and which peak close to the central binary, and extended (dashed lines), associated with older knots. Bottom: emission profiles for selected emission lines calculated from a Cloudy photoionization model using the best-fit parameters to the emission line fluxes from Epoch X1 of the X-shooter observations. The elongated profiles resolved by GRAVITY suggest photoionization by the collimated radiation as the heating mechanism. The steeper profiles measured by GRAVITY relative to the Cloudy model could be explained by screening effects due to the large area covering factor of the bullets in the jets. |
The emission profiles of the compact components, extending to approximately a few mas, suggest that each individual knot is composed of bullets emitted over ≲1 day (their speed of 0.26c corresponds to ≈8mas day−1), with their emission decaying with distance from the compact object. As in Paper I, we attempted to fit the jets with more localized emission profiles (such as a point source or Gaussian), but they are inconsistent with the data: an elongated structure for the jets is strongly preferred. We also note that, for the more compact components, the emission peaks substantially close ≲0.5 mas to the binary system, and is more compact than previous estimates from optical spectroscopy monitoring; for example Borisov & Fabrika (1987) derived an exponential decay of the jet emission with fall-off distance 6.7 × 1014 cm ≈ 8.2 mas for the Hα jet line. The elongated emission profiles that we measure are strongly suggestive of a continuous heating mechanism along the entire jet, which is naturally accomplished by photoionization by the collimated radiation from the inner regions close to the compact object. The reduced emission with distance could then explained by the decaying intensity of the ionizing radiation, shadowing of the radiation by closer-in bullets in the case of large area covering factor, changing bullet properties with distance, or a combination of such effects.
Furthermore, the 2017 observations allow us to probe the spatial evolution of the jet profiles from night to night. The jet lines in Epoch 1 have clearly disappeared by Epoch 2 two nights later (Fig. 1). However, the jets lines in Epochs 2 and 3 (which are separated by one night only) partly overlap. The extended component in Epoch 3 could correspond to the compact component in Epoch 2 after it has travelled ≈8 mas day−1 × 1 day, whereas a new compact component in Epoch 3 clearly appeared at the same redshift where the extended component in Epoch 2 was located. This is the first time the movement of the optical bullets has been spatially resolved, although longer observations during a single night would be needed to trace the motion of an individual component unambiguously. We note that spectroscopic monitoring of the Hα jet lines consistently shows four or more spectroscopically resolved knots in both jets with a scatter of speeds ∼3000 km s−1 (Blundell et al. 2007), so that the presence of multiple knots is in fact expected in the strongest jet lines such as Paα.
4. X-shooter data analysis
We fit the jet lines with Gaussian or Lorentzian profiles (the jet lines are usually better fit by a Gaussian, but sometimes a Lorentzian profile is clearly preferred) to estimate their central wavelength, FWHM, and total intensity. All line fits were performed with the task splot in IRAF2 (Tody 1986, 1993). Whenever jet lines were blended with other jet or stationary lines, deblending was used. For all line identifications and adopted wavelengths, the “Atomic Line List v2.05b21” (van Hoof, P.) was used. The noise for the spectral fits was estimated from the scatter in continuum regions near each line. A particularly important constraint for photoionization models of the optical bullets is the absence of ionized helium in the jets due to the lack of the He II 4686 Å line. We estimate upper limits on its flux from the known location of where the line would appear based on the measured redshifts and the FWHM from the other jet lines.
Figure 6 shows the spectrum for the first X-shooter observation of SS 433 (Epoch X1), which contains the largest number of jet lines of all epochs. Emission lines from the jet are shown in blue and red for the eastern and western jets, respectively (at this epoch, the eastern jet, which is approaching most of the time, is receding). Throughout all observations we identify up to twenty pairs of lines: Hα through Hϵ; Paα through Pa9; Brβ through Br12; and five lines of He I (5875 Å, 6678 Å, 7065 Å, 1.083 μm, 2.056 μm). The strongest hydrogen lines (Hα, Hβ, Paα, Brβ) and He I 1.083 μm often show one or two additional components (shown in cyan and orange in Fig. 6), with redshift corresponding to previous ejections according to the precession model (and which we associate with older jet knots), whereas most emission lines show only one component from the most recent or current ejection (this behavior matches what is seen in the GRAVITY observations). The average redshift for the more recent jet knots in each epoch is shown in Fig. 2 and agrees with the kinematic precession model within the nutational motion and random jitter. The strength and number of jet emission lines varies significantly between the five X-shooter epochs.
 |
Fig. 6. First X-shooter spectrum of SS 433 (Epoch X1). H I and He I emission lines from the eastern and western optical jets are shown in blue and red, respectively. Older jet ejections (cyan and orange), only present for the strongest line transitions such as Hα (second panel from top) and Paα (bottom panel), are also shown. |
4.1. Cloudy models for photoionized optical bullets
The spatial emission profiles for the optical jets resolved by GRAVITY are strongly suggestive of photoionization as the main heating mechanism of the optical jets. Therefore, we proceeded to fit the jet emission line fluxes measured from X-shooter with photoionization models.
All line emission in SS 433 originates from dense gas; a clear lower limit to the density ne ≳ 107 cm−3 follows from the absence of any forbidden lines in the spectrum (Osterbrock & Ferland 2006, p.60). The true density in the optical bullets is estimated to be ∼1013 cm−3, and the optical jets take the form of dense bullets distributed throughout the jets with a low volume filling factor ∼10−6 (Fabrika 2004). At such densities, collisional ionization from excited levels and line radiative transfer effects become important, causing strong deviations from Case B recombination; still, such densities are not high enough for local thermodynamic equilibrium (LTE) to apply to all levels, and full collisional radiative models must be used (Ferland et al. 2013, 2017). A clear sign that collisional and radiative transfer effects are important in the optical bullets is the rather flat or even inverted Hα/Hβ jet line ratio (after extinction correction).
We model the jet emission lines with the photoionization code Cloudy (Ferland et al. 2013, 2017) version c17.01. The ionizing radiation is taken to be a single blackbody. We construct a grid in bullet density, bullet size, blackbody temperature, and intensity. In addition, because SS 433 is known to have appreciable extinction, we expand the grid in AV, assuming an extinction law 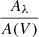 following Cardelli et al. (1989) and RV = 3.1. We attempted to fit for the He abundance, since it is likely that the donor star in SS 433 is at an advanced evolutionary stage, but it was unconstrained in our fits; therefore, we fixed a standard He abundance (0.098 by number). The abundances of other elements are taken as solar. The grid parameters and intervals are shown in Table 3. The solutions are iterated until convergence of the line optical depths. Each point in the grid gives a model intensity for each line (erg s−1 cm−2). The total number of bullets is then computed to minimize the χ2 with respect to the measured line intensities. The bullets are assumed to be identical in both jets, but the number of bullets (and therefore the kinetic power) can be different for the receding and approaching jets. We corrected the line intensities in each jet for Doppler boosting (1 + z)3 using the average measured redshift.
following Cardelli et al. (1989) and RV = 3.1. We attempted to fit for the He abundance, since it is likely that the donor star in SS 433 is at an advanced evolutionary stage, but it was unconstrained in our fits; therefore, we fixed a standard He abundance (0.098 by number). The abundances of other elements are taken as solar. The grid parameters and intervals are shown in Table 3. The solutions are iterated until convergence of the line optical depths. Each point in the grid gives a model intensity for each line (erg s−1 cm−2). The total number of bullets is then computed to minimize the χ2 with respect to the measured line intensities. The bullets are assumed to be identical in both jets, but the number of bullets (and therefore the kinetic power) can be different for the receding and approaching jets. We corrected the line intensities in each jet for Doppler boosting (1 + z)3 using the average measured redshift.
Cloudy model grid parameters.
We use the lines from the most recent jet knots (which contain a much larger number of lines) for the fits. The GRAVITY observations revealed that recent ejections have a typical exponential intensity profile as shown in Fig. 5. We integrate our Cloudy models over five radial points covering a factor of 100 in intensity. The reported best-fit intensity is the one at the base of the optical jet.
The statistical line flux errors estimated from the spectral fits are very small. The actual errors are dominated by systematic effects in the flux calibration, telluric correction, contamination by weak lines, line blending, and model uncertainties (such as collisional cross sections and line radiative transfer treatment). We estimate a 25% error in flux for all the lines, which results in 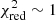 for the best-fit grid points. The parameter uncertainties are estimated by considering all the models that fall within Δχ2 = p of the best χ2 (Lampton et al. 1976), where p is the number of model parameters.
for the best-fit grid points. The parameter uncertainties are estimated by considering all the models that fall within Δχ2 = p of the best χ2 (Lampton et al. 1976), where p is the number of model parameters.
From the Cloudy model results, we derive further parameters of interest for the jets:
-
The volume filling factor of the optical bullets:
where Vbullets is the total volume in the bullets (calculated from their size and number) and
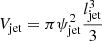 , where ψjet is the half-opening angle and ljet is the length of the jet;
, where ψjet is the half-opening angle and ljet is the length of the jet; -
The kinetic power of the optical jets:
where vjet = 0.26c, M is the total mass in the bullets (calculated from their density, size, and number).
-
The total line luminosity in the optical bullets Lbullets. This includes not only the recombination lines within X-shooter, but all of the strongest hydrogen and helium lines in the full spectrum output from Cloudy.
-
The total ionizing luminosity within the beam containing the optical bullets:
where I(r0) is the intensity at the base of the beam. The total luminosity in the collimated radiation could be higher if it is broader than the beam containing the optical bullets, which is likely the case from the presence of older jet knots that can keep radiating for a few days (Panferov & Fabrika 1993).
-
The luminosity inferred by an observer (assuming isotropy) whose line of sight is within the collimated beam:
For these estimates, we assumed ψjet = 1° and r0 = 0.4 mas and ljet = 2 mas from the GRAVITY observations. The length of the jet, ljet, is the region over which the bulk of the optical jet emission arises for the compact knot. It does not affect the intrinsic parameters of the Cloudy model, but only the derived parameters volume filling factor and kinetic power as per Eqs. (7) and (8); for instance, a larger ljet would reduce the estimated kinetic power.
Our model does not take into account screening of radiation by the bullets, which plays a role because the jets are very compact (area covering factors are high). To ensure self-consistency in the energetics, we only accept solutions with enough total luminosity in the beam to power the bullets (i.e., Lbeam > Lbullets). We also note that we assume the bullet radiation is isotropic and identical between the two jets (the only difference we allow between the two jets is in the total number of bullets), whereas differences between the luminosity of the two jets with precessional phase have been interpreted in terms of anisotropic radiation (Panferov et al. 1997; Fabrika 2004).
4.2. Results
We note that several related calculations to estimate the properties of the optical jets can be found in previous papers (e.g., Davidson & McCray 1980; Begelman et al. 1980; Bodo et al. 1985; Borisov & Fabrika 1987; Fabrika & Borisov 1987; Brown et al. 1991; Panferov & Fabrika 1993), primarily based on the Hα luminosity. These calculations have several uncertainties: unknown heating mechanism and emission line emissivity, degeneracy between density and volume filling factor, unknown extinction, optical depth effects, unknown spatial emission profile of the optical jets (e.g., jet size). The calculations presented here are based on the first optical interferometric measurements that have spatially resolved the optical jets, and on a large number of jet line species from X-shooter spectra.
Table 4 shows the model fit results for the five X-shooter epochs. Figure 7 shows the measured and model line fluxes for the first X-shooter epoch (corresponding plots for the other epochs are shown in Appendix B).
Cloudy photoionization models for the optical jets: results.
 |
Fig. 7. Measured line fluxes for the Epoch X1 X-shooter observation of SS 433 (blue) and best-fit Cloudy photoionization models (red). The models are shown for all the lines measured in at least one of the five epochs. The He II 4686 Å line flux is an upper limit since it was never detected. |
4.2.1. Bullet properties
The results confirm that the optical bullets in SS 433 are very dense, nH ∼ 1013 cm−3, and have a size R ≈ 106−107 cm. Even though they are optically thin to electron scattering (τT ∼ 0.01), many emission lines are optically thick. For the best-fit model in Epoch X1, τHα ≈ τPα ≈ 20, τHβ ≈ 4, τBrγ ≈ 2, τBr10 ≈ 0.3, τHeI6578 ≈ 5, and τHeI1.083 ≈ 0.6, so that optical depth effects in the line emission indeed have to be taken into account. The cooling in the bullets is dominated by hydrogen and helium recombination lines (∼80%), with total line luminosity ≈2 × 1037 erg s−1. Only around 15% of such luminosity is in lines within the X-shooter spectrum, with the strongest lines being the Lyman series in the UV. The total number of bullets that compose each knot is ∼1012−1015, with volume filling factor ∼10−6−10−4.
4.2.2. Jet kinetic power
We constrain the kinetic power in the optical bullets to ∼2−20 × 1038 erg s−1. This agrees with estimates from emission line modeling in the X-rays, which vary from ∼3 × 1038 to 5 × 1039 erg s−1 (e.g., Marshall et al. 2002; Brinkmann et al. 2005; Medvedev & Fabrika 2010). The collapse of the continuous X-ray jets into optical bullets must therefore be an efficient process, both in terms of mass and kinetic energy. Previous estimates from optical spectroscopy give Lkin ∼ 1039 erg s−1 (e.g., Panferov & Fabrika 1997; Fabrika & Borisov 1987).
4.2.3. Collimated radiation
The results constrain the collimated radiation to be relatively soft, T ∼ 3−4 × 104 K, and the total luminosity in the 1° beam containing the optical bullets to Lbeam ≈ 2−6 × 1037 erg s−1. Lower luminosities cannot power the jet emission lines, whereas higher luminosities and temperatures cause too intense heating and ionize helium too much. For an observer looking face-on at the collimated radiation and assuming isotropy, the inferred luminosity would be ≈7−20 × 1040 erg s−1, that is, SS 433 would appear as an extremely bright UV source. This luminosity is higher than the ∼few × 1039 erg s−1 inferred from the spectral energy distribution (SED) (Wagner 1986, although this is a rather uncertain number – see below), suggesting that indeed there is collimated radiation in SS 433 (not only thermal downgrading at low latitudes). The total intrinsic luminosity in collimated radiation depends on its opening angle, and would be ∼2 × 1039−1041 erg s−1 for angles 10 ° −50°. From modeling of the optical filaments in the W50 nebula and assuming photoionization by collimated radiation, Fabrika & Sholukhova (2008) estimated an ionizing luminosity ∼1040 erg s−1 in an opening angle ∼50°, roughly consistent with our estimates.
Figure 5 (bottom) shows the spatial emission profile for selected emission lines for the best-fit Cloudy photoionization model to Epoch X1. It assumes the bullets are distributed homogeneously over the jet with constant properties (density, size), and shows the normalized line emissivity as a function of distance r in the jet. It resembles the spatial profiles directly resolved by GRAVITY, and confirms that the different H I and He I lines have similar emission regions. The elongated, decaying exponential-like profile results from the interplay between the radiation intensity, gas density, and column density, and is a good consistency check for our photoionization models. For a given density and column density, there is an optimal intensity that will maximize the line emission of a given species by ionizing the bullet but not overheating it. Therefore, it is possible to obtain different spatial profiles (rising or decaying) depending on the combination of parameters, so that it is reassuring that the best-fit Cloudy models reproduce decaying profiles (albeit less steep than in the GRAVITY data) without an explicit requirement. A caveat of our model is that we do not consider screening of the intensity along the jet by the bullets (which happens in practice due to the large area covering factor), which is possibly the reason for the discrepancy in steepness.
Because of the possibility that SS 433 could be an ULX for an observer looking at it face-on, we attempted to constrain the X-ray luminosity in the beam containing the optical bullets. We did this through a perturbative approach: we selected the best-fit model in Epoch X1 from the analysis above, and added a second X-ray component with varying intensity, and checked at which X-ray intensity the optical emission lines are substantially affected and in clear violation of the data (e.g., by producing a too strong He II 4868 Åline). Because the main effect comes from the soft X-ray photons capable of ionizing H, He, and He+, the constraint depends on the relative contribution of soft X-ray photons to the total X-ray luminosity. To this end, we repeated the procedure for two different SEDs: a very soft one corresponding to a supersoft ultraluminous (SSUL) source, in the form of a blackbody kT = 0.14 keV, and a harder one corresponding to a hard ultraluminous (HUL) source, in the form of a blackbody kT = 0.27 keV plus a strong hard component (Kaaret et al. 2017). The corresponding SEDs and limits are shown in Fig. 8.
 |
Fig. 8. Potential SS 433 SED for a face-on observer who sees the beam radiation as the optical bullets see it. The solid blue curve shows the UV component from the best-fit Cloudy photoionization model to the line intensities in Epoch X1 of X-shooter. The orange and red lines show the upper limit to a possible X-ray component for a supersoft ultraluminous (SSUL) and hard ultraluminous (HUL) type SEDs, respectively. The dashed lines show the ground state photoionization cross sections for H, He, and He+. For SS 433 to look like an ULX for the face-on observer, its X-ray spectrum must be significantly hard, since soft X-ray photons break the H/He/He+ ionization balance in the optical bullets. |
In the case of the SSUL SED, we constrain the X-ray luminosity to be ≲10−3 of the UV component, that is, ≲5 × 1034 erg s−1 in the 1° beam containing the optical bullets or ≲1038 erg s−1 for a face-on observer. In this case, SS 433 would not be an ULX. For the HUL SED, the X-ray luminosity could be much larger, up to ≲10−1 of the UV component, that is, ≲5 × 1036 erg s−1 in the 1° beam containing the optical bullets or ≲1040 erg s−1 for a face-on observer. We conclude that SS 433 could be an ULX, as long as its X-ray spectrum is dominated by hard X-rays. Just the same, face-on ULXs (with a clear view through the funnel) are generally expected to have dominantly X-ray spectra (Kaaret et al. 2017), whereas our results suggest that SS 433 is UV dominated even in the collimated beam. This might mean that thermal downgrading happens already in the funnel of SS 433 (Begelman et al. 2006). The most promising way to find face-on SS 433-like objects in other galaxies might be to look for very bright and variable (due to jet precession) UV sources.
The X-ray luminosity of SS 433 has also been constrained from a putative reflection component ∼1035 erg s−1 in the hard X-ray spectrum ≳10 keV of SS 433 (Medvedev & Fabrika 2010; Middleton et al. 2018). Middleton et al. (2018) estimates that the intrinsic X-ray luminosity is LX ≳ 1038 erg s−1. This is consistent with our upper limits as long as the X-ray radiation is slightly less collimated (≳5°) than the beam containing the optical bullets, which is almost certainly the case from the presence of older jet knots that keep radiating for a few days (Panferov & Fabrika 1993).
4.2.4. Extinction towards SS 433
The extinction towards SS 433 is known to be large from the very red continuum spectrum but its exact value is difficult to assess. Galactic dust extinction maps give AV = 7.8 towards the direction of SS 433 (Schlegel et al. 1998; Perez & Blundell 2010), but that is an upper limit to the total integrated line of sight extinction. More recent 3D dust maps rather give AV = 5.7 ± 0.1 at d = 5.5 kpc towards SS 433 (Green et al. 2018). Strong diffuse interstellar bands (DIBs) are also present in the spectrum of SS 433 (as noted in previous work, e.g., Murdin et al. 1980; Margon 1984). The strength of DIBs has been shown to be correlated with interstellar extinction (e.g., Herbig 1975; Friedman et al. 2011; Kos & Zwitter 2013), although with substantial scatter. We measured the equivalent widths (EW) of several DIBs (5780, 5797, 5850, 6196, 6202, 6270, 6283, 6379, 6613, 6660 Å) in our X-shooter spectra and used the correlations in Friedman et al. (2011) and Kos & Zwitter (2013) to estimate AV = 5.1 ± 1.0 and AV = 5.6 ± 2.1, respectively, where the uncertainties are the 1σ scatter between the different DIBs. Therefore, there is evidence that the interstellar extinction towards SS 433 may be AV ≲ 6.0.
On the other hand, AV ≳ 7.8−8.0 has also been estimated from fitting the spectral energy distribution with a single reddened blackbody (e.g., Murdin et al. 1980; Wagner 1986; Dolan et al. 1997). This approach, however, suffers from several problems: (i) in the Rayleigh-Jeans range, the temperature of the blackbody and the extinction are very strongly correlated; (ii) there are numerous and very strong emission lines in SS 433; (iii) it is not clear whether the supercritical disk should look like a single blackbody, for example, the temperature seems to change with precession phase (Wagner 1986). Our X-shooter observations are not optimized for SED continuum fitting, but we confirm the strong degeneracy between blackbody temperature and extinction. A temperature T ≳ 20 000 (a reasonable expectation from the presence of He II 4868 Å stationary line) requires AV ≳ 7.5.
Our modeling of the jet lines yields AV ≈ 6.7 ± 0.1, which is intermediate between the lower values inferred from 3D dust maps and DIBs and those estimated from the very reddened SED. We suggest that there may be substantial AV ≳ 1 and structured circumstellar extinction in SS 433, affecting the equatorial part of the system more than the optical jets. It may be caused by dust forming from the equatorial outflows seen in radio (Paragi et al. 1999; Blundell et al. 2001) and near-infrared stationary emission lines (Waisberg et al. 2019). Mid-infrared observations of SS 433 show evidence of dust from excess emission at λ ≳ 20 μm (Fuchs et al. 2006). We speculate that mid-infrared interferometric observations with VLTI+MATISSE (Lopez et al. 2014) might resolve an extended dust torus in SS 433.
5. Conclusions
We presented a second set of GRAVITY observations of SS 433 after Paper I, as well as the first X-shooter observations of this object, focusing on the optical jets. We summarize our main conclusions from the GRAVITY observations as follows:
-
The optical jets have elongated, exponential-like spatial emission profiles, suggestive of a continuous heating process throughout the entire jet; we argue for photoionization by collimated radiation;
-
We have spatially resolved the movement of the optical bullets for the first time, finding more extended jet knots corresponding to previous jet ejections.
Using the up to twenty simultaneous pairs of measured jet line fluxes in the X-shooter observations, we have constrained properties of the optical bullets and the putative ionizing radiation with Cloudy photoionization models:
-
The optical bullets are dense, ∼1013 cm−3, and have a size ∼106−107 cm, from which optical depth effects in the jet emission lines are important;
-
The kinetic power of the optical jets is ∼2−20 × 1038 erg s−1;
-
The beamed radiation is dominantly UV with a luminosity ≈2−6 × 1037 erg s−1 in the 1° beam containing the optical bullets. An observer looking directly at the beam would infer an isotropic luminosity ≈7−20 × 1040 erg s−1, that is, SS 433 would appear as an extremely bright UV source;
-
In the photoionization picture, SS 433 could still be an ULX with a face-on observer inferring LX ≲ 1040 erg s−1, as long as the X-ray SED is dominantly hard, since soft X-ray photons destroy the H/He/He+ ionization balance in the optical bullets;
-
We constrain the extinction in the optical jets AV = 6.7 ± 0.1 and suggest there is substantial and structured circumstellar extinction in this object.
Acknowledgments
We thank the anonymous referee for the careful reading and helpful suggestions. We thank the GRAVITY Co-Is, the GRAVITY Consortium, and ESO for developing and operating the GRAVITY instrument. In particular, I.W. and J.D. thank the MPE GRAVITY team, in particular F. Eisenhauer, R. Genzel, S. Gillessen, T. Ott, O. Pfhul, and E. Sturm. We also thank the GRAVITY team members (W. Brandner, F. Einsenhauer, S. Hippler, M. Horrobin, T. Ott, T. Paumard, O. Pfhul, O. Straub, E. Wieprecht) and ESO staff who were on the mountain during the observations. We also thank P. Kervella for comments on the paper. I.W. thanks the organizers and participants of the 2018 Cloudy Workshop in Chiang Mai, Thailand, where part of this project was done, in particular Gary Ferland, Christophe Morisset, and Peter van Hoof. POP acknowledges financial support from the CNRS High Energy National Program (PNHE). POP and GD acknowledge financial support from the CNES. This research has made use of the Jean-Marie Mariotti Center SearchCal service (available at http://www.jmmc.fr/searchcal) co-developed by LAGRANGE and IPAG, CDS Astronomical Databases SIMBAD and VIZIER (available at http://cdsweb.u-strasbg.fr/), NASA’s Astrophysics Data System Bibliographic Services, NumPy (Van Der Walt et al. 2011) and matplotlib, a Python library for publication quality graphics (Hunter 2007).
References
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 156, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Sarazin, C. L., Hatchett, S. P., McKee, C. F., & Arons, J. 1980, ApJ, 238, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., & Bowler, M. G. 2004, ApJ, 616, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Mioduszewski, A. J., Muxlow, T. W. B., Podsiadlowski, P., & Rupen, M. P. 2001, ApJ, 562, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Bowler, M. G., & Schmidtobreick, L. 2007, A&A, 474, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodo, G., Ferrari, A., Massaglia, S., & Tsinganos, K. 1985, A&A, 149, 246 [NASA ADS] [Google Scholar]
- Borisov, N. V., & Fabrika, S. N. 1987, Sov. Astron. Lett., 13, 200 [NASA ADS] [Google Scholar]
- Brinkmann, W., & Kawai, N. 2000, A&A, 363, 640 [NASA ADS] [Google Scholar]
- Brinkmann, W., Fink, H. H., Massaglia, S., Bodo, G., & Ferrari, A. 1988, A&A, 196, 313 [NASA ADS] [Google Scholar]
- Brinkmann, W., Kotani, T., & Kawai, N. 2005, A&A, 431, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, J. C., Cassinelli, J. P., & Collins, II., G. W. 1991, ApJ, 378, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, D. H., & Murdin, P. 1978, Nature, 276, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & McCray, R. 1980, ApJ, 241, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Dolan, J. F., Boyd, P. T., Fabrika, S., et al. 1997, A&A, 327, 648 [NASA ADS] [Google Scholar]
- Dubner, G. M., Holdaway, M., Goss, W. M., & Mirabel, I. F. 1998, AJ, 116, 1842 [NASA ADS] [CrossRef] [Google Scholar]
- Eikenberry, S. S., Cameron, P. B., Fierce, B. W., et al. 2001, ApJ, 561, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Rees, M. J. 1979, MNRAS, 187, 13P [NASA ADS] [CrossRef] [Google Scholar]
- Fabrika, S. 2004, Phys. Rev., 12, 1 [Google Scholar]
- Fabrika, S. N., & Borisov, N. V. 1987, Sov. Astron. Lett., 13, 279 [NASA ADS] [Google Scholar]
- Fabrika, S. N., & Sholukhova, O. 2008, Microquasars and Beyond, 52 [Google Scholar]
- Fabrika, S., Ueda, Y., Vinokurov, A., Sholukhova, O., & Shidatsu, M. 2015, Nat. Phys., 11, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mexi. Astron. Astrofis., 49, 137 [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mexi. Astron. Astrofis., 53, 385 [Google Scholar]
- Friedman, S. D., York, D. G., McCall, B. J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, Y., Koch Miramond, L., & Ábrahám, P. 2006, A&A, 445, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glindemann, A. 2011, Principles of Stellar Interferometry (Berlin, Heidelberg: Springer-Verlag) [CrossRef] [Google Scholar]
- Goranskij, V. 2011, Peremennye Zvezdy, 31, 29 [Google Scholar]
- Gravity Collaboration (Petrucci, P.-O., et al.) 2017a, A&A, 602, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2017b, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, G. M., Schlafly, E. F., Finkbeiner, D., et al. 2018, MNRAS, 478, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1975, ApJ, 196, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, R. M., & Johnston, K. J. 1981, ApJ, 246, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kos, J., & Zwitter, T. 2013, ApJ, 774, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Kotani, T., Kawai, N., Matsuoka, M., & Brinkmann, W. 1996, PASJ, 48, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Lampton, M., Margon, B., & Bowyer, S. 1976, ApJ, 208, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J.-F., Bai, Y., Wang, S., et al. 2015, Nature, 528, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J., Blundell, K. M., & Goss, W. M. 2007, MNRAS, 381, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, B., Lagarde, S., Jaffe, W., et al. 2014, The Messenger, 157, 5 [NASA ADS] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Margon, B. 1984, ARA&A, 22, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Margon, B., Ford, H. C., Grandi, S. A., & Stone, R. P. S. 1979, ApJ, 233, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, H. L., Canizares, C. R., & Schulz, N. S. 2002, ApJ, 564, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, H. L., Canizares, C. R., Hillwig, T., et al. 2013, ApJ, 775, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Medvedev, A., & Fabrika, S. 2010, MNRAS, 402, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M. J., Walton, D. J., Alston, W., et al. 2018, ArXiv e-prints [arXiv:1810.10518] [Google Scholar]
- Murdin, P., Clark, D. H., & Martin, P. G. 1980, MNRAS, 193, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics Of Gaseous Nebulae And Active Galactic Nuclei (Sausalito, CA: University Science Books) [Google Scholar]
- Panferov, A. A., & Fabrika, S. N. 1993, Astron. Lett., 19, 41 [NASA ADS] [Google Scholar]
- Panferov, A. A., & Fabrika, S. N. 1997, Astron. Rep., 41, 506 [NASA ADS] [Google Scholar]
- Panferov, A. A., Fabrika, S. N., & Rakhimov, V. Y. 1997, AZh, 74, 392 [NASA ADS] [Google Scholar]
- Paragi, Z., Vermeulen, R. C., Fejes, I., et al. 1999, A&A, 348, 910 [NASA ADS] [Google Scholar]
- Perez, M. S., & Blundell, K. M. 2010, MNRAS, 408, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, W. J. 1974, ApJ, 187, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stephenson, C. B., & Sanduleak, N. 1977, ApJS, 33, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Stirling, A. M., Jowett, F. H., Spencer, R. E., et al. 2002, MNRAS, 337, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1986, in Instrumentation in Astronomy VI, ed. D. L. Crawford, Proc. SPIE, 627, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [NASA ADS] [Google Scholar]
- van den Heuvel, E. P. J., Ostriker, J. P., & Petterson, J. A. 1980, A&A, 81, L7 [NASA ADS] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
- Vermeulen, R. C., Murdin, P. G., van den Heuvel, E. P. J., et al. 1993, A&A, 270, 204 [NASA ADS] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wagner, R. M. 1986, ApJ, 308, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Waisberg, I., Dexter, J., Pfuhl, O., et al. 2017, ApJ, 844, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Waisberg, I., Dexter, J., Olivier-Petrucci, P., Dubus, G., & Perraut, K. 2019, A&A, 623, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, M. G., Stewart, G. C., Brinkmann, W., & King, A. R. 1986, MNRAS, 222, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Zealey, W. J., Dopita, M. A., & Malin, D. F. 1980, MNRAS, 192, 731 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: GRAVITY: full data and model fits
Here we show as in Fig. 3 the full K band spectrum and interferometric data, as well as the best-fit jet models, for the remaining GRAVITY observations. Compact and extended jet knots are shown in colored solid and dashed lines, respectively. In the 2017 observations, in which there is strong blending between the jets and the Brγ stationary line, a combined fit is done, but we show only the jet model for clarity. For the Brγ stationary line model and results, we refer to the companion paper on the equatorial outflows (Waisberg et al. 2019).
 |
Fig. A.1. Data and best-fit jet model for the 2016 GRAVITY observation. |
 |
Fig. A.2. Data and best-fit jet model for the 2017 Epoch 1 GRAVITY observation. |
 |
Fig. A.3. Data and best-fit jet model for the 2017 Epoch 2 GRAVITY observation. |
Appendix B: X-shooter: full data and model fits
Here we show the data and best-fit models for the remaining X-shooter epochs as in Fig. 7.
 |
Fig. B.1. Data and best-fit models for Epoch 2 of the X-shooter observations. |
 |
Fig. B.2. Data and best-fit models for Epoch 3 of the X-shooter observations. |
 |
Fig. B.3. Data and best-fit models for Epoch 4 of the X-shooter observations. |
 |
Fig. B.4. Data and best-fit models for Epoch 5 of the X-shooter observations. |
All Tables
All Figures
 |
Fig. 1. K band spectra for the three GRAVITY observations in 2017. The strongest jet emission lines are Paα and Brβ for the receding and approaching jets, respectively (the former is blended with the Brγ stationary line, the latter with stationary Pfund lines). The brightening and fading of different jet knots are visible over the three observations. Stationary emission lines are labeled in green, but are not the subject of this paper. |
| In the text | |
 |
Fig. 2. Jet redshifts (mostly approaching (eastern) jet in blue; mostly receding (western) jet in red) and position angle on sky (green) of the optical jets for each observation as a function of precessional phase. The curves were made using the kinematic model parameters in Eikenberry et al. (2001) and the precessional axis position angle in Stirling et al. (2002). The PA of the optical jets as derived from the GRAVITY data agrees well with the prediction from the radio jets. We plot both the 2016 (ϕprec ≈ 0.7) as well as the 2017 (ϕprec ≈ 0.9) GRAVITY observations. |
| In the text | |
 |
Fig. 3. Data and best-fit jet model for the 2017 Epoch 3 GRAVITY observation. Compact (recent) and extended (older) jet knots are shown in the spectrum as full and dashed lines, respectively. Stationary lines are labeled in green. There is substantial blending of the Paα lines from the receding jet with the stationary Brγ line, which also has differential visibility signatures across it. The fits are done to all lines simultaneously, but we plot only the model for jet lines for clarity. The baseline projected lengths and position angles on sky are indicated in the labels. |
| In the text | |
 |
Fig. 4. Example jet radial emission profiles (left) that can be created by the model, and corresponding differential visibility amplitudes and phases (middle, right) as a function of projected baseline length in the jet direction. The continuum is modeled as an unresolved point source, the flux ratio between the jet and the continuum is 0.5, and the wavelength is 2 μm. At the spatial scales probed by GRAVITY, more compact profiles (red) have smoother visibility curves, whereas more extended profiles (blue) show more significant substructure in the visibilities. |
| In the text | |
 |
Fig. 5. Top: collection of optical jet radial emission profiles for all GRAVITY observations. These were derived from the available jet emission lines in the K band spectrum (Brγ, Brδ, and He I 2.06 μm in the 2016 observation, and Paα and Brβ in the 2017 observations). There are two classes of profiles: compact (solid lines), associated with recent or current knots and which peak close to the central binary, and extended (dashed lines), associated with older knots. Bottom: emission profiles for selected emission lines calculated from a Cloudy photoionization model using the best-fit parameters to the emission line fluxes from Epoch X1 of the X-shooter observations. The elongated profiles resolved by GRAVITY suggest photoionization by the collimated radiation as the heating mechanism. The steeper profiles measured by GRAVITY relative to the Cloudy model could be explained by screening effects due to the large area covering factor of the bullets in the jets. |
| In the text | |
 |
Fig. 6. First X-shooter spectrum of SS 433 (Epoch X1). H I and He I emission lines from the eastern and western optical jets are shown in blue and red, respectively. Older jet ejections (cyan and orange), only present for the strongest line transitions such as Hα (second panel from top) and Paα (bottom panel), are also shown. |
| In the text | |
 |
Fig. 7. Measured line fluxes for the Epoch X1 X-shooter observation of SS 433 (blue) and best-fit Cloudy photoionization models (red). The models are shown for all the lines measured in at least one of the five epochs. The He II 4686 Å line flux is an upper limit since it was never detected. |
| In the text | |
 |
Fig. 8. Potential SS 433 SED for a face-on observer who sees the beam radiation as the optical bullets see it. The solid blue curve shows the UV component from the best-fit Cloudy photoionization model to the line intensities in Epoch X1 of X-shooter. The orange and red lines show the upper limit to a possible X-ray component for a supersoft ultraluminous (SSUL) and hard ultraluminous (HUL) type SEDs, respectively. The dashed lines show the ground state photoionization cross sections for H, He, and He+. For SS 433 to look like an ULX for the face-on observer, its X-ray spectrum must be significantly hard, since soft X-ray photons break the H/He/He+ ionization balance in the optical bullets. |
| In the text | |
 |
Fig. A.1. Data and best-fit jet model for the 2016 GRAVITY observation. |
| In the text | |
 |
Fig. A.2. Data and best-fit jet model for the 2017 Epoch 1 GRAVITY observation. |
| In the text | |
 |
Fig. A.3. Data and best-fit jet model for the 2017 Epoch 2 GRAVITY observation. |
| In the text | |
 |
Fig. B.1. Data and best-fit models for Epoch 2 of the X-shooter observations. |
| In the text | |
 |
Fig. B.2. Data and best-fit models for Epoch 3 of the X-shooter observations. |
| In the text | |
 |
Fig. B.3. Data and best-fit models for Epoch 4 of the X-shooter observations. |
| In the text | |
 |
Fig. B.4. Data and best-fit models for Epoch 5 of the X-shooter observations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.