EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 624 (April 2019) A&A, 624 (2019) A49 Full HTML
Free Access
Issue
A&A
Volume 624, April 2019
Article Number A49
Number of page(s) 17
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/201834504
Published online 08 April 2019

© ESO 2019

1 Introduction

Dozens of terrestrial planets in the habitable zone (HZ) have been found so far. Most of these planets orbit cool host stars, the so-called M dwarfs1. The Transiting Exoplanet Survey Satellite (TESS) is expected to find many more of these systems in our solar neighbourhood in the near future (Ricker et al. 2014; Sullivan et al. 2015; Barclay et al. 2018). Whether these planets can have surface conditions to sustain (complex) life is still debated (e.g. Tarter et al. 2007; Shields et al. 2016). Because of the close-in HZ, M-dwarf planets are likely tidally locked (e.g. Kasting et al. 1993; Selsis et al. 2008). To allow for habitable surface conditions they require a mechanism to redistribute the heat from the dayside to the nightside (e.g. atmospheric or ocean heat transport; Joshi et al. 1997; Joshi 2003; Selsis et al. 2008; Yang et al. 2013; Hu & Yang 2014). Another drawback of a planet lying close to its host star is the high luminosity during the pre-main-sequence phase (e.g. Ramirez & Kaltenegger 2014; Luger & Barnes 2015; Tian & Ida 2015) or that it might be subject to strong stellar cosmic rays (see e.g. Grießmeier et al. 2005; Segura et al. 2010; Tabataba-Vakili et al. 2016; Scheucher et al. 2018). On the other hand M-dwarf planets are favourable targets for the characterisation of their atmosphere. The high contrast ratio and transit depth of an Earth-like planet around cool host stars favours a detection of spectral atmospheric features. Hence, planets transiting M dwarfs are prime targets for future telescopes such as the James Webb Space Telescope (JWST; Gardner et al. 2006; Deming et al. 2009) and the European Extremely Large Telescope (E-ELT; Gilmozzi & Spyromilio 2007; Marconi et al. 2016).

Additionally model simulations show that planets with an Earth-like composition can build up increased amounts of biosignature gases like ozone (O3) and related compounds like water (H2O) and methane (CH4), which further increases their detectability (Segura et al. 2005; Rauer et al. 2011; Grenfell et al. 2013; Rugheimer et al. 2015). Knowing the ultraviolet radiation (UV) of the host star is crucial to understand the photochemical processes in the planetary atmosphere (see e.g. Grenfell et al. 2014; Rugheimer et al. 2015). M dwarfs vary by several orders in the UV flux from inactive to active stars (Buccino et al. 2007; France et al. 2016).

The approach of this study is to investigate the influence of a range of spectra of active and inactive stars with observed and modelled UV radiation on Earth-like planets in the HZ around M dwarfs. We furthermore aim to determine whether the resulting planetary spectral features could be detectable with JWST. Previous studies showed that multiple transits are needed to detect any spectral feature of an Earth-like planet with transmission or emission spectroscopy (Rauer et al. 2011; von Paris et al. 2011; Barstow et al. 2016; Barstow & Irwin 2016). Rauer et al. (2011) found that CH4 of an Earth-like planet around AD Leo (at 4.9 pc) would be detectable by co-adding at least three transits using transmission spectroscopy with JWST. To detect O3 at least ten transits would be required. For the TRAPPIST-1 planets c and d at 12.1 pc, 30 transits are needed to detect an Earth-like concentration of O3 with JWST (Barstow & Irwin 2016).

In this study we first apply a 1D atmosphere model to calculate the global and annual mean temperature profiles and the corresponding chemical profiles of Earth-like planets orbiting M dwarfs. As model input we use 12 stellar spectra including the spectra of the MUSCLES database with observed UV radiation (France et al. 2016). In contrast to Rugheimer et al. (2015) we use additional M-dwarf spectra and calculate transmission spectra of each Earth-like planet around M dwarfs with a radiative transfer model. We concentrate on transmission spectroscopy owing to the low chance of finding detectable absorption bands for temperate Earth-like planets with emission spectroscopy (see Rauer et al. 2011; Rugheimer et al. 2015; Batalha et al. 2018). We further develop a model to calculate the signal-to-noise ratio (S/N) of planetary spectral features with any kind of telescope and apply this to the modelled spectra and up-to-date JWST specifications. With the S/N we evaluate the potential to characterise the atmosphere of Earth-like exoplanets around M dwarfs.

The paper is organised as follows: in Sect. 2 we describe the atmospheric model, the scenarios, the line-by-line spectral model, and the S/N calculation. In Sect. 3 we first show the results of the atmospheric modelling and the resulting transmission spectra. Then we show the results of the S/N calculations. Section 3 presents the conclusions of this study.

2 Methods and models

2.1 Climate-chemistry model

We use a coupled 1D steady-state, cloud-free, radiative-convective photochemical model. The code is based on the climate model of Kasting et al. (1984) and the photochemical model of Pavlov & Kasting (2002) and was further developed by Segura et al. (2003), von Paris et al. (2008, 2010, 2015), Rauer et al. (2011), Gebauer et al. (2017, 2018a,b). The atmosphere in the climate module is divided into 52 pressure layers and the chemistry model into 64 equidistant altitude levels.

The radiative transfer of the climate module is separated into a short wavelength region from 237.6 nm to 4.545 μm with 38 wavelength bands for incoming stellar radiation and a long wavelength region from 1 to 500 μm in 25 bands for planetary and atmospheric thermal radiation (von Paris et al. 2015). We consider Rayleigh scattering by N2, O2, H2O, CO2, CH4, H2, He, and CO using the two-stream radiative transfer method based on Toon et al. (1989). Molecular absorption in the short wavelength range is considered for the major absorbers H2O, CO2, CH4, and O3. Molecular absorption of thermal radiation by H2O, CO2, CH4, and O3 and continuum absorption by N2, H2O, and CO2 are included (von Paris et al. 2015).

Our chemistry module includes 55 species with 217 chemical reactions. An update compared to previous model versions, for example used in Keles et al. (2018), is to consider altitude dependent CO2, O2, and N2 profiles instead of using an isoprofile as described in Gebauer et al. (2017). The photolysis rates are calculated within the wavelength range between 121.4 and 855 nm. For the effective O2 cross sections in the Schumann–Runge bands we use the values from Murtagh (1988) as described in Gebauer et al. (2018b). The mean solar zenith angle is set to 54° in the photochemistry module in order to best reproduce the 1976 U.S. Standard Atmosphere (Anderson et al. 1986). The water vapour concentrations in the troposphere are calculated using the relative humidity profile of the Earth taken from Manabe & Wetherald (1967).

2.2 Stellar Input

An important aim of this study is to investigate the influence of different spectral energy distributions (SED) on the temperature and chemical composition profiles of an Earth-like planet in the HZ around an M dwarf. We used eight observed M-dwarf spectra from the MUSCLES database2 (France et al. 2016), the observed spectra of AD Leo and GJ 644 from the VPL website3 (Segura et al. 2005), and the constructed stellar spectrum of TRAPPIST-1 with high UV activity using the method of Rugheimer et al. (2015) and O’Malley-James & Kaltenegger (2017). We note that there is no observed spectrum of TRAPPIST-1 in the UV. The spectrum used in this study is assumed and could be very different from the real spectrum. The Mega-MUSCLES HST Treasury Survey is planning to observe TRAPPIST-1 to construct a representative spectrum of this low mass M dwarf (Froning et al. 2018).

The spectra cover a range from M1.5 to M8 spectral type. For comparison we used the solar spectrum from Gueymard (2004). Table 1 lists basic parameters of all stars used in this study. Figure 1 compares all M-dwarf spectra and the solar spectrum and Fig. 2 shows the mean UV flux of each M dwarf between 170 and 240 nm. In both plots the flux is scaled so that the surface temperature of the modelled planet reaches a value of 288.15 K. The scaling values are shown in Table 2. Whereas the MUSCLESstars are classified as inactive (France et al. 2016), AD Leo and GJ 644 are often cited as active M dwarfs (e.g. Segura et al. 2005; Reiners et al. 2009; Leitzinger et al. 2010; Rauer et al. 2011; Rugheimer et al. 2015). We label the active M dwarfs with an asterisk to separate them from non-active M dwarfs. Since the real TRAPPIST-1 spectrum is unknown, we cannot make any conclusions regarding the UV activity of this star. The spectrum we adopted for this study has a low mean UV flux, since we do not label TRAPPIST-1 as active. From the MUSCLES database we used version 22 of the adapted panchromatic SED, binned to a constant resolution of 1 Å. In low S/N regions the spectra were sampled down by the MUSCLES project to avoid negative fluxes by averaging negative flux bins with their neighbours until no negative flux bins remained. The spectra of GJ 1214, GJ 436 and Proxima Centauri include zero values for some wavelength bins in the UV. For these bins we linearly interpolated the flux with the two next non-zero neighbours to achieve a better estimate of the real flux. We applied the same downsampling procedure to avoid negative and non-zero flux to the spectra of AD Leo and GJ 644.

Since the MUSCLES spectra extend only up to a wavelength of 5.5 μm, we extended the available wavelength range with the NextGen4 spectra up to 971 μm (Hauschildt et al. 1999) to avoid overestimation of the flux when scaling to 1 solar constant. For the MUSCLES spectra we took the values of the effective temperature, log g and [Fe/H] from Loyd et al. (2016). Since the NextGen spectra have a fixed grid for effective temperature, log g and [Fe/H], we took the spectra withthe most similar log g and [Fe/H] values and linear interpolated the temperature grid to the corresponding value.

The incoming stellar radiation is used up to 4.545 μm in the radiative transfer calculations. For a G-type star like the Sun ~1% of the incoming flux is neglected by the model because of this cut. For TRAPPIST-1 the flux which is not included at longer wavelengths by the model increases up to 4.6% of the total incoming radiation.

Table 1

Stellar parameters for the Sun and all M dwarfs used in this study.

2.3 Model scenarios

We model Earth-like planets around M dwarfs with N2 –O2 dominated atmospheric chemical compositions. We use 78% nitrogen, 21% oxygen, and a modern CO2 volume mixing ratio of 355 ppm as starting conditions. While in previous studies it was assumed that these concentrations are isoprofiles which stay constant with altitude, in this study only the volume mixing ratios (vmr) at the surface are held to these values. The vmr within the atmosphere are allowed to vary (see Gebauer et al. 2017 for details). The chemistry module uses Earth-like boundary conditions to reproduce mean Earth atmospheric conditions. These are kept constant for each simulation and are further described in Gebauer et al. (2017). We use the Earth’s radius and gravity and a surface pressure of 1 bar for all modelled planets. The temperature profile is calculated with the climate module depending on the chemical composition. The tropospheric water concentration is calculated via the assumption of an Earth-like relative humidity profile (see Manabe & Wetherald 1967). In contrast to Rauer et al. (2011), but following Segura et al. (2005) we scale the stellar spectra from Fig. 1 so that we reproduce the Earth’s surface temperature of 288.15 K, since the assumption of an Earth-like relative humidity may not be appropriate for higher temperatures (see e.g. Leconte et al. 2013; Godolt et al. 2015, 2016). Table 2 shows the scaling values of the stellar insolation for each star. We note that except the Earth, we do not model existing planets in this study. There are several studies investigating the potential atmosphere of Proxima Centauri b (Kreidberg & Loeb 2016; Turbet et al. 2016; Meadows et al. 2018), GJ 1214 b (Menou 2011; Berta et al. 2012; Charnay et al. 2015), GJ 436 b (Lewis et al. 2010; Beaulieu et al. 2011) and the TRAPPIST-1 planets (Barstow & Irwin 2016; de Wit et al. 2016; O’Malley-James & Kaltenegger 2017).

2.4 Line-by-line spectral model

The Generic Atmospheric Radiation Line-by-line Infrared Code (GARLIC) is used to calculate synthetic spectra between 0.4 and 12 μm (Schreier et al. 2014, 2018). The GARLIC model is based on the Fortran 77 code MIRART-SQuIRRL (Schreier & Schimpf 2001), which has been used for radiative transfer modelling in previous studies like Rauer et al. (2011) and Hedelt et al. (2013). The line parameters over the whole wavelength range are taken from the HITRAN 2016 database (Gordon et al. 2017). Additionally the Clough–Kneizys–Davies continuum model (CKD; Clough et al. 1989) and Rayleigh extinction are considered (Murphy 1977; Clough et al. 1989; Sneep & Ubachs 2005; Marcq et al. 2011). The transmission spectra are calculated using the temperature profile and the profiles of the 23 atmospheric species5, which HITRAN 2016 and our 1D climate-chemistry model have in common. We note that not all of the species are relevant for transmission spectroscopy of Earth-like atmospheres (see e.g. Schreier et al. 2018).

The radius of a planet with an atmosphere is wavelength dependent. This effect may be measured for example via transit spectroscopy. The difference between the geometric transit depth (without the contribution of the atmosphere) and the transit depth (considering the atmosphere) is called the effective height he (λ). We simulate the transmission spectra 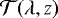T(λ,z)$\mathcal{T}(\lambda,z)$ for L = 64 adjacent tangential beams (corresponding to the 64 chemistry levels z) through the atmosphere. The effective height of each atmosphere is calculated using he(λ)=∫0∞( 1−T(λ,z)) dz.\begin{equation*}h_{\text{e}}(\lambda) = \int_{0}^{\infty} \Big(1-\mathcal{T}(\lambda,z)\Big)~\textrm{d}z. \end{equation*}(1)

thumbnail Fig. 1

Stellar input spectra, scaled to reach a surface temperature of 288.15 K, of the modelled planet and binned to a resolving power of 200. AD Leo and GJ 644 are taken from the VPL website (Segura et al. 2003), TRAPPIST-1 from O’Malley-James & Kaltenegger (2017), the other M-dwarf spectra from the MUSCLES database (France et al. 2016), and the solar spectrum from Gueymard (2004). Stars labelled with an asterisk are active M dwarfs. Top panel: UV and IR spectra up to 3 μm with linear axes. Bottom panel: UV spectra with logarithmic axes.
thumbnail Fig. 2

Mean UV flux of each M dwarf between 170 and 240 nm. Mean values are calculated from the stellar spectra, scaled as in Fig 1.

2.5 Signal-to-noise ratio model

To calculatethe S/N for potential measurements of our synthetic Earth-like planets, we further developed the background-limited S/N model used by von Paris et al. (2011) and Hedelt et al. (2013). We added the readout noise contribution to the model and calculate the duty cycle (fraction of time spent on target) to better evaluate the detectability of atmospheric spectral features. The code of von Paris et al. (2011) and Hedelt et al. (2013) is based on the photon noise model applied in Rauer et al. (2011) as follows: 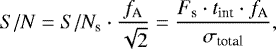S/N=S/Ns⋅fA2=Fs⋅tint⋅fAσtotal,\begin{equation*}S/N = S/N_{\text{s}} \cdot \frac{f_{\text{A}}}{\sqrt{2}} = \frac{F_{\text{s}} \cdot t_{\text{int}} \cdot f_{\text{A}}}{\sigma_{\text{total}}}, \end{equation*}(2)

where S/Ns is the stellar S/N. The stellar signal, Fs (photons s−1), is calculatedwith 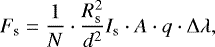Fs=1N⋅Rs2d2Is⋅A⋅q⋅Δλ,\begin{equation*} F_{\text{s}} = \frac{1}{N} \cdot \frac{R_{\text{s}}^2}{d^2} I_{\text{s}} \cdot A \cdot q \cdot \Delta \lambda, \end{equation*}(3)

where Rs is the stellar radius, Is the spectral energy flux (W m−2 μm−1), d the distance of the star to the telescope, and A the telescope area. The flux is divided by 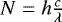N=hcλ$N = h\frac{c}{\lambda}$ (h, Planck constant, c, speed of light) to convert into number of photons. In contrast to Rauer et al. (2011) we consider a wavelength dependent total throughput, q, of the corresponding instrument. The bandwidth, Δλ (resolving power, 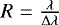R=λΔλ$R = \frac{\lambda}{\Delta \lambda}$), is dependent on the filter and disperser of the instrument in question. The additional transit depth due to the atmosphere of the planet, fA, is calculated using Rs, the planetary radius, Rp and he (Eq. (1)), i.e. 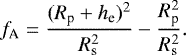fA=(Rp+he)2Rs2−Rp2Rs2.\begin{equation*}f_{\text{A}} = \frac{(R_{\text{p}} + h_{\text{e}})^2}{R_{\text{s}}^2} - \frac{R_{\text{p}}^2}{R_{\text{s}}^2}. \end{equation*}(4)

The total noise contribution, σtotal, includes photon noise, σphoton, zodiacal noise, σzodi, thermal noise σthermal, dark noise, σdark, and readout noise, σread, i.e. 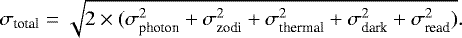σtotal=2×(σphoton2+σzodi2+σthermal2+σdark2+σread2).\begin{equation*} \sigma_{\text{total}} = \sqrt{2 \times (\sigma_{\text{photon}}^2 + \sigma_{\text{zodi}}^2 + \sigma_{\text{thermal}}^2 + \sigma_{\text{dark}}^2 + \sigma_{\text{read}}^2)}. \end{equation*}(5)

The additional factor 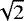2$\sqrt{2}$ is included to consider the planetary signal as a result of the difference between in and out of transit. The individual noise sources are described in more detail in von Paris et al. (2011). In constrast to von Paris et al. (2011) and Hedelt et al. (2013) we calculate the smallest number of pixels, Npixel, needed to collect at least 99% of the full stellar signal. This assumption significantly decreases the contribution due to zodiacal, thermal, dark, and readout noise by neglecting contamination of background noise dominated pixels. The number of photons per pixel is given by the point spread function (PSF) of the corresponding instrument, filter, and disperser. We use the pixel of the PSF with the highest fraction of the total signal to calculate the exposure time, texp, which is the longest time of photon integration before the collector is saturated. Possible exposure times are usually predefined by the instrument configuration. The minimum exposure time defines the saturation limits of the instrument. The number of exposures, Nexp, during a single transit is calculated via 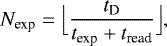Nexp=⌊tDtexp+tread⌋,\begin{equation*} N_{\text{exp}} = \Bigl\lfloor\frac{t_{\text{D}}}{t_{\text{exp}} + t_{\text{read}}}\Bigr\rfloor, \end{equation*}(6)

where tread is the readout time of the instrument configuration and tD is the transit duration. The value Nexp is rounded down to the next integer.

We calculate tD via tD = P/π × arcsin (​​(Rs + Rp)2 − b2/a),\begin{equation*}t_{\text{D}}\;{=}\;P/\pi~\times~\textrm{arcsin}\,\Big(\!\!\sqrt{(R_{\text{s}}~+~R_{\text{p}})^2~-~b^2}/{a}\Big), \end{equation*}(7)

with b = a∕Rs  cos(i). The inclination, i, was assumed to be 90° for all planets. The orbital distance, a, was calculated by 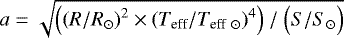a = ((R/R⊙)2×(Teff/Teff ⊙)4) / (S/S⊙)$a\;{=}\;\sqrt{\Big({(R/R_{\odot})}^2 \times {(T_{\textrm{eff}}/T_{\textrm{eff}~\odot})}^4\Big)~/~\Big(S/S_{\odot}\Big)}$ and the orbital period, P, was calculated using Kepler’s third law. The full integration time of one transit, tint is considered for the noise calculation, as well as for the calculation of the number of photons collected from the star during one transit (Fs × tint). The value tint is calculated via 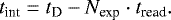tint=tD−Nexp⋅tread.\begin{equation*} t_{\text{int}} = t_{\text{D}} - N_{\text{exp}} \cdot t_{\text{read}}. \end{equation*}(8)

The instrumental readout noise, RON, is usually given per pixel and per exposure. To calculate the full readout noise during one transit we use 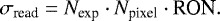σread=Nexp⋅Npixel⋅RON.\begin{equation*} \sigma_{\text{read}} = N_{\text{exp}} \cdot N_{\text{pixel}} \cdot \text{RON}. \end{equation*}(9)

Table 2

Parameters of the Earth around the Sun and Earth-like planets around M-dwarf host stars.

3 Results and discussion

3.1 Atmospheric profiles

Figures 3 and 4 show the results from the climate-chemistry model using the M dwarf and the solar spectra as incoming flux shown in Fig. 1. Compared to previous studies such as Rauer et al. (2011), Grenfell et al. (2014), and Keles et al. (2018) we use a further developed model and a set of active and inactive observed and modelled M-dwarf SEDs.

3.1.1 Temperature profile

Figure 3 shows temperature profiles for the hypothetical Earth-like planets around their corresponding host stars. All planets are placed at a distance to their host star which results in a surface temperature of 288.15 K. Table 2 shows the scaling factor of the total solar irradiance (TSI) of each planet. Without scaling the spectra, Earth-like planets around most M dwarfs would show an increased surface temperature (see e.g. Rauer et al. 2011; Rugheimer et al. 2015). In part, this is due to the shift of the emission maximum of M dwarfs to the near-IR, which leads to increased absorption of CO2 and H2O and decreased scattering at UV and visible wavelengths in the planetary atmosphere (see e.g. Kasting et al. 1993).

This effect can be intensified by an increased greenhouse heating due to the increased amount of CH4 and H2O in the troposphere of Earth-like planets around M dwarfs (see e.g. Rauer et al. 2011; Grenfell et al. 2013; Rugheimer et al. 2015). Most M-dwarf cases require decreased TSI to reach a surface temperature of 288.15 K. However, above a certain CH4 concentration, the surface temperature decreases with the same insolation. This suggests that most of the stellar irradiation is absorbed in the stratosphere, resulting in a smaller increase of the surface temperature due to reduced stellar irradiation reaching the troposphere (see also Grenfell et al. 2013). For M 1 to M 3 type stars the TSI needs to be decreased by about 8–12%. Mid M dwarfs show this saturation in greenhouse heating, resulting in a minor downscaling of 1–5%. For the synthetic planet orbiting the late M-dwarf TRAPPIST-1, the stellar flux needs to be increased by 5% to reproduce Earth’s surface temperature. Hence, the chemistry feedback counteracts the effect of the SED, which may shift the inner edge of the HZ towards shorter distances to the star for late-type M-dwarf planets compared to climate-onlysimulations such as Kopparapu (2013). Neglecting the composition change, hence assuming Earth’s compositionand carrying out climate only calculations suggest that the TSI would need to be decreased by 8–12% for all Earth-like planets around M dwarfs including TRAPPIST-1 and Proxima Centauri (not shown). Hence the chemical feedback tends to cool the planets around late-type M dwarfs. This result is consistent with the study of Ramirez & Kaltenegger (2018) who found that for planets around late M dwarfs a CH4 anti-greenhouse effect can shrink the HZ by about 20%.

Our simulations do not include effects on the radiative transfer due to clouds and hazes. This decreases the equilibrium temperature of the Earth due to the lower planetary albedo (see Table 2). The consideration of clouds can decrease or increase the surface temperature depending on the type and height of the clouds (see e.g. Kitzmann et al. 2010). Including thick hazes would likely decrease the surface temperature by a few degrees (see e.g. Arney et al. 2016, 2017). Even for climate models of the Earth it is still challenging to simulate the effect of clouds and aerosols consistently (see e.g. Pachauri et al. 2014). Hence, we do not consider clouds and hazes for this model study. Effects which would lead to a different surface temperature could be corrected by up- or downscaling the stellar flux to obtain a surface temperature of 288.15 K.

In the middle atmosphere (stratosphere and mesosphere up to 0.01 hPa) heating due to O3 absorption is decreased owing to weak UV emission of M dwarfs (see e.g. Segura et al. 2005; Grenfell et al. 2013, 2014). Therefore, no temperature inversion is present in the stratosphere, as found by Segura et al. (2005). For active and inactive early M dwarfs the temperature maximum in the middle atmosphere around 1 hPa is decreased compared to the Earth around the Sun. The enhanced heating rates due to CH4 absorption of stellar irradiation increase the temperature in the middle atmosphere by up to 60 K for late-type M-dwarf planets compared to early-type M-dwarf planets (see also Rauer et al. 2011; Grenfell et al. 2014). Increased temperatures from about 500 up to 1 hPa result in an almost isothermal vertical gradient, most pronounced for late M-dwarf planets. For emission spectroscopy the weak temperature contrast between the surface and the atmosphere reduces the spectral features, resulting in low S/N as discussed in Rauer et al. (2011).

thumbnail Fig. 3

Influence of various M-dwarf SEDs on the temperature profile (K) of an Earth-like planet. The stellar spectra of Fig. 1 are scaled to reproduce a surface temperature of 288.15 K (see Table 2). Each coloured line represents the temperature profile of the modelled hypothetical planet orbiting a different host star. Weak UV emission of M dwarfs leads to low O3 heating inthe middle atmosphere and therefore to a reduced or missing temperature inversion. Enhanced CH4 heating increases the temperature in the middle atmosphere of Earth-like planets around late-type M dwarfs by up to 60 K.

3.1.2 Responses of O3

The production of O3 in the middle atmosphere is sensitive to the UV radiation. In the Schumann–Runge bands and Herzberg continuum (from about 170 to 240 nm) molecular oxygen (O2) is split into atomic oxygen in the ground state (O3P), which reactswith O2 to form O3. The destruction of O3 is mainly driven by absorption in the Hartley (200–310 nm), Huggins (310–400 nm), and Chappuis (400–850 nm) bands. Hydrogen oxides, HOx (OH, HO2, and HO3), and nitrogen oxides, NOx (NO, NO2, and NO3), destroy O3 via catalytic loss cycles (e.g. Brasseur & Solomon 2006). All planets around inactive host stars from the MUSCLES database and TRAPPIST-1 have a reduced O2 photolysis in the Schumann–Runge bands and Herzberg continuum compared to the Earth around the Sun case (see Fig. 2 and Rugheimer et al. 2015). The decreased destruction of O3 by photolysis at wavelengths longer than ~200 nm (see Fig. 1 and Grenfell et al. 2014) can not compensate the decreased production, resulting in lower concentrations of O3 throughout the atmosphere (see Fig. 4). Earth-like planets around active M dwarfs (AD Leo and GJ 644) show strong O2 photolysis in the Schumann–Runge bands and Herzberg continuum (see Fig. 2), which results in an increase of O3 concentrations compared to planets around inactive M dwarfs (see also Grenfell et al. 2014).

3.1.3 Responses of CH4

For an Earth-like atmosphere the destruction of CH4 is mainly driven by the reaction with the hydroxyl radical, OH, (CH4 + OH → CH3 + H2O). The amount of OH in the atmosphere is closely associated with UV radiation via the source reaction with excited oxygen (O1 D): H2O + O1D → 2OH. O1 D is mainly produced by O3 photolysis (see e.g. Grenfell et al. 2007, 2013 for further details). As in previous studies (e.g. Rauer et al. 2011) we assume a constant CH4 bioflux for all our simulations. No in situ chemical production of CH4 in the atmosphere is included in the model. The effect of different CH4 biomass emissions on planets around M dwarfs was investigated by for example Grenfell et al. (2014). Compared to the Earth around the Sun, the UV photolysis of O3 is reduced for all Earth-like planets orbiting M dwarfs (see Grenfell et al. 2013). This leads to reduced O1 D and therefore OH concentrations, except for active M-dwarf planets, where OH is increased in the upper middle atmosphere (Fig. 4). The reduced OH concentrations decrease the destruction of CH4 and lead to enhanced CH4 abundances (Segura et al. 2005; Grenfell et al. 2013, 2014; Rugheimer et al. 2015). The planets around the inactive MUSCLES host stars show CH4 concentrations comparable to the results of Rugheimer et al. (2015). The active host stars have higher far UV radiation, which leads to more O3 production, increased OH concentrations in the upper middle atmosphere, and more CH4 destruction in the atmosphere of Earth-like planets compared to planets orbiting inactive host stars.

All our simulated planets around M dwarfs feature a CH4/CO2 ratio higher than 0.2, for which previous model studies suggest that hydrocarbon haze formation is favoured (see Trainer et al. 2004; Arney et al. 2016, 2017). Our model does not include hydrocarbon haze production or the impact of haze on the radiatve transfer. Arney et al. (2017) found that the surface temperature of an Earth-like planet around AD Leo would decrease by 7 K whenthe effect of hazes is considered. Such a decrease of the surface temperature by hazes would require an increase in stellar flux to obtain a surface temperature of 288.15 K. On the one hand haze production would lead to an CH4 sink, on the other hand the lower UV radiation due to UV absorption by organic haze would decrease the CH4 photolysis. The overall effect upon the resulting CH4 profile is difficult to estimate. Hence, we refer to Arney et al. (2016, 2017) who investigated the impact of organic haze on Earth-like atmospheres.

We based our simulations on the assumption of a constant CH4 bioflux for all planets. Segura et al. (2005) and Rugheimer et al. (2015) reduced the surface flux of CH4 or set a constant surface mixing ratio to limit the building up of CH4 due to the reduced destruction for Earth-like planets around late M dwarfs. Although the biosphere of an Earth-like planet around M dwarfs is likely to be different to the Earth, we cannot exclude that biofluxes might be similar.

thumbnail Fig. 4

Influence of various M-dwarf SEDs on some selected chemical atmospheric profiles of an Earth-like planet. The legend is the same as for Fig. 3.
thumbnail Fig. 5

Stellar S/N ratio over 1 h integration time of each M dwarf at 10 pc, binned to a resolution of 100. All NIRSpec filters and high resolution disperser are combined. Solid lines are calculated using the method described in Sect. 2.5 and dashed lines are calculated using the JWST ETC, Pandeia (Pontoppidan et al. 2016).

3.1.4 Responses of H2O

In the middle atmosphere the increased CH4 abundances lead to more H2O production via CH4 oxidation for Earth-like planets around M dwarfs compared to the Earth–Sun case (e.g. Segura et al. 2005; Rauer et al. 2011). In the troposphere the H2O content is related to the temperature profile and is calculated with the assumption of a relative humidity profile. Although all planets are placed at the distance to their host star where the surface temperature reaches 288.15 K, the H2O content in the upper troposphere is increased for M-dwarf planets and is close to the mixing ratio thought to lead to water loss. In this case this high mixing ratio is caused by CH4 oxidation. The temperatures in the troposphere are increased for all Earth-like M-dwarf planets compared to the Earth. This allows the atmosphere to sustain more H2O in the troposphere, even if the same H2O vmr is obtained at the surface.

3.1.5 Responses of N2O

On Earth nitrous oxide (N2O) sources are mainly surface biomass emissions. Only weak chemical sources in the atmosphere further increase the amount of N2 O in the atmosphere (see e.g. Grenfell et al. 2013). We assume constant N2 O biomass emissions for all our simulations bases on modern Earth (see e.g. Grenfell et al. 2011, 2014). The loss processes of N2 O are dominated by photolysis in the UV below 240 nm in the middle atmosphere (via N2 O + hν → N2 + O3P). We use the cross sections of Selwyn et al. (1977), which cover the wavelength range from 173 to 240 nm and peak for room temperature at around 180 nm. For Earth-like planets around M dwarfs and the Earth only ~5–10% of N2O is destroyed via catalytic reaction with O1D (see e.g. Grenfell et al. 2013). The resulting N2O is therefore closely related to the SED around 180 nm (see Fig. 2). The SED in the far UV range is dominated by the activity of the M dwarf and has a lower dependence on the spectral type (France et al. 2013). Since active M dwarfs emit strongly in the far UV, planets orbiting active M dwarfs show reduced N2 O abundances in comparison to planets around inactive M dwarfs. Similar to Rugheimer et al. (2015) we do not find a dependence of the N2O abundances on the type of the M dwarf using observed stellar spectra. The amount of N2 O in the atmosphere of Earth-like planets is mainly dependent on the incoming radiation in the wavelength range between 170 and 240 nm of the host star (see Fig. 2). For modelled spectra Rugheimer et al. (2015) show that N2 O increases for Earth-like planets around late-type M dwarf.

3.1.6 Responses of CO2

The CO2 production is mainly driven by the reaction CO + OH → CO2 + H. The increased CH4 oxidation in the middle atmosphere leads to an increase in CO for Earth-like planets around M dwarfs compared to the Earth–Sun case (Fig. 4). CO2 is mainly destroyed by photolysis in the far UV. At wavelengths longer than 120 nm the photolysis of CO2 is strongest between 130 and 160 nm (e.g. Huestis & Berkowitz 2011). Despite the strong emission of AD Leo in the far UV, Gebauer et al. (2017) found a 40% increase of CO2 abundances in the upper middle atmosphere of an Earth-like planet around AD Leo due to an increase of OH and CO at these altitudes compared to the Earth around the Sun. Even for lower abundances of OH in the upper middle atmosphere, we find that CO2 increases in the middle atmosphere for all M-dwarf planets because of the large amounts of CO. The enhancement of the CO2 production was not taken into account in previous studies, such as Rauer et al. (2011) and Grenfell et al. (2014), where CO2 was kept constant. At the surface all scenarios show a CO2 volume mixing ratio of 355 ppm.

3.2 Stellar S/N

Just a fraction of the measured stellar signal of the order of a few parts per million (ppm) is blocked by the atmosphere of a terrestrial planet during a transit. Hence, to calculate the S/N of the atmosphere of the planet, we first need to know the stellar S/N (S/Ns). The radius of the star and the distance to the star are also important to determine the stellar signal in addition to the spectral type, (Eq. (2)). Figure 5 shows the S/Ns for all M dwarfs at 10 pc, observed for an integration time of 1 h, using all high resolution JWST NIRSpec filters (G140H/F070LP, G140H/F100LP, G235H/F170LP, G395H/F290LP). The specifications used to calculate the S/N using the NIRSpec filters can be found in Appendix A.1. We binned the S/N to a constant resolution of 100 over the entire wavelength range (Δλ = 10 nm at 1 μm and Δλ = 50 nm at 5 μm). We chose the highest S/N for all overlapping bins of two filters. We note that in practise it is not possible to observe several NIRSpec filters at the same time. Gaps in the wavelength coverage at ~1.3, ~2.2, and ~3.8 μm result from aphysical gap between the detectors6.

At 10 pc, all M dwarfs except GJ 644 are observable over the entire wavelength range using high resolution spectroscopy (HRS). For the low wavelength filters GJ 644 reaches the saturation limit at around 11.5 pc. The Sun, placed at 10 pc, is not observable at any wavelength using NIRSpec due to saturation of the detector. The SED of M dwarfs peaks between 0.7 (early M dwarfs) and 1.1 μm (late M dwarfs). Because of the broader bandwidth with increasing wavelengths the S/N does not decrease significantly towards longer wavelengths. Nielsen et al. (2016) showed that the S/N for GJ 1214 reduces by a factor of 3 from 1.5 to 4 μm when using a constant bandwidth. The early M dwarfs are near the saturation limit, which results in a significant reduction of the S/N due to changes in the detector duty cycle (with shorter exposures) and additional readout noise (see also Nielsen et al. 2016). Early-type M dwarfs have larger S/N than late-type M dwarfs at the same distance owing to the combined effect of effective temperature and stellar radius.

The solid lines of Fig. 5 show the S/N calculated using the method described in Sect. 2.5. Our S/N model can be applied to any space and ground-based telescope. In comparison to the previous S/N model version of Hedelt et al. (2013) we added the readout noise contribution and saturation limits to the code. We plan to further develop this model and include exozodiacal dust contamination and the influence of star spots on the S/N of transmission and emission spectroscopy.

To verify our S/N model we compared the calculations to results from the JWST Exposure Time Calculator (ETC), Pandeia (Pontoppidan et al. 2016). The S/N calculated with Pandeia are shown as dashed lines in Fig. 5. For all stars and wavelengths we find that our calculations are in good agreement with the S/N calculated with Pandeia. For both calculations GJ 644 is just observable using G395H/F290LP. This confirms that the saturation limits of the NIRSpec HRS are also in agreement.

3.3 Transmission spectra

The top panel of Fig. 6 shows the transmission spectra of each simulated hypothetical Earth-like planet around an M dwarf. The transmission spectra are shown as the wavelength dependent effective height (see Eq. (1)). We binned the line-by-line effective height of each planet to a resolving power of 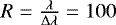R=λΔλ=100$R = \frac{\lambda}{\Delta\lambda} = 100$ over the entire wavelength range. We calculated the effective height of the Earth around the Sun for comparison. Dominant absorption features are H2O at 1.4 and 6.3 μm, CO2 at 2.8 and 4.3 μm and O3 at 9.6 μm, comparable to observed and modelled transmission spectra of the Earth (Pallé et al. 2009; Kaltenegger & Traub 2009; Vidal-Madjar et al. 2010; Bétrémieux & Kaltenegger 2013; Yan et al. 2015; Schreier et al. 2018).

We do not consider clouds and hazes when calculating the transmissivity of the atmosphere. The consideration of clouds would essentially limit the minimum effective height to the height of the cloud deck (e.g. Benneke & Seager 2013; Bétrémieux & Kaltenegger 2014; Bétrémieux & Swain 2017). For the Earth the cloud layer is low and therefore the extent of the absorption feature is affected by only a few kilometres (e.g. Schreier et al. 2018). The consideration of hazes in the atmosphere would effect the spectral appearance of the planet (see e.g. Kempton et al. 2011; Kreidberg et al. 2014). For Earth-like planets hazes affect the plantary spectra mostly at wavelengths below about 3.2 μm (see Arney et al. 2016, 2017). For hazy atmospheres the transit depth is increased between the absorption features of, for example CH4, H2O and O2 (atmospheric windows), leading to a lower separability of the individual spectral bands.

For Earth-like planets around M dwarfs the amount of H2O and CH4 in the middle atmosphere is increased by several orders of magnitude (Fig. 4). Since CH4 and H2O are strong absorbers in the near-IR, increased abundances result in a decreased transmissivity and larger effective heights at most wavelengths compared to the Earth around the Sun (see also Rauer et al. 2011). In the middle atmosphere CH4 is more abundant than H2O for Earth-like planets around M dwarfs. Hence, the spectral features at 1.1 and 1.4 μm are dominated by CH4 absorption as also shown by Barstow et al. (2016). Larger temperatures in the middle atmosphere of planets around late M dwarfs (Fig. 3) lead to an expansion of the atmosphere by more than 10 km compared to planets around early M dwarfs (Table 3). This, together with enhanced absorption of CH4 and H2O, results in an overall increased effective height for mid to late M-dwarf planets. Most spectral features of Earth-like planets around inactive M dwarfs are larger as a consequence of increased concentrations of CH4, H2O, and N2 O compared to planets around active M dwarfs. Just the spectral feature of O3 is largest for active M-dwarf planets because of the increased O2 photolysis in the UV, resulting in an enhanced O3 layer.

Most other studies have used existing planets and have applied assumed atmospheres to spectral models (Shabram et al. 2011; Barstow et al. 2015, 2016; Barstow & Irwin 2016; Morley et al. 2017). In comparison to these studies the calculated concentrations of most biosignatures and related compounds are increased owing to the consideration of the chemical response of the atmosphere to M-dwarf spectra. Hence, the effective height of the atmosphere in our study is larger at most wavelengths and the detectability of most spectral features is increased.

3.4 Planetary S/N

3.4.1 Signal-to-noise ratio with constant resolution at 10 pc

For the bottom panel of Fig. 6 we combined all available JWST NIRSpec and MIRI filter-disperser combinations to calculate the highest corresponding S/N of the planetary spectral features during one transit. The specifications of all JWST instruments used in this study can be found in Appendix A. As already discussed in Sect. 3.1.4 certain wavelength regions are not observable with low or medium resolution for bright stars due to saturation effects. Scenarios for GJ 1214, Proxima Centauri, and TRAPPIST-1 are observable with NIRSpec medium resolution spectroscopy at 10 pc below 5 μm. GJ 644 at 10 pc is only observable at wavelengths longer than 3 μm. All other M dwarfs can also be observed below 5 μm via high resolution spectroscopy. For wavelengths longer than 5 μm MIRI specifications are used to calculate the S/N. The Sun placed at 10 pc is only observable with MIRI MRS, with roughly one-third of the quantum efficiency upto 10 μm compared to MIRI LRS (Rieke et al. 2015a; Glasse et al. 2015).

An increasing stellar radius increases the S/N of the star (Fig. 5) but decreases the transit depth of the planet (Table 2). The effective height of the CO2 feature at 4.3 μm differs only by 10 km between early and late M-dwarf planets owing to similar CO2 abundances of the simulated atmospheres (see top panel of Fig. 6). The S/N of this feature is however twice as large for late-type M-dwarf planets than for early to mid M-dwarf planets due to the smaller stellar radius. Despite the high stellar signal, the GJ 644 planet has the lowest S/N owing to the exceptionally large radius of the host star. The consideration of the readout noise and the reduction of total exposure time due to the increased number of detector readouts (shorter duty cycle) has an impact on the S/N of bright targets. For GJ 644 at 10 pc half of the transit time is needed for detector readouts using the filter-disperser G395H/F290LP. For fainter targets like TRAPPIST-1 the duty cycle increases. Only 3% of the transit time is lost for TRAPPIST-1 at 10 pc due to detector readouts. Hence, the detectability of the spectral features is further improved for close mid to late-type M-dwarf planets. For late-type M-dwarf planets we expect the highest S/N compared to earlier M-dwarf planets (see e.g. de Wit & Seager 2013). The hypothetical Earth-like planet around the M5.5 star Proxima Centauri, placed at 10 pc, has a higher S/N than the planet around the M8 star TRAPPIST-1 placed at 10 pc for all spectral features at wavelength shorter than 3 μm. Comparing the theoretical radii from Reid (2005), TRAPPIST-1 has a slightly bigger radius and Proxima Centauri a smaller radius than expected forthis spectral type. The spectra of very low mass stars show strong atomic lines mainly from K I and Ti I between 1 and 1.3 μm, water vapour bands in the near-IR and CO bands at 2.3–2.4 μm (Allard et al. 2001). These bands coincide with the absorption features found for the modelled Earth-like atmospheres and decrease theS/N at these wavelengths. We note that M dwarfs later than M6 are affected by dust formation, which increases the uncertainty of the spectral models (Allard et al. 2012).

As mentioned in Sect. 3.3 we do not consider the effect of clouds and hazes on the transmission spectra. Since we use the geometric transit depth (i.e. the planetary radius without atmosphere) as reference to calculate the S/N, the increase of the effective height from additional absorption, scattering, or reflection would not influence the S/N of the spectral bands of, for example CH4 or H2O, at low wavelengths.

The atmospheres of Earth-like planets around mid to late M dwarfs have much higher S/N at most absorption features compared to early M-dwarf planets. Nevertheless, at 10 pc a single transit is not enough to detect any spectral feature using JWST with a fixed resolution of 100 due to the maximum S/N of only around 1.5. In the next section we want to investigate whether absorption bands would be detectable when taking into account the entire spectral feature.

Table 3

Height, H, and temperature, T, at 100 and at 0.1 hPa for all simulated atmospheres of Earth-like planets around M dwarfs and the Earth.

thumbnail Fig. 6

Top panel: effective height of all hypothetical Earth-like planets orbiting M dwarfs for a fixed resolving power of 100. Bottom panel: combined S/N using all high or medium resolution NIRSpec and MIRI filters up to 11 μm for all M-dwarf planets at 10 parsecs integrated over a single transit and a resolving power of 100.
thumbnail Fig. 7

Transit depth of all hypothetical Earth-like planets around their M-host stars for a fixed resolving power of 100 (coloured lines). The error bars show two sigma (standard deviation), single transit errors for selected spectral features, and selected M-dwarf planets at 10 parsecs with optimised wavelength bins. In black: calculated using high resolution JWST NIRSpec BOTS disperser and filter. In grey: calculated using NIRCam weak lens filters and high resolution NIRCam grism filters. Central wavelengths and bandwidths are calculated individually to distinguish between spectral absorption features (see Sect. 3.4.2).

3.4.2 S/N for spectral features at 10 pc

In Fig. 7 we show transmission spectra with improved detectability of each spectral features by calculating the bandwidth and central wavelength of each spectral feature. We maximise the lower limit of the error bar (lower value at the two sigma deviation) by shifting the central wavelength and increasing the bandwidth until the optimal value is found. Increasing the bandwidth decreases the noise contamination. But if the selected band spans over a wider wavelength range than the absorption feature, the mean effective height decreases. We note that for a nonsymmetric-Gaussian distribution of the absorption feature, the central wavelength is not necessarily the wavelength of the peak absorption. The selected bandwidth and central wavelength also depend on the overall S/N. For low S/N it is favourable to integrate over a broad wavelength range, including the wings of the spectral feature to decrease the noise contamination. If the noise is low, the bandwidth can be narrow to maximise the transit depth of the absorption feature. To detect a spectral feature it needs to be separated from an atmospheric window with a low effective height. We find the bandwidth and central wavelength of atmospheric windows by minimising the upper limit of the error bar (upper value at the two sigma deviation) between two absorption features.

Figure 7 shows the detectability of the spectral features using NIRSpec in black and NIRCam in grey. For NIRCam we use five fixed filters in weak lens mode between 1.3 and 2.2 μm. We omit the narrow-band filters owing to the very low resulting S/N. At longer wavelengths we use the NIRCam grism mode to calculate the error bars. The advantage of using NIRCam would be that observations of one weak lens filter at short wavelengths could be performed simultaneously with one filter-grism at longer wavelengths.

No feature would be distinguishable from an atmospheric window with a single transit for early M-dwarf planets at 10 pc except for the planet around GJ 581, which has a small radius. For mid to late M dwarfs several absorption features could be distinguishable from an atmospheric window within two sigmas with just a single transit. These are CH4/H2O at 1.15 and 1.4 μm; the CH4 at 1.8, 2.3 and 3.4 μm; and the H2O/CO2 at 2.7 μm. The CO2 feature at 4.3 μm could be separated from one of the atmospheric windows below 1.7 μm if simultaneous observations of both wavelength ranges were to be provided. Barstow et al. (2016) showed that just a few transits would be necessary to detect CO2 at 4.3 μm for an Earth around an M 5 star at 10 pc. For an Earth the detection of the H2O and CO2 feature at 2.7 μm would require more than ten transits due to the lower abundances of H2O in the Earth’s middle atmosphere compared to our calculated amounts.

Figure 8 shows that the planets around the later M dwarfs with a distinguishable CH4 feature at 3.4 μm reach an S/N of at least 3. For real observations we expect additional sources of variability like stellar spots (Pont et al. 2008; Zellem et al. 2017; Rackham et al. 2018) and exozodiacal dust (Roberge et al. 2012; Ertel et al. 2018). For this study we consider an S/N of 5 to be sufficient to detect a spectral feature.

thumbnail Fig. 8

Signal-to-noise ratio of the CH4 feauture at 3.4 μm for a single transit of each M-dwarf planet at 10 pc.
thumbnail Fig. 9

Number of transits needed to reach an S/N of 5 for selected spectral features of M-dwarf planets and the Earth-Sun case and different distances to the star. Central wavelength and bandwidths are shown in Table 4. The suddenreductions of the needed observation time happen when there are changes in the duty cycle and when a filter-disperser combination with a higher throughput can be used.

3.4.3 Detectability of spectral features up to 100 pc

The optimal central wavelengths and bandwidths to reach an S/N of 5 are independent from the distance to the star and differ just by a few nanometres between the M-dwarf planets. Table 4 shows the mean central wavelengths, bandwidths, and resolving power for each spectral feature.

In Fig. 9 we show the number of transits necessary to reach an S/N of 5 for the selected spectral features at the given central wavelengths and resolving power. The saturation limit is reached if the minimum integration time is equal to the frame time. We do not consider partial saturation as proposed by Batalha et al. (2018). The saturation limit to observe the entire wavelength range is about 6.3 at J band. Early M dwarfs reach this limit at around 6–10 pc. Mid- to late-type M dwarfs are fully observable at 1–3 pc. A G2 star like the Sun is observable at short wavelengths only beyond a distance of about 30 pc. The O3 feature at 9.6 μm and the H2O feature at 6.3 μm can be observed at shorter distances using MIRI MRS. We note that the sudden reductions of the needed observation time are due to changes in the duty cycle (more frames per integration) as shown by Nielsen et al. (2016) and changes of the considered filter-disperser combination. We always plot the lowest number of transits needed for detection in cases in which a feature can be observed with several filter-disperser combinations.

Because of the high saturation limit and lower S/N (Fig. 8), none of the spectral features of Earth-like planets around early M dwarfs would be observable with a single transit. For Earth-like planets around late-type M dwarfs lying closer than 4 pc, all selected spectral features except O3 are detectable with a single transit. By co-adding 10 transits, CH4 is detectablebetween the saturation limit and 10 pc for most M-dwarf planets. Rauer et al. (2011) found that at a distance of 4 pc the CH4 absorption band of an Earth-like atmosphere around an M5 star would reach an S/N of 3 using JWST observations. Owing to the consideration of a broader bandwidth and by taking into account realistic throughputs, our new analysis shows an improved detectability of CH4. For the planet around the M4.5 star, GJ 1214, with a comparable atmosphere to the Earth-like planet around the M5 star modelled by Rauer et al. (2011), we find that even at a larger distance of 7 pc, a single transit is sufficient to reach an S/N of 5.

The O3 feature at 9.6 μm is more difficult to detect because of the low stellar signal at longer wavelengths and the low abundances of O3 of Earth-like planets around inactive M dwarfs. The planet around the active M-dwarf AD Leo has a similar O3 column as the present Earth. If AD Leo were to have a transiting Earth-like planet in the HZ, around 50 transits or more than three years of total observing period would be required to detect O3 with JWST. This is in agreement with the results of Rauer et al. (2011). Only 10 transits are necessary to detect O3 at 4 pc for the hypothetical Earth-like planets around the later type M-dwarfs Proxima Centauri and TRAPPIST-1, which have a lower O3 concentration than the planet around AD Leo.

All modelled atmospheres of planets around different M dwarfs show an increased amount of H2O in the middle atmosphere compared to the Earth–Sun case (Fig. 4). The H2O feature at 6.3 μm is detectable for mid to late M-dwarf planets at 10 pc by co-adding 10 transits. We find that 20 transits are necessary to detect H2O in the atmosphere of the hypothetical Earth-like planet around the M 2.5 star, GJ 581, at 12 pc (J-band magnitude 8). This is comparable to results from Kopparapu et al. (2017), who showed that a detection of a 10 ppm H2O feature observing an M 3 star would require around 30 transits at J-band magnitude 8.

Previous studies investigated the potential detectability of the TRAPPIST-1 planets using predefined atmospheres (see e.g. Barstow & Irwin 2016; Morley et al. 2017; Kopparapu et al. 2017; Krissansen-Totton et al. 2018). We calculate the detectability of an Earth-like planet around TRAPPIST-1 considering the effect of the stellar spectrum on the atmosphere of the planet. At least 9 transits are required to detect CO2 of the Earth-like planet around TRAPPIST-1 at 12.1 pc. Morley et al. (2017) found that a 1 bar Venus-like atmosphere of TRAPPIST-1e (TRAPPIST-1f) can be characterised by co-adding 4 (17) transits. The O3 feature at longer wavelengths requires the observation of more transits for a detection. Barstow & Irwin (2016) concluded that 30 transits are needed to detect O3 at Earth abundances for TRAPPIST-1c and TRAPPIST-1d. Our model calculation shows that the O3 levels wouldbe reduced for an Earth-like planet around TRAPPIST-1. Furthermore, at longer wavelengths there is a significant contribution of zodiacal noise for faint targets. Hence, we find that 170 transits are needed to detect O3, which is much more than found by Barstow & Irwin (2016), who did not consider zodiacal noise. The time span over which the Earth-like planet in the HZ around TRAPPIST-1 needs to be observed for 170 transits would be more than two years, assuming white noise only and that each transit would improve the S/N perfectly. Hence, it would be difficult to detect O3 with JWST in the atmosphere around an Earth-like planet by transmission spectroscopy, even for a close late-type M-dwarf like TRAPPIST-1. The detectabilityof CH4, H2O, and CO2 is improved for M-dwarf planets compared to the Earth because of the larger concentrations of these species in their atmospheres. Up to a distance of about 10 pc CH4, H2O, and CO2 would be detectable in the atmosphere of Earth-like planets orbiting mid- to late-type M-dwarf planets with 10 transits. In Sect. 3.4.4 we show for which potential TESS findings within 15 pc it would be possible to characterise the Earth-like planetary atmospheres.

Table 4

Mean central wavelengths, λc, bandwidths, Δλ and resolving power for selected spectral features and an S/N of 5.

3.4.4 Detectability of spectral features of hypothetical TESS findings

The TRAPPIST-1 planets will be among the main future targets for atmospheric characterisation. The TESS satellite will find more transiting exoplanets in the solar neighbourhood (Barclay et al. 2018). We used the TESS catalogue of cool dwarf targets (Muirhead et al. 2018) to calculate the S/N of potential TESS findings. From this catalogue we selected all M dwarfs within 15 pc. The distances themselves are not included in the catalogue. Hence, we took the distance of the M dwarfs in the northern sky from Dittmann et al. (2016) and in the southern sky from Winters et al. (2014). We complemented the distances with the data from the CARMENES input catalogue (Cortés-Contreras et al. 2017) and with data from Lépine & Gaidos (2011). For values which are present in two or more catalogues, we used the most recent reference. For consistency we used the values for the M dwarfs shown in Table 1. The spectra until 5.5 μm were taken from the PHOENIX model7 (Husser et al. 2013). At wavelengths longer than 5.5 μm we extendedthe spectra with NextGen (Hauschildt et al. 1999). Since NextGen and PHOENIX have a fixed grid for effective temperature, log g and [Fe/H], we took the spectra assuming a log g of 5 cgs and a [Fe/H] of 0.0 dex and linear interpolate the temperature grid to the corresponding value.

Figure 10 shows which hypothetical Earth-like planets around M dwarfs within 15 pc would have a detectable feature for asingle transit observation using JWST. To calculate the S/N of each spectral feature we used the modelled atmosphere of the planets around the M dwarfs with the most similar effective temperature (see Table 1). For 36 of the 915 hypotheticalM-dwarf planets at least one spectral feature would however be detectable with a single transit observation. The saturation of the NIRSpec HRS limits the detectability of the planetary atmosphere to stellar effective temperatures of lower than about 3300 K and distances larger than about 8 pc. Bright targets can only be observed at longer wavelengths with MIRI. Proxima Centauri and Barnard’s star, which are the two closest M dwarfs, are too bright for NIRSpec HRS. The H2O feature at 6.3 μm of a hypotheticaltransiting Earth-like planet would be detectable using MIRI. For the planets around late-type M dwarfs Wolf 359 and DX Cancri, CO2, H2O, and CH4 would be detectable with a single transit. Because of the large CH4 abundances, the detection of CH4 in the atmosphere of a hypothetical Earth-like planet around mid- to late-type M dwarfs would be possible up to about 10 pc. Three of the 36 M dwarfs have confirmed planets found by radial velocity measurements (Proxima Centauri, Ross 128, and YZ Ceti). Grey dots show the S/N of the strongest spectral feature. We find 267 hypothetical planets with an S/N of at least 3 for one or more spectral features, including two host stars with confirmed transiting planets (TRAPPIST-1 and GJ 1132) and two early M dwarfs, GJ 581 and Ross 605. For these planets, at least one spectral feature could be detected by co-adding 5 transits.

Table 5 shows the number of transits required to detect H2O, CH4, CO2, and O3 assuming an Earth-like planet around the 11 closest M dwarfs with a confirmed transiting planet8. O3 would not be detectable with JWST for any of the synthetic planets owing to the long observation time required. The detection of CH4 would be possible with JWST in a reasonable amount of observation time for an Earth-like planet in the HZ around GJ 1132, TRAPPIST-1, GJ 1214, and LHS 1140.

thumbnail Fig. 10

Detectability of hypothetical nearby Earth-like planets around M dwarfs with a single transit. Coloured dots show planets with an S/N of at least 5 for the corresponding spectral features (H2O: blue, CH4: green and CO2: red). Morethan one colour means that multiple spectral features can be detected with a single transit. The sizes of the grey dots indicate the highest S/N of all spectral features. The numbers inside the coloured dots correspondto the following host stars: 1: Proxima Centauri, 2: Barnard’s star, 3: Wolf 359, 4: Ross 154, 5: Ross 248, 6: Ross 128, 7: GJ 15 B, 8: DX Cancri, 9: GJ 1061, 10: YZ Ceti, 11: Teegarden’s star, 12: Wolf 424, 13: L 1159-16, 14: GJ 1245 B, 15: GJ 1245 A, 16: GJ 412 B, 17: LHS 2090, 18: GJ 1116, 19: LHS 1723, 20: GJ 1005, 21: L 43-72, 22: GJ 3737, 23: GL Virginis, 24: GJ 1128, 25: LSPM J2146+3813, 26: Ross 619, 27: G 161-7, 28: GJ 4053, 29: G 141-36, 30: SCR J0740-4257, 31: GJ 1286, 32: LHS 1070, 33: SCR J0838-5855, 34: NLTT 40406, 35: GJ 3146, 36: LSPM J0539+4038.
Table 5

Number of transits, NTr, required to detect H2O, CH4, CO2, and O3 with JWST for an Earth-like planet in the HZ of the corresponding host star.

4 Summary and conclusions

We use a range of stellar spectra to investigate the influence of the SED on the atmosphere of Earth-like planets in the HZ around M dwarfs and their detectability by JWST via transmission spectroscopy. The simulations of M-dwarf planets show an increase of CH4, H2O, and CO2 in the middle atmosphere compared to the Earth around the Sun. The abundances of O3 increase for planets around active M dwarfs and decrease for planets around inactive M dwarfs. The results of the atmosphere simulations are in agreement with previous model studies (Segura et al. 2005; Rauer et al. 2011; Grenfell et al. 2013, 2014; Rugheimer et al. 2015). For Earth-like planets around early- to mid-type M dwarfs the stellar insolation needs to be downscaled to reproduce the surface temperature of the Earth (see also Segura et al. 2005). For late M-dwarf planets like the hypothetical Earth-like planet around TRAPPIST-1 we find that the chemistry feedback requires an upscaling of the stellar insolation to reach the surface temperature of the Earths.

One of the main goals of this study was to investigate the detectability of spectral features of the simulated atmospheres. We use a sophisticated S/N model including readout noise contribution and consideration of saturation limits and the duty cycle for each target. Although the model is applicable to any current or future telescope, we limit our analysis to transmission spectroscopy with JWST. We verify the results of our S/N model with the JWST ETC, Pandeia (Pontoppidan et al. 2016). We calculate the optimal central wavelengths and bandwidths to detect main spectral features of an Earth-like planet.

The detectability of atmospheric features of Earth-like planet around mid to late M dwarfs is much higher than for planets around early M dwarfs. The saturation limits of JWST allow the observation of almost all mid- to late-type M dwarfs at low wavelengths in the solar neighbourhood. For an early-type M dwarf at 10 pc, the integration time due to detector readouts can be reduced up to 50%. In comparison, for an observation of TRAPPIST-1 the detector readout time is just a few percent of the full observation time when using NIRSpec MRS or HRS. Another advantage of mid to late M-dwarf planets are the increased abundances of biosignature related compounds like CH4 and H2O and the extended atmosphere due to warmer temperatures from the upper troposphere to the mesosphere. This allows a detection of CH4 with only two transits and H2O and CO2 with less than ten transits up to a distance of about 10 pc.

We find that H2O, CO2, and CH4 could be detected in the atmosphere of a hypothetical Earth-like planet around Wolf 359 and DX Cancri with only a single transit. Within 15 pc there are 267 M dwarfs for which detection of at least one spectral feature would be possible by co-adding just a few transits. For hypothetical Earth-like planets around GJ 1132, TRAPPIST-1, GJ 1214, and LHS 1140 a detection of CH4 would require less than ten transits. The predictions of Barclay et al. (2018) have shown that terrestrial planets around mid to late M dwarfs within 15 pc are expected to be found with TESS. In this study we conclude that atmospheric features of these planets could be partly characterised with JWST.

Acknowledgement

This research was supported by DFG projects RA-714/7-1, GO 2610/1-1 and SCHR 1125/3-1. We acknowledge the support of the DFG priority programme SPP 1992 “Exploring the Diversity of Extrasolar Planets (GO 2610/2-1)”. We thank the anonymous referee for the helpful and constructive comments.

Appendix A JWST configurations

Currently operating telescopes are likely unable to detect spectral features of an Earth-like planet within a reasonable amount of observation time. This paper aims to investigate whether JWST will be able to detect biosignatures and related compounds within a few transits using transmission spectroscopy. The JWST will provide a telescope aperture of 6.5 m diameter and a collecting area of 25.4 m2 (Contos et al. 2006). For our science case we chose the observing modes of NIRCam, NIRSpec, and MIRI, which are applicable to a single bright object.

A.1 NIRSpec

The Bright Object Time Series (BOTS) mode is designed for time-resolved exoplanet transit spectroscopy of bright targets (Ferruit et al. 2012, 2014). The NIRSpec BOTS uses a fixed slit (FS) mode with the S1600A1 aperture (1.6 × 1.6 arcsec slit; Beichman et al. 2014; Birkmann 2016). For the NIRSpec modes there are three sets of disperser and filter combinations available. For low resolution spectroscopy the PRISM with a resolving power of ~ 100 covers the full NIRSpec range of 0.6–5.3 μm. Medium and high resolution spectroscopy provides four different disperser-filter combinations with a mean resolving power of ~ 1000 and ~ 2700 respectively (medium resolution: G140M/F070LP, G140M/F100LP, G235M/F170LP, G395M/F290LP; high resolution: G140H/F070LP, G140H/F100LP, G235H/F170LP, G395H/F290LP). For high resolution observations a physical gap between the detectors results in gaps in the wavelength coverage. A subarray of 512 × 32 pixel (SUB512) is used for the PRISM. For medium and high resolutions a subarray of 2024 × 32 pixel (SUB2048) is used in order to cover the full spectrum.

To increase the brightness limits it is possible to observe only half of the spectrum (SUB1024A and SUB1024B). Using SUB2048 M dwarfs have a J-band brightness limit of 6.4 ± 0.5 for the G140H and G235H disperser and a limit of 5.8 ± 0.5 for the G395H disperser (Nielsen et al. 2016). In this study we also consider the 1024 × 32 pixel subarrays, when the brightness limit for SUB2048 is reached.

Each subarray has a different single frame time, which is the same as the readout time. The frame time for SUB512 is 0.226 s, for SUB1024A and SUB1024B 0.451 s and for SUB2024 0.902 s. It is recommended to use as many frames as possible per integration because the S/N does not simply scale with the number of frames owing to changes in the detector duty cycle (Rauscher et al. 2007; Nielsen et al. 2016). The duty cycle increases with increasing number of frames. We use the frame time as a minimum exposure time and do not consider a partial saturation strategy as proposed by Batalha et al. (2018). If one pixel is saturated in a shorter time than the single frame time, the target is considered to be not observable for this filter-disperser combination.

For detailed information about NIRSpec we refer to Birkmann et al. (2016) and the on-line documentation9. The wavelength ranges, resolving powers, and throughputs of each filter-disperser combination can be found in the on-line documentation, in Birkmann (2016) and in Beichman et al. (2014). Other relevant information such as dark current (0.0092 e− s pixel−1), pixel scale (0.1 arcsec pixel−1), readout noise (6.6 e−), and full well capacity (55 100 e−) are taken from the on-line documentation. The dispersion curves and PSFs are described in Perrin et al. (2012) and were downloaded from the documentation page.

A.2 NIRCam

The NIRCam grism time-series observations allows for simultaneous observation of short wavelengths (1.3–2.3 μm) and longer wavelengths (2.4–5.0 μm; Beichman et al. 2014). To observe bright targets at short wavelengths, a weak lens is used to defocus incoming light. The expected saturation limit change for the strongest wave of defocus 8 (WLP8) in a subarray of 160 × 160 pixel is 6.5 magnitudes (Greene et al. 2010). For the medium filter centred at 1.4 μm this means a saturation limit of ~4 at K band for a G2V star, assuming 80% of the full well capacity (105 750 e−). The readout time and the minimum exposure time is 0.27864 s. We use all medium (R ≈ 10) and wide (R ≈ 4) filters available for the weak lens mode for our S/N calculations (F140M, F150W, F182M, F210M, F200W). Further information about the NIRCam weak lens mode such as dark current (0.0019 e− s pixel−1), pixel scale (0.031 arcsec pixel−1), readout noise (16.2 e−), and full well capacity (105 750 e−) are given in Greene et al. (2010) and the NIRCam documentation10.

At longer wavelengths a grism is used for slitless spectroscopy between 2.5 and 5.0 μm. The wide filters (F277W, F322W2, F356W, F444W) have a mean resolving power of ~1600 and a dispersion of 1 nm pixel−1 (Greene et al. 2016, 2017). We use the smallest grism subarray of 64 × 2048 pixel and a frame and readout time of 0.34061 s. For an M2V star the brightness limit at K band is ~4. Information on the wavelength dependent filter throughput and resolving power can be found in Greene et al. (2017). The PSFs were downloaded from11 Perrin et al. (2012). Other specifications like dark current (0.027 e− s pixel−1), pixel scale (0.063 arcsec pixel−1), readout noise (13.5 e−), and full well capacity (83 300 e−) are taken from the online documentation.

A.3 MIRI

The JWST Mid-Infrared Instrument (MIRI) provides medium resolution spectroscopy (MRS) from 4.9 to 29.8 μm and low resolution slitted and slitless spectroscopy (LRS) from 5 to 12 μm (Wright et al. 2015; Rieke et al. 2015b). The MRS mode has four channels with three sub-bands each. The resolving power for short wavelengths is 3710 and decreases for long wavelengths to 1330 (Wells et al. 2015). The brightness limits for MIRI MRS are around magnitude 4 at K band for late-type host stars for a 2 frame integration (Beichman et al. 2014; Glasse et al. 2015). For MRS there is no subarray available. The full size is 1024 × 1032 pixels, which results in a frame time and readout time of 2.775 s.

The LRS slitless mode provides the possibility to read out a subarray of 416 × 72 pixels. This decreases the frame and readout time to 0.159 s. Hence, despite the much lower resolving power of ~100 compared to MRS (Kendrew et al. 2015), the brightness limit is just 2 magnitudes fainter for the K band (magnitude 6 at K band; Beichman et al. 2014; Glasse et al. 2015). For targets brighter than magnitude 6 at K band, we always use LRS owing to the better throughput of around a factor of 3 up to 10 μm compared to MRS (Rieke et al. 2015a; Glasse et al. 2015,12). We took other specifications like dark current (0.2 e− s pixel−1), pixel scale (0.11 arcsec pixel−1), readout noise (14 e−), and full well capacity (250 000 e−) from the online documentation13 and from references therein.

References

  1. Allard, F., Hauschildt, P. H., Alexander, D. R., Tamanai, A., & Schweitzer, A. 2001, ApJ, 556, 357 [NASA ADS] [CrossRef] [Google Scholar]
  2. Allard, F., Homeier, D., & Freytag, B. 2012, Phil. Trans. R. Soc. A, 370, 2765 [CrossRef] [PubMed] [Google Scholar]
  3. Anderson, G., Clough, S., Kneizys, F., Chetwynd, J., & Shettle, E. 1986, AFGL Atmospheric Constituent Profiles (0–120 km), Tech. Rep. TR-86-0110, AFGL [Google Scholar]
  4. Anglada-Escudé, G., Rojas-Ayala, B., Boss, A. P., Weinberger, A. J., & Lloyd, J. P. 2013a, A&A, 551, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Anglada-Escudé, G., Tuomi, M., Gerlach, E., et al. 2013b, A&A, 556, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Arney, G., Domagal-Goldman, S. D., Meadows, V. S., et al. 2016, Astrobiology, 16, 873 [NASA ADS] [CrossRef] [Google Scholar]
  7. Arney, G. N., Meadows, V. S., Domagal-Goldman, S. D., et al. 2017, ApJ, 836, 49 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bailey, J., Butler, R. P., Tinney, C. G., et al. 2008, ApJ, 690, 743 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barclay, T., Pepper, J., & Quintana, E. V. 2018, ApJS, 239, 2 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barstow, J. K., & Irwin, P. G. 2016, MNRAS, 461, L92 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barstow, J. K., Aigrain, S., Irwin, P. G., Kendrew, S., & Fletcher, L. N. 2015, MNRAS, 448, 2546 [NASA ADS] [CrossRef] [Google Scholar]
  12. Barstow, J. K., Aigrain, S., Irwin, P. G., Kendrew, S., & Fletcher, L. N. 2016, MNRAS, 458, 2657 [NASA ADS] [CrossRef] [Google Scholar]
  13. Batalha, N. E., Lewis, N. K., Line, M. R., Valenti, J., & Stevenson, K. 2018, ApJ, 856, L34 [NASA ADS] [CrossRef] [Google Scholar]
  14. Beaulieu, J.-P., Tinetti, G., Kipping, D., et al. 2011, ApJ, 731, 16 [NASA ADS] [CrossRef] [Google Scholar]
  15. Beichman, C., Benneke, B., Knutson, H., et al. 2014, PASP, 126, 1134 [NASA ADS] [CrossRef] [Google Scholar]
  16. Benneke, B., & Seager, S. 2013, ApJ, 778, 153 [NASA ADS] [CrossRef] [Google Scholar]
  17. Berta, Z. K., Charbonneau, D., Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
  18. Birkmann, S. 2016, ESAC JWST “On Your Mark” Workshop, 1 [Google Scholar]
  19. Birkmann, S. M., Ferruit, P., Rawle, T., et al. 2016, in Space Telescopes and Instrumentation 2016: Optical, Infrared, and Millimeter Wave, SPIE, 9904, 99040B [Google Scholar]
  20. Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Boyajian, T. S., Von Braun, K., Van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
  22. Brasseur, G. P., & Solomon, S. 2006, Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere (Berlin: Springer Science & Business Media), 32 [Google Scholar]
  23. Buccino, A. P., Lemarchand, G. A., & Mauas, P. J. 2007, Icarus, 192, 582 [NASA ADS] [CrossRef] [Google Scholar]
  24. Butler, R. P., Vogt, S. S., Marcy, G. W., et al. 2004, ApJ, 617, 580 [NASA ADS] [CrossRef] [Google Scholar]
  25. Bétrémieux, Y., & Kaltenegger, L. 2013, ApJ, 772, L31 [NASA ADS] [CrossRef] [Google Scholar]
  26. Bétrémieux, Y., & Kaltenegger, L. 2014, ApJ, 791, 7 [NASA ADS] [CrossRef] [Google Scholar]
  27. Bétrémieux, Y., & Swain, M. R. 2017, MNRAS, 467, 2834 [NASA ADS] [CrossRef] [Google Scholar]
  28. Charnay, B., Meadows, V., Misra, A., Leconte, J., & Arney, G. 2015, ApJ, 813, L1 [NASA ADS] [CrossRef] [Google Scholar]
  29. Clough, S., Kneizys, F., & Davies, R. 1989, Atmos. Res., 23, 229 [NASA ADS] [CrossRef] [Google Scholar]
  30. Contos, A. R., Acton, D. S., Atcheson, P. D., et al. 2006, in Space Telescopes and Instrumentation I: Optical, Infrared, and Millimeter, SPIE, 6265, 62650X [NASA ADS] [Google Scholar]
  31. Cortés-Contreras, M., Béjar, V., Caballero, J., et al. 2017, A&A, 597, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Deming, D., Seager, S., Winn, J., et al. 2009, PASP, 121, 952 [NASA ADS] [CrossRef] [Google Scholar]
  33. de Wit, J., & Seager, S. 2013, Science, 342, 1473 [NASA ADS] [CrossRef] [Google Scholar]
  34. de Wit, J., Wakeford, H. R., Gillon, M., et al. 2016, Nature, 537, 69 [NASA ADS] [CrossRef] [Google Scholar]
  35. Dittmann, J. A., Irwin, J. M., Charbonneau, D., & Newton, E. R. 2016, ApJ, 818, 153 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ertel, S., Kennedy, G., Defrère, D., et al. 2018, Proc. SPIE, 10698, 106981V [Google Scholar]
  37. Ferruit, P., Bagnasco, G., Barho, R., et al. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, SPIE, 8442, 84422O [Google Scholar]
  38. Ferruit, P., Birkmann, S., Böker, T., et al. 2014, in Space Telescopes and Instrumentation 2014: Optical, Infrared, and Millimeter Wave, SPIE, 9143, 91430A [Google Scholar]
  39. France, K., Froning, C. S., Linsky, J. L., et al. 2013, ApJ, 763, 149 [NASA ADS] [CrossRef] [Google Scholar]
  40. France, K., Loyd, R. O. P., Youngblood, A., et al. 2016, ApJ, 820, 89 [NASA ADS] [CrossRef] [Google Scholar]
  41. Froning, C. S., France, K., Parke Loyd, R., et al. 2018, AAS Meeting, 231 [Google Scholar]
  42. Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
  43. Gautier III, T. N., Rieke, G., Stansberry, J., et al. 2007, ApJ, 667, 527 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gebauer, S., Grenfell, J., Stock, J. W., et al. 2017, Astrobiology, 17, 27 [NASA ADS] [CrossRef] [Google Scholar]
  45. Gebauer, S., Grenfell, J., Lehmann, R., & Rauer, H. 2018a, Astrobiology, 18, 856 [NASA ADS] [CrossRef] [Google Scholar]
  46. Gebauer, S., Grenfell, J. L., Lehmann, R., & Rauer, H. 2018b, ACS Earth and Space Chem., 2, 1112 [Google Scholar]
  47. Giampapa, M. S., Rosner, R., Kashyap, V., et al. 1996, ApJ, 463, 707 [NASA ADS] [CrossRef] [Google Scholar]
  48. Gillon, M., Triaud, A. H., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  49. Gilmozzi, R., & Spyromilio, J. 2007, The Messenger, 127, 3 [NASA ADS] [Google Scholar]
  50. Glasse, A., Rieke, G., Bauwens, E., et al. 2015, PASP, 127, 686 [NASA ADS] [CrossRef] [Google Scholar]
  51. Godolt, M., Grenfell, J., Hamann-Reinus, A., et al. 2015, Planet. Space Sci., 111, 62 [Google Scholar]
  52. Godolt, M., Grenfell, J., Kitzmann, D., et al. 2016, A&A, 592, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Gordon, I., Rothman, L., Hill, C., et al. 2017, J. Quant. Spectr. Rad. Transf., 203, 3 [Google Scholar]
  54. Greene, T., Beichman, C., Gully-Santiago, M., et al. 2010, in Space Telescopes and Instrumentation 2010: Optical, Infrared, and Millimeter Wave, SPIE, 7731, 77310C [Google Scholar]
  55. Greene, T. P., Chu, L., Egami, E., et al. 2016, in Space Telescopes and Instrumentation 2016: Optical, Infrared, and Millimeter Wave, SPIE, 9904, 99040E [Google Scholar]
  56. Greene, T. P., Kelly, D. M., Stansberry, J., et al. 2017, J. Astron. Telesc. Instrum. Syst., 3, 035001 [NASA ADS] [CrossRef] [Google Scholar]
  57. Grenfell, J. L., Stracke, B., von Paris, P., et al. 2007, Planet. Space Sci., 55, 661 [NASA ADS] [CrossRef] [Google Scholar]
  58. Grenfell, J. L., Gebauer, S., von Paris, P., et al. 2011, Icarus, 211, 81 [NASA ADS] [CrossRef] [Google Scholar]
  59. Grenfell, J., Gebauer, S., Godolt, M., et al. 2013, Astrobiology, 13, 415 [NASA ADS] [CrossRef] [Google Scholar]
  60. Grenfell, J. L., Gebauer, S., Paris, P. v., Godolt, M., & Rauer, H. 2014, Planet. Space Sci., 98, 66 [Google Scholar]
  61. Grießmeier, J.-M., Stadelmann, A., Motschmann, U., et al. 2005, Astrobiology, 5, 587 [NASA ADS] [CrossRef] [Google Scholar]
  62. Gueymard, C. A. 2004, Sol. Energy, 76, 423 [NASA ADS] [CrossRef] [Google Scholar]
  63. Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
  64. Hedelt, P., von Paris, P., Godolt, M., et al. 2013, A&A, 553, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Hu, Y., & Yang, J. 2014, Proc. Natl. Acad. Sci., 111, 629 [Google Scholar]
  66. Huestis, D. L., & Berkowitz, J. 2011, Adv. Geosci. Planet. Sci. 25, 229 [Google Scholar]
  67. Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Joshi, M. 2003, Astrobiology, 3, 415 [NASA ADS] [CrossRef] [Google Scholar]
  69. Joshi, M., Haberle, R., & Reynolds, R. 1997, Icarus, 129, 450 [NASA ADS] [CrossRef] [Google Scholar]
  70. Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
  71. Kasting, J. F., Pollack, J. B., & Crisp, D. 1984, J. Atmos. Chem., 1, 403 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  72. Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  73. Keles, E., Grenfell, J. L., Godolt, M., Stracke, B., & Rauer, H. 2018, Astrobiology, 18, 116 [NASA ADS] [CrossRef] [Google Scholar]
  74. Kempton, E. M.-R., Zahnle, K., & Fortney, J. J. 2011, ApJ, 745, 3 [NASA ADS] [CrossRef] [Google Scholar]
  75. Kendrew, S., Scheithauer, S., Bouchet, P., et al. 2015, PASP, 127, 623 [NASA ADS] [CrossRef] [Google Scholar]
  76. Kitzmann, D., Patzer, A., von Paris, P., et al. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Kopparapu, R. K. 2013, ApJ, 767, L8 [NASA ADS] [CrossRef] [Google Scholar]
  78. Kopparapu, R. K., Wolf, E. T., Arney, G., et al. 2017, ApJ, 845, 5 [NASA ADS] [CrossRef] [Google Scholar]
  79. Kraus, A. L., Tucker, R. A., Thompson, M. I., Craine, E. R., & Hillenbrand, L. A. 2011, ApJ, 728, 48 [NASA ADS] [CrossRef] [Google Scholar]
  80. Kreidberg, L., & Loeb, A. 2016, ApJ, 832, L12 [NASA ADS] [CrossRef] [Google Scholar]
  81. Kreidberg, L., Bean, J. L., Désert, J.-M., et al. 2014, Nature, 505, 69 [NASA ADS] [CrossRef] [Google Scholar]
  82. Krissansen-Totton, J., Garland, R., Irwin, P., & Catling, D. C. 2018, AJ, 156, 114 [NASA ADS] [CrossRef] [Google Scholar]
  83. Leconte, J., Forget, F., Charnay, B., Wordsworth, R., & Pottier, A. 2013, Nature, 504, 268 [NASA ADS] [CrossRef] [Google Scholar]
  84. Leitzinger, M., Odert, P., Hanslmeier, A., et al. 2010, CEAB, 34, 123 [NASA ADS] [Google Scholar]
  85. Lépine, S., & Gaidos, E. 2011, AJ, 142, 138 [NASA ADS] [CrossRef] [Google Scholar]
  86. Lewis, N. K., Showman, A. P., Fortney, J. J., et al. 2010, ApJ, 720, 344 [NASA ADS] [CrossRef] [Google Scholar]
  87. Loyd, R. O. P., France, K., Youngblood, A., et al. 2016, ApJ, 824, 102 [NASA ADS] [CrossRef] [Google Scholar]
  88. Luger, R., & Barnes, R. 2015, Astrobiology, 15, 119 [NASA ADS] [CrossRef] [Google Scholar]
  89. Lurie, J. C., Henry, T. J., Jao, W.-C., et al. 2014, AJ, 148, 91 [NASA ADS] [CrossRef] [Google Scholar]
  90. Manabe, S., & Wetherald, R. T. 1967, J. Atmos. Sci., 24, 241 [Google Scholar]
  91. Marconi, A., Di Marcantonio, P., D’Odorico, V., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, SPIE, 9908, 990823 [Google Scholar]
  92. Marcq, E., Belyaev, D., Montmessin, F., et al. 2011, Icarus, 211, 58 [NASA ADS] [CrossRef] [Google Scholar]
  93. Meadows, V. S., Arney, G. N., Schwieterman, E. W., et al. 2018, Astrobiology, 18, 133 [NASA ADS] [CrossRef] [Google Scholar]
  94. Menou, K. 2011, ApJ, 744, L16 [NASA ADS] [CrossRef] [Google Scholar]
  95. Morley, C. V., Kreidberg, L., Rustamkulov, Z., Robinson, T., & Fortney, J. J. 2017, ApJ, 850, 121 [NASA ADS] [CrossRef] [Google Scholar]
  96. Muirhead, P. S., Dressing, C. D., Mann, A. W., et al. 2018, AJ, 155, 180 [NASA ADS] [CrossRef] [Google Scholar]
  97. Murphy, W. F. 1977, J. Chem. Phys., 67, 5877 [NASA ADS] [CrossRef] [Google Scholar]
  98. Murtagh, D. 1988, Planet. Space Sci., 36, 819 [NASA ADS] [CrossRef] [Google Scholar]
  99. Neves, V., Bonfils, X., Santos, N. C., et al. 2014, A&A, 568, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  100. Nielsen, L. D., Ferruit, P., Giardino, G., et al. 2016, in Space Telescopes and Instrumentation 2016: Optical, Infrared, and Millimeter Wave, SPIE, 9904 99043O [Google Scholar]
  101. O’Malley-James, J. T., & Kaltenegger, L. 2017, MNRAS, 469, L26 [NASA ADS] [CrossRef] [Google Scholar]
  102. Pachauri, R., Meyer, L., & IPCC, 2014, Climate Change 2014: Synthesis Report.Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change [Google Scholar]
  103. Pallé, E., Osorio, M. R. Z., Barrena, R., Montañés-Rodríguez, P., & Martín, E. L. 2009, Nature, 459, 814 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  104. Pavlov, A. A., & Kasting, J. 2002, Astrobiology, 2, 27 [NASA ADS] [CrossRef] [Google Scholar]
  105. Perrin, M. D., Soummer, R., Elliott, E. M., Lallo, M. D., & Sivaramakrishnan, A. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, SPIE, 8442, 84423D [Google Scholar]
  106. Pettersen, B. R., & Coleman, L. A. 1981, ApJ, 251, 571 [NASA ADS] [CrossRef] [Google Scholar]
  107. Pont, F., Knutson, H., Gilliland, R., Moutou, C., & Charbonneau, D. 2008, MNRAS, 385, 109 [NASA ADS] [CrossRef] [Google Scholar]
  108. Pontoppidan, K. M., Pickering, T. E., Laidler, V. G., et al. 2016, in Observatory Operations: Strategies, Processes, and Systems VI, SPIE, 9910, 991016 [Google Scholar]
  109. Rackham, B. V., Apai, D., & Giampapa, M. S. 2018, ApJ, 853, 122 [NASA ADS] [CrossRef] [Google Scholar]
  110. Ramirez, R. M., & Kaltenegger, L. 2014, ApJ, 797, L25 [NASA ADS] [CrossRef] [Google Scholar]
  111. Ramirez, R. M., & Kaltenegger, L. 2018, ApJ, 858, 72 [NASA ADS] [CrossRef] [Google Scholar]
  112. Rauer, H., Gebauer, S. v., Paris, P. v., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  113. Rauscher, B. J., Fox, O., Ferruit, P., et al. 2007, PASP, 119, 768 [NASA ADS] [CrossRef] [Google Scholar]
  114. Reid, I. 2005, New Light on Dark Stars Red Dwarfs, Low-Mass Stars, Brown Stars, eds. I. N. Reid and S. L. Hawley (Chichester: Praxis Publishing Ltd) [Google Scholar]
  115. Reid, N., & Gilmore, G. 1984, MNRAS, 206, 19 [NASA ADS] [Google Scholar]
  116. Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
  117. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  118. Rieke, G., Ressler, M., Morrison, J. E., et al. 2015a, PASP, 127, 665 [NASA ADS] [CrossRef] [Google Scholar]
  119. Rieke, G., Wright, G., Böker, T., et al. 2015b, PASP, 127, 584 [NASA ADS] [CrossRef] [Google Scholar]
  120. Roberge, A., Chen, C. H., Millan-Gabet, R., et al. 2012, PASP, 124, 799 [NASA ADS] [CrossRef] [Google Scholar]
  121. Rugheimer, S., Kaltenegger, L., Segura, A., Linsky, J., & Mohanty, S. 2015, ApJ, 809, 57 [NASA ADS] [CrossRef] [Google Scholar]
  122. Scheucher, M., Grenfell, L., Wunderlich, F., et al. 2018, ApJ, 863, 1 [NASA ADS] [CrossRef] [Google Scholar]
  123. Schreier, F., & Schimpf, B. 2001, in IRS 2000: Current Problems in Atmospheric Radiation, eds. W. Smith & Y. Timofeyev (Hampton, VA: A. Deepak Publishing), 381 [Google Scholar]
  124. Schreier, F., Garcia, S. G., Hedelt, P., et al. 2014, J. Quant. Spectr. Rad. Transf., 137, 29 [NASA ADS] [CrossRef] [Google Scholar]
  125. Schreier, F., Städt, S., Hedelt, P., & Godolt, M. 2018, Mol. Astrophys., 11, 1 [NASA ADS] [CrossRef] [Google Scholar]
  126. Segransan, D., Perrier, C., Udry, S., et al. 2000, A&A, 364, 665 [NASA ADS] [Google Scholar]
  127. Segura, A., Krelove, K., Kasting, J. F., et al. 2003, Astrobiology, 3, 689 [Google Scholar]
  128. Segura, A., Kasting, J. F., Meadows, V., et al. 2005, Astrobiology, 5, 706 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  129. Segura, A., Walkowicz, L. M., Meadows, V., Kasting, J., & Hawley, S. 2010, Astrobiology, 10, 751 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  130. Selsis, F., Kaltenegger, L., & Paillet, J. 2008, Phys. Scr., 2008, 014032 [NASA ADS] [CrossRef] [Google Scholar]
  131. Selwyn, G., Podolske, J., & Johnston, H. S. 1977, Geophys. Res. Lett., 4, 427 [NASA ADS] [CrossRef] [Google Scholar]
  132. Shabram, M., Fortney, J. J., Greene, T. P., & Freedman, R. S. 2011, ApJ, 727, 65 [NASA ADS] [CrossRef] [Google Scholar]
  133. Shields, A. L., Ballard, S., & Johnson, J. A. 2016, Phys. Rep., 663, 1 [NASA ADS] [CrossRef] [Google Scholar]
  134. Sneep, M., & Ubachs, W. 2005, J. Quant. Spectr. Rad. Transf, 92, 293 [NASA ADS] [CrossRef] [Google Scholar]
  135. Sullivan, P. W., Winn, J. N., Berta-Thompson, Z. K., et al. 2015, ApJ, 809, 77 [NASA ADS] [CrossRef] [Google Scholar]
  136. Tabataba-Vakili, F., Grenfell, J., Grießmeier, J.-M., & Rauer, H. 2016, A&A, 585, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. Tarter, J. C., Backus, P. R., Mancinelli, R. L., et al. 2007, Astrobiology, 7, 30 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  138. Tian, F., & Ida, S. 2015, Nat. Geosci., 8, 177 [NASA ADS] [CrossRef] [Google Scholar]
  139. Toon, O. B., McKay, C., Ackerman, T., & Santhanam, K. 1989, J. Geophys. Res., 94, 16287 [NASA ADS] [CrossRef] [Google Scholar]
  140. Trainer, M. G., Pavlov, A. A., Curtis, D. B., et al. 2004, Astrobiology, 4, 409 [NASA ADS] [CrossRef] [Google Scholar]
  141. Turbet, M., Leconte, J., Selsis, F., et al. 2016, A&A, 596, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. van Leeuwen, F. 2008, VizieR Online Data Catalog: I/311 [Google Scholar]
  143. Vidal-Madjar, A., Arnold, L., Ehrenreich, D., et al. 2010, A&A, 523, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  144. von Braun, K., Boyajian, T. S., Kane, S. R., et al. 2011, ApJ, 729, L26 [NASA ADS] [CrossRef] [Google Scholar]
  145. von Braun, K., Boyajian, T. S., Kane, S. R., et al. 2012, ApJ, 753, 171 [NASA ADS] [CrossRef] [Google Scholar]
  146. von Braun, K., Boyajian, T. S., van Belle, G. T., et al. 2014, MNRAS, 438, 2413 [NASA ADS] [CrossRef] [Google Scholar]
  147. von Paris, P., Rauer, H., Grenfell, J. L., et al. 2008, Planet. Space Sci., 56, 1244 [NASA ADS] [CrossRef] [Google Scholar]
  148. von Paris, P., Gebauer, S., Godolt, M., et al. 2010, A&A, 522, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  149. von Paris, P., Cabrera, J., Godolt, M., et al. 2011, A&A, 534, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  150. von Paris, P., Selsis, F., Godolt, M., et al. 2015, Icarus, 257, 406 [NASA ADS] [CrossRef] [Google Scholar]
  151. Wells, M., Pel, J.-W., Glasse, A., et al. 2015, PASP, 127, 646 [NASA ADS] [CrossRef] [Google Scholar]
  152. Winters, J. G., Henry, T. J., Lurie, J. C., et al. 2014, AJ, 149, 5 [NASA ADS] [CrossRef] [Google Scholar]
  153. Wright, G., Wright, D., Goodson, G., et al. 2015, PASP, 127, 595 [NASA ADS] [CrossRef] [Google Scholar]
  154. Yan, F., Fosbury, R. A., Petr-Gotzens, M. G., et al. 2015, IJA, 14, 255 [Google Scholar]
  155. Yang, J., Cowan, N. B., & Abbot, D. S. 2013, ApJ, 771, L45 [NASA ADS] [CrossRef] [Google Scholar]
  156. Zellem, R. T., Swain, M. R., Roudier, G., et al. 2017, ApJ, 844, 27 [NASA ADS] [CrossRef] [Google Scholar]
5

OH, HO2, H2O2, H2CO, H2O, H2, O3, CH4, CO, N2O, NO, NO2, HNO3, ClO, CH3Cl, HOCl, HCl, ClONO2, H2S, SO2, O2, CO2, N2.

All Tables

Table 1

Stellar parameters for the Sun and all M dwarfs used in this study.

In the text
Table 2

Parameters of the Earth around the Sun and Earth-like planets around M-dwarf host stars.

In the text
Table 3

Height, H, and temperature, T, at 100 and at 0.1 hPa for all simulated atmospheres of Earth-like planets around M dwarfs and the Earth.

In the text
Table 4

Mean central wavelengths, λc, bandwidths, Δλ and resolving power for selected spectral features and an S/N of 5.

In the text
Table 5

Number of transits, NTr, required to detect H2O, CH4, CO2, and O3 with JWST for an Earth-like planet in the HZ of the corresponding host star.

In the text

All Figures

thumbnail Fig. 1

Stellar input spectra, scaled to reach a surface temperature of 288.15 K, of the modelled planet and binned to a resolving power of 200. AD Leo and GJ 644 are taken from the VPL website (Segura et al. 2003), TRAPPIST-1 from O’Malley-James & Kaltenegger (2017), the other M-dwarf spectra from the MUSCLES database (France et al. 2016), and the solar spectrum from Gueymard (2004). Stars labelled with an asterisk are active M dwarfs. Top panel: UV and IR spectra up to 3 μm with linear axes. Bottom panel: UV spectra with logarithmic axes.
In the text
thumbnail Fig. 2

Mean UV flux of each M dwarf between 170 and 240 nm. Mean values are calculated from the stellar spectra, scaled as in Fig 1.
In the text
thumbnail Fig. 3

Influence of various M-dwarf SEDs on the temperature profile (K) of an Earth-like planet. The stellar spectra of Fig. 1 are scaled to reproduce a surface temperature of 288.15 K (see Table 2). Each coloured line represents the temperature profile of the modelled hypothetical planet orbiting a different host star. Weak UV emission of M dwarfs leads to low O3 heating inthe middle atmosphere and therefore to a reduced or missing temperature inversion. Enhanced CH4 heating increases the temperature in the middle atmosphere of Earth-like planets around late-type M dwarfs by up to 60 K.
In the text
thumbnail Fig. 4

Influence of various M-dwarf SEDs on some selected chemical atmospheric profiles of an Earth-like planet. The legend is the same as for Fig. 3.
In the text
thumbnail Fig. 5

Stellar S/N ratio over 1 h integration time of each M dwarf at 10 pc, binned to a resolution of 100. All NIRSpec filters and high resolution disperser are combined. Solid lines are calculated using the method described in Sect. 2.5 and dashed lines are calculated using the JWST ETC, Pandeia (Pontoppidan et al. 2016).
In the text
thumbnail Fig. 6

Top panel: effective height of all hypothetical Earth-like planets orbiting M dwarfs for a fixed resolving power of 100. Bottom panel: combined S/N using all high or medium resolution NIRSpec and MIRI filters up to 11 μm for all M-dwarf planets at 10 parsecs integrated over a single transit and a resolving power of 100.
In the text
thumbnail Fig. 7

Transit depth of all hypothetical Earth-like planets around their M-host stars for a fixed resolving power of 100 (coloured lines). The error bars show two sigma (standard deviation), single transit errors for selected spectral features, and selected M-dwarf planets at 10 parsecs with optimised wavelength bins. In black: calculated using high resolution JWST NIRSpec BOTS disperser and filter. In grey: calculated using NIRCam weak lens filters and high resolution NIRCam grism filters. Central wavelengths and bandwidths are calculated individually to distinguish between spectral absorption features (see Sect. 3.4.2).
In the text
thumbnail Fig. 8

Signal-to-noise ratio of the CH4 feauture at 3.4 μm for a single transit of each M-dwarf planet at 10 pc.
In the text
thumbnail Fig. 9

Number of transits needed to reach an S/N of 5 for selected spectral features of M-dwarf planets and the Earth-Sun case and different distances to the star. Central wavelength and bandwidths are shown in Table 4. The suddenreductions of the needed observation time happen when there are changes in the duty cycle and when a filter-disperser combination with a higher throughput can be used.
In the text
thumbnail Fig. 10

Detectability of hypothetical nearby Earth-like planets around M dwarfs with a single transit. Coloured dots show planets with an S/N of at least 5 for the corresponding spectral features (H2O: blue, CH4: green and CO2: red). Morethan one colour means that multiple spectral features can be detected with a single transit. The sizes of the grey dots indicate the highest S/N of all spectral features. The numbers inside the coloured dots correspondto the following host stars: 1: Proxima Centauri, 2: Barnard’s star, 3: Wolf 359, 4: Ross 154, 5: Ross 248, 6: Ross 128, 7: GJ 15 B, 8: DX Cancri, 9: GJ 1061, 10: YZ Ceti, 11: Teegarden’s star, 12: Wolf 424, 13: L 1159-16, 14: GJ 1245 B, 15: GJ 1245 A, 16: GJ 412 B, 17: LHS 2090, 18: GJ 1116, 19: LHS 1723, 20: GJ 1005, 21: L 43-72, 22: GJ 3737, 23: GL Virginis, 24: GJ 1128, 25: LSPM J2146+3813, 26: Ross 619, 27: G 161-7, 28: GJ 4053, 29: G 141-36, 30: SCR J0740-4257, 31: GJ 1286, 32: LHS 1070, 33: SCR J0838-5855, 34: NLTT 40406, 35: GJ 3146, 36: LSPM J0539+4038.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.