| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201834286 | |
| Published online | 08 March 2019 | |
Plasma heating by magnetoacoustic wave propagation in the vicinity of a 2.5D magnetic null-point
1
Center for mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
e-mail: 876.sabri@gmail.com, Somaiyeh.Sabri@kuleuven.be
2
Department of Theoretical Physics and Astrophysics, Physics Faculty, University of Tabriz, PO Box 51664, Tabriz, Iran
e-mail: s.sabri@tabrizu.ac.ir
3
Research Institute for Astronomy and Astrophysics of Maragheh (RIAAM), Iran
Received:
19
September
2018
Accepted:
8
January
2019
Context. Magnetohydrodynamic (MHD) waves have significant potential as a plasma heating mechanism. Finding a suitable wave dissipation mechanism is a very tough task, given the many observational constraints on the models, and this has resulted in the development of an important research community in solar physics. The magnetic field structure has an important role in the solar corona heating. Here, we investigate in detail current sheet mode generation via magnetic reconnection and mode conversion releases some of the free magnetic energy and produces heating. In addition, energy conversion is discussed completely. Moreover, nonlinear effects on density variations and, in turn, mode conversion are pursued.
Aims. In order to assess the role of magnetoacoustic waves in plasma heating, we have modeled in detail a fast magneto-acoustic wave pulse near a magnetic null-point in a finite plasma-β. The behavior of the propagation and dissipation of the fast magneto-acoustic wave is investigated in the inhomogeneous magnetically structured solar corona. Particular attention is given to the dissipation of waves and coronal heating and energy transfer in the solar corona, focusing on the energy transfer resulting from the interaction of fast magneto-acoustic waves with 2.5D magnetic null-points.
Methods. The shock−capturing Godunov−type PLUTO code was used to solve the ideal MHD set of equations in the context of wave-plasma energy transfer.
Results. It is shown that magneto-acoustic waves could be a viable candidate to contribute significantly to the heating of the solar corona and maintain the solar corona at a temperature of a few million degrees. The temperature is not constant in the corona. Coronal heating occurs near magnetic null points. It is found that magnetic reconnection, phase mixing and mode conversion contribute to the heating. Moreover, nonlinear fast and slow magnetoacoustic waves are decoupled except in β = 1 layer.
Key words: magnetohydrodynamics (MHD) / waves / methods: numerical / Sun: corona
© ESO 2019
1. Introduction
Understanding the processes involved in the heating of the plasma is important and difficult problem. The mechanism of magnetohydrodynamic (MHD) wave heating in the solar atmosphere has been recently investigated by Arregui (2015). High resolution observations have emphatically illustrated the presence of MHD waves in solar prominences (Lin et al. 2007, 2009; Hillier et al. 2013), spicules (He et al. 2009; Okamoto & De Pontieu 2011) and coronal loops (McIntosh et al. 2011; Wang et al. 2012; Anfinogentov et al. 2013; Nistico et al. 2013). The observed oscillations are the manifestation of MHD waves that may play an important role in coronal heating (Oliver 2009; Mackay et al. 2010; Arregui & Asensio Ramos 2011; Pesnell et al. 2012). The interaction of MHD waves with solar atmospheric plasma structures provides some insight into the energy transfer mechanisms in the solar atmosphere. The outcome of these interactions contributes to coronal heating and initiates the solar wind acceleration which directly affects us on Earth.
The key step in coronal heating is to recognize a mechanism for converting the magnetic energy to the plasma heating. Since classical dissipation coefficients are so negligible in the corona, thus plasma heating needs the generation of very steep gradients in very small spatial scales. However, velocity gradients result in the heating by viscous dissipation, but magnetic gradients that are so steep around the magnetic null point lead to the heating by magnetic reconnection and ohmic dissipation. Some numerical simulations have explained how the generation of the current sheets occur but as the energy conversion in these models is highly questionable, we discuss it here.
Two fundamentally different types of methods are proposed to solve the coronal heating problem. These are the so-called alternative current (AC) and direct current (DC) mechanisms. AC methods depend on MHD waves induced by plasma motions in and below the photosphere that travel through the solar atmosphere and reach the corona and are guided by magnetic flux tubes. In the corona, they can dissipate by creating AC current sheets via phase-mixing and resonant absorption. However, DC mechanisms depend on the magnetic field reconnection. Magnetic reconnection can release sufficient amounts of energy for coronal heating (Markus 2001).
Syrovatskii & Eksperim (1966), Bulanov & Syrovatskii (1980), and Bulanov et al. (1990, 1992) analytically studied the deformation of a magnetic field in a compressible conducting medium in the vicinity of zero filed lines. Therefore an X line is a natural structure that can be used in order to investigate a basic plasma phenomenon such as magnetic reconnection (Bulanov et al. 1986). The analysis of exact self-similar solutions of the full nonlinear equations in order to describe the magnetic field collapse near the magnetic null point, pursued by different studies (Imshennik & Syrovatskii 1967; Bulanov & Ol’shanetskii 1984, 1985).
Takeuchi & Shibata (2001) performed MHD simulations in 2.5D and found that the energy flux of Alfvén waves is sufficiently high to generate both coronal heating and spicule production. Slow magneto-acoustic modes are also thought to contribute to coronal heating. Suzuki (2004) showed that slow magneto-acoustic modes may indeed play a role in coronal heating and the acceleration of the low-speed solar wind. Bonet et al. (2008) discussed waves that are excited by torsional motions in the photosphere or by magnetic reconnection and found that such waves propagated into the corona and could dissipate their energy there through linear and nonlinear mechanisms.
A magnetic null-point is a point in the reconnection site where the magnetic field is zero. We note that the presence of magnetic null-points is proportional to the complexity of the magnetic flux distribution (Close et al. 2004; Longcope & Parnell 2009). Magnetic null points in the solar corona are basic configurations for inducing magnetic reconnection. There exists strong gradients of the magnetic field in magnetic null points which are accompanied by high plasma density which produces gradients of Alfvén speed (Provornikova et al. 2016).
Many processes in astrophysics and plasma physics are related to the magnetic reconnection and magnetic energy dissipation such as planetary magnetosphere, solar flares and fusion plasma instabilities. Using laser pulses, it becomes experimentally possible to investigate the magnetic filed annihilation. The corresponding theoretical and experimental studies have been reviewed (Bulanov et al. 2009, 2015).
Magnetic reconnection has proved adequate for triggering various solar features; all of which play a significant role in the sequence of events that seem interesting to us in the context of coronal seismology. Magnetic reconnection is very important in plasma physics, because through this mechanism energy previously stored in a magnetic field structure may suddenly be released and transformed into thermal and kinetic energy causing plasma heating, bulk plasma motions and particle acceleration. In the case of the solar corona, MHD waves and magnetic reconnection are often investigated separately despite the effective relation between these two phenomena. Indeed, violent magnetic reconnection events excite waves which can perturb the magnetic null points and trigger reconnection events (McLaughlin et al. 2009; Lee et al. 2014). Magnetic null points have an important effect on transforming the wave energy in the corona (Tarr et al. 2017).
Nakaraikov et al. (1997) considered compressibility and nonlinear effects and found that Alfvén waves propagation excited fast magnetoacoustic waves via phase mixing and that those fast waves moved across magnetic field lines and went away from the phase mixing layer. As they propagated and dissipated, these fast magnetoacoustic waves cause indirect heating of plasma.
The transient behavior of linear waves around null points, and its consequences for solar physics, have been extensively studied (McLaughlin et al. 2011). A series of investigations into linear MHD wave propagation in the vicinity of 2D β = 0 null points are carried out by McLaughlin & Hood (2004, 2005, 2006). These studies have led to two key results for the linear regime: a) fast and Alfvén waves accumulate at predictable regions of null point topology, regardless of the initial configuration and b) these wave modes remain district and decoupled without any interaction.
A variation of density results in a variation of sound and Alfvén speeds. This inhomogeneity of the characteristic speeds leads to an infinite set of the eigenfrequencies or a continuum in the MHD spectrum. One of the consequences of the Alfvén continuum is the possibility of resonant absorption of the Alfvén wave energy at resonant layers where the local Alfvén frequency matches the frequency of the wave (Poedts et al. 1989a,b, 1990a,b). When considering a monochromatic wave driver in the system, on the other hand, resonant damping plays possibly an essential role in the wave dissipation. Another wave dissipation mechanism is the wave-to-wave interaction. Collisions of waves and shocks occur at all times in the corona, which significantly increases nonlinearity and shock strengths. Thurgood & McLaughlin (2013) found that in nonlinear MHD, mode conversion can occur at regions of inhomogeneous Alfvén speed, suggesting that the decoupled nature of waves may not be extended to the nonlinear regime.
Due to the refraction effect, fast magnetoacoustic waves are focused toward the null point which resulting in the accumulation of current density and ohmic heating at the null point. Linear 2D, beta = 0 null points are thus predicted as locations of preferential heating due to passing fast magnetoacoustic waves.
McLaughlin et al. (2008), and Thurgood & McLaughlin (2012) confirmed that these two key features carry over. These extensions also add further dynamics considering β ≠ 0 introduces the slow mode which interacts with the fast wave.
McLaughlin & Hood (2004) investigated the nature of linear fast magnetoacoustic and Alfvén waves in a β = 0 regime. They solved the 2D linearized MHD equations numerically and compared the results with a WKB approximation. It was found that the fast mode was focused at the null point and generated the current density at that point. Thus, ohmic dissipation would extract the wave energy there. This illustrates that the null points play an important role in the rapid dissipation of fast magnetoacoustic waves and be the locations where wave heating will occur in the corona. They also found out that there was no evidence of X-point collapsing. Therefore, they conclude that wave heating would naturally occur at coronal null points. They suggested that other steps need to be taken to investigate the effects of pressure on the system. Fast waves can now pass through the null points and then perhaps take wave energy away from that area. To include the coupling of the waves, one needs to include the next terms in the approximation. The WKB approximation becomes degenerate at the points VA = Cs regions where the Alfvén speed and sound speed are equal. Therefore, this method cannot be used to pursue mode conversion.
McLaughlin et al. (2008), investigate the nature of nonlinear fast magnetoacoustic waves about a 2D magnetic X-point to include nonlinear effects. They found that propagation of the fast magnetoacoustic waves leads to the hot jet excitation which heats the plasma and significantly bends the local magnetic filedlines. Moreover, the nonlinear wave passes through the null point. We extend this work with considering β ≠ 0 plasma that introduces slow magnetoacoustic waves to the system. Therefore, the mode conversion effect takes place at the layer that sound and Alfvén speeds are equal (VA = Cs).
Due to the finite beta, a driving fast wave will excite a slow wave. In the current study, we investigated this by taking into account magnetoacoustic waves coupling with considering the energy evolution. However, this effect was studied previously by the propagation of the slow and fast waves and behavior of them not by the energy evolution. Previous studies, find no evidence of the fast wave traveling through the null in finite beta regime. Then they conclude that perhaps it is because of that sound speed is so tiny at the null point and it dissipates.
The behavior of the nonlinear fast wave around a 2D magnetic null point was investigated by McLaughlin et al. (2009). They find that, for sufficiently large driving amplitudes, magnetoacoustic shock waves developed, they passed through the null point and caused magnetic reconnection.
The condition that the MHD pulse must have in order to reach the magnetic null-point is discovered by Gruszecki et al. (2011). Although nonlinear shocks are highly dependent on the initial amplitude of waves, by decreasing the amplitude to width ratio of the pulse, the shock would later be experienced and, hence, it would be closer to the null-point. When the initial amplitude and width ratio of the pulse are less than a specific value, shock formation is prevented enabling the MHD wave and null-point interaction.
The interaction of MHD waves with magnetic null-points exercises our knowledge on the educational aspects of the solar atmosphere. The attention to MHD waves has been increased with the successful detection of MHD waves in coronal loops and plumes by recent observations from the TRACE and SOHO spacecrafts. MHD seismology has been quickly increased in solar physics research in recent years. These mechanisms allow defining the physical quantities and structures of solar features by the analysis of wave propagating through the plasma (Robert et al. 1984; Verwichte et al. 2004; McEwan et al. 2006).
Therefore, we aim to study the nonlinear dynamics considering the interaction of the magneto-acoustic waves with magnetic null-points in the contexts of MHD waves and energy evolution in the solar atmosphere and coronal heating. The understanding of coronal heating is essential not only for our insight into solar physics but also about its significant influence on the interplanetary and Earth space environments. The solar atmosphere creates the solar wind that can generate magnetic storms during the peak time of solar activity by substantially disturbing the magnetosphere of the Earth causing telecommunication and navigation interruptions and disruptions and other damages. MHD waves are obvious agents to transport energy from the solar surface into the solar atmosphere.
Coronal heating and acceleration of the solar wind by dissipation of fast and slow MHD waves through the formation of MHD shocks were studied with 1D MHD models, by for example, Orta et al. (2003) and Suzuki (2004). However, the role of MHD waves in coronal heating needs to be explored in detail and better quantification.
In numerical simulations without explicit physical dissipation some terms have been taken into account in the equations. Basically, there are two types of ‘dissipation’: The first one is physical dissipation which is associated with the generations of shocks. When a Riemann solver is used, as in the present study, this kind of dissipation is important. The second dissipation mechanism is numerical one which is affiliated with the truncation errors from the applied numerical discretization. In this case, magnetic shear or the advocation of shear flows could lead to some “numerical dissipation”. It must be noted that, in order to get realistic results, this dissipation mechanism needs a high numerical resolution to limit the numerical dissipation, real resistive and/or viscous dissipation (Matsumoto & Suzuki 2002).
We include some discussion about the role of wave energy in the heating of the solar corona. This is how the present study will be presented in the remainder of this paper: the domain and model under consideration are specified before stating the basic equations and equilibrium conditions. After presenting the domain configuration and numerical code, we discuss simulations to study the action of a magneto-acoustic pulse in the vicinity of a magnetic null-point. This enables investigating the induced perturbations due to the magneto-acoustic waves around a magnetic null-point and, hence, the transport and transfer of energy in this regard. In the final section, our conclusions are stated.
2. Basic equations and equilibrium conditions
The MHD theory is implemented to model the macroscopic dynamics of magneto-acoustic waves propagating in a plasma medium that hosts a magnetic null-point. The effects of solar gravity, plasma viscosity and resistivity have been neglected, so we do not consider any explicit dissipation terms in our equations. Therefore, one of the key problems in solar physics is to describe the way in which the solar corona could be heated to few millions of degrees when the resistive dissipation is assumed to be negligible (Klimchuk 2006). Parker (1972, 1979) explained possible mechanism of coronal heating and termed it topological dissipation. They claimed that the magnetic field in an ideal plasma has natural tendency to make tangential discontinuities that is current singularities. The current sheets are so intense that can cause significant dissipation even in the negligible resistivity of the solar corona. Thus, the ideal MHD equations are used in the following form:
where ρ, V, B, and P respectively represent the plasma density, plasma velocity, magnetic field, and plasma pressure. The constants μ and γ denote the magnetic permeability and the ratio of the specific heats, where we have μ = 4π × 10−7 Hm−1 and γ = 5/3. When magnetic field and nonlinearity are included together, the problem of MHD wave propagation around a magnetic null-point is intractable analytically and MHD equations are to be solved numerically. The main aim of this simulation is to investigate the roles of the background magnetic structure and nonlinear effects on the propagation and evolution of MHD waves and resulting effects on plasma heating.
Oscillations in coronal plasma are generated by sudden disturbances such as solar flares or filament eruptions. For a better representation of actual events that often create waves and oscillations in the solar corona, we have considered the excitation of perturbations by localized disturbances. The experimental setup configured in this study is based on a 2.5D X−type null-point in the (x, y) plane with a magneto-acoustic pulse initialized near the null-point (see Fig. 1). The setup is chosen to figure out how the propagation of this initial pulse affects the plasma heating, transforming and dissipation of the energies. We consider the initial magnetic field as
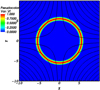 |
Fig. 1. Indicative lines of the equilibrium magnetic field structure and contours of the initial fast pulse at t = 0, (Vf = Vfastwave = (V × B) · z). |
where B0 represents a characteristic magnetic field strength and L is the length scale for magnetic field variations. The background magnetic field is force free. The theory of which is so important in numerous astrophysical situations (Marsh 1996; Sturrock 1994). As, in the solar corona, the magnetic energy dominates the other kinds of the energy such as thermal, kinetic and gravitational potential energy. Thus, at this situation Lorentz force of the magnetic field is approximately zero and magnetic structure is force free. The scenario of the numerical simulation is as follows: a circular magneto-acoustic pulse given by
and
is introduced in the vicinity of a magnetic null-point, 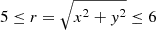 , where we have set Vz = 0, and A0 = 1 as the initial amplitude of the circular magneto-acoustic pulse. We note that the selection for the initial magneto-acoustic pulse may somehow be similar to the magneto-acoustic (m = 0) mode investigated by Gruszecki et al. (2011). In order to prevent or limit the occurrence of phase mixing in the initial phase of the simulation, we consider the background plasma density to be uniformed. Of course, due to nonlinearity in the later phase, phase-mixing does occur and contributes to the dissipation of the waves. The specific quantitative values of the initial equilibrium are taken to be consistent with the typical parameters of the solar coronal plasma: ρ0 = 10−12 kg m−3 and cs = 0.129 Mm s−1. Typical values of the initial pulse are r0 = 1 Mm and r1 = 5 Mm. We note that the equilibrium plasma has been considered as static.
, where we have set Vz = 0, and A0 = 1 as the initial amplitude of the circular magneto-acoustic pulse. We note that the selection for the initial magneto-acoustic pulse may somehow be similar to the magneto-acoustic (m = 0) mode investigated by Gruszecki et al. (2011). In order to prevent or limit the occurrence of phase mixing in the initial phase of the simulation, we consider the background plasma density to be uniformed. Of course, due to nonlinearity in the later phase, phase-mixing does occur and contributes to the dissipation of the waves. The specific quantitative values of the initial equilibrium are taken to be consistent with the typical parameters of the solar coronal plasma: ρ0 = 10−12 kg m−3 and cs = 0.129 Mm s−1. Typical values of the initial pulse are r0 = 1 Mm and r1 = 5 Mm. We note that the equilibrium plasma has been considered as static.
3. Numerical results and discussion
3.1. Numerical method
The experimental setup of the present study is solved in the context of MHD theory. The MHD Eqs. (1)–(5) are solved numerically using a high−resolution shock−capturing code, PLUTO, that is an appropriate and robust tool for studying nonlinear dynamics of magnetized fluid (Mignone et al. 2007). This code is appropriate for explicit time−dependent computations, where we implemented the Godunov method (approximate Riemann solver). Like most other codes, PLUTO works with dimensionless quantities. Therefore, by defining the three main parameters ρ0, L0, and V0, all other physical quantities of the system are made dimensionless in a consistent manner. The PLUTO code is designed to solve a system of conservation laws on structured meshes based on a finite-difference or finite-volume method. In the simulations presented and discussed here, we applied the finite difference discretization. In order to take into account the dissipative effects, the Godunov-type shock-capturing Riemann solver scheme was implemented in the present study with adaptive mesh refinement that resolves the current sheet and magnetic reconnection dynamics in detail. We applied HLLD scheme which is an approximate Riemann solver that have robustness and inexpensive numerical cost (Miyoshi & Kusano 2005). The PLUTO code enables solving the full nonlinear MHD equations in one to three dimensions. In the present numerical experiments, we apply the 2.5D option to ideal MHD, meaning that all the physical quantities depend only on two coordinates but their fields can have three components, including a component in the ignorable direction.
The magnetic field B is defined on cell faces in order to keep ∇ ⋅ B = 0 at all times in the entire computational domain. We simulated the plasma dynamics in a domain with ( − 10, 10)×(−10, 10)×(−10, 10) Mm and 1400 × 1400 × 1400 grid points. Since our main goal is to study the behavior of waves in the vicinity of a magnetic null-point, a stretched grid has been used to focus the majority of the grid points close to the null-point. Therefore, we set 1200 × 1200 × 1200 grid points in the numerical domain ( − 6, 6)×(−6, 6)×(−6, 6) Mm with an effective resolution of δx ≈ δy ≈ δz ≈ 1/100.
Waves in the solar atmosphere often have high amplitudes that are to be assumed nonlinear. The previous investigations of nonlinear waves in the solar atmosphere have been interested especially in coronal heating. The study of fully nonlinear problems is only numerically possible. In our experiments, an initially symmetric nonlinear fast magneto-acoustic pulse at a specific distance from a magnetic null-point is kicked toward the isothermal null-point.
In the early phase of the experiment, the initial pulse, due to the spatial variation of the phase speed, has been divided into two oppositely propagating waves. Now, since steep gradients exist in the Alfvén waves speed around the magnetic null-point, the behavior of the waves is highly affected by this inhomogeneity. Moreover, the propagation of the MHD waves also affects the plasma parameters such as density and temperature. We want to study the effect of the propagation of the MHD waves on the temperature and demonstrate the possible contribution of MHD waves to the coronal heating.
3.2. Current sheet and plasma heating
The requirements for the coronal heating model have changed drastically in recent years. The main challenge used to be to obtain a heating process with the same efficiency in both open and closed magnetic configurations for the numerous time and length scales observed in the corona. Also, it is not known to what extend MHD waves are excited in the solar corona by magnetic reconnection phenomena nor whether plasma inhomogeneities couple these waves. However, it is now clear that the temperature is not constant in the solar corona. The main interest of this study is to investigate the aspects of magneto-acoustic wave dissipation as a possible heating mechanism in the corona. This problem has been extremely studied under numerous assumptions and in the various regions of the solar corona. The origin of such temperature increases can thus be of a magnetic nature. The exact physical mechanisms and their contribution to the heating remain unknown and we intend to investigate these more in detail.
We pursed the perturbation of the plasma temperature due to the propagation of the magneto-acoustic waves by initially introducing symmetric fast magneto-acoustic wave. In fact, for the present situation with β ≠ 0, we also had slow magneto-acoustic disturbances. The magneto-acoustic waves propagation in the vicinity of the reconnection current sheet modifies the magnitude of the plasma density and magnetic field strength and thus the magnitude of the Alfvén speed.
In this line, we aim to study the nonlinear aspects of the dynamic behavior due to the interaction of the magneto-acoustic waves with magnetic null-points in the context of MHD waves and coronal heating. The propagation of the MHD waves is accompanied by the variation of the density, pressure and temperature of the plasma. Figure 2 shows the spatial variation of the temperature.
 |
Fig. 2. Spatial variation of the temperature. Contours a till b show the gradual increase of temperature for −3.3 ≤ x ≤ 3.3, −3.2 ≤ x ≤ 3.2 (a at t = 0.6 s, b at t = 1.14 s, c at t = 1.3 s and d at t = 3.52 s). The significant increase in plasma temperature is shown in the last two plots respectively at t = 6.02 s for −2.7 ≤ x ≤ 2.7, −2.6 ≤ x ≤ 2.6 and t = 7.6 s for −1.5 ≤ x ≤ 1.5, −1.5 ≤ x ≤ 1.5. This increase due to the propagation of magneto-acoustic waves and their interaction with the magnetic configuration. The black lines in the lower figure denote magnetic field lines. |
We observe a gradual increase of the temperature in the four first panels (plots a till b). A significant increase of the temperature was seen at t = 6.02 s and, especially, at t = 7.6 s in the last panels of Fig. 2. We find a very prominent increase in temperature at t = 7.6 s so that the temperature reaches its maximum value obtained in this simulation. We now realize that the temperature is not constant in the corona. At a point near the magnetic null point, heating takes place. This means that due to the nonlinearity and β ≠ 0, magnetoacoustic waves go through the null point.
McLaughlin & Hood (2004) investigated the nature of linear fast magnetoacoustic in a β = 0. They solved the 2D linearized MHD equations numerically and compared the results with a WKB approximation. They find that the fast mode was focused at the null point and generated the current density at that point. Thus, ohmic dissipation would extract the wave energy there. This illustrates that the null points play an important role in the rapid dissipation of fast magnetoacoustic waves and be the locations where wave heating will occur in the corona. They also find that there is no evidence of X-point collapsing. Therefore, they conclude that wave heating would naturally occur at coronal null points.
However, in this work with considering the nonlinearity and β ≠ 0 we found that plasma heating occurs at a point near the magnetic null point, not at the null. The last panel in Fig. 2 plots in a limited area that the heating point is observed clearly as well as the magnetic filed structure. It is shown that the structure of the magnetic filed is being changed. Thus, we expect that magnetic reconnection takes place at that point. Previous studies, have found no evidence of the fast wave traveling through the null in finite beta regime. Thus, they concluded that perhaps it is because of that sound speed is so tiny at the null point and it dissipates.
In this work, we show that due to the nonlinearity and β ≠ 0, fast and slow magnetoacoustic waves pass through the null point. It causes the null point to collapse to form a current sheet in which reconnection can release magnetic energy.
Due to the impulsive heating, the thermal pressure increases to drive the flow along the magnetic field. In the solar corona, it is obvious that the characteristic scale of inhomogeneity in the perpendicular direction to the magnetic field is much smaller than the one along the magnetic field. Therefore, high thermal conductivity is induced along the magnetic field lines. The propagation of the magneto-acoustic waves compresses the plasma and bends the magnetic field lines, which is very interesting in the context of the explanation of the coronal heating.
Various analytical and numerical investigations offer the role of thin current sheets in the corona that could explain the observed plasma heating (Parker 1988; Gudiksen & Nordlund 2005; Ofman 2009; Peter & Bingert 2012). An interesting domain that hosts such phenomena is the neighborhood of a magnetic reconnection site. Magnetic reconnection is an event that comes into play when the plasma magnetic field structure experiences changes (Petschek 1964; Forbes & Priest 1987; Craig & McClymont 1991). Magnetic reconnection has been assumed to be the essential procedure in most solar activities (Parker 1972, 1988; Priest 1981; Priest & Forbes 2000). The fundamental scenario is that due to the non−potential flux, free energy is generated in the form of current sheets in the corona. The magnetic free energy is released by magnetic reconnection and leads to the coronal plasma heating Klimchuk (2006), Rappazzo et al. (2008), or in violent mass ejections Lynch et al. (2008, 2009), Pariat et al. (2009) and particle acceleration as in flare models Miller et al. (1997), Darke et al. (2006). Thus, the generation of current singularities which generically term current sheets is crucial process in solar activity, so we investigated the behavior of the current sheets at this work.
Parker (1972) suggested that the dissipation from thin current filaments could be the energy source of coronal heating. This can be due to the resistive dissipation of the small scale currents continuously generated by magneto-acoustic waves propagation. As we see in Fig. 3, the magnetic field generate current filaments so dissipation of them leads to the plasma heating according to the Fig. 2. It is interesting that the heating point at t = 7.6 s in the last panel of Fig. 2 is coincidence to the high thin current sheet place at the last panel of Fig. 3. Therefore, it is found that MHD waves propagation generates multiple small scale current sheets in the vicinity of the magnetic null-point and it leads to the plasma heating by ohmic dissipation. For efficient dissipation of waves in the corona, extremely small length scales must be created due to the huge local magnetic Reynolds numbers. Such small length scales can be created by dynamical evolution or as proposed in chromospheric and transition region reconnection. We focused on the importance of the generation of electric current density and presence of the compressive magneto-acoustic modes which could play a significant role in creating the required small dissipative length scales. To solve these complex kinds of the problems, we used the best available numerical methods. The PLUTO code, mentioned above, is able to handle both discontinuities, such as shocks, and current sheets that are generated in nonlinear regimes. With the continuous variation of the Alfvén speed, energy can be carried across the magnetic field and dissipated in a thin resonance layer. By neglecting the dissipation terms in ideal MHD equations, it is assumed that dissipation processes that accompany the heating are significantly important in this narrow layer.
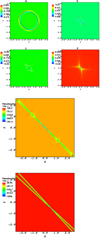 |
Fig. 3. Spatial variation of the current density. The contours a till b show the gradual current density variation for −3.3 ≤ x ≤ 3.3, −3.2 ≤ x ≤ 3.2 (a at t = 0.6 s, b at t = 1.14 s, c at t = 1.3 s, and d at t = 3.52 s). The significant variation in current density is shown in the last two plots for −2.7 ≤ x ≤ 2.7, −2.6 ≤ x ≤ 2.6 respectively at t = 6.02 s and t = 7.6 s. This shows that the place of current sheet generation is coincident with the heating place because of the ohmic dissipation. |
A detailed numerical study of the full mechanisms of mode conversion, phase mixing and plasma heating in complex modules including nonlinearity has not yet been undertaken. We explore more about the plasma heating by mode conversion and phase mixing by temporal profiles of oscillation in the following.
3.3. Energy conversion and phase mixing
This line is focused on the allegedly important contribution of MHD waves to coronal heating in the context of energy evolution. Figure 4 shows the energy of the MHD waves including magnetic, kinetic and internal (acoustic) energies. The potential energy consists of the magnetic and internal (or acoustic) energy. The study of MHD waves in terms of their propagation features and energy transport and transfer capabilities is vital for solving the plasma heating problem. Compressible magneto-acoustic waves can dissipate their energy in many different ways such as resonant absorption (Goossens & De Groof 2001), turbulent mixing (Van Ballegooijen et al. 2011), viscosity (Braginskii 1965), mode conversion (Ulmschneider et al. 1991) and thermal conduction (Ofman & Aschwanden 2002). Arregui & Asensio Ramos (2011), studied the detailed energy transfer by standing waves via analyzing the Poynting flux in a 2D configuration.
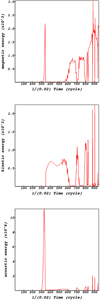 |
Fig. 4. Time variation of magneto-acoustic waves magnetic, kinetic and acoustic energies at the null point (0, 0, 0). Time on the horizontal axis is normalized to Alfvén cycle times. |
The role of MHD waves in the coronal heating needs to be explored in detail and be quantified carefully. In this work, however, the importance of the nonlinear effects of magneto-acoustic wave heating is emphasized by considering the mode conversion and phase mixing effects.
Mode conversion has been found to be a notable dissipation mechanism for MHD waves which could play an important role in solar coronal heating (Kudoh et al. 1998; Moriyasu et al. 2004), and also in the generation of the slow and fast solar wind (Suzuki & Inutsuka 2006). For the mode conversion mechanism, the density fluctuation is decisive for efficient wave dissipation. Mode conversion happens wherever the sound and Alfvén speed are equal (i.e., in plasma β = 1 layer), it takes place mainly when the nonlinear effects are large. Nonlinear effects can be expressed by the ratio of the azimuthal to longitudinal velocities or magnetic fields. In this layer, mode conversion of the slow mode into the fast magneto-acoustic facilitates the rapid dissipation of wave energy to the plasma and then plasma heating occurs. As is known, when fast and slow magneto-acoustic waves across the plasma layer where β ≃ 1, wave mixing occurs which means that waves show both acoustic and magnetic qualities. This effect is shown in Fig. 4 where we see approximately the same initial evolution of the magnetic and acoustic wave energies (cf. the peak at about 7.6 s in both plots). Apart from this layer, fast and slow nonlinear magneto-acoustic waves are decoupled while fast mode has a dominant magnetic character but the slow mode has mostly an acoustic character. Thurgood & McLaughlin (2013) conclude that in nonlinear MHD, mode conversion could occur at regions of inhomogeneous Alfvén speed, suggesting that the decoupled nature of waves may not be extended to the nonlinear regime. Then, we show the decoupled behavior of nonlinear fast and slow modes. It means that apart from the β ≃ 1 layer, slow and fast magneto-acoustic waves are decoupled. This means that basic concepts of wave mixing and transformation are valid in 2.5D magnetic configuration.
However, the behavior of the magnetic energy is initially governed by the density perturbations kicked by the MHD wave propagation. Indeed, the initial peak in magnetic energy in Fig. 4 is in accordance with the plasma density profile. We find that background flow has a substantial influence on the wave dynamics in a plasma had already been noted by (Chagelishvili et al. 1994). Also, Tikhonchuk et al. (1995), Terradas & Ofman (2004) investigated density perturbations due to nonlinear MHD waves.
Heating of the plasma by MHD waves can occur through two main methods. The first is a direct momentum transfer from the MHD waves to the plasma by the Lorentz force. In the second-order, the nonlinear approximation of the waves results in a ponderomotive force due to the magnetic field perturbation (Ofman & Davila 1997). However, since the nonlinear effects are highly dependent on the wave amplitude and width (Gruszecki et al. 2011), high amplitude perturbations in the density are created which enables phase mixing Heyvaerts & Priest (1983). In Fig. 5, we present the time evolution of the plasma density and current density. When MHD waves move along an inhomogeneous magnetized plasma, due to the variation of the Alfvén speed, the wave front becomes significantly deformed. The gradients that are produced in the wave front lead to the creation of electric currents and flows. It is found that strong plasma density compressions can be produced in reconnection current sheets. Chen et al. (2013) studied the trajectories of electron beams in a flare and found the presence of steep density gradients near the flare regions. These observations show that reconnection sites with high compressions exist in the corona that is also illustrated in Fig. 5.
 |
Fig. 5. Time variation of plasma density and electrical current density at the null point (0,0,0). |
The explanation for such a phenomenon is connected to the nonlinearity due to the transverse gradients in the Alfvén speed (Nakaraikov et al. 1997). This proves that since the system is adiabatic, the only player for energy dissipation is the nonlinearity that leads to the magnetic reconnection, phase mixing and mode conversion.
In Fig. 6 we show that the atmospheric inhomogeneities have more observable consequences for the wave magnetic variables than for the wave velocity variables (cf. the peak in the magnetic field due to the density peak), this result is in line with the previous one, obtained by Murawski & Musielak (2010) and Perera et al. (2015). Transformation of the magnetic energy into the kinetic energy occurs due to the small-scale currents produced as a result of variations in the phase speeds of the waves in magnetic inhomogeneities. This is also due to non-uniformity of the velocity which causes an additional coupling of the MHD waves, although we here deal with pure magneto-acoustic waves without any Alfvén mode, this means that energy can be transferred from one wave mode to another. We found that the energy flux of the magneto-acoustic waves into the null-point may indeed provide a sufficient amount of energy to heat the corona, as claimed by Pekunlu et al. (2001). Transforming the magnetic energy to the kinetic one occurs due to the small scale currents. This means that energy can be transferred from one wave mode to another. This also means that there is the equipartition of the wave kinetic and magnetic energies in magneto-acoustic waves as illustrated in Fig. 4. The equipartition of the magnetic and kinetic energy was not observed in the case of Alfvén wave (Sabri et al. 2018).
 |
Fig. 6. Time variation of velocities and magnetic field in the x and y directions at the null point (0,0,0). |
As shown in Fig. 4, it is clear that dominant mode is a slow magneto-acoustic wave, which is replaced by the weak fast wave when it disappears. It is sensible that magnetic energy density is the dominant contribution in low−β plasma, but it rapidly releases and transforms into thermal (internal) and kinetic energy. Several mechanisms such as magnetic reconnection, phase mixing, and mode conversion have an important contribution in damping of this mode. Different processes such as mode conversion and magnetic reconnection convert fast mode wave to the slow one which results in plasma heating. Besides, we inferred that the attenuation of the slow magneto-acoustic mode has a greater effect on the time evolution of the current density or the oscillatory behavior of the system. This stronger attenuation of slow magneto-acoustic mode results from wave scattering in inhomogeneous plasma, which also verifies our claim.
4. Summary and discussion
Despite numerous observational and theoretical investigations, the solar coronal heating problem remained unsolved. We are interested in studying the coronal heating and oscillatory behavior of different characteristics by magneto-acoustic wave propagation by implementing the PLUTO code. This code solves full nonlinear MHD equations. The interaction of MHD waves with magnetic null-points exercises our knowledge on the educational aspects of the solar atmosphere. The fast and slow magneto-acoustic waves have been considered respectively propagating along the perpendicular and parallel directions with respect to background magnetic field. These waves produce nonlinear effects in the x-y plane. MHD waves are a diagnostic tool in plasma heating phenomena. The null-point structure, preconditions, equilibrium variables and assumptions are studied for coronal conditions. The behavior of propagation and dissipation of fast magneto-acoustic wave are investigated in the inhomogeneous magnetically structured solar corona. However, the detailed analysis of the propagation and dissipation of the magnetoacoustic waves leads us to the eight key results below:
-
1.
We find a very noticeable increase in temperature at t = 7.6 s such that it reached the maximum. We now know that the temperature is not constant in the corona.
-
2.
Continuously operating external forces such small scale current sheets, phase mixing and mode conversion damped energy into the medium, and turned it into the heating. High current sheet excitation, mode conversion, and phase mixing took place simultaneously with the heating.
-
3.
The behavior of the magnetic energy at the first time is governed by the density perturbations kicked by the MHD waves propagation. The density perturbations are signatures of induced compressive perturbations by the compressible magneto-acoustic waves. We show that background flow has influenced the wave dynamics in a plasma.
-
4.
We find that strong plasma density compressions can be produced in reconnecting current sheets.
-
5.
When fast and slow magneto-acoustic waves cross the layer where β ≃ 1, wave mixing occurs which means that waves show a mixture of acoustic and magnetic behaviors. Apart from this layer, fast and slow magneto-acoustic waves are decoupled. Mode conversion of slow and fast modes at the equipartition layer where the plasma β ≃ 1, leads to rapid dissipation of the wave energy to the plasma and, therefore, results in plasma heating.
-
6.
Transforming the magnetic energy to the kinetic one occurs due to the small scale currents. This means that energy can be transferred from one wave mode to another one. This also means that there is the equipartition of the wave kinetic and magnetic energies in magneto-acoustic waves.
-
7.
It is found that the energy of the wave accumulates at one point near the magnetic null point and leads to the significant heating of that point. Also, we show that the nonlinear induced density perturbations cause the magnetic energy variation and then frequently transforming magnetic energy to kinetic and thermal energy.
-
8.
We find that density and magnetic field gradients play an important role in the dissipation of energy in the solar corona. Moreover, MHD waves act as energy carriers and can transport energy to the corona and even transfer it to the small scales, enabling localized plasma heating to occur there.
Finding a suitable wave dissipation mechanism is a very tough task, given the many observational constraints on the models, which has resulted in an important research community in solar physics. In the present work, magnetic reconnection, phase mixing, and mode conversion are considered to be the main dissipative mechanism. Indeed, nonlinear effects lead to density variations and these are, in turn, accompanied by mode conversion. Thus, suitable conditions for magneto-acoustic wave heating are strongly dependent on these nonlinear effects.
Acknowledgments
This work has been supported by KU Leuven and financially supported by Maragheh (RIAAM). For the computations we used the infrastructure of the VSC/Flemish Supercomputer Center, funded by the Hercules foundation and the Flemish Government−department EWI. Visualization was done with the help of VisIt software (Childs et al. 2012).
References
- Anfinogentov, S., Nistico, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I. 2015, Trans. Roy. Soc. Lond. Ser. A, 373, 20140261 [Google Scholar]
- Arregui, I., & Asensio Ramos, A. 2011, ApJ, 740, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Bonet, J. A., Marquez, I., Sanchez Almeida, J., Cabello, I., & Domingo, V. 2008, ApJ, 687, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [Google Scholar]
- Bulanov, S. V., & Ol’shanetskii, M. A. 1984, Phys. Lett. A, 100, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Bulanov, S. V., & Ol’shanetskii, M. A. 1985, Sov. J. Plasma Phys., 11, 425 [NASA ADS] [Google Scholar]
- Bulanov, S. V., & Syrovatskii, S. I. 1980, Sov. J. Plasma Phys., 6, 661 [NASA ADS] [Google Scholar]
- Bulanov, S. V., Butov, I. Ya, Gvaladze, Yu S, et al. 1986, Sov. J. Plasma Phys., 12, 180 [Google Scholar]
- Bulanov, S. V., Pegoraro, F., & Shasharina, S. G. 1990, Plasma Phys. Controlled Fusion, 32, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Bulanov, S. V., Pegoraro, F., & Shasharina, S. G. 1992, Plasma Phys. Controlled Fusion, 34, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Bulanov, S. V., Esirkepov, T. Z., Habs, D., Pegoraro, F., & Tajima, T. 2009, Eur. Phys. J. D, 55, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bulanov, S. V., Esirkepov, T. Z., Kando, M., et al. 2015, Plasma Phys. Rep., 41, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Chagelishvili, G. D., Rogava, A. D., & Segal, I. N. 1994, Phys. Rev. E, 50, 4283 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, B., Bastian, T. S., White, S. M., & Gray, D. E. 2013, ApJ, 763, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Childs, H., Brugger, E., & Whitlock, B. 2012, High Performance Visualization Enabling Extreme Scale Scientific Insight (Chapman & Hall/CRC Computational Science), 357 [Google Scholar]
- Close, R. M., Parnell, C. E., & Priest, E. R. 2004, Sol. Phys., 225, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & McClymont, A. N. 1991, ApJ, 371, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Darke, J. F., Swisdak, M., Che, H., & Shay, M. A. 2006, Nature, 443, 553 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Forbes, T. G., & Priest, E. R. 1987, Rev. Geophys., 25, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Goossens, M., & De Groof, A. 2001, Phys. Plasmas, 8, 2371 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., Vasheghani Farahani, S., Nakariakov, V. M., & Arber, T. D. 2011, A&A, 531, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gudiksen, B. V., & Nordlund, A. 2005, ApJ, 618, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- He, J. S., Tu, C. Y., & Marsch, E. 2009, A&A, 497, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Hillier, A., Morton, R. J., & Erdelyi, R. 2013, ApJ, 779, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Imshennik, V. S., & Syrovatskii, S. I. 1967, Sov. Phys. JETP, 26, 656 [NASA ADS] [Google Scholar]
- Klimchuk, J. A. 2006, Sol. Phys., 234, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kudoh, T., Matsumoto, R., & Shibata, K. 1998, ApJ, 508, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, E., Lukin, V. S., & Linton, M. G. 2014, A&A, 569, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, Y., Engvold, O., Rouppe van der Voort, L. H. M., & van Noort, M. 2007, Sol. Phys., 246, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y., Soler, R., & Engvold, O. 2009, ApJ, 704, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Longcope, D. W., & Parnell, C. E. 2009, Sol. Phys., 254, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Antiochos, S. K., DeVore, C. R., Luhmann, J. G., & Zurbuchen, T. H. 2008, ApJ, 683, 333 [Google Scholar]
- Lynch, B. J., Antiochos, S. K., Luhmann, J. G., & DeVore, C. R. 2009, ApJ, 697, 1918 [NASA ADS] [CrossRef] [Google Scholar]
- Mackay, D. H., Karpen, J. T., Ballester, J. L., Schmieder, B., & Aulanier, G. 2010, Space Sci. Rev., 151, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Markus, J. A. 2001, ApJ, 560, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, G. E. 1996, Force-Free Magnetic Fields: Solutions, Topology and Applications (World Scientific) [CrossRef] [Google Scholar]
- Matsumoto, T., & Suzuki, T. K. 2002, Astron. Soc., 1 [Google Scholar]
- McEwan, M. P., Donnelly, G. R., Diaz, A. J., & Roberts, B. 2006, A&A, 460, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McIntosh, S. W., De Pontieu, B., & Carlsson, M. 2011, Nature, 475, 477 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2004, A&A, 420, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2005, A&A, 435, 313 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Hood, A. W. 2006, A&A, 452, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., Ferguson, J. S. L., & Hood, A. W. 2008, Sol. Phys., 251, 563 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, J. A., De Moortel, I., Hood, A. W., & Brady, C. S. 2009, A&A, 493, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., Hood, A. W., & De Moortel, I. 2011, Space Sci. Rev., 158, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Miller, J. A., Cargill, P. J., Emslie, A. G., et al. 1997, J. Geophys. Res., 102, 14631 [NASA ADS] [CrossRef] [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Moriyasu, S., Kudoh, T., Yokoyama, T., & Shibata, K. 2004, ApJ, 601, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Murawski, K., & Musielak, Z. E. 2010, A&A, 37, 518 [Google Scholar]
- Nakaraikov, V. M., Roberts, B., & Murawski, K. 1997, Sol. Phys., 175, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Nistico, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L. 2009, ApJ, 694, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Aschwanden, M. J. 2002, ApJ, 576, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Ofman, L., & Davila, J. M. 1997, ApJ, 476, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T. J., & De Pontieu, B. 2011, ApJ, 736, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, R. 2009, Space Sci. Rev., 149, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Orta, J. A., Huerta, M. A., & Boynton, G. C. 2003, ApJ, 529, 592 [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1972, ApJ, 174, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1979, Cosmical Magnetic Fields (Oxford University Press) [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Pekunlu, E. R., Cakirli, O., & Ozetken, E. 2001, MNRAS, 326, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Perera, H. K., Musielak, Z. E., & Murawski, K. 2015, MNRAS, 450, 3 [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Peter, H., & Bingert, S. 2012, A&A, 548, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petschek, H. E. 1964, in Proc. AAS-NASA Symp. Phys. Solar Flares, ed. W. N. Hess (Washington, DC: NASA), 425 [Google Scholar]
- Poedts, S., Goossens, M., & Kerner, W. 1989a, Sol. Phys., 123, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Poedts, S., Kerner, W., & Goossens, M. 1989b, Plasma Phys., 42, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Poedts, S., Goossens, M., & Kerner, W. 1990a, ApJ, 360, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Poedts, S., Goossens, M., & Kerner, W. 1990b, Comput. Phys. Commun., 59, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 1981, Solar Flare Magnetohydrodynamics (Newark: Gordon and Breach) [Google Scholar]
- Priest, E. R., & Forbes, T. 2000, Magnetic Reconnection: MHD Theory and Applications (Cambridge University Press) [CrossRef] [Google Scholar]
- Provornikova, E., Laming, J. M., & Lukin, V. S. 2016, ApJ, 852, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2008, ApJ, 677, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Robert, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Sabri, S., Vasheghani Farahani, S., Ebadi, H., Hosseinpour, M., & Fazel, Z. 2018, MNRAS, 479, 4991 [NASA ADS] [CrossRef] [Google Scholar]
- Sturrock, P. A. 1994, Plasma Physics: An Introduction to the Theory of Astrophysical, Geophysical and Laboratory Plasmas (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Suzuki, T. K. 2004, MNRAS, 349, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K., & Inutsuka, S. I. 2006, Space Phys., 111, 6101 [Google Scholar]
- Syrovatskii, S. I., & Eksperim, Zh 1966, Teoret. Fiz, 50, 1133 [Google Scholar]
- Takeuchi, A., & Shibata, K. 2001, ApJ, 546, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Tarr, L. A., Linton, M., & Leake, J. 2017, ApJ, 837, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., & Ofman, L. 2004, ApJ, 610, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Thurgood, J. O., & McLaughlin, J. A. 2012, A&A, 545, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thurgood, J. O., & McLaughlin, J. A. 2013, A&A, 555, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tikhonchuk, V. T., Rankin, R., Frycz, P., & Samson, J. C. 1995, Phys. Plasmas, 2, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Ulmschneider, P., Zaehringer, K., & Musielak, Z. E. 1991, A&A, 241, 625 [NASA ADS] [Google Scholar]
- Van Ballegooijen, A. A., Asgari Targhi, M., Cranmer, S. R., & DeLuca, E. E. 2011, ApJ, 736, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Ofman, L., Davila, J. M., & Su, Y. 2012, ApJ, 718, L102 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Indicative lines of the equilibrium magnetic field structure and contours of the initial fast pulse at t = 0, (Vf = Vfastwave = (V × B) · z). |
| In the text | |
 |
Fig. 2. Spatial variation of the temperature. Contours a till b show the gradual increase of temperature for −3.3 ≤ x ≤ 3.3, −3.2 ≤ x ≤ 3.2 (a at t = 0.6 s, b at t = 1.14 s, c at t = 1.3 s and d at t = 3.52 s). The significant increase in plasma temperature is shown in the last two plots respectively at t = 6.02 s for −2.7 ≤ x ≤ 2.7, −2.6 ≤ x ≤ 2.6 and t = 7.6 s for −1.5 ≤ x ≤ 1.5, −1.5 ≤ x ≤ 1.5. This increase due to the propagation of magneto-acoustic waves and their interaction with the magnetic configuration. The black lines in the lower figure denote magnetic field lines. |
| In the text | |
 |
Fig. 3. Spatial variation of the current density. The contours a till b show the gradual current density variation for −3.3 ≤ x ≤ 3.3, −3.2 ≤ x ≤ 3.2 (a at t = 0.6 s, b at t = 1.14 s, c at t = 1.3 s, and d at t = 3.52 s). The significant variation in current density is shown in the last two plots for −2.7 ≤ x ≤ 2.7, −2.6 ≤ x ≤ 2.6 respectively at t = 6.02 s and t = 7.6 s. This shows that the place of current sheet generation is coincident with the heating place because of the ohmic dissipation. |
| In the text | |
 |
Fig. 4. Time variation of magneto-acoustic waves magnetic, kinetic and acoustic energies at the null point (0, 0, 0). Time on the horizontal axis is normalized to Alfvén cycle times. |
| In the text | |
 |
Fig. 5. Time variation of plasma density and electrical current density at the null point (0,0,0). |
| In the text | |
 |
Fig. 6. Time variation of velocities and magnetic field in the x and y directions at the null point (0,0,0). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \rho \left[\frac{\partial {\boldsymbol{V}}}{\partial t} + ({\boldsymbol{V}}\cdot \nabla ){\boldsymbol{V}}\right]= \left(\frac{1}{\mu }\nabla \times {\boldsymbol{B}}\right)\times {\boldsymbol{B}}-\nabla P, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34286-18/aa34286-18-eq1.gif)
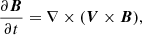
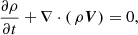
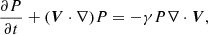
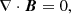
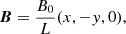
![$$ \begin{aligned} {\boldsymbol{V}}_{\rm {x}}={\boldsymbol{A}}_{\mathrm{0} } \sin \left[\pi \frac{\sqrt{x^2+y^2}-r_1}{r_0}\right]\frac{B_{\rm y}}{(B_{\rm x})^2+(B_{\rm y})^2}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34286-18/aa34286-18-eq7.gif)
![$$ \begin{aligned} {\boldsymbol{V}}_{\mathrm{y} }={\boldsymbol{A}}_{\rm {0}} \sin \left[\pi \frac{\sqrt{x^2+y^2}-r_1}{r_0}\right]\frac{B_x}{(B_{\rm x})^2+(B_{\rm y})^2}, \end{aligned} $$](/articles/aa/full_html/2019/03/aa34286-18/aa34286-18-eq8.gif)