| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A201 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834557 | |
| Published online | 21 February 2019 | |
Two new free-floating or wide-orbit planets from microlensing
1
Warsaw University Observatory,
Al. Ujazdowskie 4,
00-478
Warszawa,
Poland
e-mail: pmroz@astrouw.edu.pl
2
Code 667, NASA Goddard Space Flight Center,
Greenbelt,
MD
20771,
USA
3
Department of Astronomy, University of Maryland,
College Park,
MD
20742,
USA
4
Korea Astronomy and Space Science Institute,
Daejon
34055,
Republic of Korea
5
Department of Earth and Space Science, Graduate School of Science, Osaka University,
Toyonaka,
Osaka
560-0043,
Japan
6
IPAC,
Mail Code 100-22, Caltech, 1200 E. California Blvd.,
Pasadena,
CA
91125,
USA
7
Department of Astronomy, Ohio State University,
140 W. 18th Ave.,
Columbus,
OH
43210,
USA
8
Department of Physics, University of Warwick,
Coventry
CV4 7AL,
UK
9
University of Canterbury, Department of Physics and Astronomy,
Private Bag 4800,
Christchurch
8020,
New Zealand
10
Korea University of Science and Technology,
Daejeon
34113,
Republic of Korea
11
Max-Planck-Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
12
Department of Physics, Chungbuk National University,
Cheongju
28644,
Republic of Korea
13
Harvard-Smithsonian Center for Astrophysics,
60 Garden St.,
Cambridge,
MA
02138,
USA
14
Physics Department and Tsinghua Centre for Astrophysics, Tsinghua University,
Beijing
100084,
PR China
15
School of Space Research, Kyung Hee University,
Yongin,
Kyeonggi
17104,
Republic of Korea
16
Institute for Space-Earth Environmental Research, Nagoya University,
Nagoya
464-8601,
Japan
17
Institute of Natural and Mathematical Sciences, Massey University,
Auckland
0745,
New Zealand
18
Department of Physics, University of Auckland,
Private Bag
92019,
Auckland,
New Zealand
19
Department of Earth and Planetary Science, Graduate School of Science, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo
113-0033,
Japan
20
Instituto de Astrofísica de Canarias,
Vía Láctea s/n,
38205
La Laguna,
Tenerife,
Spain
21
Department of Astronomy, Graduate School of Science, The University of Tokyo,
7-3-1 Hongo,
Bunkyo-ku,
Tokyo
113-0033,
Japan
22
National Astronomical Observatory of Japan,
2-21-1 Osawa,
Mitaka,
Tokyo
181-8588,
Japan
23
School of Chemical and Physical Sciences, Victoria University,
Wellington,
New Zealand
24
Institute of Space and Astronautical Science,
Japan Aerospace Exploration Agency,
3-1-1 Yoshinodai,
Chuo, Sagamihara,
Kanagawa,
252-5210,
Japan
25
University of Canterbury Mt. John Observatory,
PO Box 56,
Lake Tekapo
8770,
New Zealand
26
Department of Physics, Faculty of Science, Kyoto Sangyo University,
603-8555
Kyoto,
Japan
27
School of Physics and Astronomy and Wise Observatory, Tel-Aviv University,
Tel-Aviv
6997801,
Israel
Received:
1
November
2018
Accepted:
9
January
2019
Planet formation theories predict the existence of free-floating planets that have been ejected from their parent systems. Although they emit little or no light, they can be detected during gravitational microlensing events. Microlensing events caused by rogue planets are characterized by very short timescales tE (typically below two days) and small angular Einstein radii θE (up to several μas). Here we present the discovery and characterization of two ultra-short microlensing events identified in data from the Optical Gravitational Lensing Experiment (OGLE) survey, which may have been caused by free-floating or wide-orbit planets. OGLE-2012-BLG-1323 is one of the shortest events discovered thus far (tE = 0.155 ± 0.005 d, θE = 2.37 ± 0.10μas) and was caused by an Earth-mass object in the Galactic disk or a Neptune-mass planet in the Galactic bulge. OGLE-2017-BLG-0560 (tE = 0.905 ± 0.005 d, θE = 38.7 ± 1.6μas) was caused by a Jupiter-mass planet in the Galactic disk or a brown dwarf in the bulge. We rule out stellar companions up to a distance of 6.0 and 3.9 au, respectively. We suggest that the lensing objects, whether located on very wide orbits or free-floating, may originate from the same physical mechanism. Although the sample of ultrashort microlensing events is small, these detections are consistent with low-mass wide-orbit or unbound planets being more common than stars in the Milky Way.
Key words: planets and satellites: detection / gravitational lensing: micro
© ESO 2019
1 Introduction
Theories of planet formation predict the existence of free-floating (rogue) planets that are not gravitationally tethered to any host star. These objects could have formed in protoplanetary disks around stars, as “ordinary” planets, and could have been ejected as a result of various mechanisms, including planet–planet dynamical interactions (e.g., Rasio & Ford 1996; Weidenschilling & Marzari 1996; Marzari & Weidenschilling 2002; Chatterjee et al. 2008; Scharf & Menou 2009; Veras et al. 2009), ejections from multiple-star systems (e.g., Kaib et al. 2013; Sutherland & Fabrycky 2016), stellar flybys (e.g., Malmberg et al. 2011; Boley et al. 2012; Veras & Moeckel 2012), dynamical interactions in stellar clusters (e.g., Hurley & Shara 2002; Spurzem et al. 2009; Parker & Quanz 2012; Hao et al. 2013; Liu et al. 2013), or the post-main-sequence evolution of the host star(s) (e.g., Veras et al. 2011, 2016; Kratter & Perets 2012; Voyatzis et al. 2013).
It is believed that low-mass planets are more likely to be scattered to wide orbits or ejected than giant, Jupiter-mass planets. Calculations of Ma et al. (2016), which are based on the core accretion theory of planet formation, predict that most free-floating planets should be of Earth mass. Rogue planets are more likely to form around FGK-type stars, because they are scattered into wide orbits following close encounters with gas giant planets, which are more likely to form around massive stars. The typical total ejected mass is about 5−20 M⊕ and about 10–20% of all planetary systems should give rise to rogue planets. Similarly, Barclay et al. (2017), using N-body simulations of terrestrial planet formation around solar-type stars, estimated that about 2.5 terrestrial-mass planets are ejected per star in the Galaxy during late-stage planet formation, but these numbers strongly depend on the adopted initial conditions.
Free-floating planetary-mass objects can also be formed by the fragmentation of gas clouds, in a way similar to that in which stars form. Star formation processes are believed to extend down to 1− 4 MJup (Boyd & Whitworth 2005; Whitworth & Stamatellos 2006). This parameter space cannot be probed with the current surveys of young stellar clusters and star-forming regions, which are unable to detect objects less massive than 5− 6 MJup (Peña Ramírez et al. 2012; Lodieu et al. 2013; Mužić et al. 2015). Free-floating planetary-mass objects may also form from small molecular cloudlets that have been found in H II regions, although it is unclear whether these clouds may contract (Gahm et al. 2007; Grenman & Gahm 2014).
Gravitational microlensing is the only method that enables us to find Earth-mass free-floating planets. A gravitational microlensing event occurs when a lens (free-floating planet or star) is very closely aligned with a distant source star, with the angular separation smaller than the Einstein radius of the lens 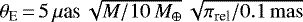 (here, M is the lens mass, πrel = πl − πs is the relative lens-source parallax, and πl and πs are parallaxes to the lens and source, respectively). The gravitational field of the lens can focus light rays of the source, causing a transient brightening of the source to an Earth-based observer. As typical lens-source proper motion in the direction of the Galactic center is μrel = 5 mas yr−1, timescales of microlensing events due to Earth-mass lenses are very short tE = θE∕μrel ≈ 10−3 yr ≈ 0.4 d.
(here, M is the lens mass, πrel = πl − πs is the relative lens-source parallax, and πl and πs are parallaxes to the lens and source, respectively). The gravitational field of the lens can focus light rays of the source, causing a transient brightening of the source to an Earth-based observer. As typical lens-source proper motion in the direction of the Galactic center is μrel = 5 mas yr−1, timescales of microlensing events due to Earth-mass lenses are very short tE = θE∕μrel ≈ 10−3 yr ≈ 0.4 d.
Because angular radii of giant source stars in the Galactic bulge ρ* = 6 μas(R∕10 R⊙) (πs∕0.125 mas) are comparable to angular Einstein radii of planetary-mass lenses, light curves of giant-source events attributed to free-floating planets should exhibit strong finite source effects (as each point on the source surface is magnified by a different amount). Detection of the finite source effects in the light curve allows us to measure θE, which can place additional constraints on the mass of the lens. Direct calculations of the lens mass require additional information on πrel, but the parallax measurement is challenging for such short events (see Introduction in Mróz et al. 2018).
Microlensing events on timescales shorter than 2 d have been traditionally attributed to unbound planets. A statistical analysis of 474 events discovered by the Microlensing Observations in Astrophysics (MOA) group led to the claim of an excess of events on timescales of 1–2 d (corresponding to Jupiter-mass lenses) and the suggestion that they are caused by a sizable population of Jupiter-mass wide-orbit or free-floating planets (Sumi et al. 2011). The analysis of a larger data set collected during the years 2010–2015 of the fourth phase of the Optical Gravitational Lensing Experiment (OGLE-IV) did not confirm these findings (Mróz et al. 2017). Mróz et al. (2017) found a 95% upper limit on the frequency of Jupiter-mass rogue planets in the Milky Way of 0.25 per star. They detected, however, a few very short events (tE < 0.5 d), which could be attributed to Earth- and super-Earth-mass free-floating planets. Their sampling was, however, insufficient to detect finite source effects. See Mróz et al. (2017, 2018) for a detailed discussion.
The only known ultrashort microlensing event that exhibited prominent finite source effects, OGLE-2016-BLG-1540, was identified by Mróz et al. (2018) in the OGLE data from the 2016 observing season. This event was likely caused by a Neptune-mass free-floating planet, as inferred from the measurement of the angular Einstein radius. Encouraged by this discovery, we searched for short-timescale microlensing events in the OGLE data from the 2017 season and complemented them with photometric observations from the Korea Microlensing TelescopeNetwork (KMTNet). We also searched for short-duration microlensing events with giant sources in the archival OGLE data collected during the 2010–2015 period. Here, we report the discovery and characterization of two microlensing events, OGLE-2012-BLG-1323 and OGLE-2017-BLG-0560, which can be attributed to free-floating planets. We show that, although the sample of these events is small, these detections are consistent with terrestrial-mass wide-orbit or unbound planets being more common than stars in the Milky Way.
2 Observations
Microlensing event OGLE-2017-BLG-0560 was announced on 2017 April 16 by the OGLE Early Warning System (Udalski 2003). This event was located at equatorial coordinates of RA = 17h51m 51.s 33, Dec = −30°27′31.′′4 (J2000.0) in the field BLG534, which was observed with a cadence of 60 min. The OGLE survey operates from Las Campanas Observatory, Chile, and uses a dedicated 1.3 m Warsaw Telescope, equipped with a mosaic CCD camera with a field of view of 1.4 deg2 (see Udalski et al. 2015 for details of the survey). This event was also observed by three identical 1.6 m telescopes from the KMT Network (Kim et al. 2016), which are located at the Cerro Tololo Inter-American Observatory (CTIO; Chile), the South African Astronomical Observatory (SAAO; South Africa), and the Siding Spring Observatory (SSO; Australia). The event was located in the two overlapping fields BLG01 and BLG41, each observed with a cadence of 30 min. For the modeling, we used observations collected between March 7 and May 26, 2017.
The second event analyzed in this paper, OGLE-2012- BLG-1323, was also discovered by the OGLE Early Warning System, on 2012 August 21. This event is located at equatorial coordinates of RA = 18h00m18.s51, Dec = −28°35′01.′′7 (J2000.0) in the field BLG512, which was monitored with a cadence of 20 min. This event was not previously identified as a free-floating planet candidate (Mróz et al. 2017), owing to its extremely low amplitude (below 0.1 mag).
We supplement OGLE observations with the data from the MOA (Bond et al. 2001) and Wise groups (Shvartzvald et al. 2016). MOA observations were collected using the 1.8 m telescope at Mt. John University Observatory in New Zealand (Sumi et al. 2013). Wise observations were taken with the 1 m telescope at Wise Observatory in Israel equipped with the LAIWO camera.
All data were taken in the I band except for MOA data; the MOA group uses a custom wide filter, which is effectively the sum of the standard R and I filters. Photometry was extracted using custom implementations of the difference image analysis technique: Woźniak (2000; OGLE), Albrow (2017; KMTNet and Wise), and Bond et al. (2001; MOA).
3 Light curve modeling
Light curvesof both events are well described by the extended-source point-lens model (Fig. 1), which is defined by four parameters: t0 (time of the closest lens-source approach), u0 (impact parameter in Einstein radius units), tE (event timescale), and ρ = θ*∕θE (normalizedradius of the source, i.e., the ratio of the angular radius of the source θ* to the angular Einsteinradius θE). Two additional parameters (for each observatory and filter) are needed to describe the source star flux (Fs) and unmagnified flux of the blend (Fb). When the blend flux is allowed to vary, the best-fit solutions are characterized by negative blending (Fb < 0). We therefore, following the approach of Mróz et al. (2018), kept Fb = 0 constant, but we also added in quadrature 0.05 mag to the uncertainty of the source brightness.
The best-fit parameters and their uncertainties are shown in Table 1. The uncertainties are estimated using the Markov chain Monte Carlo technique (Foreman-Mackey et al. 2013) and represent 68% confidence intervals of marginalized posterior distributions.
To describe the brightness profile of the source star, we adopted the square-root limb-darkening law, described by two parameters Γ and Λ (which are filter-dependent; Yoo et al. 2004). If allowed to vary, Γ and Λ are strongly correlated. We thus kept limb-darkening coefficients constant, using the limb-darkening models of Claret & Bloemen (2011; see Table 1 for their numerical values). We used ATLAS models and assumed a solar metallicity, microturbulent velocity of 2 km s−1, and surface gravity of log g = 2.0 (Γ and Λ are weakly dependent on log g if log g ≤ 2.0), as is appropriate for giant sources.
The archival light curve of OGLE-2017-BLG-0560 shows low-amplitude (0.02 mag), semi-regular variability that is typical of OGLE small amplitude red giants (Wray et al. 2004). The strongest pulsation period in the 2017 data is18.9 d. As the effective duration of the event (3 days) is much shorter than the pulsation period, we expected that the inferred model parameters should not be strongly influenced by the variability of the source. Additional modeling, in which we assume that the flux of the source varies sinusoidally with a period of 18.9 d, results in almost identical microlensing parameters (within the error bars) to those of the model with the constant source.
We also searched for terrestrial parallax signal (Gould et al. 2009; Yee et al. 2009; Freeman et al. 2015) in the light curve of OGLE-2012-BLG-1323, but the χ2 improvement was insignificant (Δχ2 = 1) and the limits on the microlens parallax were very poor. We did not fit the parallax model to the light curve of OGLE-2017-BLG-0560 because of the low-level variability of the source.
Finally, we also searched for possible binary lens models. Short-duration events may be caused by close binary lenses (when the projected separation s, in Einstein radius units, is much smaller than 1), when the source crosses a small triangle-shaped caustic that is far (~ 1∕s) from the center of mass. The expected light curves are asymmetric, unless the source is larger than the caustic. In that case the light curve may superficially look like an extended-source point-lens event, except that it has a more extended tail. We found that the best-fitting close binary models are disfavored by Δχ2 of several hundred for OGLE-2012-BLG-1323 and even more for OGLE-2017-BLG-0560. The latter event has a large amplitude (≈ 1 mag), but the peak magnification in close binary models is usually much lower than that, unless the source is small (ρ < 0.001) and the light curve is asymmetric. We cannot rule out that the lens is a wide-orbit planet; we discuss these cases in Sect. 4.3.
 |
Fig. 1 Light curves of two ultrashort microlensing events. Upper panel: OGLE-2012-BLG-1323. Lower panel: OGLE-2017-BLG-0560. Both events show strong finite-source effects, which allows us to measure their angular Einstein radii. |
4 Physical parameters
4.1 Source stars
Model parameters can be translated into physical parameters of the lens provided that the angular radius of the source star is known. Here we use a standard technique (Yoo et al. 2004) of measuring the offset of the source from the centroid of red clump giants in the calibrated color–magnitude diagram in a 2′ × 2′ region around the event (about 5 pc × 5 pc at the Galactic center distance; Fig. 2). Because we lack color observations collected during the two events, our best estimate for the color of the source is the color of the baseline star. This is further supported by the lack of evidence for blending in the I-band light curves and the low probability of bright unmagnified blends. As the intrinsic color (Bensby et al. 2011) and dereddened brightness of the red clump (Nataf et al. 2013) are known toward a given direction, we are able to calculate the dereddened color and brightness of the source. Subsequently, we use color–color (Bessell & Brett 1988) and color–surface brightness (CSB; Kervella et al. 2004) relations for giants to measure the angular radius of the source star1. We also use the color–temperature relations of Houdashelt et al. (2000a,b) and Ramírez & Meléndez (2005) to estimate the effective temperature of the source. The angular Einstein radius is θE = θ*∕ρ and the relative lens-source proper motion (in the geocentric frame) is μrel,geo = θE∕tE. The heliocentric correction (v⊕,⊥πrel∕au, where v⊕,⊥ is the Earth’s velocity projected on the sky), which should be added vectorially, is on the order of 3πrel yr−1 and is negligible unless the lens is nearby (closer than 1 kpc from the Sun). The physical parameters of the source star and lens are given in Table 1.
 |
Fig. 2 OGLE-IV color–magnitude diagrams for stars in 2′× 2′ regions around OGLE-2012-BLG-1323 and OGLE-2017-BLG-0560. Sources are marked with blue squares and are likely located in the Galactic bulge. If sources were M dwarfs, they would have absolute I-band magnitudesof 9.75 (OGLE-2012-BLG-1323) and 13.90 (OGLE-2017-BLG-0560; Pecaut & Mamajek 2013) and would be located at a distance of 140 and 16 pc, respectively, which contradicts the Gaia DR2 parallaxes (0.15 ± 0.14 mas and 0.23 ± 0.19 mas, respectively). |
Short-timescale microlensing events exhibiting finite source effects.
4.2 Proper motion of source stars
Because source stars are bright and lenses contribute little (if any) light, the absolute proper motions of the sources can be found in the second Gaiadata release (DR2; Gaia Collaboration 2016, 2018). We recall, however, that the Gaia performance in the crowded regions of the Galactic center is poor, especially for faint sources. Figure 3 shows proper motions of stars located within 4′ of the sources. In both cases source proper motions are consistent with those of Galactic bulge stars (represented by red clump and red giant branch stars), although proper motions measured relative to the mean velocity of the bulge are high. This contributes to the high relative lens-source proper motion of OGLE-2017-BLG-0560 and its very short timescale.
 |
Fig. 3 Gaia DR2 proper motions of stars within 4′ of OGLE-2012-BLG-1323 (left panel) and OGLE-2017-BLG-0560 (right panel). Blue contours correspond to the main-sequence stars (Galactic disk population) and red contours to giants (bulge population). Solid contours enclose 68 and 95% of all objects. The source is marked with a black dot. The black dashed circle corresponds to the relative source-lens proper motion of 5.6 mas yr−1 (left panel) and 15.6 mas yr−1 (right panel). |
4.3 Constraints on the host star
If the trajectory of the source passed near a putative host star, we would detect additional anomalies in the light curves of both events. As we have not found any, we are able to provide only lower limits on the projected star-planet separation, using the method of Mróz et al. (2018). In short, the description of a binary lens requires three additional parameters: mass ratio q, separation s (in Einstein radius units), and angle α between the source trajectory and binary axis. We consider a 0.3 M⊙ host located either in the Galactic disk (πrel = 0.1 mas) or in the bulge (πrel = 0.01 mas), which corresponds to θE,host = 0.49 mas or 0.16 mas, respectively. Then, for each pairof mass ratio 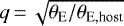 and separation s, we simulate 180 OGLE light curves (spanning from 2010 March 4 through 2017 October 30) with uniformly distributed α, and calculate the fraction of light curves that show signatures of the putative host star (see Fig. 4). For OGLE-2012-BLG-1323 we find a 90% lower limits of 11.8 au for the disk case (4.9 Einstein radii of the host) and 6.0 au for the bulge host (4.5 Einstein radii of the host). The formal 90% limits for OGLE-2017-BLG-0560 are 9.3 and 3.9 au, respectively, but the sensitivity to additional anomalies in the light curve is reduced, owing to low-level variability of the source.
and separation s, we simulate 180 OGLE light curves (spanning from 2010 March 4 through 2017 October 30) with uniformly distributed α, and calculate the fraction of light curves that show signatures of the putative host star (see Fig. 4). For OGLE-2012-BLG-1323 we find a 90% lower limits of 11.8 au for the disk case (4.9 Einstein radii of the host) and 6.0 au for the bulge host (4.5 Einstein radii of the host). The formal 90% limits for OGLE-2017-BLG-0560 are 9.3 and 3.9 au, respectively, but the sensitivity to additional anomalies in the light curve is reduced, owing to low-level variability of the source.
5 Discussion
The two microlensing events presented in this paper and OGLE-2016-BLG-1540 (Mróz et al. 2018) share a number of similarities (Table 1). All events occurred on bright giant stars (with estimated angular radii of 9.2– 34.9μas) and their relative lens-source proper motions are high (5.6−15.6 mas yr−1). All three events show prominent finite source effects, which led to the measurement of the angular Einstein radius. The fact that all three events occurred on bright, large sources is surprising as less than 3% of all known events are found with sources brighter than I = 16 mag. Moreover, the microlensing event rate Γ is proportional to the area of the sky swept by the Einstein ring: Γ ∝ θEμrel. The high lens-source relative proper motion makes an event more likely to be found, but events with μrel> 10 mas yr−1 are very rare (Han et al. 2017).
Strong finite source effects make the duration of an event longer, especially if ρ ≫ 1, which makes giant source events easier to detect. The typical timescale t* of such an event is comparable to the time needed for the lens to cross the chord of the source:
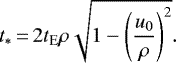 (1)
(1)
Monitoring of giant-star microlensing events, as advocated by the Hollywood strategy of Gould (1997), is therefore a promising way of studying free-floating planets.
On the other hand, the peak magnification Apeak in the absence of blending declines with the source size (Gould & Gaucherel 1997):
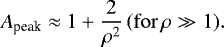 (2)
(2)
The OGLE Early Warning System alerts events that brighten by at least 0.06 mag (Udalski 2003), which corresponds to ρ ≲ 6, but the search algorithm of Mróz et al. (2017) is sensitive to lower magnifications. Equation (1) also explains why the impact parameter of OGLE-2012-BLG-1323 is poorly measured (cf. Table 1): for large sources (ρ = 5) changing the impact parameter from u0 = 0 to u0 = 1 leads to an increase in tE of only 2%, which is already included in the reported uncertainties.
The mass of the lens depends on the angular Einstein radius θE and the relative parallax πrel:
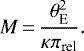 (3)
(3)
For both events, the masses cannot be unambiguously determined because the microlens parallaxes cannot be measured. For lenses located in the Galactic disk (πrel ≈ 0.1 mas) the masses are 2.3 M⊕ and 1.9 MJup for OGLE-2012-BLG-1323 and OGLE-2017-BLG-0560, respectively. If the lenses are located in the Galactic bulge (πrel ≈ 0.01 mas), they have higher masses of about 23 M⊕ or 20 MJup, respectively.
The mass of the lens can be further constrained by employing the Bayesian analysis. If we assume a Galactic model and a mass function of lenses, we can estimate the mass of the lens that most likely reproduces the observations (Einstein radius and proper motion) given the model. However, as we probe extreme events, we must be cautious that the inferred masses will depend on priors that may be derived from data on objects whose properties lie well beyond the range of those being probed. We used the Galactic model of Bennett et al. (2014) and two planetary mass functions as the prior. The first mass function (d N∕dM ∝ M−1.3), taken from Sumi et al. (2011), overpredicts the number of short-timescale events (Mróz et al. 2017). The second function (d N∕dM ∝ M−1.8) is steeper, which is consistent with the findings of Clanton & Gaudi (2016) and Suzuki et al. (2016), and better describes the event timescale distribution of Mróz et al. (2017). The posterior distributions favor Galactic bulge lenses, but the allowed range of masses is very broad (see Table 2). The median masses of the Bayesian results,
![\[ M\,{=}\,(0.038,1.5,100)\,M_{\textrm{Jup}}, \vspace*{-1pt}\]](/articles/aa/full_html/2019/02/aa34557-18/aa34557-18-eq6.png)
when combined with the angular Einstein radius values in Table 1,
![\[ \theta_{\textrm{E}}\,{=}\,(2.37,9.2,38.7)\,\mu{\textrm{as}}, \vspace*{-1pt}\]](/articles/aa/full_html/2019/02/aa34557-18/aa34557-18-eq7.png)
correspond to lens-source relative parallaxes of
![\[ \pi_{\textrm{rel}}\,{=}\,(0.019,0.007, 0.002)\,\rm{mas} \vspace*{-1pt}\]](/articles/aa/full_html/2019/02/aa34557-18/aa34557-18-eq8.png)
for the three events OGLE-2012-BLG-1323, OGLE-2016- BLG-1540, and OGLE-2017-BLG-0560, respectively.
The ultrashort timescale event OGLE-2012-BLG-1323 (tE = 0.155 ± 0.005 d) is almost certainly caused by a planetary-mass object (Earth- to super-Earth-mass), while the mass of OGLE-2016-BLG-1540 (tE = 0.320 ± 0.003 d) is poorly constrained. The rate of events due to brown dwarfs and stars with timescales shorter than 0.32 d (0.155 d) is just 10−5 (5 × 10−7) of the total event rate (Mróz et al. 2017).
It is not possible to determine, without further high-resolution follow-up observations, whether these planets are free-floating or are located at very wide orbits. Owing to their high relative lens-source proper motions, such searches will be possible in the near future with current instruments or next-generation telescopes (Gould 2016). As the sources are bright, separations of ~ 100 mas are required to resolve the putative host stars; such separations will be reached in the late 2020s.
Presently, there are no observational constraints on the frequency of bound Earth- and super-Earth-mass wide-orbit planets as their detection is challenging with the current techniques. For example, Poleski et al. (2014) found a 4 MUranus planet at projected separation of 5.3 Einstein radii and Sumi et al. (2016) discovered a Neptune analog at projected separation of 2.4 Einstein radii. Planet-formation theories, such as the core accretion model (Ida & Lin 2004), predict very few low-mass planets at wide orbits because the density of solids and gas in a protoplanetary disk is very low at such large separations. It is believed that Uranus and Neptune formed closer to the Sun, near Jupiter and Saturn, and were subsequently scattered into wide orbits (Thommes et al. 1999, 2002). Likewise, multiple protoplanets of up to a few Earth masses can be scattered to wide orbits and eventually ejected by growing gas giants (e.g., Chatterjee et al. 2008; Izidoro et al. 2015; Bromley & Kenyon 2016; Silsbee & Tremaine 2018). From the point of view of microlensing observations, these objects, whether bound or free-floating, are in practice indistinguishable.
While making statistical inferences out of such a small sample of events is risky, we show that these detections are consistent with low-mass lenses being common in the Milky Way, unless it is just a coincidence that the events occurred on bright giant stars. According to models presented by Mróz et al. (2017), about 2.8 × 10−3 of all events should be caused by Earth- and super-Earth-mass lenses (on timescales tE < 0.5 d) if there were one such object per each star. About 50 events with giant sources brighter than I = 16 are found in OGLE high-cadence fields annually, thus we expect to find 2.8 × 10−3 × 50 = 0.1 very short microlensing events with giant sources annually (about one event during the entire OGLE-IV time span) if the probability of detection is the same for events due to free-floating planets and stars. In reality, the detection efficiency for bright events on timescales of O(1 d) is a factor of 2–4 lower than for stellar events (Mróz et al. 2017). Thus, our findings support the conclusions of Mróz et al. (2017) that such Earth-mass free-floating (or wide-orbit) planets are more common than stars in the Milky Way.
 |
Fig. 4 Probability of detecting the putative host star as a function of star-planet separation. Solid curves correspond to the lens located in the Galactic bulge (πrel = 0.01 mas) and dashed curves to the lens in the Galactic disk (πrel = 0.1 mas). |
Posterior distributions for the lens mass calculated from the Bayesian analysis.
Acknowledgements
P.M. acknowledges support from the Foundation for Polish Science (Program START) and the National Science Center, Poland (grant ETIUDA 2018/28/T/ST9/00096). The OGLE project has received funding from the National Science Center, Poland, grant MAESTRO 2014/14/A/ST9/00121 to A.U. Work by A.G. was supported by AST-1516842 from the US NSF. I.G.S. and A.G. were supported by JPL grant 1500811. A.G. received support from the European Research Council under the European Union’s Seventh Framework Programme (FP 7) ERC Grant Agreement n. [321035]. This research has made use of the KMTNet system operated by the Korea Astronomy and Space Science Institute (KASI) and the data were obtained at three host sites of CTIO in Chile, SAAO in South Africa, and SSO in Australia. Work by C.H. was supported by a grant (2017R1A4A1015178) from the National Research Foundation of Korea. The MOA project is supported by JSPS KAKENHI Grant Numbers JSPS24253004, JSPS26247023, JSPS23340064, JSPS15H00781, and JP16H06287. This research was supported by the I-CORE program of the Planning and Budgeting Committee and the Israel Science Foundation, Grant 1829/12. D.M. and A.G. acknowledge support from the US-Israel Binational Science Foundation.
References
- Adams, A. D., Boyajian, T. S., & von Braun K. 2018, MNRAS, 473, 3608 [Google Scholar]
- Albrow, M. 2017, MichaelDAlbrow/pyDIA: Initial Release on Github [Google Scholar]
- Barclay, T., Quintana, E. V., Raymond, S. N., & Penny, M. T. 2017, ApJ, 841, 86 [Google Scholar]
- Bennett, D. P., Batista, V., Bond, I. A., et al. 2014, ApJ, 785, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessell, M. S., & Brett, J. M. 1988, PASP, 100, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Boley, A. C., Payne, M. J., & Ford, E. B. 2012, ApJ, 754, 57 [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [Google Scholar]
- Boyd, D. F. A., & Whitworth, A. P. 2005, A&A, 430, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromley, B. C., & Kenyon, S. J. 2016, ApJ, 826, 64 [Google Scholar]
- Chatterjee, S., Ford, E. B., Matsumura, S., & Rasio, F. A. 2008, ApJ, 686, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Clanton, C., & Gaudi, B. S. 2016, ApJ, 819, 125 [Google Scholar]
- Claret, A., & Bloemen, S. 2011, A&A, 529, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Fouque, P., & Gieren, W. P. 1997, A&A, 320, 799 [NASA ADS] [Google Scholar]
- Freeman, M., Philpott, L. C., Abe, F., et al. 2015, ApJ, 799, 181 [Google Scholar]
- Gahm, G. F., Grenman, T., Fredriksson, S., & Kristen, H. 2007, AJ, 133, 1795 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A. 1997, in Variables Stars and the Astrophysical Returns of the Microlensing Surveys, eds. R. Ferlet, J.-P. Maillard, & B. Raban (France: Editions Frontières), 125 [Google Scholar]
- Gould, A. 2016, J. Korean Astron. Soc., 49, 123 [Google Scholar]
- Gould, A., & Gaucherel, C. 1997, ApJ, 477, 580 [Google Scholar]
- Gould, A., Udalski, A., Monard, B., et al. 2009, ApJ, 698, L147 [Google Scholar]
- Grenman, T., & Gahm, G. F. 2014, A&A, 565, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. A. T. 2004, MNRAS, 353, 903 [Google Scholar]
- Han, C., Udalski, A., Sumi, T., et al. 2017, ApJ, 843, 59 [Google Scholar]
- Hao, W., Kouwenhoven, M. B. N., & Spurzem, R. 2013, MNRAS, 433, 867 [Google Scholar]
- Houdashelt, M. L., Bell, R. A., & Sweigart, A. V. 2000a, AJ, 119, 1448 [Google Scholar]
- Houdashelt, M. L., Bell, R. A., Sweigart, A. V., & Wing, R. F. 2000b, AJ, 119, 1424 [Google Scholar]
- Hurley, J. R., & Shara, M. M. 2002, ApJ, 565, 1251 [Google Scholar]
- Ida, S., & Lin,D. N. C. 2004, ApJ, 604, 388 [Google Scholar]
- Izidoro, A., Morbidelli, A., Raymond, S. N., Hersant, F., & Pierens, A. 2015, A&A, 582, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaib, N. A., Raymond, S. N., & Duncan, M. 2013, Nature, 493, 381 [Google Scholar]
- Kervella, P., Bersier, D., Mourard, D., et al. 2004, A&A, 428, 587 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, J. Korean Astron. Soc., 49, 37 [Google Scholar]
- Kratter, K. M., & Perets, H. B. 2012, ApJ, 753, 91 [Google Scholar]
- Liu, H.-G., Zhang, H., & Zhou, J.-L. 2013, ApJ, 772, 142 [Google Scholar]
- Lodieu, N., Dobbie, P. D., Cross, N. J. G., et al. 2013, MNRAS, 435, 2474 [Google Scholar]
- Ma, S., Mao, S., Ida, S., Zhu, W., & Lin, D. N. C. 2016, MNRAS, 461, L107 [Google Scholar]
- Malmberg, D., Davies, M. B., & Heggie, D. C. 2011, MNRAS, 411, 859 [Google Scholar]
- Marzari, F., & Weidenschilling, S. J. 2002, Icarus, 156, 570 [Google Scholar]
- Mróz, P., Udalski, A., Skowron, J., et al. 2017, Nature, 548, 183 [Google Scholar]
- Mróz, P., Ryu, Y.-H., Skowron, J., et al. 2018, AJ, 155, 121 [Google Scholar]
- Mužić, K., Scholz, A., Geers, V. C., & Jayawardhana, R. 2015, ApJ, 810, 159 [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., & Quanz, S. P. 2012, MNRAS, 419, 2448 [Google Scholar]
- Peña Ramírez, K., Béjar, V. J. S., Zapatero Osorio, M. R., Petr-Gotzens, M. G., & Martín, E. L. 2012, ApJ, 754, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Poleski, R., Skowron, J., Udalski, A., et al. 2014, ApJ, 795, 42 [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [Google Scholar]
- Rasio, F. A., & Ford, E. B. 1996, Science, 274, 954 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scharf, C., & Menou, K. 2009, ApJ, 693, L113 [Google Scholar]
- Shvartzvald, Y., Maoz, D., Udalski, A., et al. 2016, MNRAS, 457, 4089 [Google Scholar]
- Silsbee, K., & Tremaine, S. 2018, AJ, 155, 75 [Google Scholar]
- Spurzem, R., Giersz, M., Heggie, D. C., & Lin, D. N. C. 2009, ApJ, 697, 458 [Google Scholar]
- Sumi, T., Kamiya, K., Bennett, D. P., et al. 2011, Nature, 473, 349 [Google Scholar]
- Sumi, T., Bennett, D. P., Bond, I. A., et al. 2013, ApJ, 778, 150 [Google Scholar]
- Sumi, T., Udalski, A., Bennett, D. P., et al. 2016, ApJ, 825, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, A. P., & Fabrycky, D. C. 2016, ApJ, 818, 6 [Google Scholar]
- Suzuki, D., Bennett, D. P., Sumi, T., et al. 2016, ApJ, 833, 145 [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 1999, Nature, 402, 635 [Google Scholar]
- Thommes, E. W., Duncan, M. J., & Levison, H. F. 2002, AJ, 123, 2862 [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Udalski, A., Szymański, M. K., & Szymański, G. 2015, Acta Astron., 65, 1 [NASA ADS] [Google Scholar]
- Veras, D., & Moeckel, N. 2012, MNRAS, 425, 680 [Google Scholar]
- Veras, D., Crepp, J. R., & Ford, E. B. 2009, ApJ, 696, 1600 [Google Scholar]
- Veras, D., Wyatt, M. C., Mustill, A. J., Bonsor, A., & Eldridge, J. J. 2011, MNRAS, 417, 2104 [Google Scholar]
- Veras, D., Mustill, A. J., Gänsicke, B. T., et al. 2016, MNRAS, 458, 3942 [Google Scholar]
- Voyatzis, G., Hadjidemetriou, J. D., Veras, D., & Varvoglis, H. 2013, MNRAS, 430, 3383 [Google Scholar]
- Weidenschilling, S. J., & Marzari, F. 1996, Nature, 384, 619 [Google Scholar]
- Whitworth, A. P., & Stamatellos, D. 2006, A&A, 458, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woźniak, P. R. 2000, Acta Astron., 50, 421 [NASA ADS] [Google Scholar]
- Wray, J. J., Eyer, L., & Paczyński, B. 2004, MNRAS, 349, 1059 [Google Scholar]
- Yee, J. C., Udalski, A., Sumi, T., et al. 2009, ApJ, 703, 2082 [Google Scholar]
- Yoo, J., DePoy, D. L., Gal-Yam, A., et al. 2004, ApJ, 603, 139 [Google Scholar]
As both sources are very red, it is important to determine how well the empirical CSB relations are calibrated in this range. The relation of Kervella et al. (2004) was derived for giants with colors
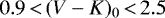 , but it agrees well with the earlier relation by Fouque & Gieren (1997), which is valid in a wider color range. Groenewegen (2004) published a CSB relation for M giants (
, but it agrees well with the earlier relation by Fouque & Gieren (1997), which is valid in a wider color range. Groenewegen (2004) published a CSB relation for M giants (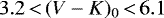 ), which gives angular radii that are systematically 10% lower than those based on Kervella et al. (2004):
θ* = 10.9 ± 0.7μas (OGLE-2012- BLG-1323) and
θ* = 29.8 ± 1.9μas (OGLE-2017-BLG-0560). Adams et al. (2018) recently published a new CSB relation for giants (
), which gives angular radii that are systematically 10% lower than those based on Kervella et al. (2004):
θ* = 10.9 ± 0.7μas (OGLE-2012- BLG-1323) and
θ* = 29.8 ± 1.9μas (OGLE-2017-BLG-0560). Adams et al. (2018) recently published a new CSB relation for giants ( ), from which we find
θ* = 11.5 ± 0.9μas (OGLE-2012-BLG-1323) and
θ* = 32.3 ± 2.3μas (OGLE-2017-BLG-0560), in good agreement with our determination.
), from which we find
θ* = 11.5 ± 0.9μas (OGLE-2012-BLG-1323) and
θ* = 32.3 ± 2.3μas (OGLE-2017-BLG-0560), in good agreement with our determination.
All Tables
All Figures
 |
Fig. 1 Light curves of two ultrashort microlensing events. Upper panel: OGLE-2012-BLG-1323. Lower panel: OGLE-2017-BLG-0560. Both events show strong finite-source effects, which allows us to measure their angular Einstein radii. |
| In the text | |
 |
Fig. 2 OGLE-IV color–magnitude diagrams for stars in 2′× 2′ regions around OGLE-2012-BLG-1323 and OGLE-2017-BLG-0560. Sources are marked with blue squares and are likely located in the Galactic bulge. If sources were M dwarfs, they would have absolute I-band magnitudesof 9.75 (OGLE-2012-BLG-1323) and 13.90 (OGLE-2017-BLG-0560; Pecaut & Mamajek 2013) and would be located at a distance of 140 and 16 pc, respectively, which contradicts the Gaia DR2 parallaxes (0.15 ± 0.14 mas and 0.23 ± 0.19 mas, respectively). |
| In the text | |
 |
Fig. 3 Gaia DR2 proper motions of stars within 4′ of OGLE-2012-BLG-1323 (left panel) and OGLE-2017-BLG-0560 (right panel). Blue contours correspond to the main-sequence stars (Galactic disk population) and red contours to giants (bulge population). Solid contours enclose 68 and 95% of all objects. The source is marked with a black dot. The black dashed circle corresponds to the relative source-lens proper motion of 5.6 mas yr−1 (left panel) and 15.6 mas yr−1 (right panel). |
| In the text | |
 |
Fig. 4 Probability of detecting the putative host star as a function of star-planet separation. Solid curves correspond to the lens located in the Galactic bulge (πrel = 0.01 mas) and dashed curves to the lens in the Galactic disk (πrel = 0.1 mas). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


