EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 622 (February 2019) A&A, 622 (2019) A94 Full HTML
Free Access
Issue
A&A
Volume 622, February 2019
Article Number A94
Number of page(s) 7
Section Galactic structure, stellar clusters and populations
DOI https://doi.org/10.1051/0004-6361/201834477
Published online 01 February 2019

© ESO 2019

1. Introduction

The formation of the Galactic bulge is a debated topic within the context of galaxy evolution (e.g. Renzini et al. 2018). Recent studies on low-Galactic-latitude fields revealed a complex scenario with a combination of different stellar populations including metal-poor and metal-rich components with different spatial distribution, kinematics, and possibly also distinct ages (Babusiaux et al. 2010, 2014). These studies indicate that the moderately metal-poor population component corresponds to a spheroidal old population, and the metal-rich one is confined to a bar/disc. These two components contain respectively 48% and 52% of the stars according to Zoccali et al. (2018).

The globular clusters (GCs) projected in the direction of the Galactic bulge can be used as population tracers and can help to constrain the bulge formation and evolution models. This work is part of an effort to study the globular clusters of the inner bulge as presented, for example, in Barbuy et al. (1998, 2018a,b) and Bica et al. (2016).

Proper motions derived using data from ground-based and space telescopes, in particular from Gaia, together with orbital calculations for bulge GCs are now becoming available (e.g. Casetti-Dinescu et al. 2013; Moreno et al. 2014; Rossi et al. 2015; Pérez-Villegas et al. 2018; Vasiliev 2019). These studies show that there are some systematic trends in the orbital parameters, possibly related also to metal abundances, indicating “families” of GCs with distinct origins. The present study is dedicated to two moderately metal-poor GCs, Terzan 10 and Djorgovski 1, with metallicity [Fe/H] ∼ −1.0 (Ortolani et al. 1995, 1997; Harris 1996, edition 2010). These clusters are located at low Galactic latitudes and therefore in very reddened and crowded regions.

Terzan 10 (ESO521–SC16), discovered by Terzan (1971), is located at J2000 α = 18h02m57.8s, δ = −26°04″, with Galactic coordinates l = 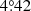4 . ° 42 $ 4{{\overset{\circ}{.}}}42 $, b = − 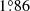1 . ° 86 $ 1{{\overset{\circ}{.}}}86 $. We point out that the coordinates and designations in Ortolani et al. (1997) were mistyped.

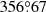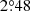Djorgovski 1, discovered by Djorgovski (1987), is located at α = 17h47m28.7s, δ = −33°03′59″, with Galactic coordinates l = 356 . ° 67 $ 356{{\overset{\circ}{.}}}67 $, b = − 2 . ° 48 $ 2{{\overset{\circ}{.}}}48 $.

Recent studies of the bulge area have provided a series of new GCs and candidates (Minniti et al. 2018; Camargo 2018; Ryu & Lee 2018; Bica et al. 2018; Piatti 2018). A consistent derivation of parameters (distance, reddening, age) requires deep high-resolution images however, and the samples already known are still lacking accurate values for these parameters; a good example is provided by the two GCs studied here. A useful approach that has been leading to newly derived distances is the systematic observation of variables, in particular in the VISTA Variables in the Via Lactea (VVV) survey (Saito et al. 2012). Using RR Lyrae detected with VVV and other sources, Alonso-García et al. (2015) derived a distance for Terzan 10.

The main goal of this work is to obtain accurate distances, which, together with kinematical data including recent literature providing radial velocities, and the proper motions obtained from Gaia Data Release 2 (hereafter Gaia DR2; Gaia Collaboration 2018a), allow us to reconstruct their orbital parameters.

Observations are described in Sect. 2, we present Hubble Space Telescope (HST) colour-magnitude diagrams (CMDs) with superimposed red giants measured with Gaia in Sect. 3, cluster parameters and orbits are derived for Terzan 10 and Djorgovski 1 (hereafter Djorg 1) in Sect. 4, and conclusions are drawn in Sect. 5.

2. Observations and data reduction

For this work we used the available HST observations of the central regions of the clusters. For Terzan 10 we made use of the observations collected during the mission GO-14074 (PI: Cohen, mean epoch 2016.4) in F606W with the Wide Field Channel (WFC) of the Advanced Camera for Survey (ACS), and in F160W with the IR channel of the Wide Field Camera 3 (WFC3). Djorg 1 data were collected with ACS/WFC in F606W and F814W filters during the mission GO-9799 (PI: Rich, mean epoch 2004.15).

For the data reduction we adopted the software kitchen_sync2 described in detail in Nardiello et al. (2018). Briefly, using flc images and perturbed empirical PSF arrays, the software analyses all the exposures simultaneously to find and measure the sources. We refer the reader to Nardiello et al. (2018) and Bellini et al. (2017) for a detailed description of this approach.

Magnitudes have been calibrated into the Vega-mag system by comparing aperture photometry on drc images against our PSF-fitting photometry and adopting the photometric zero-points given by the ACS Zero-points calculator1 in the case of ACS/WFC observations, and by Kalirai et al. (2009) in the case of WFC3/IR data.

Terzan 10 and Djorg 1 I-band images, collected with EFOSC2 at NTT in 2012, are presented in Figs. 1 and 2. Terzan 10 is very compact (c = 0.8) according to the structural analysis of Bonatto & Bica (2008). Djorg 1 is rather loose with no evidence of post-core collapse (Trager et al. 1993).

thumbnail Fig. 1.

NTT 180s I image of Terzan 10. North is up, east to the right. Size is 2 × 2 arcmin2.

thumbnail Fig. 2.

NTT 240s I image of Djorgovski 1. North is up, east to the right. Size is 2 × 2 arcmin2.

3. Colour-magnitude diagrams and cluster parameters

Table 1 gives basic parameters taken from the literature for the sample clusters. Only recently, metallicities, and in particular the radial velocities, of the two sample clusters were derived from spectroscopic data. For Djorg 1, medium-resolution spectra were obtained with FORS2 at VLT in the region of the CaII triplet lines (CaT) by Vásquez et al. (2018). The CaT calibrations developed by Saviane et al. (2012) and improved in Vásquez et al. (2018) appear to be reliable. For Terzan 10, Geisler et al. (in prep.) obtained high-resolution CRIRES at VLT spectra of three stars, having derived their metallicities and radial velocities.

Table 1.

Literature values.

Figures 3 and 4 show the Gaia DR2 proper motion values for all stars in common between HST and Gaia (upper panels) in Terzan 10 and Djorg 1, respectively. Magenta dots identify red giant branch members of both clusters, located within < 10 arcsec and < 20 arcsec of the centres of Terzan 10 and Djorg 1, respectively. For Terzan 10, the lower panels of Fig. 3 show mF606W vs. mF606W−mF160W CMDs for the original (left panel), and differential-reddening-corrected (right panel) photometry.

thumbnail Fig. 3.

Terzan 10: upper panels: Gaia DR2 proper motions for the stars in common between the HST catalogue and Gaia DR2; magenta dots are the stars located within 15 arcsec from the cluster centre that also have a proper motion < 2 mas yr−1 from the mean motion of the cluster (i.e. −6.96, −2.45 mas yr−1). Bottom panels: mF606W vs. mF606W−mF160W CMD before (left-hand panel) and after (right-hand panel) the differential-reddening correction. Grey points are all the stars in the HST catalogue; black points are the stars in the HST catalogue that are located within 15 arcsec from the cluster centre; magenta points are the stars in common with Gaia DR2 catalogue that are located within 15 arcsec from the cluster centre and have a proper motion < 2 mas yr−1 from the mean motion of the cluster.

thumbnail Fig. 4.

Djorg 1: upper panels: Gaia DR2 proper motions for the stars in common between the HST catalogue and Gaia DR2; magenta dots are the stars located within 8 arcsec from the cluster centre that also have a proper motion < 2 mas yr−1 from the mean motion of the cluster (i.e. −4.99, −8.32 mas yr−1). Bottom panels: mF606W vs. mF606W−mF814W CMD before (left-hand panel) and after (right-hand panel) the differential-reddening correction. Grey points are all the stars in the HST catalogue; black points are the stars in the HST catalogue that are located within 10 arcsec from the cluster centre; magenta points are the stars in common with Gaia DR2 catalogue that are located within 10 arcsec from the cluster centre and have a proper motion < 2 mas yr−1 from the mean motion of the cluster.

It appears that the observed CMD (left panel) is better defined, in particular the blue horizontal branch. This is due to the fact that differential-reddening corrections need a well-defined cleaned sequence of bona fide member stars. For this reason, in the subsequent analysis we use the original photometric data for Terzan 10.

For Djorg 1, the upper panels from Fig. 4 are similar to Fig. 3; the lower panels of Fig. 4 show the mF606W vs. mF606W−mF814W CMDs that correspond to the original photometry (left panel), and to differential-reddening corrected CMD data (right panel). In this case the differential-reddening-corrected CMD is improved relative to the observed one, and is therefore adopted for the analysis.

The differential-reddening corrections were carried out following the procedures employed by Milone et al. (2012), briefly described as follows. In the mF606W vs. mF606W−mF814W CMD of Djorg 1, and mF606W vs. mF606W−mF160W CMD of Terzan 10, for a given target star, we selected the 40 closest cluster stars and measured their mean colour offset from the fiducial cluster sequence (along the reddening correction). This quantity is the local estimate of the differential reddening to be used to correct the magnitude of the target star.

For both clusters a blue horizontal branch is clearly detected. This morphology together with their moderately metal-poor metallicity indicates that the clusters should be very old, as, for example, NGC 6522 and HP 1 (Kerber et al. 2018a,b).

Figures 5 and 6 show the mF606W vs. mF606W−mF160W non-differential-reddening-corrected CMDs for Terzan 10, and mF606W vs. mF606W−mF814W differential-reddening-corrected CMDs for Djorg 1. In order to minimize the contamination by field stars and to use only well measured stars in the isochrone-fitting procedure, we selected stars located between 1.5 arcsec and 11.0 arcsec (30 < r < 220 in pixels) from the centre of Terzan 10 (Fig. 5) and within 20 arcsec (r <  400 pixels) from the centre of Djorg 1 (Fig. 6). These radial interval selections are slightly different relative to those used for Figs. 3 and 4.

thumbnail Fig. 5.

Terzan 10: mF606W vs. mF606W−mF160W CMD, for an extraction with 1.5 arcsec < r < 11 arcsec. A BaSTI alpha-enhanced isochrone of Z = 0.001, and 13 Gyr is overplotted.

thumbnail Fig. 6.

Djorg 1: mF606W vs. mF606W−mF814W differential-reddening-corrected CMD. The data correspond to a central extraction of r <  20 arcsec. A BaSTI alpha-enhanced isochrone of Z = 0.001, and 13 Gyr is overplotted.

The BaSTI (Pietrinferni et al. 2004, 2006) alpha-enhanced isochrone of Z = 0.001 and 13 Gyr is overplotted in both these figures. The alpha-enhanced BaSTI isochrones were corrected for reddening-dependent effective temperatures, as discussed in Ortolani et al. (2017). This correction mainly shrinks the CMDs in colours, and the fit quality greatly improves for very reddened clusters, such as Djorg 1.

In the derivations of cluster parameters below, the effect of the uncertainty on metallicity is negligible: a change of [Fe/H] ± 0.1 has a minor effect on the distance. This corresponds to a reddening difference of E(606 − 160) = ± 0.03 mag or A(606) = ± 0.04, producing a distance error of ±0.02 kpc. The effect on the Horizontal Branch (HB), corresponding to a difference in the absolute HB magnitude from the models, is a variation of only ΔM(606)HB = ±0.02 mag. Combining the two effects (they affect the distance modulus in the same way) we get a total error in the distance of ±0.04 kpc, which is very small compared to other effects. The error in the distance is then a combination of the photometric errors, contamination, reddening and [Fe/H]; the first two are likely dominating however.

3.1. Terzan 10

From the isochrone fit, we derive an apparent distance modulus of (m − M)F606W = 21.1 ± 0.1. Measuring AF606W = 6.02 ± 0.05 in the CMD, an absolute distance modulus (m − M)0 = 15.08 is obtained. A reddening E(F606W − F160W) = 4.83 converts to E(B − V)=2.17. We used the standard value of RV = AV/E(B − V) = 3.1. The corresponding visual absorption AV = 4.83/0.718 = 6.73, where the factor AV/AF606W is given in the PARSEC isochrone site (Bressan et al. 2012). Finally, a distance from the Sun of d⊙ = 10.3 ± 1 kpc is obtained.

Alonso-García et al. (2015) obtained a distance d⊙ = 10.3 kpc by selecting possible RR Lyrae members. Our previous analysis of Terzan 10, given in Ortolani et al. (1997), provided E(B − V)=2.40, and a distance of Terzan 10 to the Sun a factor two closer to us. Those data were not deep enough, and the horizontal branch was barely detected. The present, deeper data give a reliable distance based on a now clear blue HB, in very good agreement with Alonso-García et al. (2015).

3.2. Djorgovski 1

Table 1 shows that there are large discrepancies in metallicity and distance measurements, but not in reddening. The aim of the present work is to solve the distance ambiguity in the literature, by using deep high-resolution images and optimized CMDs from differential-reddening corrections.

From the isochrone fit, we derive an apparent distance modulus of (m − M)F606W = 19.6 ± 0.1. A measurement of AF606W = 4.76 ± 0.05 in the CMD and an absolute distance modulus (m − M)0 = 14.85 is obtained. A reddening E(F606W − F814W) = 1.63 converts to E(B − V)=1.66. The corresponding visual absorption is AV = 5.16. Finally, we get a distance to the Sun of d⊙ = 9.3 ± 0.5 kpc.

4. Orbits of Terzan 10 and Djorg 1

For the first time, we are able to estimate the probable Galactic orbit of both clusters, Terzan 10 and Djorg 1. This is due to the combination of the proper motions from Gaia DR2 given by Vasiliev (2019), the recent radial-velocity determinations using CaT spectra that were obtained with the FORS2 at VLT and CRIRES at VLT (Vásquez et al. 2018; Celeste Parisi, priv. comm.), and the accurate distances calculated in this work.

For the Galactic model, we employed an axisymmetric background that includes a Sérsic bulge, an exponential disc generated by the superposition of three Miyamoto-Nagai potentials (Miyamoto & Nagai 1975) following the recipe made by Smith et al. (2015), and a Navarro-Frenk-White (NFW) density profile (Navarro et al. 1997) to model the dark-matter halo, which has a circular velocity V0 = 241 km s−1 at R0 = 8.2 kpc (Bland-Hawthorn & Gerhard 2016). For the Galactic bar, we used a triaxial Ferrer’s ellipsoid, where all the mass from the bulge component is converted into a bar. For the bar potential, we consider a total bar mass of 1.2 × 1010 M⊙, an angle of 25° with the Sun-major axis of the bar, a gradient of pattern speed of the bar of Ωb = 45, 50, and 55 km s−1 kpc−1, and a major axis extension of 3.5 kpc. We keep the same bar extension, even though we change the bar pattern speed.

The integration of the orbits was made with the NIGO tool (Rossi 2015a), which includes the potentials mentioned above. The equations of motion are solved numerically using the Shampine–Gordon algorithm (for details, see Rossi 2015b). We adopted the right-handed, Galactocentric Cartesian system, x toward the Galactic centre, and z toward the Galactic North Pole. The initial conditions of Terzan 10 and Djorg 1 are obtained from the observational data, coordinates, heliocentric distance, radial velocity, and absolute proper motions given in Table 2. The velocity components of the Sun with respect to the local standard of rest are (U, V, W)⊙ = (11.1, 12.24, 7.25) km s−1 (Schönrich et al. 2010). In order to estimate the effect of the uncertainties associated to the clusters’ parameters, we use the Monte Carlo method to generate a set of 1000 initial conditions for each cluster, taking into account the errors of distance, heliocentric radial velocity, and absolute proper motion components. With such initial conditions, we integrate the orbits forward for 10 Gyr. For each orbit, we calculate the perigalactic distance rmin, apogalactic distance rmax, the maximum vertical excursion from the Galactic plane |z|max, and the eccentricity defined by e = (rmax − rmin)/(rmax + rmin).

Table 2.

Parameters for the orbit integration.

The results of the orbit integration are shown in Fig. 7, displaying the probability densities of the orbits in the x − y and R − z projection co-rotating with the bar. The red and yellow colours exhibit the region of the space that the orbits of Terzan 10 (left panels) and Djorg 1 (right panels) cross most frequently. The black curves are the corresponding orbits using the central values of the cluster observational parameters.

thumbnail Fig. 7.

Probability density map for the x − y and R − z projections of the 1000 orbits for Terzan 10 (left panels) and Djorg 1 (right panels). The orbits are co-rotating with the bar frame. The bar pattern speed, Ωb, is given in units of km s−1 kpc−1. The red and yellow colors correspond to the larger probabilities. The black lines show the orbits using the central values presented in Table 2.

Ranges in perigalactic distance, apogalactic distance, maximum vertical height and eccentricity are presented in Fig. 8, for Terzan 10 (top panels) and Djorg 1 (bottom panels), the different colours represent the angular velocities investigated here. The orbits of Terzan 10 have radial excursions between ∼0.1 and ∼30 kpc, with maximum vertical excursions from the Galactic plane between ∼1 and ∼20 kpc, and eccentricities e >  0.7. For Djorg 1, the radial excursion is between ∼0.1 and ∼20 kpc, with maximum vertical excursions from the Galactic plane between ∼0.1 and ∼6 kpc, and eccentricities e >  0.75. The eccentricity distribution of Djorg 1 clearly shows a double peak that is related to the double peak also presented in the perigalactic distance: the smaller perigalactic distances with rmin ∼ 2 kpc (left peak in first panel) correspond to the higher eccentricities e >  ∼0.9 (right peak in fourth panel). The variation of the angular velocity seems to have a negligible effect on the orbits for both clusters.

thumbnail Fig. 8.

Distribution of orbital parameters for Terzan 10 (top panels) and Djorg 1 (bottom panels), perigalactic distance rmin, apogalactic distance rmax, maximum vertical excursion from the Galactic plane |z|max, and eccentricity. The colours show the different angular speed of the bar, Ωb = 45 (blue), 50 (orange), and 55 (green) km s−1 kpc−1.

In Table 3 we present average orbital parameters of the set of orbits for Terzan 10 and Djorg 1, where the errors provided in each column are obtained by considering the 16th and 84th percentile of the distribution. The orbital characteristics of both clusters are inconsistent with orbits of bulge GCs that have [Fe/H] ∼ −1.0 (Pérez-Villegas et al. 2018), meaning that these clusters are intruders in the Galactic bulge, and their orbital parameters are more consistent with GCs that belong to the halo or a thick disc component.

Table 3.

Monte Carlo average orbital parameters of Terzan 10 and Djorg 1.

5. Discussions and conclusions

Terzan 10 and Djorg 1 were selected given that they are moderately metal-poor ([Fe/H] ∼ −1.0) as listed in Barbuy et al. (1998, 2009), and they are projected close to the Galactic centre. The aim is to identify genuine old bulge clusters, such as NGC 6522 (Barbuy et al. 2014; Kerber et al. 2018a), HP 1 (Ortolani et al. 2011; Barbuy et al. 2016; Kerber et al. 2018b), and NGC 6558 (Barbuy et al. 2018a,b). Furthermore, due to difficulties of crowding and absorption, there are very few studies of these clusters, and discrepancies are found in literature parameters.

Deep CMDs were obtained using HST optical/infrared filters (F606W, F160W) for Terzan 10, and (F606W, F814W) for Djorg 1. Since the field contamination is very high, it was only possible to correct the CMD of Djorg 1 for differential reddening. The CMDs are deep and accurate enough to reveal blue horizontal branches for both clusters. We derived reddening and distance values that supersede the literature uncertainties reported in Table 1.

We estimated the absolute total magnitude for the sample clusters by counting red giant branch stars above the horizontal branch level, and taking into account the cluster profiles. Based on the absolute total magnitudes of template clusters in Harris (1996, 2010 edition), for the RGB counts we used 13 GCs, especially selecting distant halo GCs so as to include as many giants as possible, according to the CMDs given by M. Castellani2. We obtain 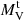M V t $ M_{\mathrm{V}}^{\mathrm{t}} $ = −5.8 ± 0.4 for both clusters, which is fainter than the values of −6.35 and −6.98 for Terzan 10 and Djorg 1, respectively, given in Harris (1996, 2010 edition). These results are comparable to most Palomar clusters, which are more luminous than ultra-faint clusters (e.g. Kim & Jerjen 2015; Luque et al. 2016), and fainter than classical halo clusters. This faint magnitudes suggest a mass loss along their trajectories crossing the bulge and disc in many orbits (Aguilar et al. 1988). Together with Gaia proper motions, radial velocities from the recent literature, and our improved distances, we were able to reach our ultimate objective of computing their orbits. The high values of proper motions and radial velocities lead to apogalactic distances of about 10−20 kpc, characterising Terzan 10 and Djorg 1 as halo clusters. Therefore, although these clusters are projected in the central parts of the bulge, they are halo intruders.

2

http://gclusters.altervista.org/, by M. Castellani, INAF, Osservatorio Astronomico di Roma.

Acknowledgments

We are grateful to Celeste Parisi and Doug Geisler for providing the radial velocity of Terzan 10, in advance of publication. SO and DN acknowledge partial support by the Università degli Studi di Padova Progetto di Ateneo CPDA141214 and BIRD178590 and by INAF under the program PRIN-INAF2014. APV acknowledges a FAPESP grant no. 2017/15893-1. BB and EB acknowledge grants from the brazilian agencies CAPES – Finance code 001, CNPq and FAPESP.

References

  1. Aguilar, L., Hut, P., & Ostriker, J. P. 1988, ApJ, 335, 720 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alonso-García, J., Dékány, I., Catelan, M., et al. 2015, AJ, 149, 99 [NASA ADS] [CrossRef] [Google Scholar]
  3. Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Babusiaux, C., Katz, D., Hill, V., et al. 2014, A&A, 563, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Barbuy, B., Bica, E., & Ortolani, S. 1998, A&A, 333, 117 [NASA ADS] [Google Scholar]
  6. Barbuy, B., Zoccali, M., Ortolani, S., et al. 2009, A&A, 507, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Barbuy, B., Chiappini, C., Cantelli, E., et al. 2014, A&A, 570, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Barbuy, B., Cantelli, E., Vemado, A., et al. 2016, A&A, 591, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Barbuy, B., Muniz, L., Ortolani, S., et al. 2018a, A&A, 619, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Barbuy, B., Chiappini, C., & Gerhard, O. 2018b, ARA&A, 56, 223 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bellini, A., Anderson, J., Bedin, L. R., et al. 2017, ApJ, 842, 6 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bica, E., Barbuy, B., & Ortolani, S. 2016, PASA, 33, 28 [Google Scholar]
  13. Bica, E., Minniti, D., Bonatto, C., & Hempel, M. 2018, PASA, 35, 25 [Google Scholar]
  14. Bland-Hawthorn, J., & Gerhard, O. 2016, ARA&A, 54, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Bonatto, C., & Bica, E. 2008, A&A, 479, 741 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  17. Camargo, D. 2018, ApJ, 860, L27 [NASA ADS] [CrossRef] [Google Scholar]
  18. Casetti-Dinescu, D. I., Girard, T. M., Jílková, L., et al. 2013, AJ, 146, 33 [NASA ADS] [CrossRef] [Google Scholar]
  19. Davidge, T. J. 2000, ApJS, 126, 105 [NASA ADS] [CrossRef] [Google Scholar]
  20. Djorgovski, S. 1987, ApJ, 317, L13 [NASA ADS] [CrossRef] [Google Scholar]
  21. Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
  22. Gaia Collaboration (Brown, A. G. A., et al.) 2018a, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gaia Collaboration (Helmi, A., et al.) 2018b, A&A, 616, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kalirai, J. S., MacKenty, J., Bohlin, R., et al. 2009, Space Telescope WFC Instrument Science Report [Google Scholar]
  26. Kerber, L. O., Nardiello, D., Ortolani, S., et al. 2018a, ApJ, 853, 15 [NASA ADS] [CrossRef] [Google Scholar]
  27. Kerber, L. O., Libralato, M., Souza, S., et al. 2018b, MNRAS, submitted [Google Scholar]
  28. Kim, D., & Jerjen, H. 2015, ApJ, 799, 73 [NASA ADS] [CrossRef] [Google Scholar]
  29. Luque, E., Queiroz, A., Santiago, B., et al. 2016, MNRAS, 458, 603 [NASA ADS] [CrossRef] [Google Scholar]
  30. Milone, A., Piotto, G., Bedin, L. R., et al. 2012, A&A, 540, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Minniti, D., Geisler, D., Alonso-García, J., et al. 2018, ApJ, 849, L24 [Google Scholar]
  32. Miyamoto, M., & Nagai, R. 1975, PASJ, 27, 533 [NASA ADS] [Google Scholar]
  33. Moreno, E., Pichardo, B., & Velázquez, H. 2014, ApJ, 793, 110 [NASA ADS] [CrossRef] [Google Scholar]
  34. Nardiello, D., Libralato, M., Piotto, G., et al. 2018, MNRAS, 481, 3382 [NASA ADS] [CrossRef] [Google Scholar]
  35. Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
  36. Ortolani, S., Bica, E., & Barbuy, B. 1995, A&A, 296, 680 [NASA ADS] [Google Scholar]
  37. Ortolani, S., Bica, E., & Barbuy, B. 1997, A&AS, 126, 319 [Google Scholar]
  38. Ortolani, S., Barbuy, B., Momany, Y., et al. 2011, ApJ, 737, 31 [NASA ADS] [CrossRef] [Google Scholar]
  39. Ortolani, S., Cassisi, S., & Salaris, M. 2017, Galaxies, 5, 28 [NASA ADS] [CrossRef] [Google Scholar]
  40. Pérez-Villegas, A., Rossi, L., Ortolani, S., et al. 2018, PASA, 35, 21 [Google Scholar]
  41. Piatti, A. E. 2018, MNRAS, 477, 2164 [NASA ADS] [CrossRef] [Google Scholar]
  42. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 167 [NASA ADS] [Google Scholar]
  43. Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2006, ApJ, 642, 797 [NASA ADS] [CrossRef] [Google Scholar]
  44. Renzini, A., Gennaro, M., Zoccali, M., et al. 2018, ApJ, 863, 16 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rossi, L. J. 2015a, Astrophysics Source Code Library [record ascl:1501.002] [Google Scholar]
  46. Rossi, L. J. 2015b, Astron. Comput., 12, 11 [NASA ADS] [CrossRef] [Google Scholar]
  47. Rossi, L., Ortolani, S., Bica, E., Barbuy, B., & Bonfanti, A. 2015, MNRAS, 450, 3270 [NASA ADS] [CrossRef] [Google Scholar]
  48. Ryu, J., & Lee, M.-G. 2018, ApJ, 863, L38 [NASA ADS] [CrossRef] [Google Scholar]
  49. Saito, R. K., Minniti, D., Dias, B., et al. 2012, A&A, 544, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Saviane, I., Da Costa, G. S., Held, E. V., et al. 2012, A&A, 540, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Schönrich, R., Binney, J., & Dehnen, W. 2010, MNRAS, 403, 1829 [NASA ADS] [CrossRef] [Google Scholar]
  52. Smith, R., Flynn, C., Candlish, G. N., Fellhauer, M., & Gibson, B. K. 2015, MNRAS, 448, 2934 [NASA ADS] [CrossRef] [Google Scholar]
  53. Terzan, A. 1971, A&A, 12, 457 [NASA ADS] [Google Scholar]
  54. Trager, S. C., Djorgovski, S., & King, I. R. 1993, ASPC, 50, 347 [NASA ADS] [Google Scholar]
  55. Valenti, E., Ferraro, F. R., & Origlia, L. 2010, MNRAS, 402, 1729 [NASA ADS] [CrossRef] [Google Scholar]
  56. Vasiliev, E. 2019, MNRAS, in press [arXiv:1807.09775] [Google Scholar]
  57. Vásquez, S., Saviane, I., Held, E. V., et al. 2018, A&A, 619, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Zoccali, M., Valenti, E., & Gonzalez, O. A. 2018, A&A, 618, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Literature values.

In the text
Table 2.

Parameters for the orbit integration.

In the text
Table 3.

Monte Carlo average orbital parameters of Terzan 10 and Djorg 1.

In the text

All Figures

thumbnail Fig. 1.

NTT 180s I image of Terzan 10. North is up, east to the right. Size is 2 × 2 arcmin2.
In the text
thumbnail Fig. 2.

NTT 240s I image of Djorgovski 1. North is up, east to the right. Size is 2 × 2 arcmin2.
In the text
thumbnail Fig. 3.

Terzan 10: upper panels: Gaia DR2 proper motions for the stars in common between the HST catalogue and Gaia DR2; magenta dots are the stars located within 15 arcsec from the cluster centre that also have a proper motion < 2 mas yr−1 from the mean motion of the cluster (i.e. −6.96, −2.45 mas yr−1). Bottom panels: mF606W vs. mF606W−mF160W CMD before (left-hand panel) and after (right-hand panel) the differential-reddening correction. Grey points are all the stars in the HST catalogue; black points are the stars in the HST catalogue that are located within 15 arcsec from the cluster centre; magenta points are the stars in common with Gaia DR2 catalogue that are located within 15 arcsec from the cluster centre and have a proper motion < 2 mas yr−1 from the mean motion of the cluster.
In the text
thumbnail Fig. 4.

Djorg 1: upper panels: Gaia DR2 proper motions for the stars in common between the HST catalogue and Gaia DR2; magenta dots are the stars located within 8 arcsec from the cluster centre that also have a proper motion < 2 mas yr−1 from the mean motion of the cluster (i.e. −4.99, −8.32 mas yr−1). Bottom panels: mF606W vs. mF606W−mF814W CMD before (left-hand panel) and after (right-hand panel) the differential-reddening correction. Grey points are all the stars in the HST catalogue; black points are the stars in the HST catalogue that are located within 10 arcsec from the cluster centre; magenta points are the stars in common with Gaia DR2 catalogue that are located within 10 arcsec from the cluster centre and have a proper motion < 2 mas yr−1 from the mean motion of the cluster.
In the text
thumbnail Fig. 5.

Terzan 10: mF606W vs. mF606W−mF160W CMD, for an extraction with 1.5 arcsec < r < 11 arcsec. A BaSTI alpha-enhanced isochrone of Z = 0.001, and 13 Gyr is overplotted.
In the text
thumbnail Fig. 6.

Djorg 1: mF606W vs. mF606W−mF814W differential-reddening-corrected CMD. The data correspond to a central extraction of r <  20 arcsec. A BaSTI alpha-enhanced isochrone of Z = 0.001, and 13 Gyr is overplotted.
In the text
thumbnail Fig. 7.

Probability density map for the x − y and R − z projections of the 1000 orbits for Terzan 10 (left panels) and Djorg 1 (right panels). The orbits are co-rotating with the bar frame. The bar pattern speed, Ωb, is given in units of km s−1 kpc−1. The red and yellow colors correspond to the larger probabilities. The black lines show the orbits using the central values presented in Table 2.
In the text
thumbnail Fig. 8.

Distribution of orbital parameters for Terzan 10 (top panels) and Djorg 1 (bottom panels), perigalactic distance rmin, apogalactic distance rmax, maximum vertical excursion from the Galactic plane |z|max, and eccentricity. The colours show the different angular speed of the bar, Ωb = 45 (blue), 50 (orange), and 55 (green) km s−1 kpc−1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.