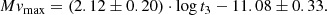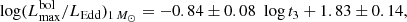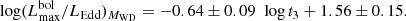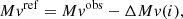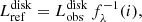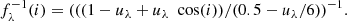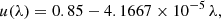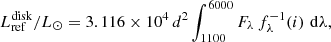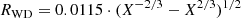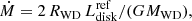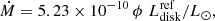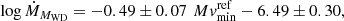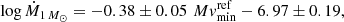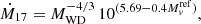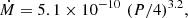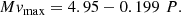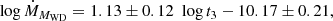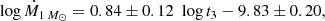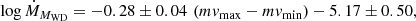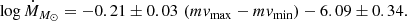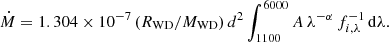| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A186 | |
| Number of page(s) | 16 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834238 | |
| Published online | 19 February 2019 | |
A UV and optical study of 18 old novae with Gaia DR2 distances: mass accretion rates, physical parameters, and MMRD⋆
1
INAF – Ossservatorio Astronomico di Trieste, Via Tiepolo 11, 34143 Trieste, Italy
e-mail: selvelli@oats.inaf.it
2
European Southern Observatory, Karl Schwarzschild-Str. 2, 85748 Garching, Germany
e-mail: rgilmozz@eso.org
Received:
13
September
2018
Accepted:
25
December
2018
We combine the results of our earlier study of the UV characteristics of 18 classical novae (CNe) with data from the literature and with the recent precise distance determinations from the Gaia satellite to investigate the statistical properties of old novae. All final parameters for the sample include a detailed treatment of the errors and their propagation. The physical properties reported here include the absolute magnitudes at maximum and minimum, a new maximum magnitude versus rate of decline (MMRD) relation, and the inclination-corrected 1100–6000 Å accretion disk luminosity. Most importantly, these data have allowed us to derive a homogenous set of accretion rates in quiescence for the 18 novae. All novae in the sample were super-Eddington during outburst, with an average absolute magnitude at maximum of −7.5 ± 1.0. The average absolute magnitude at minimum corrected for inclination is 3.9 ± 1.0. The median mass accretion rate is log Ṁ1 M⊙ = −8.52 (using 1 M⊙ as WD mass for all novae) or log ṀMWD = −8.48 (using the individual WD masses). These values are lower than those assumed in studies of CNe evolution and appear to attenuate the need for a hibernation hypothesis to interpret the nova phenomenon. We identified a number of correlations among the physical parameters of the quiescent and eruptive phases, some already known but others new and even surprising. Several quantities correlate with the speed class t3 including, unexpectedly, the mass accretion rate (Ṁ). This rate correlates also with the absolute magnitude at minimum corrected for inclination, and with the outburst amplitude, providing new and simple ways to estimate Ṁ through its functional dependence on (more) easily observed quantities. There is no correlation between Ṁ and the orbital period.
Key words: novae, cataclysmic variables / ultraviolet: stars / stars: distances / accretion, accretion disks
Based mainly on INES data from the IUE satellite. Other UV data utilized in this paper were obtained from the Multimission Archive at the Space Telescope Science Institute (MAST), see Paper I. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
© ESO 2019
1. Introduction
Old novae are the quiescent stage of systems that have undergone a historical classical nova explosion. Classical novae (CNe) are members of the class of cataclysmic variables (CVs), that is, close binary systems in which a white dwarf (WD) accretes hydrogen-rich material through an accretion disk from a low-mass, near-main-sequence companion. The “classical nova” phenomenon is a thermonuclear runaway (TNR) event that occurs when the accreted mass on the surface of the WD is large enough for the pressure at the base of the semi-degenerate shell to initiate nuclear reactions; see Starrfield et al. (1985), Shara (1989), Bode & Evans (2008), and Jose (2016) for comprehensive reviews.
Theoretical models for the outburst (hereafter OB) of CNe (see Shara et al. 1986; Livio 1992a; Prialnik & Kovetz 1992) require low mass accretion rates (hereafter Ṁ) during quiescence (10−11 − 10−9 M⊙ yr−1). Only at these rates does the material at the base of the H-rich envelope remain degenerate enough to ensure the observed strong “flash”. Instead, the available observations of old novae indicate higher Ṁ, of order 10−9 − 10−8 M⊙ yr−1. This apparent disagreement represents a disturbing problem in our understanding of the classical nova phenomenon (Prialnik & Kovetz 1992).
Ṁ is a fundamental parameter for our understanding of the evolution of CVs in general because these systems evolve under the effect of mass transfer. Angular momentum losses are required for mass transfer to occur at all (Hameury 1994). The standard paradigm of CV evolution assumes that angular momentum losses are driven by mechanisms such as magnetic wind braking (Verbunt & Zwaan 1981), dominating in systems with Porb > 3 h, and gravitational radiation (Paczyński 1967; King 1988), dominating in systems with Porb < 3 h, see also Spruit & Ritter (1983), Howell et al. (1997, 2001), Knigge (2006), and Knigge et al. (2011).
A major problem in the theory comes from the large spread (by at least one order of magnitude) in the mass transfer rates at a given orbital period (Patterson 1984; Warner 1995; Kolb 2001; Spruit & Taam 2001; Woudt et al. 2012). Explanations for this discrepancy requiring intermittent cycles produced by nova explosions (Shara et al. 1986) or by irradiation or mass loss effects (King et al. 1996) have been proposed.
It should be stressed, however, that reliable statements about Ṁ – the non plus ultra of binary evolution according to Patterson (2011) – can be found only for objects with well-determined distance and reddening, and by observations covering the satellite UV range (hereafter, simply UV) because the bulk of the accretion luminosity is emitted in this spectral region (Wade & Hubeny 1998). The homogeneous UV data on spectral energy distributions (SEDs) in Paper I are therefore of high relevance for this topic, and since old novae are (unlike other CVs, e.g., DNe) nearly stable accretors (Honeycutt et al. 1998; Retter & Naylor 2000; Puebla et al. 2007) their accretion luminosity and Ṁ can be determined with higher precision.
We note that throughout this paper accretion rate is used to indicate the mass transfer rate through the disk (the one that we derive from the observed disk luminosity). Other kinds of accretion rates that may be at play in these systems, for example the mass-loss rate from the donor, the accretion rate on to the WD, or the mass loss from the disk (e.g., via a wind or outflow through the boundary layer) cannot be determined from our data, and should not be confused with the accretion through the disk.
In Paper I (Selvelli & Gilmozzi 2013), we studied all available UV spectra of old novae. This provided a homogeneous determination of several characteristics (and their errors) of the 18 objects in the sample: the reddening E(B − V), the SED (well described by a power law), and the total UV-integrated flux. Paper I concluded that the UV SED is associated to radiation emitted by an accretion disk, that the disk accounts for most of the observed UV and optical flux, and that the contributions by the WD and the cool companion are of second order. The data also indicated that the quiescent state of classical novae is characterized by a nearly constant UV luminosity over a time interval of decades.
In this paper we combine the results from Paper I with data in the literature to derive physical parameters, revisit some known relations (e.g., the MMRD) and determine precise values of for Ṁ during the quiescence phase.
The second release of the Gaia data (Gaia Collaboration 2018) occurred while we were finalizing this paper and we decided to use the Gaia distances instead of the ones from HST/FGS or other parallax determinations (e.g., expansion) used earlier. The new distances mostly fall within the errors of the old ones, but with superior precision. We have propagated the new input to all derived physical quantities.
2. The basic parameters and their uncertainties
Table 1 contains the basic data for the novae of our sample obtained both from the literature (e.g., the magnitudes mvmin and mvmax, the rates of decline t2 and t3, the orbital period P, the system inclination, and the time ΔT elapsed from the OB at time of the UV observations, etc.) and from Paper I (e.g., the reddening Av and the UV-integrated flux distribution, etc). The orbital periods are mostly from Ritter & Kolb (2011). The orbital period of HR Lyr is quite uncertain; we adopted P = 0.1d from Leibowitz et al. (1995). For a discussion of the data regarding the system inclination see Sect. 8.
Data.
An important aspect of this paper is the determination of the uncertainties in the values of the basic physical quantities and their propagation to the final, most significant parameters, for example the accretion luminosity and Ṁ. All basic and derived parameters in this study contain error bars. For the basic parameter data (mvmin, mvmax, t3, Porb, etc.), we assumed as nominal value the average of the various values found in the literature (with some degree of personal judgement, e.g., in identifying multiple values in different old publications coming from the same source, sometime without attribution). We considered as “error bar” the semi-difference of their range; we are aware that in doing so we are probably overestimating the errors, but using the range rms as if the values were homogenous and normally distributed did not appear to be warranted, and we preferred to follow McLaughlin (1941) precept of “erring on the side of conservatism” when dealing with error estimates.
We found in Paper I that the most important source of error in the estimate of the UV SED, which is fundamental for the calculation of the disk luminosity, derives from the uncertainty in the estimate of the reddening correction, since this quantity directly affects the value of the index α in the power-law approximation of the SED and, as a consequence, the λ−integrated flux. See Paper I for the relevant values.
A detailed description of the handling of the propagation of errors is in Appendix A.
2.1. A note on the fits in the figures
There are some figures showing correlations in this paper, and they include linear fits between variables (or their log). We have chosen to show both the direct (y vs. x) and inverse (x vs. y) fits (dotted lines) because in most instances it is not obvious which variable is the independent one and we felt that this way gives a clearer idea of the range of slopes. We also show Deming (1943) regressions (as dashed lines), which account for errors in both x and y and therefore are, in our opinion, more realistic than standard 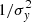 weighted fits. The fit coefficients in the text refer to the Deming regressions.
weighted fits. The fit coefficients in the text refer to the Deming regressions.
Whenever possible, novae are identified in the figures by unique three-letter labels.
2.2. Comments on parameters derived from the WD mass
Physical parameters that depend on the WD mass are derived in this paper for two separate cases: that of an identical white dwarf mass (MWD ≡ 1.0 M⊙) for all objects, and that of individual white dwarf masses, as determined from the literature and from the methods described in Sect. 10.
For clarity, the parameters are identified with subscripts 1 M⊙ or MWD, respectively.
In this way we can explore the role played by the WD mass on the parameters depending on it, and check for possible bias associated to this assumption (in particular avoiding the possible degeneracy between the WD mass and the parameters, for example t3, used to derive it): if a correlation exists for the 1 M⊙ case it is highly unlikely that the one for the individual WD masses is due to parameter degeneracy.
3. The distances in Gaia Data Release 2
The Gaia Data Release 2 (Gaia Collaboration 2018) provides precise positions, proper motions, and parallaxes for an unprecedented number of objects, that is, more than 1.3 billion (Luri et al. 2018). Data for all 18 novae of our sample are contained in this release. Their uncertainties are in most cases below 20% and this would allow a simple inversion of the parallax to derive the corresponding distance. However, following the considerations contained in Luri et al. (2018) and Bailer-Jones et al. (2018), we avoided this “naive” approach, which is allegedly a biased and very noisy estimator and tends to overestimate the true distance. Therefore, the assumed distance values are the point distance estimates rest in Table 1 of Bailer-Jones et al. (2018), contained in the table of geometric distance under the schema gaiadr2-complements at the Gaia TAP service of the Astronomisches Rechen Institut (ARI)1. The comparison between the 1/π and the rest distance estimates indicates a progressive relative increase in the difference ratio (1/π − rest)/rest with larger distances, for example, from about 1% at 300 pc to about 10% near 3000 pc. It is worth noting that distances from the nebular expansion parallax for T Aur, V446 Her, V533 Her, and CP Lac are in fair agreement with Gaia distances
It is instead surprising, and worth reporting, that the Gaia distances of V603 Aql (311 ± 7) and DQ Her (494 ± 6) are in noticeable contrast with those derived from the HST-Fine Guidance Sensor, both ∼25% lower at 249 ± 8 and 386 ± 31, respectively; see Harrison et al. (2013).
The Gaiarest distances from Bailer-Jones et al. (2018), with the corresponding errors, are in Col. 4 of Table 1.
4. The nova magnitude at maximum
This quantity is derived from mvmax, Av, and the distance using the common relation Mvmax = mvmax + 5 − 5log d − Av. The three quantities on the right-hand side have uncertainties that are outlined below:
-
mvmax: Due to the uncertain definition of the peak visual magnitude. Here, the uncertainties are higher for objects with faster decline. For the peak magnitude we used the average of the values from the literature.
-
Av : Here one can find large uncertainties even for well-studied objects, depending on the method adopted: that is, UV bump, IR maps, or Balmer decrement. We used the visual extinction Av (Paper I) from a homogeneous set of good-quality data, by the method of removal of the wide interstellar dust UV absorption bump centered around 2200 Å.
-
Distance: The Gaia astrometric distances have errors that derive from the uncertainties in the parallax and possible systematic errors; see Bailer-Jones et al. (2018) and Riess et al. (2018) for details. In Table 1 we assumed as error the semi-difference of
 .
.
The derived values of Mvmax are reported in Col. 1 of Table 2. The average of the absolute magnitude at maximum for the novae in the sample (BT Mon excluded; see Sect. 11.2) is −7.51 ± 0.96. This value is in excellent agreement with the results of Shafter et al. (2011) and Shafter (2013, 2017) who found −7.5 ± 0.8 for the average magnitude of Galactic novae.
Results.
5. The MMRD revisited with the new Gaia distances
The empirical relation between the absolute optical magnitude at maximum and the rate of decline tn of a nova light-curve (MMRD) provides insight into the nova phenomenon (faster novae are intrinsically brighter than slower ones) and is a convenient method for estimating the distance of Galactic novae in the absence of other more direct estimates (although possibly not as relevant in the Gaia era). The MMRD gives an estimate of Mvmax, and hence the distance can be derived if the apparent magnitude at maximum, the tn values, and the visual extinction are known. It should be stressed, however, that with Gaia the MMRD becomes better calibrated than ever before, making it an invaluable tool for extragalactic studies.
Since the pioneering work by Mclaughlin (1945) a number of MMRD relations for Galactic and extragalactic novae have been proposed by different authors (see della Valle & Gilmozzi 2002 for a review), the most recent ones being those of the S-shaped curve of della Valle & Livio (1995), and the linear relation of Downes & Duerbeck (2000). The first theoretical explanation of the MMRD relationship for CNe was proposed by Shara (1981). More recently, Hachisu & Kato (2006, 2007, 2010) proposed a theoretical explanation of the general trend observed in the empirical MMRD curve, in the context of the “universal decline law” Mv = 2.5log t3 − 11.6.
The validity of the MMRD relation for extragalactic novae, where the uncertainties in the distances are much lower, was confirmed by Darnley et al. (2006), Shafter et al. (2011, 2012), and Shafter (2013) from a photometric and spectroscopic study of a great number of novae in M 31, M 33, and the Large Magellanic Cloud. The peak nova luminosity appears clearly correlated with the rate of decline, that is, the more luminous novae generally fade the fastest.
Instead, Kasliwal et al. (2011), in a study of a more limited number of extragalactic novae found a subclass of faint and fast objects which fall below the MMRD relation. The presence of faint and fast extragalactic novae was confirmed by the observation of the recurrent nova M 31-12a (Darnley et al. 2015) and by the survey of novae in M 87 by Shara et al. (2017). Also, Cao et al. (2012), in a study of PTF- and Galex-based light curves of 29 novae in M 31, a subset of all the CNe in M 31, found significant scatter and a number of outliers in the MMRD distribution.
While some of this scatter is possibly due to the uncertainties in the determination of the visual extinction, in the case of Galactic novae there may be substantial uncertainties in the determination of distances from expansion parallaxes when the ejecta are not spherically symmetric (see Wade et al. 2000 for general considerations on this topic). Shore (2012, 2013, 2014) also pointed out the role played by the aspherical geometry of the ejecta near maximum light, with a range of opening angles and inclinations, on the observed scatter in the MMRD relation.
In view of the above, it is understandable that the availability of the new Gaia distances represents an irresistible temptation to test and recalibrate the MMRD relation using the data of our 17 novae with the reliable Gaia distances and the homogeneous E(B − V) values. We excluded BT Mon from this sample because of the uncertainties in its rate of decline, t3, and its mvmax value (see Sect. 11.2).
The data in the MMRD diagram are affected by the uncertainties in Mvmax discussed in Sect. 4, and by those in t3, that is, the uncertainty on the exact time and value of the maximum light and, because of its ambiguous definition, by the uncertainty in estimating the magnitude at t3 due to the frequent presence of jitter and other fluctuations in the light curve, whose decline is rarely represented by a smooth curve (Strope et al. 2010; Burlak & Henden 2008).
The t3 values in Col. 7 of Table 1 were derived from the literature as our best estimates. As mentioned above, both the determination of the peak luminosity and that of t3 is not a straightforward procedure, especially for objects with jitter in the light curve (see Burlak & Henden 2008; Strope et al. 2010 for details). Burlak & Henden (2008) derived the photometric parameter of their sample of novae from smoothed light curves that ignore small flares. Instead, Strope et al. (2010) in their classification of nova light curves choose to use the observed light curve and to use for t3 the last time in the light curve for which the brightness was above the threshold. We also note that Strope et al. (2010) consider the jitter as “extra light” added onto the decline law.
In our sample of stars, uncertainties associated with the presence of jitter are especially evident in RR Pic. In this case, we followed the method of Burlak & Henden (2008) and the procedure of Darnley et al. (2006) for novae in M 31 and derived the t3 data from interpolation between points on the decline of the light curve, that is, from a smoothed curve between spikes, a method similar to the tracing of the continuum in a noisy spectrum. Careful examination of the first stages of the OB light curve of RR Pic, from the data published by Spencer Jones (1931) and Lunt (1926) led to an estimate of the maximum magnitude of close to 2.0, and to t2 and t3 values close to 125 and 250 days, respectively.
DK Lac is another object with an OB light curve characterized by jitter. The commonly reported value of t3 in the literature varies between 24 and 32 days (Duerbeck 1981; Cohen 1985; Duerbeck & Seitter 1987; Downes & Duerbeck 2000). However, inspection of the original studies (see Ribbe 1951; Wellmann 1951; Bertaud & Baldet 1952; Larsson-Leander 1954) indicates that these t3 values derive from an arbitrary extrapolation of the peak magnitude to a value about 0.5 mag brighter. Instead, Strope et al. (2010), based on AAVSO observations, give an exceptionally long t3 value of 202 days. This probably derives from their treatment of the presence of jitter. In our estimate, by adopting a method similar to that described above, we derived a t3 value of 60 ± 15 days, intermediate between the two extremes.
For the recalibration of the MMRD relation we adopted the Mv − log t3 “universal” decline law relation. The new MMRD (Fig. 2) is
 |
Fig. 1. A revision of the MMRD relation, using the new distances from Gaia DR2. See Sect. 2.1 for explanation of the fit lines. |
 |
Fig. 2. Correlation between the bolometric luminosity at maximum (in units of Eddington luminosity) and the speed class t3. Top panel: LEdd computed using individual WD masses. Bottom panel: LEdd computed using MWD = 1 M⊙ for each nova. |
Even with only 17 data points this MMRD has a tight correlation (r = 0.93, rms = 0.38 mag) and thanks to the superior precision of the Gaia distances, confirms that the linear fit between log t3 and Mvmax is the appropriate functional dependence. We believe that this result strengthens the validity of the universal decline law as the correct description of the MMRD.
While the current paper was very close to submission, a study on nova distances and MMRD appeared (Schaefer 2018) in which the author concludes that the MMRD relation is too poor and should no longer be used.
We note here that out of our sample of 18 objects, 15 are in common with the larger sample of Schaefer (2018) and that for 10 of these objects our parameter values are close to those of Schaefer. For V603 Aql and V446 Her we have different mvmax, while for V446 Her, DK Lac, and RR Pic we have different t3 values. As explained above, our mvmax and t3 values come from careful examination of many sources in the literature data (including Strope et al. 2010) and all contain error bars, unlike those in Schaefer (2018). The difference in the t3 values may perhaps be explained by the different method to estimate t3 when jitter is present (as in the case e.g., of DK Lac and RR Pic).
Unlike Schaefer (2018) we have not included BT Mon in our MMRD because of the uncertainty in its mvmax and t3 values (see Sect. 11.2 for a more detailed discussion). Schaefer instead included BT Mon in his “gold” sample, declared it a “confident outlier” and used it as a particularly clear example against the MMRD.
6. The absolute magnitude 15 days after maximum
Buscombe & de Vaucouleurs (1955) noted that about 15 days after maximum all novae have an absolute magnitude (Mv15) close to −5.2 ± 0.1, independent of the speed class. More recent studies are those of Pfau (1976; Mb15 = −5.74 ± 0.60), Cohen (1985; Mv15 = −5.60 ± 0.45), van den Bergh & Younger (1987; Mv15 = −5.23 ± 0.16), Capaccioli et al. (1989; Mv15 = −5.69 ± 0.42) and Downes & Duerbeck (2000; Mv15 = −6.05 ± 0.44).
Ferrarese et al. (2003), using extragalactic novae in M 49, derived Mv15 = −6.36 ± 0.43. Darnley et al. (2006), using the POINT-AGAPE microlensing survey of M 31, derived Mr15 = −6.3 ± 0.9 and Mi15 = −6.3 ± 1.0, for the SLOAN r′ and i′ filters, but because of the large scatter concluded that there was no evidence of a M15 relationship. Very recently, Shara et al. (2018), from a HST survey for novae in M87, found instead support for the M15 relation and derived Mv15 = −6.37 ± 0.46.
Following a welcome suggestion by the referee we recalibrated the Mv15 relation using 17 Galactic novae of our sample (BT Mon excluded) with Gaia DR2 distances, homogeneous reddening correction from our UV-based study (Paper I), and mv15 data from the literature. For 11 objects the mv15 values are from Cohen (1985), Downes & Duerbeck (2000), and the compilation by Kantharia (2017). For the remaining 6 objects (Q Cyg, DN Gem, DI Lac, HR Lyr, GI Mon, V841 Oph) the mv15 data are derived from the light curves by Shapley (1933), Cecchini & Gratton (1942), Gaposchkin (1957), and McLaughlin (1960). We also used the AAVSO light curves, and additional information from Duerbeck (1987) and Shara et al. (1989). For the choice of the final values and the estimate of the errors, for which no information is given in the literature, we have taken into consideration the uncertainties in mvmax and its timing, and the scatter in the light curves, to derive conservative estimates of the errors.
Column 2 of Table 3 gives mv15 with associated uncertainties (typically 0.2–0.3 mag). The Mv15 values with their final errors (propagated from the relevant data in Table 1) are in Col. 3. The arithmetic mean is Mv15 = −5.58 ± 0.41, while the weighted one is Mv15 = −5.71 ± 0.40. A comparison with earlier data should be made using the first value since all previous averages were arithmetic ones.
Apparent and absolute magnitude 15 days after maximum.
We note that:
-
The small error of the mean (∼0.40 mag) lends support to the use of Mv15 as a standard candle for Galactic novae.
-
Our average values are quite close to those of previous Mv15 estimates based on Galactic novae, in spite of the less reliable values for distance and Av used in those studies.
-
Our average is substantially different from that of Shara et al. (2018) for novae in M 87 (−6.37 ± 0.46) and of Ferrarese et al. (2003) for novae in M 49 (−6.36 ± 0.43). In fact, none of our objects have an individual value as high as the average of either study. This may indicate possible issues with the distances to the two galaxies, or suggest some systematic differences between the properties of extragalactic CNe and those of our galaxy.
-
Our average value is close to the theoretical values derived by Hachisu & Kato (2015) for 0.7–1.05 M⊙ WDs using their “CO nova 4” models (Mv15 = −5.4 ± 0.4) and for 0.7–1.3 M⊙ WDs with the “Ne nova 2” ones (Mv15 = −5.6 ± 0.3).
7. The luminosity at maximum and the Eddington limit
It is generally assumed that the maximum emitted luminosity by a self-gravitating object in hydrostatic equilibrium cannot exceed LEdd. However, nature has somehow found a way to circumvent this restriction and novae are well studied systems exhibiting super-Eddington luminosities for a relatively long period close to maximum light. See Hayes et al. (1990); Shaviv (1998), and Kato & Hachisu (2007) for general considerations.
The bolometric luminosity at maximum can be derived from (Mvmax + BC), where we use a bolometric correction of −0.15 ± 0.05 which is intermediate between the values commonly found in the literature (−0.25, Duerbeck 1981; −0.1, Livio 1994; −0.10, Duerbeck 1992a,b). Subsequently, 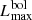 is computed using the standard relation Lλ = 3.03 × 10(35 − 0.4 Mλ). We note that the caveats in Sect. 5 on the sources of errors and uncertainties in the determination of Mvmax and t3 apply here as well.
is computed using the standard relation Lλ = 3.03 × 10(35 − 0.4 Mλ). We note that the caveats in Sect. 5 on the sources of errors and uncertainties in the determination of Mvmax and t3 apply here as well.
The value of LEdd can be estimated using the relations given by MacDonald (1983), LEdd = 2.5 × 1038 (1 + X)−1 MWD erg s−1, or by Warner (1995) and Shaviv (1998), LEdd = 6.5 × 104 MWD (1 + X)−1 L⊙ erg s−1, where MWD is in units of M⊙ and X is the hydrogen mass fraction. For X = 0.7 and MWD = 1 M⊙, LEdd ∼ 1.4 × 1038 erg s−1. Iben & Tutukov (1984) give a slightly different relation: LEdd = 4.6 × 104(MWD − 0.26) L⊙ that gives LEdd ∼ 1.31 × 1038 erg s−1 for a 1.0 M⊙ white dwarf.
In the following we adopt 1.4 × 1038 erg s−1 for the average Eddington luminosity of a 1.0 M⊙ WD. Using the relation by Warner (1995) and Shaviv (1998), LEdd was also computed for individual WD masses. Column 3 of Table 2 gives 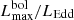 ratios for MWD = 1 M⊙.
ratios for MWD = 1 M⊙.
All objects appear super Eddington, with a clear dependence of the ratio on the speed class, fast objects being strongly super-Eddington; see also Yaron et al. (2005). For LEdd(1 M⊙) the ratio varies from ∼19.2 for the fastest objects, for example CP Pup (t3 ∼ 8 days), to ∼1.0 for the slowest novae, for example HR Del (t3 ∼ 230 days). The corresponding ratios for LEdd(MWD) are 16.6 and 1.1.
A clear correlation exists between 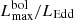 and log t3 (see Fig. 2) whose fits (computed as described in Sect. 2.2) give:
and log t3 (see Fig. 2) whose fits (computed as described in Sect. 2.2) give:
The fact that such a definite relation exists could appear as trivial, because 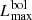 is tightly associated to Mvmax, LEdd is proportional to MWD, i.e., almost a constant (∼0.9 ± 0.2), and the MMRD is a relation between Mvmax and t3. However, while the MMRD “describes” the fact that faster novae are brighter in a way common to all,
is tightly associated to Mvmax, LEdd is proportional to MWD, i.e., almost a constant (∼0.9 ± 0.2), and the MMRD is a relation between Mvmax and t3. However, while the MMRD “describes” the fact that faster novae are brighter in a way common to all, 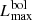 /LEdd vs. t3 (thanks to the new Gaia distances) also gives physical information: it confirms that all novae are super-Eddington, the more so the faster they are.
/LEdd vs. t3 (thanks to the new Gaia distances) also gives physical information: it confirms that all novae are super-Eddington, the more so the faster they are.
8. The absolute magnitude at minimum
The absolute magnitude at minimum is derived from the apparent magnitude mvmin using the common relation Mvmin = mvmin + 5 − 5log d − Av.
Warner (1986, 1987) defined this Mvmin as the apparent absolute magnitude since in CVs the observed flux depends on the system inclination angle.
Assuming that the visual radiation originates in a nonirradiated disk (see the results of Paper I), the “apparent” absolute magnitude Mvobs must be corrected for the inclination angle of the disk (see Warner 1987) by a term ΔMv(i) to obtain an absolute magnitude averaged over all directions, variously defined as the “standard”, “reference”, or “average” absolute magnitude (we use “reference” in the following):
where ΔMv(i)= − 2.5log[(1 + 1.5cosi)cosi] according to Warner (1987). This relation is derived from a more general λ-dependent prescription of Paczynski & Schwarzenberg-Czerny (1980) in the specific case of a limb-darkening parameter f−1 ∼ 0.6 for the V region (see Sect. 9). The ΔMv(i) correction accounts for both geometrical and limb-darkening effects.
The visual reference magnitude would correspond to the “apparent” one if viewed at an angle of about 57°.
The correction for inclination to be applied to the apparent visual magnitude can reach −5 mag for systems seen at high inclination angles (eclipsing objects) while that for systems seen nearly pole-on is of about +1 mag.
Regrettably, the system inclination angle is, in general, not accurately determined, except for the few systems that exhibit definite or grazing eclipses. It is a fortunate circumstance, however, that the correction for inclination is critical only for systems with high inclination (eclipses) while it is not so critical for systems with uncertain (i.e., mid or low) inclination.
The adopted values for the inclination (see Table 1) are mostly from the compilation by Ritter & Kolb (2011), complemented with other information from the literature, i.e., Warner (1987), Duerbeck (1992a,b), Downes & Duerbeck (2000), Peters & Thorstensen (2006), Puebla et al. (2007), and Darnley et al. (2012). We assumed our best estimate from the various values in the literature as the nominal value of i, with an indicative “error” given by half the range of values. The errors extend to ±15 degrees for systems with uncertain inclination. A typical magnitude range associated with this error depends on the inclination, and varies between 0.5 (i = 30) and 0.9 mag (i = 45).
Column 10 of Table 2 gives the reference absolute magnitude 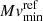 whose average value is 3.88 ± 1.01. The intrinsically most luminous object in quiescence is BT Mon.
whose average value is 3.88 ± 1.01. The intrinsically most luminous object in quiescence is BT Mon.
8.1. Comments on the inclination of individual objects
V446 Her, CP Lac, Q Cyg, DK Lac, HR Lyr and GI Mon lack reliable inclination values from the literature. However, from the absence of eclipses one can set an upper limit of about 60° for i. In a few cases, in order to derive an estimate of i we employed the method of Warner (1986), who pointed out that a definite correlation exists between the system inclination angle and the equivalent width of the hydrogen and helium emission lines observed in quiescence. Comments on individual objects are below.
-
In the case of V446 Her, an additional constraint comes from the high K1 value (about 106 km s−1) reported by Thorstensen & Taylor (2000). Inserting this value in the mass function, with P = 0.207, MWD = 1.09, M2 = 0.46 M⊙ (from the Period–M2 relation, see Knigge 2006; Selvelli et al. 2008) one derives that i ∼ 57 (i = 55 if MWD = 1.0). We adopted 57 ± 8°.
-
For CP Lac, similar considerations are based on the K1 value (about 100 km s−1) reported by Peters & Thorstensen (2006). Inserting this K1 in the mass function, with P = 0.145, MWD ∼ 1.0, M2 = 0.26 M⊙ one derives i values in the range 55–65 degrees, with a limited range for reasonable MWD values. Smaller values of i would require unlikely small values of K1, less than 80 km s−1, not compatible with the observed RV amplitude. We therefore adopted i = 60 ± 5°. This agrees with the possible detection of shallow eclipses in the light curve from time-resolved photometry of the system (Rodríguez-Gil & Torres 2005).
-
For Q Cyg, Warner (1987) gives i ∼ 50, while Peters & Thorstensen (2006) give i ∼ 26 ± 9. The optical spectrum of Ringwald et al. (1996) shows weak H-alpha emission. We adopted 26 ± 9°.
-
For DK Lac we adopted 41 ± 15 from Takei et al. (2013) and Honeycutt et al. (2011).
-
For HR Lyr we adopted 30 ± 15 based on the Warner (1987) estimate (0–30) and on the presence, although not prominent, of H and helium emission lines in the spectrum (Harrison et al. 2013).
-
For GI Mon we adopted 45 ± 15. The optical spectrum (see Bianchini 1991; Bianchini et al. 1992; Liu & Hu 2000) shows weak hydrogen and HeII 4686 emission lines. A recent SALT spectrum of GI Mon (Tomov et al. 2015) also shows weak HeII 4686 and H-beta emission lines. The equivalent width of H-alpha suggests a moderately low inclination. This seems confirmed by the presence of modulations in the light curve (Woudt et al. 2004).
-
The inclination of V841 Oph is also uncertain: Diaz & Ribeiro (2003) give a wide possible range (38 ± 30) while Peters & Thorstensen (2006) give 30 ± 10; we adopted the latter value.
9. The UV and optical disk luminosity
One of the main results of Paper I was the observational confirmation that the UV flux, whose SED is well described by a single power-law (PL) distribution, comes from an accretion disk that accounts also for the observed optical flux.
Therefore, one can estimate the total disk flux, or at least provide a reliable (lower) limit for the sum of the UV and optical contributions by integrating the power law from 1100 to 6000 Å.
We reiterate, from Paper I, that the PL indexes were derived using the Cardelli et al. (1989) reddening correction and that the difference between the actual UV flux distribution and the corresponding PL approximation is small. We also found that the observed optical magnitude agrees with the extrapolation of the PL to the V band, although on average mvobs is ∼0.17 mag fainter than mvPL, which we interpreted as due to the fact that the V light comes from the external region where the disk starts to be optically thin or has a physical edge. Alternatively it could be due to the presence of a Balmer jump, although one is not visible in the 1000–9000 Å spectrum of V603 Aql; see Fig. 15 of Paper I.
We therefore used the method described above to estimate the total flux of the disk and to derive its luminosity using the Gaia distances of Table 1.
We neglected the IR contribution to the disk luminosity by truncating the integral of the PL at 6000 Å. This is justified by the considerations above. In any case the PL contribution to this range would be small.
9.1. The UV correction for the disk inclination
If the observed SED (or its PL approximation) derives from a disk, a correction for inclination similar to that introduced in Sect. 8 for the visual magnitude is required. As mentioned there, Paczynski & Schwarzenberg-Czerny (1980) derived a general relation for the correction of the observed disk luminosity for i-related limb darkening and geometrical factors. The reference disk luminosity is
where
Here uλ is the limb darkening coefficient, whose values vary from 0.2 (IR), 0.6 (V), and 0.8 (UV), up to 1.0 (far UV). Limb darkening is an important effect, especially for flat objects such as accretion disks, and is especially important in the UV; see Diaz et al. (1996) for relevant considerations.
For physical reasons and for the sake of homogeneity in the treatment of the error propagation, rather than using separately the approximate coefficient in the relevant wavelength range, we chose to use the general equation of Paczynski & Schwarzenberg-Czerny (1980) with a limb-darkening coefficient that linearly varies with wavelength:
where the two constants were derived by imposing u(1200)=0.8 and u(5500)=0.6. Equation (4) can also be re-written as :
where d is from Table 1, 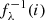 is given by Eq. (5), Fλ = A λ−α, and the constants A and α are determined from the PL approximation to the observed UV flux, as described in Paper I.
is given by Eq. (5), Fλ = A λ−α, and the constants A and α are determined from the PL approximation to the observed UV flux, as described in Paper I.
Columns 4 and 5 of Table 2 give, separately, the UV λλ 1250–3100 luminosity, as derived from the IUE reddening corrected λ−integrated flux, and the total i-corrected UV+optical disk luminosity as derived from Eq. (7).
10. The white dwarf mass and radius
A basic paradigm in the theoretical interpretation of the nova phenomenon (Starrfield et al. 1985; Livio et al. 1986; Shara 1989; Truran & Livio 1989; Livio 1994; Bode & Evans 2008) is that the OB characteristics, that is, the luminosity at maximum, the decline of the nova light curve (speed class), the mass of the ejecta, the outflow velocities, the OB recurrence time, and so on, depend primarily on the WD mass, and more weakly on other physical parameters like Ṁ, the chemical composition of the accreted material, the temperature of the WD, magnetic fields, mixing processes in the WD, and so on (see also Yaron et al. 2005; Townsley & Bildsten 2005; Kato & Hachisu 2007; Kato et al. 2013).
The white dwarf mass MWD (with its associated radius RWD) plays an important role also in quiescence because the ratio RWD/MWD explicitly appears in the relation between Ṁ and the accretion luminosity; see the following section.
Regrettably, MWD is not accurately known by direct observations because of the several and severe problems one encounters in determining the primary mass and other system parameters from the observed radial velocity curves. One example is that the velocities may not be those of the star(s), for example if they originate in or above the disk (see Wade & Horne 1988; Thorstensen et al. 1991; Marsh & Duck 1996).
Due to the fact that reliable determinations of MWD are only available for a few of our novae, and that even a rough estimate of MWD is helpful to more accurately determine the nova OB and quiescent characteristics, we made an effort to derive the masses of the remaining objects using both a semi-empirical and an empirical approach.
Livio (1992b) derived a theoretical relation between t3 and MWD (his Eq. (12): t3 = A X−1 (X−2/3 − X2/3)3/2, where X = MWD/1.433). The relation was calibrated using only the WD mass of V1500 Cyg, i.e., 1.25 M⊙, to derive A = 51.3.
Using data from Ritter & Kolb (2011) and additional literature (Horne et al. 1993; Arenas et al. 2000; Rodríguez-Gil & Martínez-Pais 2002; Smith & Vande Putte 2006; Hachisu & Kato 2007) on MWD for the seven calibrators (V603 Aql, T Aur, HR Del, DQ Her, V533 Her, GK Per, V1500 Cyg) with the “best”, though admittedly not completely satisfactory, determinations of the primary mass, we assumed the shape of the relation to be correct and recalibrated the constant A in Livio’s equation. The results are only partly satisfactory because the derived value of the constant A is relatively uncertain: 70 ± 20. However, this range in A corresponds to uncertainties of about ±0.1 M⊙ for the WD mass, a result that we consider acceptable.
In a different approach, we fitted the data of the seven calibrators with a simple linear regression of the form MWD(t)=a + b log t for both t2 and t3. The results give a = 1.384, b = −0.367 for t2, and a = 1.488, b = −0.388 for t3.
There is satisfactory agreement between the three methods. In the following we take the average of these three determinations as the value of MWD for the objects without a direct MWD estimate (see Col. 13 of Table 1, where the calibrators masses are in italics). We adopted as error bars the half difference between the minimum and maximum values.
We have not used as calibrator the reliable MWD estimate of the eclipsing object BT Mon (MWD = 1.05 M⊙) because regrettably and as mentioned above its t3 value is poorly determined.
We recall that the observed white dwarf mass distribution M1 in CVs is in the range 0.8–1.2 M⊙, but see Wijnen et al. (2015), and considerations therein on possible selection effects and on the contrast with the standard theoretical scenario. In particular, Smith & Dhillon (1998) give 0.85 ± 0.05 M⊙, Nelson et al. (2004) give 0.95 ± 0.05, Savoury et al. (2011) found 0.81 ± 0.04, Littlefair et al. (2008) give MWD ∼ 0.8, Zorotovic et al. (2011) give 0.83 ± 0.23, while Yuasa (2012) give MWD ∼ 0.88 ± 0.24 in nonmagnetic CVs.
Instead, the white dwarf mass in classical nova systems, as estimated by nova frequency, is ∼1.04–1.24 M⊙ (Ritter et al. 1991). This led Ritter et al. (1991) to conclude that classical novae are a special sample of CVs, not representative of the intrinsic properties of CVs. We will return to this in Paper III where we will revisit the nova paradigm in light of correlations we found among the nova parameters.
One limitation of our sample of CNe, based as it is on the availability of good UV spectra, is that it cannot say anything about the highest-mass WDs and their more extreme outcomes (our highest WD mass being 1.16 ± 0.2 M⊙).
10.1. The radius of the white dwarf
The radius RWD of the white dwarf enters in the relation between the disk luminosity and Ṁ. A theoretical nonrelativistic approximation of the relation between RWD and MWD gives 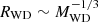 . More accurate relations between RWD and MWD were proposed by Hamada & Salpeter (1961), Nauenberg (1972), Politano et al. (1990), Cannizzo (1994), Panei et al. (2000), Wade & Hubeny (1998), and Madej et al. (2004).
. More accurate relations between RWD and MWD were proposed by Hamada & Salpeter (1961), Nauenberg (1972), Politano et al. (1990), Cannizzo (1994), Panei et al. (2000), Wade & Hubeny (1998), and Madej et al. (2004).
For this work we adopted the Nauenberg (1972) analytical relation, which is convenient for the calculations of the propagation of the uncertainties associated with MWD:
where X = MWD/1.433. This relation agrees well with previous and recent estimates of MWD and RWD. We have slightly modified the original constant (0.0112) given by Nauenberg in order to provide RWD = 8 × 10−3 R⊙ in the case of a WD with MWD = 1 M⊙, as suggested by Panei et al. (2000), Althaus et al. (2013), Barstow et al. (2015), and Barstow et al. (2017).
11. The mass accretion rate
The calculation of this parameter, fundamental for our understanding of CV evolution, requires prior knowledge of the system distance, the i-corrected accretion flux, and the mass and radius of the primary, that is, the values of all parameters being affected by uncertainties.
In principle, Ṁ can also be estimated from a comparison between the observed spectral distribution and that of synthetic models; see for example Wade & Hubeny (1998). In this case one compares the reddening-corrected (far UV) SED with that of accretion-disk models to derive the Ṁ, the distance, and the inclination. However, accretion-disk modeling has not yet reached the sophistication of stellar-atmosphere modeling and since the number of parameters in any disk model is rather large, the fitting of the data to the models does not generally provide unequivocal results.
For this reason, and especially for the availability of precise Gaia distances, we preferred an approach based on the observed UV (and optical) luminosity, after careful treatment of the various uncertainties and their propagation.
11.1. Ṁ from the disk luminosity
In this section we confidently assume that in the quiescent state between OBs most of the observed UV and optical luminosity derives from an accretion disk heated by viscous dissipation of gravitational energy. Generally, the disk emission of a cataclysmic variable dominates in the UV decreasing at longer wavelengths. We note that CVs have additional radiation sources to the accretion disks itself: for example the white dwarf, the red dwarf, the hot spot, and the boundary layer. However in systems with high Ṁ the disk is the dominating radiation source in the UV and optical ranges (Patterson 1984; Szkody 2008).
In this case, the estimate of Ṁ is not model dependent but requires knowledge of the i-corrected disk luminosity 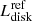 , and of MWD and RWD. If these are known, Ṁ can be calculated from the accretion luminosity:
, and of MWD and RWD. If these are known, Ṁ can be calculated from the accretion luminosity:
where it is assumed that half of the gravitational potential energy of the accreting material is liberated through viscosity in the accretion disk, the other half being released in the boundary layer between the innermost disk and the surface layer of the white dwarf (Prialnik et al. 1989; Frank et al. 2002).
In general, most of the disk accretion luminosity is emitted in the IUE UV range, while the boundary layer mostly radiates in the EUV and X-rays. Radiation at wavelengths short of Lyα is strongly absorbed and the energy is redistributed to longer wavelengths (Nofar et al. 1992).
Numerically, Ṁ can be represented by
where ϕ = 125 RWD/MWD, with radius and mass in solar units.
The “efficiency” of accretion (i.e., the luminosity associated with a given Ṁ) is strongly dependent on the compactness of the accreting object: the higher the ratio MWD/RWD, the greater the efficiency. In other words, for a given disk luminosity, Ṁ will be lower in systems with a massive white dwarf.
The parameter ϕ gives the inverse efficiency in converting Ṁ into luminosity. Clearly, this efficiency is greater than one in objects with MWD less than 1 M⊙ and lower in objects with higher MWD values. For a 1-M⊙ WD, RWD is ∼8.0 × 10−3 R⊙ and ϕ = 1.0.
Columns 6–9 of Table 2 give Ṁ separately for MWD = 1 M⊙ and for individual MWD values.
In particular for V603, HR Del, and RR Pic, the derived value for Ṁ can be considered as very reliable because for these three objects, besides precise Gaia distances, we have access to high-quality UV spectra with high S/N ratios, accurate extinction correction close to zero, and reliable estimates of the system inclination.
To compare our Ṁ values with the averages in the literature we prefer to use the median of the distribution rather than the mean because the number of points is not large, and there is no clear evidence to assume a normal distribution. One advantage of the median is that it is a more robust estimator than the mean as it is less sensitive to “outliers” in the distribution (Mana 2016; Bonamente 2013).
The median of Ṁ1 M⊙ is 3.05 × 10−9 M⊙ yr−1 (log Ṁ1 M⊙ = −8.52), while the median of ṀMWD is 3.29 × 10−9 M⊙ yr−1 (log Ṁ MWD = −8.48). These median values for Ṁ are comparable to the average value (∼ − 8.3) of log Ṁ for novae only as given in Fig. 7 of Patterson (1984). It is worth noting that in that same figure the two objects with the highest Ṁ in our sample (HR Del and BT Mon) were definite “outliers” due to their high Ṁ.
Our median Ṁ values are lower that the average Ṁ = 1.3 × 10−8 M⊙ yr−1 for quiescent novae found by Puebla et al. (2007) using accretion-disk models. They are also lower than the value (∼10−8) found for CVs monitored immediately before or after a nova OB (Iben et al. 1992). This result seems to attenuate the need for the hibernation conjecture (Shara 1989) to interpret the nova phenomenon. One of the motivations at the origin of the hibernation idea was the alleged presence, in post novae, of a disturbingly high Ṁ, of the order of 5 × 10−8 M⊙ yr−1.
11.2. Comments on individual objects
HR Del. Hr Del is an outlier in the sample, with Ṁ higher by about one order of magnitude compared to the average value of the other objects in the sample. The high Ṁ is close to the value (10−7 M⊙ yr−1) that would correspond to the steady-burning regime (see Fujimoto 1982; Nomoto 1982; Nomoto et al. 2007; Bode & Evans 2008). The reason for this continuing activity is not clear, but continuing weak thermonuclear burning may be involved (Friedjung et al. 2010). This peculiar behavior was pointed out by Selvelli & Friedjung (2003) who interpreted the presence of a strong P Cyg profile in the CIV λ 1550 resonance doublet as indicative of a strong steady outflow driven by the high disk luminosity.
V446 Her. V446 Her was considered as a low-mass transfer system (Tappert et al. 2013) and dwarf-nova behavior was reported by Honeycutt et al. (1995). Our data indicate that its Ṁ (about 10−9 M⊙ yr−1) is lower than the median, but within the dispersion of the distribution. It is surprising that dwarf-nova eruptions, which are usually interpreted as being a consequence of a thermal instability in a low-Ṁ accretion disk, may take place also in the presence of the above-reported Ṁ, a value that is close to that of other CNe in quiescence.
GK Per. Dwarf-nova behavior was reported also for GK Per (Sabbadin & Bianchini 1983). The same arguments as those of the previous paragraph are valid because Ṁ in GK Per (∼2.0 × 10−9 M⊙ yr−1) is higher than in V446 Her and close to the average Ṁ for CNe in quiescence. We recall that to estimate the Ṁ of GK Per we used only the IUE spectra with the lowest flux, that is, those corresponding to the “quiescent” DN stage. The Ṁ value for GK Per greatly exceeds the typical mass-transfer rate in DN systems in quiescence and is above the critical line for thermal instability (Osaki 1996). We note that GK Per, in spectra taken during a DN OB stage, displayed an increase by a factor of ∼70 in the UV luminosity and therefore a corresponding Ṁ as high as ∼1.4 × 10−7 M⊙ yr−1.
In conclusion, the observed quiescent Ṁ of GK Per (and V446 Her) contradict the basic assumption of the disk-instability model for the dwarf-nova phenomenon (Osaki 1996), that is, that there is no effective accretion from the disk to the WD during quiescence.
CP Pup. For the enigmatic CP Pup Ṁ ∼ 1.0 × 10−9 M⊙ yr−1 is slightly lower than our median but higher than the one (≤1.6 × 10−10 M⊙ yr−1) derived by Orio et al. (2009) via modeling of the X-ray emission only (and assuming a distance of 1600 pc, higher than the 794 pc from Gaia). Our result is in agreement with the indication of Naylor (2002) of high mass transfer.
The pre-nova magnitude (∼19.4) was much fainter than the post-nova one (∼15.0) (Schaefer & Collazzi 2010) making CP Pup the object with the highest pre-post Δm (∼5.0) and therefore with an expected Ṁ increase by a factor of about 100 in comparing the values of the pre- and post-OB phases. Our data, however, indicate Ṁ ∼ 1.0 × 10−9 M⊙ yr−1, close to that of the other ex-novae, which all returned to the pre-OB magnitude (Δm ∼ 0) and have longer orbital periods.
It is worth recalling that White et al. (1993) and Retter & Naylor (2000) suggested that CP Pup is a member of a permanent superhumps system (Osaki 1989; Patterson & Richman 1991), a new subclass of CVs with relatively short P and high mass-transfer rates.
BT Mon. This object has uncertain OB parameters: both mvmax and (consequently) t3. The nova was discovered some time after maximum light on Dec. 17, 1939, by Wachmann (1968) and independently by Whipple & Bok (1946) from plates on Dec. 23, 1939. On Harvard patrol plates the star was at 8.5 on Oct. 8, 1939, but on Sonneberg plates, Wachmann (1968) found mv = 7.6 on Sept. 24, 1939.
Schaefer & Patterson (1983) discovered five further plates providing data in OB back to Sep. 11, 1939, with an average mb ∼ 8.5, which they took to be mbmax. A similar value, mvmax = 8.1, is reported in Collazzi et al. (2009). These values are incompatible with the Gaia distance of 1412 pc: if mvmax = 8.1 and using our reddening E(B − V) = 0.24, Mvmax would have a disturbingly low value of −3.4, while novae in OB have an average Mvmax = −7.5 ± 1.0; see Sect. 4.
Therefore, mvmax had to be close to 4.0 ± 1.0, which would mean that the earliest observations were taken well after t3.
As an overdue tribute to the work of D. McLaughlin, it must be remembered that this value confirms his indication (McLaughlin 1941), based on the spectroscopic evolution and the presence of the emission lines of NIII λ 4640 when the nova was at V = 8.5, that the magnitude at maximum was about four to five magnitudes brighter than V = 8.5. Sanford (1940), based on similar considerations, also speculated that BT Mon “may well have been as bright as the third magnitude”, while Smith et al. (1998), based on the spectroscopic considerations of McLaughlin (1941), also pointed out that 4.2 should have been the faintest observed magnitude at maximum.
We also incidentally note that any mvmax > 5 would imply an Eddington ratio lower than one, in contrast with the general behavior of novae; see Sect. 7. In particular, mvmax = 8.1 would give an Eddington ratio of ∼6 × 10−2. Based on the discussion of Mv15 in Sect. 6, BT Mon should have had mv15 ∼ 6.0, also brighter than the mvmax assumed by Schaefer (2018).
As mentioned in Sect. 5, Schaefer (2018) included BT Mon in his “gold” sample and used its apparent low brightness as an argument against the validity of the MMRD.
Schaefer assumed a low brightness at maximum based on the fact that “the spectral evidence places the time of maximum around the time of start of the flat maximum”. This is surprising because it is in contradiction with his and Patterson’s 1983 paper, which he uses as a reference for the statement (see also caption to their Fig. 5), where the “spectral evidence” (from Gaposchkin 1957) was quoted to say that the magnitude at maximum might have been 3.5 magnitudes brighter than the plateau one he uses now. All this is also in contrast with the well-documented consideration by McLaughlin and Sanford reported above on the spectral evolution of BT Mon.
12. Correlations (or not) with the accretion rate
The data contained in Tables 1 and 2 provide an opportunity to test the validity of some generally accepted theoretical relations but also to investigate the possible presence of new ones. Here we outline some outstanding results that show some unexpected absence and presence of correlation between Ṁ and other system parameters. A comprehensive analysis of all correlations, using standard statistical procedures, will be presented in Paper III in the framework of revisiting the nova paradigm.
12.1. Correlation between Ṁ and the i-corrected Mvmin
It is clear from the results of Paper I and of the sections above that in old novae Ṁ is high enough to mask both the WD and the companion contributions. To quantitatively test this indication we compared the Ṁ values derived in Sect. 11 with the 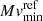 values derived in Sect. 8.
values derived in Sect. 8.
Figure 3 demonstrates the clear correlation that exists between 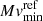 and log Ṁ1 M⊙ and log ṀMWD. In Fig. 3 (and some other figures showing Ṁ in the y-axis), the x-axis increases towards the left. This is done to maintain similarity with the Ṁ–t3 plot in Fig. 5.
and log Ṁ1 M⊙ and log ṀMWD. In Fig. 3 (and some other figures showing Ṁ in the y-axis), the x-axis increases towards the left. This is done to maintain similarity with the Ṁ–t3 plot in Fig. 5.
 |
Fig. 3. Accretion-rate correlation with the i-corrected absolute magnitude at minimum, showing that in the absence of more information |
Linear fits to the data, computed as described in Sect. 2.2, give
for Ṁ derived from the individual WD masses and for a common 1 M⊙ WD mass, respectively.
Therefore, in the absence of other spectral information, the i-corrected absolute visual magnitude of old novae and other CVs accreting at high rates (e.g., nova-like) can be used as a convenient proxy of the actual Ṁ.
It is worth comparing the results derived above with those of other estimates of Ṁ from the visual magnitude Mv.
Lipkin et al. (2001) improved the Ṁ − Mv relations presented by Retter & Leibowitz (1998) and Retter & Naylor (2000) and derived the relation
where Ṁ17 is the mass accretion rate in 1017 g s−1 and Mvref is the inclination-corrected absolute magnitude of the disk. The factor 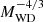 derives from the factor RWD/MWD in the assumption, generally valid for WDs with M ≤ 1 M⊙, that MR3 = const. However, this RWD − MWD relation (polytropes) is not accurate in the case of massive WDs because in this case RWD decreases with a far steeper slope as MWD increases. We have slightly modified the Lipkin et al. (2001) relation to account for a more reliable RWD/MWD relation based on the Nauenberg RWD–MWD formula.
derives from the factor RWD/MWD in the assumption, generally valid for WDs with M ≤ 1 M⊙, that MR3 = const. However, this RWD − MWD relation (polytropes) is not accurate in the case of massive WDs because in this case RWD decreases with a far steeper slope as MWD increases. We have slightly modified the Lipkin et al. (2001) relation to account for a more reliable RWD/MWD relation based on the Nauenberg RWD–MWD formula.
A comparison between our values and those derived from the modified Lipkin et al. (2001) relation indicates that, on average, the ṀWD values by Lipkin et al. (2001) are higher by a factor of about 2.5 ± 1.4. It should be noted, however, that they made the implicit assumption that the ratio Lv/Lbol has a constant value of ∼0.14; see also La Dous (1991, 1994) and Retter & Leibowitz (1998); Retter et al. (1999). Instead, our data indicate that the ratio is not constant because it depends on the slope of the SED.
12.2. No correlation between Ṁ and Porb
A long-standing and generally accepted paradigm for CVs associates higher Ṁ to systems with longer orbital periods (Howell et al. 2001). Early studies of the observed Ṁ in CVs (see Patterson 1984) indicated a strong dependence of Ṁ on the orbital period (all Ṁ values in this section are in M⊙ yr−1):
with P in hours. Patterson (2011) substantially revised this relation using a larger sample of DNe in OB, confirming the correlation between Mv (taken as a proxy for Ṁ) and P, although with a weaker linear dependence (P again in hours):
It should be stressed, however, that these results derive essentially from observations of DNe in OB and have been somewhat arbitrarily extrapolated to CVs in general and to CNe in particular. Townsley & Bildsten (2005) claim that about 50% of CNe occur in binaries accreting at Ṁ ∼ 10−9, with P ∼ 3 − 4 h, with the remaining 50% split evenly between higher Ṁ (longer P) and lower Ṁ (shorter P); Patterson et al. (2013) take as round numbers 10−8 for CNe above the period gap and 10−10 for CNe below the gap, while Iben et al. (1992) consider that the time-averaged mass transfer rate decreases from 10−8 at P ∼ 6 h to 10−11 at P ∼ 80 min.
Our data (see Fig. 4, top) show instead a flat Ṁ vs. P distribution with a relatively small scatter about a median log value close to –8.5.
 |
Fig. 4. No correlation between the accretion rate and either period P or time since explosion ΔT. Plots are in log–log for clarity. |
We note that DN Gem and DK Lac fall within the P-gap of 2.15–3.18 h (Knigge et al. 2011; Retter et al. 1999), while for HR Lyr there is some evidence that P ∼ 2.4 h also inside the gap (Leibowitz et al. 1995). However, the Ṁ values of these three objects are close to the average of the other old novae of the sample. Also, the Ṁ of CP Pup, whose P falls below the gap, is comparable to that of other novae and higher than that theoretically expected for CVs below the P-gap (see Patterson 1984; Ritter 2010; Patterson et al. 2013).
The observed flat Ṁ − P distribution of our objects apparently contradicts the generally accepted paradigm of CVs evolution. We reiterate, however, that Fig. 7 in Patterson (1984) contains mostly DNe in OB, with only eight ex-novae, and that these actually show a flat distribution of Ṁ (with average log Ṁ close to –8.3). The inclusion of these eight novae has the effect of an increase in the scatter of data in the upper part of the figure. The use of a homogeneous class of CVs (e.g., DN only) would have clearly reduced the scatter.
In conclusion, the ex-novae of our sample that fall above, inside, and below the P-gap have a median log Ṁ ∼ −8.5 with a nearly flat distribution with the orbital period P. This is a challenge to the generally accepted paradigm of CV evolution and indicates that CNe indeed represent a special class of CVs, confirming previous considerations by Ritter et al. (1991) and Livio (1994).
12.3. No correlation between Ṁ and ΔT
Figure 4 (bottom) shows no obvious correlation between Ṁ and the time elapsed since OB, HR Del being the only recent nova with high Ṁ. Due to the fact that our CNe span an interval of more than one century of nova eruptions, this is a strong indication that after the explosion Ṁ remains essentially constant during this time interval. This is in agreement with the results by Weight et al. (1994), Moyer et al. (2003), and Thomas et al. (2008) who found no correlation between Ṁ (or LUV) and the time since OB.
The case of the very old nova V841 Oph that has a relatively high Ṁ ∼ 1.8 × 10−8 M⊙ yr−1 and a steep continuum in spite of the 140 years elapsed from OB is remarkable. We note that Engle & Sion (2005) pointed out that of two UV spectra of V841 Oph taken 15 years apart, the later one had a higher flux.
Our data also indicate that if post novae enter a phase of hibernation (Shara 1989) Ṁ does not begin to decline until at least 150 years post-OB, in agreement with Thomas et al. (2008). In a recent study of candidate old novae, Tappert et al. (2015) pointed out that the two oldest novae in their sample, GR Sgr (Nova Sgr 1917) and V999 Sgr (Nova Sgr 1910), appear to have the highest luminosity, contrary to what one would expect from models of nova evolution.
12.4. Correlation between Ṁ and the speed class t3
Our data show that there is a clear correlation between Ṁ and the speed class t3 (see Fig. 5), indicating that higher Ṁ values are associated to objects with larger t3 values.
 |
Fig. 5. Accretion rate correlation with t3. Top panel: Ṁ computed using individual WD masses. Bottom panel: Ṁ computed using MWD = 1 M⊙ for each nova (to show that the correlation is not due to the possible degeneracy between t3 and MWD). |
After linearization, the logs of these two quantities, computed as described in Sect. 2.2, show the correlations:
for Ṁ derived from the individual WD masses and for a common 1 M⊙ WD mass, respectively. We note that via the MMRD this implies a correlation between Ṁ and Mvmax as well.
In the past decade models of novae have “weakened” the role of the WD mass as the dominant parameter (e.g., Townsley & Bildsten 2005; Yaron et al. 2005), showing that for any given mass a large range of Ṁ is possible. These in turn determine the ignition mass (lower for higher accretion) and the temperature at which the nova OB occurs, with the result that there is a continuum of possible OB amplitudes, and t3, for a given WD mass.
Within this context the correlation Ṁ − t3 is very surprising, as it clearly shows a one-to-one interdependence between Ṁ and the speed class. This would be particularly intriguing if t3 turns out to really be a proxy for the WD mass (as it is often assumed to be), because there are a priori no obvious reasons why novae with massive WDs should have lower Ṁ than novae with lighter WDs. The fact that heavier WD novae require a smaller total accreted mass to ignite the thermonuclear explosion (Shara et al. 2010; Glasner & Truran 2009; Yaron et al. 2005) does not seem to provide any insight into how this would control Ṁ between OBs. Furthermore, while binaries with massive WD and high Ṁ may “disappear” from the diagram because they become common envelope systems (Nomoto 1982), there appears to be no obvious way to hide the other missing MWD − Ṁ combinations (unless they become other kinds of CVs?).
A tempting speculation, if this distribution is confirmed, is that the strip populated by the old novae discussed here may define the range of Ṁ and t3 values where novae can occur. Observational Ṁ determinations for more (old) novae are clearly needed before exploring this idea any further.
12.5. Correlation between Ṁ and OB amplitude
An interesting correlation exists between the OB amplitude and Ṁ (see Fig. 6) that associates large amplitude to low Ṁ. In hindsight, this is not completely surprising given the correlation between 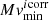 and Ṁ reported in Sect. 12.1. Unlike that correlation, which requires knowledge of several physical parameters (distance, inclination, etc.), this one has as independent variable: the observed OB amplitude (i.e., the difference between two apparent magnitudes).
and Ṁ reported in Sect. 12.1. Unlike that correlation, which requires knowledge of several physical parameters (distance, inclination, etc.), this one has as independent variable: the observed OB amplitude (i.e., the difference between two apparent magnitudes).
 |
Fig. 6. Correlation between accretion rate and the OB amplitude. Top panel: Ṁ computed using individual WD masses. Bottom panel: Ṁ computed using MWD = 1 M⊙ for each nova. |
That the correlation exists without the correction for inclination is somewhat surprising, and may be due to the fact that for most of our novae the correction is relatively small. This would also explain why DQ Her, the nova in the sample with the largest i correction, appears as an outlier in Fig. 6.
Nevertheless, this correlation provides a direct way to estimate Ṁ for any nova for which only the OB amplitude is known. Thus, the OB amplitude acts as a proxy for Ṁ, much in the way that t3 does (see Sect. 12.4). It should be noted that Schmidtobreick & Tappert (2015) suggested that novae with large OB amplitudes are candidates for low-mass-transfer-rate systems, but they assumed that the absolute magnitude of a nova explosion differs only slightly for different systems, unlike what is shown by the L/LEdd and the MMRD relations; see Figs. 1 and 2.
The fits in terms of the explicit observables, computed as described in Sect. 2.2, are
13. Concluding summary
The new and precise distances from Gaia, together with the data of Paper I and from the literature, allowed us do determine new system parameters for our sample of 18 old novae with UV data (e.g., Mvmax, 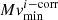 , LOB/LEdd,
, LOB/LEdd, 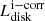 , Ṁ).
, Ṁ).
The final values include a detailed treatment of the errors and their propagation and are summarized in Table 2. Functional relations are provided in the text for all correlations (either revisited or new) presented in the paper. Our main results can be summarized as follows.
-
The average visual magnitude at maximum for the novae in the sample is −7.5 ± 1.0.
-
The bolometric luminosity of all 18 objects at maximum is equal to or above the Eddington limit, with an Eddington ratio in the range ∼1 to ∼20 for LEdd(1 M⊙), and ∼1 to ∼17 for LEdd(MWD).
-
Various parameters correlate with the speed class t3, for example Mvmax (the MMRD relation) and
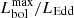 , showing that the brightest and most super-Eddington novae correspond to the shortest t3 values. These relations are (or were) also useful to derive other parameters (e.g., the distance from the MMRD since knowing t3 provides an estimate of the absolute magnitude at max).
, showing that the brightest and most super-Eddington novae correspond to the shortest t3 values. These relations are (or were) also useful to derive other parameters (e.g., the distance from the MMRD since knowing t3 provides an estimate of the absolute magnitude at max). -
The median Ṁ for the 18 old novae is log Ṁ = −8.52 for MWD ≡ 1 M⊙, and log Ṁ = −8.48 for individual MWD values. These results are not model dependent and are essentially based on the (reddening-corrected) UV luminosity after correction for inclination effects.
-
The Ṁ values are lower than those so far assumed in the studies of CNe evolution, and appear to attenuate the need for a hibernation conjecture to interpret the nova phenomenon.
-
There is a surprising correlation between Ṁ and the speed class t3 (Ṁ increasing with t3). We cannot find a simple explanation that could account for this. How, for example, does t3, a likely proxy for the WD mass, control Ṁ between OBs? Clearly this requires a more in-depth theoretical analysis. Yet, this is a useful relation that allows one to estimate Ṁ directly, and marks t3 as an extremely convenient observable to evaluate several critical parameters of classical novae.
-
The average i-corrected absolute visual magnitude at minimum of the old novae in our sample is 3.9 ± 1.0. This parameter also correlates with Ṁ, meaning that, in the absence of other spectral information, it can be used as a convenient proxy for Ṁ in old novae and other CVs accreting at high rates (e.g., nova-like).
-
Another useful correlation is the one between the OB amplitude and Ṁ. The advantage here is that the difference between two apparent magnitudes provides a direct way to estimate Ṁ for any nova for which only the OB amplitude is known.
-
There is no apparent correlation between Ṁ and the time elapsed from OB. Due to the fact that our CNe span an interval of more than one century of nova eruptions, this indicates that after the explosion Ṁ remains essentially constant during this time interval. This also indicates that if ex-novae enter a phase of hibernation (Shara 1989) Ṁ does not begin to decline until at least 150 years after OB.
-
In contrast with the commonly accepted paradigm of CV evolution based on the disrupted magnetic braking scenario (Rappaport et al. 1983; Howell et al. 2001) our data show a flat distribution with no correlation between Ṁ and the orbital period P. This suggests that novae are a special class of CVs, and confirms previous considerations by Ritter et al. (1991) and Livio (1992c, 1994); see also Zorotovic et al. (2016).
-
GK Per and V446 Her, the two ex-novae in our sample that have undergone DN eruptions, have a rather high Ṁ (∼1 − 2 × 10−9 M⊙ yr−1) during the DN quiescent phase, similar to that of the other remnants. This Ṁ value is well above the critical line for thermal instability, (Osaki 1996) and is in severe contradiction with the basic assumption in the disk instability model of no effective accretion from the disk to the WD during quiescence.
It is possible that all the correlations are an indication that the quantities we have considered depend on the same hidden parameter. This can be traced back to the WD mass: since Ṁ correlates with t3, and t3 is a likely proxy for MWD, the correlation of a parameter with Ṁ may imply a correlation with MWD. This would not be surprising, as MWD is considered a dominant parameter in the theory of novae.
The range of fit coefficients of the various correlations may in fact help us to better understand the dependences between physical quantities. Indeed, the correlations may possibly even help clarify the physics of the nova phenomenon. We will further pursue this line of reasoning in Paper III of this series.
Numpy: see www.numpy.org, and unumpy-uncertainties: see http://pythonhosted.org/uncertainties/
Acknowledgments
We wish to dedicate this paper to the memory of our friends and colleagues Angelo Cassatella and Michael Friedjung, with whom we shared inspiring discussions in the early stages of this study. We gratefully thank Elena Mason and Bob Williams for useful discussions, Carlo Morossi, Maria Grazia Franchini and Massimo Della Valle for fruitful comments, and Jorge Melnick and Jason Spyromilio for constructive debates on the intricacies of linear regressions. We thank the anonymous referee for catching a mistake in the original version, and for the useful comments and suggestions that helped us improve the paper.
References
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arenas, J., Catalán, M. S., Augusteijn, T., & Retter, A. 2000, MNRAS, 311, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Mantelet, G., & Andrae, R. 2018, AJ, 158, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, R. 1989, The Manchester Physics Series (New York: Wiley) [Google Scholar]
- Barstow, M. A., Bond, H. E., Burleigh, M. R., et al. 2015, 19th European Workshop on White Dwarfs, 493, 307 [NASA ADS] [Google Scholar]
- Barstow, M. A., Joyce, S., Casewell, S. L., et al. 2017, 20th European White Dwarf Workshop, 509, 383 [NASA ADS] [Google Scholar]
- Bertaud, C. 1952, L’Astronomie, 66, 227 [NASA ADS] [Google Scholar]
- Bertaud, C., & Baldet, F. 1952, J. Obs., 35, 108 [NASA ADS] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 1992, Data Reduction and Error Analysis for the Physical Sciences, 2nd edn. (New York: McGraw-Hill) [Google Scholar]
- Bianchini, A., & della Valle, M., Orio, M., Ogelman, H., & Bianchi, L., 1991, The Messenger, 64, 32 [NASA ADS] [Google Scholar]
- Bianchini, A., Della Valle, M., Duerbeck, H. W., & Orio, M. 1992, The Messenger, 69, 42 [NASA ADS] [Google Scholar]
- Bode, M. F., & Evans, A. 2008, in Classical Novae, 2nd edn. (Cambridge: Cambridge University Press), Cambridge Astrophysics Series, 43 [Google Scholar]
- Bonamente, M. 2013, Statistics and Analysis of Scientific Data. Series: Graduate Texts in Physics (New York: Springer) [CrossRef] [Google Scholar]
- Bruch, A., & Engel, A. 1994, A&AS, 104, 79 [NASA ADS] [Google Scholar]
- Burlak, M. A., & Henden, A. A. 2008, Astron. Lett., 34, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Buscombe, W., & de Vaucouleurs, G. 1955, Observatory, 75, 170 [NASA ADS] [Google Scholar]
- Cannizzo, J. K. 1994, ApJ, 435, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Y., Kasliwal, M. M., Neill, J. D., et al. 2012, ApJ, 752, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Capaccioli, M., Della Valle, M., D’Onofrio, M., & Rosino, L. 1989, AJ, 97, 1622 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cecchini, G., & Gratton, L. 1942, Le Stelle Nuove (Milano: U. Hoepli) [Google Scholar]
- Cohen, J. G. 1985, ApJ, 292, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., & Rosenthal, A. J. 1983, ApJ, 268, 689 [NASA ADS] [CrossRef] [Google Scholar]
- Collazzi, A. C., Schaefer, B. E., Xiao, L., et al. 2009, AJ, 138, 1846 [NASA ADS] [CrossRef] [Google Scholar]
- Darnley, M. J., Bode, M. F., Kerins, E., et al. 2006, MNRAS, 369, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Darnley, M. J., Ribeiro, V. A. R. M., Bode, M. F., Hounsell, R. A., & Williams, R. P. 2012, ApJ, 746, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Darnley, M. J., Henze, M., Steele, I. A., et al. 2015, A&A, 580, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- della Valle, M., & Livio, M. 1995, ApJ, 452, 704 [NASA ADS] [CrossRef] [Google Scholar]
- della Valle, M., & Gilmozzi, R. 2002, Science, 296, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, W. E. 1943, Statistical Adjustment of Data (New York: Wiley) [Google Scholar]
- Diaz, M. P., & Bruch, A. 1997, A&A, 322, 807 [NASA ADS] [Google Scholar]
- Diaz, M. P., & Ribeiro, F. M. A. 2003, AJ, 125, 3359 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz, M. P., Wade, R. A., & Hubeny, I. 1996, ApJ, 459, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, R. A., & Duerbeck, H. W. 2000, AJ, 120, 2007 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, R. A., Duerbeck, H. W., & Delahodde, C. E. 2001a, J. Astron. Data, 7, 6 [Google Scholar]
- Downes, R. A., Webbink, R. F., Shara, M. M., et al. 2001b, PASP, 113, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Duerbeck, H. W. 1981, PASP, 93, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Duerbeck, H. W. 1987, Space Sci. Rev., 45, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Duerbeck, H. W. 1992a, MNRAS, 258, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Duerbeck, H. W. 1992b, Acta Astron., 42, 85 [NASA ADS] [Google Scholar]
- Duerbeck, H. W., & Seitter, W. C. 1987, Ap&SS, 131, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Engle, S. G., & Sion, E. M. 2005, PASP, 117, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., Côté, P., & Jordán, A. 2003, ApJ, 599, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics (Cambridge, UK: Cambridge University Press), 398 [Google Scholar]
- Friedjung, M., Dennefeld, M., & Voloshina, I. 2010, A&A, 521, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujimoto, M. Y. 1982, ApJ, 257, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaposchkin, C. H. P. 1957, Galactic Novae (Amsterdam: North-Holland Pub. Co.) [Google Scholar]
- Glasner, S. A., & Truran, J. W. 2009, ApJ, 692, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2006, ApJS, 167, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2007, ApJ, 662, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2015, ApJ, 798, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Luna, G. J. M. 2007, ApJ, 659, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2010, ApJ, 709, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Hamada, T., & Salpeter, E. E. 1961, ApJ, 134, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Hameury, J.-M. 1994, in The Equation of State in Astrophysics, IAU Colloq., 147, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, T. E., Bornak, J., McArthur, B. E., & Benedict, G. F. 2013, ApJ, 767, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Hayes, J., Truran, J. W., Livio, M., & Shankar, A. 1990, Accretion-Powered Compact Binaries, 405 [Google Scholar]
- Horne, K., Welsh, W. F., & Wade, R. A. 1993, ApJ, 410, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Honeycutt, R. K., Robertson, J. W., & Turner, G. W. 1995, ApJ, 446, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Honeycutt, R. K., Robertson, J. W., & Turner, G. W. 1998, AJ, 115, 2527 [NASA ADS] [CrossRef] [Google Scholar]
- Honeycutt, R. K., Kafka, S., Jacobson, H., et al. 2011, AJ, 141, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Rappaport, S., & Politano, M. 1997, MNRAS, 287, 929 [NASA ADS] [Google Scholar]
- Howell, S. B., Nelson, L. A., & Rappaport, S. 2001, ApJ, 550, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., Fujimoto, M. Y., & MacDonald, J. 1992, ApJ, 384, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Jose, J. 2016, Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton: CRC Press/Taylor and Francis) [CrossRef] [Google Scholar]
- Kantharia, N. G. 2017, ArXiv e-prints [arXiv:1703.04087] [Google Scholar]
- Kasliwal, M. M., Cenko, S. B., Kulkarni, S. R., et al. 2011, ApJ, 735, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 2007, ApJ, 657, 1004 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., Hachisu, I., & Henze, M. 2013, ApJ, 779, 19 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R. 1988, QJRAS, 29, 1 [NASA ADS] [Google Scholar]
- King, A. R., Frank, J., Kolb, U., & Ritter, H. 1996, ApJ, 467, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C. 2006, MNRAS, 373, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Knigge, C., Baraffe, I., & Patterson, J. 2011, ApJS, 194, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Kolb, U. 2001, Evol. Binary and Mult. Star Syst., 229, 333 [NASA ADS] [Google Scholar]
- Kube, J., Gänsicke, B. T., & Hoffmann, B. 2002, Phys. Cataclysm. Variables Relat. Objects, 261, 678 [NASA ADS] [Google Scholar]
- La Dous, C. 1991, A&A, 252, 100 [NASA ADS] [Google Scholar]
- La Dous, C. 1994, Space Sci. Rev., 67, 1 [Google Scholar]
- Larsson-Leander, G. 1954, Stockh. Obs. Ann., 18, 3 [NASA ADS] [Google Scholar]
- Leibowitz, E. M., Mendelson, H., Gefen, G., & Retter, A. 1995, Balt. Astron., 4, 453 [NASA ADS] [Google Scholar]
- Lipkin, Y., Leibowitz, E. M., Retter, A., & Shemmer, O. 2001, MNRAS, 328, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Dhillon, V. S., Marsh, T. R., et al. 2008, MNRAS, 388, 1582 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., & Hu, J. Y. 2000, ApJS, 128, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 1992a, Cataclysm. Variab. Stars, 29, 269 [NASA ADS] [Google Scholar]
- Livio, M. 1992b, ApJ, 393, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M. 1992c, Cataclysm. Variab. Stars, 29, 4 [NASA ADS] [Google Scholar]
- Livio, M. 1994, Saas-Fee Advanced Course 22: Interacting Binaries, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., Truran, J. W., & Webbink, R. F. 1986, ApJ, 308, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Lunt, J. 1926, MNRAS, 86, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacDonald, J. 1983, ApJ, 267, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Madej, J., Należyty, M., & Althaus, L. G. 2004, A&A, 419, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mana, C. 2016, ArXiv e-prints [arXiv:1610.05590] [Google Scholar]
- McLaughlin, D. B. 1941, ApJ, 93, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Mclaughlin, D. B. 1945, PASP, 57, 69 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. B. 1960, Stellar Atmospheres, ed. J. L. Greenstein (Chicago: University of Chicago Press), 585 [Google Scholar]
- Marsh, T. R., & Duck, S. R. 1996, MNRAS, 278, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Moyer, E., Sion, E. M., Szkody, P., et al. 2003, AJ, 125, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Nauenberg, M. 1972, ApJ, 175, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Naylor, T. 2002, Classical Nova Explos., 637, 16 [NASA ADS] [Google Scholar]
- Nelson, L. A., MacCannell, K. A., & Dubeau, E. 2004, ApJ, 602, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Nofar, I., Shaviv, G., & Welirse, R. 1992, Cataclysm. Variab. Stars, 29, 65 [NASA ADS] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Saio, H., Kato, M., & Hachisu, I. 2007, ApJ, 663, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Orio, M., Mukai, K., Bianchini, A., de Martino, D., & Howell, S. 2009, ApJ, 690, 1753 [NASA ADS] [CrossRef] [Google Scholar]
- Osaki, Y. 1989, PASJ, 41, 1005 [NASA ADS] [Google Scholar]
- Osaki, Y. 1996, PASP, 108, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Paczyński, B. 1967, Acta Astron., 17, 287 [NASA ADS] [Google Scholar]
- Paczynski, B., & Schwarzenberg-Czerny, A. 1980, Acta Astron., 30, 127 [NASA ADS] [Google Scholar]
- Panei, J. A., Althaus, L. G., & Benvenuto, O. G. 2000, A&A, 353, 970 [Google Scholar]
- Patterson, J. 1984, ApJS, 54, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J. 2011, MNRAS, 411, 2695 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., & Richman, H. 1991, PASP, 103, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Patterson, J., Uthas, H., Kemp, J., et al. 2013, MNRAS, 434, 1902 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, C. S., & Thorstensen, J. R. 2006, PASP, 118, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Pfau, W. 1976, A&A, 50, 113 [NASA ADS] [Google Scholar]
- Politano, M., Livio, M., Truran, J. W., & Webbink, R. F. 1990, in Physics of Classical Novae, IAU Colloq. 122, 369, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., & Kovetz, A. 1992, ApJ, 385, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Prialnik, D., Kovetz, A., & Shara, M. M. 1989, ApJ, 339, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Puebla, R. E., Diaz, M. P., & Hubeny, I. 2007, AJ, 134, 1923 [Google Scholar]
- Rappaport, S., Verbunt, F., & Joss, P. C. 1983, ApJ, 275, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Retter, A., & Leibowitz, E. M. 1998, MNRAS, 296, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Retter, A., & Naylor, T. 2000, MNRAS, 319, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Retter, A., Leibowitz, E. M., & Naylor, T. 1999, MNRAS, 308, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Ribbe, J. 1951, PASP, 63, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., et al. 2018, ApJ, 861, 126 [Google Scholar]
- Ringwald, F. A., Naylor, T., & Mukai, K. 1996, MNRAS, 281, 192 [NASA ADS] [Google Scholar]
- Ritter, H. 2010, Mem. Soc. Astron. It., 81, 849 [NASA ADS] [Google Scholar]
- Ritter, H., & Kolb, U. 2011, VizieR Online Data Catalog: B/cb [Google Scholar]
- Ritter, H., Politano, M., Livio, M., & Webbink, R. F. 1991, ApJ, 376, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, E. L. 1975, AJ, 80, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Gil, P., & Martínez-Pais, I. G. 2002, MNRAS, 337, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Gil, P., & Torres, M. A. P. 2005, A&A, 431, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabbadin, F., & Bianchini, A. 1983, A&AS, 54, 393 [NASA ADS] [Google Scholar]
- Sanford, R. F. 1940, PASP, 52, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Savoury, C. D. J., Littlefair, S. P., Dhillon, V. S., et al. 2011, MNRAS, 415, 2025 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E. 2018, MNRAS, 481, 3033 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E., & Patterson, J. 1983, ApJ, 268, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E., & Collazzi, A. C. 2010, AJ, 139, 1831 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidtobreick, L., & Tappert, C. 2015, Acta Polytech. CTU Proc., 2, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Selvelli, P., & Friedjung, M. 2003, A&A, 401, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selvelli, P., & Gilmozzi, R. 2013, A&A, 560, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selvelli, P., Cassatella, A., Gilmozzi, R., & González-Riestra, R. 2008, A&A, 492, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shafter, A. W. 1997, ApJ, 487, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W. 2013, AJ, 145, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W. 2017, ApJ, 834, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W., Darnley, M. J., Hornoch, K., et al. 2011, ApJ, 734, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W., Darnley, M. J., Bode, M. F., & Ciardullo, R. 2012, ApJ, 752, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, H. 1933, Ann. Harv. Coll. Obs., 84, 121 [NASA ADS] [Google Scholar]
- Shara, M. M. 1981, ApJ, 243, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M. 1989, PASP, 101, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., Livio, M., Moffat, A. F. J., & Orio, M. 1986, ApJ, 311, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., Potter, M., & Shara, D. J. 1989, PASP, 101, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., Yaron, O., Prialnik, D., Kovetz, A., & Zurek, D. 2010, ApJ, 725, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., Doyle, T., Lauer, T. R., et al. 2017, ApJ, 839, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M., Doyle, T. F., Pagnotta, A., et al. 2018, MNRAS, 474, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Shaviv, N. J. 1998, ApJ, 494, L193 [NASA ADS] [CrossRef] [Google Scholar]
- Shore, S. N. 2012, Bull. Astron. Soc. India, 40, 185 [NASA ADS] [Google Scholar]
- Shore, S. N. 2013, A&A, 559, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shore, S. N. 2014, Stellar Novae: Past and Future Decades, 490, 145 [NASA ADS] [Google Scholar]
- Smith, D. A., & Dhillon, V. S. 1998, MNRAS, 301, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. C., & Vande Putte, D. 2006, Observatory, 126, 38 [NASA ADS] [Google Scholar]
- Smith, D. A., Dhillon, V. S., & Marsh, T. R. 1998, MNRAS, 296, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. M., Starrfield, S. G., Sion, E. M., et al. 2000, Allen’s Astrophys. Quant., 429 [Google Scholar]
- Spencer Jones, H. 1931, Ann. Cape Obs., 10, 9.1 [Google Scholar]
- Spruit, H. C., & Ritter, H. 1983, A&A, 124, 267 [NASA ADS] [Google Scholar]
- Spruit, H. C., & Taam, R. E. 2001, ApJ, 548, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Starrfield, S., Sparks, W. M., & Truran, J. W. 1985, ApJ, 291, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Strope, R. J., Schaefer, B. E., & Henden, A. A. 2010, AJ, 140, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Szkody, P. 2008, Astrophys. Space Sci. Lib., 352, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Takei, D., Sakamoto, T., & Drake, J. J. 2013, AJ, 145, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Tappert, C., Vogt, N., Schmidtobreick, L., Ederoclite, A., & Vanderbeke, J. 2013, MNRAS, 431, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Tappert, C., Vogt, N., Schmidtobreick, L., & Ederoclite, A. 2015, MNRAS, 450, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, J. 1997, Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements, 2nd Ed. (New York: University Science Books) [Google Scholar]
- Thomas, N. L., Naylor, T., & Norton, A. J. 2008, A&A, 483, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorstensen, J. R., Ringwald, F. A., Wade, R. A., Schmidt, G. D., & Norsworthy, J. E. 1991, AJ, 102, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Thorstensen, J. R., & Taylor, C. J. 2000, MNRAS, 312, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Tomov, T., Swierczynski, E., Mikolajewski, M., & Ilkiewicz, K. 2015, A&A, 576, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Townsley, D. M., & Bildsten, L. 2005, ApJ, 628, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Truran, J. W., & Livio, M. 1989, in White Dwarfs, IAU Colloq. 114, 328, 498 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S., & Younger, P. F. 1987, A&AS, 70, 125 [NASA ADS] [Google Scholar]
- Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]
- Wachmann, A. A. 1968, Astron. Abh. Hamburg. Sternwarte, 7, 381 [NASA ADS] [Google Scholar]
- Wade, R. A., & Horne, K. 1988, ApJ, 324, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, R. A., & Hubeny, I. 1998, ApJ, 509, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Wade, R. A., Harlow, J. J. B., & Ciardullo, R. 2000, PASP, 112, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1985, Recent Results on Cataclysmic Variables. The Importance of IUE and Exosat Results on Cataclysmic Variables and Low-Mass X-Ray Binaries, 236 [Google Scholar]
- Warner, B. 1986, MNRAS, 222, 11 [NASA ADS] [Google Scholar]
- Warner, B. 1987, MNRAS, 227, 23 [NASA ADS] [Google Scholar]
- Warner, B. 1995, Cataclysmic Variable Stars. Cambridge Astrophysics Series, 28 [Google Scholar]
- Weight, A., Evans, A., Naylor, T., Wood, J. H., & Bode, M. F. 1994, MNRAS, 266, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Wellmann, P. 1951, Z. Astrophys., 29, 112 [NASA ADS] [Google Scholar]
- Whipple, F. L., & Bok, B. J. 1946, PAAS, 10, 32 [Google Scholar]
- White, II., J. C., Honeycutt, R. K., & Horne, K. 1993, ApJ, 412, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnen, T. P. G., Zorotovic, M., & Schreiber, M. R. 2015, A&A, 577, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woudt, P. A., Warner, B., & Pretorius, M. L. 2004, MNRAS, 351, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Woudt, P. A., Warner, B., de Budé, D., et al. 2012, MNRAS, 421, 2414 [NASA ADS] [CrossRef] [Google Scholar]
- Yaron, O., Prialnik, D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Yuasa, T. 2012, Mem. Soc. Astron. It., 83, 632 [NASA ADS] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., & Gänsicke, B. T. 2011, A&A, 536, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Parsons, S. G., et al. 2016, MNRAS, 457, 3867 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The propagation of errors
We use here the term error to refer to the uncertainty in the value of a variable (this is what we have so-far referred to as a nova parameter, or a physical quantity). Propagation of errors is essential for understanding how the uncertainty in a variable affects the computations that use that variable. A basic assumption in the theory of error propagation is that that the individual variables are uncorrelated and independent and that the errors are symmetric (Gaussian), see Barlow (1989), Bevington & Robinson (1992), Taylor (1997). In this case, in the simple case of a sum (or product) of two quantities the errors (the relative errors) are added in quadrature. In the more general case of a complex function one has to compute the total derivative of that function, a task that, in some cases may be demanding.
As mentioned in Sect. 2, an important aspect of this study of novae derives from the effort we have made to estimate the errors associated to the basic physical quantities. The calculation of the error propagation up to the values of the most wanted parameters, for example the accretion disk luminosity and the accretion rate is a relatively onerous exercise. As an illustration of this we note that if one considers explicitly all the relevant parameters, the final expression for Ṁ (Eq. (10)) can be written as
It is clear from the above equation that the final value of Ṁ critically depends on quantities like the i-corrected or reference integrated flux, the distance, the white dwarf mass, and the white dwarf radius. In turn, the reference integrated flux depends on the color excess E(B − V) that determines the constant A and the index α of the PL approximation of the UV SED, and the 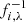 factor that takes into account both the geometrical and the limb-darkening corrections for the inclination of the system. The values of these individual parameters are all affected by uncertainties whose propagation up to the final product, the disk luminosity or Ṁ, must be correctly evaluated. To do this we utilized two separate methods: the standard pencil and paper calculation of partial derivatives and their sum, and the use of the Python (Anaconda) environment that provides specific modules and packages2 that allow a less cumbersome but “black box” calculation of complex operations in arrays with errors. Both methods yielded the same results within less than 1%. The numbers in the tables are from the Python output.
factor that takes into account both the geometrical and the limb-darkening corrections for the inclination of the system. The values of these individual parameters are all affected by uncertainties whose propagation up to the final product, the disk luminosity or Ṁ, must be correctly evaluated. To do this we utilized two separate methods: the standard pencil and paper calculation of partial derivatives and their sum, and the use of the Python (Anaconda) environment that provides specific modules and packages2 that allow a less cumbersome but “black box” calculation of complex operations in arrays with errors. Both methods yielded the same results within less than 1%. The numbers in the tables are from the Python output.
A special case is that of the power law approximation to the SED. The uncertainty in the color excess E(B − V) around the central value gives upper and lower limits of the index α and of the corresponding constant A of the PL approximation. Since alpha and A are not independent, we calculated the central value and the upper and lower limits of the integrated flux for each of the three pairs of (α, A). These integrals are slightly asymmetric so we have taken as error for the PL integral the semi-difference between the upper and lower value of the lambda integrated flux. In this way we could quadratically combine them with the relative errors determined by the uncertainties in the inclination for every (α, A) pairs. This quadratic sum gives, for each star, the total error in what we define as the reference integrated flux due to the combined uncertainties in E(B − V) and the inclination. Finally the reference integrated flux with its error has been combined with the remaining, independent parameters of Eq. (A.1), that is, d, MWD, RWD, to determine the final values, with errors, of Ṁ.
Of course, for Paper I we also explored fitting power law and reddening curve simultaneously to the UV flux. This would have had the advantage of providing symmetric fitting errors from the matrix inversion. However this method is very sensitive to the way emission and absorption lines (and in the case of IUE noise spikes) are either avoided or removed from the spectrum so that we felt more confident about the error determination through the more interactive method above.
The error propagation for all other final parameters (e.g., LEdd, i-corrected absolute magnitude), has been estimated much more easily because the associated parameters (e.g., E(B − V), distance, mvmax, mvmin) are independent of each other.
All Tables
All Figures
 |
Fig. 1. A revision of the MMRD relation, using the new distances from Gaia DR2. See Sect. 2.1 for explanation of the fit lines. |
| In the text | |
 |
Fig. 2. Correlation between the bolometric luminosity at maximum (in units of Eddington luminosity) and the speed class t3. Top panel: LEdd computed using individual WD masses. Bottom panel: LEdd computed using MWD = 1 M⊙ for each nova. |
| In the text | |
 |
Fig. 3. Accretion-rate correlation with the i-corrected absolute magnitude at minimum, showing that in the absence of more information |
| In the text | |
 |
Fig. 4. No correlation between the accretion rate and either period P or time since explosion ΔT. Plots are in log–log for clarity. |
| In the text | |
 |
Fig. 5. Accretion rate correlation with t3. Top panel: Ṁ computed using individual WD masses. Bottom panel: Ṁ computed using MWD = 1 M⊙ for each nova (to show that the correlation is not due to the possible degeneracy between t3 and MWD). |
| In the text | |
 |
Fig. 6. Correlation between accretion rate and the OB amplitude. Top panel: Ṁ computed using individual WD masses. Bottom panel: Ṁ computed using MWD = 1 M⊙ for each nova. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.