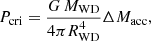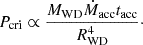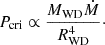EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (May 2025) A&A, 698 (2025) A251 Full HTML
Open Access
Issue
A&A
Volume 698, May 2025
Article Number A251
Number of page(s) 21
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202553762
Published online 18 June 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Classical novae are explosive stellar events that occur within close binary systems and are characterized by orbital periods spanning typically from ∼1.5 to 15 h. In the canonical scenario (see Starrfield et al. 2008, 2012, 2016; José & Shore 2008; José 2016; Chomiuk et al. 2021 for reviews), a white dwarf (WD) star is fed by a low-mass stellar companion, often a K-M main sequence star (although observations occasionally reveal the presence of more evolved companions). This mass transfer occurs as the secondary star overfills its Roche lobe, which allows matter outflows through the inner Lagrangian point of the system. The matter transferred (typically at a rate Ṁacc ∼ 10−8−10−10 M⊙ yr−1) forms an accretion disk that orbits the WD star. A fraction of this hydrogen-rich disk spirals in, gradually accumulating on top of the WD under semi-degenerate conditions. Compressional heating increases the temperature of the envelope until nuclear reactions set in, triggering a thermonuclear runaway (TNR). The TNR drives peak temperatures to around (1−4)×108 K and leads to the ejection of about ∼10−7−10−4 M⊙ of nuclear-processed material at velocities of several thousand km s−1. In fact, the suite of nuclear processes that operate during the explosion result in non-solar isotopic abundance ratios within the ejected material (Gehrz et al. 1998; Downen et al. 2013; Kelly et al. 2013).

Novae are relatively common, ranking as the second-most-frequent type of stellar thermonuclear explosions in our Galaxy, following type I X-ray bursts. Although only a handful of novae are discovered per year, typically between five and ten, predictions based on Galactic and extragalactic data suggest a much higher occurrence rate of 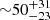∼ 50 − 23 + 31 $ {\sim }50^{+31}_{-23} $ yr−1 (Shafter 2017). This relatively high frequency is partly due to the fact that neither the WD nor the binary system are disrupted during a nova explosion, and hence, nova outbursts are expected to recur. The predicted recurrence times for classical novae lie typically in the range 104−105 yr. However, a subclass of novae, known as recurrent novae (RNe) – by definition, novae observed in outburst more than once – exhibit recurrence periods ranging from as short as 1 yr1 (e.g., M31N 2008-12a; Nishiyama & Kabashima 2008; Darnley et al. 2016, and references therein) to about 100 yr (e.g., V2487 Oph; Schaefer 2010). Such notably short recurrence times require very high mass-accretion rates, WD masses close to the Chandrasekhar limit (the mean WD mass of the ten RNe listed in Shara et al. 2018 is 1.31 M⊙), and very high initial WD luminosities or temperatures (see Starrfield et al. 1988; Yaron et al. 2005; Hernanz & José 2008). Whether these recurrence times form a nearly continuous sequence, spanning from the short values observed in RNe to the longer values predicted for classical novae, remains a topic of debate.

Recurrent novae are symbiotic systems consisting of an accreting WD and a red giant companion in wider orbits (longer orbital periods) than classical novae. Only 11 RNe have been discovered in the Milky Way2, although several others have been observed in the Andromeda Galaxy and the Large Magellanic Cloud. RNe exhibit a much broader range of orbital periods compared to classical novae, spanning from a few hours to several hundred days. Various classifications have been proposed based on different orbital periods, the presence of a plateau in the tail of the light curve, varying amplitudes and recurrence times, or distinct mechanisms driving the high mass-accretion rates inferred (see Schaefer 2010, and references therein). One well-studied RN is T Coronae Borealis (T CrB), a famous interacting binary system observed in outburst in 1866 and 1946, and likely also in 1217 and 1787 (Schaefer 2023). With a predicted recurrence period of approximately 80 yr, its next outburst is expected to occur imminently, thus motivating a thorough examination of the main characteristics of this system. Specifically, we aim to investigate the conditions required to power an outburst with a periodicity of about 80 yr. Moreover, the interest in RNe as potential progenitors of type Ia supernovae (see, e.g., Chen et al. 2011 for a model of tidally enhanced stellar wind as a possible pathway between a symbiotic system and a type Ia supernova), prompted by the likely increase in the WD mass after each outburst, further motivates the present study.

The manuscript is organized as follows: The main observational features of T CrB are summarized in Sect. 2. The input physics and initial conditions adopted in this work are presented in Sect. 3. A detailed account of the results obtained in this work is given in Sects. 4 and 5. Finally, a summary of the most relevant conclusions drawn from this research is provided in Sect. 6.

2. Observational properties of T CrB

According to Duerbeck (2009), T CrB was the first nova to be studied spectroscopically (Huggins & Miller 1866). Sanford (1949) was the first to detect radial velocity variations caused by the orbital motion in T CrB, estimating an orbital period of 230.5 days3. Subsequently, Kraft (1958) provided precise radial velocity measurements for both components of the binary system, enabling the determination of the orbital parameters and masses, sparking debate about the nature of the hot component (initially proposed to be a main-sequence star, due to its inferred mass exceeding the Chandrasekhar limit; see, e.g., Kenyon & Garcia 1986; Webbink et al. 1987, and references therein). This paradigm shifted with the analysis of satellite observations from the International Ultraviolet Explorer (IUE) by Selvelli et al. (1992), which suggested that the properties of the outburst could be better understood on the basis of a TNR on the surface of a massive WD4. Hric et al. (1998) put an end to the debate, deriving a mass of MgM = 1.38±0.2 M⊙ for the M3 giant companion overfilling its Roche lobe, and establishing a value of MWD = 1.2±0.2 M⊙ for the WD component, based on an assumed system inclination of i = 68°. Similar values have been reported by other authors (e.g., MgM = 1.14 M⊙ and MWD = 1.34 M⊙ for i = 65° in Zamanov et al. 2003; and MgM = 1.12±0.23 M⊙ and MWD = 1.37±0.13 M⊙ for i = 67° in Stanishev et al. 2004; Hachisu & Kato 1999, however, reported somewhat different values, MgM∼0.7 M⊙ and MWD = 1.35 M⊙ for i∼70°, assuming a tilted disk with an inclination of idisk∼35°). Other estimates of the WD mass in T CrB have been reported by Hachisu & Kato (2001) (MWD = 1.37 M⊙) and Shara et al. (2018) (MWD = 1.32 M⊙). Regarding the WD luminosity, Zamanov et al. (2023) provide estimates for the hot component in T CrB, assuming a distance to the source of 914 pc5: during the superactive state (2016−2022), the WD was found to have an optical luminosity of 40−110 L⊙, while in subsequent months, the luminosity decreased to 20−25 L⊙ in April–May 2023 and further to 8−9 L⊙ by August 2023.

Selvelli et al. (1992) estimated a mass-accretion rate of Ṁacc = 2.32 × 10−8 M⊙ yr−1 for T CrB during quiescence, consistent with the high values required to trigger a TNR on a massive WD. More recently, Zamanov et al. (2023), inferred a broader range for the mass-accretion rate, Ṁacc = (0.27−4.05) × 10−8 M⊙ yr−1, by linking the WD optical luminosity to the mass-accretion rate. It is also worth noting that several studies have suggested a variation of the mass-accretion rate throughout the nova cycle (see, e.g., Anupama & Prabhu 1991; Dobrotka et al. 2004; Linford et al. 2019; Luna et al. 2019).

With regard to the metallicity of the material accreted onto the WD, most studies indicate near-solar values, with some peculiar elemental features. Shahbaz et al. (1999) identified Li in the spectra of the giant star in T CrB, reporting an abundance of A(Li) = 12 + Log [N(Li)/N(H)] ∼ 0.6. This value is a factor of 4 below solar but significantly higher than those typically found in stars of the same spectral type, where no recognizable Li lines are observed. This anomaly has been attributed to either intrinsic activity in the giant star or contamination from the nova explosion. Similarly, Wallerstein et al. (2008) reported a Li abundance close to solar, with A(Li) ∼ 0.86, along with an overall metallicity consistent with solar values. More recently, Woodward et al. (2020) reported updated lithium (Li) abundance measurements for the red giant in T CrB. Using a non-irradiated (classical) 1D model atmosphere, they determined A(Li) = 1.3±0.1. When accounting for irradiation from the WD and/or the accretion disk, they found a higher value of A(Li) = 2.4±0.1. Their best-fit results were also consistent with a solar metallicity atmosphere. Pavlenko et al. (2020) also conducted abundance determinations for C, O, and Si in the photosphere of the red giant component of T CrB, complementing earlier lower-resolution spectroscopic studies by Evans et al. (2019). While the inferred elemental abundances of C, O, and Si, as well as some isotopic ratios, such as 16O/17O, 28Si/29Si, and 28Si/30Si, align with the expected composition of a red giant star after the first dredge-up, notable anomalies were observed in 12C/13C and, more strikingly, 16O/18O. These deviations are inconsistent with the normal composition of a red giant, even when accounting for possible contamination from nova ejecta7.

3. Model and input physics

The RN simulations reported in this study were performed with the hydrodynamic, Lagrangian, finite-difference, time-implicit code SHIVA (see José & Hernanz 1998; José 2016 for further details). SHIVA relies on the standard set of differential equations of stellar evolution (i.e., mass, energy, and momentum conservation, energy transport) and has been extensively used in the study of classical and recurrent nova outbursts, type I X-ray bursts, and (sub-Chandrasekhar) supernova explosions, for over 25 years. The code uses a general equation of state encompassing contributions from the degenerate electron gas, the multicomponent ion plasma, and radiation (Blinnikov et al. 1996). Coulomb corrections to the electron pressure are included, and OPAL Rosseland mean opacities have been adopted (Iglesias & Rogers 1996). Nuclear energy generation is obtained via a reaction network containing 120 species (ranging from 1H to 48Ti), linked through 630 nuclear processes, with updated rates from the STARLIB database (Sallaska et al. 2013; Iliadis, priv. comm.). Screening factors and neutrino energy losses have also been taken into account. In most simulations reported in this work, the plasma transferred from the secondary star is assumed to have solar composition (Lodders et al. 2009; see our Table 1) and is transferred at a constant rate (see, however, Sect. 4 for simulations with different metallicities). SHIVA also incorporates a time-dependent formalism for convective transport that sets in when the characteristic convective timescale becomes larger than the integration time step. Partial mixing between adjacent convective shells is modeled using a diffusion equation (Prialnik et al. 1979). No additional semi-convection or thermohaline mixing has been included.

Table 1.

Solar abundances from 1H to 48Ti and isotopic ratios (Lodders et al. 2009).

The large mean value of the WD mass in RNe reported in Shara et al. (2018), 1.31 M⊙, justifies our choice of very large values for MWD. Indeed, three different values for the mass of the white dwarf hosting the thermonuclear explosion have been explored: 1.30 M⊙, 1.35 M⊙, and 1.38 M⊙ (see, however, Sect. 5 for some additional models computed with MWD = 1.2 M⊙, to account for the existence of RNe, such as T Pyx, IM Nor, and CI Aql, whose WD masses have been reported in the range 1.21−1.23 M⊙).

For each mass, three models have been computed, corresponding to three different initial luminosity values of the WD: 0.01 L⊙, 0.1 L⊙ and L⊙. A series of tests have been conducted for each of these nine combinations of parameters, aimed at determining the mass-accretion rate at which a nova explosion occurs after 80 yr, the recurrence period inferred for T CrB. The corresponding models were flagged and further evolved through the explosion, expansion and ejection stages. For completeness, two additional models have been considered: while the matter transfer from the secondary star in the nine models discussed above was assumed to be solar, two different cases, with 0.1 Z⊙ and 10 Z⊙, were computed to examine the influence of the metallicity of the accreted material on the properties of the outburst. It is worth noting that the secondary stars in RNe are often more evolved than those in classical novae. Some evolved stars display significantly enhanced surface metallicities, reaching super-solar levels. Observations have reported metallicities up to 2−3 times the solar value in some red giants (see also Cinquegrana & Karakas 2022 for a study of asymptotic giant branch models with metallicities ranging from 3 Z⊙ to 7 Z⊙). In contrast, binary systems originating in the Galactic halo or other metal-poor environments, such as the Magellanic clouds and dwarf galaxies, are likely to contain metal-deficient stars. Within this context, the adopted metallicity range (0.1−10) Z⊙ must be regarded as exploratory, representing a variation of the solar metallicity by a factor of 10 up and down, in an attempt to quantify the role played by the metallicity of the companion star on the properties of the outbursts. All in all, 11 new hydrodynamic simulations have been performed for this study (see Table 2).

Table 2.

Models of T CrB that yield τrec = 80±0.5 yr.

4. Results

4.1. Effects of the WD mass and luminosity, the metallicity, and the accretion rate

In a nova explosion, mass ejection requires a critical pressure at the envelope's base, Pcri, which is approximately given as

P cri = G M WD 4 π R WD 4 Δ M acc , $$ P_{\mathrm {cri}} = \frac {G \, M_{\mathrm {WD}}}{4 \pi R_{\mathrm {WD}}^4} \Delta M_{\mathrm {acc}}, $$(1)

where MWD and RWD are the mass and radius of the WD hosting the explosion, and ΔMacc is the mass of the accreted envelope (Shara 1981; Fujimoto 1982). Pressures within the range Pcri∼1019−1020 dyn cm−2 must be attained, the exact value depending upon the chemical composition (Fujimoto 1982; MacDonald 1983; see also Wolf et al. 2013 and Kato et al. 2014 for more recent work on ignition masses). Higher ignition pressures lead to more violent outbursts, characterized by higher peak temperatures and a somewhat larger extension of the nuclear activity toward heavier species.

As shown in Table 3, 1.30 M⊙ WDs with an initial luminosity ranging from 0.01 to 1 L⊙, require mass-accretion rates of around 10−7 M⊙ yr−1 to drive a nova explosion after ∼80 yr of accretion of solar-composition matter. Specifically, a mass-accretion rate of 1.05×10−7 M⊙ yr−1 is required for LWD = 0.01 L⊙, while 6.1×10−8 M⊙ yr−1 is needed for LWD = 1 L⊙, showing that the lower the initial WD luminosity, the higher the mass-accretion rate required to power such an explosion in 80 yr.

Table 3.

Properties of T CrB models with MWD = 1.30 M⊙.

It is well-known that hotter (i.e., more luminous) accreting WDs attain the critical conditions to initiate a TNR earlier, thus reducing the duration of the accretion phase and the overall amount of mass accreted. A similar outcome is obtained in models characterized by higher mass-accretion rates. Accordingly, to produce an outburst after 80 yr, models with higher initial WD luminosities require lower mass-accretion rates to compensate for the reduced amount of accreted mass, in agreement with the results summarized in Table 3.

Increasing the WD mass to 1.35 M⊙ (Table 4) results in a similar pattern8, albeit with lower mass-accretion rates (a decrease by a factor of 3, compared to models computed with 1.30 M⊙). This can be understood as follows: replacing the accreted mass by the product of the mass-accretion rate, Ṁacc, and the duration of the accretion phase, tacc, Eq. (1) becomes

P cri ∝ M WD M ˙ acc t acc R WD 4 · $$ P_{\mathrm {cri}} \propto \frac {M_{\mathrm {WD}} \dot M_{\mathrm {acc}} t_{\mathrm {acc}}}{R_{\mathrm {WD}}^4}\cdot $$(2)

Taking into account that in all models reported in this work tacc=τrec = 80 yr (i.e., tacc=const.), we get

P cri ∝ M WD M ˙ R WD 4 · $$ P_{\mathrm {cri}} \propto \frac {M_{\mathrm {WD}} \dot M}{R_{\mathrm {WD}}^4}\cdot $$(3)

And recalling that more massive WDs are also more compact (i.e., they have a smaller radius), in order to achieve the same Pcri at the base of the envelope, a more massive WD requires a lower Ṁ, as shown in Tables 3 and 4.

Table 4.

Properties of T CrB models with MWD = 1.35 M⊙.

Table 5.

Properties of T CrB models with MWD = 1.38 M⊙.

Finally, an increase in the metallicity of the accreted material translates into an overall reduction in the mass-accretion rate required to achieve τrec∼80 yr (see models 138D, 138B, and 138E in Table 5). A higher metallicity favors an earlier occurrence of the TNR, due to the larger number of nuclear reactions, in particular 12C(p, γ) (see José et al. 2016), thereby shortening the overall duration of the accretion phase and decreasing the amount of mass accreted in the envelope. Accordingly, for a fixed tacc=τrec = 80 yr, models with higher metallicity require lower mass-accretion rates to compensate for the smaller accreted mass.

Tables 3–5 reveal a consistent trend: given that the accretion phase duration is fixed to 80 yr in all models, it turns out that higher accreted masses, 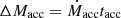Δ M acc = M ˙ acc t acc $ \Delta M_{\mathrm {acc}} = \dot M_{\mathrm {acc}} t_{\mathrm {acc}} $, are obtained in models evolved with lower LWD or Z (i.e., models requiring higher mass-accretion rates to trigger a nova explosion after tacc = 80 yr), which in turn translates into larger ignition densities and pressures in the envelope. Since pressure at the base of the envelope determines the strength of the explosion, it follows that models with lower LWD or Z (including those with lower MWD) result in more violent outbursts, characterized by higher peak temperatures (Tmax) and larger ejected masses (ΔMeje) with greater kinetic energies (K).

4.2. Nucleosynthesis

Nucleosynthesis provides valuable observables that can help identify the model that better matches the explosion of T CrB.

4.2.1. Isotopic abundances

Spectroscopic observations of the nova ejecta often provide elemental abundances only. However, a number of isotopic ratios have been accessible through high-resolution, near-IR spectroscopy (e.g., 12C/13C through the first overtone of CO in absorption; see Evans et al. 2019; Pavlenko et al. 2020 for details9). Here, we review the most important results in terms of mean (mass-averaged) isotopic abundances in the ejecta of the different models (see Tables 6–10; tables with complete yields can be found in the appendix).

Table 6.

Isotopic abundancesa of the CNOF-group nuclei in the ejecta of the main T CrB models.

Table 7.

Isotopic abundances of Ne and Na nuclei in the ejecta of the main T CrB models.

Table 8.

Isotopic abundances of Mg, Al, and Si nuclei in the ejecta of the main T CrB models.

Table 9.

Isotopic abundances of P and S nuclei in the ejecta of the main T CrB models.

Table 10.

Isotopic abundances of Ca and Sc nuclei in the ejecta of the main T CrB models.

The three models computed for MWD = 1.3 M⊙ yield identical (mean) mass fractions of H and 4He in the ejecta. Remarkably, the H content in the envelope only experienced a minor decrease of 8% through the entire outburst, while X(H)+X(4He) remained nearly constant. Indeed, very small leakage from the CNO region is observed (∑X(CNO)ini = 10−2→∑X(CNO)eje = 9.2×10−3), indicating limited nuclear activity during the explosion. Aside from H and 4He, the most abundant isotopes in the ejecta correspond to the CNO region, including 14N, 12,13C (occasionally 15N), 20Ne, and in some models 28Si and 32S, all characterized by mass fractions around ∼10−3. Predicted isotopic ratios10 in the ejecta for some important species include 12C/13C = 0.60−0.75, 16O/17O = 24−58, 16O/[18O + 18F] = 7000−8300, 28Si/29Si = 140−160, and 28Si/30Si = 1.4−5.3. With regard to 7Li(+7Be), mass fractions around 10−12 have also been obtained for these same models, revealing depletion with respect to solar values.

The MWD = 1.35 M⊙ models follow a similar pattern, displaying a notable presence of 14,15N, 12,13C, and 32S in the ejecta. However, the higher peak temperature achieved in Model 135C, Tmax = 2.71×108 K, resulted in an extension of the nuclear activity. Indeed, 40Ca reached a mass fraction of 1.3×10−3 in the ejecta, a value comparable to those of the most abundant CNO isotopes. With regard to isotopic ratios, these models yielded 12C/13C = 0.70−1.2, 16O/17O = 6.2−17, 16O/[18O + 18F] = 2400−5400, 28Si/29Si = 79−130, and 28Si/30Si = 1.0−1.2, while 7Li(+7Be) mass fractions reached values ranging between 10−12−10−11.

Similar trends are found for the MWD = 1.38 M⊙ models. The adopted mass is enough to expose the plasma to high peak temperatures (i.e., 2.92×108 K in Model 138C), which reinforced the presence of 40Ca in the ejecta, reaching 2.8×10−3 in Model 138C (about 44 times the solar value). With regard to isotopic ratios, the 1.38 M⊙ models with solar metallicity yielded 12C/13C = 0.84−1.3, 16O/17O = 4.4−11, 16O/[18O + 18F] = 1200−3500, 28Si/29Si = 48−104, and 28Si/30Si = 0.76−1.3, while 7Li(+7Be) mass fractions reached values around 10−11.

Larger variations in chemical composition within the ejecta are observed among the additional 1.38 M⊙ models evolved with different initial metallicities of the accreted matter: indeed, while the ejecta in Model 138D (Z = 0.1 Z⊙) is characterized by significant amounts of 40Ca (the third, most abundant species, after H and 4He), 14,15N, 12,13C, and 44Ca, dominance shifts toward the presence of 14,15N, 12,13C, 20Ne, and 28Si in Model 138E (Z = 10 Z⊙).

4.2.2. Elemental abundances

While some isotopic abundances can be obtained in the near IR (see Sect. 4.2.1), spectroscopic determinations often provide elemental (rather than isotopical) abundances. The main elemental abundances in the ejecta of T CrB, predicted for the different models reported in this work, are summarized in Tables 11–13.

Table 11.

Elemental abundances for T CrB models with MWD = 1.30 M⊙.

Table 12.

Elemental abundances for T CrB models with MWD = 1.35 M⊙.

Table 13.

Elemental abundances for T CrB models with MWD = 1.38 M⊙.

The influence of the initial WD luminosity and the mass-accretion rate on the elemental abundances of the ejecta can be drawn from a comparison of models with the same WD mass. Indeed, for models with MWD = 1.3 M⊙, differences in mass fractions by a factor of 3 or larger affect only P and S. For models with MWD = 1.35 M⊙, differences encompass elements such as Ne, Si, K, Ca, and Sc. For models with MWD = 1.35 M⊙, differences in elemental abundances affect Ne, Si, P, Ca, and Sc11. A cross-comparison of the variation of elemental abundances between models with different WD masses (for the same initial luminosity) reveals differences in a large variety of species, including Ne, Na, Mg, Al, Si, P, S, Ar, K, Ca, and Sc. Such differences in the elemental abundances of the ejecta could help us discriminate between the different T CrB models reported in this work. Accordingly, we urge researchers to take early spectroscopic measurements of the forthcoming outburst of T CrB with the goal of determining the elemental abundances in the ejecta and, in turn, the conditions under which outbursts in this system take place.

4.2.3. Gamma-ray emission

Previous observations of T CrB (see Sect. 2) have not revealed significant deviations from solar abundances. This justifies our choice of solar composition for the plasma transferred from the secondary star, in most of the simulations reported in this work. In this context, the amount of radioactive species in the ejecta is expected to be small.

Figure 1 shows the predicted gamma-ray spectra for a typical case, Model 130C, one of the models with higher 22Na (and also 18F) in the ejecta (see the appendix). The gamma-ray emission has been computed with a Monte Carlo code, as described in Gómez-Gomar et al. (1998). Spectra at different times after Tmax are dominated by the presence of two prominent lines, at 511 keV (generated by electron-positron annihilation, with positrons released in the decay of 18F and, to some extent, 13N) and 1275 keV (due to 22Na decay). A lower-energy continuum, powered by Comptonization of 511 keV photons – mainly effective up to 18 h after Tmax – plus contribution from positronium emission – clearly seen at 72 h, when the ejecta is less dense and Comptonization becomes less effective – is also noticed. However, fluxes corresponding to all these features are orders of magnitude smaller than those typically reported for standard models of classical novae with pre-enrichment (see, e.g., Hernanz 2008). Accordingly, no detectable gamma-ray lines are expected for the forthcoming outburst of T CrB.

thumbnail Fig. 1.

Early gamma-ray spectra of Model 130C showing the 511-keV line, the lower-energy continuum, and the 1275-keV line, from 9 h to 3 days after the explosion (Tmax).

5. Discussion

5.1. Models with mixing

The limited nuclear activity expected during the outbursts of T CrB (see Sect. 4) results from the limited mixing between the accreted material and the outer layers of the WD. This assumption is supported by the near-solar metallicities typically observed in the ejecta of most RNe, which contrasts sharply with the higher metallicities generally inferred in classical nova ejecta, typically ranging from Z∼0.2−0.5.

Several mixing mechanisms have been proposed in the literature to explain the enrichment of the accreted material with WD matter. These include diffusion-induced mixing (Prialnik & Kovetz 1984; Kovetz & Prialnik 1985; Iben et al. 1991, 1992; Fujimoto & Iben 1992), shear mixing (Durisen 1977; Kippenhahn & Thomas 1978; MacDonald 1983; Livio & Truran 1987; Kutter & Sparks 1987; Sparks & Kutter 1987; Bellomo et al. 2024), convective overshoot-induced flame propagation (Woosley 1986), mixing via gravity wave breaking on the WD surface (Rosner et al. 2001; Alexakis et al. 2004), and mixing driven by Kelvin-Helmholtz hydrodynamic instabilities in multidimensional nova models (Glasner & Livne 1995; Glasner et al. 1997, 2005, 2007, 2012; Kercek et al. 1998, 1999; Casanova et al. 2010, 2011a,b, 2016, 2018; José et al. 2020). It is likely that a combination of these mechanisms contributes to mixing during a nova outburst. However, the short time interval between outbursts in RNe likely restricts the effectiveness of the primary mixing processes responsible for the metallicity enhancement typically observed in classical novae.

For completeness, and to evaluate the impact of mixing on the nucleosynthesis occurring during RN outbursts, we conducted an additional series of simulations. These simulations were performed for WDs with masses of 1.35 M⊙ and 1.38 M⊙, assuming different (but limited) degrees of mixing between the (solar) accreted envelope and matter from the outermost WD layers: 10% and 25%. Additionally, we considered two distinct compositions for the WD hosting the explosion, carbon-oxygen (CO) and oxygen-neon (ONe), as the nature of the compact star in RNe remains a subject of debate. The main characteristics of these RN outbursts with mixing are summarized in Tables A.4. and A.5..

The injection of 12C into the envelope, originating from the underlying substrate, significantly alters the explosion dynamics and associated nucleosynthesis. A comparison of model 135C with models 135CO1 (10% mixing) and 135CO2 (25% mixing), which feature a highly C-rich substrate (X(12C) = 0.495), reveals a shortened accretion phase in the mixing models. This results in a net decrease in the total mass accreted and a corresponding reduction in the pressure at the base of the envelope at ignition. Consequently, the maximum temperature achieved during the explosion and the ejected mass are both reduced in these models with mixing. In contrast, the substantially lower 12C content in the outer layers of an ONe WD (X(12C) = 9.16×10−3) minimally impacts the explosion properties in models 135ONe1 (10% mixing) and 135ONe2 (25% mixing). Notably, in model 135C, X(12C) = 2.33×10−3 in the accreted envelope. However, mixing a solar-composition envelope with an ONe-rich substrate reduces the hydrogen content, leading to comparable values of the product X(12C) × X(1H) in the envelope for models 135C, 135ONe1, and 135ONe2.

In terms of associated nucleosynthesis, aside from 1H and 4He, the most abundant species in the ejecta of model 135C are 12,13C, 14,15N, 32S, and 40Ca. In models 135CO1 and 135CO2, 12,13C and 14N are overproduced by an order of magnitude compared to model 135C. Notably, 15N reaches X(15N) = 0.11 in model 135CO2, which is nearly 40 times the amount ejected in model 135C. Other elements significantly synthesized in the mixing models include 20Ne and 28Si in both 135CO1 and 135CO2, as well as 16,17O in model 135CO2. Models that incorporate mixing with an ONe-rich substrate are characterized by ejecta enriched in 14,15N, 12,13C, 20Ne, 28,30Si, and 32S (models 135ONe1 and 135ONe2), along with 17O and 31P (model 135ONe2). But the most striking difference between non-mixing and mixing models lies in the synthesis of the gamma-ray emitters 18F, 7Be, 22Na, and 26Al. Model 135CO produces negligible amounts of 7Be (X(7Be) ∼ 10−11) and low mass fractions of 18F (∼10−9, one hour after peak temperature), as well as 22Na and 26Al (∼10−7). In contrast, models with mixing show a substantial increase in the production of these nuclides. For models 135CO1 and 135CO2: X(7Be) ∼ 10−6−10−5, X(18F) ∼ 10−7−10−5, X(22Na) ∼ 10−6, and X(26Al) ∼ 10−6−10−5. Similarly, for models 135ONe1 and 135ONe2: X(7Be) ∼ 10−8−10−7, X(18F) ∼ 10−8−10−6, and X(22Na) and X(26Al) ∼ 10−5−10−4. Future space missions with enhanced sensitivities may have the capability to detect some of these gamma-ray lines, particularly the 511-keV line and the associated lower-energy continuum, provided that enough mixing occurs. Indeed, such observations could provide valuable constraints on the extent of mixing in RNe and offer insights into the nature of the underlying WD hosting the explosion (CO or ONe)12.

5.2. Models with 1.2 M⊙ white dwarfs

Although the most recent estimates for T CrB suggest the presence of a very massive WD, with MWD>1.3 M⊙ (Zamanov et al. 2003; Hachisu & Kato 2001; Shara et al. 2018), the existence of RNe with WD masses around 1.2 M⊙, such as T Pyx, IM Nor, and CI Aql (Shara et al. 2018), stresses the need of characterizing outbursts occurring on the surfaces of less massive WDs. To this end, we included three additional models involving 1.20 M⊙ WDs with initial luminosities of 0.01 L⊙, 0.1 L⊙, and 1 L⊙. These WDs accrete solar-composition material at the specific mass-accretion rate that triggers an explosion after 80±0.5 yr of accretion. The main characteristics of these models are summarized in Table A.6..

One of the most notable differences between these models and those computed for more massive WDs lies in the amount of mass accreted and ejected. For example, the 1.20 M⊙ models typically show values that are 2 to 3 times greater than those found in the 1.30 M⊙ models. However, the lower surface gravity of a 1.20 M⊙ WD results in lower maximum densities and pressures at the base of the accreted envelope. This leads to less violent outbursts, characterized by lower peak temperatures and a more moderate nuclear activity. The endpoint of this activity, defined as the heaviest isotope whose abundance changes by more than a factor of 2 relative to its initial value, is limited to 37Cl in the 1.20 M⊙ models. In comparison, the endpoints reach 39K and 46Ti in the 1.30 and 1.38 M⊙ models, respectively.

Nucleosynthesis is essential for distinguishing the mass of the underlying WD hosting the explosion in T CrB. While the 1.38 M⊙ models presented in this study exhibit ejecta significantly enriched in S, Cl, K, Ca, and Sc relative to solar (i.e., initial) abundances, the 1.20 M⊙ and 1.30 M⊙ models generally show solar or slightly subsolar abundances of S, K, Ca, and Sc in the ejecta (except for the relatively energetic outburst of model 130C, which yields some enhancement of S and K; see Table A.6. for details). Moreover, Si is enhanced in the 1.20 M⊙ and 1.30 M⊙ models, whereas its abundance remains near-solar or significantly depleted in the 1.38 M⊙ models. Spectroscopic determinations of the elemental abundances of these key species could prove critical for determining the mass of the underlying WD in T CrB.

6. Conclusions

The next outburst of T CrB, expected to occur imminently, motivated us to conduct a thorough examination of the main characteristics of this system and the conditions needed to power an outburst with a periodicity of about 80 yr. To this end, we constructed 11 new hydrodynamic models of the explosion of T CrB for different combinations of parameters (i.e., mass and initial luminosity of the WD, metallicity, and mass-accretion rate) that power a nova explosion in approximately 80 yr. We also reported on 8 additional hydrodynamic models that include mixing at the interface between the accreted envelope and the outermost layers of the underlying WD, and 3 models for 1.20 M⊙ WDs.

As reported in the literature (see, e.g., Starrfield et al. 1988; Hernanz & José 2008; Shara et al. 2018) and confirmed by the simulations reported in this work, extremely high mass-accretion rates, as well as high WD masses and luminosities, are necessary to drive outbursts with short recurrence periods, such as those observed in RNe. Specifically, for a system like T CrB (with τrec∼80 yr), we find that accretion rates of Ṁacc ∼ 10−8−10−7 M⊙ yr−1 are required for WD masses of MWD∼1.30−1.38 M⊙ and luminosities of LWD∼0.01−1 L⊙. Models with lower initial WD luminosities, less massive WDs, or lower metallicities in the accreted plasma require higher mass-accretion rates to power an explosion within 80 yr. Models with lower metallicities or initial WD luminosities result in higher accreted masses and ignition pressures. These conditions drive more violent outbursts, characterized by higher peak temperatures, higher ejected masses, and greater kinetic energies.

This study13 has yielded key findings, which are summarized below:

  • Aside from H and 4He, the ejecta are predominantly composed of isotopes from the CNO cycle, including 14,15N and 12,13C. In some models, significant amounts of 20Ne, 28Si, 32S, and 40Ca are also present.

  • Significant variations in the chemical composition are observed within the ejecta of 1.38 M⊙ models with different initial metallicities. For instance, the ejecta in Model 138D (Z = 0.1 Z⊙) show notable contributions from 40Ca, 14,15N, 12,13C, and 44Ca. In contrast, Model 138E (Z = 10 Z⊙) exhibits a shift in dominance toward 14,15N, 12,13C, 20Ne, and 28Si.

  • A comparative analysis of elemental abundance variations across models with different WD masses, but identical initial luminosities, reveals substantial differences in a wide range of species, including Ne, Na, Mg, Al, Si, P, S, Ar, K, Ca, and Sc. These variations within the ejecta provide a potential means to distinguish between the various T CrB models discussed in this work. Specifically, while the 1.38 M⊙ models exhibit ejecta significantly enriched in S, Cl, K, Ca, and Sc relative to solar abundances, the 1.20 M⊙ and 1.30 M⊙ models generally show solar or slightly subsolar abundances of S, K, Ca, and Sc in the ejecta (except for model 130C, which yields some enhancement of S and K). Moreover, Si is enhanced in the 1.20 M⊙ and 1.30 M⊙ models, whereas its abundance remains near-solar or significantly depleted in the 1.38 M⊙ models.

  • Gamma-ray lines (or the continuum) are not expected to be detectable during the forthcoming outburst of T CrB due to the extremely low yields of gamma-ray-emitting isotopes in the ejecta, such as 7Be, 18F, 22Na, and 26Al. However, test models that incorporate mixing with a CO- or ONe-rich substrate – characteristic of the outer layers of the underlying WD – reveal significant differences in the predicted emission profiles. Future space missions with improved sensitivity might detect the most prominent gamma-ray signatures, if enough mixing occurs. Such observations could provide constraints on the degree of mixing in RNe and help us identify the nature of the WD (CO or ONe) that hosts the explosion.

  • Additionally, we emphasize the importance of conducting early spectroscopic measurements during the next outburst of T CrB aimed at determining the abundances in the ejecta; this would shed light on the physical conditions that govern outbursts in this system.

Acknowledgments

We thank the anonymous referee for constructive comments, which helped improve the quality of the manuscript. This work has been partially supported by the Spanish MINECO grants PID2023-148661NB-I00 and PID2023-149918NB-I00, the program Unidad de Excelencia María de Maeztu CEX2020-001058-M, the E.U. FEDER funds, and the AGAUR/Generalitat de Catalunya grants SGR-386/2021 and SGR-1526/2021.

1

Models predict even shorter recurrence times, with some as brief as 50 days (Hillman et al. 2015), although no observational evidence of such systems has been reported to date.

2

KT Eridani (Nova Eridani 2009) has been claimed to be the 11th Galactic RN (Pagnotta & Schaefer 2014; Schaefer et al. 2022; Shara et al. 2024), based on the discovery of a vast super-shell (50 pc in diameter), ejected in previous eruptions, centered around that object.

3

See Hric et al. (1997) and Schaefer (2009) for more recent determinations of the orbital period in T CrB, around Porb∼227 days.

4

See Gilmozzi et al. (1991) for an alternative explanation involving a triple stellar system.

5

See Schaefer (2009) for a distance determination to T CrB of 800±140 pc.

6

A value of A(Li) ∼ 1.2 was also reported for the RN RS Oph.

7

See Figueira et al. (2025) for recent 3D simulations of the impact of the ejecta on the secondary star in the RN system U Sco.

8

See also Table 5 for 1.38 M⊙ WDs.

9

See also Evans et al. (2025) for the first near- IR spectroscopy of an extragalactic nova, the RN LMCN 1968-12a.

10

Mass fractions have been used to evaluate the corresponding isotopic ratios.

11

Multiple differences are found when models of different metallicity are considered (see Table 13 for details). The largest variations, when comparing models with Z/Z⊙ = 0.1, 1 and 10, affect Ne, Si, and P.

12

Trends similar to those observed in the 1.35 M⊙ models are also found in the 1.38 M⊙ models. See Tables A.4. and A.5. for details.

13

Another theoretical study focused on T CrB (Starrfield et al. 2025) has been published while this paper was already under review.

References

  1. Alexakis, A., Calder, A. C., Heger, A., et al. 2004, ApJ, 602, 931 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anupama, G. C., & Prabhu, T. P. 1991, MNRAS, 253, 605 [Google Scholar]
  3. Bellomo, M., Shore, S. N., & José, J. 2024, A&A, 690, A361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Blinnikov, S. I., Dunina-Barkovskaya, N. V., & Nadyozhin, D. K. 1996, ApJS, 106, 171 [Google Scholar]
  5. Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2010, A&A, 513, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2011a, A&A, 527, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Casanova, J., José, J., García-Berro, E., Shore, S. N., & Calder, A. C. 2011b, Nature, 478, 490 [NASA ADS] [CrossRef] [Google Scholar]
  8. Casanova, J., José, J., García-Berro, E., & Shore, S. N. 2016, A&A, 595, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Casanova, J., José, J., & Shore, S. N. 2018, A&A, 619, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Chen, X., Han, Z., & Tout, C. A. 2011, ApJ, 735, L31 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chomiuk, L., Metzger, B. D., & Shen, K. J. 2021, ARA&A, 59, 391 [NASA ADS] [CrossRef] [Google Scholar]
  12. Cinquegrana, G. C., & Karakas, A. I. 2022, MNRAS, 510, 1557 [Google Scholar]
  13. Darnley, M. J., Henze, M., Bode, M. F., et al. 2016, ApJ, 833, 149 [NASA ADS] [CrossRef] [Google Scholar]
  14. Dobrotka, A., Hric, L., & Petrík, K. 2004, Balt. Astron., 13, 159 [Google Scholar]
  15. Downen, L. N., Iliadis, C., José, J., & Starrfield, S. 2013, ApJ, 762, 105 [NASA ADS] [CrossRef] [Google Scholar]
  16. Duerbeck, H. W. 2009, Astron. Nachr., 330, 568 [Google Scholar]
  17. Durisen, R. H. 1977, ApJ, 213, 145 [NASA ADS] [CrossRef] [Google Scholar]
  18. Evans, A., Pavlenko, Ya. V., Banerjee, D. P. K., et al. 2019, MNRAS, 486, 3498; Erratum: MNRAS, 512, 56 [Google Scholar]
  19. Evans, A., Banerjee, D. P. K., Geballe, T. R., et al. 2025, MNRAS, 536, 1710 [Google Scholar]
  20. Figueira, J., José, J., Cabezón, R. M., & García-Senz, D. 2025, A&A, 693, A209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Fujimoto, M. Y. 1982, ApJ, 257, 752 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fujimoto, M., & Iben, I.Jr. 1992, ApJ, 399, 646 [NASA ADS] [CrossRef] [Google Scholar]
  23. Gehrz, R. D., Truran, J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110, 3 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gilmozzi, R., Selvelli, P. -L., & Cassatella, A. 1991, Accretion Powered Compact Binaries (Cambridge: Cambridge University Press), 393 [Google Scholar]
  25. Glasner, S. A., & Livne, E. 1995, ApJ, 445, L149 [NASA ADS] [CrossRef] [Google Scholar]
  26. Glasner, S. A., Livne, E., & Truran, J. W. 1997, ApJ, 475, 754 [NASA ADS] [CrossRef] [Google Scholar]
  27. Glasner, S. A., Livne, E., & Truran, J. W. 2005, ApJ, 625, 347 [NASA ADS] [CrossRef] [Google Scholar]
  28. Glasner, S. A., Livne, E., & Truran, J. W. 2007, ApJ, 665, 1321 [NASA ADS] [CrossRef] [Google Scholar]
  29. Glasner, S. A., Livne, E., & Truran, J. W. 2012, MNRAS, 427, 2411 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gómez-Gomar, J., Hernanz, M., José, J., & Isern, J. 1998, MNRAS, 296, 913 [Google Scholar]
  31. Hachisu, I., & Kato, M. 1999, ApJ, 517, L47 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hachisu, I., & Kato, M. 2001, ApJ, 558, 323 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hernanz, M. 2008, Classical Novae, 2nd edn. (Cambridge: Cambridge University Press), 252 [CrossRef] [Google Scholar]
  34. Hernanz, M., & José, J. 2008, New Astron. Rev., 52, 386 [CrossRef] [Google Scholar]
  35. Hillman, Y., Prialnik, D., Kovetz, A., & Shara, M. 2015, MNRAS, 446, 1924 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hric, L., Urban, Z., Niarchos, P., & Petrík, K. 1997, Physical Processes in Symbiotic Stars (Warsaw: Copernicus Found for Polish Astronomy), 17 [Google Scholar]
  37. Hric, L., Petrík, K., Urban, Z., Niarchos, P., & Amupama, G. C. 1998, A&A, 339, 449 [Google Scholar]
  38. Huggins, W., & Miller, W. A. 1866, R. Soc. London Proc., 15, 146 [Google Scholar]
  39. Iben, I.Jr., Fujimoto, M. Y., & MacDonald, J. 1991, ApJ, 375, L27 [Google Scholar]
  40. Iben, I.Jr., Fujimoto, M. Y., & MacDonald, J. 1992, ApJ, 388, 521 [Google Scholar]
  41. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  42. José, J. 2016, Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton, FL: CRC/Taylor and Francis) [Google Scholar]
  43. José, J., & Hernanz, M. 1998, ApJ, 494, 680 [Google Scholar]
  44. José, J., & Shore, S. 2008, Classical Novae, 2nd edn. (Cambridge: Cambridge University Press), 121 [CrossRef] [Google Scholar]
  45. José, J., Halabi, G. M., & El Eid, M. F. 2016, A&A, 593, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. José, J., Shore, S. N., & Casanova, J. 2020, A&A, 634, A5 [EDP Sciences] [Google Scholar]
  47. Kato, M., Saio, H., Hachisu, I., & Nomoto, K. 2014, ApJ, 793, 136 [CrossRef] [Google Scholar]
  48. Kelly, K. J., Iliadis, C., Downen, L. N., José, J., & Champagne, A. 2013, ApJ, 777, 130 [NASA ADS] [CrossRef] [Google Scholar]
  49. Kenyon, S. J., & Garcia, M. R. 1986, AJ, 91, 125 [Google Scholar]
  50. Kercek, A., Hillebrandt, W., & Truran, J. W. 1998, A&A, 337, 379 [NASA ADS] [Google Scholar]
  51. Kercek, A., Hillebrandt, W., & Truran, J. W. 1999, A&A, 345, 831 [NASA ADS] [Google Scholar]
  52. Kippenhahn, R., & Thomas, H. 1978, A&A, 63, 265 [NASA ADS] [Google Scholar]
  53. Kovetz, A., & Prialnik, D. 1985, ApJ, 291, 812 [Google Scholar]
  54. Kraft, R. P. 1958, ApJ, 127, 625 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kutter, G. S., & Sparks, W. M. 1987, ApJ, 321, 386 [NASA ADS] [CrossRef] [Google Scholar]
  56. Linford, J. D., Chomiuk, L., Sokoloski, J. L., et al. 2019, ApJ, 884, 8 [NASA ADS] [CrossRef] [Google Scholar]
  57. Livio, M., & Truran, J. W. 1987, ApJ, 318, 316 [Google Scholar]
  58. Lodders, K., Palme, H., & Gail, H. -P. 2009, Solar System (Berlin: Springer-Verlag) [Google Scholar]
  59. Luna, G. J. M., Nelson, T., Mukai, K., & Sokoloski, J. L. 2019, ApJ, 880, 94 [NASA ADS] [CrossRef] [Google Scholar]
  60. MacDonald, J. 1983, ApJ, 273, 289 [NASA ADS] [CrossRef] [Google Scholar]
  61. Nishiyama, K., & Kabashima, F. 2008, CBAT, IAU, http://www.cbat.eps.harvard.edu/iau/CBAT_M31.html#2008-12a [Google Scholar]
  62. Pagnotta, A., & Schaefer, B. E. 2014, ApJ, 788, 164 [Google Scholar]
  63. Pavlenko, Y. V., Evans, A., Banerjee, D. P. K., et al. 2020, MNRAS, 498, 4853 [Google Scholar]
  64. Prialnik, D., & Kovetz, A. 1984, ApJ, 281, 367 [NASA ADS] [CrossRef] [Google Scholar]
  65. Prialnik, D., Shara, M. M., & Shaviv, G. 1979, A&A, 72, 192 [NASA ADS] [Google Scholar]
  66. Rosner, R., Alexakis, A., Young, Y., Truran, J. W., & Hillebrandt, W. 2001, ApJ, 562, L177 [Google Scholar]
  67. Sallaska, A. L., Iliadis, C., Champange, A. E., et al. 2013, ApJS, 207, 18 [Google Scholar]
  68. Sanford, R. F. 1949, ApJ, 109, 81 [NASA ADS] [CrossRef] [Google Scholar]
  69. Schaefer, B. E. 2009, ApJ, 697, 721 [NASA ADS] [CrossRef] [Google Scholar]
  70. Schaefer, B. E. 2010, ApJS, 187, 275 [NASA ADS] [CrossRef] [Google Scholar]
  71. Schaefer, B. E. 2023, J. Hist. Astron., 54, 436 [CrossRef] [Google Scholar]
  72. Schaefer, B. E., Walter, F. M., Hounsell, R., & Hillman, Y. 2022, MNRAS, 517, 3864 [Google Scholar]
  73. Selvelli, P. -L., Cassatella, A., & Gilmozzi, R. 1992, ApJ, 393, 289 [NASA ADS] [CrossRef] [Google Scholar]
  74. Shafter, A. W. 2017, ApJ, 834, 196 [CrossRef] [Google Scholar]
  75. Shahbaz, T., Hauschildt, P. H., Naylor, T., & Ringwald, F. 1999, MNRAS, 306, 675 [Google Scholar]
  76. Shara, M. M. 1981, ApJ, 243, 926 [NASA ADS] [CrossRef] [Google Scholar]
  77. Shara, M. M., Prialnik, D., Hillman, Y., & Kovetz, A. 2018, ApJ, 860, 110 [NASA ADS] [CrossRef] [Google Scholar]
  78. Shara, M. M., Lanzetta, K. M., Garland, J. T., et al. 2024, MNRAS, 529, 224 [NASA ADS] [CrossRef] [Google Scholar]
  79. Sparks, W. M., & Kutter, G. S. 1987, ApJ, 321, 394 [Google Scholar]
  80. Stanishev, V., Zamanov, R., Tomov, N., & Marziani, P. 2004, A&A, 415, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Starrfield, S., Sparks, W. M., & Shaviv, G. 1988, ApJ, 325, L35 [CrossRef] [Google Scholar]
  82. Starrfield, S., Iliadis, C., & Hix, W. R. 2008, Classical Novae, 2nd edn. (Cambridge: Cambridge University Press), 77 [CrossRef] [Google Scholar]
  83. Starrfield, S., Iliadis, C., Timmes, F. X., et al. 2012, Bull. Astron. Soc. India, 40, 419 [NASA ADS] [Google Scholar]
  84. Starrfield, S., Iliadis, C., & Hix, W. R. 2016, PASP, 128, 051001 [Google Scholar]
  85. Starrfield, S., Bose, M., Woodward, C. E., et al. 2025, ApJ, 982, 89 [Google Scholar]
  86. Wallerstein, G., Harrison, T., Munari, U., & Vanture, A. 2008, PASP, 120, 492 [Google Scholar]
  87. Webbink, R. F., Livio, M., Truran, J. W., & Orio, M. 1987, ApJ, 314, 653 [NASA ADS] [CrossRef] [Google Scholar]
  88. Wolf, W. M., Bildsten, L., Brooks, J., & Paxton, B. 2013, ApJ, 777, 136 [Google Scholar]
  89. Woodward, C. E., Pavlenko, Ya. V., Evans, A., et al. 2020, AJ, 159, 231 [NASA ADS] [CrossRef] [Google Scholar]
  90. Woosley, S. E. 1986, Nucleosynthesis and Chemical Evolution (Sauverny: Geneva Observatory), 1 [Google Scholar]
  91. Yaron, O., Prialnik, D., Shara, M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
  92. Zamanov, R., Marziani, P., Stanishev, V., & Tomov, N. 2003, White Dwarfs (Dordrecht: Kluwer Academic Publishers), 353 [CrossRef] [Google Scholar]
  93. Zamanov, R., Boeva, S., Latev, G. Y., et al. 2023, A&A, 680, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

Appendix A: Detailed tables for the T CrB models computed in this work

Table A.1.

Properties of T CrB modelsa with MWD = 1.30 M⊙.

Table A.1.

continued.

Table A.2.

Properties of T CrB modelsawith MWD = 1.35 M⊙.

Table A.2.

continued.

Table A.3.

Properties of T CrB modelsa with MWD = 1.38 M⊙.

Table A.3.

continued.

Table A.4.

T CrB modelsa with mixing for MWD = 1.35 M⊙.

Table A.4.

continued.

Table A.5.

T CrB modelsa with mixing for MWD = 1.38 M⊙.

Table A.5.

Continued.

Table A.6.

T CrB modelsa with MWD = 1.20 M⊙.

Table A.6.

continued.

All Tables

Table 1.

Solar abundances from 1H to 48Ti and isotopic ratios (Lodders et al. 2009).

In the text
Table 2.

Models of T CrB that yield τrec = 80±0.5 yr.

In the text
Table 3.

Properties of T CrB models with MWD = 1.30 M⊙.

In the text
Table 4.

Properties of T CrB models with MWD = 1.35 M⊙.

In the text
Table 5.

Properties of T CrB models with MWD = 1.38 M⊙.

In the text
Table 6.

Isotopic abundancesa of the CNOF-group nuclei in the ejecta of the main T CrB models.

In the text
Table 7.

Isotopic abundances of Ne and Na nuclei in the ejecta of the main T CrB models.

In the text
Table 8.

Isotopic abundances of Mg, Al, and Si nuclei in the ejecta of the main T CrB models.

In the text
Table 9.

Isotopic abundances of P and S nuclei in the ejecta of the main T CrB models.

In the text
Table 10.

Isotopic abundances of Ca and Sc nuclei in the ejecta of the main T CrB models.

In the text
Table 11.

Elemental abundances for T CrB models with MWD = 1.30 M⊙.

In the text
Table 12.

Elemental abundances for T CrB models with MWD = 1.35 M⊙.

In the text
Table 13.

Elemental abundances for T CrB models with MWD = 1.38 M⊙.

In the text
Table A.1.

Properties of T CrB modelsa with MWD = 1.30 M⊙.

In the text
Table A.1.

continued.

In the text
Table A.2.

Properties of T CrB modelsawith MWD = 1.35 M⊙.

In the text
Table A.2.

continued.

In the text
Table A.3.

Properties of T CrB modelsa with MWD = 1.38 M⊙.

In the text
Table A.3.

continued.

In the text
Table A.4.

T CrB modelsa with mixing for MWD = 1.35 M⊙.

In the text
Table A.4.

continued.

In the text
Table A.5.

T CrB modelsa with mixing for MWD = 1.38 M⊙.

In the text
Table A.5.

Continued.

In the text
Table A.6.

T CrB modelsa with MWD = 1.20 M⊙.

In the text
Table A.6.

continued.

In the text

All Figures

thumbnail Fig. 1.

Early gamma-ray spectra of Model 130C showing the 511-keV line, the lower-energy continuum, and the 1275-keV line, from 9 h to 3 days after the explosion (Tmax).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.