| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A49 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833750 | |
| Published online | 24 January 2019 | |
Chemical composition of planet building blocks as predicted by stellar population synthesis
Institut UTINAM, CNRS UMR6213, Université Bourgogne Franche-Comté, OSU THETA Franche-Comté-Bourgogne, Observatoire de Besançon, BP 1615, 25010 Besançon Cedex, France
e-mail: nahuel.cabral@utinam.cnrs.fr
Received:
30
June
2018
Accepted:
7
November
2018
Context. Future space missions (TESS, CHEOPS, PLATO, and the JWST) will considerably improve our understanding of the formation and history of planetary systems by providing accurate constraints on planetary radius, mass, and atmospheric composition. Currently, observations show that the presence of planetary companions is closely linked to the metallicity and the chemical abundances of the host stars.
Aims. We aim to build an integrated tool for predicting the planet building blocks (PBBs) composition as a function of the stellar populations to interpret ongoing and future large surveys. The different stellar populations we observe in our Galaxy are characterized by different metallicities and α-element abundances. We here investigate the trends of the expected PBBs composition with the chemical abundance of the host star in different parts of the Galaxy.
Methods. We synthesized stellar populations with the Besançon galaxy model, which includes stellar evolutionary tracks that are computed with the stellar evolution code STAREVOL. We integrated a previously published simple stoichiometric model into this code to determine the expected composition of the PBBs.
Results. We determine the expected PBB composition around FGK stars for the four galactic populations (thin and thick disks, halo, and bulge) within the Milky Way. Our solar neighborhood simulations are in good agreement with the recent results obtained with the HARPS survey for firon, fw, and the heavy element mass fraction fZ. We present evidence of a clear dependence of firon and fw on the initial alpha abundances [α/Fe] of the host star. We find that the different initial [α/Fe] distributions in the different galactic populations lead to a bimodal distribution of PBB composition. Our simulations show an iron valley that separates PBBs with high and low iron mass fractions and a water valley that separates PBBs with high and low water mass fractions.
Conclusions. We linked host star abundances and expected PBB composition in an integrated model of the Galaxy. The trends we derive are an important step for statistical analyses of expected planet properties. In particular, internal structure models may use these results to derive statistical trends of rocky planet properties, constrain habitability, and prepare an interpretation of ongoing and future large-scale surveys of exoplanets.
Key words: planets and satellites: composition / stars: abundances
© ESO 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The correlations between planet and star properties provide key constraints on planet formation models. Space-based, Kepler and CoRoT (COnvection, ROtation and planetary Transits) telescopes, and ground-based exoplanets surveys as HARPS (High Accuracy Radial velocity Planet Searcher), have shown many dependences between the exoplanets properties and the physical properties of the host star. Moreover, the TESS (Transiting Exoplanet Survey Satellite, RICKER2015), CHEOPS (CHaracterizing ExoPlanets Satellite), and the JWST (James Webb Space Telescope) are expected to bring huge improvements in our characterizing of planets. The asteroseismic survey PLAnetary Transits and Oscillations of stars (PLATO) in particular will provide stellar properties with high accuracy (Rauer et al. 2014; Miglio et al. 2017). The main observed links between the host star chemical properties and its planet are listed below.
(i) Metallicity correlation with planet frequency. Giant planets are observed more frequently in high-metallicity stars (see, e.g., Santos et al. 2004; Fischer & Valenti 2005), which point out the crucial role of metallicity in planetary formation processes. This correlation is not observed for small planets (Sousa et al. 2011; Buchhave et al. 2012). Zhu et al. (2016) suggested that observational bias (the combination of high occurrence rate and low detection efficiency for small planets) may be the reason for the lacking metallicity correlation in small planets. Currently, the correlation with giants and the very weak correlation with small planets, if it exists, appears to be well explained by the core accretion model. In this model, giant formation efficiency is dependent on the metallicity, while small planets form even around very metal-poor stars (see, e.g., Ida & Lin 2004). We note that the tidal downsizing model also reproduces these two correlations (Nayakshin & Fletcher 2015). Moreover, the masses of heavy elements in the planets and the metallicities of their parent star may be positively correlated, but this still needs to be confirmed (Guillot et al. 2006; Thorngren et al. 2016).
(ii) The metallicity correlation with planet orbital distribution. Different observational and theoretical studies have illustrated the links between the metallicity and the orbital distributions. Beaugé & Nesvorný (2013) found that small planets (Rp < 4 R⊕) orbiting metal-poor stars present longer periods (P > 5 days) than small planets orbiting metal-rich stars. Adibekyan et al. (2013) suggested that the lack of small planets around metal-poor stars at short periods extends to up to four Jupiter masses. By analyzing 212 close-in planets from the APOGEE (APO Galactic Evolution Experiment), Wilson et al. (2018) recently showed that small planets with an orbital period shorter than 8.3 days have a host star that is richer in metals. Moreover, Dawson & Murray-Clay (2013) showed that close-in giant planets orbiting [Fe/H] < 0 host stars generally have lower eccentricities than those orbiting metal-rich stars. In this line, Buchhave et al. (2018) found that cool Jupiters (a > 1 AU) with low eccentricities (e < 0.25) on average orbit metal-poor stars.
(iii) Alpha-abundance correlation with planet frequency. Observations suggest that the correlations between chemical stellar properties and exoplanets are not limited to the metallicity. The observed abundances of specific element ratios also show interesting correlations. Iron-poor stars hosting planets are found to preferentially present enhanced alpha-element compositions (see, e.g., Haywood 2008, 2009; Adibekyan et al. 2012a,b). Interestingly, stars hosting low-mass planets (<30 M⊕) have higher Mg/Si abundance ratios than stars with giant planets (>30 M⊕; Adibekyan et al. 2015). This indicates the important role of Mg/Si ratio in the formation of these small planets. It also suggests that heavy elements such as Mg might compensate for the lack of iron in forming low-mass planets in metal-poor host stars and might explain the absence of a correlation of low-mass planets with [Fe/H]. As discussed by Adibekyan et al. (2015), the frequency oflow-mass planets should correlate with refractory elements (Mg, Si, and Fe) and not necessarily with iron alone.
Because planet properties are observed to correlate with metallicity and specific elemental ratios of the host stars, the different stellar galactic populations could produce planets with very different properties. The stellar populations in the Milky Way indeed show different metallicities and α-abundances that are dueto their different formation ways and epochs and their different chemical evolutions. The halo contains the more metal-poor stars. The disk exhibits two sequences (thick and thin disks), where the thick-disk stars are in general more metal poor and alpha enriched than thin-disk stars (see, e.g., Haywood et al. 2013). The metallicity range of the bulge is similar to that of the thin disk, but the spread in alpha abundances is far larger.
Santos et al. (2017, hereafter S17) determined the expected chemical composition of planet building blocks (PBBs) in the different galactic populations using the elemental abundances determined with the HARPS survey (Adibekyan et al. 2012b). With a simple stoichiometric model, they determined the molecular abundances and the respective mass fractions that are expected after the condensation sequence. Stellar synthetic models are particularly suitable for this type of analysis because they allow studying the properties of the thin and thick disks, halo, and bulge in detail. In line with the previous work of S17, we explore statistical trends of the PBB composition in different galactic populations. We use the Besançon galaxy model (BGM) to simulate the global and chemical properties of stars in different populations (Lagarde et al. 2017). We then apply the stoichiometric model of S17 to these synthetic populations. This allows us to reliably predict the PBB for the whole Milky Way, not only for the solar neighborhood. The development of such a coherent and integrated model is important to prepare the interpretation of future large-scale surveys of exoplanets.
The paper is structured as follows. In Sect. 2, we present the numerical tools we used in this work: the BGM model and the analytical prescriptions we used to estimate the PBB composition. In Sect. 3, we simulate the solar neighborhood, and we compare our results with the values of mass fractions obtained by S17 with the HARPS sample data. In Sect. 4, we present our results for the entire Milky Way up to 50 kpc galactic distances from the Sun and discuss the perspectives.
2 Numerical method
2.1 Besançon galaxy model
The Besançon stellar population synthesis model provides the global (e.g., M, R, and Teff) and chemical properties of stars for 54 chemical species. To reproduce the overall galaxy formation and evolution, four populations are considered: the halo, the bulge, and the thin and thick disk. Each assumes different initial mass functions (IMF) and different formation and evolution histories. In each case, the IMF is a three-slope power law. In the thin-disk population, the star formation rate is assumed to decrease exponentially with time, following Aumer & Binney (2009). The parameters of the IMF and star formation history (SFH) of the thin disk have been fit to the Tycho-2 catalog (Czekaj et al. 2014). The IMF and SFH of the thick disk and halo have been set from comparisons to photometricdata from the Sloan Digital Sky Survey (SDSS) and Two Micron All-Sky Survey (2MASS; Robin et al. 2014).
As presented by Lagarde et al. (2017, 2019; see for more details), the new version of the BGM includes a new grid of stellar evolution models that are computed with the stellar evolution code STAREVOL (e.g., Lagarde et al. 2012; Amard et al. 2016) for stars with M ≥ 0.7 M⊙. These stellar evolution tracks have been computed from the pre-main sequence to the early asymptotic giant branch at six metallicities ([Fe/H] = 0.51, 0, −0.23, −0.54, −1.2, and -2.14) and at different α-enhancements ([α/Fe] = 0.0, 0.15 and 0.30) to simulate all populations.
Data release 12 of the APOGEE spectroscopic survey (Majewski et al. 2017) has been used to determine the [α/Fe]-[Fe/H] trend for the four galactic populations:
![\begin{equation*} \mbox{[$\alpha$/Fe]}= \left\{\!\! \begin{array}{lll} 0.014+0.01406\times\mbox{[Fe/H]} \\ \hspace{0.9cm} +0.1013\times\mbox{[Fe/H]}^{2} & \mbox{thin disk, [Fe/H]\,<\,0.1}, \\ 0 & \mbox{thin disk, [Fe/H]\,>\,0.1},\\ 0.320-\mbox{e}^{(1.19375\times{\textrm{[Fe/H]}}-1.6)} & \mbox{thick disk and bulge}, \\ 0.3 & \mbox{halo}. \\ \end{array} \right. \end{equation*}](/articles/aa/full_html/2019/02/aa33750-18/aa33750-18-eq1.png) (1)
(1)
To these relations, an intrinsic Gaussian dispersion of 0.02 dex is added. Although this improvement provides a better simulation of all stellar populations in our Galaxy, we are limited to the border of the stellar grid in metallicity and alpha content −2.14 < [Fe/H] < 0.51 and 0 < [α/Fe] < 0.3 (inside black lines in Fig.1). These limits will be removed in the future as new stellar models are computed. Still, 81% of the whole sample remain after these cuts. We note that no planets have so far been detected outside our stellar metallicity limits −2.14 < [Fe/H] < 0.51. Even though future detections are not excluded, theoretical works derived a critical metallicity for forming planets (see, e.g., Johnson & Li 2012). Moreover, the vast majority of the observed planet host stars are within the 0 < [α/Fe] < 0.3 limits or very close to them (see, e.g., Adibekyan et al. 2011).
2.2 Stoichiometric model
Elemental abundance ratios such as C/O and Mg/Si1 govern the distribution and formation of chemical species in the protoplanetary disk. Because stellar atmospheres evolve slowly, the composition of a protoplanetary disk (in the early evolutive phases) can be assumed to be the same as the stellar composition (Lodders 2003; Bond et al. 2010). When solids condense from the gaseous disk, these ratios determine the planetesimal geology (Pontoppidan et al. 2014). If the C/O ratio is higher than ~0.8, almost no free oxygen is available to form silicates. The geology of planetesimals will then be dominated by carbonates (Kuchner & Seager 2005; Bond et al. 2010). When the C/O ratio is lower than ~0.8, planetesimals are dominated by magnesium-bearing silicates. In these systems, the silicate distribution will be determined by the local Mg/Si ratio. There are three regimes of mineral formation:
 |
Fig. 1 [α/Fe] abundance as a function of [Fe/H] for stars with d < 50 kpc simulated with the BGM. Thin and thick disks as well as bulge and halo stars are represented by red, blue, green, and yellow dots, respectively. Black lines indicate the selected population we used here: −2.14 < [Fe/H] < 0.51 and 0 < [α/Fe] < 0.3. |
- (1)
when Mg/Si < 1, the magnesium forms primarily pyroxene (MgSiO3) and the remainder of the silicon forms feldspars or olivine (Mg2 SiO4);
- (2)
when 1 < Mg/Si < 2, there is an equally distributed mixture of pyroxene and olivine similar to the solar system;
- (3)
when Mg/Si > 2, silicon forms olivine and the remainder of magnesium will form magnesium compounds such as MgO and MgS.
We used the stoichiometric model published in Santos et al. (2017). In this simple model, the molecular abundances in the protoplanetary disk and their mass fractions can be computed from the stellar abundances of a handful of elements. Fe, Si, Mg, O, and C together with H and He control the species expected from the equilibrium condensation of H2, He, CH4, H2 O, Fe, MgSiO3, Mg2 SiO4, and SiO2 (Lodders 2003; Bond et al. 2010). These compounds dominate the rocky interior of an Earth-like planet (see, e.g., Sotin et al. 2007).
Since we limited our synthetic population to the borders of the stellar grids (−2.14 < [Fe/H] < 0.51, 0 < [α/Fe] < 0.3), all simulated stars have 1 < Mg/Si < 2. We write here the inverted stoichiometric relations corresponding to the case 1 < Mg/Si < 2 (assuming the equations in Appendix B of S17):
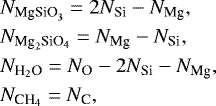 (2)
(2)
with NX the number of atoms of each species X. These relations enable the computation of the expected mass fractions of PBB: the iron-to-silicate mass fraction (firon), the water mass fraction (fw), and the summed mass in percent of all heavy elements (fZ). The expression of these fractions are given in Eqs. (1)–(3) of S17.
3 Comparison of the solar neighborhood simulation with the HARPS survey
The PPB compositions were determined using the method described in Sect. 2.2. Using the BGM, we simulated the close solar neighborhood up to 100 pc (hereafter called HARPS simulation) and the solar neighborhood up to 1 kpc (hereafter called SN simulation). We focused on FGK stars since they can be directly compared to the work of S17 on the HARPS survey. They are obviously interesting targets for future exoplanetary surveys as TESS, PLATO, and CHEOPS. Moreover, most of the currently detected planets belong to the solar neighborhood (according to the database that is available at the Extrasolar Planets Encyclopaedia2, Schneider et al. 2011, the large majority of exoplanets are within 1 kpc), therefore it is interesting to study the PBB chemical composition at close distances from the Sun.
3.1 HARPS simulation
The target selection of the HARPS sample cannot be simulated by a clear selection function and prevents us from rigorously modeling a synthetic HARPS population. In the following, we present a qualitative comparison between the results obtained by S17 with the HARPS survey and our results obtained with the HARPS simulation. When we restricted our synthetic population to the heliocentric distance, the metallicity range, and the effective temperature range of the HARPS sample used in S17, d < 100 pc, −0.83 < [Fe/H] < 0.41, and stars with an effective temperature of ±300K around solar Teff,⊙ = 5777K (see S17), we have 10237 stars: 87% thin-disk stars and 13% thick-disk stars (Table 1). Instead, the HARPS sample used by S17 includes 303 (81.7%) thin-disk stars and 68 (18.3%) thick-disk stars. We stress that the BGM can simulate all stars satisfying the mentioned range in metallicity, effective temperature and galactic distance. Instead, the HARPS sample only includes a group of them, which might introduce a bias that cannot be taken into account. Since the selection function of the HARPS survey cannot be derived, the consequent observational bias could introduce differences between the model and the results obtained with observations.
Moreover, the HARPS sample has intrinsic errors on the observed chemical abundances. To compare with the HARPS observations, the observed mean errors (see Adibekyan et al. 2011; Bertran de Lis et al. 2015; Suárez-Andrés et al. 2017) were added to the HARPS simulation using a Gaussian dispersion. Figure 2 displays the synthetic distributions of the mass fraction of iron, water, and heavy elements of the PBB around stars for each galactic stellar population in the solar neighborhood.
As shown in Fig. 2 (upper panel), the majority of the synthetic thick-disk stars have iron mass fractions within 21–36%. Using the HARPS survey, S17 found that the stellar thick-disk population has iron mass fractions ranging in the same interval. For the thin disk population, synthetic firon ranges from 26–38% in the simulation and from ~25–37% in the HARPS sample.
The synthetic thin-disk population water mass fraction range is ~48–64%, while S17 found ~40–80%. The synthetic thick-disk population ranges within ~56–72%, while S17 found ~40–90%. For the heavy elements fZ, the synthetic thin-disk population range is ~0–3.5%, while S17 found ~0.5–3.5%. The synthetic thick-disk population ranges within ~0–2.8%, while S17 found ~0.5–2.6%. Overall, we find good agreement between the distribution of the water mass fraction in the simulated and the observed sample. However, we note that our synthetic intervals are smaller than those derived by S17 using HARPS data. This could be due to the limits of the stellar grid we used in the model, since we show in Sect. 4 that fw is manly dependent on [α/Fe] (see Fig. 4). The differences may be partly explained by the typical large errors in the derivation of observed abundances for oxygen, however (see, e.g., Bertran de Lis et al. 2015; Suárez-Andrés et al. 2017), which enter the calculation of fw.
 |
Fig. 2 Mass fraction distributions, firon (upper panel), fw (middle panel), and fZ (lower panel) for the three stellar populations of the Milky Way: thin disk, thick disk, and halo. We ran the model up to distances of 100 pc. |
Summary of the simulationscontent.
3.2 Solar neighborhood simulation
Table 2 summarizes the average values of firon, fw, and fZ and their corresponding standard deviations for PBB that belong to each of the stellar populations. We list in the table the results obtained for the three simulations of this work: the HARPS simulation, the SN simulation, and the Milky Way simulation (discribed in the next section). To be more general and avoid focusing on a specific survey, we did not include a Gaussian dispersion in the chemical abundances for the SN simulation and the Milky Way simulation. In addition, the results for the HARPS simulation are given with and without a Gaussian dispersion.
The SN simulation includes larger galactic distances (d < 1 kpc) than the HARPS simulation (d < 100 pc). Again to be more general, the SN simulation was not restricted to the HARPS range in metallicity and in effective temperature. The synthetic sample had a total of 14 850 705 stars: 78.9% from the thin disk, 21% from the thick disk, and <0.001% from the halo (Table 1). Our simulation shows that the average values are very similar for d < 100 pc (HARPS simulation with and without a Gaussian dispersion) and for d < 1 kpc (SN simulation) within a given galactic population. However, we recall that the proportions of thin and thick disk stars are substantially different. For d < 1 kpc, the fraction of thick-disk stars is twice (21%) that for d < 100 pc (13%). This affects the average values of all galactic populations in Table 2. When we include a larger portion of thick-disk stars at our synthetic sample, we included more α-enhanced stars, and ⟨firon⟩ therefore decreases while ⟨fw⟩ increases. The α-enhanced stars also have lower metallicity, and therefore ⟨fZ⟩ increases. The average PBB composition changes as a function of the heliocentric distance.
In spite of the low statistics available in the study of S17 (371 stars), we note the overall good agreement with our simulations in the iron, water, and heavy element mass fractions. We developed a new version of the BGM to simulate the PBB chemical composition in the solar neighborhood using the stoichiometric model developed by S17 and taking into account stellar and galactic evolution. In the following section we extend the analysis to the whole Galaxy.
Average mass fraction values for iron and water, and for the mass percentage of heavy elements, in the different galactic populations.
4 Chemical trends in the Milky Way predicted by the BGM
We now investigate the general trends for the whole Milky Way. To do this, we simulated the FGK sample to distances up to 50 kpc from the Sun (hereafter called MW simulation). This large volume covers the Galaxy up to the external parts. As for the SN simulation, we did not include Gaussian dispersion on the chemical abundances for this simulation to be general and to avoid focusing on a specific survey. Our simulation had a total of 4 850 600 000 stars: 42% from the thin disk, 27% from the thick disk, 30% from the bulge, and 1% from the halo (Table 1).
Average values of firon, fw, and fZ are given in Table 2. Figure 3 presents the distributions of iron, water, and heavy element mass fractions of PBB as a function of the galactic populations. The four populations present significant differences in their values of the iron and water mass fractions. This means that we can expect different compositions for rocky planets.
When all stellar populations are taken together, the iron mass fraction is between 20 and 32%. The thin-disk stars host PBB with a higher iron mass fraction (⟨firon⟩ = 30%) than other stellar populations: ⟨firon⟩ = 23.5, 20.4, and 26.2% for thick disk, halo, and bulge, respectively (see top panel of Fig. 3 and Table 2). The water mass fraction of PBB in the thin disk (⟨wf ⟩ = 58.1%) is lower than in other populations (⟨wf⟩ = 61.6, 63, and 60.1% for thick disk, halo, and bulge, respectively, see middle panel of Fig. 3).
If we are able to distinguish thin-disk stars from stars of the other populations, we can deduce from our galactic model the approximate composition (iron and water mass fractions) of the planets observed by a given survey. Determining the galactic population (using kinematics, e.g., from Gaia, and/or an accurate α-abundance determination) could improve our knowledge on initial conditions, such as planetesimal composition, of planet formation models.
4.1 Water and iron valleys
Figure 4 shows the [α/Fe] ratio of FGK stars simulated with the BGM as a function of stellar metallicity, color-coded with the mass fraction of iron (top panel), water (middle panel), and heavy elements (bottom panel) of PBB. The stellar alpha abundance appears to be crucial when determining the iron and the water mass fractions of PBB. Figure 4 shows that the iron (upper panel) and water (middle panel) fractions in PBB are strongly dependent on the alpha abundance in stars and less so on their metallicity, whereas the proportion of heavy elements (bottom panel) essentially depends on the metallicity of the star. It is worth noting that S17 quantitatively described a dependence of firon on [Si/Fe] and qualitativelydescribed a dependance on [Fe/H] based on the chemical abundances observed by HARPS (371 stars). Using the BGM, we here showed that firon and fw are mainly function of [α/Fe] (Fig.4). We recall that the PBB compositions are dependent on the stellar abundances, which are here predicted with the evolutionary model STAREVOL. The detailed predictions of abundances with this model allow us to clearly show that firon and fw are essentially dependent on alpha elements.
As shown in Fig. 3, the synthetic population computed with the BGM predicts a distinct distribution between the thin-disk stars with iron-rich PBB and other stellar populations with water-rich PBB, implying a significant dip in the number of stars around firon ~ 28% and fw ~ 59%. These iron and water valleys results from the stellar alpha content distributions in the synthetic stellar populations. The density of stars around solar metallicity and [α/Fe] ~ 0.1 is lower as a result of the known gap between the thin and the thick disk. Since we derive that firon and fw are mainly function of [α/Fe], we understand why this gap translates into a bimodal distribution in the firon and fw histograms. In other words, the synthetic population computed with the BGM shows the iron and water valleys because of the clear dependence of firon and fw on [α/Fe]. We underline that these valleys are not dependent on the limits in metallicity (−2.14 < [Fe/H] < 0.51) and alpha abundances (0 < [α/Fe] < 0.3) we used in this analysis.
Interestingly, the HARPS simulation also presents a water valley around fw = 62% (middle panel of Fig. 2) that separates the thin and thick disks. Moreover, firon histograms from the thin and thick disks intersect around 28% (top panel of Fig. 2), as in the iron valley present in the MW simulation. The HARPS data are compatible with the iron and water valleys (see the left panels of Fig. 1 in S17), but less clearly than in our simulations because of their small statistics (371 stars). These valleys, not mentioned by S17, are clearly predicted by our simulation through the larger statistics. Better statistics, in particular larger spectroscopic surveys on FGK stars, may indirectly constrain the iron and water valleys at any distance from the Sun. Moreover, if we are able to determine the galactic origin of stars in a larger sample, we might be able to confirm our findings on the valleys between the thin disk and the other galactic populations.
 |
Fig. 3 Mass fraction distributions, firon (upper panel), fw (middle panel), and fZ (lower panel) for the four stellar populations of the Milky Way: thin disk, thick disk, halo, and bulge. We ran the model up to distances of 50 kpc. |
4.2 Expected planet formation efficiency
Observations show a clear correlation between giant planet frequency and stellar metallicity. This is usually explained in the frame of the core accretion model (Pollack et al. 1996). When we assume that the protoplanetary disk metallicity scales with stellar metallicity (Pontoppidan et al. 2014), the amount of condensible solids is higher in metal-rich stars, and more building blocks are available for planet formation. In the context of the core accretion model, more building blocks implies a higher probability of collision (Inaba et al. 2001) and consequently an enhanced efficiency for planet formation (see, e.g., Ida & Lin 2004). Thus, the host star metallicity is believed to determine the amount of solid material available to be accreted by the planetary embryos.
As shown in the bottom panel of Fig. 4, the heavy element mass fraction fZ correlates with stellar metallicity and weakly with the initial alpha abundances. Thus, the more-metallic stars of the thin disk and the bulge present higher average values of fZ, 1.3 and 1.5%, respectively, while metal-poor stars of the halo and the thick disk have average values of fZ, 0.2 and 0.7%, respectively. Values are summarized in Table 2. In the context of the core accretion mechanism, the bulge and the halo may have the highest and lowest frequency of giant planets of the Galaxy, respectively.
4.3 Expected exoplanet composition
Based on the expected chemical composition of PBBs, we can discuss the expected exoplanet composition. As mentioned by S17, the stoichiometric model predicts for the Sun firon ~ 33%, fw ~ 60%, and fZ ~ 1.3%. This value of firon is similar to the values observed in the meteorites and the rocky planets of the solar system, Earth, Venus, and Mars (see, e.g., Drake & Righter 2002). Solar fw and fZ are also compatible with the values found by Lodders (2003; fw = 67.11% and fZ = 1.31%).
When we compare the solar values with the values obtained by the HARPS simulation and the SN simulation, we observe that the synthetic thin disk stars present a PBB chemical composition that is compatible with the values of the solar system. Stars of the thin disk could produce planets with compositions similar to those of the rocky planets in the solar system. Metal-poor stars of the thick disk might produce planets with lower iron mass. Similar results are obtained by S17 with HARPS observations.
Additionally, we derive in Sect.3 that the PBB composition is function of the heliocentric distance in the solar neighborhood. This is because the fraction of each galactic population is changing with the heliocentric distance. The MW simulation includes naturally less thin disk stars (42% in the MW simulation and ~79% in the SN simulation), such that the fraction of rocky planets may decrease. On the other hand, the bulge presents the closest PBB compositions to the solar ones, and should also be able to host rocky planets with solar-system-like composition. Halo stars should produce planets with low iron mass fraction but rich water content. Currently there is only one planetary mass object detected in the bulge, the brown dwarf OGLE-2017-BLG-1522Lb (Jung et al. 2018) and there is no planet detected orbiting halo stars.
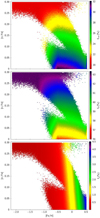 |
Fig. 4 Iron-to-silicate mass fraction, firon (upper panel), the water mass fraction, fw (middle panel), and the heavy element mass fraction fZ (lower panel) for the four stellar populations of the Milky Way: thin disk, thick disk, halo, and bulge. We ran the model up to distances of 50 kpc. |
5 Conclusion
We compared the chemical composition trends of PBBs in the different galactic populations of the Milky Way. To this aim, we computed a stellar population synthesis that included the simulation of stellar surface chemical abundances. Then, we used the simple stoichiometric model derived by S17 to estimate the PBB composition based on the chemical properties of stars generated by the BGM. This work extends the study of S17 with HARPS data to the whole Galaxy. Our results were obtained with stellar chemical abundances predicted by the BGM and not from observations, which makes comparisons particularly interesting. The new version of the BGM, including the simple stoichiometric model derived by S17, appears to be a powerful tool for predicting the chemical composition of PBB, which is crucial for preparing an interpretation of ongoing and future large-scale surveys of exoplanet search.
We ran the BGM to generate a synthetic sample of FGK stars. In the simulation of the Milky Way, we computed the model up to 50 kpc to establish general trends for our Galaxy. In the simulation of the solar neighborhood, we analyzed trends up to 1 kpc, where the majority of exoplanets have been observed. We also compared our results with those that S17 obtained with the HARPS survey. Overall, we found a very good agreement with the results of S17 based on the HARPS observations. In spite of the weak statistics of the HARPS sample, the range of values on firon, fw, and fZ is similar. We list the main results we obtained with the Milky Way simulation below.
-
Alpha content dependence. Our simulations show a clear dependence of the iron and water mass fractions on the initial alpha content [α/Fe] of the host stars. We showed that this dependence explains the iron and water valleys well. Mass fractions are found to be dependent on the metallicity as well, but to a lesser degree. These dependencies have strong implications on the chemical composition trends of PBB with the galactic populations.
-
Iron and water valleys. Different galactic populations (thin and thick disk, halo, and bulge) are known to have different metallicities and a different alpha content [α/Fe] distribution. The clear dependence on [α/Fe] leads to a bimodal distribution of the firon and fw histograms between the thin disk stars and the other galactic populations: the iron and water valleys. These valleys are predicted by our simulations to be at firon ~ 28% and fw ~ 59%.
-
PBB trends. Our solar neighborhood simulations (d < 1 kpc) show that the thin disk is expected to present iron-rich and water-poor PBB, while the thick disk should have iron-poor but water-rich PBB. Similar results are found by S17 with the HARPS observations, although their results are limited to 100 pc. In this work we simulated the whole Milky Way, enabling us to study the bulge population as well. The bulge appears to have intermediate values of firon and fw between those of the thin and thick disk. Its mass fraction values overlap those of the thin disk. It may produce rocky planets similar to those of the solar system. We found a clear dependence of the PBB composition on heliocentric distance. The fraction of thin-disk stars decreases with distance, while the fraction of thick-disk and bulge stars increases. These latter are predicted to be alpha-rich, which affects the values of firon and fw.
It is important to mention a limitation related to the determination of the galactic origin of observed stars. It is currently not possible to rigorously determine the galactic population of an observed star in a straightforward way. There is no irrevocable criterion (or combination of criteria) that could give certainty whether a star belongs the thin or thick disk. The galactic population origin of the HARPS sample was determined following criteria based on the alpha-content and metallicity (see Adibekyan et al. 2012b). A modified classification method for the observed HARPS populations might lead to different PBB composition trends. Chemical abundances from spectroscopic data combined with the precise astrometry of the Gaia mission (Gaia Collaboration 2016) will allow us to better characterize the galactic populations and consequently improve comparative analyses such as we presented here considerably. Cross-matching planet properties from future large exoplanetary surveys and the galactic origin of the host stars based on Gaia data is expected to provide precise constraints on the iron and water valleys, for instance.
Several studies showed that the bulk composition is crucial for determining the internal structure of a planet. Typically, when planetary radius and mass are known, the mass and radius of the different internal layers remain largely degenerated (Valencia et al. 2007). It has been shown that the chemical bulk composition (in particular, the Mg/Si and Fe/Si ratios) enables fixing the detailed internal structure (see, e.g., Dorn et al. 2015). Thus, it becomes crucial to estimate the chemical bulk composition. We recall that the calculations done in this work are not a prediction of the final planet composition, and with this caveat, the present paper provides some answers. The mass fractions computed here can be used as indicators of tendencies for PBB compositions and as proxies for the expected planet chemical compositions. Our results may be used as a starting step to predict the expected rocky planet properties in the different galactic populations.
The determinations of accurate stellar and planetary masses and radii distributions from the TESS, CHEOPS, and PLATO space-missions will provide unique constraints to the currently predicted statistical trends of planet composition (or proxy of those compositions as PBB compositions). Moreover, so far, the stellar grids of the BGM include stellar abundances only for M > 0.7 M⊙. This excludes the large majority of M stars, which are thought to be interesting targets to discover rocky planets in habitable zones. M stars are one of the main goals of the TESS mission and of ground-based large programs with HARPS (Bonfils et al. 2013)and the new instrument SPIRou at the Canada-France-Hawaii Telescope (Delfosse et al. 2013). The present study will be extended to M stars in a future work.
References
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., et al. 2012a, A&A, 543, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012b, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 560, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V., Santos, N. C., Figueira, P., et al. 2015, A&A, 581, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amard, L., Palacios, A., Charbonnel, C., Gallet, F., & Bouvier, J. 2016, A&A, 587, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Beaugé, C., & Nesvorný, D. 2013, ApJ, 763, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A&A, 576, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bond, J. C., O’Brien, D. P., & Lauretta, D. S. 2010, ApJ, 715, 1050 [NASA ADS] [CrossRef] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Buchhave, L. A., Bitsch, B., Johansen, A., et al. 2018, ApJ, 856, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Czekaj, M. A., Robin, A. C., Figueras, F., Luri, X., & Haywood, M. 2014, A&A, 564, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. A. 2013, ApJ, 767, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Donati, J.-F., Kouach, D., et al. 2013, in SF2A-2013: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. L. Cambresy, F. Martins, E. Nuss, & A. Palacios, 497 [Google Scholar]
- Dorn, C., Khan, A., Heng, K., et al. 2015, A&A, 577, A83 [EDP Sciences] [Google Scholar]
- Drake, M. J., & Righter, K. 2002, Nature, 416, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillot, T., Santos, N. C., Pont, F., et al. 2006, A&A, 453, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2008, A&A, 482, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M. 2009, ApJ, 698, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 616, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Inaba, S., Tanaka, H., Nakazawa, K., Wetherill, G. W., & Kokubo, E. 2001, Icarus, 149, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. L., & Li, H. 2012, ApJ, 751, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Jung, Y. K., Udalski, A., Gould, A., et al. 2018, AJ, 155, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Kuchner, M. J., & Seager, S. 2005, ArXiv e-prints [arXiv:astro-ph/0504214] [Google Scholar]
- Lagarde, N., Decressin, T., Charbonnel, C., et al. 2012, A&A, 543, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagarde, N., Robin, A. C., Reylé, C., & Nasello, G. 2017, A&A, 601, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lagarde, N., Reylé, C., Robin, A. C., et al. 2019, A&A, 621, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Miglio, A., Chiappini, C., Mosser, B., et al. 2017, Astron. Nachr., 338, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Nayakshin, S.,& Fletcher, M. 2015, MNRAS, 452, 1654 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Bergin, E. A., et al. 2014, Protostars and Planets VI (Tucson, AZ: University of Arizona Press), 363 [Google Scholar]
- Rauer, H., Catala, C., Aerts, C., et al. 2014, Exp. Astron., 38, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Robin, A. C., Reylé, C., Fliri, J., et al. 2014, A&A, 569, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Adibekyan, V., Dorn, C., et al. 2017, A&A, 608, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez-Andrés, L., Israelian, G., González Hernández, J. I., et al. 2017, A&A, 599, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thorngren, D. P., Fortney, J. J., Murray-Clay, R. A., & Lopez, E. D. 2016, ApJ, 831, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Valencia, D., Sasselov, D. D., & O’Connell, R. J. 2007, ApJ, 665, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. F., Teske, J., Majewski, S. R., et al. 2018, AJ, 155, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., Wang, J., & Huang, C. 2016, ApJ, 832, 196 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Average mass fraction values for iron and water, and for the mass percentage of heavy elements, in the different galactic populations.
All Figures
 |
Fig. 1 [α/Fe] abundance as a function of [Fe/H] for stars with d < 50 kpc simulated with the BGM. Thin and thick disks as well as bulge and halo stars are represented by red, blue, green, and yellow dots, respectively. Black lines indicate the selected population we used here: −2.14 < [Fe/H] < 0.51 and 0 < [α/Fe] < 0.3. |
| In the text | |
 |
Fig. 2 Mass fraction distributions, firon (upper panel), fw (middle panel), and fZ (lower panel) for the three stellar populations of the Milky Way: thin disk, thick disk, and halo. We ran the model up to distances of 100 pc. |
| In the text | |
 |
Fig. 3 Mass fraction distributions, firon (upper panel), fw (middle panel), and fZ (lower panel) for the four stellar populations of the Milky Way: thin disk, thick disk, halo, and bulge. We ran the model up to distances of 50 kpc. |
| In the text | |
 |
Fig. 4 Iron-to-silicate mass fraction, firon (upper panel), the water mass fraction, fw (middle panel), and the heavy element mass fraction fZ (lower panel) for the four stellar populations of the Milky Way: thin disk, thick disk, halo, and bulge. We ran the model up to distances of 50 kpc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


