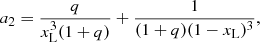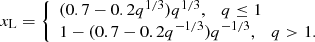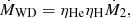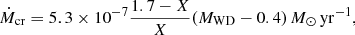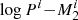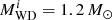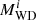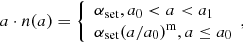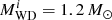| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833010 | |
| Published online | 24 January 2019 | |
The progenitors of type-Ia supernovae in semidetached binaries with red giant donors
1
Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, PR China
e-mail: liudongdong@ynao.ac.cn, wangbo@ynao.ac.cn
2
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650216, PR China
3
University of Chinese Academy of Sciences, Beijing 100049, PR China
4
Center for Astronomical Mega-Science, Chinese Academy of Sciences, Beijing 100012, PR China
Received:
13
March
2018
Accepted:
25
November
2018
Context. The companions of the exploding carbon-oxygen white dwarfs (CO WDs) that produce type-Ia supernovae (SNe Ia) have still not been conclusively identified. A red-giant (RG) star can fill this role as the mass donor of the exploding WD − this channel for producing SNe Ia has been named the symbiotic channel. However, previous studies on this channel have given a relatively low rate of SNe Ia.
Aims. We aim to systematically investigate the parameter space, Galactic rates, and delay time distributions of SNe Ia arising from the symbiotic channel under a revised mass-transfer prescription.
Methods. We adopted an integrated mass-transfer prescription to calculate the mass-transfer process from a RG star onto the WD. In this prescription, the mass-transfer rate varies with the local material states. First, we obtain the parameter space that leads to SNe Ia by evolving a large number of semidetached WD+RG systems with the Eggleton stellar-evolution code. Second, we investigate the Galactic rates and delay-time distributions of SNe Ia using a binary population synthesis method.
Results. The parameter space of WD+RG systems that can produce SNe Ia is enlarged significantly judging by our calculations. This channel could produce SNe Ia with intermediate and old ages, contributing up to 5% of all SNe Ia in the Galaxy. Our model increases the SN Ia rate from this channel by a factor of five. We suggest that the symbiotic systems RS Oph and T CrB are strong candidates for the progenitors of SNe Ia.
Key words: binaries: close / stars: evolution / supernovae: general / white dwarfs
© ESO 2019
1. Introduction
Type-Ia supernovae (SNe Ia) are good distance indicators in cosmology. They revealed the accelerating expansion of the universe and led to the discovery of dark energy (e.g., Howell 2011; Meng et al. 2015). It is generally believed that SNe Ia result from the thermonuclear explosions of carbon-oxygen white dwarfs (CO WDs) in binaries (e.g., Hoyel & Fowler 1960; Nomoto et al. 1984). However, the identity of the mass donor for the exploding CO WD is still not fully confirmed (e.g., Podsiadlowski et al. 2008; Wang & Han 2012; Maoz et al. 2014; Ruiz-Lapuente 2014). The mass donor could be a main sequence (MS) star, a red giant (RG) star, or a helium (He) star in the single-degenerate (SD) model, in which the CO WD that accretes H-/He-rich matter may produce an SN Ia when its mass approaches the Chandrasekhar limit (MCh; e.g., Whelan & Iben 1973; Nomoto et al. 1984; Li & van den Heuvel 1997; Langer et al. 2000; Han & Podsiadlowski 2004; Chen & Li 2007; Wang et al. 2009). The mass donor may also be another CO WD in the double-degenerate (DD) model, in which the merger of the double WDs may produce SNe Ia (e.g., Iben & Tutukov 1984; Webbink 1984; Han 1998; Nelemans et al. 2001; Toonen et al. 2012). In addition, some other progenitor models have been proposed to explain the observed diversity of SNe Ia, such as for example the double-detonation model, the core-degenerate model, the collisional WD model, the single star model, the WDs near black hole model, and so on (for recent reviews see Wang 2018; Soker 2018; Livio & Mazzali 2018).
In the single-degenerate model, the primary WDs can accrete H-rich matter from RG stars and form SNe Ia when they grow close to MCh in terms of mass. This formation channel is known as the symbiotic channel (e.g., Whelan & Iben 1973; Kenyon 1986; Kenyon et al. 1993; Munari & Renzini 1992; Hachisu et al. 1996; Li & van den Heuvel 1997; Yungelson & Livio 1998; King et al. 2003; Lü et al. 2006, 2009; Chen et al. 2011). Although the actual number of symbiotic stars in the Galaxy is still unknown (e.g., Mikołajewska 2012; Rodríguez-Flores et al. 2014), many symbiotic systems have been observed (e.g., Belczyński et al. 2000; Miszalski & Mikołajewska 2014; Li et al. 2015). In these systems, the symbiotic novae T CrB and RS Oph are possible progenitor candidates for SNe Ia (Kraft 1958; Brandi et al. 2009). Patat et al. (2007) detected Na I absorption lines with low expansion velocities in SN 2006X, and speculated that the companion of the exploding WD may be an early RG star, although Chugai (2008) argued that the absorption lines detected in SN 2006X cannot be formed in the RG wind. Voss & Nelemans (2008) suggested that the progenitor of SN 2007on may be a WD+RG system after studying the pre-explosion X-ray images at the same position. In addition, the surviving companions of SNe Ia from the symbiotic channel may be related to the formation of single low-mass He WDs in observations (e.g., Justham et al. 2009; Wang & Han 2010).
However, previous studies argued that the rate of SNe Ia from the symbiotic channel is relatively low (e.g., Li & van den Heuvel 1997; Yungelson & Livio 1998; Han & Podsiadlowski 2004). These studies usually adopted a surface boundary condition to calculate the process of Roche-lobe overflow (RLOF), as follows:
where Ṁ2 is the mass-transfer rate, rstar is the radius of the lobe-filling star, rlobe is the radius of its Roche lobe and C is a constant (see Han et al. 2000). The constant C is usually set to be 1000 M⊙ yr−1. According to this prescription, the exceeding mass of the donor star would be transferred onto the accretor immediately as soon as the donor star exceeds its Roche-lobe, since (rstar/rlobe − 1) is always less than 0.001 once Eq. (1) is used. In this case, the mass-transfer rate in WD+RG systems is usually relatively high, resulting in two cases that prevent the formation of SNe Ia: (1) A common envelope (CE) may be formed if the mass-transfer is dynamically unstable (e.g., Ivanova et al. 2013). The binary is likely to merge after the formation of a CE, which prevents the formation of SNe Ia. If the CE can be ejected, the binary may evolve into a CO WD+He WD system or a CO WD+He-burning star system (e.g., Han et al. 2000). The CO WD+He-burning star system may evolve to double CO WDs and then produce SNe Ia via the DD model (Ruiter et al. 2013; Liu et al. 2016, 2018). (2) The stellar wind driven by the WD radiation may blow away too much accreted matter from the surface of the WD, preventing the WD from growing in mass to MCh.
The local gas density and sound velocity in the region around the inner Lagrange point L1 of a RG star are significantly lower than those of a MS star. Furthermore, hydrodynamic estimates of the dimensionless parameter C are of the order of M2/Porb (Paczyński & Sienkiewicz 1972; Eggleton 2006) and therefore the parameter C may also be smaller in a binary system containing a RG star rather than a MS star due to the larger orbital period. Previous studies usually employed the same mass-transfer prescription presented in Eq. (1) for WD+RG systems and WD+MS systems. Thus, the constant C in Eq. (1) is too large for semidetached WD+RG systems in the previous simulations, which may overestimate Ṁ2 when the RG star fills its Roche-lobe. Lubow & Shu (1975) proposed that the mass-transfer process can be investigated by integrating the local gas density and sound velocity over the plane that is perpendicular to the line of centres connecting the two stars, and passing through the inner Lagrangian point. By assuming that the equation of state of stars obeys an adiabatic power law, and that the mass outflow is laminar and occurs along equipotential surfaces, Ge et al. (2010) obtained an approximated prescription for the mass-transfer process. In this prescription, Ṁ2 is a function of local material states, which is equivalent to a variable C in Eq. (1). In this case, the exceeding mass will be transferred at a limited rate (C is around M/Porb) when the RG star fills its Roche-lobe. Thus, Ṁ2 is lower than that of previous models, leading to a lower mass-loss rate and more matter being accumulated onto the primary WD. Ge et al. (2015) also found that the critical mass ratio for the formation of a CE becomes larger compared with the results given by Hjellming & Webbink (1987), implying that more interacting binaries would experience stable mass-transfer processes (see also Passy et al. 2012; Pavlovskii & Ivanova 2015).
In this work, we adopted the integrated mass-transfer prescription described in the Appendix of Ge et al. (2010) to investigate the semidetached symbiotic channel for producing SNe Ia. In Sect. 2, we show the methods for detailed binary evolution computations and the corresponding results. The method for and results of synthesizing a binary population are provided in Sect. 3. We present a discussion in Sect. 4 and finally a summary in Sect. 5.
2. Detailed binary evolution computations
2.1. Methods
We use the Eggleton stellar evolution code (Eggleton 1973) to follow the binary evolution of semidetached WD+RG systems. The typical Pop I composition is adopted for the initial MS models with H fraction X = 0.7, He fraction Y = 0.28, and metallicity Z = 0.02. In this work, we do not calculate the structure of the WD and consider it as a point mass. When the WD grows in mass to MCh (set to be 1.378 M⊙), an SN Ia explosion is assumed to occur. In this work, we adopted the integrated mass-transfer prescription presented in the Appendix of Ge et al. (2010) to calculate the RLOF in semidetached WD+RG systems (see also Kolb & Ritter 1990). The mass-transfer rate
where RL is the effective Roche-lobe radius, G is the gravitational constant, M2 is the donor mass, Γ is the adiabatic index, ρ is the local gas density, and P is the local gas pressure. The integration is from the Roche-lobe potential energy (ϕL) to the stellar surface potential energy (ϕs). The potential energy is written as
in which R is the donor radius. The coefficient f(q) is a slowly varying function of the mass ratio q:
in which a2 is defined as
where xL is simply but accurately approximated as
The accreted H-rich matter from RG stars first burns into He. The He experiences He flashes and burns into C and O, which is then accumulated onto the surface of the WD. The mass growth rate of the WDs (ṀWD) is defined as
where ηH is the mass accumulation efficiency for H-shell burning from Wang et al. (2010), and ηHe is the mass accumulation efficiency for He-shell flashes from Kato & Hachisu (2004) 1. When Ṁ2 is larger than the critical mass-transfer rate Ṁcr described in Nomoto (1982), we assume that the accreted H stably burns into He at the rate of Ṁcr, and the rest of the H-rich matter would be blown away in the form of the optically thick wind (e.g., Hachisu et al. 1996). The critical mass accretion rate is written as
where X is the mass fraction of H and MWD is the mass of the primary WD in units of M⊙. When Ṁ2 is lower than Ṁcr, the following assumptions are adopted (e.g., Wang et al. 2010): (1) the H-shell burning is stable and no matter is lost from the binary when 1/2 Ṁcr < Ṁ2 < Ṁcr; (2) a very weak H-shell flash occurs and no matter is lost from the binary when 1/8 Ṁcr < Ṁ2 < 1/2Ṁcr; (3) the H-shell flash becomes so strong that no matter is accumulated onto the WD when Ṁ2 < 1/8Ṁcr. We also assume that the mass loss depletes the specific orbital angular momentum of the primary WD. In our calculations, we do not consider the effect of the mass stripping from the RG caused by the optically thick wind (see Hachisu et al. 1999).
2.2. Results
Figure 1 shows a typical example of binary-evolution computations, in which the WD accretes H-rich material from a RG star and explodes as an SN Ia when its mass reaches MCh. Here, we set the initial WD mass 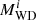 to 1.0 M⊙, the initial mass of donor star
to 1.0 M⊙, the initial mass of donor star 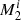 to 1.2 M⊙, and the orbital period to log (Pi/day) = 2.4. When the mass donor evolves to the RG stage, it expands quickly and fills its Roche-lobe. The crosses in panel a indicate the position where the donor begins to fill its Roche-lobe, which also corresponds to the position of t = 0 in panel b. Subsequently, the binary will experience four phases shown in panel b before an SN Ia is produced: (1) At the beginning (t = 0), Ṁ2 is lower than 1/8 Ṁcr, during which the H-shell flash is relatively strong and no matter is accumulated onto the surface of the WD. (2) At about t = 2.4 × 105 yr, Ṁ2 increases to be larger than 1/8 Ṁcr but still smaller than Ṁcr, during which the H-shell burns stably or flashes very weakly, and all of the accreted H-rich matter is assumed to be burned into He. However, some of the matter would be lost due to the He flashes. (3) At about t = 3.8 × 105 yr, Ṁ2 becomes larger than Ṁcr, and the binary enters the optically thick wind stage, during which the transferred H-rich matter stably burns into He at the rate of Ṁcr, while the rest of the H-rich matter is assumed to be blown away via the optically thick wind. (4) At about t = 8.3 × 105 yr, the binary enters the H-shell burning phase again, and subsequently the very weak H-shell flash phase. The primary WD grows in mass to MCh and explodes as an SN Ia at about t = 1.42 × 105 yr. At this moment, the mass of the RG star is
to 1.2 M⊙, and the orbital period to log (Pi/day) = 2.4. When the mass donor evolves to the RG stage, it expands quickly and fills its Roche-lobe. The crosses in panel a indicate the position where the donor begins to fill its Roche-lobe, which also corresponds to the position of t = 0 in panel b. Subsequently, the binary will experience four phases shown in panel b before an SN Ia is produced: (1) At the beginning (t = 0), Ṁ2 is lower than 1/8 Ṁcr, during which the H-shell flash is relatively strong and no matter is accumulated onto the surface of the WD. (2) At about t = 2.4 × 105 yr, Ṁ2 increases to be larger than 1/8 Ṁcr but still smaller than Ṁcr, during which the H-shell burns stably or flashes very weakly, and all of the accreted H-rich matter is assumed to be burned into He. However, some of the matter would be lost due to the He flashes. (3) At about t = 3.8 × 105 yr, Ṁ2 becomes larger than Ṁcr, and the binary enters the optically thick wind stage, during which the transferred H-rich matter stably burns into He at the rate of Ṁcr, while the rest of the H-rich matter is assumed to be blown away via the optically thick wind. (4) At about t = 8.3 × 105 yr, the binary enters the H-shell burning phase again, and subsequently the very weak H-shell flash phase. The primary WD grows in mass to MCh and explodes as an SN Ia at about t = 1.42 × 105 yr. At this moment, the mass of the RG star is 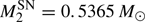 with a 0.42 M⊙ He core, and the orbital period is log (PSN/day) = 2.8178. In Fig. 2, we present the evolution of the same binary using the traditional mass-transfer prescription shown in Eq. (1) for a comparison. From this figure, we can see that the mass-transfer rate increases rapidly after the RG fills its Roche-lobe, which may lead to the formation of a CE.
with a 0.42 M⊙ He core, and the orbital period is log (PSN/day) = 2.8178. In Fig. 2, we present the evolution of the same binary using the traditional mass-transfer prescription shown in Eq. (1) for a comparison. From this figure, we can see that the mass-transfer rate increases rapidly after the RG fills its Roche-lobe, which may lead to the formation of a CE.
 |
Fig. 1. A typical binary evolution for producing SN Ia via the symbiotic channel. In panela, the solid curve represents the evolutionary track of the mass donor in the Hertzsprung–Russell diagram, and the dash-dotted curve shows the evolution of the orbital periods. The crosses in this panel represent the positions where mass transfer starts. In panelb, the evolution of Ṁ2, ṀWD, and MWD as a function of time are shown as solid, dashed, and dash-dotted curves, respectively. The position of t = 0 corresponds to the moment when the RG fills its Roche-lobe. The mass-transfer process can be divided into four phases: (1) the strong H-shell flash phase; (2) the stable H-shell burning or the weak H-shell flash phase; (3) the optically thick wind phase; (4) the stable H-shell burning or the weak H-shell flash phase. The asterisks in both panels indicate the position where an SN Ia explosion occurs. |
 |
Fig. 2. Similar to Fig. 1, but for a comparison using the traditional method to calculate the mass-transfer rate. |
We evolved more than 460 WD+RG systems, for which the initial masses of the WDs are in the range of 1.0−1.3 M⊙, the initial masses of the donors range from 0.7 to 2.0 M⊙ and the initial orbital periods are ∼1−630 days. Thus, we obtained the initial parameter space for the production of SNe Ia via the symbiotic channel. Figure 3 shows the parameter space of WD+RG systems for producing SNe Ia with an initial WD mass of 1.2 M⊙. For a comparison, we show the results of Li & van den Heuvel 1997). This figure shows that the grid from the present work has larger initial donor masses and shorter initial orbital periods. In these regions, Ṁ2 would be so high that the binary enters a CE process or a strong, optically thick wind process in the model of Li & van den Heuvel (1997), preventing them from forming SNe Ia.
 |
Fig. 3. Regions of WD+RG systems at their formation moment in the initial orbital period−initial secondary mass ( |
Figure 4 presents the initial parameter space for the production of SNe Ia, and the final regions of WD+RG systems at the moment of SN Ia explosions in the orbital period–secondary mass (logP−M2) plane, in which 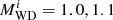 and 1.2 M⊙. We found that
and 1.2 M⊙. We found that 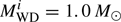 is the minimum initial WD mass for producing SNe Ia as its region almost vanishes. We also found that the symbiotic systems RS Oph and T CrB could form SNe Ia via the symbiotic channel (for more details, see Sect. 4). The WDs in the binaries beyond these initial contours cannot grow in mass to MCh: binaries beyond the left boundaries will experience strong H-shell flashes that will blow away too much material, while binaries beyond the right boundaries will undergo a rapid mass-transfer process as a result of the rapid expansion of the RG stars, leading to the mass-loss of too much material in the form of the optically thick wind. We note that the mass donor with the shortest orbital period for the case of
is the minimum initial WD mass for producing SNe Ia as its region almost vanishes. We also found that the symbiotic systems RS Oph and T CrB could form SNe Ia via the symbiotic channel (for more details, see Sect. 4). The WDs in the binaries beyond these initial contours cannot grow in mass to MCh: binaries beyond the left boundaries will experience strong H-shell flashes that will blow away too much material, while binaries beyond the right boundaries will undergo a rapid mass-transfer process as a result of the rapid expansion of the RG stars, leading to the mass-loss of too much material in the form of the optically thick wind. We note that the mass donor with the shortest orbital period for the case of 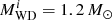 would fill its Roche lobe at the bottom of its RG branch. For binaries below the lower boundaries, the primary WDs can grow in mass but cannot reach MCh due to the small masses of the donors. The upper boundaries are constrained by the high mass-transfer rate owing to a large mass ratio, leading to the formation of a CE. The wind-accreting channel of symbiotic stars may also slightly contribute to the formation of SNe Ia, which is not considered in this work as its contribution is almost negligible (e.g., Yungelson & Livio 1998).
would fill its Roche lobe at the bottom of its RG branch. For binaries below the lower boundaries, the primary WDs can grow in mass but cannot reach MCh due to the small masses of the donors. The upper boundaries are constrained by the high mass-transfer rate owing to a large mass ratio, leading to the formation of a CE. The wind-accreting channel of symbiotic stars may also slightly contribute to the formation of SNe Ia, which is not considered in this work as its contribution is almost negligible (e.g., Yungelson & Livio 1998).
 |
Fig. 4. Initial and final regions of WD+RG systems for producing SNe Ia with various |
3. Binary population synthesis
3.1. Methods
By employing the Hurley rapid binary evolution code (see Hurley et al. 2002), we conduct a series of Monte Carlo simulations in a binary population synthesis (BPS) approach to calculate the rates and delay times of SNe Ia. In each simulation, we evolve a sample of 4 × 107 primordial binaries until the formation of WD+RG systems. The metallicity in our simulations is set to be 0.02. We assume that an SN Ia will be produced if the parameters of the formed lobe-filling WD+RG system are located in the initial regions for producing SNe Ia in Fig. 4.
The following initial parameters and basic assumptions of the Monte Carlo BPS computations are adopted:
- (1)
All stars are assumed to be in binary systems, and their orbits are assumed to be circular.
- (2)
The initial mass function of Kroupa (2001) is adopted for the primordial primaries, in which the masses of the primordial primaries (M1) are in the range of 0.01−100 M⊙.
- (3)
For the primordial secondary mass (M2), we simply adopt a constant mass ratio (q′ = M2/M1) distribution, that is, n(q′) = 1, in which 0 < q′≤1.
- (4)
The initial distribution of separations a is supposed to be constant in loga for wide binaries, and fall off smoothly for close binaries (see Eggleton et al. 1989), as follows:
in which we assume αset ≈ 0.07, m ≈ 1.2, a0 = 10 R⊙ and a1 = 5.75 × 106 R⊙. (5) The standard energy prescription from Webbink (1984) is employed to describe the CE ejection process, in which the uncertain parameters αCE and λ are combined as a single parameter and set to be αCEλ = 0.5, 1.0, and 1.5 for comparison. (6) The star formation rate is adopted to be constant (5M⊙ yr−1) for the Galaxy over the past 15 Gyr-pagination (see Yungelson & Livio 1998; Willems & Kolb 2004; Han & Podsiadlowski 2004), or alternatively, modeled as a delta function (a single star burst of 1010 M⊙ in stars).
The formation channel of WD+RG systems is similar to that in Wang et al. (2010). The primordial primary fills its Roche-lobe when it evolves to the thermal pulsing asymptotic giant branch. In this case, the mass transfer is dynamically unstable, leading to the formation of a CE. If the CE can be ejected, the primordial primary becomes a CO WD. After that, a WD+RG system will be formed when the primordial secondary evolves to its RG phase. The parameters of primordial binaries for producing SNe Ia via the symbiotic channel are M1, i ∼ 5.0−6.5 M⊙, 0.15 < M2, i/M1, i < 0.5, and Pi ∼ 600−5000 days.
3.2. Results
Figure 5 presents the evolution of SN Ia rates from the symbiotic channel with different values of αCEλ, in which a constant star formation rate of 5M⊙ yr−1 is adopted. This figure shows that the Galactic rates of SNe Ia are in the range of ∼0.5−1.3 × 10−4 yr−1. The Galactic SN Ia birthrate in observations is about 3−4 × 10−3 yr−1 (e.g., Cappellaro et al. 1997). Thus, the semidetached symbiotic channel may contribute up to 5% of all SNe Ia in the Galaxy. We note that the SN Ia rate increases with αCEλ. This is because the orbital period of the binaries evolving from CE ejections would be larger for a larger value of αCEλ, resulting in more WD+RG systems located in the SN Ia production region in Fig. 3. For comparison, the traditional method for calculating the mass-transfer rate yields a contribution of only 1% under the same star formation rate (i.e., 5M⊙ yr−1; e.g., Han & Podsiadlowski 2004; Wang et al. 2010). Obviously, our model increases the rate of SNe Ia from the symbiotic channel by a factor of five. However, the rate of SNe Ia arising from the semidetached symbiotic channel is still low, as most WD+RG systems lie outside of the initial parameter space for producing SNe Ia. Further investigation is required if the symbiotic channel is the primary source of SNe Ia. Otherwise, some other explosion mechanisms or formation channels are required (e.g., Tout 2005; Wang & Han 2012).
 |
Fig. 5. Evolution of SN Ia rates in the Galaxy as a function of time based on the symbiotic channel. The solid, dashed, and dash-dotted curves represent the cases with αCEλ = 0.5, 1.0 and 1.5, respectively. |
Figure 6 shows the theoretical delay time distributions of SNe Ia from the symbiotic channel. A single starburst of 1010 M⊙ in stars is assumed here. According to the symbiotic channel, the SN Ia delay times range from about 400 Myr–10 Gyr, indicating that this channel mainly contributes to the observed SNe Ia in the intermediate and old populations. We note that Wang et al. (2010) suggested that the symbiotic channel only contributes to SN Ia rates in old populations. The present work extends the contribution of the symbiotic channel to the SN Ia rates in the intermediate populations.
 |
Fig. 6. Delay time distributions of SNe Ia from the symbiotic channel, in which a star burst of 1010 M⊙ in stars is adopted. The open circles are from Totani et al. (2008), and the filled triangles, the filled circles, the filled squares, and the open square represent, respectively, observed results from Maoz et al. (2010, 2011, 2012) and Graur & Maoz (2013), all of which have been rescaled by Maoz & Graur (2017). |
Figure 7 presents the density distribution of WD+RG systems that produce SNe Ia in the 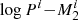 plane. For a comparison, we also show the initial contour for producing SNe Ia with
plane. For a comparison, we also show the initial contour for producing SNe Ia with 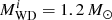 . From this figure, we can see that the orbital periods of the majority of WD+RG systems are mainly distributed from about 15 d to the right boundary of the initial contour, and the donor masses lie in the range from 1.0 M⊙ to 1.8 M⊙. The contribution of the remaining space to the SN Ia rates is negligible. Here, αCEλ is adopted to be 1.5. We note that the absolute number of WD+RG systems will decrease and the relative number will not change significantly if we adopt a lower value of αCEλ.
. From this figure, we can see that the orbital periods of the majority of WD+RG systems are mainly distributed from about 15 d to the right boundary of the initial contour, and the donor masses lie in the range from 1.0 M⊙ to 1.8 M⊙. The contribution of the remaining space to the SN Ia rates is negligible. Here, αCEλ is adopted to be 1.5. We note that the absolute number of WD+RG systems will decrease and the relative number will not change significantly if we adopt a lower value of αCEλ.
 |
Fig. 7. Density distribution of WD+RG systems producing SNe Ia. Here, αCEλ is set to be 1.5 and 4 × 107 primordial samples are included. The solid contour is the initial parameter space of WD+RG systems for producing SNe Ia with |
4. Discussion
In the present work, we adopted an improved method to calculate the mass-transfer rate, and found that the parameter space for producing SNe Ia via the semidetached symbiotic channel is significantly enlarged. The mass-transfer prescription adopted here is based on a power-law adiabatic assumption, which is still under debate. Woods & Ivanova (2011) argued that the envelope of the RG will not expand adiabatically, when the mass-loss timescale is comparable with the local thermal timescale of the superadiabatic outer surface layer of the envelope. In this case, our model might underestimate Ṁ2, and thus we might obtain an upper limit of the parameter space for producing SNe Ia.
The Galactic SN Ia rates calculated by the revised mass-transfer prescription are five times larger than that when assuming the traditional mass-transfer prescription. However, the present work only provides an upper limit for the SN Ia rate from the symbiotic channel. There are still some uncertainties in our BPS calculations:
- (1)
From Fig. 5, we can see that different CE models may result in a difference in the SN rate that may modify it by a factor of three. Some recent studies indicate that the value of αCEλ for WD+MS systems may be much lower than 1 (∼0.25; e.g., Zorotovic et al. 2010, 2014; Toonen & Nelemans 2013; Camacho et al. 2014). The rates of SNe Ia would decrease to ∼0.4 × 10−4 yr−1 if αCEλ were adopted to be 0.25.
- (2)
We adopted a constant initial-mass ratio distribution in our calculations and note that the predicted rates of SNe Ia will decrease sharply when an extreme uncorrelated mass ratio distribution is adopted (e.g., Wang et al. 2010).
- (3)
In Fig. 5, we assumed a constant star formation rate of 5M⊙ yr−1 for the Galaxy over the past 15 Gyr, which has been calibrated by assuming that a binary with its primary mass larger than 0.8 M⊙ is formed each year (see Iben & Tutukov 1984; Han et al. 1995; Hurley et al. 2002). However, recent studies suggested that the current Galactic star formation rate is about 1.9 ± 0.4 M⊙ yr−1 (see Chomiuk & Povich 2011). If the Galactic star formation rate is adopted to be 2 M⊙ yr−1, the Galactic rates of SNe Ia from the symbiotic channel decrease to ∼0.2−0.6 × 10−4 yr−1, contributing to at most 2% of all SNe Ia in the Galaxy.
- (4)
We note that the binary fraction may vary with the primordial primary mass (e.g., van Haaften et al. 2013). In the present work, we simply assume that about 50% of binary systems have orbital periods shorter than 100 yr, and that there is an equal binary number per logarithmic interval for wide systems with orbital periods longer than 100 yr. If the binary fraction is less than 50%, the SN Ia rate may also be overestimated.
- (5)
The age of the Galactic disk is around 10 Gyr, which is less than the Hubble timescale adopted in Fig. 5. However, the value of this timescale has almost no influence on the final results as the Galactic rates of SNe Ia are almost constant once t is larger than 10 Gyr.
Generally, if the different assumptions listed above are adopted in our BPS calculations, the Galactic SN Ia rate may also decrease by a factor of five, similar to that due to the different mass-transfer prescription. However, the argument still holds that the relative rates increase due to the new mass-transfer prescription.
There are some other alternative paths for producing SNe Ia via the symbiotic channel, such as for example the mass-stripping model, the aspherical stellar wind model, the tidally enhanced stellar wind model, and so on.
- (1)
Hachisu et al. (1999) proposed a mass-stripping model to stabilize the mass-transfer process and avoid the formation of a CE, in which the stellar wind from the WD collides with the RG surface and strips some of the mass from the RG. We note that this model can reproduce the basic features of the observed light curves of two supersoft X-ray sources (RX J0513.9−6951 and V Sagittae), although the predicted light curves may be influenced by a coefficient defined as the ratio of the mass-stripping rate to the optically thick wind-mass-loss rate (see Hachisu & Kato 2003a,b).
- (2)
Lü et al. 2009 assumed an aspherical stellar wind with an equatorial disk from a RG to investigate the symbiotic channel of SNe Ia, leading to a higher SN Ia rate. However, the results of Lü et al. 2009 are strongly affected by the mass-loss rate and the outflow velocity of the equatorial disk.
- (3)
Chen et al. 2011 adopted the tidally enhanced stellar wind assumption presented by Tout & Eggleton (1988) to study the symbiotic channel, and found that the parameter space for producing SNe Ia was enlarged. Chen et al. (2011) estimated that the SN Ia rates from the symbiotic channel would increase to be 6.9 × 10−3 yr−1 using Eq. (1) of Iben & Tutukov (1984). We note that Eq. (1) of Iben & Tutukov (1984) may overestimate the rate since some parameter space for producing SNe Ia may not contribute to the SN Ia rate. Importantly, the rate obtained by Chen et al. (2011) strongly depends on a tidal wind enhancement parameter Bw, which is still poorly understood and may critically influence the predicted SN Ia rate; the parameter space for producing SNe Ia would shrink dramatically if a lower value of Bw were adopted (see Chen et al. 2011).
In the symbiotic channel, some of the matter would be blown away from the system before the SN explosion, mainly due to the optically thick wind when Ṁ2 > Ṁcr. This blown-away matter would remain as circumstellar matter. We found that the circumstellar matter in SN Ia explosions has masses of up to ∼1.0 M⊙. Some direct evidence has been found for the existence of circumstellar matter in the normal SN Ia SN 2006X (e.g., Patat et al. 2007). The symbiotic channel may be responsible for SN 2006X-like events (see also Patat et al. 2007; Voss & Nelemans 2008).
In the observations, there are many symbiotic novae that are progenitor candidates of SNe Ia. For instance, RS Oph and T CrB are two symbiotic systems that both consist of a massive WD and a lobe-filling RG star. RS Oph has a 1.2−1.4 M⊙ WD and a 0.68−0.80 M⊙ RG star with an orbital period of 454.1 ± 0.41 days (Brandi et al. 2009), and T CrB has a ∼1.2 M⊙ WD and a ∼0.7 M⊙ RG star with an orbital period of ∼227.6 days (Kraft 1958; Belczyński & Mikołajewska 1998). Recently, Mikołajewska & Shara (2017) suggested that the WD in RS Oph is a CO WD according to their analysis of its spectra, which strongly supports the idea that RS Oph will form an SN Ia. The binary parameters of RS Oph and T CrB are located in the regions for producing SNe Ia in Fig. 3, which indicates that they can form SNe Ia in their future evolution via the semidetached symbiotic channel.
Some published observations support the existence of single low-mass He WDs with masses lower than 0.45 M⊙ (e.g., Marsh et al. 1995; Kilic et al. 2007), which may correspond to the surviving companions of SNe Ia from the symbiotic channel (e.g., Justham et al. 2009; Wang & Han 2010). Marietta et al. (2000) suggested that about 96%−98% of the envelope in the RG stars will be stripped during SN Ia explosions, leading to the formation of single He WDs. From our calculations, we find that the surviving companion stars are single He WDs with masses in the range of 0.19−0.45 M⊙. In addition, if the companion survives after SN explosion, it is likely to have large velocities (e.g., Justham et al. 2009). We also found that the orbital velocity of the remaining He WD at the moment of thermonuclear explosion is in the range of 17−91 km s−1 estimated by the prescription of Justham et al. (2009). Meanwhile, Kasen (2010) suggested that the interaction between the SN ejecta and the companion star would produce detectable optical/UV emission in the hours to days following the SN explosion. The early UV emission caused by the SN ejecta–companion interaction has recently been observed, such as in SN iPTF14atg and SN 2012cg for example (e.g., Cao et al. 2015; Marion et al. 2016). Because the distribution of orbital separations at the moment of SN explosion in our BPS calculations (see Fig. 7) is quite similar to that when assuming the traditional mass-transfer prescription (e.g., see Fig. 1 of Liu et al. 2015), we do not expect that the influence of the revised mass-transfer prescription on the early optical/UV emission caused by the SN ejecta–companion interaction is dramatic. However, there is still no conclusive proof for the existence of surviving companions (e.g., Badenes et al. 2007; Graham et al. 2015), which still requires further investigation.
5. Summary
In this work, we added an integrated mass-transfer prescription into the Eggleton stellar evolution code to investigate the symbiotic channel for producing SNe Ia. We evolved a large number of WD+RG systems, and obtained an SN Ia production space that is significantly enlarged. We then carried out a series of BPS computations with this parameter space and found that the SN Ia rates are in the range of ∼0.5−1.3 × 10−4 yr−1, which is five times larger than that when assuming the traditional mass-transfer prescription. The delay times of SNe Ia from the symbiotic channel range from 400 Myr to 10 Gyr, contributing to SNe Ia in the intermediate and old populations. The surviving companions of SNe Ia from the symbiotic channel may evolve to 0.19−0.45 M⊙ single He WDs. We suggest that the symbiotic channel is a possible way to form SN 2006X-like events. We note that the rate of symbiotic systems could provide some constraints on the progenitor candidates and rates of SNe Ia from the symbiotic channel. However, the population of symbiotic systems is still not particularly well known, and more observations of the symbiotic systems are required.
We note that the values of ηHe from different studies are quite different, for instance, the value of ηHe can range from ∼0.4 to ∼0.9 for MWD = 1.3 M⊙ and Ṁ2 = 10−6 M⊙ yr−1 (e.g., Yoon et al. 2004; Kato & Hachisu 2004; Piersanti et al. 2014; Wang et al. 2015; Brooks et al. 2016; Wu et al. 2017).
Acknowledgments
We acknowledge useful comments and suggestions from the anonymous referee. We thank Philipp Podsiadlowski, Xiangcun Meng and Hailiang Chen for their helpful discussions. We also thank Yan Gao for his kind help in improving the language of this paper. This work is partly supported by the NSFC (Nos. 11673059, 11873085, 11390374, 11521303, 11673058, 11573016, 11733008 and 11322324), CAS (Nos. QYZDB-SSW-SYS001 and KJZD-EW-M06-01), and Yunnan Province (Nos. 2014FB189, 2017HC018 and 2018FB005).
References
- Badenes, C., Hughes, J. P., Bravo, E., & Langer, N. 2007, ApJ, 662, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Belczyński, K., & Mikołajewska, J. 1998, MNRAS, 296, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Belczyński, K., Mikołajewska, J., Munari, U., Ivison, R. J., & Friedjung, M. 2000, A&AS, 146, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandi, E., Quiroga, C., Mikołajewska, J., Ferrer, O. E., & Garca, L. G. 2009, A&A, 497, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brooks, J., Bildsten, L., Schwab, J., & Paxton, B. 2016, ApJ, 821, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Camacho, J., Torres, S., García-Berro, E., et al. 2014, A&A, 566, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cao, Y., Kulkarni, S. R., Howell, A. D., et al. 2015, Nature, 521, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellaro, E., & Turatto, M. 1997, in Thermonuclear Supernovae, eds. P. Ruiz-Lapuente, R. Cannal, & J. Isern (Dordrecht: Kluwer), 77 [CrossRef] [Google Scholar]
- Chen, W. C., & Li, X. D. 2007, ApJ, 658, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Han, Z., & Tout, C. A. 2011, ApJ, 735, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Chomiuk, L., & Povich, M. S. 2011, AJ, 142, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Chugai, N. N. 2008, Astron. Lett., 34, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1973, MNRAS, 163, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 2006, Evolutionary Processes in Binary and Multiple Stars (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Eggleton, P. P., Fitchett, M. J., & Tout, C. A. 1989, ApJ, 347, 998 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, H., Hjellming, M. S., Webbingk, R. F., Chen, X., & Han, Z. 2010, ApJ, 717, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Ge, H., Webbink, R. F., Chen, X., & Han, Z. 2015, ApJ, 812, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, M. L., Nugent, P. E., Sullivan, M., et al. 2015, MNRAS, 454, 1948 [NASA ADS] [CrossRef] [Google Scholar]
- Graur, O., & Maoz, D. 2013, MNRAS, 430, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2003a, ApJ, 590, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., & Kato, M. 2003b, ApJ, 598, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1996, ApJ, 470, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Hachisu, I., Kato, M., & Nomoto, K. 1999, ApJ, 522, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z. 1998, MNRAS, 1998, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., & Podsiadlowski, Ph 2004, MNRAS, 350, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Z., Podsiadlowski, Ph, & Eggleton, P. P. 1995, MNRAS, 272, 800 [NASA ADS] [Google Scholar]
- Han, Z., Tout, C. A., & Eggleton, P. P. 2000, MNRAS, 319, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Hjellming, M. S., & Webbink, R. F. 1987, ApJ, 318, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A. 2011, Nat. Commun., 2, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyel, F., & Fowler, W. A. 1960, ApJ, 132, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanova, N., Justham, S., Chen, X., et al. 2013, A&ARv, 21, 59 [Google Scholar]
- Justham, S., Wolf, C., Podsiadlowski, Ph, & Han, Z. 2009, A&A, 493, 1081 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasen, D. 2010, ApJ, 708, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, M., & Hachisu, I. 2004, ApJ, 613, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J. 1986, The Symbiotic Stars (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Kenyon, S. J., Mario, L., Mikołajewska, J., & Tout, C. A. 1993, ApJ, 407, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Kilic, M., Stanek, K. Z., & Pinsonneault, M. H. 2007, ApJ, 671, 761 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. R., Rolfe, D. J., & Schenker, K. 2003, MNRAS, 341, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Kolb, U., & Ritter, H. 1990, A&A, 236, 385 [NASA ADS] [Google Scholar]
- Kraft, R. P. 1958, ApJ, 127, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, N., Deutschmann, A., Wellstein, S., & Höflich, P. 2000, A&A, 362, 1046 [NASA ADS] [Google Scholar]
- Li, X., & van den Heuvel, E. P. J. 1997, A&A, 322, L9 [NASA ADS] [Google Scholar]
- Li, J., Mikolajewska, J., Chen, X. F., et al. 2015, RAA, 15, 1332 [NASA ADS] [Google Scholar]
- Liu, Z., Moriya, T. J., & Stancliffe, R. J. 2015, MNRAS, 454, 1192 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Wang, B., Podsiadlowski, Ph, & Han, Z. 2016, MNRAS, 461, L3653 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Wang, B., & Han, Z. 2018, MNRAS, 473, 5352 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Mazzali, P. 2018, Phys. Rep., 736, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Lü, G., Yungelson, L., & Han, Z. 2006, MNRAS, 372, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Lü, G., Zhu, C., Wang, Z., & Wang, N. 2009, MNRAS, 396, 1086 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., & Graur, O. 2017, ApJ, 848, 25 [Google Scholar]
- Maoz, D., Keren, S., & Avishay, G.-Y. 2010, ApJ, 722, 1879 [Google Scholar]
- Maoz, D., Mannucci, F., Li, W., et al. 2011, MNRAS, 412, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Brandt, T. D. 2012, MNRAS, 426, 3282 [NASA ADS] [CrossRef] [Google Scholar]
- Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Marietta, E., Burrows, A., & Fryxell, B. 2000, ApJS, 128, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Marion, G. H., Brown, P. J., Vinkó, J., et al. 2016, ApJ, 820, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Marsh, T. R., Dhillon, V. S., & Duck, S. R. 1995, MNRAS, 275, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Meng, X., Gao, Y., & Han, Z. 2015, IJMPD, 24, 1530029 [NASA ADS] [CrossRef] [Google Scholar]
- Mikołajewska, J. 2012, Balt. Astron., 21, 5 [NASA ADS] [Google Scholar]
- Mikołajewska, J., & Shara, M. M. 2017, ApJ, 847, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Miszalski, B., & Mikołajewska, J. 2014, MNRAS, 440, 1410 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., & Renzini, A. 1992, ApJ, 397, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Nelemans, G., Yungelson, L. R., Zwart, S. F. P., & Verbunt, F. 2001, A&A, 365, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K. 1982, ApJ, 253, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F. K., & Yokoi, K. 1984, ApJ, 286, 644 [Google Scholar]
- Paczyński, B., & Sienkiewicz, R. 1972, Acta Astron., 22, 73 [NASA ADS] [Google Scholar]
- Passy, J. C., Herwig, F., & Paxton, B. 2012, ApJ, 760, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Chandra, P., Chevalier, R., et al. 2007, Science, 317, 924 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Pavlovskii, K., & Ivanova, N. 2015, MNRAS, 449, 4415 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Tornambé, A., & Yungelson, L. R. 2014, MNRAS, 445, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Podsiadlowski, Ph, Mazzali, P., Lesaffre, P., Han, Z., & Förster, F. 2008, New Astron. Rev., 52, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiter, A. J., Sim, S. A., Pakmor, R., et al. 2013, MNRAS, 429, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lapuente, P. 2014, New Astron. Rev., 62, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Flores, E. R., Corradi, R. L. M., Mampaso, A., et al. 2014, A&A, 567, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soker, N. 2018, Sci. Chin. Phys. Mech. Astron., 61, 049502 [NASA ADS] [CrossRef] [Google Scholar]
- Toonen, S., & Nelemans, G. 2013, A&A, 557, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toonen, S., Nelemans, G., & Portegies, Z. S. 2012, A&A, 546, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Totani, T., Morokuma, T., Oda, T., Doi, M., & Yasuda, N. 2008, PASJ, 60, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Tout, C. A. 2005, in The Astrophysics of Cataclysmic Variables and Related Objects, eds. J.-M. Hameury, & J.-P. Lasota (San Francisco: ASP), ASP Conf. Ser., 330, 279 [NASA ADS] [Google Scholar]
- Tout, C. A., & Eggleton, P. P. 1988, MNRAS, 231, 823 [NASA ADS] [CrossRef] [Google Scholar]
- van Haaften, L. M., Nelemans, G., Voss, R., et al. 2013, A&A, 552, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voss, R., & Nelemans, G. 2008, Nat, 451, 802 [Google Scholar]
- Wang, B. 2018, Res. Astron. Astrophys., 18, 49 [Google Scholar]
- Wang, B., & Han, Z. 2010, MNRAS, 404, L84 [NASA ADS] [Google Scholar]
- Wang, B., & Han, Z. 2012, New Astron. Rev., 56, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Meng, X., Chen, X., & Han, Z. 2009, MNRAS, 395, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Li, X.-D., & Han, Z. 2010, MNRAS, 401, 2729 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, B., Li, Y., Ma, X., et al. 2015, A&A, 584, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webbink, R. F. 1984, ApJ, 277, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Willems, B., & Kolb, U. 2004, A&A, 419, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woods, T. E., & Ivanova, N. 2011, ApJ, 739, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C., Wang, B., Liu, D., & Han, Z. 2017, A&A, 604, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, S.-C., Langer, N., & Scheithauer, S. 2004, A&A, 425, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yungelson, L., & Livio, M. 1998, ApJ, 497, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., Gänsicke, B. T., & Nebot Gómez-Morán, A. 2010, A&A, 520, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., Schreiber, M. R., García-Berro, E., et al. 2014, A&A, 568, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1. A typical binary evolution for producing SN Ia via the symbiotic channel. In panela, the solid curve represents the evolutionary track of the mass donor in the Hertzsprung–Russell diagram, and the dash-dotted curve shows the evolution of the orbital periods. The crosses in this panel represent the positions where mass transfer starts. In panelb, the evolution of Ṁ2, ṀWD, and MWD as a function of time are shown as solid, dashed, and dash-dotted curves, respectively. The position of t = 0 corresponds to the moment when the RG fills its Roche-lobe. The mass-transfer process can be divided into four phases: (1) the strong H-shell flash phase; (2) the stable H-shell burning or the weak H-shell flash phase; (3) the optically thick wind phase; (4) the stable H-shell burning or the weak H-shell flash phase. The asterisks in both panels indicate the position where an SN Ia explosion occurs. |
| In the text | |
 |
Fig. 2. Similar to Fig. 1, but for a comparison using the traditional method to calculate the mass-transfer rate. |
| In the text | |
 |
Fig. 3. Regions of WD+RG systems at their formation moment in the initial orbital period−initial secondary mass ( |
| In the text | |
 |
Fig. 4. Initial and final regions of WD+RG systems for producing SNe Ia with various |
| In the text | |
 |
Fig. 5. Evolution of SN Ia rates in the Galaxy as a function of time based on the symbiotic channel. The solid, dashed, and dash-dotted curves represent the cases with αCEλ = 0.5, 1.0 and 1.5, respectively. |
| In the text | |
 |
Fig. 6. Delay time distributions of SNe Ia from the symbiotic channel, in which a star burst of 1010 M⊙ in stars is adopted. The open circles are from Totani et al. (2008), and the filled triangles, the filled circles, the filled squares, and the open square represent, respectively, observed results from Maoz et al. (2010, 2011, 2012) and Graur & Maoz (2013), all of which have been rescaled by Maoz & Graur (2017). |
| In the text | |
 |
Fig. 7. Density distribution of WD+RG systems producing SNe Ia. Here, αCEλ is set to be 1.5 and 4 × 107 primordial samples are included. The solid contour is the initial parameter space of WD+RG systems for producing SNe Ia with |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \dot{M}_{2}= -C \mathrm{max}\left[0,{\left(\frac{r_{\rm star}}{r_{\rm lobe}}-1\right)^{3}}\right], \end{aligned} $$](/articles/aa/full_html/2019/02/aa33010-18/aa33010-18-eq1.gif)
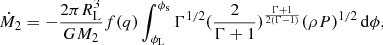
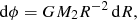
![$$ \begin{aligned} f(q)\equiv \frac{q}{r_{\rm L}^{3}(1+q)}\frac{1}{[a_{2}(a_{2}-1)]^{1/2}}, \end{aligned} $$](/articles/aa/full_html/2019/02/aa33010-18/aa33010-18-eq4.gif)