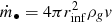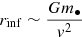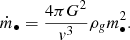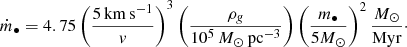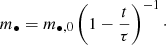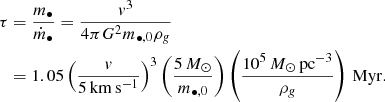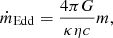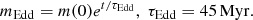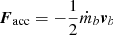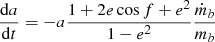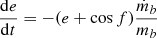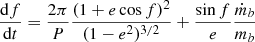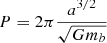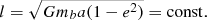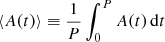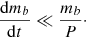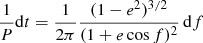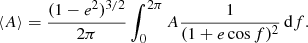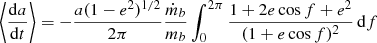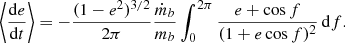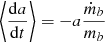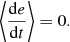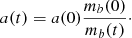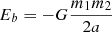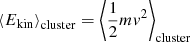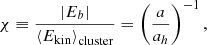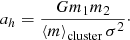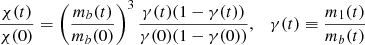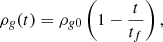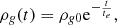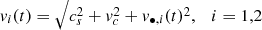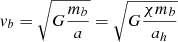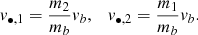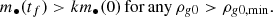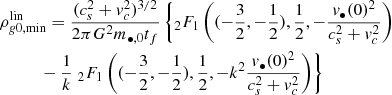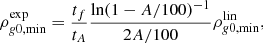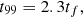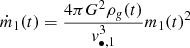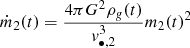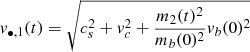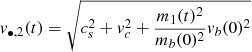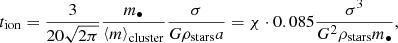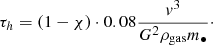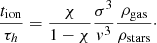EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 621 (January 2019) A&A, 621 (2019) L1 Full HTML
Free Access
Issue
A&A
Volume 621, January 2019
Article Number L1
Number of page(s) 8
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/201834609
Published online 03 January 2019

© ESO 2019

1. Introduction

The majority of gravitational wave (GW) signals produced by binary black holes (BBH) and observed by LIGO (Abbott et al. 2016a,b, 2017a,b,c; LIGO Scientific Collaboration & Virgo Collaboration 2018) involve high stellar mass black holes (BHs) ∼(20 − 50) M⊙. In particular, recently LIGO Scientific Collaboration & Virgo Collaboration (2018) released new data indicating that 75% of the BHs, observed in 10 BBH GW signals, have masses greater than 20 M⊙. We investigate here a possible origin of such high mass BHs. In the, so called, dynamical channel (Abbott et al. 2016c), the BBH is assumed to be formed and get hardened in the dense environment of a stellar cluster, such as a globular cluster (GC) or nuclear star cluster (NSC), by dynamical processes. We examine the possibility that a BBH can grow by accretion of primordial gas during the cluster’s early formation era.

Globular clusters seem to contain little or no interstellar gas today. However, there is accumulated evidence that they underwent prolonged star formation early in their lifetimes (Gratton et al. 2012) and therefore should have started life as a dense gas cloud, called a protoglobular cluster or primordial cluster. It is uncertain to what extent these primordial clusters share the same properties as the young massive clusters (YMC) observed today (see Portegies Zwart et al. 2010 and references therein). For a vast range of values for the stellar formation efficiency ∼(10 − 90)%, the mass of primordial gas remaining after the first formation event in a primordial cluster is of the same order of the cluster’s stellar mass. Therefore, there is a huge gas reservoir, available for accretion, immediately after the first formation event. The BBH accretion efficiency will depend strongly on the relevant timescales of the depleting and accreting processes.

In star-forming regions, the phenomena of radiation, stellar winds and energetic explosions are expected to clear away the surrounding gas within a few Myr from the onset of formation (e.g., Voss et al. 2010; Galván-Madrid et al. 2013; Krumholz et al. 2014). However, this is not necessarily true for sufficiently massive clouds. Since feedback processes are proportional to the total mass, while the gravitational binding energy to the square of the mass, there should exist a critical mass, depending on the size of the cloud, above which the feedback processes become ineffective. Sufficiently compact clusters such as NSCs and massive GCs are candidate regions in which this may occur. In fact, it has been shown that a key parameter controlling gas expulsion is indeed compactness, namely the mass over size of the cluster (Krause et al. 2012, 2016; Silich & Tenorio-Tagle 2017, 2018).

The precise mechanism for gas depletion in primordial GCs is still unknown, while proposals abound in the literature with most of them focusing on stellar winds and supernovae explosions (Spergel 1991; Thoul et al. 2000; Fender et al. 2005; Moore & Bildsten 2011; Herwig et al. 2012; Krumholz et al. 2014; Krause et al. 2016; Silich & Tenorio-Tagle 2017, 2018). The gas expulsion may dramatically affect the evolution of the cluster (Marks et al. 2008; Kruijssen 2012) and especially in connection with the presence of multiple stellar populations (D’Ercole et al. 2008; Conroy 2012; Renzini et al. 2015). It has been argued that the superbubbles formed by winds and supernova explosions (Bagetakos et al. 2011; Krause et al. 2013; Jaskot et al. 2011; Fierlinger et al. 2016; Yadav et al. 2017), which are the primary candidates supposed to expel the primordial gas, undergo a Rayleigh–Taylor instability in sufficiently massive (≳107 M⊙) proto-clusters preventing this gas expulsion (Krause et al. 2012). Krause et al. (2012) propose further that, in this case, the power released by accretion of primordial gas onto dark remnants could be sufficient to expel the gas. Leigh et al. (2013) have further elaborated the idea and proposed that in any cluster that is able to form massive stars, the primordial gas is depleted exactly due to the accretion onto BHs. They find that accreting BHs can deplete the whole gas reservoir within only as few as 10 Myr.

Here, we do not focus on the effect of the accreting BHs to the gas reservoir, but on the effect of accretion to the BBHs of the cluster. We assume that the gas depletion occurs rapidly in a timescale of few Myr, independently of any specific depletion scenario. We further assume that the cluster can generate at least one stellar mass BBH, that may be found inside the clusters’ core ≲1 pc within a few Myr from the onset of the first formation event. This assumption is justified, since most massive stars are formed as binaries (Sana et al. 2012) and furthermore they sink rapidly, in relevant timescales, to the center due to mass segregation and dynamical friction (Spitzer 1987; Binney & Tremaine 2008). In fact, it has been calculated recently (Leigh et al. 2014) that accretion of gas (gas damping) accelerates mass segregation resulting to timescale of less than 1 Myr.

Moreover, the timescales considered are much shorter than the Gyr timescale that the recoil mechanism of BBH-BH three-body encounters operate and which may eject BBHs out of the cluster (Sigurdsson & Hernquist 1993). In addition, following numerous pieces observational evidence of X-ray emitting black holes (Maccarone et al. 2007, 2011; Barnard et al. 2011; Shih et al. 2010; Strader et al. 2012), it has become evident in the last decade that the recoil mechanism is not effective in dense GCs, which seem to contain a significant population (≲1000) of BHs and BBHs in their core (see Morscher et al. 2015 and references therein).

Our main result below is that in a protoglobular cluster a sufficient amount of primordial gas can be accreted on a BBH, before the gas may be depleted, to increase the mass of each BBH member to values ∼30 M⊙, consistent with high mass BBH LIGO detections (LIGO Scientific Collaboration & Virgo Collaboration 2018). We further calculate, in case of isotropic accretion, the degree that a BBH gets harder (with the “hardness” χ(t) defined below in Eq. (B.19)) due to accretion. We discuss this issue along with our conclusions in Sect. 3.

The present analysis suggests that in addition to the two primary channels (Abbott et al. 2016c) for formation and hardening of BBH that may be detected by LIGO (the “dynamical” in dense stellar environments and the “isolated” channel in isolated environment), an additional formation and hardening channel of BBH operates due to accretion of gas in dense primordial stellar clusters.

In the next section we present our results, while the basic calculations are given in the appendices. In Appendix A we briefly describe the mechanism of isotropic accretion, in Appendix B we show our calculation of the hardening of a BBH due to isotropic accretion and in Appendix C we present the equations that describe the evolution of the BBH members. In Appendix D we discuss the timescale of ionization of a soft binary versus that of the hardening due to accretion.

2. Results

The isotropic, spherically symmetric accretion is described by the Bondi formula for each BBH member, as in Appendix A. During isotropic accretion, the binary is hardened as we show in Appendix B. The accumulation of mass by BBH members results in a decrease of the separation due to angular momentum preservation.

The formation of a thin disk may, however, significantly decrease the accretion rate. Radiation emission during accretion could negatively impact the accretion rates due to gas heating and ionization via inverse Compton scattering (King 2003). Under this perspective the Bondi accretion analysis corresponds to nearly maximum possible accretion rate. On the other hand, Eddington-limited accretion should be much closer to the true rate if accretion proceeds via angular-momentum redistribution within a disk that radiates (King & Pounds 2003). It may be regarded for our problem as corresponding to nearly minimum accretion effectiveness being linearly depending on BH mass as in Eq. (A.7).

Regarding the gas loss, we investigate two cases; a linear gas loss rate, as in (C.1) and an exponential gas loss rate, as in (C.2). We do not worry about the cause of the depletion. Our results are independent of any specific depletion scenario as long as its loss rate lies within these two marginal gas loss models.

In Appendix C we show our calculation of the minimum possible initial gas density ρg0, min, as in (C.7) and (C.8) for hard and soft binaries and for several initial BH masses so that m•(tf)=30 M⊙. The result is plotted in Fig. 1. We find that ρg0, min ∼ (104 − 105) M⊙ pc−3, gas density values relevant to proto-globular clusters. The number density of gas in a primordial cluster is estimated to be ∼106 cm−3 and the temperature a few thousand Kelvin degrees (∼5000 K) (D’Ercole et al. 2008; Maccarone & Zurek 2012; Calura et al. 2015). These values give cs ∼ 5 and ρg ∼ 5 × 104 M⊙ pc−3 for the speed of sound and the gas density, respectively, in agreement with our above result. Moreover, the gas density value may be even higher. A primordial cluster is estimated (Fall & Zhang 2001; Kruijssen & Portegies Zwart 2009; Conroy 2012) to be 10–100 times more massive than the resulting GC. Typical galactic GCs have mass ∼5 × (104 − 105) M⊙ (the mean mass of galactic GCs is ∼2 × 105 M⊙ (Harris 1998)) and therefore originate from primordial clusters of mass 5 × (105 − 107) M⊙. Let us consider a primordial cluster with mass 107 M⊙, and assume that the formation efficiency is 0.4. If the half mass radius of the gas’ distribution is rc ∼ 3 pc then the mean gas density inside rc is ∼106 M⊙ pc−3, a value much higher than the one given above. Unfortunately, the exact conditions prevailing in the center of a primordial cluster are unknown.

thumbnail Fig. 1.

Minimum initial density of the gas (ρg0, min), given in Eq. (C.7), required for a BBH with equal mass BH members so that each member reaches mass 30 M⊙ by Bondi accretion inside this gas’ density environment and until time tf when the gas is completely depleted, assuming a constant mass loss rate of the gas (C.1). For an exponential gas loss law (C.2), the time t99 needed for 99% depletion is t99 = 2.3tf, for the same values of all other parameters. We also assume in both figures cs = 5 km s−1, σ = vc = 6 km s−1 where we denote, respectively, the speed of sound of the gas, the velocity dispersion of the stars and the velocity of the binary with respect to the cluster. We consider three cases, each member having initial mass m0 = 5 M⊙ (blue solid line), 10 M⊙ (red dashed-dotted line) or 15 M⊙ (yellow dashed line). Left panel: we assume an initially slightly hard binary with χ(0)=1 ⇔ a(0)=ah(0). It is evident that in order for a BH with initial mass ∼(5 − 10) M⊙ to grow up to 30 M⊙ within tf = 5 Myr, assuming by this time there is complete gas depletion, would require an initial gas’ density ∼(5 − 15)×104 M⊙ pc−3. These minimum density values correspond to the exponential gas loss law with 99% depletion at time t99 = 11.5 Myr. The density values are half for tf = 10 Myr for both linear and exponential cases. We took into account the hardening of the binary during accretion. Right panel: we calculate ρg0, min w.r.t. the initial hardness expressed by the quantity logχ−1(0) for tf = 5 Myr in the linear case of gas loss. This time corresponds to t99 = 11.5 Myr in the case of exponential gas loss. It is evident that soft binaries accrete gas more effectively than very hard ones. A hard binary a(0)/ah(0)=0.1 with BH members each of mass (5 − 10) M⊙ requires ρg0, min = (8 − 50)×104 M⊙ pc−3 while a soft one a(0)/ah(0)=10 requires only (5 − 13)×104 M⊙ pc−3. By the time the gas is depleted a soft binary gets hard in case of isotropic accretion as demonstrated below, in Fig. 2.
Open with DEXTER

Then, in Fig. 2 we present a demonstrative example of a BBH becoming more massive and harder by accretion. In particular, we consider both Bondi and Eddington-limited accretion cases in order to generate the masses of GW signal GW150914, as a representative of the signals involving high (m• >  20 M⊙) BH masses. These can originate in BBHs with originally light BH members (∼8 − 10 M⊙), which increased their masses rapidly, within ∼10 Myr in Bondi accretion and ∼50 Myr in Eddington-limited case, assuming that the gas is 99% depleted by exponential loss within this time.

thumbnail Fig. 2.

Evolution of BH masses m1, m2 (red lines) and BBH hardness (minus logarithm) χ(t)=ah(t)/a(t) (blue lines) plotted until the time the gas reservoir of a primordial cluster is completely depleted for an exponential loss law (for a linear law the depletion time for the same mass growth is about half) so that the BHs attain the mass values of the GW signal GW150914, namely m1(tend)=36 M⊙, m2(tend)=29 M⊙. We assume cs = 5 km s−1, σ = 6 km s−1 and the orbital velocity of the BBH w.r.t. the cluster to be constant vc = 4.5 km s−1 which corresponds to a circular orbit of the barycenter at a distance ∼0.15 pc from the center of the cluster. Assuming vc = σ will add about 8 Myr. Left panels: we consider spherically symmetric Bondi accretion and solve the system (C.10) and (C.11). The initial gas density is ρg(0)=5 × 104 M⊙ pc−3. We find that the time needed is 12 Myr for a(0)/ah(0)=1, corresponding to the soft-hard boundary, in the upper panel and m1(0)=8.35 M⊙, m2(0)=8.03 M⊙, while we consider a soft binary in the lower panel with a(0)/ah(0)=5 ⇔ χ(0)=0.2 and m1(0)=7.91 M⊙, m2(0)=7.54 M⊙. The hard BBH gets about 62 harder, while the soft 74 times harder becoming very hard at the end of the process χ(tend)=14.8. Both the mass increase and hardening effects are more intense for the soft binary in agreement with Fig. 2b. Right panels: we consider Eddington-limited accretion in a disk, as in Eq. (A.7), depicted with solid lines and we plot in the same graph the Bondi case with dotted lines. We assume initial gas density ρg(0)=104 M⊙ pc−3. The time needed for a similar growth to the Bondi case is about four times larger with respect to the left panels, namely 50 Myr with a little higher initial masses m1(0)=11.85 M⊙, m2(0)=9.55 M⊙. We note that in order to achieve the same final mass in the same time with Bondi accretion, the initial masses are much lower, namely m1(0)=6.40 M⊙, m2(0)=6.29 M⊙ in the hard case and m1(0)=5.54 M⊙, m2(0)=5.40 M⊙ in the soft one. In case of angular momentum preservation (or loss to the disk) the BBH gets harder in Eddington-limited accretion as well, though it is less severe than in the Bondi case. The soft binary gets hard attaining χ(tend)=5.6.
Open with DEXTER

We note that in case of Bondi accretion a very small initial mass difference between the two BHs grows fast leading to significant final mass difference at the end. Also, due to dynamical friction that is not taken into account here, the time by which the soft binary becomes hard is overestimated and it should become even harder at the end.

We find that for the aforementioned parameter values of Fig. 2, a soft BBH with χ(0)=0.2 gets hardened due to mass increase, in case of angular momentum preservation, by a factor 28–74 becoming hard, χ(tend)=5.6 − 14.8, at the end of the process, where the lower values correspond to Eddington-limited case and upper ones to Bondi case. Soft binaries that would normally dissolve due to three-body encounters (Heggie–Hills law) they may get hard (χ(tf)> 1) due to accretion that forces their concentration in the center. However, the simultaneous operation of three-body encounters should act counter to this effect, so that not all soft binaries should be subject to such a drastic accretion effect and not under all conditions. The timescales of ionization of soft binaries (D.1) and hardening (D.2) are comparable at least for mildly soft binaries inside the core of a proto-globular cluster with ρgas greater than ρstars (see Eq. (D.3)). The inclusion of both dynamical friction and close encounters needs much further investigation and will be presented elsewhere.

3. Conclusions

Our basic results are summarized in Figs. 1 and 2. We conclude that:

  1. BHs with initial masses (5 − 10) M⊙, members of a BBH, require initial gas density environment ∼(104 − 105) M⊙ pc−3 in order to become as massive as 30 M⊙ by isotropic accretion of gas within a time of ∼12 Myr for 99% gas depletion following an exponential gas loss. Such gas density values are expected to occur in the centers of primordial clusters, while the aforementioned gas depletion timescales are in direct agreement with simulations of gas depletion due to feedback from star formation in primordial clusters Calura et al. (2015; see Appendix C).

  2. The GW signals involving high mass (≳20 M⊙) BHs can originate at BBHs with light BH members, each of mass ∼8 M⊙, that became sufficiently massive (in particular 36 M⊙ and 29 M⊙ for GW150914) by gas accretion in primordial clusters within gas depletion time of 12 Myr for exponential gas loss and Bondi accretion and an initial gas density 5 × 104 M⊙ pc−3.

  3. In the case of the more conservative Eddington-limited accretion in a radiative thin disk, the time needed for the BBH to grow at similar proportion to the Bondi case is ∼50 Myr and for slightly higher initial BH masses ∼10 M⊙. The two accretion cases may be regarded as upper and lower limits so that the precise timescale should lie somewhere between 10 and 50 Myr.

  4. The BBHs get hardened during isotropic accretion due to conservation of angular momentum, proportionally to the third power of mass, as in Eq. (B.21).

  5. The mass increase and hardening effects are more intense for soft binaries, which it is possible to become hard due to isotropic gas accretion before being dissolved due to three-body encounters, especially for mildly soft binaries in a stellar or BH subcluster immersed in a much denser gas environment (see Eq. (D.3)).

Depending on the conditions prevailing in the primordial cluster and the specifics of the BBH and the environment it is embedded in, there may or may not be formed a gas accretion (mini)disk with some thickness. Recent simulations (Farris et al. 2014; Shi & Krolik 2015) show that accretion in the presence of a thin disk is not significantly suppressed compared to the accretion rate expected for a single black hole with the binary mass. Therefore, our results will be valid regarding the mass increase effect even in the case of the presence of a disk, while the precise arithmetic corrections are expected to be small according to 3D simulations (Shi & Krolik 2015). A qualitative picture may be given as follows. Provided that the disk cannot be stable and grow beyond some size and mass because of (and not only) being immersed inside a dense gas density environment there should operate some form of continuity principle. For any amount of gas mass that enters some prescribed radius which encloses the BBH and the disk, an almost equal amount of mass is accreted onto the BHs instead of accumulating on the disk. Nevertheless, this issue requires further investigation.

Regarding the effect of minidisks to the hardening of the BBH due to accretion, we emphasize that simulations show that orbital angular momentum tends to be removed from the BBH either due to “spiral shocks” (Spruit 1987; Ryan & MacFadyen 2017; Ju et al. 2016; Arzamasskiy & Rafikov 2018; Tang et al. 2017) or magnetohydrodynamic effects (Konigl 1989; Subramanian & Becker 1999). These effects are small and in any case they accelerate the hardening. According to this literature, our estimation for the hardening rate is in fact a lower limit and it can be even higher in the presence of minidisks. We note, however, that some authors (Miranda et al. 2017) contradict the aforementioned literature, and a general consensus has not as yet been achieved.

In addition, it has been argued that dynamical friction due to the gas generates torques which tend to harden the binary (Sánchez-Salcedo & Chametla 2014). This will add up to the effect we put forward here.

Apart from not considering more involved and detailed accretion models, in our analysis we also did not take into account dynamical friction from the stellar component affecting the very soft binaries neither the many and complex dynamical effects arising from close encounters. Refinements and more detailed analysis will follow. Our main message is that the accretion in primordial clusters seems to have drastic consequences regarding the BH mass function and BBH merger rates in GCs. Not only can it not be ignored, but also we feel urged to consider the mechanism in much more involved and realistic scenarios to quantify more precisely its effect.

Finally, the possibility that the gas is depleted in proto-globular clusters primarily due to the accretion by dark remnants which leads to the formation of either a dense, highly populated, BH subcluster (Breen & Heggie 2013; Morscher et al. 2015; Chatterjee et al. 2017; Weatherford et al. 2018; Askar et al. 2018) that may form a disk (Roupas et al. 2017; Meiron & Kocsis 2018) or an IMBH (for observational evidence see e.g., Gebhardt et al. 2002, 2005; Noyola et al. 2008; Sun et al. 2013; Feldmeier et al. 2013; Perera et al. 2017; Mezcua 2017; Kızıltan et al. 2017) needs further investigation. Certainly, our calculations provide indirect support to these scenarios.

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016a, Phys. Rev. Lett., 116, 061102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016b, Phys. Rev. Lett., 116, 241103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016c, ApJ, 818, L22 [NASA ADS] [CrossRef] [Google Scholar]
  4. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017a, Phys. Rev. Lett., 118, 221101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  5. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017b, ApJ, 851, L35 [NASA ADS] [CrossRef] [Google Scholar]
  6. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017c, Phys. Rev. Lett., 119, 141101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  7. Arzamasskiy, L., & Rafikov, R. R. 2018, ApJ, 854, 84 [NASA ADS] [CrossRef] [Google Scholar]
  8. Askar, A., Arca Sedda, M., & Giersz, M. 2018, MNRAS, 478, 1844 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bagetakos, I., Brinks, E., Walter, F., et al. 2011, AJ, 141, 23 [NASA ADS] [CrossRef] [Google Scholar]
  10. Barnard, R., Garcia, M., Li, Z., Primini, F., & Murray, S. S. 2011, ApJ, 734, 79 [NASA ADS] [CrossRef] [Google Scholar]
  11. Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton, NJ: Princeton University Press) [Google Scholar]
  12. Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  13. Breen, P. G., & Heggie, D. C. 2013, MNRAS, 436, 584 [NASA ADS] [CrossRef] [Google Scholar]
  14. Calura, F., Few, C. G., Romano, D., & D’Ercole, A. 2015, ApJ, 814, L14 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chatterjee, S., Rodriguez, C. L., & Rasio, F. A. 2017, ApJ, 834, 68 [NASA ADS] [CrossRef] [Google Scholar]
  16. Conroy, C. 2012, ApJ, 758, 21 [NASA ADS] [CrossRef] [Google Scholar]
  17. D’Ercole, A., Vesperini, E., D’Antona, F., McMillan, S. L. W., & Recchi, S. 2008, MNRAS, 391, 825 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fall, S. M., & Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef] [Google Scholar]
  19. Farris, B. D., Duffell, P., MacFadyen, A. I., & Haiman, Z. 2014, ApJ, 783, 134 [NASA ADS] [CrossRef] [Google Scholar]
  20. Feldmeier, A., Lützgendorf, N., Neumayer, N., et al. 2013, A&A, 554, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Fender, R. P., Maccarone, T. J., & van Kesteren, Z. 2005, MNRAS, 360, 1085 [NASA ADS] [CrossRef] [Google Scholar]
  22. Fierlinger, K. M., Burkert, A., Ntormousi, E., et al. 2016, MNRAS, 456, 710 [NASA ADS] [CrossRef] [Google Scholar]
  23. Galván-Madrid, R., Liu, H. B., Zhang, Z.-Y., et al. 2013, ApJ, 779, 121 [NASA ADS] [CrossRef] [Google Scholar]
  24. Gebhardt, K., Rich, R. M., & Ho, L. C. 2002, ApJ, 578, L41 [NASA ADS] [CrossRef] [Google Scholar]
  25. Gebhardt, K., Rich, R. M., & Ho, L. C. 2005, ApJ, 634, 1093 [NASA ADS] [CrossRef] [Google Scholar]
  26. Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hadjidemetriou, J. D. 1963, Icarus, 2, 440 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hadjidemetriou, J. D. 1966, Icarus, 5, 34 [NASA ADS] [CrossRef] [Google Scholar]
  29. Harris, W. E. 1998, in Saas-Fee Advanced Course 28: Star Clusters, eds. L. Labhardt, & B. Binggeli (Berlin, Heidelberg: Springer) [Google Scholar]
  30. Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
  31. Herwig, F., VandenBerg, D. A., Navarro, J. F., Ferguson, J., & Paxton, B. 2012, ApJ, 757, 132 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hills, J. G. 1975, AJ, 80, 809 [NASA ADS] [CrossRef] [Google Scholar]
  33. Jaskot, A. E., Strickland, D. K., Oey, M. S., Chu, Y.-H., & García-Segura, G. 2011, ApJ, 729, 28 [NASA ADS] [CrossRef] [Google Scholar]
  34. Ju, W., Stone, J. M., & Zhu, Z. 2016, ApJ, 823, 81 [NASA ADS] [CrossRef] [Google Scholar]
  35. King, A. 2003, ApJ, 596, L27 [NASA ADS] [CrossRef] [Google Scholar]
  36. King, A. R., & Pounds, K. A. 2003, MNRAS, 345, 657 [NASA ADS] [CrossRef] [Google Scholar]
  37. Kızıltan, B., Baumgardt, H., & Loeb, A. 2017, Nature, 542, 203 [NASA ADS] [CrossRef] [Google Scholar]
  38. Konigl, A. 1989, ApJ, 342, 208 [NASA ADS] [CrossRef] [Google Scholar]
  39. Krause, M., Charbonnel, C., Decressin, T., et al. 2012, A&A, 546, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Krause, M., Fierlinger, K., Diehl, R., et al. 2013, A&A, 550, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Krause, M. G. H., Charbonnel, C., Bastian, N., & Diehl, R. 2016, A&A, 587, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Kruijssen, J. M. D. 2012, MNRAS, 426, 3008 [NASA ADS] [CrossRef] [Google Scholar]
  43. Kruijssen, J. M. D., & Portegies Zwart, S. F. 2009, ApJ, 698, L158 [NASA ADS] [CrossRef] [Google Scholar]
  44. Krumholz, M. R., Bate, M. R., Arce, H. G., et al. 2014, Protostars and Planets VI, 243 [Google Scholar]
  45. Leigh, N. W. C., Böker, T., Maccarone, T. J., & Perets, H. B. 2013, MNRAS, 429, 2997 [NASA ADS] [CrossRef] [Google Scholar]
  46. Leigh, N. W. C., Mastrobuono-Battisti, A., Perets, H. B., & Böker, T. 2014, MNRAS, 441, 919 [NASA ADS] [CrossRef] [Google Scholar]
  47. LIGO Scientific Collaboration, & Virgo Collaboration 2018, ArXiv e-prints [arXiv:1811.12907] [Google Scholar]
  48. Maccarone, T. J., & Zurek, D. R. 2012, MNRAS, 423, 2 [NASA ADS] [CrossRef] [Google Scholar]
  49. Maccarone, T. J., Kundu, A., Zepf, S. E., & Rhode, K. L. 2007, Nature, 445, 183 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  50. Maccarone, T. J., Kundu, A., Zepf, S. E., & Rhode, K. L. 2011, MNRAS, 410, 1655 [NASA ADS] [Google Scholar]
  51. Marks, M., Kroupa, P., & Baumgardt, H. 2008, MNRAS, 386, 2047 [NASA ADS] [CrossRef] [Google Scholar]
  52. Maschberger, T. 2013, MNRAS, 429, 1725 [NASA ADS] [CrossRef] [Google Scholar]
  53. Meiron, Y., & Kocsis, B. 2018, ApJ, submitted [arXiv:1806.07894] [Google Scholar]
  54. Mezcua, M. 2017, Int. J. Mod. Phys. D, 26, 1730021 [NASA ADS] [CrossRef] [Google Scholar]
  55. Miranda, R., Muñoz, D. J., & Lai, D. 2017, MNRAS, 466, 1170 [NASA ADS] [CrossRef] [Google Scholar]
  56. Moore, K., & Bildsten, L. 2011, ApJ, 728, 81 [NASA ADS] [CrossRef] [Google Scholar]
  57. Morscher, M., Pattabiraman, B., Rodriguez, C., Rasio, F. A., & Umbreit, S. 2015, ApJ, 800, 9 [NASA ADS] [CrossRef] [Google Scholar]
  58. Noyola, E., Gebhardt, K., & Bergmann, M. 2008, ApJ, 676, 1008 [NASA ADS] [CrossRef] [Google Scholar]
  59. Perera, B. B. P., Stappers, B. W., Lyne, A. G., et al. 2017, MNRAS, 468, 2114 [NASA ADS] [CrossRef] [Google Scholar]
  60. Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
  61. Renzini, A., D’Antona, F., Cassisi, S., et al. 2015, MNRAS, 454, 4197 [NASA ADS] [CrossRef] [Google Scholar]
  62. Roupas, Z., Kocsis, B., & Tremaine, S. 2017, ApJ, 842, 90 [NASA ADS] [CrossRef] [Google Scholar]
  63. Ryan, G., & MacFadyen, A. 2017, ApJ, 835, 199 [NASA ADS] [CrossRef] [Google Scholar]
  64. Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley-Interscience), 393 [Google Scholar]
  65. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  66. Sánchez-Salcedo, F. J., & Chametla, R. O. 2014, ApJ, 794, 167 [NASA ADS] [CrossRef] [Google Scholar]
  67. Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars: The Physics of Compact Objects (New York: Wiley-Interscience), 663 [CrossRef] [Google Scholar]
  68. Shi, J.-M., & Krolik, J. H. 2015, ApJ, 807, 131 [NASA ADS] [CrossRef] [Google Scholar]
  69. Shih, I. C., Kundu, A., Maccarone, T. J., Zepf, S. E., & Joseph, T. D. 2010, ApJ, 721, 323 [NASA ADS] [CrossRef] [Google Scholar]
  70. Sigurdsson, S., & Hernquist, L. 1993, Nature, 364, 423 [NASA ADS] [CrossRef] [Google Scholar]
  71. Silich, S., & Tenorio-Tagle, G. 2017, MNRAS, 465, 1375 [NASA ADS] [CrossRef] [Google Scholar]
  72. Silich, S., & Tenorio-Tagle, G. 2018, MNRAS, 478, 5112 [NASA ADS] [CrossRef] [Google Scholar]
  73. Spergel, D. N. 1991, Nature, 352, 221 [NASA ADS] [CrossRef] [Google Scholar]
  74. Spitzer, L. 1987, Dynamical Evolution of Globular Clusters (Princeton, NJ: Princeton University Press), 191 [Google Scholar]
  75. Spruit, H. C. 1987, A&A, 184, 173 [NASA ADS] [Google Scholar]
  76. Strader, J., Chomiuk, L., Maccarone, T. J., Miller-Jones, J. C. A., & Seth, A. C. 2012, Nature, 490, 71 [NASA ADS] [CrossRef] [Google Scholar]
  77. Subramanian, P., & Becker, P. A. 1999, BAAS, 31, 993 [NASA ADS] [Google Scholar]
  78. Sun, M.-Y., Jin, Y.-L., Gu, W.-M., et al. 2013, ApJ, 776, 118 [NASA ADS] [CrossRef] [Google Scholar]
  79. Tang, Y., MacFadyen, A., & Haiman, Z. 2017, MNRAS, 469, 4258 [NASA ADS] [CrossRef] [Google Scholar]
  80. Thoul, A., Jorissen, A., Goriely, S., et al. 2000, in Liège International Astrophysical Colloquia, eds. A. Noels,P. Magain, D. Caro, et al., 35, 567 [NASA ADS] [Google Scholar]
  81. Voss, R., Diehl, R., Vink, J. S., & Hartmann, D. H. 2010, A&A, 520, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Weatherford, N. C., Chatterjee, S., Rodriguez, C. L., & Rasio, F. A. 2018, ApJ, 864, 13 [NASA ADS] [CrossRef] [Google Scholar]
  83. Yadav, N., Mukherjee, D., Sharma, P., & Nath, B. B. 2017, MNRAS, 465, 1720 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Accretion of gas by BHs

The spherically symmetric accretion of gas with density ρg by a BH with mass m• is described by the Bondi formula (Bondi 1952), which is an application of the continuity equation

(A.1)

where v is the inward velocity of the gas and rinf is the radius of influence of the BH, that is, the space within which the BH’s gravitational potential dominates the gas dynamics. Assuming

(A.2)

we get

(A.3)

We scale Eq. (A.3) as

(A.4)

Now, for ρg = const in time, we get

(A.5)

where m•, 0 = m•(t = 0) and

(A.6)

This defines the characteristic timescale of the process, when there appears a runaway effect if there is no explicit gas loss and the implicit loss due to accretion is neglected.

Eddington-limited accretion rate is given by the formula (Rybicki & Lightman 1979)

(A.7)

where c is the speed of light, κ the electron scattering opacity and η the radiation efficiency we assume to be η = 0.1. This value corresponds to the formation of a gas accretion disk (Shapiro & Teukolsky 1983). We get

(A.8)

Appendix B: Hardening of BBH due to isotropic accretion

Hadjidemetriou (1963, 1966) has shown that isotropic mass increase or loss of a binary can be described by a dragging force

(B.1)

acting on the total mass mb = m1 + m2, mi = 1, 2 denotes the mass of each member. He calculated, using the Lagrange method of variation of Keplerian elements, that it is in this case

(B.2)

(B.3)

(B.4)

where a, e, and f are the semi-major axis, the eccentricity and the true anomaly respectively and we denote

(B.5)

the period of the orbit. It is straightforward to verify that the specific angular momentum is conserved

(B.6)

We then consider the secular evolution of the mean value of any quantity A(t) over the time P

(B.7)

assuming slow accretion within one period

(B.8)

Equation (B.3) becomes in this limit

(B.9)

and therefore we get for the mean value of any quantity A(t) within time P that

(B.10)

Thus, we get for the secular evolution of the orbit

(B.11)

(B.12)

After performing the integration we get

(B.13)

(B.14)

We infer that the eccentricity is secularly conserved and the separation a evolves secularly like

(B.15)

The same result we deduce from the conservation of angular momentum (B.6) assuming e = const.

However, the crucial quantity, which determines the dynamical evolution of the binary due to close encounters, is not a. According to the “Heggie–Hills law” (Heggie 1975; Hills 1975) soft binaries get softer on average and hard ones get harder due to close, mainly thee-body, encounters, in which a hard binary is one with

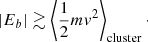(B.16)Eb is the internal energy of the binary

(B.17)

and

(B.18)

the mean kinetic energy per star of the cluster. Therefore the quantity which determines the dynamical evolution of a binary inside a cluster is the quantity

(B.19)

we shall call hardness. The quantity ah is a characteristic separation

(B.20)

which follows from Eq. (B.19). In the followings we will assume for the mean stellar mass of the primordial cluster ⟨m⟩cluster = 0.36 M⊙, as estimated recently by Maschberger (2013). The quantity ah defines the soft-hard boundary χ = 1 ⇔ a = ah. The higher the value of χ the harder the binary. Binaries that have become hard enough, that is, their binding energy is higher than the mean stellar energy χ >  1, will most probably continue to get harder and eventually merge. Therefore we are interested in determining how soft may a BBH be in order to become hard by accretion before the gas is completely depleted from the cluster.

Using Eqs. (B.15) and (B.19) we conclude that the binary’s hardness increases proportional to the third power of mass due to isotropic accretion

(B.21)

and therefore it is very sensitive to mass increase.

Appendix C: Evolution of accreting BBH

We wish to estimate the degree that a primordial BBH can become more massive and harder by accretion of primordial gas and by the time the gas is completely depleted. This calculation will allow us to conclude on whether it is possible the BBHs of the GW signals GW150914, GW170104 and GW170814, corresponding to initial BBH masses mBBH ∼ (50 − 65) M⊙ to originate from low mass BBHs (mBBH ∼ 15 M⊙) that have been grown and hardened rapidly by accretion inside a proto-globular clusters’ core.

In our analysis we need some estimation on the gas depletion time and the rate of gas depletion in primordial clusters. Calura et al. (2015) estimate that within ∼14 Myr the gas is 99% depleted by star formation feedback processes in a primordial cluster with initial total mass ∼107 M⊙. They find that within the first 3 Myr about 40% of the gas is lost, while the gas is completely depleted by 30 Myr. It is evident in their analysis that there is an approximate linear mass loss of gas for a time lapse ∼5 Myr starting after the first Myr, in which time interval occurs the most effective and rapid mass loss while until time ∼30 Myr the rest gas mass is slowly depleted. Therefore, for a linear gas density loss within the time tf when the gas is completely depleted

(C.1)

the more realistic and strict values of tf should be about ∼5 Myr and up to ∼10 Myr. For an exponential law like

(C.2)

the value of te should be ∼3 Myr in order to have more than 99% depletion at ∼14 Myr.

We next wish to calculate the minimum initial gas density ρg0, min inside which a BH of initial mass m•(0) -member of a BBH- should move, in order to grow in mass by a certain amount within a definite time lapse. Then we can compare with the estimated gas density in primordial clusters ρg ∼ 5 ⋅ (104 − 105) M⊙ pc−3 (see Appendix A).

We assume that the relative vertical speed v with which the gas is absorbed by the ith BBH member equals

(C.3)

where cs, vc, and v•, i are the speed of sound of the gas cloud, the circular speed of the center of mass of the binary with respect to the cluster center, and the orbital velocity of the member BH of the binary with respect to the center of mass. This equation follows if one assumes that all directions are equivalent. We assume cs = 5 km s−1 as estimated previously in Appendix A. For an initially hard binary χ(0)≳1 we assume vc = σ with the stellar velocity dispersion in the core equal to σ = 6 km s−1 (Binney & Tremaine 2008). The value of v•, i(0) follows from the value of the initial hardness as follows. The orbital velocity of the fiducial particle is

(C.4)

where ah is given in Eq. (B.20). The orbital velocity of each member BH with respect to the center of mass of the binary is

(C.5)

Assuming m1 = m2 ≡ m• = mb/2 and using Eq. (C.1) we calculate ρg0, min so that the BH mass is grown k times, meaning

(C.6)

By integrating Eq. (A.3), we get for the linear gas loss case (C.1)

(C.7)

where 2F1 is the hypergeometric function. For the exponential gas loss (C.2) we get

(C.8)

where tA is the time by which A% of the gas density is depleted. Therefore, for the same initial gas density we get

(C.9)

where t99 denotes the time by which 99% of the gas density is depleted.

The evolution of each BBH member may be calculated by solving the system of equations

(C.10)

(C.11)

where

(C.12)

(C.13)

and ah(t) is given in Eq. (B.20).

Appendix D: Ionization vs accretion

The ionization (desolution by a single encounter) timescale of a soft BBH is (Heggie 1975)

(D1)

where we used the definition of χ and ah, Eqs. (B.19) and (B.20) and assumed equal masses for the BBH members and mass ⟨m⟩cluster for the single scattering star. The evaporation (desolution by numerous encounters) timescale is of the same order of magnitude tev ∝ σ/GρstarsalnΛ (Binney & Tremaine 2008).

Combining Eqs. (A.5), (A.6), and (B.15) we find the timescale τh at which a soft binary (χ <  1) may get hard (χ ≥ 1) due to Bondi accretion

(D2)

Dividing (D.1) by (D.2) we get

(D3)

All Figures

thumbnail Fig. 1.

Minimum initial density of the gas (ρg0, min), given in Eq. (C.7), required for a BBH with equal mass BH members so that each member reaches mass 30 M⊙ by Bondi accretion inside this gas’ density environment and until time tf when the gas is completely depleted, assuming a constant mass loss rate of the gas (C.1). For an exponential gas loss law (C.2), the time t99 needed for 99% depletion is t99 = 2.3tf, for the same values of all other parameters. We also assume in both figures cs = 5 km s−1, σ = vc = 6 km s−1 where we denote, respectively, the speed of sound of the gas, the velocity dispersion of the stars and the velocity of the binary with respect to the cluster. We consider three cases, each member having initial mass m0 = 5 M⊙ (blue solid line), 10 M⊙ (red dashed-dotted line) or 15 M⊙ (yellow dashed line). Left panel: we assume an initially slightly hard binary with χ(0)=1 ⇔ a(0)=ah(0). It is evident that in order for a BH with initial mass ∼(5 − 10) M⊙ to grow up to 30 M⊙ within tf = 5 Myr, assuming by this time there is complete gas depletion, would require an initial gas’ density ∼(5 − 15)×104 M⊙ pc−3. These minimum density values correspond to the exponential gas loss law with 99% depletion at time t99 = 11.5 Myr. The density values are half for tf = 10 Myr for both linear and exponential cases. We took into account the hardening of the binary during accretion. Right panel: we calculate ρg0, min w.r.t. the initial hardness expressed by the quantity logχ−1(0) for tf = 5 Myr in the linear case of gas loss. This time corresponds to t99 = 11.5 Myr in the case of exponential gas loss. It is evident that soft binaries accrete gas more effectively than very hard ones. A hard binary a(0)/ah(0)=0.1 with BH members each of mass (5 − 10) M⊙ requires ρg0, min = (8 − 50)×104 M⊙ pc−3 while a soft one a(0)/ah(0)=10 requires only (5 − 13)×104 M⊙ pc−3. By the time the gas is depleted a soft binary gets hard in case of isotropic accretion as demonstrated below, in Fig. 2.
Open with DEXTER
In the text
thumbnail Fig. 2.

Evolution of BH masses m1, m2 (red lines) and BBH hardness (minus logarithm) χ(t)=ah(t)/a(t) (blue lines) plotted until the time the gas reservoir of a primordial cluster is completely depleted for an exponential loss law (for a linear law the depletion time for the same mass growth is about half) so that the BHs attain the mass values of the GW signal GW150914, namely m1(tend)=36 M⊙, m2(tend)=29 M⊙. We assume cs = 5 km s−1, σ = 6 km s−1 and the orbital velocity of the BBH w.r.t. the cluster to be constant vc = 4.5 km s−1 which corresponds to a circular orbit of the barycenter at a distance ∼0.15 pc from the center of the cluster. Assuming vc = σ will add about 8 Myr. Left panels: we consider spherically symmetric Bondi accretion and solve the system (C.10) and (C.11). The initial gas density is ρg(0)=5 × 104 M⊙ pc−3. We find that the time needed is 12 Myr for a(0)/ah(0)=1, corresponding to the soft-hard boundary, in the upper panel and m1(0)=8.35 M⊙, m2(0)=8.03 M⊙, while we consider a soft binary in the lower panel with a(0)/ah(0)=5 ⇔ χ(0)=0.2 and m1(0)=7.91 M⊙, m2(0)=7.54 M⊙. The hard BBH gets about 62 harder, while the soft 74 times harder becoming very hard at the end of the process χ(tend)=14.8. Both the mass increase and hardening effects are more intense for the soft binary in agreement with Fig. 2b. Right panels: we consider Eddington-limited accretion in a disk, as in Eq. (A.7), depicted with solid lines and we plot in the same graph the Bondi case with dotted lines. We assume initial gas density ρg(0)=104 M⊙ pc−3. The time needed for a similar growth to the Bondi case is about four times larger with respect to the left panels, namely 50 Myr with a little higher initial masses m1(0)=11.85 M⊙, m2(0)=9.55 M⊙. We note that in order to achieve the same final mass in the same time with Bondi accretion, the initial masses are much lower, namely m1(0)=6.40 M⊙, m2(0)=6.29 M⊙ in the hard case and m1(0)=5.54 M⊙, m2(0)=5.40 M⊙ in the soft one. In case of angular momentum preservation (or loss to the disk) the BBH gets harder in Eddington-limited accretion as well, though it is less severe than in the Bondi case. The soft binary gets hard attaining χ(tend)=5.6.
Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.