| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201833634 | |
| Published online | 15 January 2019 | |
Emission of Joule heating events in simulations of the solar corona
1
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029, Blindern 0315, Oslo, Norway
2
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern 0315, Oslo, Norway
e-mail: charalambos.kanella@astro.uio.no
Received:
13
June
2018
Accepted:
14
November
2018
Context. Nanoscale events in cooperation with steady heating from a slow heating mechanism, such as slow-burning current-sheets, could be able to heat the corona; however, their observational traces are hard to detect via current instrumentation. After we locate heating events in magnetohydrodynamic (MHD) simulations and synthesise observational data, we extract observational signatures of small-scale events.
Aims. Our mission is threefold. The first goal is to observe the manifestation of small-scale events via three observational tools: intensity maps of three extreme ultraviolet (EUV) filters in the Atmospheric Imaging Assembly (AIA) instrument with resolution better than that in AIA images, emission measure (EM) analysis, and time-lag maps. The second goal is to identify the reason why we cannot quantify the energy release from observed events. The third goal is to study the differences between the radiation from isolated heating events and that from the whole corona.
Methods. We employed a three-dimensional magnetohydrodynamic (3D-MHD) simulation using the Bifrost code. We simulated the atmosphere of a network embedded in the quiet Sun (QS), and we identified 3D heating events in the corona in several time-steps. Then we synthesised the three observational tools for two cases. First, we considered information from the total column mass in the corona, and then we considered only regions that exhibit heating events.
Results. We report on the differences between the two regions of investigation, which also consist of the evidence to justify why observers cannot identify small-scale heating events in observations. We found that the combination of multiple heating events at different cooling phases along the line of sight gives the impression of thin elongated threads of events. For this reason, the EM as a function of temperature has a multi-thermal distribution. Both the radiation and the emission measure of the isolated heating events have values at least ten times lower than the signal calculated from the total corona. We also found that heating events move together with diffuse emission from the slow heating mechanism, and for this reason we cannot differentiate between the two. In addition, we find that the frequency of heating events and their intensity affect the EM distribution as a function of temperature. We also find that the filter’s intensity, EM, and time-lag maps of heating events are different to those incorporating information from the total column mass of the corona. However, the two regions have, on average, comparable values, which are slightly smaller than the analytical cooling timescales calculated for an optically thin and radiation-dominated atmosphere.
Key words: magnetohydrodynamics (MHD) / Sun: corona / Sun: flares / Sun: UV radiation
© ESO 2019
1. Introduction
After almost eight decades of wondering how the solar corona reaches the high temperatures we observe (Grotrian 1939), the question is one of the longest-standing in astrophysics. One possible heating mechanism is nanoflares (Parker 1983a,b): numerous small-scale impulsive events based on the idea of magnetic reconnection. Though this mechanism is theoretically very promising, in practice, however, its validation has been proven a difficult task.
The research community has so far been unable to validate the proposed mechanism, due to the limitations of current instrumentation. Solar flares in general, follow a distribution where the number of flares per energy interval is a power law with a critical power-law index −δ. Much effort has gone into identifying the value of δ because if the value of δ is above two, the nanoflares will dominate the energy output from solar flares. Large flares are not frequent enough to maintain the solar corona at MK temperatures, so if flares are the main heat source of the corona, nanoflares need to provide more energy than the larger flares. Until now, a large fraction of observational studies have provided values of δ of less than two (see Table 9 in Aschwanden et al. 2016 for an overview), but more importantly the value of δ seems to be dependent on the region investigated and more importantly on the instrument used. It is at the same time very difficult to estimate the full energy release from a flare, for a number of reasons. The intensity observed in a spectral window range can give an estimate of the energy, but the density and temperature is hard to quantify, as is the flare size along the line of sight. For these reasons other more easily observational parameters are often collected, most often the peak flux. The complication is of course that the peak flux and the total released energy might not have a common proportionality factor at both low and high energies, making an estimate of the power-law exponent for the peak flux of flares potentially different than for the total energy. For certain instruments with longer exposure times, the exposure time makes the peak flux an integration over the true flare evolution. It is likely that small energy flares last a shorter time than high-energy flares, and such an integration effect would then affect short-lived and long-lived flares differently.
To form a better view of how heating events manifest themselves in observations, and to understand the reasons why we cannot quantify the energy release from observed heating events, we simulated a part of the solar corona using the Bifrost code. Then we used a relatively new method to identify three-dimensional heating events, and we followed their evolution in time. Finally, we synthesised observations for the whole corona and for the flaring regions in isolation to compare the two cases. The observations we synthesised are the three single-peak EUV channels (171 Å, 193 Å, 211 Å) of the AIA instrument (Title et al. 2006; Lemen et al. 2012) on the Solar Dynamic Observatory (SDO, Schwer et al. 2002). From these synthetic observables, we calculate emission measure (EM), and time-lag between the pairs the AIA filters.
This paper discusses the difference between the radiative signal from the heating events in isolation and the signal from the whole simulated corona. The remainder of this paper is organised in the following way. In Sect. 2 we explain the methods and tools employed to generate and analyse the data. In Sect. 3 we briefly describe the Bifrost code, the physics of the model, and the parameters chosen for analysis; in Sect. 4 we display the results of our investigation; and in Sect. 5 we discuss our findings and derive some conclusions that might help observers in the study of a magnetic network embedded in the quiet Sun (QS).
2. Methods and tools
In this and previous works (Kanella & Gudiksen 2017, 2018), we identify Joule heating events in simulations of a solar magnetic network region using the numerical code Bifrost (Gudiksen et al. 2011). For the details of the numerical code and the simulation, we refer to these papers. Here, we only briefly describe the code and simulation.
3. Model
In this section we first describe the numerical code very briefly and the physical processes involved in the simulation, then we explain the code set-up, and finally we elaborate on the model used for the purpose of this paper.
3.1. Numerical method
The Bifrost code (Gudiksen et al. 2011) is a massively parallel code that can simulate a stellar environment from the convective zone up to the corona with decent resolution. The code can describe the different parts of the solar atmosphere in detail using several physical processes and boundary conditions as requested by the user. It solves a closed set of three-dimensional magnetohydrodynamic (3D-MHD) partial differential equations together with equations that describe radiative transport and thermal conduction. It solves the system of equations on a Cartesian grid using sixth-order differential operators, fifth-order interpolation operators, along with a third-order Hyman method with variable time-step.
The code considers the different physical processes that occur in the convective zone, the photosphere, the chromosphere, and the corona and for each simulation, it is possible to include or exclude some of these processes depending on the subject of the study. The simulation results we used are similar to the simulation available as part of the IRIS data release (Carlsson et al. 2016) except the detailed hydrogen non-equilibrium ionisation is not included. It includes full radiative transfer, which incorporates the scattering between optically thin and thick regions in the atmosphere; the radiative transfer in the outer part of the solar atmosphere, which is optically thin from the upper chromosphere up to the corona; the radiative transfer in the chromosphere, which is optically thin in the continuum and optically thick in numerous spectral lines; and thermal conduction along the magnetic field.
Radiative and conductive processes are parts of the equation of internal energy, which has the form
where e is the internal energy per unit volume, u the velocity vector, P the gas pressure, and Qc the heating/cooling derived via the Spitzer thermal conduction along the magnetic field (Spitzer 1962). Here QJ represents the Joule heating, which is expressed as QJ ∝ η (∇ × B)2, where η is the numeric diffusivity and B the magnetic field vector; QVi is the viscous heating, which is expressed as QVi ∝ ν (∇× u)2, where ν is the fluid viscosity; Λ is the cooling or heating produced by the emission or absorption of radiation. In the corona, radiative transfer is optically thin, and thus, radiative loss Λ can be reduced to radiative cooling Qthin = −nHnef(T), where nH is the number density of hydrogen, ne is the number density of electron, and f(T) is a temperature function that can be computed assuming ionisation equilibrium. The third term on the right-hand side expresses mechanical work, while the two terms on the left-hand side represent how internal energy changes in a Lagrangian system of reference.
In our analysis, a necessary quantity for the calculation of the synthetic AIA filters is electron density. To calculate electron density, nel we assume ionisation equilibrium.
3.2. Simulation set-up
We simulated the Sun spanning a volume 24 × 24 × 16.8Mm3 and separated into 7683 grid-cells. The cell-size in the horizontal plane is constant (dx = dy = 31.25 km), where the vertical grid-spacing varies so as to resolve the magnetic field, temperature, and pressure scale heights. Vertical spacing therefore has values as low as 26.1 km in the photosphere, chromosphere, and transition region, and increases slowly up to 165 km in the corona. The vertical axis starts 2.5Mm below the photosphere and ends 14.3Mm above it. The horizontal boundary conditions are periodic, and the vertical (z-direction) are open. The lower boundary remains in hydrostatic equilibrium allowing convective flows to enter and leave. By controlling the entropy of inflowing material at the bottom boundary, the effective temperature at the photosphere is kept constant at 5780 K.
The main free parameter in the code set-up is the magnetic field. It has the form of two relatively strong magnetic regions with opposite polarities to imitate a network region. The magnetic field at the first step of the simulation is vertical at the bottom boundary, and extrapolated assuming potential field. We continually introduced a 100 Gauss horizontal field in the bottom boundary. This injection ensures the well-known “salt and pepper” structure of the magnetic field in the QS (see Carlsson et al. 2016, for more details).
3.3. Model description and general behaviour
Magnetic networks should produce numerous reconnection events, due to the small scales of the magnetic flux distribution, so this should be an ideal region to study small-scale reconnection events. Since magnetic reconnection is a topological phenomenon, it is difficult to identify each reconnection event without a detailed study of the magnetic configuration of each event, but the indirect effect of reconnection is easier to identify. Therefore, the study of the Joule heating term in the Bifrost code is our best proxy for such topological events. Magnetic reconnection depends on, among other things, the degree of magnetic field distortion; currents are manifestations of magnetic field distortion in MHD and when there is inclination between the magnetic field and currents, magnetic reconnection can occur.
In this model, the solar corona is heated mostly by the Joule heating term included in Eq. (1). A fraction of this term is from impulsive heating events, while the remainder is from a combination of slow-burning currents due to a lower energy release mechanism and unresolved small-scale heating events not detected by our method (Kanella & Gudiksen 2017). The code computes the Joule heating via a non-constant electric resistivity. We keep numerical resistivity as low as possible to achieve stability of the explicit code (Gudiksen et al. 2011).
Resistivity on scales larger than the particle resistivity, is a combination of the unresolved structure of the magnetic and electric fields. It is obvious that the Sun is able to employ a resistivity that is much larger than the theoretical particle resistivity, most likely due to small-scale instabilities in the current sheet. More precisely, simulations have shown that resistivity increases locally at the reconnection sites. Ugai & Tsuda (1977) have shown that microscopic instabilities (e.g. tearing instability; Furth et al. 1963) within a current sheet can increase resistivity locally and thus, magnetic reconnection proceeds faster. Resistivity is also enhanced in regions of high magnetic stressing. According to Aulanier et al. (2006), current sheets in high magnetic stressing regions becomes thinner and the magnetic field gradients larger. As a result, current density increases and that leads to an enhanced resistivity.
We chose to investigate coronal heating and cooling in a fixed-size box specified at a specific temporal window. Our region of interest (ROI) starts at height 3.28Mm above the photosphere where the temperature is 1MK at t = 1130 s of solar time, and extends to 12.8Mm above the photosphere. The ROI is resolved by 768 × 768 × 331 grid-cells, which is equivalent to a 24 × 24 × 9.5Mm3 box. We investigate a temporal window that starts at 650 s of solar time and finishes at 3500 s, having a snapshot cadence of 30 s.
The beginning of the time sequence is still affected by the initial conditions. Vertical flows are apparent throughout the whole corona at any instant. At the beginning of the simulation, we find downflows at every layer (see bottom right panel in Fig. 1). After approximately 800 s of solar time, the averaged flow changes direction. At this point and for almost 800 s, the uz amplitude varies widely and drops while time elapses. After this point, the atmosphere progresses towards a more stable configuration.
Figure 1 demonstrates the evolution of the planar averaged temperature T, mass density ρ, Joule heating QJ, and vertical velocity uz at six different heights in the solar corona. Except uz, all the quantities are stratified along height throughout the total temporal window of investigation. Focusing at a fixed time, we note that Joule heating decreases with height. This occurs because Joule heating scales with the magnetic energy density, which also drops with height. Mass density drops with height as well, whereas temperature increases.
All four parameters in Fig. 1 show significant changes in the first 1500 s. Later in time, when the simulation has settled down and balance between heating and cooling has been achieved, changes in the four quantities are smaller. The density profile closer to the lower corona exhibits more fluctuations than the higher corona probably due to upflows of evaporated chromospheric plasma. Fluctuations in the vertical component of the velocity field might be due to the net effect of propagating waves, and upflows from evaporated chromospheric plasma.
The evolution of the planar averaged Joule heating in the corona exhibits a fluctuating behaviour that persists at every height in the solar corona. The reason is the random nature of the magnetic field distortion that depends on the energy release of the Joule heating term. When an energy release happens the stresses in the magnetic field relax, while the mechanical drivers in the photosphere and the convective zone build up energy again, thus making it possible for another release of energy.
Electron density drops exponentially with height, and fluctuates with time in the same way as mass density does in the lower left panel in Fig. 1. We expect radiation to behave similarly because emission scales as a function of square electron density. Electron density fluctuations in the lower corona are greater than those in the upper part because chromospheric evaporation adds hot material to the corona. It is speculated and implicitly observed (Testa et al. 2014) that magnetic reconnection accelerates electrons towards the chromosphere causing evaporation. In our case, we do not simulate accelerated electron. Instead, if pulses of heating leave the corona via thermal conduction (i.e. the dissipative thermal flare model by Brown et al. 1979; Smith & Lilliequist 1979), then chromospheric evaporation is also triggered in a similar manner, simulating similar effects to the ones caused by accelerated electrons.
 |
Fig. 1. Evolution of four planar averaged parameters at different heights. Top left panel: temperature. Top right panel: joule heating. Bottom left panel: mass density. right panel: vertical component of velocity field. Positive values indicate downflow. |
The method we employ and which is described in both Kanella & Gudiksen (2017, 2018) relies on being able to find spikes in the Joule heating, and then following the negative gradient in all directions until the gradient at some level of the heating E0 becomes very small. The 3D isosurface of the Joule heating at level E0 around that spike then gives the event volume, and the total energy of the event can be calculated. The method is repeated for the next spike. This method makes it possible to use different values for E0 for each spike. We note that E0 is a free parameter and is chosen based on pre-specified criteria, such as the maximum volume among all volumes with different E0.
The method consists of identifying different events at different thresholds and chooses the ones that satisfy pre-specified criteria. The volume that has Joule heating, but is not identified as being part of an event is puzzling. There is no single and typical effect that leads to the volumes with Joule heating not identified as an event in this study, but in this work we refer to these regions as diffusion regions. It is interesting how the percentage we resolve with our method (2%−13%) is closed to the diffuse emission in between strands of well-defined loops. Such diffuse emission composes 60%−90% of the total emission in the EUV of active regions (Del Zanna & Mason 2003; Viall & Klimchuk 2011). Note also that our identification method is a conservative method because we try to avoid to attribute mistakenly more energy to an identified event.
Since observations cannot distinguish nanoflares and constant Joule heating by low gradients in the magnetic field, we synthesised AIA filters in our simulations to study emission in both of the regions found in this simulation.
We chose to analyse the EUV passbands of the AIA instrument. The AIA instrument observes the solar atmosphere in seven filters covering a variety of UV, EUV, and visible bandpasses. Six of theses filters emit mainly due to iron emission lines; the importance of lines depends on the ROI: different lines have different contributions in the chromosphere (CH), quiet Sun (QS), active region (AR), and flares.
Assuming optically thin plasma and ionisation equilibrium1 the intensity of an AIA filter is then expressed as
where ΔT is equal to 0.1 dex Kelvin, RAIA is the instrument response function, and ϕ(Te) is the differential emission measure (DEM).
Figure 2 illustrates the temperature sensitivity of the three AIA filters we use in this study as a function of electron temperature normalised to their respective maximum values (RAIA(Te) in Eq. (2)). Filters 94 Å and 131 Å have double temperature sensitivity at both low and high temperatures, while filter 335 Å has broad temperature sensitivity; therefore, these filters are not useful in our study. Filters 171 Å, 193 Å, and 211 Å are narrow bandpasses with a single peak, which makes these filters good observational tools for studying the QS.
 |
Fig. 2. Temperature response function of three EUV filters of the AIA instrument normalised to their respective maximum values. |
The EUV filters of the AIA span a wide temperature spectrum, which makes them a strong observational tool. AIA images have a pixel size equal to 1.2 arcsec (900 km), which is not small enough to resolve the loop braiding that is essential to observe magnetic reconnection directly. Therefore, small-scale changes in the coronal structure remain unresolved because resolution must be less than 300 km (Brooks et al. 2013). For this reason, we do not use the AIA resolution; we use instead our simulation’s horizontal grid-size.
To study emission, we synthesise three observational tools, namely synthetic AIA filters, cross-correlation, and emission measure. Our method is different to others in the way that we apply these tools, not only on 2D images of a simulated solar corona (known as the all region case), but also on images where we only consider contributions from regions that exhibit heating events (known as the flaring case).
3.4. Synthetic AIA filters
In this section, we describe how we synthesised the EUV AIA filters using data from the MHD simulation. To calculate the filters’ intensities, we used the aia_get_response.pro function included in the SolarSoft version of IDL. The current function used at the time of calculation (5 December 2016) is version 6, dated 11 March 2016. The temperature response functions, as illustrated in Fig. 2, use atomic data from the CHIANTI database version 7.1.3 (Dere et al. 1997; Landi et al. 2013) assuming coronal abundances. The temperature response function of each EUV filter is a contribution from numerous spectra lines and continuum; a list with count rates predicted for several ions for each filter is tabulated in O’Dwyer et al. (2010). Then, we introduced the calculated electron density together with the response function into Eq. (2), and calculated the intensity. We repeated the procedure, also to generate an off-limb view of the solar corona.
3.5. Cross-correlation and cooling timescale
Cross-correlation and derived time-lag maps compose a useful tool for checking the sequence of filters in which cooling proceeds after a heating event has occurred in the solar atmosphere. Cross-correlation is widely used to study either the impulsive or the constant heating character of coronal loops (e.g. Viall & Klimchuk 2012, 2016; Lionello et al. 2016; Tajfirouze et al. 2016a,b).
In the current study, we use the MATLAB xcorr.m function to compute the cross-correlation coefficients and time-lags between a pair of signals. The light curves are normalised so that the auto-correlation of each component is one; the coefficients therefore range between 0 and 1. We then choose the maximum coefficient, and the corresponding time-lag between the two sequences. The process is repeated for the three combinations between the AIA EUV filters in Fig. 2 at each pixel (in total 768 × 768 pixels) for light curves starting at 650 s and ending at 3500 s having a 30 s cadence. We repeated the method assuming information from only regions that exhibit Joule heating events. In this case, we only considered pixels that had at least one identified heating event along the line of sight in the 3D ROI.
To better understand the cooling process we compared the observed time-lag values between filters with the theoretical cooling timescales derived when considering only radiation-driven cooling. We use the formula of radiative cooling timescale derived by Bian et al. (2016). In an optically thin atmosphere dominated by radiation, the temperature evolution formula has the form
where Λ(T) = χT−l is the radiative loss function (e.g. Cox & Tucker 1969). For the temperature range 104 < T < 107, constants are equal to χ = 1.2 × 10−19 and l = 1/2. Integrating Eq. (3) and reforming the result we derive the radiative cooling timescale tcool, which has the form
where 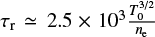 . We note that cooling proceeds from T0 to T(t) in time t = tcool. We use the averaged electron density of our ROI that is ne =2.32 × 109 cm−3. The temperature values correspond to the peak of the temperature response function of each filter: T171Å = 8.9× 105 K, T193Å = 1.6× 106 K, and T211Å = 1.8 × 106 K.
. We note that cooling proceeds from T0 to T(t) in time t = tcool. We use the averaged electron density of our ROI that is ne =2.32 × 109 cm−3. The temperature values correspond to the peak of the temperature response function of each filter: T171Å = 8.9× 105 K, T193Å = 1.6× 106 K, and T211Å = 1.8 × 106 K.
3.6. Emission measure
Another powerful tool is EM because it quantifies the amount of emitting material. We calculate EM in MHD by integrating the squared ne along the line of sight we investigate. This way, we constructed EM maps in top and side view. Another strategy we employed in this work is the selection of small patches in the top view images and calculation of an averaged EM in the region as a function of temperature.
4. Results
In this section we present the results of our analysis. In Sect. 4.1 we describe results from the radiation analysis; in Sect. 4.2 we describe the results from cross-correlation analysis; and in Sect. 4.3 we present the outcomes from the emission measure analysis.
4.1. Radiation
The results presented in this section are based on the resolution of the simulation. For comparison, we reduced our resolution to that of the AIA pixel, and found that the averaged intensity of the 2D image of the 171Å filter agree with Raftery et al. (2011). Their observations, like ours, correspond to emission from a magnetically active patch embedded in the QS.
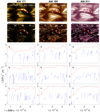 |
Fig. 3. Top row: intensity of three EUV AIA filters for the total column mass case (i.e. all regions). The three red cycles, selected in 171Å filter at t = 2990, track intensity at every time-step. Second row: same as in top row but for regions that exhibit only heating events (i.e. flaring). Third to fifth rows: plots of the evolution of intensity. Red coloured lines depict intensity calculated assuming total column mass, while blue-coloured lines depict intensity evolution for regions that exhibit only heating events. Pixel size is the simulations pixel size. |
Next we investigated the intensity in the AIA passbands from the indentified localised Joule heating events and for the whole ROI. The results are presented in Fig. 3, where the top row is the intensity from the whole ROI seen from the top and the second row is the intensity from the identified heating events at t = 2990. It should be noted that the intensity from the heating events themselves generally are only a small percentage of the total intensity. This is even more apparent when looking at the three lower rows of Fig. 3, where the intensity at three different locations is shown. We select three points on a loop in AIA 171Å at the specific snapshot and check what happens in all filters through time. Pixel (a) targets the foot-point of a loop, pixel (b) the top of it, and pixel (c) the half-distance between foot-point and apex. The intensity from the whole corona exhibits a flickering character for all regions, whereas in regions exhibiting heating events the light curves are bursty and intermittent. We also identify 50, 90, and 105 heating events at each point (a to c, respectively) that occurred during the total time span. For all three locations and in all filters the many heating events never produce more than roughly 1% of the intensity. Equally interesting, is that this seems to be constant for all the heating events in all the filters.
The combination of multiple heating events along one horizontal direction at different cooling phases gives the impression of individual threads of radiating material in side view. In Figs. 4 and 5 we can see that threads are embedded in a diffuse region forming loop-like structures that move around.
To clarify whether motions in Fig. 4 are real lateral motions or apparent ones, we followed a loop in time. We tracked the intensity evolution of an almost 3Mm long slit placed across the loop, and plotted a time-distance map of intensity for every EUV AIA filter for two cases: all regions and flaring-only regions. We placed the slit in a way that captures the lateral motion of a coronal strand as observed at t = 2990 s through 171Å filter. We find that the loop moves at almost 3 km s−1, which is also confirmed through the velocity field calculated by the Bifrost code, u = 2.5 km s−1. Different slits positioned at different locations along the same loop show different velocities. The top part of the loop moves faster than the foot-points indicating a loop that moves as a rigid body. However, such motions are not the rule. In addition, we observe that the motion of the loop is apparent in all time-distance maps, where the intensity is coherent but fading.
The second row of panels in Fig. 4 illustrates the radiation from the sites of Joule heating events. The corresponding time-distance maps are also illustrated in the fourth row of panels. We note that the time-distance maps of intensity of the flaring-only regions is quite different to the case of all regions. The time-distance map of flaring events is dominated by multiple short-lived events scattered along the slit, suggesting that they might be following the motion of the loop-like structure. In general, a comparison between the intensity time-distance maps of the two cases (all regions and flaring-only regions) shows dissimilar patterns.
4.2. Cross-correlation analysis and radiative cooling
In Fig. 6, we illustrate time-lag maps for two cases: the total column mass and locations of Joule heating events. Table 1 lists the averaged time-lag for all region and flaring-only region cases of each pair neglecting zero values. Surprisingly, the averaged time-lags of the two regions are similar even though the maps are entirely different. Coherent structures of non-zero temporal offsets mostly appear in the central region where magnetic cancellation is the strongest. In the images of only heating events, concentrations of seemingly elongated and irregular-shaped features around the magnetic polarities and in between space are apparent. The differences between the time-lags of each pair for every region is also apparent in the percentages of surface coverage by non-zero time-lags included in Table 1. We note that the positive temporal offset between filters with the specific ordering we use in our study indicates cooling, whereas negative offset indicates heating.
In the current study, we found that time-lag maps are mostly dominated by zero temporal offsets due to overlapping of the temperature response functions of AIA filters. Our conclusion is based on the fact that since cooling proceeds very quickly the number of pixels that exhibit zero time-lags will be larger between filters if their temperature functions overlap more than others. For example, the relatively small percentage of surface coverage by non-zero time-lags we observe in pair 211–193Å (see Table 1) compared to pair 211–171Å is due to the larger overlapping between the temperature response functions of the former pair. This result agrees with what was suggested by Viall & Klimchuk (2012), who explained that zero temporal offsets are due to very fast cooling.
 |
Fig. 4. Top row: intensity of three EUV AIA filters for the total column mass case (all regions). The red line represents a slit with one pixel width on top of a loop-like structure chosen at t = 2990 s in the 171Å filter. Second row: same as the top row, but for regions exhibiting heating events. Third and fourth rows: time-distance maps of intensity. The dashed white line indicates the time-step used for the slit. Velocity was calculated in the range denoted by the blue line. We measured distance and velocity from the south side of red and blue lines, respectively. Intensity is in units of DN/s/pix. |
 |
Fig. 5. Side view of the AIA filter intensity at t = 2990 s for the total column mass case (top row), and regions displaying only events (bottom row). Intensity is in units of DN/s/pix. |
Using Eq. (4), we calculated the theoretical cooling timescale of an optically thin atmosphere that is static and its cooling process is dominated by only radiation. The ordering of the theoretical cooling time is similar to the time-lag values from cross-correlation; the closer the temperatures, the quicker the cooling. We also note that the theoretical cooling timescales and the observed temporal offsets are comparable, the former being just few times larger than the latter.
 |
Fig. 6. top row: time-lag maps between pairs of filters considering total column mass of the solar corona. Negative values indicate that the first component lagged behind the second one. bottom row: same as in the top group of images, but for regions that exhibit only heating events. The percentages of surface coverage by non-zero time-lags are listed in Table 1. |
4.3. Emission measure analysis
We use EM to study the multi-thermal properties of the plasma in the solar corona by combining the EUV filters of the AIA instrument.
Illustrations of EM in Figs. 7 and 8 map out the heating in the corona in top and side view, respectively, for different temperature regimes. We calculated the EM for two cases: emission assuming the total column mass of the ROI including flaring and diffuse regions, and emission considering only regions identified as heating events. We calculated that diffuse regions account for 96%–99% of the total emission through the time of investigation.
The magnetic field has a decisive role on how heating and cooling is arranged in the ROI. In EM maps, we identify three different regions of emitting plasma as they are positioned with respect to the magnetic field configuration: magnetic polarities, regions around the polarity inversion line (PIL), and the rest of the regions, which we call the residual region.
We note that emitting plasma from the total column mass, and from regions exhibiting only heating events follows similar trends at any instant. The EM structure at t = 2990 s shows that emitting plasma in the two coolest temperature spectra is faded and positioned everywhere in the low corona except around and above the strong polarities (see Fig. 7). On the contrary, plasma in the third temperature spectrum occurs primarily in regions around the two polarities, and stretches towards the top boundary of the ROI (Fig. 8). Plasma in the fourth temperature spectrum lies across the PIL in the mid- and upper-atmosphere, whereas EM in the lower corona is significantly fainter.
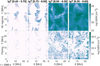 |
Fig. 7. Emission measure in four temperature regimes at t = 2990 s of solar time when considering information from the total column mass of the corona (top row), and only for heating events (bottom row). |
To further check the differences between the two regions, and their thermal properties, we also computed the averaged EM as a function of temperature in three areas chosen in 193Å filter at t = 2990 s (Figs. 9 and 10). We plotted the averaged EM as a function of temperature using temperature binning equal to 0.01 dex K. We chose a smaller binning than usually used by observers because it provides more detail. We choose regions (a), (b), and (c) on top of a diffuse loop, at the core of an intense loop, and on top of the negative magnetic polarity, respectively. The three rectangular shapes are identical and have grid cell dimensions of 50 × 40, equivalent to 1562×1250Km2 surfaces. We also calculated the average number of events per pixel throughout the 2850 s of investigation and we find 186, 105, and 76 events in regions (a), (b), and (c) respectively. We note that the number and the location of heating events with respect to the magnetic field affect the temperature of the emitting material and the amplitude of the emission. The larger the frequency of events, the higher the emission is in hot temperature bins.
Figures 9 and 10 also display the multi-thermal behaviour of loops and what we call here strands. In the former case, the EM spans coherently and almost monotonically a wide range of temperatures, whereas in the latter case multiple EM peaks dominate in the distribution of EM.
 |
Fig. 9. Left panel: synthetic filters of the SDO/AIA 193Å filter. Right panel: averaged EM vs. temperature at three different regions. |
5. Discussion and conclusions
We consider the emission from a coronal strand in our synthetic images to be a combination of heating events at different locations, different times, and at different cooling phases; the combination of these factors exhibits a temperature range that spans a relatively small spectrum of values. A group of strands, as illustrated in Figs. 3, 5, 7, and 8, blend with the diffuse region and together compose a multi-thermal coronal loop.
Since the observed strands are parts of loops, and are manifestations of the same heating mechanism, both exhibit similar characteristics at the same locations. The strands in the corona, like the diffuse region of a loop-like structure, appear only in the lower corona across the PIL and in regions with strong magnetic flux cancellation (Figs. 7 and 8). Hot material is mostly located at the magnetic poles in the lower corona where magnetic energy is very large. Hot emitting material also appears everywhere in the mid- and upper corona because the magnetic field in these regions is weaker, and thus distortion of the magnetic field occurs with ease, triggering multiple events and heating the region. This result agrees with the study of Jiang et al. (2015), who found that high intensity is emitted in regions exhibiting frequent microflares. Strands and diffuse regions exhibit strong EM in the temperature range log10T([6.05−6.35]) Kelvin in the low and mid-corona. This occurs because small motions in the photosphere create magnetic field blending (and thus heating) in the lower corona that is larger than magnetic field blending at locations higher in the atmosphere.
Extreme ultraviolet emission as observed via the AIA instrument mostly consists of radiation from the diffuse regions. Light curves of regions with diffuse emission in AIA filters (see red light curves in Fig. 3) display flickering behaviour. The mechanism of flickering could be due to the bursty and highly intermittent character of Joule heating events. However, the evolution of the signal received from events (blue light curves in Fig. 3) is at least one order of magnitude fainter, a value that is smaller than the magnitude of flickering. Post-effects of impulsive events could also justify to some extent the flickering. According to Kato et al. (2016), Provornikova et al. (2018), sound waves triggered after a heating event travel and interact with plasma. In addition, Tajfirouze et al. (2016b,a) found that flickering was caused by pressure waves triggered by highly discontinuous heating that travelled back and forth along the observed threads of combined events. Identification of pressure waves in our analysis is beyond the scope of this work, but it might be worth studying these effects in greater detail in the future.
The difference between the identified strands and the diffuse region is appparent not only in the various intensity maps, but also in the time-distance maps of intensity that trace the motion of the structures. For example, the specific loop we investigate in Fig. 4 has a lateral motion that is apparent in all intensity time-distance maps, exhibiting coherent but fading intensity. The same time-distance maps of the heating events display a different behaviour. The short-lived signatures of events with small spatial extent seem to follow the motion of the loop by appearing at the same locations in the equivalent time-distance map of the loop.
In our analysis, we find that most of the emission is generated in diffuse regions. The mechanism of the diffuse emission is, according to Viall & Klimchuk (2011, 2012), Fuentes & Klimchuk (2016), Lionello et al. (2016), Dahlburg et al. (2016), either due to steady heating from a slow heating mechanism, e.g. slow-burning currents, or due to frequent heating events that give the impression of continuous diffuse heating. From our analysis, we cannot identify the exact heating mechanism of the diffuse region. The uncertainty is due to resolution issues that every identification method encounters. If the slow heating we see is indeed a superposition of small numerous heating events, the simulation is not able to resolve them, and the individual energy contributions is very low.
We speculate that the physical mechanism of the diffuse emission is not very different to the one that generates the heating events. In one of our previous studies (Kanella & Gudiksen 2018), we found that the ratio between Joule heating attributed to heating events and the total Joule heating remained almost constant, while the total Joule heating was increased by more than a factor of two. As a consequence, the diffuse emission could not be due to any physical mechanism that just distorts the magnetic field. For example, global oscillations of the solar surface that introduce propagating sound waves (p-mode waves) to the solar atmosphere or the effects of chromospheric evaporation could not produce such behaviour. However, diffuse emission could be a combination of unresolved events, numerical noise, or a physical mechanism that distorts the magnetic field in a less impulsive or non-impulsive manner. Such a mechanism could be MHD waves generated at the reconnection sites that travel along the magnetic field, while also distorting it, or magnetic field gradients caused by pressure waves triggered by highly discontinuous events (Tajfirouze et al. 2016b,a). Undoubtedly, the identification of the real physical mechanism of the diffuse emission is a major challenge in understanding the heating in the solar corona, and is something that we will work on in the future in a more aggressive manner by performing simulations with better resolution.
The magnitude of heating in the corona from heating events depends on two factors: the frequency of events and how strong they are. Regarding the frequency of events, the EM in region (a) in Fig. 10, where we calculated the largest number of events, lies preferably in the hottest temperature bins, while the EM in region (b), where fewer events occur, lies within a cooler temperature range. This is because the higher the frequency of the heating events, the shorter the waiting time between successive events. Therefore, a region does not have time to cool down significantly with respect to regions that exhibit less frequent events; a conclusion that is consistent with Fuentes & Klimchuk (2016), Barnes et al. (2016). The amount of energy released from the heating events also plays an important role. The EM in region (c), which is on top of the strong magnetic polarity where a small number of impulsive heating events occur, shows that a few but energetic events keep the plasma hot. It is obvious that without the explicit identification of heating events, what we have deduced from our analysis about heating events cannot be explicitly inferred.
The combination of multiple heated structures at different locations with different temperatures exhibits an overall multi-thermal behaviour, which is apparent in plots of EM as a function of temperature (see Figs. 9 and 10). Multiple peaks and minima in the latter figure suggest a combination of multiple strands experiencing either heating events or are at different cooling phases along the line of sight. For example, region (b) in Fig. 10 exhibits multiple peaks across a large range of the temperature spectrum because it is a region that has cool low-lying and hot high-lying emitting material (see off-limb view of EM maps in Fig. 8). Similar multi-thermal behaviour is also apparent in the EM as a function of temperature when considering emission from the total corona; however, the EM distribution in that case is smoother.
An important question is whether we can observe signatures of multi-temperature strands in real QS observations, or traces of different frequency of small-scale heating events. Unfortunately, diffuse emission, as displayed in AIA images and EM maps, hides the information we receive from heating events.
If observers are ever able to isolate small-scale heating events and perform cross-correlation between different filters, they will notice that the resulting time-lag maps of only heating events are very different than those of the diffuse region. These time-lag maps exhibit regular and irregular shapes of small chunks that compose thin and elongated shapes around the magnetic polarities and their in-between space, such as those in the intensity maps in Fig. 3. They will notice that these structures consist of groups of smaller short-lived bursts that have similar time-lags. Interestingly, they will also observe that the averaged non-zero time-lags of heating events are comparable, and in some cases even larger, than those of the diffuse region (see Table 1). The reason is that the light curves of heating events consist of multiple events that occurred at different heights and at various cooling phases. This is similar to the case of having a major event where, during its evolution, another event occurs prolonging its EUV emission. This case is well studied by Qiu & Longcope (2016), who found that when heating events occur during the impulsive phase of another event, then the decay of EUV emission is prolonged. Hence, the gradual phase of a heating event is not considered solely abundant by only cooling.
The discrepancy between the theoretical radiative cooling timescale and that derived via cross-correlation of the AIA filters implies that radiation cannot be the only effect responsible for cooling. In the loops investigated here, the strands never reach the radiation dominated cooling phase where radiation should be the dominant cooling mechanism. This either means that the loops are then reheated before the radiation dominated phase begins or that the density drops sufficiently quickly to extend the radiative cooling timescale to the point where the conduction can stay important.
In this work, we are able to synthesise three observational tools and watch how heating events are manifested. In synthetic AIA filters, the combination of multiple heating events along the line of sight and strands of different cooling phases and locations give the impression of individual threads of radiating material. The radiation from the heating events is very weak, a fact that is also repeated in the EM analysis. EM also reveals that the combination of multiple heating events along the line of sight exhibits multi-thermal emission. This occurs because the signal at specific locations consists of low-lying and hot high-lying material. Cross-correlation analysis shows that small-scale events on average have relatively large temporal-offsets due to the way a light curve is formed: multiple heating events in strands that then cool down through the synthetic AIA filters. Interestingly the temporal offsets of filter pairs are comparable with the analytic radiative cooling timescale calculated for a radiation dominated cooling atmosphere.
We believe that real observations cannot detect small-scale events, at least with the EUV filters of the AIA instrument, even when considering smaller pixel-sizes. The evidence for this statement is as follows: 1) intensity and EM from heating events are at least an order of magnitude lower than the values calculated using the total column mass of the corona; 2) heating events and the diffuse region exhibit similar characteristics in visual inspection of EM and intensity maps. For example, cool low-lying and hot high-lying loops incorporate similar characteristics with strand structures of heating events. Another example is the similarity in the top-view appearance of both regions; 3) since identified events are parts of a loop, they follow the motions of the latter without having the chance to differentiate from it.
For the best identification of small-scale heating events, the resolution limit and the ability to study the size of an event along the line of sight are vital. In the current study, the projected areas of the 3D heating events are so small that they have values well below the 900 km × 900 km pixel-size of the AIA instrument. The identified events cover surfaces with values around a few simulation pixels (our simulation pixel size is 31 km). A necessary condition for the best possible identification of heating events that will allow us to infer the released thermal energy is also the size of an event along the line of sight because the combination of numerous projected events at different cooling phases along the line of sight can give a different impression of what an event looks like to how it is in reality. In conclusion, our model and identification method performed in 4D space-time can provide information that observations, due to their limitations, cannot.
According to Kawate et al. (2016), the assumption of ionisation equilibrium breaks in case where large flares cause chromospheric evaporation (CE) and temperature rise as high as 10 MK.
Acknowledgments
This research was supported by the Research Council of Norway through its Centres of Excellence scheme, project number 262622, and through grants of computing time from the Programme for Supercomputing.
References
- Aschwanden, M. J., Crosby, N. B., Dimitropoulou, M., et al. 2016, Space Sci. Rev., 198, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., Pariat, E., Démoulin, P., & DeVore, C. R. 2006, Sol. Phys., 238, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, W. T., Cargill, P. J., & Bradshaw, S. J. 2016, ApJ, 833, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, N. H., Watters, J. M., Kontar, E. P., & Emslie, A. G. 2016, ApJ, 833, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, D. H., Warren, H. P., Ugarte-Urra, I., & Winebarger, A. R. 2013, ApJ, 772, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. C., Spicer, D. S., & Melrose, D. B. 1979, ApJ, 228, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, D. P., & Tucker, W. H. 1969, ApJ, 157, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlburg, R. B., Einaudi, G., Taylor, B. D., et al. 2016, ApJ, 817, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Del Zanna, G., & Mason, H. E. 2003, A&A, 406, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C., & Young, P. R. 1997, A&AS, 125 [Google Scholar]
- Fuentes, M. L., & Klimchuk, J. A. 2016, ApJ, 828, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Furth, H. P., Killeen, J., & Rosenbluth, M. N. 1963, Phys. Fluids, 6, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Grotrian, W. 1939, Naturwissenschaften, 27, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, F., Zhang, J., & Yang, S. 2015, PASJ, 67, 1 [NASA ADS] [Google Scholar]
- Kanella, C., & Gudiksen, B. V. 2017, A&A, 603, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanella, C., & Gudiksen, B. V. 2018, A&A, 617, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kato, Y., Steiner, O., Hansteen, V., et al. 2016, ApJ, 827, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kawate, T., Keenan, F. P., & Jess, D. B. 2016, ApJ, 826, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Young, P. R., Dere, K. P., Del Zanna, G., & Mason, H. E. 2013, ApJ, 763, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lionello, R., Alexander, C. E., Winebarger, A. R., Linker, J. A., & Mikifa, Z. 2016, ApJ, 818, 129 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dwyer, B., Del Zanna, G., Mason, H. E., Weber, M. A., & Tripathi, D. 2010, A&A, 521, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1983a, ApJ, 264, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1983b, ApJ, 264, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Provornikova, E., Ofman, L., & Wang, T. 2018, Adv. Space Res., 61, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, J., & Longcope, D. W. 2016, ApJ, 820, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Raftery, C. L., Bloomfield, D. S., Gallagher, P. T., et al. 2011, Sol. Phys., 286, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Schwer, K., Lilly, R. B., Thompson, B. J., & Brewer, D. A. 2002, AGU Fall Meeting Abstracts, 2002, SH21C [Google Scholar]
- Smith, D. F., & Lilliequist, C. G. 1979, ApJ, 232, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases 2nd edn. (New York: Interscience) [Google Scholar]
- Tajfirouze, E., Reale, F., Peres, G., & Testa, P. 2016a, ApJ, 817, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Tajfirouze, E., Reale, F., Petralia, A., & Testa, P. 2016b, ApJ, 816, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Testa, P., De Pontieu, B., Allred, J., et al. 2014, Science, 346 [Google Scholar]
- Title, A. M., Hoeksema, J. T., & Schrijver, C. J., Aia Team 2006, in COSPAR Meeting, 36th COSPAR Scientific Assembly, 36 [Google Scholar]
- Ugai, M., & Tsuda, T. 1977, J. Plasma Phys., 17, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2011, ApJ, 738, 24 [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2012, ApJ, 753, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2016, ApJ, 828, 6 [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Evolution of four planar averaged parameters at different heights. Top left panel: temperature. Top right panel: joule heating. Bottom left panel: mass density. right panel: vertical component of velocity field. Positive values indicate downflow. |
| In the text | |
 |
Fig. 2. Temperature response function of three EUV filters of the AIA instrument normalised to their respective maximum values. |
| In the text | |
 |
Fig. 3. Top row: intensity of three EUV AIA filters for the total column mass case (i.e. all regions). The three red cycles, selected in 171Å filter at t = 2990, track intensity at every time-step. Second row: same as in top row but for regions that exhibit only heating events (i.e. flaring). Third to fifth rows: plots of the evolution of intensity. Red coloured lines depict intensity calculated assuming total column mass, while blue-coloured lines depict intensity evolution for regions that exhibit only heating events. Pixel size is the simulations pixel size. |
| In the text | |
 |
Fig. 4. Top row: intensity of three EUV AIA filters for the total column mass case (all regions). The red line represents a slit with one pixel width on top of a loop-like structure chosen at t = 2990 s in the 171Å filter. Second row: same as the top row, but for regions exhibiting heating events. Third and fourth rows: time-distance maps of intensity. The dashed white line indicates the time-step used for the slit. Velocity was calculated in the range denoted by the blue line. We measured distance and velocity from the south side of red and blue lines, respectively. Intensity is in units of DN/s/pix. |
| In the text | |
 |
Fig. 5. Side view of the AIA filter intensity at t = 2990 s for the total column mass case (top row), and regions displaying only events (bottom row). Intensity is in units of DN/s/pix. |
| In the text | |
 |
Fig. 6. top row: time-lag maps between pairs of filters considering total column mass of the solar corona. Negative values indicate that the first component lagged behind the second one. bottom row: same as in the top group of images, but for regions that exhibit only heating events. The percentages of surface coverage by non-zero time-lags are listed in Table 1. |
| In the text | |
 |
Fig. 7. Emission measure in four temperature regimes at t = 2990 s of solar time when considering information from the total column mass of the corona (top row), and only for heating events (bottom row). |
| In the text | |
 |
Fig. 8. Same as Fig. 7, but the emission measure here is projected in side-view. |
| In the text | |
 |
Fig. 9. Left panel: synthetic filters of the SDO/AIA 193Å filter. Right panel: averaged EM vs. temperature at three different regions. |
| In the text | |
 |
Fig. 10. Same as in Fig. 9, but for regions exhibiting only heating events. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



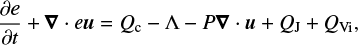
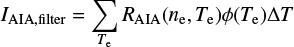
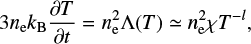
![$ \begin{equation} t_{\rm cool} = \tau_{\rm r} \left[1- \left(\frac{T(t)}{T_0}\right)^{3/2}\right] {\rm s}, \end{equation} $](/articles/aa/full_html/2019/01/aa33634-18/aa33634-18-eq4.gif)