| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833289 | |
| Published online | 10 January 2019 | |
Properties of small meteoroids studied by meteor video observations
Astronomical Institute of the Czech Academy of Sciences,
Fričova 298,
251 65
Ondřejov,
Czech Republic
e-mail: vojacek@asu.cas.cz
Received:
23
April
2018
Accepted:
12
November
2018
Aims. The complex study of millimetre-sized meteoroids can reveal more about the structure and origin of population of these meteoroids.
Methods. Double-station video observations, paired with spectroscopic video observations, were used to study small meteoroids. In total 152 sporadic and shower meteors of maximum brightness between magnitude −5 and +3 were analysed. Spectral classification was based on time-integrated intensities of lines of Na, Mg, and Fe. Meteor light curves and deceleration were fitted by the grain erosion model. Heliocentric orbits of all meteors were computed. Monochromatic light curves were constructed in order to study differential ablation. The length of meteor wakes was evaluated as well.
Results. The variety of properties among millimetre-sized meteoroids proved different sources and histories of this material. Meteoroids that contain small grains tend to release their sodium early. For given grain sizes, the sodium in Na-poor meteoroids is released earlier than in meteors without sodium depletion. Overall, meteoroids with sodium depletion are revealed to have different structures: they have stronger material without very small grains and they do not show very bright wakes. Two iron meteoroids on Halley-type orbits were observed, thereby supporting the idea of large-scale mixing of material in the early solar system. The distribution of grain sizes of Jupiter-family members was in good agreement with results from the COSIMA instrument on the ROSETTA probe.
Key words: meteorites, meteors, meteoroids
© ESO 2019
1 Introduction
Direct video observations paired with spectral observations are increasingly used for meteor studies. Meteor spectra can reveal information about individual meteoritic elements. Time-resolved spectral lines can provide new information about meteoroids. Models of meteoroid fragmentation can give us the estimation of physical parameters of small interplanetary bodies (Ceplecha et al. 1998).
We combined spectral observations with a study of the fragmentation of meteoroids. There are valuable works that used both spectral observations and studies of meteoroid fragmentation. But they usually used a limited sample of meteoroids (Borovička 2010; Borovička et al. 2014) or the study of material properties was somewhat limited (Matlovič et al. 2017; Bloxam & Campbell-Brown 2017). We applied both the study of meteoroid fragmentation and spectral analysis of a broader sample of meteors. All known spectral types of meteors were used. Representative samples of members of major showers were included. A number of sporadic meteors with both cometary and asteroidal orbits have provided the necessary diversity.
2 Instrumentation and observations
2.1 Data source
The video observations performed by the Department of Interplanetary Matter of the Ondřejov Observatory were the source of data for this work. We used observations that took place between years 2004 and 2014, during the periods of activity of major meteor showers (Quadrantids, Lyrids, η-Aquarids, Perseids, Draconids, Orionids, Leonids, and Geminids). Some of the data in this work have already been used in our previous papers. The catalogue of Vojáček et al. (2015) presented 84 spectra from our sample. All Draconids were used for the work of Borovička et al. (2014). Data for three Leonids meteors from the Tajikistan expedition were published in the work of Koten et al. (2011). The meteor numbered 07406018 was already analysed in the work of Borovička et al. (2008). We included these previously analysed meteors to present a complete sample.
2.2 Observations and equipment
Most of the video observations were performed in the Czech Republic at the Ondřejov – Kunžak observatories (distance 92.5 km). The Ondřejov–Barrandov and Ondřejov–Třebíč observatories with distances 32.2 and 109.2 km, respectively, were occasionally used for observations. Three Leonids, one Taurid, and two sporadic meteors from the Leonid observation campaign in Tajikistan in 2009 and seven Draconids from the Draconid observation campaign in Italy in 2011 were used. The observations were carried out with S-VHS camcorders with second-generation image intensifiers: until 2005, the Dedal-41 intensifier was used and after 2005 Mullard XX1332 was used. The Arsat 1.4/50 mm lens was used most of the time. With this lens the field of view was 54° with the Mullard intensifier (Borovička et al. 2008) and with the Dedal intensifier the field of view was 25° (Borovička& Jenniskens 2000). One direct camera and one spectral camera were operated from the first station and one direct camera was operated from the second station.
For meteor spectra, a Milton Roy spectral grating with 600 grooves mm−1 blazed to 470 nm was used. The resulting dispersion for the 1.4∕50 mm lens and the Dedal intensifier was 1.15 nm pix−1 in the first order (Borovicka et al. 1999). We measure the resulting dispersion for the 1.4∕50 mm lens and the Mullard intensifier to be 2.7 nm pix−1 in the first order.
2.3 Data processing
To automatically search for meteors, the detection software MetRec (Molau 1999) was used. The final meteor records were then cut from these recordings as an uncompressed AVI files with resolution 768 × 576 pixels × 8 bit and 25 images per second.
Meteors that were suitable for this work were selected from the digitised records. We included only meteors observed from both stations with most of their paths inside the field of view of the direct cameras. We selected meteors with bright enough spectra, in which at least some spectral lines were visible. We excluded bright meteors if their spectra were saturated. We included only meteors that had at least the most important part of the spectrum (500–800 nm) inside the field of view of the spectral camera.
We focussed on sporadic meteors and a representative selection of major showers meteors was made. The total number of meteors used for further processing was 152 with magnitudes between −5 and +3 (corresponding sizes between 1 and 30 mm), of which 121 were sporadic meteors and 31 meteors were members of major showers. The Southworth–Hawkins D-criterion (Southworth & Hawkins 1963) was used for the determination of the meteor shower membership. All sporadic meteors showed the criterion to any major shower higher than DSH = 0.2. On the other hand, all values of D-criterion for all major shower members were lower than DSH = 0.1.
The photometry and positions of each meteor were measured manually. We computed atmospheric trajectories and heliocentric orbits with the least squares method (Borovička 1990). For the photometric mass, the luminous efficiency of Pecina & Ceplecha (1983) was used.
The calibration of spectral wavelengths was carried out using the wavelengths of well-known atomic lines of the meteor emission. The wavelength calibrated spectra were then manually fitted in the FIT SPectra (FITSP) software developed at Ondřejov Observatory. Intensities of spectral components, the temperature of the Planck emission, and the vibrational and rotational temperature of nitrogen bands were changed manually. The fitting was done on each frame separately. We obtained the time-resolved meteor spectra. One temperature was sufficient for all frames for the Planck continuum and for the nitrogen bands. All spectra were calibrated for spectral sensitivity of the system. We were also able to sum all spectra along the trajectory. This way we obtained the estimation of total intensities for corresponding multiplets.
Meteor spectra were numbered chronologically with SZ (indicating the Dedal intensifier) or SX (indicating the Mullard intensifier) prefixes. The direct camera recordings were coded in the format YYMDDXXX, where XXX is the chronological number of the meteor (counting starts at the beginning of the night) and DD is the day of the month when the observation started. Months M were coded as follows: the numerals 1–9 indicate January–September, and A, B, and C represent October, November, and December, respectively. Detailed information about observations, equipment and data processing can be found in Vojáček et al. (2015).
3 Spectral and orbital classification of small meteoroids
3.1 Spectral classification
To classify different spectral populations of small meteors, we used the spectral classification of Borovička et al. (2005) that uses relative intensities of Na I, Mg I, and Fe I lines. Meteors are divided into several classes. The mainstream group contains thenormal class and the Na-poor, Na-enhanced, and Fe-poor classes. The non-mainstream classes are Na-free, Na-rich, and iron class. We found two meteors, for which only atmospheric lines and molecular bands were visible and marked these as spectra with atmospheric lines. Normal chondritic composition is expected for the corresponding meteoroids but thanks to their low masses and high velocities only atmospheric lines were bright enough for our system. Results of the classification can be seen in a Mg–Na–Fe ternary graph in Fig. 1. The meteor position in the ternary graph represents the computed relative intensities of three spectral lines (Mg I – 2, Na I – 1, and Fe I – 15). In Fig. 1 we can see the black curve that represents the expected theoretical positions for meteoroids of chondritic composition. The Na/Mg ratio also depends on the meteor velocity.
According to Fig. 2, the Na/Mg ratio is independent of the speed for meteoroids with v ≳ 35 km s−1. The sodium starts to prevail in the spectra of slow meteoroids, thanks to lower temperature and higher volatility of sodium. More information about the spectral classification can be found in the work of Borovička et al. (2005) and Vojáček et al. (2015).
 |
Fig. 1 Classification of meteor spectra in ternary graph. Every spectral group is represented with a different symbol. The black line shows the theoretical position of meteors with normal chondritic composition and was taken from the work of Borovička et al. (2005). The position depends on the speed of the meteor. The speed in km s−1 is indicated with numbers above the line. |
 |
Fig. 2 Na/Mg line intensity ratio as a function of the meteor speed. Iron- and Na-free meteors were excluded owing to the high uncertainty in the determination of the Na and Mg line intensities for their spectral classes. Meteors classified as normal were fitted. The fit was divided into three segments. |
3.2 Beginning heights
Beginning heights of meteoroids in the atmosphere can give us information about the strength of the material (Ceplecha 1988). For a given velocity, the stronger material (iron, Na-depleted classes) begin at lower heights. This can be seen in Fig. 3. Almost all meteors had their beginnings in the field of view of the camera. Five normal meteors with their beginnings out of the field were included, since the parts of the trajectory that were not observed were negligible. These meteors are indicated in Fig. 3. Only the Fe-poor meteor 04811066 (spectral number SZ2266) had a non-negligible part at the beginning out of the field of view. We excluded this meteor from Fig. 3.
 |
Fig. 3 Beginning height as dependence of the velocity. Different classes are indicated with different symbols. Meteors with beginning out of field of view are indicated with black squares. Uncertainties for beginning heights and velocities were negligible for display in the graph. |
3.3 Trajectories and orbital classification
Observed meteors showed orbits with a wide variety of orbital elements. Five classes of meteoroid orbits were defined by Borovička et al. (2005) as follows:
Sun-approaching orbits (SA): q < 0.2 AU.
Ecliptic shower orbits (ES): members of ecliptical meteor showers such as the Taurid meteors and other showers with orbits close to the boundary between asteroids and Jupiter-family comets.
Halley-type orbits (HT): TJ < 2 or 2 < TJ < 3 and i > 45°.
Jupiter-family orbits (JF): 2 < TJ < 3 and i < 45° and Q > 4.5 AU.
Asteroidal-chondritic orbits (A-C): TJ > 3 or Q <4.5 AU.
Figures 4 and 5 show some orbital elements of studied meteoroids. Regions of orbital classes according to above classification are shown. Not all classes are possible to distinguish from others in these 2D figures (Sun-approaching in Fig. 5 and ecliptic in Figs. 4 and 5).
 |
Fig. 4 Perihelion and aphelion of measured meteoroids. If possible, regions of given orbital classes are indicated in colour. For precise definition of orbital classes, see Sect. 3.3. The horizontal line at 5 AU represents aphelion at Jupiter orbit. |
 |
Fig. 5 Inclination and Tisserand parameter of measuerd meteoroids. If possible, regions of given orbital classes are represented in colour. For precise definition of orbital classes see Sect. 3.3. |
3.3.1 Iron meteoroids
Fifteen meteors were classified as iron. All of these are sporadic meteors. Most of these meteors have typical asteroidal–chondritic orbits. Their aphelion distances Q are below 4.5 AU and their Tisserand parameters TJ are greater than 3. On the other hand, five iron meteors have different orbits. The meteoroid SX001 have perihelion of 0.11 AU can be classified as a Sun-approaching meteoroid. The meteoroids SX661 and SX1194 can be classified as Jupiter-family meteoroids, but their asteroidal origin cannot be excluded, since the inclination is only 1.5° and 3° and the aphelion of 4.7 AU for both of these meteors is not particularly high.
The most surprising was the discovery of two iron meteors with Halley-type orbits. Their orbital parameters are in Table 1. Although both of these orbits are somewhat transitional between Halley-type and Jupiter-family orbits, they showed inclinations more than 60°. The measurement of orbit for the meteoroid with spectrum SX1938 is not particularly precise. The uncertainty for Tisserand parameter is high (TJ = 1.7 ± 1.0). Another iron class meteor with a Halley-type orbit was the meteor with spectrum SZ2410. High inclination (i = 63.2 ± 0.2°) and overall accurate orbit measurement assigns a clearly Halley-type orbit.
Orbital elements of meteoroids classified as iron with Halley-type orbits.
3.3.2 Na-free meteoroids
Two different sources for members of the Na-free class can be observed: the Sun-approaching population with small perihelion and the Halley-type population with high inclinations.
Sun-approaching meteoroids
Almost all meteoroids with perihelion distance q < 0.2 AU are Na-free or Na-poor. This is in agreement with the conclusion of Borovička et al. (2005). Two exceptions to the Na-free, Na-poor dominance in the Sun-approaching orbital class were found. One is the iron meteoroid SX001, which also does not contain sodium. The second exception is the Geminid meteor SX336 with a normal type of spectrum. This meteor is discussed in detail in Sect. 6.3.
Cometary Na-free meteoroids
These 10 Na-free meteors do not approach the Sun as close as the Sun-approaching meteors. Nine of these have Halley-type orbits. The orbit of meteor SX1073 was classified as Jupiter-family type. As suggested in Borovička et al. (2005) the reason for Na depletion in these types of orbits might be the long exposure to cosmic rays on the surface of comets during their residence in the Oort cloud. This process can lead to the formation of an Na-free refractory crust.
3.3.3 Na-rich meteoroids
Two spectra are classified as Na-rich. Both meteoroids have Jupiter-family-type orbits. Their velocities are small at v =13.4 and v = 12.0 km s−1, respectively. High relative sodium intensity can be caused by high sodium abundance in a meteoroid or by very low velocity. More meteors with very low velocities would be more helpful for accurate classification.
3.3.4 Normal meteoroids
This class contains both cometary and asteroidal meteoroids. Only part of these meteoroids have typical chondritic composition. Many of these show somewhat fainter Fe lines. Except for one Na-enhanced meteor with an ecliptical shower type orbit (SX820), all of the remaining meteoroids with ecliptical orbits are classified as normal. Most of the shower meteors were classified as normal, but some shower meteors were Na-poor or Na-free. There were no iron, Na-enhanced or Na-rich meteors among the shower meteors.
3.3.5 Fe-poor meteoroids
Five meteoroids are classified as Fe-poor. Four of the Fe-poor meteoroids have cometary Halley-type orbits. Their beginning heights suggest that these meteoroids have lower material strength; their ablation beginning heights are usually high (see Fig. 3).
A transitional orbit between asteroidal–chondritic and ecliptical was computed for the meteoroid with spectrum SZ2466 with Tisserand parameter Tj = 3.0. The asteroidal–chondritic orbit is not expected for fragile Fe-poor bodies. Unfortunately, recordings from both stations do not contain the beginning and end of this meteor. Thus, we cannot reliably compute the atmospheric trajectory and the orbit. We decided to omit this meteor from further study of orbits and atmospheric trajectories.
3.3.6 Na-poor meteoroids
Na-poor meteoroids are the transition between normal and Na-free meteoroids. Like Na-free meteoroids, some of these Na-poor meteors have low perihelion and others have cometary orbits. Thus, they probably have the same two origins as the Na-free meteoroids.
3.3.7 Na-enhanced meteoroids
Five meteor spectra are classified as Na-enhanced. The meteoroid with spectrum SX500 has a typical asteroidal–chondritic orbit. Orbits for SX498 and SX1197 are classified as Jupiter-family types. The meteoroid with spectrum SX820 has ecliptical shower type orbit and meteor SX1057 is classified with a Halley-type orbit. There is wide variety of orbital types among Na-enhanced meteoroids.
Na-enhanced meteors have usually low velocities with one exception. The SX1057 meteor with high velocity (v = 69.4 km s−1), and clearly Halley-type orbit, showed increased intensity of sodium for given speed (see Fig. 2).
4 Fragmentation model
We used thefragmentation model developed by Borovička et al. (2007). The model uses the dustball concept with quasi-continuous fragmentation. Gradual erosion is releasing grains continuously from the surface of the meteoroid. The released grains then ablate (evaporate) as single bodies.
The inputs are light curves and curves of deceleration. The goal is to find the best fit for these curves. Equations of ablation and erosion are used. Among the free parameters of the fit are the initial mass and initial velocity, ablation coefficient, energy per unit cross section necessary to start the erosion, bulk density, erosion coefficient, number of fragmented grains, and mass distribution of these grains. Useful parameters are the upper and lower limits for grain masses (GUML; GLML).
From our data, we are not able to determine the density of individual grains. Therefore we assumed a grain density of δg = 3000 kg m−3. If this density is different, the grain mass and number of grains need to be changed accordingly. If the meteor was identified as iron, we assumed the grain density to be δg = 6000 kg m−3.
Some external parameters were fixed. The drag coefficient Γ was assumed to equal unity. We used spherical grains and the shape factor A = 1.21. As the luminous efficiency τ, we used the Pecina & Ceplecha (1983) function. As a model of the atmosphere, the empirical model NRLMSISE-00 (Picone et al. 2002) was used to compute the density of the atmosphere ρ.
We do not list parameter errors since the grid-search method used for parameter search gave unrealistically small formal errors. We found that there can be multiple local minimums with comparable values of χ2 function. The formal errors, reflecting the shape of the χ2 function near the minimum, therefore do not reflect the real uncertainties of some parameters. We discuss the uncertainties and possible correlations between parameters in Sect. 7.5.
In a similar analysis, Kikwaya et al. (2011) first performed a broad global search for eight free parameters of the fragmentation model of Campbell-Brown & Koschny (2004). The grain mass distribution was, nevertheless, fixed, and was refined only in the second step. Three mass bins were used. Errors were discussed mainly for meteoroid densities and were found numerically.
Figure 6 shows an example of four meteors, their light curves, and deceleration curves. Measurements from each station are represented by points. The fitting curve is the result of the fragmentation model. We chose four different types of light-curve shapes as examples. The deceleration curve shows the dependence of the length difference on the atmospheric trajectory of the meteoroid. The length difference is the difference between the measured real position of the meteor and the computed position for no deceleration. The violet line is the result of fitting with the fragmentation model and represents the computed length difference of the brightest point of the meteor. Some meteors show signs of at least two phases of fragmentation; we can see the sudden brightening of the light curve. This is the case of the meteor 08927101 (spectrum SX788). We tried to fit these light curves and deceleration curves with two phases of erosion. This way we could estimate physical differences between these two parts.
For most meteors, we did not observe the meteor before fragmentation starts. For these cases, it is hard to estimate the bulk density since every change in bulk density can be compensated by the change of the erosion coefficient to obtain the same fit. This is the result of equations that are used by the fragmentation model (Borovička et al. 2007).
 |
Fig. 6 Examples of different shapes of light curves and their corresponding deceleration curves for four meteors. Light curves are represented on the left; deceleration curves on the right. Only data used for model are shown. |
4.1 Porosity and energy to start fragmentation
The porosity p of meteoroids is computed from the bulk density of the meteoroid δ and from the grain density δg: p = 1 − δ∕δg. The grain density was assumed according to the spectral type (see above).
Figure 7 shows the dependence of the porosity on the energy necessary to start fragmentation Es. The less porous the material is, the more energy is needed to start fragmentation. We can see in the upper panel that Na-free, Na-poor, and iron meteoroids were usually less porous (compared to the normal class) and these types needed more energy to start fragmentation. All but three Na-poor and Na-free members had porosities lower than 0.7. The Na-poor and Na-free meteoroids with low porosity were mostly Sun-approaching. The Na-poor and Na-free members with higher porosity were of cometary origin. Most members of the normal class showed high porosity. We can clearly see a cluster of normal meteoroids with porosity higher than 0.7 and Es around 1 MJ s−2. As expected, the iron members had low porosity, p < 0.2. Members ofthe Na-enhanced and Na-rich groups were porous, with p > 0.5. The Sun-approaching meteoroids were generally less porous. The cometary (both Halley and Jupiter family) meteoroids had porosities inthe whole range, but porous material prevailed. Members of the asteroidal–chondritic class showed three groups: one with very porous material, a second with an average porosity, and a third with a very low porosity.
 |
Fig. 7 Porosity p as a function of the energy necessary to start the fragmentation. Upper panel: different spectral classes are indicated with different colours. Lower panel: different orbital classes are indicated with different colours. A–C stands for the asteroidal–chondritic class. |
4.2 Grain sizes
Grains released in the model can have different masses. These masses were grouped in mass bins. A power-law mass distribution was assumed. Since density of grains and spherical shape is assumed, grain sizes and grain masses are equivalent. Grain numbers and grain masses varied for individual meteoroids. Grain masses were approximately between 10−10 g and 3 × 10−2 g (corresponding sizes 5 μm–2.5 mm). The total number of grains released during fragmentation for individual meteoroids was approximately from 102 up to 108.
Figure 8 shows histograms of grain sizes for the spectral classes. The power-law fits are shown except for the Na-enhanced class. The normal spectral group show a high diversity of grain masses and grain numbers. The Na-free and Na-poor classes show similar, but not exactly the same histograms. The histograms are divided into two parts. In case of Na-free class, the part of grains larger than ≈ 100 μm is fitted withthe fit index − 6.4 and the part with smaller grains is fitted with the index − 1.1. The numberof small grains of Na-free class members do not increase as much compared to other classes. Moreover, there are no grains smaller than 30 μm. The Na-poor meteoroids tend to contain more small grains than the Na-free class. On the other hand, only three members containe grains smaller than 100 μm. The fit index − 1.7 for grains smaller than ≈ 200 μm also shows smaller increase of number of small grains compared to other, non-sodium-depleted, classes. The Na-enhanced class contains only four modelled meteoroids, all of which have very different grain distributions and a reliable power-law fit of the whole class is not possible. The different orbital classes of these four meteoroids are indicated in the figure. The other spectral classes also contain only a small number of modelled meteoroids (iron: 4, Fe-poor: 3, Na-rich: 2, and atmospheric lines: 2).
The COSIMA instrument on the ROSETTA spacecraft collected a number of cometary particles when orbiting Comet 67/P Churyumov-Gerasimenko. Hornung et al. (2016) measured the sizes of captured grains. The particle sizes were from 15 μm up to ≈ 300 μm and a total number of particles was 7524. A histogram of grain sizes was fitted by a power-law function with index − 3.3. Since the comet is a member of the Jupiter-family comets, we tried to compare results of Hornung et al. (2016) with our sample of meteoroids on Jupiter-family orbits. The power-law fit of our data had an index of − 3.4 and it was in good agreement with Hornung et al. (2016). The histogram of grain sizes up to 450 μm for the Jupiter family is given in Fig. 9.
Figure 9 shows histograms of grain sizes for other orbital classes as well. Except for the ecliptical and asteroidal class, these have similar values of fit indexes as the power-law fit. Histograms for Sun-approaching and ecliptical class are not so smooth as histograms of asteroidal and cometary classes. It might be caused by the fact that these classes are created only on the basis of orbital similarity. The meteoroids with cliptical and the Sun-approaching orbits do not have similar origins as the cometary and asteroidal classes.
 |
Fig. 8 Histograms of grain sizes of different spectral classes. The power-law fits are shown for all classes except for the Na-enhanced class. |
 |
Fig. 9 Histograms of grain sizes of different orbital classes. The power-law fits are shown. The power-law fit of grain sizes captured by ROSETTA with index − 3.3 taken from Hornung et al. (2016) is shown in the Jupiter-family histogram. |
4.3 Irons and the fragmentation model
Iron meteors are usually faint and short and it is hard to observe deceleration. Only four iron meteors of a total of 15 could be modelled bythe fragmentation model. Meteors SX692 and SX701 were on asteroidal–chondritic orbits; SX001 was Sun-approaching and SZ2410 was on a Halley-type orbit.
The range of bulk densities was from 5000 to 5700 kg m−3, and porositywas low, as expected, from 0.16 to 0.05. The energy necessary to start fragmentation was among the highest for iron meteors. Most of the iron meteors had a very small total number of grains and number of grains in the first released bin (from 12 to 153), but the SX692 meteor had 2 × 105 grains in the first bin. The SX692 meteor contained the smallest grains with grain upper mass limit of only 3 × 10−7 kg (one of the lowest). The overall highest ablation coefficient was for the iron meteor SX701 (σ = 0.08 s2 km2). In contrast, other iron meteors had very low values of the ablation coefficient (σ < 0.013 s2 km2). The erosion coefficient was among the highest for SX692 and SX701 and low for SX001 and SZ2410. Despite only four modelled meteoroids, we can clearly see different physical parameters for asteroidal–chondritic iron meteors and for iron meteors on other orbits (Sun-approaching and Halley).
4.4 Meteors impossible to model
The fragmentation model was successfully applied to 94 of the total number of 152 meteors. The remaining 38% of all meteors could not be modelled. There are only 3 modelled meteors among 17 meteors shorter than 15 km, because short meteors hardly show any deceleration. Among meteors longer than 15 km, 21 did not show deceleration or showed only a small deceleration and the fragmentation model could not be successfully applied as it needs decelerated meteoroids. Ten meteoroids showed sufficient deceleration and the measurements were precise, but we could not find a combination of meteoroid parameters for the fragmentation model to fit these curves. Thirteen meteoroids with inaccurate measurements that did not allow modelling were omitted from further analysis. Examples of the deceleration curves and the light curves (and best achieved fits, if possible) for meteoroids not modelled are shown in Fig. 10.
We looked at the F parameter defined as the position of the maximum brightness on the light curve of the meteor in the interval from 0 to 1 (Fleming et al. 1993). The ablation of a single body predicts the light curve with a slow rise and a rapid decrease after the maximum brightness is reached, the theoretical F value for single bodies is ≈0.65 (Murray et al. 1999). The group that was not modelled because there was no deceleration even if the meteors were long enough may be suspected to be single bodies. The average F value for this group was 0.65 ± 0.15. This value suggests that they were single bodies, but the larger standard deviation indicates wide variety of F values. There were meteoroids with F value higher than 0.8 (possible single bodies), but there were meteoroids with F values smaller than 0.4. This study shows that it is hard to develop a model of meteoroid ablation and fragmentation that can match all observations.
 |
Fig. 10 Examples of light curves and their corresponding deceleration curves for meteors that were impossible to model. Deceleration curves are indicated on the left side and light curves on the right side. The best achieved fit is shown. The average F number of appropriate light curves are shown. |
5 Morphology
It is believed that wakes are formed by eroded grains from the meteoroid body (Campbell-Brown et al. 2013). Smaller grains are decelerated more than grains of larger sizes. The larger the difference between largest and smallest grains, the longer the wake should be.
We investigated all meteor videos and we tried to evaluate meteor shapes, lengths, and visibility of wakes. The brightness of the wake was determined by the operator as the brightness relative to the meteor head. We marked meteors with
no wakes
short or faint wakes
bright or long wakes
The resolution of our system is ≈ 200 m∕px at the 100 km distance. Small faint wakes were usually 3–15 px long, corresponding length is ≈ 600 m–3 km, assuming perpendicular flight and 100 km distance. Bright long wakes were usually 15–100 px long, corresponding length is ≈3–20 km.
We did not observe any dependence of wake appearance on the ratio of largest to smallest grains. This confirms the conclusion of Campbell-Brown et al. (2013) that the erosion model we used does not predict meteor wakes correctly for all cases.
We compared these “wake” groups with spectral classification of given meteors (Fig. 11). For the normal spectral class, meteors with no wake (38% of all normal meteors) and short wake prevail (46%), but meteors with long and bright wakes are not negligible (16%). On the other hand, there is only one case with bright wake for Na-poor class and no bright wake for Na-free case. Meteors with no wake or short wake are present in similar amount (48%: 48% for Na-poor and 45%: 55% for Na-free). The iron meteors with no wake prevail among this spectral class (67% meteors with no wake). Other spectral classes contain onlya small number of meteors.
Several meteors showed endings with elongated ends and with similar brightnesses along their whole length. This is typical for Draconids (Borovička et al. 2007). We observed this phenomenon for three sporadic meteors and for five (out of seven) Draconid meteors.
We compared parameters of these three meteors obtained from the fragmentation model with the parameters of all Draconid meteors. Some of these parameters are listed in Table 2. We can notice that most of the parameters of the three sporadic meteors are very similar. On the other hand, both the bulk density and erosion coefficient varied. We obtained high densities for meteors 06730083 (1700 kg m−3) and 08728233 (1100 kg m−3). The bulk density of 450 kg m−3 for meteoroid 08728233 is lower and more similar to Draconid meteoroids. We have to be aware of the uncertainty for bulk density (at least a factor of two), since we did not observe the three sporadic meteors before the fragmentation started. Theother parameters of the three sporadic meteors were similar to Draconid meteoroids, even though the parameters of individual Draconid meteoroids varied a little bit. For more details about Draconids, see Borovička et al. (2014).
 |
Fig. 11 Fraction of three different wake types for different spectral classes. |
Fragmentation model parameters for meteors with elongated ending, compared to results of Draconid meteors.
6 Combining spectral analysis and results of fragmentation modelling
6.1 Monochromatic light curves and differential ablation
The monochromatic light curves of three meteoric lines of Mg I, Na I, and Fe I were constructed in order to study differential ablation. Vondrak et al. (2008) developed a chemical ablation model and concluded that Na and K is released ≈ 10 − 15 km higher than other (less volatile) major elements (Si, Fe, and Mg) in very small meteoroids. Janches et al. (2009) observed the micrometeoroid differential ablation using a radar observation.
We studied the height where half of the individual element was radiated out. This quantity was computed by integrating the monochromatic light curve along the trajectory. The height where the integral reaches half of its total value is the height where half of the element was radiated out. The difference between heights where half of the sodium and magnesium is radiated is shown in Fig. 12. When the sodium was released earlier, the value of the difference was positive. We excluded the Na-free and iron meteoroids and meteors with only atmospheric lines in their spectra from the figure.
The dependence of the difference between these heights for Na and Mg on grain sizes was discovered. As shown in Fig. 12, the smaller the grains, the earlier is Na released in comparison with Mg. The Pearson correlation coefficients are evaluated for the normal and Na-poor class. The correlation of normal class is rN = − 0.48 and for the Na-poor class this correlation is rP = − 0.52. These values are close to the limit between strong and medium correlation, which is considered to be − 0.5.
Moreover, Na-poor meteoroids tend to release their sodium earlier in comparison with normal meteoroids. Of 21 meteors classified as Na-poor, 11 were successfully modelled. We show the monochromatic light curves of these 11 modelled meteors in Fig. 13. These are sorted according to the value of the lower grain mass limit from lowest to highest. The sodium light curve for Na-poor meteors usually does not start earlier than the magnesium line, but the sodium can end earlier than the magnesium. The brightening of Na and Mg at the beginning suggests that the release rate for sodium and magnesium is more or less the same, but since there is less sodium in the meteoroid, this element simply “runs out”.
 |
Fig. 12 Difference of heights where half of the mass of sodium and magnesium was lost as a function of lower mass limit of grains. Fits for the normal class (purple line) and for the Na-poor class (green line) are shown. Correlations for normal (rN) and Na-poor(rP) classes are shown. |
 |
Fig. 13 Monochromatic light curves of Na-poor modelled meteors. The panels are sorted according to the lower grain mass limit, from the lowest (SX1738) to the highest (SX2133) value. The lower grain mass limit in grams is shown in each figure. |
6.2 Second stage of fragmentation
Several meteoroids show two stages of fragmentation detected as primary and secondary brightening in the light curve. The erosion model was applied only to a fraction of the initial mass. The rest of the body was unaffected (it only ablated) until some point, where it started to fragment in the second stage.
A total of 15 meteors showed two stages of fragmentation. Their white light light curves and monochromatic light curves can be seen in Fig. 14. Parameters for both stages, as a result of the modelling, are shown in Table 3.
We classify nine meteors as shower meteors, of which four are Draconids. Since there are a total of seven Draconids in this work, it seems that two stages of fragmentation are typical for this shower. Moreover, all three Taurid meteors show two stages of fragmentation. One Lyrid meteor and one Geminid meteor remain. Of all 121 sporadic meteors, only 6 required second-stage erosion modelling.
The orbits are cometary or Sun-approaching. Of the six members of the Jupiter family, four meteors are Draconids. Most of the meteors with two stages of fragmentation are classified as normal. There are two (SX1041, SX2133) meteors classified as Na-poor, both of which are sporadic. Other spectral classes do not show two stages of fragmentation.
As can be seen in Table 3, the ablation coefficient σ is the same for both stages of fragmentation in all meteors except for the Geminid meteor 06C13136 (SX336). On the other hand, the erosion coefficient η is usually different. According to Fig. 14, the brightening during the second stage is caused sometimes by the brightening of only one line (e.g. the Mg line in SX2133) and sometimes by multiple lines at once (e.g. SX804, SXDRA06). If the brightening in the second stage is caused by magnesium, the erosion coefficient η is smaller in the second stage. If the brightening in the second stage is caused by sodium, the erosion coefficient η is usually similar or larger in the second stage. If the monochromatic light curve is more complicated, the erosion coefficient η usually stays similar.
The amount of mass that is subjected to the second fragmentation varies among individual meteoroids from only 10% ofthe initial mass up to 70% of the initial mass. The masses and sizes of grains vary widely. The grain masses in the second stage of erosion are between six orders of magnitude larger and four orders of magnitude smaller than in the first erosion. But for most meteoroids, the difference is within two orders of magnitude. The second-stage fragmentation of Draconids contains one of the smallest grains we encountered (~ 10 μm).
 |
Fig. 14 Meteors with two stages of erosion. Light curves in white light and monochromatic light curves of Na, Mg, and Fe are shown. The scale for intensity for white light is in absolute magnitudes. For monochromatic light curves, the intensity is in arbitrary units (linear scale). |
Results of the fragmentation model for cases with two stages of erosion.
6.3 SX336 Geminid meteor
The Geminid meteor SX336 is a special case. As all Geminids, this meteor is Sun-approaching. The spectrum is classified as normal. It isone of two meteoroids with a Sun-approaching orbit that is not classified as Na-poor or Na-free; the other meteor is classified as iron. Although the relatively large lower mass grain limit predicts later release of sodium, this meteor differs a lot from the dependence in Fig. 12. According to Fig. 14, magnesium and iron lines show two maxima, while sodium shows only one maximum at the end of the light curve. The slope of the sodium light curve is more or less constant until the maximum. It only increases a little bit after the start of the second stage of fragmentation.
The erosion started at an altitude of 104 km and ended at an altitude of 87 km. The energy to start the erosion was 1.2 × 106 J m−2. As shown inTable 3, the number of grains in the first stage was two orders of magnitude higher than in the second stage. There were only large (millimetre sizes) grains released during the second stage. The ablation coefficient σ was five times larger for the second stage, i.e. the ablation was faster in the second stage. On the contrary, the erosion coefficient η was one order of magnitude larger for the first stage. In other words, the erosion in the form of larger grains was slower in the second stage. In the first stage, about 1.5 × 103 grains were released, and in the second stage, only 19 grains were released.
The Geminids are well known for variations of the amount of sodium in their spectra (Borovička 2010). Čapek & Borovička (2009) suggested that the porosity and the grain sizes play a key role in the rate of this depletion in interplanetary space. Meteoroids with smaller grains deplete sodium faster during their passages around the Sun.
The SX336 meteoroid contained large grains both in the first and in the second stage of erosion. In the first stage there were also smaller grains, but in the second stage of erosion there were only large grains (more than 1 mm in size).
The different parts contained different relative amounts of sodium and magnesium. The part with smaller grains fragmented first. Thanks to faster depletion of sodium on the orbit for smaller grains, there was less sodium than expected for chondritic composition and we observed brighter magnesium line and weak sodium line. The material in the second stage of erosion was different. Thanks to larger grains, the depletion of the sodium was much slower or did not take place at all. The relative intensity of the sodium line corresponded to the chondritic composition during the secondary fragmentation. Owing to different amounts of sodium depletion for these two different parts of the meteoroid, we could observe much later release of sodium than was typical for the given lower mass grain limit.
6.4 Sun-approaching meteoroids
Since Čapek & Borovička (2009) predicted sodium depletion in connection with grain sizes, we compared our observed results with their theoretical work. According to Table 4, the bulk density δ is relatively high for Sun-approaching meteoroids, thus the porosity is not high. The energy necessary to start the erosion Es is from 1 × 106 to 1 × 107 J m−2 and is generally higher for meteors with lower perihelia. According to the work of Čapek & Borovička (2009), the sizes of grains for Geminids are supposed to be in the size range ≈ 100–400 μm. Three of four modelled Geminids have grain sizes in the range ≈ 60–270 μm. Only the SX336 meteoroid has grain sizes in the range of ≈ 200–2300 μm. According to the results of Čapek & Borovička (2009), the smaller the grains and the smaller the perihelion is q, the more likely that the meteoroids lose sodium. We included the values of perihelion distance and grain sizes in the Table 4. These values are visualised in Fig. 15. It is clear that among the Sun-approaching class most of the Na-free meteoroids contain small grains and have low perihelia. Na-poor meteoroids contain slightly larger grains or their perihelia are larger for the given grain size. The meteoroid with the largest grains is the SX336 Geminid, which is classified as normal. These trends are expected. In general (compared to other meteoroids) the Sun-approaching orbital class contains relatively larger grains. Still these grains are small enough for the sodium depletion to take place.
Parameters for the Sun – approaching members sorted according to the perihelion.
 |
Fig. 15 Perihelion and the smallest grain sizes for all Sun-approaching meteoroids. Every colour represents a different spectral class. |
7 Discussion
We reduced, measured, and analysed 152 sporadic and shower meteors. They were observed from (at least) two stations using video observations, both in white light and using a spectral grating. Reduced meteor spectra were classified according to spectral classification of faint meteors (Borovička et al. 2005). Meteors were also classified according to their orbits. Moreover, the morphology of the meteors was studied. To study atmospheric fragmentation of meteoroids, we used the fragmentation model developed by Borovička et al. (2007).
7.1 Spectral classification and orbits
Our data confirmed the existence of spectral classes defined by Borovička et al. (2005) and their associations with orbital classes (Fig. 1). We found two spectra containing only atmospheric lines. Atmospheric lines are the strongest lines in fast meteors and meteoric lines were probably below the detection limit in these cases. The surprise of the spectral classification was one sodium-enhanced meteor with very high velocity (Fig. 2).
Another surprising result was the occurrence of two iron meteoroids on Halley-type orbits. Although there are asteroids on Halley-type orbits called Damocloids, they are believed to be dormant cometary nuclei and their composition is probably the same as comets on Halley-type orbits. We compared the two iron meteor orbits with the latest list of Damocloids and found no association according to the Southworth–Hawkins D-criterion (Southworth & Hawkins 1963). For meteoroids originated in the asteroid belt it is unlikely to change their orbits to Halley-type orbit. Jupiter can greatly increase the eccentricity of meteoroids, but this process cannot increase the inclination above ≈ 40°. Both iron meteoroids showed inclinations over 60°.
The material might have originated in the young solar system when some planetesimals formed very quickly and this fast process allowed them to differentiate. Some of these planetesimals might be transported to the Oort cloud by the then-migrating Jupiter. According to the Grand Tack model (Walsh et al. 2011) Jupiter migrated up to within 1.5 AU of the Sun and subsequently migrated outwards. This migration was potentially responsible for the transportation of some planetesimals into the Oort cloud. There had to be collisions that allowed the escape of the differentiated iron material as meteoroids. Thus, the Grand Tack is one possible scenario that might be responsible for a small number of iron meteoroids on Halley-type orbits (Dr. Nesvorný, priv. comm.).
The Stardust mission discovery of calcium–aluminium-rich inclusions (CAIs) and other high-temperature materials that are closely analogous to meteoritic components in the comet 81P/Wild 2 (Brownlee et al. 2012) was a surprise. Brownlee et al. (2012) suggested that this inner solar system material was probably transported beyond the orbit of Neptune, where they accreted along with ice and organic components to form comet Wild 2. Their best data came from a restricted set of solid materials. The studied components that were sufficiently strong that they did not fragment during capture in aerogel were from 2 μm to a few 10 μm in diameter. Larger components were rare. Our iron meteoroids were of millimetre size in diameter and although the comet Wild 2 is on Jupiter-family-type orbit, we think that even the Halley-type comets can contain differentiated solid inclusions. Nevertheless, the origin of iron meteoroids on Halley-type orbits might also be different. Further investigation is needed.
In the study of Kikwaya et al. (2011) a meteoroid with one of the highest densities (σ = 4495 ± 600 kg m−3) showed a high inclination of 150° and the orbit was reminiscent of Halley-type comets, although it was classified as Sun-approaching. They concluded that it was probably an iron-rich inclusion from a Halley-type comet, or it was a thermally processed meteoroid that has lost its volatiles and has been sintered.
7.2 Meteor wakes
Our data agree with the finding of Fisher et al. (2000) that significant wakes are absent in many faint sporadic meteors. Their theoretical work suggested that detection of wakes would be favoured in slow cometary meteors. In our sample, meteoroids of cometary origin (Halley, Jupiter family, ecliptic) with velocity less than 30 km s−1 make up 41% of all meteors with faint wakes and they make up 52% of all meteors with bright wakes. Fast cometary meteoroids (v ≥ 50 km s−1) make up 42% of all meteors without wakes.
Subasinghe et al. (2016), on the other hand, found that most cometary and asteroidal meteoroids fragmented with long distinct trails (more than 80%). The low resolution of our video did not allow us to study meteor wakes in detail and could underestimate the number of meteors with wakes. But the amount of meteors without wakes in our sample is substantial. Only Draconids and three sporadic meteors showed elongated endings.
The model can give us brightness profiles of individual meteors. We compared these profiles with the wake classification. In some cases, there was a disagreement with observation. This fact strengthens the conclusion of Campbell-Brown et al. (2013) that the erosion model we used is not accurate in the simulation of wakes. Future work on the formation of wakes will be needed.
Analyses of spectral classes and wake classes showed that spectral classes that usually do not contain very small grains (Na-poor, Na-free) usually have no or only small wakes. This is in agreement with the general assumption that smaller grains are more dragged and decelerated than larger grains and thus the larger difference in grain sizes causes longer wakes.
7.3 Spectral classification and physical parameters
The energy necessary for the start of erosion, Es, is a robust parameter of the modelling. It was highest for the iron class (up to Es ≈ 4 × 107 J m−2). Members of the iron, Na-poor, and Na-free classes showed the highest energies Es. The meteoroid with the lowest value of Es was a member of the Fe-poor class with Es ≈ 1 × 105 J m−2.
Only two Fe-poor meteors were modelled. Their material was fragile, with rather small grains. The meteoroid SZ2428 was one of the most porous in our work. We did not observe much difference for ablation of sodium and magnesium for Fe-poor meteoroids.
The sodium-depleted material showed rather low values of porosity. We did not observe much difference in physical properties of sodium-depleted meteoroids, whether they were on Sun-approaching orbits or on cometary orbits. The erosion and the ablation coefficients tend to be low – the rate of erosion and ablation is slower for given grain sizes for sodium-depleted meteoroids than for other meteoroids. The Na-poor and Na-free meteors usually do not contain very small grains with one exception, the meteoroid 12421069 (SX1738) contained one of the smallest grains in our study. Na-poor meteoroids tend to release sodium earlier for a given grain size. During the flight in the atmosphere, sodium is released at the same rate as magnesium, but the smaller amount of sodium “runs out” at some point of the flight (Fig. 13). All these results for Na-poor (and Na-free) meteoroids lead to the conclusion that these classes have a different structure compared to the normal chondritic class. Figure 16 shows a schematic idea of these differences. They do not contain grains larger than the other classes; in fact, some Normal meteoroids contained larger grains than any other Na-poor member. But unlike other classes, they usually do not contain very small grains. The smallest grains were probably depleted during close approaches to the Sun or by exposure to cosmic rays. The Na-poor and Na-free classes do not form long wakes; this is probably because they contain fewer grains.
Iron meteors have recently been studied by Campbell-Brown (2015) and Čapek & Borovička (2017). Čapek & Borovička (2017) and Girin (2017) suggested that ablation is in the form of droplets released from a liquid layer at the surface of the body. So the grains in our model can be in fact iron droplets in this case.
Na-enhanced and Na-rich meteors were mostly slow and more massive than average meteoroids, and have larger grains and porous material. But the only Na-enhanced meteoroid on a Halley-type orbit had lower mass and smaller grains. It was also the most porous meteoroid among Na-enhanced and Na-rich meteoroids. We did not observe much difference in the ablation of sodium and magnesium for Na-rich and Na-enhanced meteoroids.
Most meteoroids in our work were classified as normal. They showed normal chondritic composition, often with somewhat fainter Fe lines. They had a mixture of asteroidal and cometary orbits and had a dominance of cometary orbits. Most of the normal meteoroids had higher porosities (above ≈ 0.7). We observed a wide range of differences for the release of sodium and magnesium. Except for showers with low perihelia, most of the shower meteoroids were of normal spectral class.
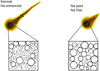 |
Fig. 16 Schematic representation of the difference between Na-poor and Na-free classes, inner structure, compared to the normal and Na-enhanced classes. |
7.4 Two stages of the erosion and the implication to line intensites
The two stages of erosion of small meteoroids helped us to learn more about the structure and composition of meteoroids and to better understand the processes of the erosion and the evaporation of meteoroids during the flight in the atmosphere.
Ten percent of meteors showed two stages of erosion. The shower meteors showed higher percentage of cases with a second stage of erosion. The orbital classification showed that meteoroids on cometary orbits are more prone to two stages of erosion. There were no meteoroids on asteroidal orbits with two stages of erosion. This suggests why we observed the discrepancy between sporadic and shower meteors, since most of the meteor showers have cometary origin.
The GIADA instrument on the Rosetta mission collected 300 particles and found two families of these particles (Fulle et al. 2015): compact particles with sizes ranging from 0.03 to 1 mm and fluffy aggregates (from 0.2 to 2.5 mm). We can expect that these materials can be mixed together in some meteoroids of cometary origin. The model of Mukai & Fechtig (1983) proposed that material increased its bulk density owing to solar heating. If this process can affect only part of the small Sun-approaching meteoroid (owing to the short exposure time), it needs to be proved further. The asteroidal millimetre-sized meteoroids, on the other hand, seem to be more uniform.
The comparison of the parameters in both stages of erosion showed that if we observe two stages of erosion, it is probably a consequence of two different structures of the same material within one meteoroid. The same ablation coefficient in both erosion stages shows that the ability of the material to ablate is the same, even though the grain sizes were different in these stages. Thus, we think that the type of material was the same or very similar. On the other hand, the differences in the erosion coefficients (and thus the ability to erode) and the differences in grain sizes between two stages of erosion suggest that the structure of the same material can be different within one meteoroid.
We observed that if the brightening in the second stage of the erosion was caused by sodium, the grains in the second stage were in general smaller and the rate of erosion was higher or similar, compared to the first stage. If the brightening was caused by magnesium in the second stage, the grains were larger and the rate of erosion was lower. We can imagine that smaller grains with a higher ratio of surface to volume help the more volatile sodium to evaporate faster from the grain compared to the magnesium. In the case of larger grains, the evaporation of the sodium is slower and thus the spectral line is less pronounced. This is in an agreement with the results in Sect. 6.1 (see Fig. 12).
This encourages us to conclude that the shape of monochromatic light curves depends not only on the chemical composition of the material, but also on the structure of the material itself.
7.5 Meteoroid densities
Kikwaya et al. (2011) studied densities of millimetre-sized meteoroids. They obtained densities for different orbital classes. The most significant results they found is high densities for Jupiter-family meteoroids. The average density was δ = 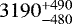 kg m−3, suggesting ordinary chondritic composition with low porosity. Their average density for meteoroids on Halley-type orbits was much lower, δ =
kg m−3, suggesting ordinary chondritic composition with low porosity. Their average density for meteoroids on Halley-type orbits was much lower, δ = 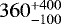 kg m−3. Our results were different. We assumed the grain density to be the same for all non-iron meteors: δ = 3000 kg m−3 and thus our highest possible density for non-irons was still lower than the average density for meteoroids on Jupiter-family meteors observed by Kikwaya et al. (2011). In our sample, the average value of density for meteoroids on Jupiter-family orbits was δ = 850 ± 110 kg m−3 (median δM = 695 kg m−3). The range of values was from 99 to 2100 kg m−3. Our lower value is more in agreement with the concept of low density cometary material. We admit that the densities derived by our modelling are questionable for cases when the ablation was not observed before erosion (uncertaintyat least by factor of two). We observed ablation before erosion only for 12 meteoroids, of which 3 of were on Jupiter-family orbits and we can be more sure about their density. The sporadic meteor 14505037 showed density δ = 800 kg m−3; the Draconids had very low densities: DRA03 δ = 99 kg m−3, DRA06 δ = 390 kg m−3. These low densities are expected for Draconids, and the density of the meteor 14505037 is close to the average density for Jupiter-family members. Thus, we think that high average density for meteoroids of Jupiter-family orbits is unlikely. But since the Stardust mission found μm sized CAIs and other high-temperature materials similar to meteoritic components in debris from Jupiter-family comet 81P/Wild (Brownlee et al. 2012), individual high-density meteoroids of cometary origin are possible.
kg m−3. Our results were different. We assumed the grain density to be the same for all non-iron meteors: δ = 3000 kg m−3 and thus our highest possible density for non-irons was still lower than the average density for meteoroids on Jupiter-family meteors observed by Kikwaya et al. (2011). In our sample, the average value of density for meteoroids on Jupiter-family orbits was δ = 850 ± 110 kg m−3 (median δM = 695 kg m−3). The range of values was from 99 to 2100 kg m−3. Our lower value is more in agreement with the concept of low density cometary material. We admit that the densities derived by our modelling are questionable for cases when the ablation was not observed before erosion (uncertaintyat least by factor of two). We observed ablation before erosion only for 12 meteoroids, of which 3 of were on Jupiter-family orbits and we can be more sure about their density. The sporadic meteor 14505037 showed density δ = 800 kg m−3; the Draconids had very low densities: DRA03 δ = 99 kg m−3, DRA06 δ = 390 kg m−3. These low densities are expected for Draconids, and the density of the meteor 14505037 is close to the average density for Jupiter-family members. Thus, we think that high average density for meteoroids of Jupiter-family orbits is unlikely. But since the Stardust mission found μm sized CAIs and other high-temperature materials similar to meteoritic components in debris from Jupiter-family comet 81P/Wild (Brownlee et al. 2012), individual high-density meteoroids of cometary origin are possible.
To estimate robustness of output model parameters, we varied the expected grain density δg of three meteors (07407021, 08927015, 12815056) in the range from 2500 to 5000 kg m−3 with the 500 kg m−3 step. During these variations the energy necessary to start the erosion Es did not change. The ablation coefficient σ and the bulk density δ changed within the factor of 2. Grain numbers and masses varied more. The grain lower mass limit changed up to one order for some cases.
7.6 Differential ablation
The shapes of monochromatic light curves of Na, Mg, and Fe varied for individual meteors. Both the early and late release of sodium was observed. The difference in the ablation for sodium and magnesium depended on the sizes of grains of meteoroids. The early release of sodium was typical for meteoroids that contained small grains. This is in agreement with the concept of differential ablation. Small grains are heated thoroughly and sodium can escape from their whole volume earlier than major elements are ablated. Early release of sodium and small grains were more typical for Halley-type meteors. The Jupiter-family members did not contain grains as small as Halley-type meteoroids.
However, small grains also mean easier loss of sodium in interplanetary space in case that meteoroid orbit approaches the Sun. We clearly observed higher sodium depletion for meteoroids with low perihelia and small grains. The same effect was responsible for the behaviour of the Geminid meteor SX336. Smaller grains in the first stage of fragmentation contained a small amount of sodium. During the second stage of fragmentation, only large grains with a higher amount of sodium were released.
8 Conclusions
Our study of small meteoroids combined the results of fragmentation modelling with spectral observations of a large quantity of diverse meteoroids. We found that the size of the grains of meteoroids can affect the release of sodium from the body during the flight in the atmosphere as well as during close approaches to the Sun. Meteoroids with small grains tend to release sodium earlier. We also found that the Na-poor class tends to release their sodium earlier in the upper part of the trajectory. We compared size distribution of modelled grains in meteoroids on Jupiter-family orbits with the new results of the ROSETTA study of the Comet 67/P Churyumov-Gerasimenko and found good agreement. Finally, we found evidence of iron meteoroids on Halley-type orbits. This may be proof of the complicated evolution of the early solar system. We are aware that even though the model we used was usually in agreement with other models and results of other works as well as with studies of cometary material from spacecraft missions, it does not work well in some areas (e.g. simulation of meteor wakes). The population of millimetre-sized meteoroids is heterogeneous and future models should be more complex to reflex this variety. Meteor morphology observed by high-resolution narrow field cameras will be crucial for testing the models.
Acknowledgements
We would like to thank Margaret Campbell-Brown and Juraj Tóth for their valuable comments to the Ph.D. thesis of the first author, which was the basis of this work. The language correction made by Margaret Campbell-Brown really improved the style of this work. We would like to thank referee Jeremie Vaubaillon for his valuable comments that improved this work. We would like to thank to David Nesvorný for his idea of the iron on Halley orbit scenario. We would also like to thank Jan Mánek for the operation of the station Barrandov. This work was supported by the grant 16-00761S of the Grant Agency of the Czech Republic, GA ČR.
Appendix A Orbital elements of meteoroids
Orbital elements of meteoroids.
References
- Bloxam, K., & Campbell-Brown, M. 2017, Planet. Space Sci., 143, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J. 1990, Bull. Astr. Inst. Czechosl., 41, 391 [NASA ADS] [Google Scholar]
- Borovička J. 2010, in 26th IMC Proceedings of the International Meteor Conference, Bareges, France, 2007, eds. J. Rendtel & J. Vaubaillon (Hove, Belgium: International Meteor Organization), 42 [Google Scholar]
- Borovička, J., & Jenniskens, P. 2000, Earth Moon Planets, 82, 399 [NASA ADS] [Google Scholar]
- Borovicka, J., Stork, R., & Bocek, J. 1999, Meteor. Planet. Sci., 34, 987 [Google Scholar]
- Borovička, J., Koten, P., Spurný, P., Boček, J., & Štork, R. 2005, Icarus, 174, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J., Spurný, P., & Koten, P. 2007, A&A, 473, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borovička, J., Koten, P., Spurný, P., & Štork R. 2008, Earth Moon Planets, 102, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J., Koten, P., Shrbený, L., Štork, R., & Hornoch, K. 2014, Earth Moon Planets, 113, 15 [Google Scholar]
- Brownlee, D., Joswiak, D., & Matrajt, G. 2012, Meteor. Planet. Sci., 47, 453 [Google Scholar]
- Campbell-Brown, M. 2015, Planet. Space Sci., 118, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 418, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Campbell-Brown, M. D., Borovička, J., Brown, P. G., & Stokan, E. 2013, A&A, 557, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Čapek, D., & Borovička J. 2009, Icarus, 202, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Borovička J. 2017, Planet. Space Sci., 143, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z. 1988, Bull. Astr. Inst. Czechosl., 39, 221 [NASA ADS] [Google Scholar]
- Ceplecha, Z., Borovička, J., Elford, W. G., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, A. A., Hawkes, R. L., Murray, I. S., Campbell, M. D., & LeBlanc, A. G. 2000, Planet. Space Sci., 48, 911 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming,D. E. B., Hawkes, R. L., & Jones, J. 1993, in Meteoroids and Their Parent Bodies, eds. J. Stohl & I. P. Williams (Bratislava: Astronomical Institute Slovak Academy of Sciences), 261 [Google Scholar]
- Fulle, M., Della Corte, V., Rotundi, A., et al. 2015, ApJ, 802, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Girin, O. G. 2017, A&A, 606, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hornung, K., Merouane, S., Hilchenbach, M., et al. 2016, Planet. Space Sci., 133, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Janches, D., Dyrud, L. P., Broadley, S. L., & Plane, J. M. C. 2009, Geophys. Res. Lett., 36, L06101 [NASA ADS] [CrossRef] [Google Scholar]
- Kikwaya, J.-B., Campbell-Brown, M., & Brown, P. G. 2011, A&A, 530, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koten, P., Fliegel, K., Vítek, S., & Páta, P. 2011, Earth Moon Planets, 108, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Matlovič, P., Tóth, J., Rudawska, R., & Kornoš L. 2017, Planet. Space Sci., 143, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Molau, S. 1999, in 17th IMC Proceedings of the International Meteor Conference, Stara Lesna, Slovakia, 1998 [Google Scholar]
- Mukai, T., & Fechtig, H. 1983, Planet. Space Sci., 31, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, I. S., Hawkes, R. L., & Jenniskens, P. 1999, Meteor. Planet. Sci., 34, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Pecina, P., & Ceplecha, Z. 1983, Bull. Astr. Inst. Czechosl., 34, 102 [NASA ADS] [Google Scholar]
- Picone, J. M., Hedin, A. E., Drob, D. P., & Aikin, A. C. 2002, J. Geophys. Res., 107, 1468 [Google Scholar]
- Southworth, R. B., & Hawkins, G. S. 1963, Smithsonian Contrib. Astrophys., 7, 261 [Google Scholar]
- Subasinghe, D., Campbell-Brown, M. D., & Stokan, E. 2016, MNRAS, 457, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Vojáček, V., Borovička, J., Koten, P., Spurný, P., & Štork R. 2015, A&A, 580, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vondrak, T., Plane, J. M. C., Broadley, S., & Janches, D. 2008, Atmos. Chem. Phys., 8, 7015 [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Fragmentation model parameters for meteors with elongated ending, compared to results of Draconid meteors.
All Figures
 |
Fig. 1 Classification of meteor spectra in ternary graph. Every spectral group is represented with a different symbol. The black line shows the theoretical position of meteors with normal chondritic composition and was taken from the work of Borovička et al. (2005). The position depends on the speed of the meteor. The speed in km s−1 is indicated with numbers above the line. |
| In the text | |
 |
Fig. 2 Na/Mg line intensity ratio as a function of the meteor speed. Iron- and Na-free meteors were excluded owing to the high uncertainty in the determination of the Na and Mg line intensities for their spectral classes. Meteors classified as normal were fitted. The fit was divided into three segments. |
| In the text | |
 |
Fig. 3 Beginning height as dependence of the velocity. Different classes are indicated with different symbols. Meteors with beginning out of field of view are indicated with black squares. Uncertainties for beginning heights and velocities were negligible for display in the graph. |
| In the text | |
 |
Fig. 4 Perihelion and aphelion of measured meteoroids. If possible, regions of given orbital classes are indicated in colour. For precise definition of orbital classes, see Sect. 3.3. The horizontal line at 5 AU represents aphelion at Jupiter orbit. |
| In the text | |
 |
Fig. 5 Inclination and Tisserand parameter of measuerd meteoroids. If possible, regions of given orbital classes are represented in colour. For precise definition of orbital classes see Sect. 3.3. |
| In the text | |
 |
Fig. 6 Examples of different shapes of light curves and their corresponding deceleration curves for four meteors. Light curves are represented on the left; deceleration curves on the right. Only data used for model are shown. |
| In the text | |
 |
Fig. 7 Porosity p as a function of the energy necessary to start the fragmentation. Upper panel: different spectral classes are indicated with different colours. Lower panel: different orbital classes are indicated with different colours. A–C stands for the asteroidal–chondritic class. |
| In the text | |
 |
Fig. 8 Histograms of grain sizes of different spectral classes. The power-law fits are shown for all classes except for the Na-enhanced class. |
| In the text | |
 |
Fig. 9 Histograms of grain sizes of different orbital classes. The power-law fits are shown. The power-law fit of grain sizes captured by ROSETTA with index − 3.3 taken from Hornung et al. (2016) is shown in the Jupiter-family histogram. |
| In the text | |
 |
Fig. 10 Examples of light curves and their corresponding deceleration curves for meteors that were impossible to model. Deceleration curves are indicated on the left side and light curves on the right side. The best achieved fit is shown. The average F number of appropriate light curves are shown. |
| In the text | |
 |
Fig. 11 Fraction of three different wake types for different spectral classes. |
| In the text | |
 |
Fig. 12 Difference of heights where half of the mass of sodium and magnesium was lost as a function of lower mass limit of grains. Fits for the normal class (purple line) and for the Na-poor class (green line) are shown. Correlations for normal (rN) and Na-poor(rP) classes are shown. |
| In the text | |
 |
Fig. 13 Monochromatic light curves of Na-poor modelled meteors. The panels are sorted according to the lower grain mass limit, from the lowest (SX1738) to the highest (SX2133) value. The lower grain mass limit in grams is shown in each figure. |
| In the text | |
 |
Fig. 14 Meteors with two stages of erosion. Light curves in white light and monochromatic light curves of Na, Mg, and Fe are shown. The scale for intensity for white light is in absolute magnitudes. For monochromatic light curves, the intensity is in arbitrary units (linear scale). |
| In the text | |
 |
Fig. 15 Perihelion and the smallest grain sizes for all Sun-approaching meteoroids. Every colour represents a different spectral class. |
| In the text | |
 |
Fig. 16 Schematic representation of the difference between Na-poor and Na-free classes, inner structure, compared to the normal and Na-enhanced classes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


