| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833038 | |
| Published online | 03 January 2019 | |
NuSTAR observations of heavily obscured Swift/BAT AGNs: Constraints on the Compton-thick AGNs fraction
IAASARS, National Observatory of Athens, I. Metaxa & V. Pavlou, 15236
Greece
e-mail: ig@noa.gr
Received:
16
March
2018
Accepted:
31
August
2018
The evolution of the accretion history of the Universe has been studied in unprecedented detail owing to recent X-ray surveys performed by Chandra and XMM-Newton. A focus on the most heavily obscured or Compton-thick active galactic nuclei (AGNs) is missing in these studies. These AGNs evade detection even in X-ray surveys owing to their extreme hydrogen column densities, which exceed 1024 cm−2. Recently, the all-sky hard X-ray survey performed by Swift/BAT brought a breakthrough, allowing the detection of many of these AGNs. This is because of the very high energy bandpass (14–195 keV) of this instrument, which helps to minimise attenuation effects. In our previous work, we identified more than 50 candidate Compton-thick AGNs in the local Universe, corresponding to an observed fraction of about 7% of the total AGNs population. This number can only be converted to the intrinsic Compton-thick AGNs number density if we know their exact selection function. This function sensitively depends on the form of the Compton-thick AGN spectrum, that is the energy of their absorption turnover, photon-index and its cut-off energy at high energies, and the strength of the reflection component on the matter surrounding the nucleus. For example, the reflection component at hard energies 20–40 keV antagonises the number density of missing Compton-thick AGNs in the sense that the stronger the reflection the easier these sources are detected in the BAT band. In order to constrain their number density, we analysed the spectra of 19 Compton-thick AGNs that have been detected with Swift/BAT and have been subsequently observed with NuSTAR in the 3–80 keV band. We analysed their X-ray spectra using the MYTORUS models which properly take into account the Compton scattering effects. These were combined with physically motivated Comptonisation models, which accurately describe the primary coronal X-ray emission. We derived absorbing column densities that are consistent with those derived by the previous Swift/BAT analyses. We estimate the coronal temperatures to be roughly between 25 and 80 keV corresponding to high energy cut-offs roughly between 75 and 250 keV. Furthermore, we find that the majority of our AGNs lack a strong reflection component in the 20–40 keV band placing tighter constraints on the intrinsic fraction of Compton-thick AGNs. Combining these results with our X-ray background synthesis models, we estimate a percentage of Compton-thick AGNs in the local Universe of ≈20 ± 3 % relative to the type-II AGNs population.
Key words: X-rays: general / X-rays: diffuse background / X-rays: galaxies / quasars: supermassive black holes
© ESO 2019
1. Introduction
The vast majority of galaxies contain a supermassive black hole in their centres (e.g. Ferrarese & Merritt 2000). A fraction of these emit copious amounts of radiation as in-falling matter forms an accretion disc around the black hole. These active galactic nuclei (AGNs) constitute at least half of the galaxy population (Ho et al. 1997a,b). The majority of AGNs are covered by veils of dust and gas (e.g. Ricci et al. 2017), which probably have a toroidal form (Wada et al. 2009). In most cases this obscuring screen can obliterate the optical emission and reradiate in the IR. X-rays can more easily penetrate these obscuring screens. However, in the most extreme obscuration even the X-ray radiation can be blocked. These Compton-thick AGNs have column densities that exceed 1024 cm−2. In this case, the X-rays are Compton scattered on the free electrons of the obscuring screen. As these heavily obscured AGNs represent the evasive side of the accretion history of the Universe, it is of primary importance to detect these objects. However, the methods employed to constrain their number appear to give diverging results.
The most commonly used method is that of X-ray background synthesis models. The spectrum of the X-ray background, that is the integrated X-ray light produced by all X-ray sources in the history of the Universe, presents a peak at 20–30 keV as measured by the HEAO-1, XMM-Newton, BeppoSAX, and the INTEGRAL missions (e.g. Gruber et al. 1999; Frontera et al. 2007; Churazov et al. 2007; Moretti et al. 2009). X-ray background synthesis models attempt to reconstruct the spectrum of the X-ray background using the AGN luminosity function, together with a model for the AGN X-ray spectrum. These models have been pioneered by Comastri et al. (1995) and were later refined by Gilli et al. (2007), Treister et al. (2009), Draper & Ballantyne (2009), Akylas et al. (2012), Vasudevan et al. (2013), Ueda et al. (2014), and Esposito & Walter (2016). A significant number of Compton-thick AGNs are necessary to reproduce the hump of the X-ray background. However, their fraction remains uncertain with figures ranging roughly between 10% and 50%. This discrepancy is attributed mainly to the fact that there is a degeneracy between the required fraction of Compton-thick AGNs and the strength of the total AGNs population reflection component. This reflection component originates from scattering and subsequent absorption of the X-ray radiation on surrounding cold material (e.g. George & Fabian 1991) and results in the flattening of the observed AGN spectrum. The higher the AGNs population reflection component the lower the number of Compton-thick AGNs are required. Interestingly enough, the reflection component strength does not refer to the Compton-thick AGNs but to the average reflection component of the total AGNs population.
Recently, attention has shifted to the direct detection of Compton-thick AGNs using X-ray spectroscopy. The sensitive observations performed with Chandra and XMM-Newton allowed the detection of many faint candidate Compton-thick AGNs in the 2–10 keV band, mainly in the Chandra Deep Field South area (e.g. Georgantopoulos et al. 2013; Brightman et al. 2014; Buchner et al. 2015), resulting in the derivation of the Compton-thick AGN luminosity function and its evolution. Additional studies have focussed on the ultra-hard band above 10 keV where the X-ray attenuation is less severe. The Neil Gehrels Swift, INTEGRAL, and NuSTAR missions, which operate in this band, readily provide this possibility. The burst alert telescope (BAT) hard X-ray instrument on board Neil Gehrels Swift is continuously performing an all-sky survey in the 14–195 keV band. As this instrument does not carry imaging X-ray optics it can probe flux limits of only a few times 10−12 erg cm−2 s−1. Ricci et al. (2015) and Akylas et al. (2016) analysed the X-ray spectra of 688 candidate AGNs in the 70-month BAT all-sky survey (Baumgartner et al. 2013). Fitting the X-ray spectra using Bayesian statistics, Akylas et al. (2016) found about 50 Compton-thick AGNs candidates in overall agreement with the results of Ricci et al. (2015). The observed fraction of Compton-thick AGNs amounts to about 7% of the total AGNs population. This number can be extrapolated to the intrinsic fraction of Compton-thick AGNs, only by knowing the exact X-ray spectrum of Compton-thick AGNs, i.e. their selection function. Akylas et al. (2016) found that the intrinsic fraction of Compton-thick AGNs in the local Universe is between 10% and 30%, assuming a reflection component that contributes between 0 and 5% to the total 2–10 keV flux. These estimates are in good agreement with the estimates of Ricci et al. (2015), Burlon et al. (2011), and Malizia et al. (2009). The advantage of the above direct methods is that only knowledge of the X-ray spectrum of Compton-thick AGNs is required instead of the average AGNs population.
In this paper, we present an X-ray spectral analysis of the Compton-thick AGNs in Akylas et al. (2016), which has publicly available NuSTAR spectra. The imaging X-ray optics of NuSTAR (Harrison et al. 2013) allow the derivation of excellent quality spectra. These are used to constrain with the highest accuracy yet, the fraction of Compton-thick AGNs in the local Universe. We adopt Ho = 75 km s−1 Mpc−1, ΩM = 0.3, and ΩΛ = 0.7 throughout the paper.
2. X-ray sample and data
2.1. Burst Alert Telescope
The Neil Gehrels Swift gamma-ray burst (GRB) observatory (Gehrels et al. 2004) was launched in November 2004 and has been continually observing the hard X-ray (14–195 keV) sky with the BAT instrument. The BAT is a large, coded-mask telescope optimised to detect transient GRBs and is designed with a very wide field of view of ∼60 × 100°. The observation strategy of Neil Gehrel Swift is to observe targets with the narrow field-of-view X-ray telescope (XRT), in the 0.3–10 keV band until a new GRB is discovered by BAT, at which time Neil Gehrel Swift automatically slews to the new GRB to follow up with the narrow field instruments until the X-ray afterglow is below the XRT detection limit. Baumgartner et al. (2013) presented the catalogue of sources detected in 70 months of observations with BAT. The BAT 70 month survey has detected 1171 hard X-ray sources down to a flux level of 10−11 erg cm−2 s−1. The majority of these sources are AGNs.
Akylas et al. (2016) have analysed the X-ray spectra of these sources employing Bayesian statistics. These authors considered 688 sources classified according to the NASA/IPAC Extragalactic Database in the following types: (i) 111 galaxies, (ii) 292 Seyfert I (Sy 1.0-1.5), (iii) 262 Seyfert II (Sy 1.7-2.0), and (iv) 23 sources of other types of AGNs. Radio-loud AGNs were excluded since their X-ray emission might be dominated by the jet component. Quasi Stellar Objects (QSOs) have been also excluded from the analysis since the fraction of highly absorbed sources within this population is negligible. These authors have combined the BAT with the XRT data (0.3–10 keV) at softer energies adopting a Bayesian approach to fit the data using Markov chains. This allowed us to consider all sources as potential Compton-thick candidates at a certain level of probability. Fifty-three sources present a non-zero probability of being Compton-thick corresponding to 40 effective Compton-thick sources. These represent 7% of the sample in excellent agreement with the figure reported in Ricci et al. (2015) and Burlon et al. (2011). Out of these, 38 sources have a probability of more than 70% being Compton-thick.
2.2. NuSTAR
The Nuclear Spectroscopic Telescope Array, NuSTAR, (Harrison et al. 2013) launched in June 2012, is the first orbiting X-ray observatory that focusses light at high energies (E > 10 keV). It consists of two co-aligned focal plane modules (FPMs), which are identical in design. Each FPM covers the same 12 × 12 arcmin portion of the sky and comprises four cadmium-zinc-telluride detectors. The NuSTAR array operates between 3 and 79 keV and provides an improvement of at least two orders of magnitude in sensitivity compared to previous hard X-ray orbiting observatories, E> 10 keV. This is because of its excellent spatial resolution, which is 58 arcsec half-power diameter. The energy resolution is 0.4 and 0.9 keV at 6 and 60 keV, respectively.
All the 38 candidate Compton-thick objects in Akylas et al. (2016) with a probability > 70% have either been observed or are scheduled for observation with NuSTAR. We analysed the 19 sources that are currently publicly available. The details of the NuSTAR observations for each object are given in Table 1. We extracted the spectra from each FPM using a circular aperture region of 30 arcsec radius corresponding to ∼50% NuSTAR encircled energy fraction (ECF). We processed the data with the NuSTAR Data Analysis Software (NUSTARDAS) v1.4.1within HEASOFT v6.15. The NUPIPELINE script was used to produce the calibrated and cleaned event files using standard filter flags. We extracted the spectra and response files using the NUPRODUCTS task.
NuSTAR observations.
3. X-ray spectral modelling
Recently, sophisticated spectral models have been developed that estimate the detailed spectra of Compton-thick AGNs, that is they take into account Compton scattering and reprocessing by Compton-thick material that surrounds the nucleus. These include the models of Brightman & Nandra (2011) and the models of Yaqoob & Murphy (2011). Both models employ Monte Carlo simulations to account for Compton scattering and the geometry of the obscuring screen. The models of Brightman & Nandra (2011) refer to both spherical coverage and a torus geometry. These estimate self-consistently the Compton scattering along the line of sight as well as the reflection from surrounding matter. Instead, the toroidal Compton-thick X-ray re-processor model, MYTORUS of Murphy & Yaqoob (2009) and Yaqoob & Murphy (2011), uses a torus geometry. The torus has a diameter that is characterised by the equatorial column density, NH, Z. The model assumes a configuration in which the global covering factor of the re-processor is 0.5, corresponding to a solid angle subtended by the torus of 2π. The Yaqoob & Murphy (2011) model employs three separate components: the line of sight component, Z, an absorbed reflected component along the line of sight, S90, and an unabsorbed reflected component S0. In our spectral fits, we chose to employ the spectral models of Yaqoob & Murphy (2011). This is because this model allows for free relative normalisations between the different components in contrast to the self-consistent models of Brightman & Nandra (2011). Then the Yaqoob & Murphy (2011) model can accommodate differences in the actual geometry and time delays between direct, scattered, and fluorescent line photons. We note that the reflected emission is modelled using the appropriate column density instead of being modelled using reflection on a slab of infinite column density, cf. the PEXRAV model Magdziarz & Zdziarski (1995). The full general geometrical set-up of this model can be visualised in Fig. 2 of Yaqoob (2012).
In detail, our modelling consists of the following components. a) An unabsorbed power law originates from scattered emission on Compton-thin material, usually referred as the “soft excess” in type-2 AGNs b) The direct zeroth order primary emission absorbed by the line-of-sight column NH, Z is denoted by the multiplicative model mytorus_Ezero. Following Yaqoob (2012), we used the physically motivated model COMPTT of Titarchuk (1994). This model estimates the scattering of soft accretion disc photons on a hot thermal corona with temperature kT and optical depth τ. According to this thermal Comptonisation model the resulting cut-off energy is ∼3kT. There is dependence between the optical depth and temperature of the corona in the sense that the higher the temperature of the corona the lower the value of τ. In the case where the optical depth cannot be constrained from the spectral fits, we chose to fix the value of the optical depth to τ = 2. This value corresponds roughly to a photon index of Γ ≈ 1.9 for a coronal temperature of kT ∼ 50 keV (the average value estimated in our spectral fits below) in the case of spherical geometry (Titarchuk 1994; Longair 2011). The mean photon-index value observed in AGNs is Γ = 1.9 (Nandra & Pounds 1994) and is also the best fit photon index found in our X-ray background synthesis models Akylas et al. (2012). c) A reflected absorbed component S90 with a column density NH, S90 is denoted by the model mytorus_scattered. d) A reflected unabsorbed component, S0, from a column density NH, S0 could possibly originate from the back-side of the torus. e) An FeKα, FeKβ, and ionised Fe lines at 6.4, 7.02 and 6.7 keV, respectively, is denoted by the model MYTL arising from the line of sight absorbed scattered radiation. f) The same lines as above are denoted again by the model MYTL arising from unabsorbed scattered radiation. We assume that all the above column densities have the same value. The normalisations of the two scattered components and of the zeroth order component are allowed to vary independently. In XSPEC notation, the model can be written as
The scattering models mytorus_scatteredkT and atablemytl correspond to a temperature kT of the corona obtaining discrete values between 16 and 100 keV. The use of these models requires an iterative process. More specifically, it is necessary to have a priori knowledge of the primary radiation spectrum and in particular of the cut-off to estimate the output reflection spectrum. In the MYTORUS models, this is a free parameter in the zeroth component spectrum but not in the reflection spectra. In the first run we give an initial cut-off energy of 50 keV as an input to estimate the reflection components S0 and S90. Then the exact cut-off energy is estimated from the fit to the zeroth order component. This value is fed back to the reflection components and the process is repeated. In the above process we leave the NuSTAR and BAT normalisations untied. We use the XSPEC v12.8 spectral fitting package (Arnaud et al. 1996). The appropriate Galactic absorption column density has been included in all fits. Owing to the high number of counts we employ the χ2 statistic. We bin the spectra, using the task GRPPHA so that they contain at least 20 counts per bin. All errors quoted refer to the 90% confidence level.
4. Results
The spectral fitting results are given in Table 2. In the following subsections we discuss separately our findings regarding the hydrogen column density, the high energy cut-off and the reflection fraction. Finally, we discuss the implications of our spectral modelling for the intrinsic number of Compton-thick AGNs
MYTORUS Spectral fits.
4.1. Absorbing column density
The distribution of the column densities is presented in Fig. 1. The column densities found by NuSTAR are in very good agreement with those previously found by Neil Gehrels Swift (Akylas et al. 2016). Akylas et al. (2016) found a much higher column density for only one source (NGC 7212). The current NuSTAR results confirm the lower column density reported by Ricci et al. (2015). This difference is most probably because the Neil Gehrels Swift/XRT data have limited photon statistics while Ricci et al. (2015) have combined the BAT data with XMM-Newton spectra obtaining better quality photon statistics at energies below 10 keV. Recently, Marchesi et al. (2018) published a NuSTAR analysis of Compton-thick AGNs from the Neil Gehrels Swift/BAT list of Ricci et al. (2015). Marchesi et al. (2018) found that a number of candidate Compton-thick AGNs in Ricci et al. (2015) may present lower column densities. There are 15 common objects between our sample and that of Marchesi et al. (2018). According to these authors four objects appear to have column densities somewhat lower than 1024 cm−2. These are NGC 1194, NGC 6232, NGC 1229, and 2MASSXJ09235371−3141305. According to our NuSTAR analysis, NGC 1194 is above the Compton-thick threshold while NGC 1229 and 2MASSXJ09235371−3141305 are consistent with being Compton-thick within the errors. In the case of NGC 1229, although the source is unambiguously heavily obscured (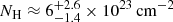 ) the column density derived lies well below the Compton-thick limit. For many other sources, for example NGC 1068, Circinus, NGC 424, NGC 3079, NGC 4945, and NGC 5643, NuSTAR spectral fits have been presented elsewhere (Bauer et al. 2015; Arévalo et al. 2014; Baloković et al. 2014; Puccetti et al. 2014, 2016; Koss et al. 2015; Annuar et al. 2015; Marchesi et al. 2018). In general, our results are consistent with the work cited above.
) the column density derived lies well below the Compton-thick limit. For many other sources, for example NGC 1068, Circinus, NGC 424, NGC 3079, NGC 4945, and NGC 5643, NuSTAR spectral fits have been presented elsewhere (Bauer et al. 2015; Arévalo et al. 2014; Baloković et al. 2014; Puccetti et al. 2014, 2016; Koss et al. 2015; Annuar et al. 2015; Marchesi et al. 2018). In general, our results are consistent with the work cited above.
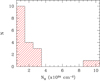 |
Fig. 1. Column density distribution for all 19 sources in our sample. |
As can be seen from Fig. 1, there is a clear tendency to detect mildly obscured Compton-thick AGNs with column densities a few times 1024cm−2. This has been first noticed by Burlon et al. (2011) who showed that the BAT instrument is unbiased only up to column densities of only 2 × 1024 cm−2. We observe only two heavily Compton-thick source with a column density around 1025 cm−2. Owing to their diminished X-ray emission, these heavily obscured sources can be detected only if they are relatively nearby. A similar effect is observed in INTEGRAL observations of Compton-thick AGNs (Malizia et al. 2009). Although the number of Compton-thick AGNs is relatively limited in the current sample, Akylas et al. (2016) using a much larger sample noticed that the column density distribution is fully consistent with a flat Compton-thick column density distribution between 1024 and 1026 cm−2.
4.2. High energy cut-off
In column (3) of Table 2 we give the derived coronal temperature. The cut-off energy corresponds to ∼3kT (Titarchuk 1994). For three objects the coronal temperature could not be constrained (2MFGC2280, NGC 5643, and NGC 7130). The mean energy of the coronal temperature of the remaining 16 sources is kT ≈ 50 keV corresponding to a high energy cut-off of about EC ∼ 150 keV. The distribution of the coronal temperature is given in Fig. 3. In the case of the three sources above where the coronal temperature could not be well constrained, we fixed the temperature at 50 keV to estimate the reflected emission.
It is interesting to compare the estimated cut-off with other high energy spectral studies of Compton-thick AGNs. Dadina (2007) estimated the cut-off energy in a number of nearby AGNs using data from the BeppoSAX mission, which observes in the 2–100 keV range. There are eight sources in common between our sample and that of Dadina (2007). Owing to the limited photon statistics at high energies, Dadina (2007) were able to constrain the high-energy cut-off in only two of these sources: NGC 1068, with EC > 116 keV, and NGC 4945, with 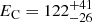 keV. These values are entirely consistent with our combined NuSTAR and BAT analysis. Ricci et al. (2017) derived the cut-off energy of the Compton-thick AGNs in his sample using a combination of XMM-Newton, Chandra, and Neil Gehrels Swift spectra (both XRT and BAT). For comparison with the present work, the cut-off energies, EC ∼ 3kT, derived by Ricci et al. (2017), are given in column (5) of Table 2. In many cases, there is reasonable agreement between the two analyses. However, there are at least four cases in which the results are clearly at odds. These are Circinus, ESO137−34, NGC 6232, and 2MASXJ09235371. This discrepancy could be partly attributed to the different spectral models used, that is the power-law model with an exponential cut-off versus the Comptonisation models. Ricci et al. (2017) have determined the average cut-off energy for their Compton-thick sources. When they excluded the lower and upper limits, they found a very low high energy cut-off for their Compton-thick AGNs (EC ≈ 43 ± 15 keV). Taking lower and upper limits into account by means of the Kaplan-Meier estimator, they estimated a much higher value for the cut-off EC ∼ 450 ± 64 keV. We found a mean high energy cut-off of EC ∼ 3kT ≈ 150 keV, excluding the three sources above where the cut-off energy could not be constrained. It is also interesting to compare with the work of Dadina (2007) who derived the average X-ray spectrum of 42 type-2 AGNs using BeppoSAX data. They found a cut-off energy of EC = 376 ± 42 keV. This is significantly higher than the cut-off energy of our Compton-thick sources.
keV. These values are entirely consistent with our combined NuSTAR and BAT analysis. Ricci et al. (2017) derived the cut-off energy of the Compton-thick AGNs in his sample using a combination of XMM-Newton, Chandra, and Neil Gehrels Swift spectra (both XRT and BAT). For comparison with the present work, the cut-off energies, EC ∼ 3kT, derived by Ricci et al. (2017), are given in column (5) of Table 2. In many cases, there is reasonable agreement between the two analyses. However, there are at least four cases in which the results are clearly at odds. These are Circinus, ESO137−34, NGC 6232, and 2MASXJ09235371. This discrepancy could be partly attributed to the different spectral models used, that is the power-law model with an exponential cut-off versus the Comptonisation models. Ricci et al. (2017) have determined the average cut-off energy for their Compton-thick sources. When they excluded the lower and upper limits, they found a very low high energy cut-off for their Compton-thick AGNs (EC ≈ 43 ± 15 keV). Taking lower and upper limits into account by means of the Kaplan-Meier estimator, they estimated a much higher value for the cut-off EC ∼ 450 ± 64 keV. We found a mean high energy cut-off of EC ∼ 3kT ≈ 150 keV, excluding the three sources above where the cut-off energy could not be constrained. It is also interesting to compare with the work of Dadina (2007) who derived the average X-ray spectrum of 42 type-2 AGNs using BeppoSAX data. They found a cut-off energy of EC = 376 ± 42 keV. This is significantly higher than the cut-off energy of our Compton-thick sources.
Our results are not significantly affected by the choice of τ = 2.0 in the cases where the photon statistics is limited. For example, in the case of NGC 3079 if we choose τ = 1.5, the resulting temperature becomes kT = 39 ± 19 keV. For this temperature of the corresponding photon index would be Γ ≈ 2.0.
4.3. Reflection component
The fraction of the reflected emission in the 20–40 keV band plays an important role in the prediction of the intrinsic fraction of Compton-thick AGNs in the sense that as the reflected emission becomes higher, the number of Compton-thick AGNs required is reduced. This is because the higher the reflection the easier it is to detect Compton-thick AGNs in the BAT band and hence the number of missing Compton-thick AGNs is relatively small. The reflection fraction is given in column (6) of Table 2. This is defined as the ratio of the unabsorbed reflection component S0 versus the total flux, i.e. the sum of the line-of-sight component Z and the two scattered components S0 and S90. Four sources appear to be reflection dominated as the reflection radiation fraction is near unity. These are NGC 1068, Circinus, NGC 424, and NGC 5643. A typical spectrum of a source with a strong reflection component (NGC 5643) is shown in Fig. 5. There is not a clear correlation between the strength of the reflection component and the column density in these sources. For example, NGC 424 and NGC 5643 have moderate Compton-thick column densities 1.3 ×1024cm−2. The vast majority of the sources have moderate strength reflection components below 0.23. There are eight sources in which the best-fit reflection component is negligible i.e. well below 0.01. The distribution of the reflection fraction is given in Fig. 2. The mean reflection fraction is 0.22. In analogy to the commonly used PEXRAV model (Magdziarz & Zdziarski 1995), which estimates the reflection to an infinite slab, we find that a fraction of 0.22 corresponds to a reflection strength R≈1. This is equivalent to a reflection fraction of ∼3% in the 2–10 keV band.
4.4. Intrinsic fraction of Compton-thick AGNs
In this section we estimate the intrinsic number of Compton-thick AGNs in the Universe using the population synthesis models developed by Akylas et al. (2012). The X-ray background synthesis models have been primarily devised to predict the number of Compton-thick AGNs based on their contribution to the X-ray background spectrum and in particular at its energy peak around 20–30 keV. The X-ray background synthesis models predict the number of AGNs and their contribution to the X-ray background spectrum at any redshift, luminosity, and column density. The necessary ingredients are the AGN luminosity function and the typical AGN spectrum. Treister et al. (2009) first pointed out that uncertainties on the measurements of the X-ray background are substantially large to hamper an accurate prediction of the number of Compton-thick AGNs. Instead these authors proposed that the INTEGRAL or BAT number counts of Compton-thick AGNs place tighter constraints. In this manner, the X-ray background synthesis models could be used to extrapolate the observed number counts to the intrinsic population number counts. In a similar approach, Burlon et al. (2011) used the observed Compton-thick AGNs number counts and predict the intrinsic Compton-thick AGNs counts by assuming a relation between the observed and intrinsic Compton-thick flux. This conversion sensitively depends on the typical Compton-thick AGN spectrum. Using a simple spectrum and by deriving the intrinsic NH distribution, Burlon et al. (2011) derived an intrinsic Compton-thick AGN contribution of ∼20%.
We fold the full observed spectral distribution as described by the parameters NH, kT, and the reflection fraction (see Figs. 1–3) in our X-ray population synthesis models. Then, the remaining unknown parameter is the intrinsic fraction of Compton-thick AGNs. We find that in order to match the observed Compton-thick AGNs counts in the BAT 14–195 keV band with our models, we need an intrinsic fraction of ∼20% relative to the type-II AGNs population (NH > 1022 cm−2); see Fig. 4. This corresponds to a Compton-thick fraction of 15% relative to the total AGNs population. The statistical error on this figure is 3%. This is derived from the number of Compton-thick AGNs (53 ± 7) used to derive the logN − logS. The uncertainties on the spectral parameters estimated above have not been taken into account in this error estimate.
 |
Fig. 2. Reflection fraction distribution (frefl = Flux[S0]/(Flux[Z]+Flux[S90]+Flux[S0] ) in the 20–40 keV band for all 19 sources in our sample. |
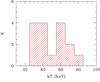 |
Fig. 3. Coronal temperature distribution as estimated using the COMPTT model of Titarchuk (1994, 16 sources). The three sources in which kT is unconstrained have been excluded. |
 |
Fig. 4. Number count distribution of the Compton-thick AGNs derived from the Neil Gehrels Swift-BAT survey in Akylas et al. (2016, black solid line). The red dashed line denotes the prediction of the X-ray population synthesis model of Akylas et al. (2012). Using the spectral parameters found in our spectral fits, we find that the Compton-thick AGNs fraction should be 20% of the type-2 AGNs population to agree with the observed logN − logS. |
 |
Fig. 5. NGC 5643: a characteristic spectrum of an AGN with a high reflection component. Top panel: folded spectrum. Bottom panel: unfolded spectrum; the blue sold line denotes the unabsorbed component S0. The straight dotted line represents the soft power-law component while the other dotted line denotes the absorbed reflection component S90. In both panels black and red denote the two FPM NuSTAR detectors while green corresponds to the BAT detector. |
Recently, Masini et al. (2018) estimated the Compton-think fraction of Compton-thick sources, using NuSTAR observations in the UKIDSS Ultra deep field. These authors found an observed Compton-thick fraction of 8.4 ± 2% in the 8–24 keV band at a flux of 2.7 × 10−14 erg cm−2 s−1. Making corrections for their non-detected XMM-Newton sources this fraction becomes 11.5 ± 2.0. This is in agreement with the 1σ upper limit of our model predictions, which is ≈10% at this flux.
5. Summary and conclusions
Direct spectroscopic observations of AGNs in the local Universe, using Neil Gehrels Swift/BAT samples, find a fraction of Compton-thick AGNs of about 7% of the total AGN population (Burlon et al. 2011; Ricci et al. 2015; Akylas et al. 2016; Marchesi et al. 2018). This figure can be extrapolated to the intrinsic number of Compton-thick AGNs by assuming a spectral model for the Compton-thick AGN spectrum (e.g. Burlon et al. 2011). The spectral parameters of interest are the photon index, strength of the reflection component, column density distribution, and primary emission cut-off energy. The reflection of material on cold matter surrounding the nucleus results in the flattening of the spectrum around 20–30 keV. Therefore the higher the reflection the easier it is to detect Compton-thick AGNs in the 14–195 keV band and hence the lower the number of missing Compton-thick AGNs (the lower the intrinsic fraction). The high energy cut-off works in the opposite way. The lower the value of the cut-off energy, the higher the intrinsic number of Compton-thick AGNs as these would not be easily detected in the BAT band. For example, if the high energy cut-off were ≈50 keV (see e.g. Ricci et al. 2017), the fraction of Compton-thick AGNs would increase to about 50%. We note that in contrast cut-offs higher than 150 keV would not significantly affect our results.
Aiming to constrain the intrinsic fraction of Compton-thick AGNs in the local Universe, we explored the spectrum of a large number Compton-thick AGNs. We analysed the combined NuSTAR/BAT spectra of 19 candidate Compton-thick AGNs (at the 70% confidence level) in the sample of Akylas et al. (2016). We modelled the spectra using the MYTORUS models of Yaqoob (2012), which take into account absorption and reflection from Compton-thick material. The primary X-ray emission from a hot corona is modelled with a physically motivated model (Titarchuk 1994). Our results can be briefly summarised as follows:
We derive absorbing column densities that are consistent with those derived by the previous Neil Gehrels Swift/BAT analyses by Ricci et al. (2015) and Akylas et al. (2016). We estimate that the coronal temperatures lie between 25 and 80 keV corresponding to high energy cut-offs roughly between 75 and 240 keV. The mean cut-off energy is 150 keV. We find that a large fraction of our AGNs lack a significant reflection component in the 20–40 keV band. The average reflection fraction is ∼0.22. The resulting spectral parameters are used to place constraints on the intrinsic fraction of Compton-thick AGNs. Using the above spectral results in combination with our synthesis models, we extrapolate the observed fraction of Compton-thick AGNs to the intrinsic fraction. We find that the Compton-thick AGNs fraction is 20 ± 3% of the type-II AGNs population.
Acknowledgments
We would like to thank the anonymous referee for comments and suggestions that helped to improve the paper. We acknowledge the use of MYTORUS spectral models by Yaqoob & Murphy (2011). We would also like to thank Tahir Yaqoob for his help and suggestions in the application of the above models. The research leading to these results has received funding from the European Union’s Horizon 2020 Programme under the AHEAD project (grant agreement n. 654215).
References
- Akylas, A., Georgakakis, A., Georgantopoulos, I., Brightman, M., & Nandra, K. 2012, A&A, 546, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Akylas, A., Georgantopoulos, I., Ranalli, P., et al. 2016, A&A, 594, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Annuar, A., Gandhi, P., Alexander, D. M., et al. 2015, ApJ, 815, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Arévalo, P., Bauer, F. E., Puccetti, S., et al. 2014, ApJ, 791, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Baloković, M., Comastri, A., Harrison, F. A., et al. 2014, ApJ, 794, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, F. E., Arévalo, P., Walton, D. J., et al. 2015, ApJ, 812, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJ, 207, 19 [Google Scholar]
- Brightman, M., & Nandra, K. 2011, MNRAS, 413, 1206 [CrossRef] [Google Scholar]
- Brightman, M., Nandra, K., Salvato, M., et al. 2014, MNRAS, 443, 1999 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2015, ApJ, 802, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Burlon, D., Ajello, M., Greiner, J., et al. 2011, ApJ, 728, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Sunyaev, R., Revnivtsev, M., et al. 2007, A&A, 467, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comastri, A., Setti, G., Zamorani, G., & Hasinger, G. 1995, A&A, 296, 1 [NASA ADS] [Google Scholar]
- Dadina, M. 2007, A&A, 461, 1209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draper, A. R., & Ballantyne, D. R. 2009, ApJ, 707, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Esposito, V., & Walter, R. 2016, A&A, 590, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Frontera, F., Orlandini, M., Landi, R., et al. 2007, ApJ, 666, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Georgantopoulos, I., Comastri, A., Vignali, C., et al. 2013, A&A, 555, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- George, I. M., & Fabian, A. C. 1991, MNRAS, 249, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gruber, D. E., Matteson, J. L., Peterson, L. E., & Jung, G. V. 1999, ApJ, 520, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997a, ApJS, 112, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., Filippenko, A. V., & Sargent, W. L. W. 1997b, ApJ, 487, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Koss, M. J., Romero-Cañizales, C., Baronchelli, L., et al. 2015, ApJ, 807, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Longair, M. S. 2011, High Energy Astrophysics [Google Scholar]
- Magdziarz, P., & Zdziarski, A. A. 1995, MNRAS, 273, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Malizia, A., Stephen, J. B., Bassani, L., et al. 2009, MNRAS, 399, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesi, S., Ajello, M., Marcotulli, L., et al. 2018, ApJ, 854, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Masini, A., Comastri, A., Baloković, M., et al. 2016, A&A, 589, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masini, A., Civano, F., Comastri, A., et al. 2018, ApJS, 235, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Moretti, A., Pagani, C., Cusumano, G., et al. 2009, A&A, 493, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, K. D., & Yaqoob, T. 2009, MNRAS, 397, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., & Pounds, K. A. 1994, MNRAS, 268, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Comastri, A., Fiore, F., et al. 2014, ApJ, 793, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Puccetti, S., Comastri, A., Bauer, F. E., et al. 2016, A&A, 585, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, C., Ueda, Y., Koss, M. J., et al. 2015, ApJ, 815, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Treister, E., Urry, C. M., & Virani, S. 2009, ApJ, 696, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Hasinger, G., Miyaji, T., & Watson, M. G. 2014, ApJ, 786, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Mushotzky, R. F., & Gandhi, P. 2013, ApJ, 770, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Papadopoulos, P. P., & Spaans, M. 2009, ApJ, 702, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Yaqoob, T. 2012, MNRAS, 423, 3360 [NASA ADS] [CrossRef] [Google Scholar]
- Yaqoob, T., & Murphy, K. D. 2011, MNRAS, 412, 1765 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Column density distribution for all 19 sources in our sample. |
| In the text | |
 |
Fig. 2. Reflection fraction distribution (frefl = Flux[S0]/(Flux[Z]+Flux[S90]+Flux[S0] ) in the 20–40 keV band for all 19 sources in our sample. |
| In the text | |
 |
Fig. 3. Coronal temperature distribution as estimated using the COMPTT model of Titarchuk (1994, 16 sources). The three sources in which kT is unconstrained have been excluded. |
| In the text | |
 |
Fig. 4. Number count distribution of the Compton-thick AGNs derived from the Neil Gehrels Swift-BAT survey in Akylas et al. (2016, black solid line). The red dashed line denotes the prediction of the X-ray population synthesis model of Akylas et al. (2012). Using the spectral parameters found in our spectral fits, we find that the Compton-thick AGNs fraction should be 20% of the type-2 AGNs population to agree with the observed logN − logS. |
| In the text | |
 |
Fig. 5. NGC 5643: a characteristic spectrum of an AGN with a high reflection component. Top panel: folded spectrum. Bottom panel: unfolded spectrum; the blue sold line denotes the unabsorbed component S0. The straight dotted line represents the soft power-law component while the other dotted line denotes the absorbed reflection component S90. In both panels black and red denote the two FPM NuSTAR detectors while green corresponds to the BAT detector. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \mathrm{model}&= wa[1]*(po[2]+ \nonumber \\&comptt[3]*etable{mytorus\_Ezero}[4] + \nonumber \\&atable {mytorus\_scatteredkT}[5]+ \nonumber \\&atable {mytorus\_scatteredkT}[6] + \nonumber \\&atable{mytl}[7]) \nonumber \\&atable{mytl}[8])). \nonumber \end{aligned} $$](/articles/aa/full_html/2019/01/aa33038-18/aa33038-18-eq1.gif)