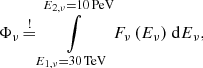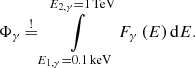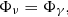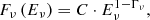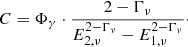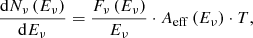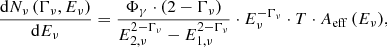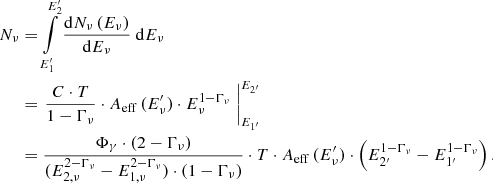| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A174 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834183 | |
| Published online | 14 December 2018 | |
Fermi/LAT counterparts of IceCube neutrinos above 100 TeV
1 Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
e-mail: felicia.krauss@uva.nl
2 GRAPPA, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
3 Department of Physics, Indian Institute of Technology Kharagpur, Kharagpur, West Bengal, 721302, India
4 Oskar Klein Centre and Dept. of Physics, Stockholm University, 10691 Stockholm, Sweden
5 Dr. Remeis Sternwarte & ECAP, Universität Erlangen-Nürnberg, Sternwartstrasse 7, 96049 Bamberg, Germany
6 Institut für Theoretische Physik und Astrophysik, Universität Würzburg, Emil-Fischer-Str. 31, 97074 Würzburg, Germany
7 Centre for Space Research, North-West University, Private Bag X6001, Potchefstroom, 2520, South Africa
8 Theoretical Astrophysics, T-2, MS B227, Los Alamos National Laboratory, Los Alamos, NM, 87545, USA
9 Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD, 21218, USA
Received:
3
September
2018
Accepted:
17
October
2018
The IceCube Collaboration has published four years of data and the observed neutrino flux is significantly in excess of the expected atmospheric background. Due to the steeply falling atmospheric background spectrum, events at the highest energies are most likely extraterrestrial. In our previous approach we have studied blazars as the possible origin of the High-Energy Starting Events (HESE) neutrino events at PeV energies. In this work we extend our study to include all HESE neutrinos (which does not include IC 170922A) at or above a reconstructed energy of 100 TeV, but below 1 PeV. We study the X-ray and γ-ray data of all (∼200) 3LAC blazars that are positionally consistent with the neutrino events above 100 TeV to determine the maximum neutrino flux from these sources. This larger sample allows us to better constrain the scaling factor between the observed and maximum number of neutrino events. We find that when we consider a realistic neutrino spectrum and other factors, the number of neutrinos is in good agreement with the detected number of IceCube HESE events. We also show that there is no direct correlation between Fermi/LAT γ-ray flux and the IceCube neutrino flux and that the expected number of neutrinos is consistent with the non-detection of individual bright blazars.
Key words: neutrinos / galaxies: active / quasars: general / BL Lacertae objects: general
© ESO 2018
1. Introduction
The detection of high-energy PeV neutrinos in the first three years of operations of the IceCube detector (Aartsen et al. 2013, 2014; IceCube Collaboration 2013) has led to a great effort to find the astrophysical origin of these neutrinos. Proposed counterparts include Sagittarius A*, (choked-jet) gamma-ray bursts (GRBs), active galactic nuclei (AGN), fast radio bursts (FRBs), star formation galaxies, magnetar flares, accretion disks, ultraluminous X-ray sources, and tidal disruption events (Tamborra & Ando 2016; Bednarek 2016; Bechtol et al. 2017; Bustamante et al. 2017; Fujita et al. 2017; Guépin & Kotera 2017; Aartsen et al. 2017; Albert et al. 2017; Fahey et al. 2017). Among these candidate sources, blazars have found particular interest (Krauß et al. 2014; Kadler et al. 2016; IceCube Collaboration et al. 2018) However, several studies have found that blazars alone are unlikely counterparts because they have only a small contribution to the neutrino spectrum for all of the IceCube neutrinos (Turley et al. 2016; Murase & Waxman 2016; Aartsen et al. 2016; Feyereisen et al. 2017; Ando et al. 2017; Neronov et al. 2017; Zhang & Li 2017). Constraints from multiplets indicate that BL Lacs do not contribute strongly to the observed neutrinos, but the same is not true for FSRQs (Murase et al. 2018). Moreover, the γ-ray brightest AGN sky show only a weak positional agreement with HESE neutrinos, demonstrating that the > 100 TeV IceCube signal is not simply dominated by a small number of the γ-ray brightest blazars. Instead, a larger number of sources have to contribute to the signal, with each individual source having only a low Poisson probability for producing an event in multi-year integrations of current neutrino detectors (Aartsen et al. 2015; Müller et al. 2018).
Owing to the steeply falling atmospheric background with increasing energy, PeV events are highly likely of extraterrestrial origin. For this reason, we have concentrated in our previous works on such events at energies above 1 PeV (Krauß et al. 2014; Kadler et al. 2016). Between 100 TeV and 1 PeV, the HESE analysis of the IceCube team has found 16 additional events (Aartsen et al. 2014), whose individual “signalness” is reduced, however, so that only about 14 out of these 16 events can be expected to be of astrophysical origin (Aartsen et al. 2014; IceCube Collaboration 2015).
In addition to the HESE analysis, IceCube has published six Extremely High Energy (EHE) events via GCN1. One of these EHE event alerts has recently prompted an intriguing coincidence of a track-like IceCube neutrino event above 100 TeV, IC 170922A (GCN #21916), with a blazar outburst (Tanaka et al. 2017; IceCube Collaboration et al. 2018; IceCube Collaboration 2018). While the signalness of the recent event is only ∼56%, this new coincidence is reminiscent of another blazar outburst found at the same time and position as a 2 PeV neutrino event (Kadler et al. 2016), but due to the track-like nature of the event, the chance coincidence is substantially lower, on the order of 3σ. If one > 100 TeV neutrino is indeed associated with a blazar, it appears straightforward to test whether viable blazar candidates exist in the fields of the 16 published HESE neutrino events between 100 TeV and 1 PeV. In this paper, we study possible blazar counterparts to the four-year IceCube HESE neutrinos above 100 TeV and below 1 PeV. We collect multiwavelength data from X-ray to high-energy γ rays and describe the high-energy peak in the spectral energy distribution (SED) with a logarithmic parabola. From the integrated energy flux we calculate the maximum number of neutrinos. This large sample of neutrinos and possible candidate sources allows us to constrain a scaling factor between the observed number of neutrinos and the maximum number of neutrinos calculated from the energy flux. This was previously constrained and explained by Kadler et al. (2016), but was only based on the sky area of one neutrino event (∼800 deg2), and referred only to PeV neutrino events. We further study if the non-detection of neutrinos from some bright blazars and the small number of source candidates for neutrinos with small angular uncertainties are still consistent with blazars as the origin of IceCube PeV neutrinos.
In Sect. 2 we explain the methods, including the data analysis and SED generation. In Sect. 3 we show the results, discussing the expected number of neutrinos and how we scale that number. Section 4 lists caveats of the methods and how they affect the results. In the final section we discuss the results and implications for hadronic blazars. Neutrino event numbers and SEDs are shown in the appendix.
2. Methods
2.1. IceCube HESE events
In Table 1, we give the full list of HESE events above 100 TeV in four years of IceCube data (IceCube Collaboration 2015). Sources above 1 PeV are listed, but not considered in this study, as we have investigated them before (Krauß et al. 2014; Kadler et al. 2016).
IceCube four-year HESE events above 100 TeV.
2.2. X-ray data
The maximum possible neutrino flux of a blazar can be derived from the integrated X-ray to γ-ray high-energy emission hump (see Krauß et al. 2014, and Sect. 2.5). In order to measure this, we need a sufficient spectral coverage. Unfortunately, this is not always available because of a lack of coverage at X-ray energies for a large number of (low-peaked) faint LAT sources. For high-peaked blazars we often lack information in the TeV energy range. X-ray data have been taken from the public Swift archives. The Neil Gehrels Swift Observatory observes in the 0.3–10 keV energy range. We obtained observations in the time range of the four-year IceCube period (May 1, 2010–April 30, 2014), unless data were only available outside this time range, in which case these data were used. For sources without Swift/XRT observations we used the recently updated Second ROSAT All-Sky Survey (2RXS). The available count rates where converted into fluxes using the factor 1.08 × 10−11 erg cm−2 s−1, which assumes a photon index of Γ = 1.7 and an absorption of 3 × 1020 cm−2 (Boller et al. 2016).
Several sources that are in the IceCube neutrino uncertainty fields are not observed by Swift and were further not detected by ROSAT. For these sources we used the flux limit of the RASS catalog as an upper limit. This contributes a large factor to the uncertainties of our study.
Swift/XRT data were prepared and extracted with the standard tools using HEASoft (v. 6.3.2). After running the xrtpipeline to apply the newest calibration, the target source was extracted using XSELECT with a circle of 20 pixels (47.146′′), centered on the source. The background was extracted using an annulus centered on the source, with radii of 50 (117.866′′) and 70 pixels (165.012′′), while ensuring that no sources lie in the background region.
2.3. 3LAC
In addition to the X-ray data, the Fermi/LAT data cover the high energies. As calculating LAT spectra is computationally expensive, we used the spectra from the 3FGL catalog that are identical in time integration to the 3LAC catalog (Acero et al. 2015). This time range overlaps by 2.5 years with the IceCube period. Variability in the sources adds another systematic uncertainty to our study, but we expect that the effects of more quiescence and flaring combined in all sources will more or less cancel out, and be small in comparison to modeling uncertainties. Furthermore, we expect that the 3FGL spectra are a reasonable approximation of four-year averaged spectra in the IceCube time period. We note that some (especially weak) sources (e.g., 1RXS J194422.6−452326) show a rising component with detections above 10 GeV. Such a component can often be explained with background from the Sun, for instance (Acero et al. 2015).
2.4. Broadband spectral energy distributions
As a first step, we rebinned the Swift X-ray data where available. We rebinned to constrain the spectrum to ten bins, while ensuring that each bin is above a signal-to-noise ratio (S/N) of 4.47 to ensure the validity of χ 2 statistics. In sources where we have a slightly lower S/N, we rebinned to an S/N of 1.5 and used Cash statistics. Data with fewer photons (rebinning to an S/N of 1.5 and fewer than 2 bins) were excluded and are not shown in this paper.
In the case of high-peaked sources, the X-ray data sometimes clearly lie on the synchrotron peak. Therefore the X-ray data were modeled with an absorbed power law (tbnew2), using the fixed Galactic NH (Kalberla et al. 2005), the vern cross-sections (Verner et al. 1996) and the wilm abundances (Wilms et al. 2000). From the best fit to the Swift/XRT data, we selected only those spectra with Γ < 2.3, ensuring that only X-ray data on the high-energy peak are included in the final SED model. For ROSAT, only the flux in the full energy band is available, so data cannot be excluded based on indices.
We constructed the SEDs and then fit them with an absorbed logarithmic parabola in the Interactive Spectral Interpretation System (ISIS; Houck & Denicola 2000). The data were fit in detector space, with the exception of Fermi/LAT data. Upper limits were not taken into account for spectral modeling, so in those cases, the best fit is based solely on Fermi/LAT data. In a few rare cases, the Fermi/LAT spectrum is not consistent with the X-ray index and was not used for spectral modeling (see, e.g., 1RXS J1958.6−301119). The details of the SED modeling approach are described in detail by Krauß et al. (2016).
2.5. Maximum number of neutrinos
From the best fit to the high-energy SED, we calculated the integrated energy flux in the energy range 0.1 keV–1 TeV to ensure that the range covers the peak of the high-energy component. We then followed our previous method of calculating the maximum neutrino number from the integrated energy flux of the high-energy peak of the broadband spectrum (see Krauß et al. 2014; Kadler et al. 2016). We estimated the neutrino energy flux from the electromagnetic energy flux assuming pion photoproduction and isospin symmetry. This yields
with the neutrino flux Fν(Eν) and the integrated neutrino energy flux Φν. The energy boundaries of 30 TeV and 10 PeV have been based on FSRQs, whose neutrinos spectra are expected to peak at PeV energies (Mannheim 1993b). If the true spectrum extends lower or higher, the neutrino estimates would be lower. However, our goal is to estimate whether there is enough power in this energy band to explain the IceCube neutrinos. The integrated electromagnetic energy flux is given by
Numerical evaluation of pion production Mücke et al. (2000) shows that
is a good approximation for most astrophysical scenarios. This approach yields a strict upper limit on the flux (or a maximum possible number of neutrinos that can be detected), because it assumes that the high-energy peak is purely hadronic and that the neutrino flux is emitted as a δ-function at the observed neutrino energy. In the following section, we discuss corrections to this maximum assumption for the neutrino flux needed to derive realistic expectation values.
2.6. Neutrino spectrum correction
Of course, monoenergetic neutrino production is unrealistic, and a power-law distribution is a more realistic assumption. In the proton blazar model, most of the flux is emitted at energies of 1000 PeV (for BL Lacs) and at ∼PeV energies (for FSRQs; Biermann & Strittmatter 1987); a Γν = 2.58 spectrum is inconsistent with both. A pp-component from protons leaking from the jet and diffusing through the host galaxy is steeper (Γν = 2.3) but not boosted, and thus comes from the larger number of radio galaxies. We assume that the integrated electromagnetic energy flux Φγ equals the integrated neutrino energy flux Φν, where E1, γ = 0.1 keV and E2, γ = 1 TeV gives the lower and higher energies, respectively, which were used to obtain the integrated electromagnetic flux. E1, ν = 30 TeV and E2, ν = 10 PeV then specify the energy range in which the neutrino spectrum was defined. The HESE best-fit photon index of Γν = 2.58 was obtained from the energy range 60 TeV–3 PeV (IceCube Collaboration 2015), although noting that a spectrum this steep is inconsistent with predictions from photo-hadronic source models (Mannheim 1995). This can be used to correct for a more realistic neutrino spectrum. We assume that the neutrinos follow a power-law flux distribution
with a photon index of the neutrino spectrum Γν = 2.58 and a normalization constant C. Integrating Eq. (4) and solving Eq. (3) for the normalization constant yields
The number of observed neutrinos per given energy is given by
where Aeff is the effective area of the neutrino instrument at a given neutrino energy for either the southern or the northern hemisphere (see Fig. 1), T = 1347 days is the IceCube time range, and Fν is the neutrino flux, dependent on the energy. Combining Eqs. (4), (5), and (6) gives
 |
Fig. 1. IceCube effective area for all neutrino flavors for the northern and southern hemisphere as given by IceCube Collaboration (2013). |
where Eν is the energy of the detected neutrino event. In order to obtain the total number of neutrinos per source in the energy range 100 TeV–1 PeV, we integrated Eq. (7). As the IceCube effective area is dependent on energy (see Fig. 1), we integrated numerically over each energy bin of the effective area, where Aeff (Eν) is constant. The integral of one single bin at the neutrino energy 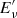 is given by
is given by
The resulting neutrino numbers are given in Table A.1 in the sixth column (νscale, int), but we note that this does not give the expected number of neutrinos per neutrino event, but per source in the whole energy range. We note that the total number of scaled, integrated neutrinos is representative for the total expected number of neutrinos from blazars. We note that the true correction factors are smaller if a fraction of the energy flux lies outside of the chosen window (e.g., BL Lac emission above 10 PeV, if the proton blazar model is correct, and below 30 TeV if a steep spectrum with Γν = 2.58 is true). Furthermore, such a steep spectrum cannot be true to below a few TeV without overproducing γ rays, or overproducing the nonthermal output of jets.
3. Results
There are 179 3LAC sources consistent with IceCube HESE events between 100 TeV and 1 PeV. We find that most of the sources can be described well by the model (see Fig. 2), and when this is not true, it is mostly due to a lack of data. In Fig. B.1–B.13 we show the SEDs of all sources including their best-fit model. Here we discuss the results obtained from the neutrino calculation.
 |
Fig. 2. Example SED with good Swift/XRT data that is well described by a logarithmic parabola (solid line). The unabsorbed model is shown as a dashed line. Residuals are shown in the lower panel. The energy range that is used for integrating the electromagnetic flux is given by the blue bar. The SEDs of the other sources are given in Fig. B.1–B.13. |
The resulting neutrino numbers are given in Table A.1, where the sources that are the strongest neutrino producers are listed first3. We note that in some fields the predicted number of neutrinos is dominated by the brightest sources, while in others the expected output is distributed fairly evenly across the individual sources.
The maximum number of neutrinos obtained for all sources is Nmax, all = 493, which clearly exceeds the 16 detected neutrinos between 100 TeV and 1 PeV. Correcting this for the neutrino spectrum and integrating lowers this value, yielding a total of 97 neutrinos. This is still larger than the detected number of neutrinos. Applying the empirical factor from Kadler et al. (2016) yields a total of 4 neutrinos.
Given the contributions from atmospheric neutrinos in this sample, this suggests that blazars could contribute largely to the observed neutrino signal in this energy range. However, our calculations show that the energy range over which blazars emit neutrinos and the spectral shape strongly affect neutrino estimates.
To calculate the number of neutrinos for individual events, we used all sources that are consistent with the uncertainty region of the neutrino event. To calculate the total number, we exclude sources that appeared several times, as the uncertainty regions overlap (see Fig. 3).
 |
Fig. 3. Hammer-Aitoff projection of the sky in right ascension and declination including all HESE events above 100 TeV (red), and above 1 PeV (gray) in four years of data, with their respective R50 error circles. The 3FGL position of the 3LAC sources consistent with the error circles are shown in gray crosses and the number of the IceCube event is marked above the plus sign, which marks the best-fit position of the origin of the neutrino event. |
3.1. Scaling factor
Another aspect to consider is which properties of the sources can further lower the neutrino number (in addition to the neutrino spectrum). Kadler et al. (2016) used an empirical scaling factor, comparing the observed event to the expected maximum number of neutrinos. This yields an empirical scaling of ∼0.0089. Based on IceCube Collaboration (2015), we assumed 10% atmospheric neutrino events above 100 TeV, that is to say, two cosmic events. The empirical scaling factor is then given by femp = 14/493 = 0.028, which is close to femp = 0.0089 that we derived from the IC35 field alone (Kadler et al. 2016).
The empirical scaling factor is explained by a combination of neutrino flavor, blazar class, and spectrum factor. We expect to not detect the neutrino flavors in IceCube data equally well (Learned & Pakvasa 1995; Aartsen et al. 2015), which would further reduce the number of detected neutrinos by ∼1/2, which, even with the spectrum correction, would be in excess of the detected neutrino events.
It is unclear if all blazars contribute equally, that is, if FSRQs are more or less hadronic than BL Lac-type objects. This could account for the second factor (∼1/2). The third factor is the effect of the neutrino spectrum. As we already took this into account, we added another factor. Assuming a more realistic lepto-hadronic SED than in our previous approach, that is, a high-energy peak that is not purely hadronic, we further lowered the number of neutrinos. As we do not know how hadronic blazars are, the exact value remains uncertain. Here we assumed that all 14 cosmic neutrinos in the energy range were produced by blazars (including FSRQs and BL Lacs). Applying the neutrino flavor factor and the spectral correction yields an expected number of 97 ⋅ 0.5 ⋅ 0.5 = 24 neutrino events. To lower this to the detected number of events requires only 56.2% of the high-energy emission to originate from hadronic interactions. This estimate neglects contributions from other sources and from unresolved blazars.
3.2. Full-sky approximation
While we only calculated the SED for the sources that are consistent with the neutrino events, in search for possible excesses, the full sky contribution must be considered. This effect of overestimating the neutrino flux is related to the Eddington bias (Strotjohann et al. 2018), which overestimates the neutrino flux when only a small number of events is considered. The neutrino expectations were calculated for all 16 neutrino uncertainty regions, which cover an area of 5590.88 degrees2. If we assume that the neutrino uncertainty regions are representative of the rest of the sky, we can scale the calculated neutrino numbers to the full sky (41 253 degrees2). The resulting total number of neutrinos is Nmax, all, fullsky = 3634, which yields a scaled number of neutrinos Nscale, fullsky = 712. Applying the other factors from Kadler et al. (2016) yields Nf, fullsky = 178. Comparing these numbers to the observed 14 cosmic neutrinos yields that only 7.9% of blazar high-energy emission is of hadronic origin, for blazars to explain all cosmic neutrinos in the 100 TeV–10 PeV range. If this is true, a correlation bet-ween high-energy electromagnetic and neutrino flux cannot be expected.
3.3. Effect of the neutrino spectrum
We assumed a power law for the neutrino spectrum, which might be an incorrect assumption. Furthermore, here we assumed that all neutrinos from a source are produced within the given energy range of 100 TeV–10 PeV, which neglects higher- and lower-energy neutrinos. The proton blazar model predicts a hard spectrum (Mannheim 1995), which is inconsistent with the measured IceCube index of Γ = 2.58. Even when this soft spectrum is used, calorimetrically blazars can explain the observed neutrino events above 100 TeV.
3.4. Energy range
The number of neutrinos that might be produced by the sources listed here depends on many factors, such as the selected neutrino spectrum. However, the basic input is the integrated electromagnetic flux of the source. The specific energy range of integration does not affect the expected number of neutrinos (as long as the peak is covered). This shows, however, that the expected number of neutrinos is dependent on the total integrated high-energy flux (assuming it is purely hadronic), not on the Fermi/LAT flux alone, for instance. This is illustrated in Fig. 4, where we compare the 3FGL energy flux with the expected number of neutrinos.
 |
Fig. 4. Calculated maximum number of neutrinos vs. the total integrated model flux between 1 keV and 1 PeV (top panel) and the calculated number of neutrinos vs. the given 3FGL flux (bottom panel). This illustrates that the Fermi/LAT flux alone is not a good predictor of expected neutrino numbers. |
4. Discussion
In this section we discuss possible problems with our method and other caveats. We discuss the high number of neutrinos that were calculated, as well as the impact of blazar variability on the neutrino number. We also discuss the problems related to the sparse broadband coverage and faint sources.
4.1. High neutrino numbers
The highest maximum number of neutrinos has been predicted for the source PKS 1830−211, with 50 predicted neutrinos. This is due to its steep spectra and the subsequent parabola, which peaks at high fluxes in the MeV band. However, when we scale this value and others to a realistic neutrino spectrum, the predicted neutrino number falls to 11 expected events for this source in the 100 TeV–1 PeV energy range, and to 3 neutrinos when the other scaling factors are applied. This is still above the detected number of neutrinos. However, when we take into account that most sources are expected to have a strong or even dominant leptonic contribution, this values becomes much lower, consistent with a non-detection. It is further unclear whether some sources are purely leptonic, while others have a strong hadronic component, or if this “hadronicness” is similar in all blazars.
4.2. Blazar variability
For many sources in our sample, multiwavelength observations are sparse, especially for fainter and less well-known sources, and simultaneous data are often not available. In such cases, the individual narrow-band observations from different epochs combined into an SED might not be representative of the true average SED because of source variability between the epochs. As many of the sources are faint and barely detected by Fermi/LAT, it is impossible to generate light curves for many of these sources in order to study their variability. Furthermore, multiple observations or monitoring in other wavebands is only available for a very small number of sources.
4.3. Broadband coverage
As observations are sparse, the SED coverage is far from ideal. Many of the SEDs are constrained by only ROSAT upper limits, as no Swift/XRT pointings are available or the S/N is not sufficient for spectral fitting. Furthermore, several Fermi/LAT spectra have upper limits, yielding only one or two energy bands with detections (TS > 25) in extreme cases. This sparse coverage, as well as neglecting the synchrotron peak, leads to over- or underestimates of the electromagnetic flux and therefore of the number of neutrinos. We estimate that this could change the integrated flux to a factors of a few, but would not greatly affect the total number of neutrinos.
4.4. Faint sources
As neutrinos have a very long mean free path, we can observe neutrinos from objects that are too faint to be resolved with current instruments. We therefore estimate additional neutrinos from faint, unresolved blazars. A rough estimate can be obtained from the extragalactic γ-ray background (EGB). Between 50% and 80% of the EGB is expected to be from blazars (Inoue & Totani 2009; Ackermann et al. 2015). This total integrated flux from unresolved blazars is a factor of 2 higher than the total integrated value for resolved blazars (Krauß et al. 2015). Furthermore, unbeamed sources, such as radio galaxies, are also expected to contribute to the neutrino (and to the extragalactic γ-ray background).
4.5. Source classes
Blazars can further be separated into FSRQs and BL Lacs depending on their jet power. While FSRQs are the more likely counterparts for neutrinos in the IceCube energy range (due to interactions with thermal UV photons from the accretion disk; Mannheim 1993a), some authors have considered only BL Lac objects (Righi et al. 2017). It is unclear how the opacity problem in these sources can be overcome since BL Lacs are generally optically thin to the absorption of TeV γ rays and thus are very inefficient in producing neutrinos at IceCube energies (Bahcall & Waxman 2001). However, possible exceptions are being discussed, for example by Ansoldi et al. (2018), Murase et al. (2018).
5. Conclusions
We have constructed SEDs for all 3LAC counterparts to IceCube HESE neutrino events between 100 TeV and 1 PeV. We also showed that the Fermi/LAT energy flux does not yield a good estimate of the neutrino flux. From the integrated energy flux, we estimated the maximum number of neutrino events from all blazars Nν = 493, which is in agreement with our previous work, where we found that blazars are easily able to explain the neutrino signal based on their electromagnetic output at high energies (Krauß et al. 2014). When a power-law neutrino spectrum with a spectral index Γν = 2.58 is adopted, this number is reduced to 97 neutrinos events. These numbers also show no strong neutrino excesses from individual sources (> 3 neutrino events) when the other scaling factors are applied, consistent with the non-detection of high-energy neutrino multiplets from bright sources.
Applying the empirical factor from Kadler et al. (2016) to the maximum number of neutrino events instead of using the correction to the neutrino spectrum reduces this to four neutrino events. Another factor that could reduce the number of neutrinos would be the “hadronicness” of the source, which accounts for the fraction of the high-energy emission that is actually due to photo-meson production. We find that if 56.2% of the high-energy electromagnetic flux originates from hadronic emission, this is sufficient to explain the IceCube neutrino events above 100 TeV. When these numbers are scaled to the full sky, we obtain a total number of neutrinos Nmax, all, fullsky = 3634, the scaled number of neutrinos Nscale, fullsky = 712, and Nf, fullsky = 178. Comparing these numbers to the observed 14 cosmic neutrinos yields that only 7.9% of blazar high-energy emission is of hadronic origin, for blazars to explain all cosmic neutrinos in the 100 TeV–10 PeV range. If this is true, a correlation between high-energy electromagnetic and neutrino flux cannot be expected.
Considering the systematic uncertainties as well as the caveats, we argue that blazars can contribute strongly to the 100 TeV–1 PeV energy range. Considering a realistic neutrino spectrum and other aspects of blazar physics reduces the amount of neutrinos we expect to detect from these sources, but is still larger than the detected number of neutrinos and constrains the “hadronicness” of blazars. The recently detected TXS 0506+056 (which is not a HESE event and not detected in four years of data), which is in agreement with the track event IC 170922A, is a tantalizing hint at a blazar connection, which is why further study is necessary (IceCube Collaboration et al. 2018).
Available at https://gcn.gsfc.nasa.gov/gcn3_archive.html. GCN numbers available for 5 EHE events: 19787, 20247, 20929, 21916, 22105. The sixth event is online at https://gcn.gsfc.nasa.gov/notices_amon/6888376_128290.amon
Available at: http://pulsar.sternwarte.uni-erlangen.de/wilms/research/tbabs/
Acknowledgments
We thank the journal referee for the helpful comments. We thank A. Heijboer for the useful discussions regarding the results. F. K. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 653477. B. W. acknowledges funding from the DAAD RISE program. This research has made use of ISIS functions (ISISscripts) provided by ECAP/Remeis observatory and MIT (http://www.sternwarte.uni-erlangen.de/isis/).
References
- Aartsen, M. G., Abbasi, R., Abdou, Y., et al. 2013, Phys. Rev. Lett., 111, 021103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2014, Phys. Rev. Lett., 113, 101101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2015, Phys. Rev. Lett., 114, 171102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aartsen, M. G., Abraham, K., Ackermann, M., et al. 2016, Phys. Rev. Lett., 117, 241101 [Google Scholar]
- Aartsen, M. G., Ackermann, M., Adams, J., et al. 2017, ApJ, 843, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., & Ajello, M. 2015, ApJS, 218, 23 [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2015, ApJ, 799, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Albert, A., André, M., Anghinolfi, M., et al. 2017, Phys. Rev. D, 96, 022005 [Google Scholar]
- Ando, S., Feyereisen, M. R., & Fornasa, M. 2017, Phys. Rev. D, 95, 103003 [NASA ADS] [CrossRef] [Google Scholar]
- Ansoldi, S., Antonelli, L. A., Arcaro, C., et al. 2018, ApJ, 863, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J., & Waxman, E. 2001, Phys. Rev. D, 64, 023002 [NASA ADS] [CrossRef] [Google Scholar]
- Bechtol, K., Ahlers, M., Di Mauro, M., et al. 2017, ApJ, 836, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W. 2016, ApJ, 833, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, P. L., & Strittmatter, P. A. 1987, ApJ, 322, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Boller, T., Freyberg, M. J., Trümper, J., et al. 2016, A&A, 588, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bustamante, M., Heinze, J., Murase, K., & Winter, W. 2017, ApJ, 837, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Fahey, S., Kheirandish, A., Vandenbroucke, J., & Xu, D. 2017, ApJ, 845, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Feyereisen, M. R., Tamborra, I., & Ando, S. 2017, JCAP, 3, 057 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, Y., Murase, K., & Kimura, S. S. 2017, JCAP, 4, 037 [NASA ADS] [CrossRef] [Google Scholar]
- Guépin, C., & Kotera, K. 2017, A&A, 603, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. Manset, N., Veillet, C., & Crabtree, D., ASP Conf. Ser., 216, 591 [NASA ADS] [Google Scholar]
- IceCube Collaboration 2013, Science, 342, 1242856 [Google Scholar]
- IceCube Collaboration 2015, ICRC 2015 (The Hague: The Netherlands) [Google Scholar]
- IceCube Collaboration 2018, Science, 361, 147 [NASA ADS] [Google Scholar]
- IceCube Collaboration, Fermi-LAT, MAGIC, et al. 2018, Science, 361, eaat1378 [NASA ADS] [Google Scholar]
- Inoue, Y., & Totani, T. 2009, ApJ, 702, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Kadler, M., Krauß, F., Mannheim, K., et al. 2016, Nat. Phys., 12, 807 [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krauß, F., Kadler, M., Mannheim, K., et al. 2014, A&A, 566, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krauß, F., Wang, B., Baxter, C., et al. 2015, 5th Fermi Symp. Proc., eConf C141020.1 [Google Scholar]
- Krauß, F., Wilms, J., Kadler, M., et al. 2016, A&A, 591, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Learned, J. G., & Pakvasa, S. 1995, Astropart. Phys., 3, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K. 1993a, Phys. Rev. D, 48, 2408 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K. 1993b, A&A, 269, 67 [NASA ADS] [Google Scholar]
- Mannheim, K. 1995, Astropart. Phys., 3, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Mücke, A., Rachen, J. P., Engel, R., et al. 2000, Nucl. Phys. B Proc. Suppl., 80, C810 [Google Scholar]
- Müller, C., Kadler, M., Ojha, R., et al. 2018, A&A, 610, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murase, K., & Waxman, E. 2016, Phys. Rev. D, 94, 103006 [NASA ADS] [CrossRef] [Google Scholar]
- Murase, K., Oikonomou, F., & Petropoulou, M. 2018, ApJ, 865, 124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neronov, A., Semikoz, D. V., & Ptitsyna, K. 2017, A&A, 603, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Righi, C., Tavecchio, F., & Guetta, D. 2017, A&A, 598, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strotjohann, N. L., Kowalski, M., & Franckowiak, A. 2018, A&A, submitted, [arXiv:1809.06865] [Google Scholar]
- Tamborra, I., & Ando, S. 2016, Phys. Rev. D, 93, 053010 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y. T., Buson, S., & Kocevski, D. 2017, ATel, 10791 [Google Scholar]
- Turley, C. F., Fox, D. B., Murase, K., et al. 2016, ApJ, 833, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, B. T., & Li, Z. 2017, JCAP, 3, 024 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Number of neutrinos
Neutrino numbers for all sources.
Appendix B: High-energy spectral energy distributions
This appendix shows the SEDs of all sources in the sample.
 |
Fig. B.1. Broadband SEDs for IceCube event IC 2. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
 |
Fig. B.2. Broadband SEDs for IceCube event IC 4. |
 |
Fig. B.3. Broadband SEDs for IceCube event IC 12. |
 |
Fig. B.4. Broadband SEDs for IceCube event IC 17. |
 |
Fig. B.5. Broadband SEDs for IceCube event IC 22. |
 |
Fig. B.6. Broadband SEDs for IceCube event IC 26. |
 |
Fig. B.6. continued. |
 |
Fig. B.7. Broadband SEDs for IceCube event IC 30. |
 |
Fig. B.8. Broadband SEDs for IceCube event IC 33. |
 |
Fig. B.9. Broadband SEDs for IceCube event IC 39. |
 |
Fig. B.9. continued. |
 |
Fig. B.10. Broadband SEDs for IceCube event IC 40. |
 |
Fig. B.11. Broadband SEDs for IceCube event IC 46. |
 |
Fig. B.12. Broadband SEDs for IceCube event IC 48. |
 |
Fig. B.13. Broadband SEDs for IceCube event IC 52. |
All Tables
All Figures
 |
Fig. 1. IceCube effective area for all neutrino flavors for the northern and southern hemisphere as given by IceCube Collaboration (2013). |
| In the text | |
 |
Fig. 2. Example SED with good Swift/XRT data that is well described by a logarithmic parabola (solid line). The unabsorbed model is shown as a dashed line. Residuals are shown in the lower panel. The energy range that is used for integrating the electromagnetic flux is given by the blue bar. The SEDs of the other sources are given in Fig. B.1–B.13. |
| In the text | |
 |
Fig. 3. Hammer-Aitoff projection of the sky in right ascension and declination including all HESE events above 100 TeV (red), and above 1 PeV (gray) in four years of data, with their respective R50 error circles. The 3FGL position of the 3LAC sources consistent with the error circles are shown in gray crosses and the number of the IceCube event is marked above the plus sign, which marks the best-fit position of the origin of the neutrino event. |
| In the text | |
 |
Fig. 4. Calculated maximum number of neutrinos vs. the total integrated model flux between 1 keV and 1 PeV (top panel) and the calculated number of neutrinos vs. the given 3FGL flux (bottom panel). This illustrates that the Fermi/LAT flux alone is not a good predictor of expected neutrino numbers. |
| In the text | |
 |
Fig. B.1. Broadband SEDs for IceCube event IC 2. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.2. Broadband SEDs for IceCube event IC 4. |
| In the text | |
 |
Fig. B.3. Broadband SEDs for IceCube event IC 12. |
| In the text | |
 |
Fig. B.4. Broadband SEDs for IceCube event IC 17. |
| In the text | |
 |
Fig. B.5. Broadband SEDs for IceCube event IC 22. |
| In the text | |
 |
Fig. B.6. Broadband SEDs for IceCube event IC 26. |
| In the text | |
 |
Fig. B.6. continued. |
| In the text | |
 |
Fig. B.7. Broadband SEDs for IceCube event IC 30. |
| In the text | |
 |
Fig. B.8. Broadband SEDs for IceCube event IC 33. |
| In the text | |
 |
Fig. B.9. Broadband SEDs for IceCube event IC 39. |
| In the text | |
 |
Fig. B.9. continued. |
| In the text | |
 |
Fig. B.10. Broadband SEDs for IceCube event IC 40. |
| In the text | |
 |
Fig. B.11. Broadband SEDs for IceCube event IC 46. |
| In the text | |
 |
Fig. B.12. Broadband SEDs for IceCube event IC 48. |
| In the text | |
 |
Fig. B.13. Broadband SEDs for IceCube event IC 52. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.