| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201834101 | |
| Published online | 07 December 2018 | |
Determination of physical parameters of particle-accelerating colliding-wind binaries based on generalized partition considerations
Space Sciences, Technologies and Astrophysics Research (STAR) Institute, University of Liège, Quartier Agora, 19c, Allée du 6 Août, B5c, 4000 Sart Tilman, Belgium
e-mail: Michael.DeBecker@uliege.be
Received:
17
August
2018
Accepted:
7
October
2018
The sub-set of massive binaries known to accelerate particles, the so-called category of particle-accelerating colliding-wind binaries (PACWBs), constitutes a valuable laboratory for investigating the non-thermal physics in stellar environments. In particular, their synchrotron emitter status allows us to derive some basic properties of their population of relativistic electrons. In this paper, considerations about energy partitions (not restricted to equipartition or minimum energy) are developed to derive relevant physical parameters of PACWBs in an appropriate assumption context. This approach was applied to three PACWBs with known stellar wind and orbital parameters, along with rather well-known radio properties. For long-period systems, a local magnetic field of the order of 0.1–10 mG was determined for a wide range of assumptions on partition parameters, while values of a few G are obtained for the shorter period system we investigated. Normalization parameters of the relativistic electron populations were also determined. Synchrotron self-absorption appears to be an unlikely turn-over process for long-period systems, while it may compete with free-free absorption for a shorter period object. Our results are discussed in the context of the energy budget of non-thermal processes in PACWBs, and prospects for high energy emission are also addressed. The sensitivity of this approach, applied for the first time to PACWBs, was also investigated through a critical discussion of the dependence of determined physical quantities on adopted and assumed parameters. Even though this method is certainly not adequate to reproduce the physics of PACWBs in detail, it offers the advantage of allowing for the determination of valuable average quantities provided a few fundamental parameters and measurements are known, without the need of any detailed hydrodynamic and radiative modelling. In the absence of any relevant measurement of non-thermal radiation in the high-energy domain, the method presented here constitutes the most straightforward and accessible approach to date to discuss physical parameters that are relevant for the non-thermal physics of PACWBs.
Key words: stars: massive / binaries: general / radiation mechanisms: non-thermal / acceleration of particles / radio continuum: stars / magnetic fields
© ESO 2018
1. Introduction
Evidence for the production of synchrotron radiation in several systems made of massive stars (OB type and their evolved Wolf-Rayet counterparts) opened the door for the investigation of non-thermal physics in these environments. The requirement of the existence of a population of relativistic electrons to produce synchrotron radiation provides evidence that an efficient particle acceleration process is at work. Most probably, this process should be diffusive shock acceleration (DSA, Drury 1983) in the presence of strong shocks in the colliding-wind region (see e.g. Eichler & Usov 1993; De Becker 2007). The sub-population of colliding-wind massive binaries known to accelerate particles is referred to as particle-accelerating colliding-wind binaries (PACWBs, De Becker & Raucq 2013). About 40 systems are included in the catalogue of PACWBs, and prospects for an extension of the catalogue are highly anticipated. As a result of their particle accelerator status, these systems are considered as contributors to the production of Galactic cosmic rays (De Becker et al. 2017).
Addressing the issue of particle acceleration and non-thermal processes in Galactic environments immediately leads to a comparison with shell-type supernova remnants (SNR). PACWBs and SNRs have shock physics in common, including particle acceleration through DSA and non-thermal emission of radiation. Significant differences between the two classes of objects exist, however. First of all, the shock geometry of PACWBs adopts a folded cone-like shape, while to some extent, spherical symmetry holds for SNRs. Shock properties (pre-shock velocity, shocked material density, etc.) in SNRs change gradually as the shell expands through the interstellar medium. The variation timescale is thus that of the expansion. However, the binary nature of PACWBs introduces a more stringent variability timescale, that is, the orbital period (typically between a few weeks and potentially centuries, according to the current census of the catalogue members). During the orbit, provided it is eccentric, shock properties may change very significantly, therefore affecting all the downstream physics (including particle acceleration and non-thermal emission). Finally, the radiative environment also presents significant differences. In particular, the dominant radiative energy density in PACWBs comes from the photospheric radiation field from the stars, resulting in a significant impact on relativistic electron populations. In particular, inverse Compton scattering is likely the most efficient cooling process for electrons, thus converting a substantial fraction of their energy into high-energy radiation.
Non-thermal emission processes offer the opportunity of investigating physical parameters characterizing not only relativistic particles, but also the astrophysical environment itself. A relevant example is the determination of the magnetic field strength in a few SNRs on the basis of synchrotron radio emission measurements, as in the case of W44 (Castelletti et al. 2007), with a value of a few tens of μG. These considerations also allow deriving relevant information about the energetics of these synchrotron emitters. It is important to mention, however, that these estimates are based on the assumption of equipartition between magnetic energy and relativistic particle energy, which is not necessarily physically justified (Dubner & Giacani 2015).
Similarly, the case of PACWBs deserves to be investigated in order to derive physical parameters related to the synchrotron emission process revealed by radio observations. However, the situation is significantly more complicated through the periodically variable geometry and physical parameters. In addition, PACWBs are known to be composite (thermal + non-thermal) radio emitters, with a thermal free-free emission that inevitably affects any attempt to measure the synchrotron contribution. This introduces more requirements in terms of extraction of information from radio measurements. The objective of this study is to consider the specificities of PACWBs in a general approach allowing for the determination of relevant physical parameters based on their synchrotron emission. It is intended to derive average parameters starting with physically motivated assumptions, focusing on observational measurements, without any use of self-consistent modelling of these objects. Such an approach is intended to be easy to use, and likely to be applied to any system provided the required observational measurements are available. The outcome of the approach described here is also expected to enhance the interest of conducting observations of PACWBs by improving their connections with the underlying physics.
The paper is organized as follows. The general approach and method are described in Sect. 2. Section 3 presents the results of the application of this method to a few stellar systems, after a short description of the target selection procedure. Section 4 consists of a general and critical discussion of the approach and of its results. Finally, the concluding remarks are presented in Sect. 5.
2. General approach
2.1. Theoretical formalism
The basic idea followed here is to estimate the average magnetic field strength in the synchrotron emission region on the basis of simple partition considerations between the magnetic field and relativistic particles on the one hand, and relativistic electrons and protons on the other hand. The general formalism adopted here follows globally the standard approach for estimating the magnetic field of synchrotron sources (e.g. Rybicki & Lightman 1979; Longair 1992; Condon & Ransom 2016), although the present study is not restricted to minimum energy or equipartition, which are not necessarily physically justified. Details on this formalism are presented in Appendix A. This work will thus make use of two partition parameters: one for the ratio of magnetic to particle energy densities (ηmag), and one for the ratio of total relativistic particles to relativistic electron energy densities (η).
First of all, the average magnetic field of the synchrotron emission region can be estimated using Eq. (1), provided the emitting volume and the spectral luminosity are reasonably determined, and assuming adequate values for the integration boundaries for the synchrotron spectrum (νmin and νmax), as described in Appendix A:
The magnetic field strength clearly is directly dependent on partition parameters. A specific discussion of all parameters relevant for this approach is given in Sect. 2.2. In the specific case where the magnetic partition parameter ηmag = 3/4, coincident with minimum total (magnetic + particles) energy, Eq. (1) recovers the usual form traditionally used for synchrotron sources (see e.g. Rybicki & Lightman 1979).
When the magnetic field strength is calculated, the normalization parameter of the relativistic particle population (K) can be determined as well, making use of Eq. (2) (see Eq. A.4):
This K parameter, along with the electron index (p) determined from the measurement of the synchrotron spectral index (α), leads to an overall characterization of the population of relativistic electrons responsible for the measured synchrotron spectrum.
When these quantities are determined, considerations about the energy budget can be addressed, in particular, magnetic and relativistic particle energy densities can easily be determined. According to the adopted partition assumptions, energy densities more specific to electron and protons, respectively, can be determined (see details in Appendix A). The energy budget is discussed in Sect. 4.5.
We clarify that the approach adopted here is not intended to provide an in-depth description of the non-thermal physics and energetic of PACWBs. In particular, it is implicitly assumed here that both relativistic electrons and protons (and potentially heavier nuclei) are characterized by the same power-law index, with an overall partition parameter distributing the total energy between particles. The intention is to achieve an overall and average view of physical parameters in these environments, in direct connection with average observational quantities measured through radio observations. A more detailed view of the physics of PACWBs would require self-consistent modelling of the hydrodynamics and non-thermal physics, including cooling and transport processes that are likely to affect relativistic particles in massive binaries. Such an investigation would be beyond the scope of this study.
2.2. Relevant parameters
Particle partition. Partition parameters defined in Sect. 2.1 have to be assumed to lie between reasonable boundaries. For the relativistic particle partition parameter, a strict lower boundary would correspond to energy injection in electrons only (assuming protons and heavier charged particles are neglected). A frequent assumption is to consider η = 100, in agreement with some measurements of this parameter in Galactic cosmic ray spectra. Another frequently adopted value is η = 10. We refer to Merten et al. (2017) for a deeper discussion. In this study, the empirically reasonable range of η = 1…100 is adopted.
Magnetic partition. Anticipating the most adequate value for the magnetic partition parameter ηmag is much more problematic. Without any independent measurement of the local magnetic field and relativistic particle content, we can only conjecture on the most appropriate range of values. A conservative range of value to be explored in this study is set to be 0.01 ≤ ηmag ≤ 100, centred on the frequently adopted assumption of equipartition.
Emitting volume. In the absence of high angular resolution radio imaging using very long baseline interferometry (VLBI) techniques, we cannot directly access any information on the synchrotron-emitting volume. However, this is a crucial parameter, as seen for instance in Eq. (1). We therefore have to make physically justified assumptions. For this purpose, we adopted a simple geometry as described in Fig. 1. We assumed that the emitting volume can be represented by a spherical cap. It would be convenient to express this volume in a simple way, as a function of an easily accessible geometrical quantity related to its orbit, such as the distance between the centre of the star with the less powerful stellar wind and the stagnation point of the colliding-wind region (rB). The latter quantity is given by 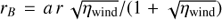 , where the wind momentum rate ratio is ηwind = (ṀB/ṀA) (V∞,B/V∞,A) (based on mass-loss rates and terminal velocities of the stellar winds of components A and B), r is the relative separation depending on the orbital phase (calculated using orbital parameters), and a is the major axis of the system.
, where the wind momentum rate ratio is ηwind = (ṀB/ṀA) (V∞,B/V∞,A) (based on mass-loss rates and terminal velocities of the stellar winds of components A and B), r is the relative separation depending on the orbital phase (calculated using orbital parameters), and a is the major axis of the system.
According to Eichler & Usov (1993), the size of the synchrotron-emitting region can be set to w = π rB . The volume of a spherical cap can be written 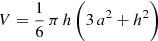 . Assuming for the sake of simplicity a geometrical thickness h ∼ 2a/3 (see Fig. 1) and considering w ∼ 2a, one obtains V ∼ 5 rB
3. In an eccentric system, this volume will thus significantly change as a function of the orbital phase, as expected. It is also important to clarify that the approximate character of this estimate of the volume does not constitute a severe issue considering the 2/7 power dependence of B on this parameter, as we discuss in Sect. 4.4.
. Assuming for the sake of simplicity a geometrical thickness h ∼ 2a/3 (see Fig. 1) and considering w ∼ 2a, one obtains V ∼ 5 rB
3. In an eccentric system, this volume will thus significantly change as a function of the orbital phase, as expected. It is also important to clarify that the approximate character of this estimate of the volume does not constitute a severe issue considering the 2/7 power dependence of B on this parameter, as we discuss in Sect. 4.4.
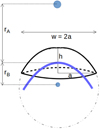 |
Fig. 1. Illustration of the synchrotron-emitting region as a spherical cap (thick solid black lines). The thick blue curve represents the contact discontinuity of the wind-wind interaction region wrapped around the star with the weakest wind (lower blue filled circle). |
Valid frequency range. The synchrotron emission should be significantly active over a few orders of magnitudes in frequency. It is not so straightforward to estimate the most relevant frequency boundaries to consider, however. In view of the negative slope of synchrotron spectra, we can consider that νmax is probably not higher than 100 GHz, where certainly thermal processes will clearly dominate. For νmin, it is a priori difficult to exactly determine where the synchrotron emission starts. The lower frequency part of the synchrotron spectrum is affected by turn-over (see Sect. 4.3) that is poorly investigated so far for this category of synchrotron radio emitter. A lower boundary of 10 MHz is considered, which is close to the Earth ionospheric cut-off. A discussion of the sensitivity of the results on the adopted value for νmin and νmax is presented in Sect. 4.4.
Spectral luminosity. The spectral luminosity is expressed by the following relation:
The flux density (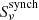 ) is measured at a given frequency (ν) and the distance (d) has to be known.
) is measured at a given frequency (ν) and the distance (d) has to be known.
We recall, however, that PACWBs are composite radio emitters, including thermal emission from the stellar winds in addition to the synchrotron emission. Only VLBI observations of long-period systems (at least a few years) would allow us to resolve the synchrotron emission without any significant contamination by the thermal emission from the stellar winds. In most cases, the measured flux densities Sν have to be corrected for the thermal emission (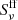 ) in order to isolate the synchrotron contribution (
) in order to isolate the synchrotron contribution (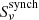 ), that is,
), that is,
as two stellar winds (A and B) contribute to the thermal emission (see Appendix B). It is also important to note that the above relation provides a lower limit on the synchrotron contribution, as the synchrotron flux density can be significantly reduced by free-free absorption by the stellar winds material. We therefore do not access the intrinsic synchrotron emission through observations, but instead measure a quantity that is attenuated. Therefore it is highly recommended to select a measurement at a not so low frequency to minimize the impact of free-free absorption. Such an attenuation is however less severe when long-period (at least a few years) systems are considered. In addition, depending on the geometry of the system, especially for short-period systems or eccentric systems close to periastron, a small fraction of the thermal emission from a stellar wind can be absorbed by the companion wind. Accounting for this effect would require a full treatment of the radiative transfer in the binary system, which is far beyond the scope of thisstudy. Finally, we should mention that our estimate of the free-free emission from the stellar winds does not consider the removal of the spatial region filled with the companion wind. In particular for the weakest wind, this fraction may be significant. For the dominant wind, this effect is probably not critical. In addition, as illustrated in the examples discussed in Sect. 3.2, the thermal contribution from the stellar winds does not appear to be very strong, and correcting for it with a factor of a few would not severely affect the results we present here.
In practice, for a given stellar classification of the components of the system, individual stellar and wind parameters can be retrieved from several published studies. For O-type stars, typical values for Teff on the one hand and for Ṁ and V∞ on the other can be obtained from Martins et al. (2005) and Muijres et al. (2012), respectively. For Wolf-Rayet stars, a typical value for these parameters can be found, for instance, in Crowther (2007) and Sander et al. (2012). On the basis of these values, the expected thermal free-free flux density of individual winds (Sν ff, A and Sν ff, B) can be predicted following the approach detailed in Appendix B. The successive use of Eqs. (4) and (3) yields the spectral luminosity.
Spectral index. The spectral index is determined from radio spectra and is expected be constant in the assumed valid frequency range. However, the effective synchrotron spectral index cannot be directly measured, as the thermal free-free contributions (for low-to-medium angular resolution observations) are included in the flux density measurements. In most cases, we have to estimate the spectral index on the basis of flux densities corrected for the contamination by thermal emission (see above),
where subscripts 1 and 2 stand for two distinct frequencies where the flux density has been measured. For non-thermal processes, this spectral index is expected to be negative. In equations developed and written in Appendix A, the spectral index is α = −α′, in agreement with the conventions adopted in our approach (i.e. Sν ∝ ν −α).
We note that the influence of free-free absorption on the measurement of the spectral index can be significant as the absorption depends intimately on the frequency. The sensitivity of our results with respect to α is discussed in Sect. 4.4.
2.3. Method
The procedure is illustrated in Fig. 2, with the various steps as described below:
-
For a specific object, the first step consists of selecting radio observations that yield reliable values of measured flux densities at a given orbital phase. We recall that flux densities, and likely α, are expected to vary significantly as a function of the orbital phase. Typically, epochs with good signal-to-noise ratio measurements at two frequencies with a clear non-thermal signature should be preferred.
-
Adequate values of the stellar and wind parameters are required in order to feed Eq. (B.1) and thus estimate expected flux densities of the free-free thermal radio emission from individual stellar winds.
-
The measured flux densities are then corrected for the thermal contributions in order to obtain an estimate of the synchrotron contribution
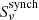 (Eq. (4)).
(Eq. (4)). -
The corrected flux densities are used to compute a corrected spectral index of the synchrotron spectrum (Eq. (5)), along with the corresponding spectral luminosity Lν at the selected frequency ν (Eq. (3)).
-
The orbital parameters of the system must be checked to derive the orbital separation and use this geometrical information to estimate the emitting volume V.
-
For a set of assumptions on the partition parameters, the magnetic field in the synchrotron-emitting region (B) can be determined using Eq. (1).
-
Every determination of the magnetic field allows us to determine the normalization parameter of the population of relativistic particles (K) using Eq. (2).
-
The determination of the magnetic field also allows us to compute the magnetic energy density (Umag) in the emitting region.
-
On the basis of the Umag and of partition parameters, the energy densities in electrons and other relativistic particles can easily be determined.
These steps can be repeated for any orbital phase of the system investigated, provided relevant radio measurements exist at these specific epochs. As we discuss in Sect. 4.5, energy densities constitute highly valuable quantities for energy budget considerations. These results are also used to derive order-of-magnitude estimates of the high-energy inverse Compton scattering emission from these objects.
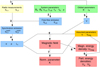 |
Fig. 2. Block diagram of the various steps involved in our approach to determine the physical parameters. The meaning of the numbers associated with every step is explained in Sect. 2.3. Yellow shows measured quantities, green the required parameters, blue represents intermediate computed quantities, orange shows assumed quantities, and red the output physical quantities. |
3. Application to a few systems
3.1. Selection of objects
The approach described above requires the knowledge of some information about the objects of interest (see Table 1). This places some stringent constraints on the list of objects that are adequate for a determination of physical parameters on the basis of synchrotron radio emission measurements. In addition to radio measurements at least at two distinct frequencies, information about the orbit and on the spectral classification is required. Among the few systems fulfilling these criteria, we selected three systems spread over the parameter space of PACWBs presented in De Becker & Raucq (2013): a short-period O-type system (Cyg OB2 #8A), a long-period O-type system (HD 167971), and a long-period WR + O system (WR 140).
Adopted parameters for the three selected systems.
3.2. Results
3.2.1. Cyg OB2#8A
The comparison of the minimum masses determined by De Becker et al. (2004) to the expected absolute masses predicted by Martins et al. (2005) allows us to compute a likely value for the inclination i. The latter quantity is needed to determine the absolute dimensions of the orbit on the basis of the projected semi-major axes given by De Becker et al. (2004). The wind momentum rate ratio was estimated on the basis of stellar wind parameters given by Muijres et al. (2012) adequate for the spectral classification of the members of the system. The estimate of the wind momentum rate ratio allows us to compute the distance between the star with the weaker wind and the stagnation point (rB). This allows us to estimate the emitting volume (see Sect. 2.2). The distance is taken from Reipurth & Schneider (2008). Relevant parameters are summarized in Table 1.
Cyg OB2 #8A is the shortest period O + O system with a significant synchrotron emission component clearly associated with its colliding-wind region. From the radio measurements quoted by Blomme et al. (2010), we selected the values obtained on 21 December 1984, corresponding to orbital phase 0.49 (see Table 2). We selected this orbital phase because it displays an obvious non-thermal index between 6 and 20 cm, with reasonable relative errors on the flux densities. At most orbital phases, either simultaneous measurements at two frequencies, a detection at 20 cm, or a good signal-to-noise ratio is lacking. A clearer synchrotron signature at that selected orbital phase is not surprising: close to apastron, when the stellar separation is larger, a more significant part of the synchrotron emission region is likely to emerge from the opaque stellar winds. The estimate of the synchrotron component of the radio emission is obtained by correcting the measured flux densities for the computed thermal flux densities. The corrected flux densities yield a spectral index α′ of about –0.72, while the uncorrected (measured) one is –0.69.
Selected and computed radio quantities.
We applied the approach described in Sect. 2.1, assuming various values for η, for a range of values of ηmag. Results are shown in Fig. 3. As expected, the logarithm representation produces a linear trend with a slope consistent with the 2/7 power found in Eq. (1). In line with the same equation, curves obtained for η values differing by one order of magnitude are vertically shifted by less than a factor 2. Where measurements allowed estimating the electron and proton content of cosmic ray populations, η values between 10 and 100 seem to be more appropriate (Merten et al. 2017). It seems a priori unlikely that the energy injection is exclusively directed to electrons, but we recall that synchrotron radiation provides only evidence for electron acceleration. We therefore considered η values equal to 1, 10 and 100, as shown by the curves plotted in Figs. 3 and 4. The magnetic field strength accounting for the measured radio emission (according to the approach followed in this study) should be in the range 0.1–4 G. Such high values could partly be explained by the quite short stellar separation in this short-period system. If the magnetic field is of stellar origin (thus not produced in the wind-wind interaction region), its geometrical dilution due to its photospheric distance is rather weak. Assuming a local magnetic field scaling as 1/r2 (in the radial regime that should be valid up to distances of the order of 10 R⋆, Usov & Melrose 1992), with r being the distance between the stagnation point and the stellar photosphere (of the order of 5 stellar radii at the selected orbital phase), we can extrapolate that the photospheric field ranges between 2 and 100 G. However, this extrapolation does not take into account a likely magnetic amplification in the colliding-wind region, which would reduce the extrapolated surface field by a significant factor. As a result, the magnetic field strength values plotted in Fig. 3 are compatible with surface fields below the detection limit of current spectropolarimetric measurements (see e.g. Neiner et al. 2015).
 |
Fig. 3. Magnetic field strength as a function of ηmag for three different values of η for Cyg OB2 #8A. |
The magnetic energy density, the energy density in relativistic particles, and the sum of both are plotted in Fig. 4 as a function of ηmag for the three assumed values of η. The total energy density (magnetic + particles) presents a minimum close to equipartition (ηmag = 1), in agreement with the standard minimum energy and equipartition considerations.
 |
Fig. 4. Energy densities as a function of ηmag for three different values of η for Cyg OB2 #8A. Black, blue, and red curves represent the total (in black), the magnetic (Umag, in red), and the relativistic particles (Upart, in blue) energy densities. |
3.2.2. HD 167971
HD 167971 was selected among O-type long-period systems as it is the brightest O-type synchrotron radio emitter included in the catalogue of PACWBs. The main difficulty comes from its triple system status (see e.g. Leitherer et al. 1987; Davidge & Forbes 1988; De Becker et al. 2012). This is a system of three massive stars, with two colliding-wind regions. According to the conventions adopted in De Becker (2015), the members of the short-period binary are referred to as components Aa and Ab, while the third more distant star is component B. The colliding-wind region in the close binary system (whose period is only about three days) is certainly too short to allow any putative synchrotron radiation to escape the opaque stellar winds. The bright non-thermal radio emission thus comes from the wind-wind interaction in the wider orbit, with a period of about 20 years, as supported by the radio light curves published by Blomme et al. (2007). The most recent orbital elements published for the long-period orbit come from Le Bouquin et al. (2017).
The adopted stellar wind and orbital parameters are quoted in Table 1. Adequate stellar wind parameters were selected from Muijres et al. (2012) for the three components, according to their spectral classification. The distance is taken from Reipurth (2008). Individual parameter values for components Aa and Ab are quoted for the short-period binary (referred to as A). Individual free-free flux densities were computed following the approach detailed in Appendix B.
The radio measurements were taken from Blomme et al. (2007). Orbital phase 0.88 was selected as it is close to maximum emission with a clear non-thermal spectral index (see Table 2). Estimates of the magnetic field following the same approach as in Sect. 3.2.1 are presented in Fig. 5. The magnetic field strength is several orders of magnitude lower than for Cyg OB2 #8A. Typically, B lies between a few 0.1 mG and about 10 mG, depending on the adopted values for the partition parameters. The much lower values derived for HD 167971 as compared to Cyg OB2 #8A are in principle in fairly good agreement with the expected trend of a lower local magnetic field in the wind-wind interaction region, accounting for the much longer distance to the star (if B originates from the stars). In this case, we note that the distance to the colliding-wind region measured from the star is large enough to consider the toroidal regime valid, with a 1/r dependence of the magnetic field strength. This also has consequences on the energy densities plotted in Fig. 6, which are much lower than for Cyg OB2 #8A.
3.2.3. WR 140
WR 140 is certainly the best-known long-period WR + O binary, with a period of about 8 years and a very high eccentricity (∼0.9). The most recent orbital parameters are those published by Fahed et al. (2011). For the stellar wind parameters, we used the typical value for a WC7 star given by Crowther (2007) and intermediate values between giant and supergiant O5.5 stars given by Muijres et al. (2012), according to the spectral classification proposed by Fahed et al. (2011). The adopted distance is that proposed by Dougherty et al. (2011). All relevant parameters are quoted in Table 1.
This system has benefited from in-depth investigations in the radio domain, at various frequencies and with various angular resolutions. The radio measurements used in this study are taken from Dougherty et al. (2003). The Very Large Array measurements obtained at orbital phase 0.783 were arbitrarily selected among several measurements that similarly fulfil our main selection criteria (bright radio emission, with a clear non-thermal spectral index). Other measurements in the same part of the orbit (but before the decrease of the measured emission as the system approaches periastron) would give similar results. Flux densities at 4.9 and 8.4 GHz were selected, and were corrected for the free-free contribution of the stellar winds following the same approach as for the O-type systems discussed above (see Table 2).
Globally, estimates of the local magnetic field lie in a similar range as for HD 167971, that is, typically a few (down to a fraction of) mG (see Fig. 7), and the same holds for energy densities plotted in Fig. 8. For the magnetic field, values derived here are in agreement with the equipartition value derived by Dougherty et al. (2003) in the framework of their model for a long-period WR + O binary. On the other hand, Eichler & Usov (1993) at a similar orbital phase estimated B ∼ 0.03 G, which is compatible with the results we obtain at equipartition with η close to 10 (in agreement with the assumption made by Eichler & Usov 1993). Such a B strength leads to a magnetic energy density of the order of 3.5 × 10−5 erg cm−3. It should also be noted that Eichler & Usov (1993) expressed the relativistic particle energy density in terms of fraction of the ram pressure (Ugas) at the stagnation point, Upart = ϵ Ugas with 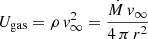 , where ρ is the gas density. With the numbers quoted in Table 1, Ugas is of a few 0.1 erg cm−3 for the WC wind. With the Upart value obtained at equipartition for η = 10, ϵ is of the order of 10−5, which is significantly below the 0.01 value assumed by Eichler & Usov (1993). Certainly a very detailed modelling of the non-thermal physics in these environments is required to clarify the most adequate values of the partition parameters, including ϵ.
, where ρ is the gas density. With the numbers quoted in Table 1, Ugas is of a few 0.1 erg cm−3 for the WC wind. With the Upart value obtained at equipartition for η = 10, ϵ is of the order of 10−5, which is significantly below the 0.01 value assumed by Eichler & Usov (1993). Certainly a very detailed modelling of the non-thermal physics in these environments is required to clarify the most adequate values of the partition parameters, including ϵ.
4. Discussion
4.1. Local magnetic field
The magnetic field derived from this approach is in the range of 0.1–10 mG for longer period systems, while it is closer to the G level for the short-period system. This is a priori in agreement with the expectations from a magnetic field of stellar origin, affected by a geometrical dilution as a function of the radial distance to the stars. As longer period systems are characterized by longer distances between stars and the wind collision region, local magnetic fields should on average be lower (considering photospheric fields of the same order of magnitude). We also mention that local magnetic field amplification is expected in such environments (Falceta-Gonçalves & Abraham 2012), which further blurs the link between our estimate of the local magnetic field and the (undetermined) field strength at the surface of both stars in the binary system. We note that the quite high values obtained for the short-period system are largely related to the much smaller emitting volume (in the denominator of Eq. (1)), in direct relation with the smaller dimensions of the orbit, while much larger volumes contribute to the emission in long-period binaries.
The magnetic field values reported here should be considered with some caution, however. First of all, the synchrotron emission level is intimately dependent on the magnetic energy density, which is certainly not homogeneous. In particular, local fluctuations of the magnetic field will affect the integrated/average synchrotron flux that is measured through radio observations. This effect is certainly expected to lead to an overestimate of the actual average magnetic field in the emission region. In particular, the measurement of synchrotron radiation is restricted to the brightest part of the emitting region, introducing a bias in the determination of higher field strengths.
4.2. Relativistic electrons properties
It is not straightforward to estimate the typical range of Lorentz factors for relativistic electrons required to produce synchrotron radiation in a given photon frequency range. The typical photon frequency indeed depends on both the local magnetic field and electron Lorentz factor (see Eq. (2)). Any photon frequency can thus result from any B − γ combination. However, our estimate of the magnetic field in various sources allows us to lift this degeneracy.
Generalizing, we plotted the typical Lorentz factor required for given values of the magnetic field for two typical photon frequencies, that is, 500 MHz and 10 GHz (see Fig. 9). The two selected frequencies reasonably bracket the frequencies where synchrotron radiation is measured in PACWBs. For instance, with typical B values reported for HD 167971 and WR 140, adequate Lorentz factors are in the range between a few 100 and a few 1000 (with higher values required for higher frequencies). However, in the case of the shorter period system Cyg OB2 #8A, values between a few 10 and a few 100 are enough, considering the stronger local magnetic field.
 |
Fig. 9. Lorentz factor required to produce synchrotron radio photons at frequencies of 500 MHz and 10 GHz as a function of the magnetic field strength in the synchrotron emission region. Ranges appropriate for the long-period and short-period results are indicated by thick horizontal lines. |
In addition to the adequate range of Lorentz factors, we can estimate the normalization parameters of the population of relativistic electrons (K) using Eq. (A.4). Results are plotted in the upper panels of Figs. 10–12 for the three targets discussed in Sect. 3.2. K clearly is quite sensitive to the assumptions made on the partition parameters, with, as expected, a power-law decrease as a function of increasing ηmag. K is also larger when lower values of η are considered.
 |
Fig. 10. Upper panel: normalization factor of the relativistic electrons population for Cyg OB2 #8a. Lower panel: corresponding SSA turn-over frequency. Both quantities are plotted as a function of ηmag for three assumed values of η. |
A last quantity relevant for characterizing the role of relativistic electrons in the physics of PACWBs is their energy density, which is easily computed on the basis of the energy densities in relativistic particles plotted (in blue) in Figs. 4, 6 and 8. Depending on the adopted value for η, for instance for ηmag = 1, Ue lies in the range 5 × 10−4–10−3 erg cm−3 for Cyg OB2 #8A, 10−8–10−7 erg cm−3 for HD 167971, and 10−8–10−7 erg cm−3 for WR 140. The actual value of η is anticipated to have a significant impact on the relative weights of leptonic and hadronic radiative process, with some consequences on the capability of these objects to contribute to the non-thermal high energy emission and to the production of Galactic cosmic-rays. One also has to clarify that the much larger energy density in electrons for the short period system may be misleading, and the physical quantity that carry a significant importance for a putative detection of non-thermal leptonic processes is the total energy amount. Multiplying the energy densities reported above by the respective volumes of the synchrotron emission region of these systems leads to similar energy reservoirs in relativistic electron energy. Short period systems should therefore not necessarily be considered a priori as much brighter non-thermal radio emitters, despite the much higher values derived for energy densities in relativistic electrons.
4.3. Synchrotron-Self Absorption
It is always relevant to check for the potential occurrence of synchrotron-self absorption (SSA) in synchrotron sources. For a slab of emitting (and absorbing) material of thickness l measured along the line of sight, we may estimate the SSA opacity χ(ν) (see e.g. Rybicki & Lightman 1979), which depends on the frequency. The switch between optically thick and optically thin regimes occurs close to a unit optical depth, namely τ(ν)=χ(ν) l = 1 (with χ(ν) expressed in cm−1). This optical depth identity thus allows deriving an expression for the SSA turn-over frequency,
with
provided B and K have been determined, and assuming a thickness l equivalent to the size of the emitting region. For this purpose, as a rough approximation, l is considered to be the width of the emission region (w, defined in Sect. 2.2).
Our results are plotted in the lower panel of Figs. 10–12 for the three targets. The turn-over frequency is quite close to (or even below) the MHz level, thus even below the Earth ionospheric cut-off, for the two long-period systems (HD 167971 and WR 140). SSA is thus very unlikely to significantly affect synchrotron spectra from this type of source. However, for Cyg OB2 #8a, the SSA turn-over frequency is of a few 100 MHz, and even close to the GHz level for high values of ηmag and high values of η. These frequencies are clearly located in the range of usual observation frequencies, as a result of a more abundant population of SSA absorbers and of a stronger local magnetic field. However, it is very likely that in such shorter period systems, other turn-over processes such as free-free absorption (FFA) and the Razin-Tsytovitch effect are quite efficient as well (see e.g. Dougherty et al. 2003). In particular, the higher plasma density surrounding the synchrotron emission region in short-period PACWBs will severely absorb radio photons. At first sight, FFA may dominate the turn-over, but detailed radiative transfer based on a sophisticated hydrodynamic code is necessary to clarify the respective roles of various turn-over processes in massive binary systems. The FFA is the only orientation-dependent turn-over process affecting measured synchrotron spectra of massive binaries. The full configuration of the system from the point of view of the observer changes greatly as a function of the orbital phase. An adequate description of the impact of FFA would thus require a detailed description of the distribution of the (shocked and un-shocked) material in the system. Such a study is beyond the scope of the present paper which focuses on the non-thermal physics of PACWBs and will be addressed in future works for specific systems. Let’s however mention for instance the results published by Williams et al. (1990) who estimated the FFA optical depth for WR 140 at various orbital phases, and showed that it can vary very significantly as a function of the orbital phase. In particular, the FFA optical depth is expected to deeply depend on which wind is crossed by the line of sight in very asymmetric systems such as WR + O binaries. In shorter period systems, the synchrotron emission region is surrounded by denser layers of material, and it is expected to undergo on average a more severe free-free absorption. A dedicated inspection of the turn-over processes is needed for any specific system being investigated, but in principle, we cannot reject the possibility that SSA may compete with FFA and the Razin-Tsytovitch effect in the low-energy cut-off of the synchrotron spectrum of short-period binaries.
4.4. Influence of adopted parameters
Our estimate of the magnetic field based on Eq. (1) is influenced by the values we adopt for several parameters. It is interesting to note that the dependence of B with respect to several parameters is somewhat smoothed out thanks to the 2/7 power. A striking effect of this power dependence is obvious in Figs. 3, 5, and 7, when the curves obtained for different values of the proton-to-electron partition parameter (η) are compared. A difference of a factor 10 in η translates into less than a factor 2 in B. When switching from η = 1–100, B increases by about a factor 3.7. The same dependence is valid for ηmag as well, with the same moderate impact on the value of B.
The same dependence holds for the emitting volume as well. It is clear that our approach to estimating the emitting volume yields only an approximate value. Assuming that our approach leads to an uncertainty of a factor 10 in the typical dimension of the emitting region, this would translate into a factor 103 in the volume, which in turn affects the estimate of the local magnetic field by a factor of about 7. At the level of approximation of the simple approach developed here, this is adequate to at least provide reasonable estimates of the magnetic field given some assumptions are made for partition parameters.
The method followed here also presents significant dependences on other quantities, such as the photon index of the synchrotron spectrum (corrected for the thermal emission contributions) and adopted frequency boundaries to integrate the radio emission (νmin and νmax). In order to investigate the impact of the adopted values on these parameters, one test case (i.e. WR 140) was selected with different sets of these parameters (with η set to 100 and ηmag set to 1, for the sake of simplicity). The adopted parameter grid considers minimum and maximum frequencies shifted by a factor 10, and shifts of 0.2 for the spectral index. The results are summarized in Table 3. It is clear that the most sensitive dependence is that of the spectral index. When magnetic field values obtained for very different α are compared, B values that differ by more than an order of magnitude are derived. This emphasizes that it is mandatory to accurately determine the basic properties of synchrotron spectra from radio measurements. In particular, the effect of FFA on the determination of α deserves special attention, as has been pointed out by Williams et al. (1990) in the case of WR 140. On the other hand, the impact of the adopted frequency boundaries seems to be minor (much less than an order of magnitude), as anticipated in Sect. 2.2. For the effect on the SSA turn-over frequency, we can expect differences of up to about one order of magnitude, depending on the adopted value for α (within the range covered by our exploration of the parameter space). This may have a more significant effect on short-period systems, where it seems that νSSA may lie in the range of a few 100 MHz. A significant increase of the SSA turn-over frequency may result from a change in the adopted spectral index value. As a consequence, we cannot completely rule out a tight competition between SSA and FFA for the turn-over of the synchrotron spectrum in shorter period binaries.
Effect of the adopted parameters on the output values.
4.5. Energy budget
The determination of magnetic and relativistic particle energy densities allows us to address the question of the energy budget more quantitatively, in line with the general discussion presented by De Becker & Raucq (2013). We first compute the total energy in the magnetic field and in non-thermal particles,
At least for order-of-magnitude purposes, we also consider a dynamical timescale (tdyn) defined as the time required for material to cross a distance typical of the emission region at the flow speed, taken as the wind velocity,
We can thus express so-called magnetic and non-thermal powers,
These quantities deserve to be compared to the energy pool that feeds the non-thermal physics, namely the wind kinetic power, which can be expressed by the following relation:
Using Eqs. (8)–(10), we can determine power ratios as follows:
The last power ratio constitutes a measurement of the non-thermal efficiency, that is, the efficiency to convert wind mechanical energy into particle acceleration in general. From this, the electron acceleration efficiency ratio would be defined as
We computed tdyn and Pkin,wind for all systems considered in this paper. For the wind kinetic power, we added the individual kinetic power of all individual winds to obtain a total value, representative of the total amount of mechanical power available in the system. All values are summarized in Table 4. The results of the application of Eqs. (11)–(13) are plotted in Figs. 13–15, for Cyg OB2 #8a, HD 167971, and WR 140, respectively, for the same ranges of ηmag and η values as adopted in Sect. 3.2.
Dynamical timescale (tdyn), total wind kinetic power (Pkin,wind), and total radio synchrotron luminosity (Lsynch) for the three targets.
 |
Fig. 13. fmag (top panel), fpart (middle panel), and fe (bottom panel) for Cyg OB2 #8a as a function of ηmag, for three assumed values of η. |
Our results clearly show that both magnetic field and non-thermal particles are at sub-partition with respect to the mechanical wind energy, which constitutes a strict boundary condition to validate our approach. First of all, it would be quite unexpected that the magnetic field energy in the synchrotron-emitting region be similar to (or at least a significant fraction of) the wind total energy. Such a scenario would indeed induce a strong coupling between the wind plasma and the magnetic field, which is not supported by our current understanding of the physics of colliding winds in massive binaries. On the other hand, the non-thermal energy injected into relativistic particles comes from the wind kinetic power, and more specifically, from the fraction of that mechanical energy that is effectively injected into the colliding-wind region. Here again, a value of fpart closer to unity would not make any sense. The order of magnitudes of fpart shown in Figs. 13–15 are in fair agreement with the educated-guess values proposed by De Becker & Raucq (2013). We note, as expected, that this non-thermal efficiency factor depends severely on the system that is considered, with significantly higher values for the short-period system.
We note that the quantity Pe(=fe Pkin,wind) constitutes the most consistent upper limit on the expected inverse Compton (IC) luminosity produced by these systems (see Sect. 4.6). Any non-thermal leptonic emission process should indeed not produce more radiation than permitted by the energy content of relativistic electrons.
One word of caution is needed to close this discussion on the energy budget. As clarified in Sect. 4.1, our approach very likely over-estimates the magnetic field strength. As a result, the energy budget is significantly biased toward over-estimated values of Pmag and Ppart. The curves plotted in Figs. 13–15 may accordingly have to be down-shifted. On the other hand, the discussion in Sect. 4.4 reveals that the estimate of the magnetic field is somewhat sensitive to the spectral index of the synchrotron spectrum. We anticipate that the intrinsic spectral index (i.e. corrected for the free-free absorption) is significantly affected, as absorption is more severe at lower frequencies (see e.g. Williams et al. 1990; Dougherty et al. 2003). For instance, a change of α from 0.26 to 0.46 would lead to an increase of B by a factor 6 (see Table 3 for WR 140). For a given set of partition parameters, this would lead to an increase of a factor 36 in Umag(∝B 2), with similar repercussions on the energetics of the system. The energy budget discussion presented here therefore allows us to discuss relevant trends, but absolute and accurate numbers must wait for a more detailed modelling.
4.6. Expectations at high energies
The idea that massive binaries should be non-thermal high-energy emitters is not new, as illustrated notably by the work by Benaglia & Romero (2003). The existence of a population of relativistic electrons opens the possibility that non-thermal emission could also be produced at high energies. Considering the presence of the strong radiation field from the stellar photospheres in massive binary systems, inverse Compton (IC) scattering is the most likely candidate (se e.g. Pittard & Dougherty 2005; De Becker 2007). If the same relativistic electron population produces the radio synchrotron radio emission and the high-energy IC scattering (in the Thomson regime), the following relation is frequently used:
where the radiative energy density, measured at the distance of the stagnation point of the wind-wind interaction region (e.g. at rA from star A and at rB from star B), is given by
with Lbol,A and Lbol, B the bolometric luminosities of components A and B, respectively. On the basis of our estimate of the magnetic energy density, we can derive predictions of the total inverse Compton luminosity:
where the synchrotron luminosity (Lsynch) results from the integration of the spectral luminosity between frequencies νmin and νmax,
Values of the integrated synchrotron luminosity (Eq. (17)) and of the radiative energy density (Eq. (15)) at the selected orbital phases for the three targets are given in Table 5. The bolometric luminosities are those given by Martins et al. (2005) for the spectral types specified in Table 1, except for WR 140, whose value is taken from Crowther (2007). Distances to the stagnation point measured from each component (rA and rB) are given in Table 1.
Selected and computed quantities for the estimate of the IC luminosity.
We predicted values for the IC luminosity in the same ranges of ηmag and η as adopted in previous sections. For Cyg OB2 #8A, the curves plotted in Fig. 16 point to a strict upper limit of the IC luminosity of about 1035 erg s−1 for the adopted set of assumed parameters. The maximum value occurs for the lower values of ηmag and η. The minimum value of a few 1031 erg s−1 is obtained for the highest values for the two partition parameters. This is expected as the latter situation considers that the total energy is dominated by the magnetic field (at the expense of non-thermal particles) and the energy in these particles is dominantly injected into protons (at the expense of electrons).
 |
Fig. 16. Predicted IC luminosity (LIC ) for Cyg OB2 #8a as a function of ηmag for three assumed values of η. |
For HD 167971 and WR 140 (see Figs. 17 and 18, respectively), globally the IC luminosity is higher by about three orders of magnitude than in the case of Cyg OB2 #8A. This is quite counter-intuitive as we a priori expect shorter period systems to by brighter IC sources because of the shorter distance to the stellar photospheres. This difference partly comes from the brighter synchrotron radio emission, which acts as some kind of scaling factor for IC predictions using Eq. (16). Another important factor is the magnetic energy density, which is much lower in these long period systems. Even though the higher radiative energy density of the short-period system may at first sight act in favour of a bright high-energy IC emission, all in all, the indirect influence of other factors points to a brighter expected IC emission in longer period systems.
The predicted IC luminosities for the long-period systems are obviously on average much too optimistic, in particular when these numbers are compared to the total wind kinetic power quoted in Table 4. This clearly points to the strict limitation of the approach adopted here, which is based on simple assumptions without any adequate and modern modelling. It is indeed quite reasonable to consider that LIC should be only a small fraction of Pkin,wind. For instance, a significant increase in the magnetic field strength would accordingly reduce the predicted IC luminosities. However, this increase is not expected to be too high, otherwise it would lead to a severe increase of the fmag and fpart ratios (see Sect. 4.5) and therefore generate another inconsistency. The high IC luminosity is related to the high radiative energy density. Any attenuation of the photospheric radiation field in the colliding-wind region would reduce the IC emission accordingly. The sensitivity and accuracy of our approach does not allow us to clarify the most appropriate set of parameters leading to reasonable IC luminosities without increasing the magnetic field strength too far. This simple approach to anticipate the IC emission level is thus quite approximate and is not meant to compete with a more detailed modelling allowing for a more appropriate description of the non-thermal physics, including predictions at high energies (Pittard & Dougherty 2005; Reimer et al. 2006; del Palacio et al. 2016).
Finally, we wish to clarify that the luminosities computed here are total IC luminosities, integrated over the full spectrum, which certainly covers several orders of magnitude in photon energy. This is especially important if these numbers are to be discussed in the context of the attempts made in the past years to measure an IC emission from massive binaries in X-rays. If we define LIC the total IC luminosity in a wide photon energy range, for example, between Emin and Emax, we can define the IC luminosity (LIC, band) in a narrower band, for instance, between Emin, band and Emax, band. Considering a power-law IC emission with constant spectral index equal to the synchrotron index α, we can write
Assuming the total IC photon energy range such that Emin = 0.1 keV and Emax = 1 GeV (for a long-period system such as WR 140, the highest energy reached by electrons would be of a few GeV, Eichler & Usov 1993; we note that such a high upper limit is intentionally adopted as a conservative limit), and an observation energy band typical of the bandpass of current soft X-ray observatories (e.g. Emin, band = 0.1 keV and Emax, band = 10 keV), a total IC luminosity of 1037 erg s−1 (see e.g. WR 140 at equipartition, for η = 10, with α = 0.26) would lead to LIC, band ∼ 3 × 1032 erg s−1. This luminosity drops by at least one order of magnitude if much higher values for the partition parameters are considered. This represents only a small fraction of the total IC luminosity. The non-thermal X-ray luminosity in that band would be, as expected, much too weak to compete with the much more powerful thermal X-ray emission that is due to the colliding winds (i.e. in the 1033–1034 erg s−1 range for the O-type PACWBs discussed in this paper, De Becker 2015). Similarly, attempts to detect non-thermal hard X-rays (above 10 keV) require observations with instruments that are characterized by a sensitivity that is good enough to measure the fraction of the total IC emission that is effectively produced in that energy band. However, in the latter case, there is no thermal emission component likely to compete with the expected non-thermal emission. With the example illustrated above, in the 10–79 keV range typical of the hard X-ray instruments on board the NuStar satellite (Harrison et al. 2013), LIC, band ∼ 1033 erg s−1. At a distance of 2 kpc, this translates into a flux of about 10−12 erg cm−2 s−1, which is in the range of the detection level of the non-thermal hard X-ray emission reported for Eta Car by Hamaguchi et al. (2018). In the gamma-ray regime, we estimate for instance the energy emission in the 80–150 MeV range for the e-ASTROGAM mission1, where the sensitivity is expected to be of the order of 10−12 erg cm−2 s−1. The number used here above for WR 140 lead to a IC luminosity of the order of a few 1035 erg s−1, which translates into a flux of the order of a few 10−10 erg cm−2 s−1. We caution, however, as stated above, that the predicted IC luminosities presented here are significantly overestimated. As a result, the actual flux may lie much closer to the sensitivity limit mentioned above.
The discussion developed in this section is especially useful in the context of order-of-magnitude estimates. Relevant refinements should notably consider, for a specific system, what the upper and lower limits on photon energies in the non-thermal spectrum are to be. This would allow clarifying the values that are to be injected in the denominator terms of Eq. (18). We also recall that currently there is no clear warranty that the spectral index is constant throughout the relativistic electron spectrum. Only accurate measurements in hard X-rays and γ-rays would allow us to characterize the shape of the spectrum in detail. Finally, we note that a strict upper limit on the IC luminosity should come from the energy content in non-thermal particles (see the Ppart quantity in Sect. 4.5), and in particular relativistic electrons (Pe). As a result, all quantities considered here should be scaled down to fit the latter requirement. We therefore caution that the predictions based on Eq. (16) appear too severely overestimated (especially for long-period systems), and that a more physically justified strict upper limit on the energy available for IC emission needs to come from the more consistent (with respect to our general approach) energy budget considerations developed in Sect. 4.5.
4.7. Comparison to other approaches
The method followed here is based on the magnetic field determination as a function of partition assumptions for the magnetic field and relativistic particles. This approach deviates from the more restrictive minimum energy assumption proposed first time by Burbidge (1956), as we explicitly explore a wider parameter space covering any value of partition parameters.
The limitations inherent to this partition method have been pointed out by several studies. We first mention the work by Pohl (1993), for instance. The author developed a more rigorous approach to calculating the steady-state populations and energy densities of relativistic electrons and protons, assuming both are injected in the acceleration process with the same initial energy. This method allows removing the usual partition assumption for electrons and protons. These refinements allowed Pohl (1993) to achieve an improvement of a factor 2 in the determination of the magnetic field strength in the galaxy M 51. However, we note that a refinement by a factor 2 is not that significant in the context of this study here, which aims mainly at providing adequate and physically justified orders of magnitude for relevant parameters (including the magnetic field). In addition, the basic equal injection energies for various particles also constitutes an assumption, with no specific warranty that it could apply to the case of PACWBs.
A revised equipartition and minimum energy formula has also been proposed by Beck & Krause (2005). This alternative approach instead used the number density ratio in electrons and protons. However, this refined method still assumed a constant number density ratio of protons and electrons over a given limited range of particle energies. It is also assumed that the same total number of protons and electrons are accelerated. Moreover, according to Beck & Krause (2005), the revised estimates of the magnetic field in the synchrotron emission region deviate by a factor ∼2 with respect to the classical equipartition estimates. Here again, the improvement of this more demanding approach is negligible at the approximation level of our description of the non-thermal physics of PACWBs.
Finally, it is worth mentioning that an alternative determination of the magnetic field may be achieved provided high-energy inverse Compton scattering is measured simultaneously with the radio synchrotron measurement (i.e. at the same orbital phase). If the relativistic electron population responsible for both processes is the same, the ratio of synchrotron-to-inverse Compton luminosities should scale with the ratio of magnetic-to-radiative energy densities (see also Sect. 4.6), allowing for the determination of B in the colliding-wind region (see e.g. De Becker 2007). This has not been achieved so far, however. The reason is the lack of detection of high-energy non-thermal emission from synchrotron radio emitters. The conditions that are likely to lead to the measurement of the two emission components are certainly different, if complementary (De Becker et al. 2017). To date, the only PACWB identified as a particle accelerator thanks to high-energy measurements is Eta Car (Farnier et al. 2011; Leser et al. 2017; Hamaguchi et al. 2018), but it is not known as a synchrotron radio emitter. We also mention the more recent claim of γ-ray emission from the WR + O binary WR 11 based on Fermi observations (Pshirkov 2016; Reitberger et al. 2017). If the physical association of the γ-ray source with the massive binary can be confirmed, WR 11 would be the second example of a non-thermal high-energy emitter, without an indication of synchrotron radio emission (Benaglia 2016). Undoubtedly, the development of high-energy observatories with the required sensitivity to measure non-thermal high-energy emission from PACWBs constitutes a key step to proceed in our understanding of their non-thermal physics.
5. Summary and conclusions
The purpose of this paper was to provide physically justified values for several parameters relevant for the non-thermal physics in PACWBs. We used simple partition considerations to build parameter grids allowing for an overall estimate of the magnetic field strength in their synchrotron emission region. This approach is based on the one hand on an assumed partition between the magnetic field energy density and the relativistic particle energy density, and on the other hand on the partition between electron and proton energy densities. This is the first time such an approach is used in the framework of this class of objects, while similar approaches (but restricted to equipartition) have been applied for decades to the case of emblematic synchrotron sources such as radio galaxies and supernova remnants.
The requirements for this method include a good knowledge of stellar wind parameters, along with a good description of the orbit. Other important inputs are the measured flux densities of the target in the radio domain, which need to be corrected for the contamination by the thermal free-free emission from the individual winds (not resolved by most radio observations). This precaution is especially important for PACWBs, and not at all required for other synchrotron radio sources such as SNRs and radio galaxies. This correction was provided according to the standard model for the free-free emission from expanding stellar envelopes as a function of wind properties, including appropriate adjustments for wind clumping. The correction for the free-free emission is necessary for both the flux densities and the resulting spectral index.
As a test case, this method was applied to three massive systems with rather well-known stellar wind and orbital parameters. The sample of targets consisted of two long-period systems (one O + O type and one WC + O type) and a short-period O + O system. Our results suggest that typical values for the average magnetic field in the synchrotron emission region probably are of the order of mG, while values closer to the G level are anticipated for the short-period system. These significant differences are in line with the trend expected for the geometrical dilution of a photospheric or stellar magnetic field up to the location of the colliding-wind region (combined with a likely magnetic amplification effect). The estimate of the magnetic field (B) as a function of partition parameters allowed us to determine the average normalization parameter (K) for the relativistic particle population. The simultaneous knowledge of B and K is necessary to determine the SSA turn-over frequency. For the long-period systems, the turn-over frequency is of the order of a few MHz, which is well below the Earth ionospheric cut-off. Such frequencies are well below the expected free-free absorption turn-over frequency, certainly of the order of a fraction of GHz for most systems. As a result, SSA is unlikely to affect the measured synchrotron spectrum of long-period systems. However, for the short-period system, the SSA turn-over appears at a few 100 MHz, and may approach GHz for some partition assumptions. The turn-over of the synchrotron spectrum for short-period systems may thus be affected by SSA, in addition to free-free absorption. The very different magnetic environments likely encountered in short- and long-period systems also has consequences on the typical Lorentz factors of relativistic electrons that are necessary to produce synchrotron radio emission in the measured relevant frequency range for PACWBs, that is, from 10–100 for short-period systems to a few 100–1000 for long-period systems. Order-of-magnitude estimates for the IC luminosity were also computed. However, our predictions are much too optimistic for long-period systems. We caution that the simple estimates produced here would never compete with more detailed approaches that rely on a more consistent modelling.
It must be clarified that the approach presented here would deserve to be applied to more systems, upon availability of the required information, in order to check whether the trends observed for long-period and short-period binaries are confirmed on a larger sample of targets. This constitutes a real motivation to pursue observational efforts to derive orbital elements and obtain accurate radio measurements of massive binaries. In addition, repeating such investigations along the orbit of some specific eccentric systems is probably likewise quite instructive for following the evolution of the magnetic field and energy densities as a function of the orbital phase. This would require a detailed use of radio data time-series along with a careful inspection of the effect of the varying free-free absorption, which is beyond the scope of this study. The rather low emission level of PACWBs in hard X-rays suggests actual values of ηmag and η should be reasonably high, that is, significantly higher than 1. Lower values lead to predicted IC luminosities that are too high considering the wind kinetic power of these objects.
This approach is affected by significant inherent limitations, in particular considering the implicit assumption that relativistic protons and electrons share a constant and identical index for the power-law distributions of both types of particles. Relaxing this limitation would require a much more detailed description of the particles distributions, based on an appropriate modelling of the cooling and transport processes that (differently) affect electrons and other relativistic particles. It would also require appropriate measurements of non-thermal high-energy radiation, which is still lacking for all synchrotron radio emitters. We also emphasize the high sensitivity of physical parameters to the synchrotron spectral index. Accurate measurements combined with appropriate corrections for free-free absorption and emission constitute a strong requirement. To date, the considerations developed here constitute the most straightforward approach to derive relevant average values for many physical parameters involved in the non-thermal physics of PACWBs.
Acknowledgments
The author warmly thanks the anonymous referee for a very positive and constructive report that significantly helped to improve the manuscript. The ADS database was used for the bibliography.
References
- Beck, R., & Krause, M. 2005, Astron. Nachr., 326, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Benaglia, P. 2016, PASA, 33, e017 [NASA ADS] [CrossRef] [Google Scholar]
- Benaglia, P., & Romero, G. E. 2003, A&A, 399, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blomme, R., De Becker, M., Runacres, M. C., van Loo, S., & Setia Gunawan, D. Y. A. 2007, A&A, 464, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blomme, R., De Becker, M., Volpi, D., & Rauw, G. 2010, A&A, 519, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burbidge, G. R. 1956, ApJ, 124, 416 [NASA ADS] [CrossRef] [Google Scholar]
- Castelletti, G., Dubner, G., Brogan, C., & Kassim, N. E. 2007, A&A, 471, 537 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Condon, J., & Ransom, S. 2016, Essential Radio Astronomy (Princeton, NJ: Princeton University Press) [CrossRef] [Google Scholar]
- Crowther, P. A. 2007, ARA&A, 45, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Davidge, T. J., & Forbes, D. 1988, MNRAS, 235, 797 [NASA ADS] [Google Scholar]
- De Becker, M. 2007, A&ARv., 14, 171 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M. 2015, MNRAS, 451, 1070 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M., & Raucq, F. 2013, A&A, 558, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Becker, M., Rauw, G., & Manfroid, J. 2004, A&A, 424, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Becker, M., Sana, H., Absil, O., Le Bouquin, J.-B., & Blomme, R. 2012, MNRAS, 423, 2711 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M., Benaglia, P., Romero, G. E., & Peri, C. S. 2017, A&A, 600, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- del Palacio, S., Bosch-Ramon, V., Romero, G. E., & Benaglia, P. 2016, A&A, 591, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dougherty, S. M., Pittard, J. M., Kasian, L., et al. 2003, A&A, 409, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dougherty, S. M., Trenton, V., & Beasley, A. J. 2011, Bull. Soc. Roy. Sci. Liège, 80, 658 [NASA ADS] [Google Scholar]
- Drew, J. E. 1990, in Properties of Hot Luminous Stars, ed. C. D. Garmany, ASP Conf. Ser., 7, 230 [NASA ADS] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Dubner, G., & Giacani, E. 2015, A&ARv., 23, 3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eichler, D., & Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Fahed, R., Moffat, A. F. J., Zorec, J., et al. 2011, MNRAS, 418, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Falceta-Gonçalves, D., & Abraham, Z. 2012, MNRAS, 423, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Farnier, C., Walter, R., & Leyder, J.-C. 2011, A&A, 526, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamaguchi, K., Corcoran, M. F., Pittard, J. M., et al. 2018, Nat. Astron., 2, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bouquin, J.-B., Sana, H., Gosset, E., et al. 2017, A&A, 601, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leitherer, C., Forbes, D., Gilmore, A. C., et al. 1987, A&A, 185, 121 [NASA ADS] [Google Scholar]
- Leitherer, C., Chapman, J. M., & Koribalski, B. 1995, ApJ, 450, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Leser, E., Ohm, S., & Füßling, M. 2017, in 35th Int. Cosmic Ray Conf, Proceedings of Science, 301, 717 [Google Scholar]
- Longair, M. S. 1992, High Energy Astrophysics, 2nd ed. (Cambridge University Press) [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merten, L., Becker Tjus, J., Eichmann, B., & Dettmar, R.-J. 2017, Phys., 90, 75 [Google Scholar]
- Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neiner, C., Grunhut, J., Leroy, B., De Becker, M., & Rauw, G. 2015, A&A, 575, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panagia, N., & Felli, M. 1975, A&A, 39, 1 [Google Scholar]
- Pittard, J. M., & Dougherty, S. M. 2005, Massive Stars and High-Energy Emission in OB Associations, 57 [Google Scholar]
- Pohl, M. 1993, A&A, 270, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Pshirkov, M. S. 2016, MNRAS, 457, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reimer, A., Pohl, M., & Reimer, O. 2006, ApJ, 644, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B. 2008, The Young Cluster NGC 6604 and the Serpens OB2 Association, ed. B. Reipurth (ASP), 590 [Google Scholar]
- Reipurth, B., & Schneider, N. 2008, Star Formation and Young Clusters in Cygnus, ed. B. Reipurth (ASP), 36 [Google Scholar]
- Reitberger, K., Kissmann, R., Reimer, A., & Reimer, O. 2017, ApJ, 847, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Runacres, M. C., & Owocki, S. P. 2002, A&A, 381, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley-Interscience) [Google Scholar]
- Sander, A., Hamann, W.-R., & Todt, H. 2012, A&A, 540, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usov, V. V., & Melrose, D. B. 1992, ApJ, 395, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, P. M., van der Hucht, K. A., Pollock, A. M. T., et al. 1990, MNRAS, 243, 662 [NASA ADS] [Google Scholar]
- Wright, A. E., & Barlow, M. J. 1975, MNRAS, 170, 41 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Magnetic field
We assume a synchrotron-emitting region with a volume V, producing a spectrum with spectral index α = (p − 1)/2 that is valid for a relativistic electron energy spectrum defined as
where K is the normalization parameter of the relativistic electron population.
Using the expression of the emissivity J(ν) (energy per unit time, per unit volume, per unit frequency) for a population of relativistic electrons in cgs units as given by Rybicki & Lightman (1979), the spectral luminosity can be expressed as follows:
with
and
is made of Gamma functions (Γ) dependent on the electron index (p) only. This set of equations will in turn allow us to express the normalization parameter of the relativistic electron population,
For energetic considerations, we adopt the following partition relations:
The latter relation is especially designed to consider any assumed partition between magnetic field and relativistic particles, and not only minimum energy or equipartition, as frequently assumed (e.g. Rybicki & Lightman 1979; Longair 1992; Condon & Ransom 2016).
The magnetic energy density is expressed by
and the relativistic particle energy density is
The maximum intensity of synchrotron radiation from one electron occurs at a frequency ν = 0.29 νc, where νc is the critical frequency (see e.g. Rybicki & Lightman 1979),
Assuming an isotropic distribution of pitch angles θ ( ), we obtain the typical frequency of synchrotron photons produced by electrons with Lorentz factor γ in a magnetic field B (considering relativistic electrons with v ∼ c),
), we obtain the typical frequency of synchrotron photons produced by electrons with Lorentz factor γ in a magnetic field B (considering relativistic electrons with v ∼ c),
Using the direct relation between the electron energy E and the Lorentz factor (E = γ me c 2), and including all constants in a given constant C, we have
with
As a result, we can express the integration boundaries of Eq. (A.8) in terms of frequencies:
Starting with Eq. (A.6), and using Eqs. (A.7), (A.8), (A.1), and (A.4), we can derive an expression for the average magnetic field in the synchrotron emitting region:
with
Appendix B: Free-free radio emission
The free-free emission by individual stellar winds can be calculated on the basis of the equations established by Wright & Barlow 1975 (or equivalently, by Panagia & Felli 1975),
with
and, in the Rayleigh-Jeans limit,
The Gaunt factor is expressed, according to Leitherer et al. (1995), as
The electron temperature (Te) is set as 0.5 times the effective temperature (Teff), as suggested by Drew (1990). d is the distance to the stellar system. For O-type stars, we assume solar abundances and a partial ionization, leading to values of the molecular weight (μ), the mean electron number (Z), and the RMS ionic charge (γ) of 1.8, 1.0, and 1.0, respectively. For a WC wind mainly made of He, these parameters were set to 4.0, 1.0, and 1.0, respectively. Details on these quantities and the way to compute them are given by Leitherer et al. (1995).
We note that the Ṁ parameter is multiplied by the square root of the clumping factor (fcl), accounting for the dependence of the free-free emission process on the square of the density of the emitting plasma (see e.g. Puls et al. 2006). As a result, the free-free flux density accounting for clumping ( ) is related to the flux density of smooth wind (
) is related to the flux density of smooth wind (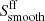 ) with the same mass-loss rate in this way:
) with the same mass-loss rate in this way:
Stellar winds are radio optically thick, and consequently, the measured free-free emission comes from their outer parts. As a result, the clumping factor that is adequate for correcting radio flux densities is the one that is valid in the outer wind. According to the predictions by Runacres & Owocki (2002), fcl converges asymptotically to a value of the order of 4 for various sets of model parameters. This is the value we adopted in this study.
All Tables
Dynamical timescale (tdyn), total wind kinetic power (Pkin,wind), and total radio synchrotron luminosity (Lsynch) for the three targets.
All Figures
 |
Fig. 1. Illustration of the synchrotron-emitting region as a spherical cap (thick solid black lines). The thick blue curve represents the contact discontinuity of the wind-wind interaction region wrapped around the star with the weakest wind (lower blue filled circle). |
| In the text | |
 |
Fig. 2. Block diagram of the various steps involved in our approach to determine the physical parameters. The meaning of the numbers associated with every step is explained in Sect. 2.3. Yellow shows measured quantities, green the required parameters, blue represents intermediate computed quantities, orange shows assumed quantities, and red the output physical quantities. |
| In the text | |
 |
Fig. 3. Magnetic field strength as a function of ηmag for three different values of η for Cyg OB2 #8A. |
| In the text | |
 |
Fig. 4. Energy densities as a function of ηmag for three different values of η for Cyg OB2 #8A. Black, blue, and red curves represent the total (in black), the magnetic (Umag, in red), and the relativistic particles (Upart, in blue) energy densities. |
| In the text | |
 |
Fig. 5. Same as Fig. 3, but for HD 167971. |
| In the text | |
 |
Fig. 6. Same of Fig. 4, but for HD 167971. |
| In the text | |
 |
Fig. 7. Same as Fig. 3, but for WR 140. |
| In the text | |
 |
Fig. 8. Same as Fig. 4, but for WR 140. |
| In the text | |
 |
Fig. 9. Lorentz factor required to produce synchrotron radio photons at frequencies of 500 MHz and 10 GHz as a function of the magnetic field strength in the synchrotron emission region. Ranges appropriate for the long-period and short-period results are indicated by thick horizontal lines. |
| In the text | |
 |
Fig. 10. Upper panel: normalization factor of the relativistic electrons population for Cyg OB2 #8a. Lower panel: corresponding SSA turn-over frequency. Both quantities are plotted as a function of ηmag for three assumed values of η. |
| In the text | |
 |
Fig. 11. Same as Fig. 10, but for HD 167971. |
| In the text | |
 |
Fig. 12. Same as Fig. 10, but for WR 140. |
| In the text | |
 |
Fig. 13. fmag (top panel), fpart (middle panel), and fe (bottom panel) for Cyg OB2 #8a as a function of ηmag, for three assumed values of η. |
| In the text | |
 |
Fig. 14. Same as Fig. 13, but for HD 167971. |
| In the text | |
 |
Fig. 15. Same as Fig. 13, but for WR 140. |
| In the text | |
 |
Fig. 16. Predicted IC luminosity (LIC ) for Cyg OB2 #8a as a function of ηmag for three assumed values of η. |
| In the text | |
 |
Fig. 17. Same as Fig. 16, but for HD 167971. |
| In the text | |
 |
Fig. 18. Same as Fig. 16, but for WR 140. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} B = \Bigg [\frac{8\pi \,\eta \,\eta _{\text{mag}}\,L_\nu \,G(\alpha )}{V}\Bigg ]^{\frac{2}{7}}.\end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq1.gif)
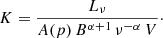
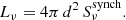
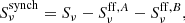
![$$ \begin{aligned} \alpha {^\prime } = \frac{\log \Bigg [\frac{S_{\nu ,1}^\mathrm{synch}}{S_{\nu ,1}^\mathrm{synch}}\Bigg ]}{\log \bigg [\frac{\nu _1}{\nu _2}\bigg ]},\end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq10.gif)
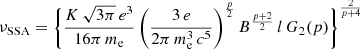
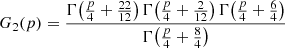
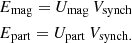
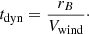
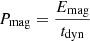
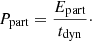
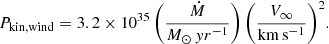
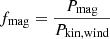
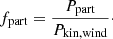
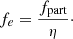
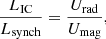
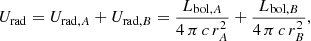
![$$ \begin{aligned} L_{\rm IC} = \frac{L_{\rm synch}}{U_{\rm mag}}\,\bigg [\frac{L_{\mathrm{bol},A}}{4\,\pi \,c\,r_A^2} + \frac{L_{\mathrm{bol},B}}{4\,\pi \,c\,r_B^2}\bigg ],\end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq31.gif)
![$$ \begin{aligned} L_{\rm synch} = \frac{L_\nu \,\nu ^{\alpha }}{(1 - \alpha )}\,\bigg [\nu _{\rm max}^{1 - \alpha } - \nu _{\rm min}^{1 - \alpha }\bigg ]. \end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq32.gif)
![$$ \begin{aligned} L_{\rm IC,band} = L_{\rm IC}\,\frac{\bigg [E_{\rm max,band}^{1-\alpha } - E_{\rm min,band}^{1-\alpha }\bigg ]}{\bigg [E_{\rm max}^{1-\alpha } - E_{\rm min}^{1-\alpha }\bigg ]}\cdot \ \end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq33.gif)
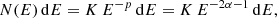
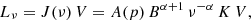
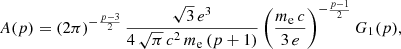
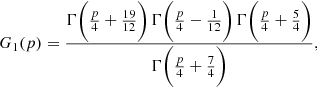
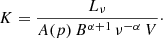
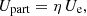
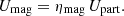
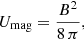
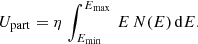
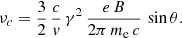
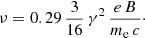
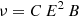
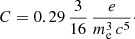
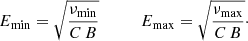
![$$ \begin{aligned} B = \Bigg [\frac{8\pi \,\eta \,\eta _{\rm mag}\,L_\nu \,G(\alpha )}{V}\Bigg ]^{\frac{2}{7}} \end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq49.gif)
![$$ \begin{aligned} G(\alpha ) = \frac{1}{p-2}\,\frac{C^{\alpha - 1/2}}{A(p)}\,\nu ^\alpha \,\bigg [\nu _{\rm min}^{-\alpha + 1/2} - \nu _{\rm max}^{-\alpha + 1/2}\bigg ]. \end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq50.gif)
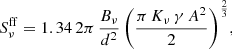
![$$ \begin{aligned} K_\nu = 3,68\,10^8\,Z^2\,\sqrt{T_{\rm e}}\,\nu ^{-3}\,\bigg [1 - \exp \bigg (-\frac{h\nu }{kT_{\rm e}}\bigg )\bigg ]\,{ g}_{\rm ff}, \end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq52.gif)
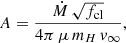
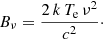
![$$ \begin{aligned} { g}_{\rm ff} = 9.77\,\Bigg [1 + 0.13\,\log \bigg (\frac{T_{\rm e}^{3/2}}{Z\,\nu }\bigg )\Bigg ]\cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa34101-18/aa34101-18-eq55.gif)