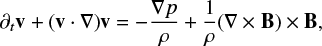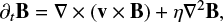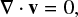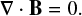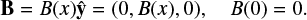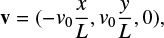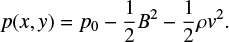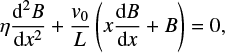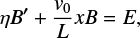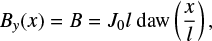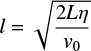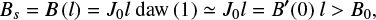| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A159 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201833752 | |
| Published online | 12 December 2018 | |
Flows and magnetic field structures in reconnection regions of simulations of the solar atmosphere: Do flux pile-up models work?
1
Department of Mathematics, Physics and Electrical Engineering, Northumbria University, Newcastle upon Tyne NE1 8ST, UK
e-mail: shelyag@gmail.com
2
Department of Mathematics, University of Waikato, P. B. 3105, Hamilton, New Zealand
3
Plasma Dynamics Group, Department of Automatic Control and Systems Engineering, University of Sheffield, Sheffield S1 3JD, UK
4
Plasma Dynamics Group, School of Mathematics and Statistics, University of Sheffield, Sheffield S3 7RH, UK
5
Instituto de Geofísica, Unidad Michoacán, Universidad Nacional Autónoma de México, Morelia, Michoacán, Mexico
6
Laboratorio de Inteligencia Artificial y Supercómputo., Instituto de Física y Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Morelia, Michoacán, Mexico
Received:
1
July
2018
Accepted:
21
September
2018
Aims. We study the process of magnetic field annihilation and reconnection in simulations of magnetised solar photosphere and chromosphere with magnetic fields of opposite polarities and constant numerical resistivity.
Methods. Exact analytical solutions for reconnective annihilations were used to interpret the features of magnetic reconnection in simulations of flux cancellation in the solar atmosphere. We used MURaM high-resolution photospheric radiative magneto-convection simulations to demonstrate the presence of magnetic field reconnection consistent with the magnetic flux pile-up models. Also, a simulated data-driven chromospheric magneto-hydrodynamic simulation is used to demonstrate magnetic field and flow structures, which are similar to the theoretically predicted ones.
Results. Both simulations demonstrate flow and magnetic field structures roughly consistent with accelerated reconnection with magnetic flux pile-up. The presence of standard Sweet–Parker type reconnection is also demonstrated in stronger photospheric magnetic fields.
Key words: Sun: atmosphere / Sun: magnetic fields / Sun: photosphere / Sun: chromosphere
© ESO 2018
1. Introduction
The observational term “cancellation” describes the disappearance of magnetic flux of either sign at the polarity inversion line that separates the magnetic fragments with opposite polarity in the solar photosphere (Livi et al. 1985; Martin et al. 1985). Photospheric cancellation appears to be a key dynamic process in the removal of solar magnetic flux and in the formation and evolution of solar filaments (Martens & Zwaan 2001; Martin et al. 2008; Panasenco et al. 2014). Cancellation remains a subject of active research, based on the data from several instruments, including the Solar Dynamics Observatory (Zeng et al. 2013; Yardley et al. 2016).
Observations of evolving magnetic features in the photosphere strongly suggest that magnetic reconnection in a photospheric or chromospheric current sheet, rather than simple submergence, is the cancellation mechanism (Martin 1990; Chae 2012). Photospheric magnetic fragments originate as bipoles but cancel with external fields. Fragments with the same polarity do not cancel each other out on encounter but rather merge to form a single larger magnetic feature, whereas cancelling fragments of opposite polarity usually slow down on encounter, indicating that mutual interaction takes place. On the theoretical side, a model of flux pile-up reconnection in a Sweet–Parker current sheet (Parker 1957), suitably modified for a compressible, weakly ionised photospheric plasma, can explain the properties of cancelling magnetic features, such as the speeds of the cancelling magnetic fragments and the flux cancellation rates, inferred from the data (Litvinenko 1999; Litvinenko et al. 2007; Park et al. 2009).
Magnetic energy release in a chromospheric reconnecting current sheet leads to bulk heating of the chromospheric plasma, balanced by radiative cooling (Litvinenko & Somov 1994). Except for very small cancelling features, thermal conduction can be neglected. Radiation is the dominant mechanism of energy loss from the chromospheric current sheet. The high density and low temperature in the current sheet also mean that particle acceleration by the reconnection electric field is inefficient (Litvinenko 2015).
Reconnection also converts a part of the free magnetic energy into the kinetic energy of reconnection jets. The jets travel with a local Alfvén speed vA which is of order a few km s−1 in the photosphere. Hα and magnetogram data do indeed show that photospheric cancellation is accompanied by plasma upflows (Litvinenko & Martin 1999; Bellot Rubio & Beck 2005) and downflows (Chae et al. 2004). The speeds of ubiquitous quiet-Sun jets (Martínez Pillet et al. 2011) are consistent with the reconnection outflow speeds in the range of 3–10 km s−1, predicted by photospheric reconnection models (Litvinenko 1999; Litvinenko et al. 2007).
Much faster chromospheric jets are associated with explosive events, detected by ultraviolet (UV) and extreme-ultraviolet (EUV) observations of the upper chromosphere and transition region. The explosive events correlate with photospheric cancellation (Dere et al. 1991) or, more generally, with changes of the photospheric magnetic structure (Muglach 2008). The photospheric jets with speeds of the order of a few km s−1 and the chromospheric jets with speeds of up to 100 km s−1 are thought to be direct signatures of magnetic reconnection at the corresponding heights (Innes et al. 1997; Nelson et al. 2016). High-resolution observations of Ellerman bombs (Watanabe et al. 2011; Vissers et al. 2013) suggest that local photospheric reconnection can cause the magnetic field relaxation on a larger scale, leading to the photospheric and chromospheric jet generation (Reid et al. 2015). Additionally, Yan et al. (2015) argued that self-absorption features in transition region lines imply similar magnetic field changes in a range of observational phenomena (explosive events, blinkers, Ellerman bombs), which only differ by the height of a magnetic reconnection site. It appears, therefore, that photospheric cancellation can create favourable conditions for the generation of the photospheric and chromospheric jets, either directly or by triggering the release of stored magnetic energy on a larger scale.
In this paper, we have used a combination of numerical magneto-hydrodynamic simulations and exact analytical solutions for magnetic field reconnection to demonstrate the presence of magnetic pile-up mechanism, accelerating reconnection process. Also, we demonstrate the presence of outflows produced by the reconnection with magnetic pile-up.
The paper is organised as follows. In Sect. 2, we outline an analytical model for reconnection with magnetic field pile-up. Section 3 describes the simulation setup we use for the analysis of reconnection regions in photospheric magneto-convection simulations. In Sect. 4, using averaging over the current sheet surroundings in the simulated reconnection regions, we demonstrate presence of magnetic pile-up, consistent with the theoretical model. Section 5 is devoted to the simulated chromospheric reconnection and flow structure in the reconnection region. Section 6 concludes our findings.
2. Analytical models of magnetic annihilation with flux pile-up
Magnetic flux pileup merging (annihilation) is one of the few models of magnetic reconnection for which detailed analytical description is available (Priest & Forbes 2000). Exact analytical solutions for the annihilation of planar magnetic fields, driven by a stagnation-point flow in an incompressible resistive plasma, were discovered by Clark (1964, 1965) and independently by Parker (1973) and Sonnerup & Priest (1975). Later the solutions were generalised to describe reconnective annihilation of magnetic fields in a current sheet in two and three dimensions (Craig & Henton 1995; Craig et al. 1995; Craig & Fabling 1996) and incorporate numerous potentially important effects, such as plasma viscosity (Craig & Litvinenko 2012) and a non-vanishing curvature of the current sheet (Watson & Craig 2002; Litvinenko 2013). Although no analogous exact solutions for magnetic merging in a compressible plasma had been obtained, the incompressible reconnection model with flux pileup was argued to yield robust magnetic reconnection scalings (Litvinenko & Craig 2003).
Predictions of the analytical theory of flux pileup merging were found to be in good quantitative agreement with the results of numerical simulations performed in a two-dimensional periodic geometry (Heerikhuisen et al. 2000). We are not yet aware of a detailed application of the theory to simulation results obtained in a more realistic geometry lacking a high symmetry, which motivates us to employ the analytical model to investigate how the geometry of magnetic merging controls the observable signatures of magnetic reconnection in our simulations of the photospheric dynamics. Specifically we are interested in the role played by the velocity and magnetic field geometry in quantifying the rate of magnetic energy dissipation and the generation of vertical reconnection-related jets. Following Craig et al. (1995), we present an illustrative solution in the limiting case of the planar annihilating magnetic field lines that is parallel to the plane of the velocity field of a stagnation-point flow.
We seek solutions of the governing magnetohydrodynamic (MHD) equations for the velocity v and magnetic field B in an incompressible resistive plasma: the momentum equation
the induction equation
the incompressible continuity equation
and the divergence-free condition for the magnetic field
Here, ρ is the plasma density, η is the magnetic diffusivity, and p is the plasma pressure. The magnetic field in the equations is normalised by 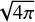 for convenience.
for convenience.
To emphasise the key features of the model, we considered the simplest case of magnetic field annihilation in a flat current sheet located at x = 0:
Suppose that the merging is driven by an incompressible plasma flow of the form
where L > 0 is the characteristic lengthscale and v0 is the inflow speed at an outer boundary. Since the magnetic field lines are parallel to the plane of the velocity field, they are driven together by the stagnation-point flow. The resulting magnetic field build-up at the entrance to the sheet leads to a thinner sheet and a faster rate of magnetic energy dissipation. The equation of motion gives the pressure profile
The induction equation (Eq. (2)) becomes
which, after integrating once, reduces to
where E = ηJ0 is the merging electric field, and J0 = B′(0) is the integration constant corresponding to the electric current density at the centre of the current sheet. The equation is integrated to yield the magnetic field profile
where
is the thickness of the current sheet, and daw denotes Dawson’s integral (e.g. Oldham et al. 2009).
For comparison with the simulations, analysed below, we assume the mean flow speed in the domain (v0 ∼ 3 km s−1), the characteristic length, corresponding to the granular spatial scale (L ∼ 1 Mm), and the constant magnetic diffusivity η = 2 × 1010 cm2 s−1, which is used to ensure numerical stability of the simulations. The resulting theoretical profile of the magnetic field across the current sheet is shown in Fig. 1. The exact solution gives the scaling for the magnetic pile-up region and current sheet thickness, which is of the order of 30–40 km, as is evident from the figure.
 |
Fig. 1. Dawson function, corresponding to the reconnecting magnetic field profile around the current sheet. The current sheet thickness l was chosen according to the simulation parameters. |
 |
Fig. 2. Horizontal cuts of the temperature (left panel) and the vertical component of magnetic field (right panel) in the domain, taken at a height of ∼300 km above the continuum formation height. Small-scale temperature enhancements up to 7700 K indicate current sheets in the centres of magnetic reconnection regions. These regions can be clearly seen in the right panel, where magnetic fields of opposite polarities merge. The reconnection region example, shown in Fig. 3, is located at (2,3) Mm. |
The main feature of the solution is that thinner sheets, faster inflows, and larger dissipation rates are possible when the field build-up is strong, so the magnetic field at the entrance to the current sheet is greater than B0,
where B0 is the magnetic field far from the current sheet. Such situations are likely to be the case in a high-beta photospheric plasma.
 |
Fig. 3. Algorithm for determining the magnetic field and flow structure around reconnection current sheets, and magnetic field and flow structure around a simulated photospheric reconnection region. Left panel: an example of the averaging algorithm used for diagnostics of the simulated data. The background image is the horizontal cut of the temperature at the height of 300 km above the average continuum formation height. It shows the temperature enhancements in the current sheet region due to the current dissipation. The axes units are grid cells with 6.25 km per grid cell. The green lines are constructed to align with the direction of the strongest change of vertical component of magnetic field at each point of the current sheet. The velocities are projected onto the direction parallel to the strongest gradient direction. Right panel: the vertical component of magnetic field. Arrows indicate the horizontal plasma flow direction. A flow, converging towards the reconnection region is clearly visible. |
3. Numerical model of the solar photosphere with reconnecting magnetic fields
We used the MURaM code (Vögler et al. 2005) to produce the data on plasma parameters in photospheric reconnection events. The code solves the system of radiative magneto-hydrodynamic equations with constant resistivity. The numerical setup is essentially a higher-resolution version of the one used by Nelson et al. (2013), and is only briefly described here. The horizontal extent of the domain is 6 × 6 Mm, which are resolved by 960 × 960 grid cells. The vertical extent is 1.6 Mm, resolved by 320 grid cells. This leads to the resolution of 6.25 km and 5 km per grid cell in the horizontal and vertical directions, respectively. The domain is positioned such that the continuum formation layer is located 1 Mm above the bottom boundary. Four-bin non-grey radiative transport is used in the simulation. The side boundary conditions are periodic, the top boundary is closed, and the bottom boundary is open for flows.
To simulate small-scale reconnection events in the integranular lanes of photospheric convection, we used a 4 × 4 checkerboard pattern of vertical magnetic field with constant unsigned strength of 200 G. The magnetic field configuration was added into a well-developed non-magnetic self-consistent convection model. Then the model is evolved for ten minutes of physical time. During these, the magnetic field, after initial uniform field annihilation phase, gets advected into the intergranular lanes of simulated granulation. The inter-granular magnetic field concentrations with the (nearly vertical) field strength of ∼1.7 kG randomly move along inter-granular lanes, being buffeted by the granular flows with the mean speed 〈vh〉 ≈ 2.8 km s−1 at the photospheric level, occasionally come in close proximity to each other and reconnect. This leads to appearance of current sheets, which resistively dissipate and heat the plasma. Such events are demonstrated in Fig. 2. In the figure, the horizontal cuts of temperature and of the vertical component of magnetic field at the height of 300 km above the average continuum formation layer in the domain are shown. Small-scale temperature enhancements (left panel) up to 7700 K, which is 3000 K higher than the average temperature at the corresponding height, clearly indicate the locations at which the opposite polarity magnetic fields reconnect (right panel of the figure). These events are studied in the following section.
 |
Fig. 4. Reconnection and magnetic flux pile-up. Left column: vertical magnetic field map around the reconnection region. Green boxes identify the averaging regions. Middle and right columns: average vertical magnetic field and the horizontal inflow into the current sheet dependences on the distance from the current sheet, respectively. The first three rows demonstrate the magnetic flux pile-up at the scale predicted by the pile-up reconnection model. The fourth row shows stronger reconnecting magnetic fields and does not show the localised enhancements of the vertical magnetic field in proximity of the current sheet. |
4. Simulated reconnection events
A number of reconnection events have been identified in the simulated time series. In order to reveal the features corresponding to magnetic flux cancellation in these events, some averaging is required to remove local fluctuations of the flow and magnetic field due to turbulent convection. Therefore, to analyse the structure of magnetic field and flow surrounding the identified reconnection regions, we designed a programme, which computes the average profiles of vertical magnetic field and speed of inflow into the reconnection regions.
An example of identified reconnection region is shown in Fig. 3. The temperature and vertical component of magnetic field are shown in the left and right panels of the figure, respectively. The reconnection current sheet region is, as expected, located in the region of strongest change in the magnetic field, which includes the change of the polarity. To numerically localise the reconnection current sheet, we computed the gradient of the vertical component of magnetic field d = ∇ Bz. The maximum of the gradient therefore identifies the location of the current sheet. A unit vector in the direction of the strongest change of the vertical magnetic field 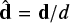 identifies then the direction, over which the inflow speed and the magnetic field profile are measured. The direction sign is chosen that way the gradient of the magnetic field is positive in the current sheet. The horizontal components of velocity are projected onto the direction, therefore, the positive sign of flow speed corresponds to the inflow into the current sheet from the left. Finally, the net velocity component relative to the current sheet was subtracted from the velocity profiles.
identifies then the direction, over which the inflow speed and the magnetic field profile are measured. The direction sign is chosen that way the gradient of the magnetic field is positive in the current sheet. The horizontal components of velocity are projected onto the direction, therefore, the positive sign of flow speed corresponds to the inflow into the current sheet from the left. Finally, the net velocity component relative to the current sheet was subtracted from the velocity profiles.
This routine was repeated in the selected region of the current sheet for each of its pixels, identified as the maximum of the magnetic field gradient. Thus, the averaging was performed over the model slices, interpolated onto the direction of the strongest change of the magnetic field, and centred at the current sheet location. The result of the routine is demonstrated in the left panel of Fig. 3. The green lines show the directions of averaging. The averaging was done over the distance interval ± 150 km from the current sheet.
Examples of the magnetic field and flow structure around the identified reconnections are shown in Fig. 4. The examples were selected according to the following requirements. The thickness of the magnetised region has to be significantly larger than the thickness of the current sheet. Also, we aimed to select the regions with smooth flows around the reconnection region. The selection is carried out by visual inspection. Finally, we aimed for averaging over 50 or more automatically constructed rays.
 |
Fig. 5. Vertical magnetic field component (left panel) and the perpendicular velocity structure in the magnetic flux cancellation region of the cromospheric simulation. |
 |
Fig. 6. Magnetic field geometry and velocity structure in the reconnection region. The background greyscale image shows the vertical cut (x and z are horizontal and vertical directions respectively) of the vertical component of the magnetic field in the domain. Height z = 0 corresponds to the photospheric level. Solid curves show the magnetic field lines (colours correspond to the magnetic field direction). The horisontal velocity component in the plot corresponds to the velocity, perpendicular to the current sheet. The thin black dash-dotted line shows the height, where the parameters for Fig. 5 were measured. |
Maps of the vertical component of magnetic field are shown in the left column of Fig. 4. The averaging regions are identified as green boxes in the panels. The resulting average vertical magnetic field and reconnection inflow depedencies on the distance from the current sheet are shown in the second and third columns, respectively. The first three rows clearly show magnetic field pile-up around the reconnection region at x = 0. The profile of the vertical component of magnetic field is in a good agreement with the theoretical model profile shown in Fig. 1, demonstrating magnetic field intensification around the neutral line x = 0. The distance between the local maxima is of the order of 10–20 km, again in a good agreement with the theoretical model of flux pile-up reconnection. The flows around the reconnection regions show smooth behaviour, gradually decreasing in magnitude towards the current sheet, roughly corresponding to the linear dependence of inflow as required by Eq. (6).
The event shown in the fourth row of Fig. 4 differs significantly from the first three reconnection events. Here, the magnetic field further away from the reconnection region is significantly (by a factor of almost two) stronger than in the previous cases. The magnetic field profiles do not exhibit the flux pile-up near the reconnection region, and the flow structure shows the behaviour opposite to the required by Eq. (6). Indeed, the flow velocity increases towards the reconnection region, leading to the velocity gradient of 4 km s−1, while in the cases with magnetic flux pile-up the corresponding gradient is about 2 km s−1. This indicates a different reconnection regime, more consistent with the standard Sweet–Parker reconnection with the (large, but for numerical stability reasons only) constant resistivity.
Summarising the above, in resistive magneto-convection photospheric simulations with constant resistivity and opposite polarities of magnetic field, two magnetic field cancellation regimes are observed. In weaker magnetic fields, the flux pile-up regime of reconnection with a smooth inflow into the reconnection region and characteristic amplification of the magnetic field near the current sheet is identified. Therefore, the magnetic field cancellation and the magnetic energy release is intensified by the flux pile-up process. Contrary to the previous case, in stronger magnetic fields the flow profile shows a sharp jump across the reconnection region, while the magnetic field does not intensify, therefore indicating a different, Sweet–Parker-like, reconnection mechanism.
5. Chromospheric reconnection and outflows
Similar velocity and magnetic field features were found in a simulation of ideal resistive chromospheric reconnection. The simulation is based on potential (current-free) extrapolation of the photospheric magnetic field, obtained from a low-resolution bipolar MURaM simulation (Shelyag et al. 2012; Nelson et al. 2013). The three-dimensional force-free magnetic field structure is then embedded into a hydrostatic chromospheric model and released to evolve for 60 s of physical time. The simulation was carried out in a 3D numerical domain of the size x ∈ [0,6], y ∈ [0,6], z ∈ [0,10] Mm, covered with 240 × 240 × 400 grid cells (the effective resolution is 25 km in each direction). The constant magnetic diffusivity value used in the code is η = 1012 cm2 s−1. This large diffusivity value gives the thickness of the current sheet l ≈ 500 km, according to Eq. (11). Further detail and simulation processes are provided in González-Avilés et al. (2018).
The simulation is analysed in a similar manner to the described in Sect. 3. The vertical component of the reconnecting magnetic field and the horizontal velocity, perpendicular to the manually identified current sheet, measured at the height of 1 Mm above the photospheric level are shown in Fig. 5. The constant velocity at the current sheet position was subtracted from the data. As can be seen in the figure, the situation in this simulation is more complex. In the left part of the region around the current sheet (x < 0), a clear pattern of magnetic pile-up (local increase of magnetic field with nearly linear inflow into the reconnection region) is present. However, in the right part of the reconnection region (x > 0), where the magnetic field is about three times stronger than in the left part, no pile-up is observed, and the structure is consistent with the fourth row of Fig. 4 and with Sweet–Parker-like reconnection.
Figure 6 shows the magnetic field geometry and the velocity structure in the vertical domain cut along the direction perpendicular to the current sheet. The simulation demonstrates a diverging velocity field, caused by compression of magnetic field lines of opposite polarities in the horizontal direction with the flow at around 1 Mm. This leads to appearance of the velocity null-point at x = 800 km and z = 1000 km, chromospheric upflow, emerging from the reconnection region above the null-point, and a downflow below it.
6. Conclusions
A relatively simple, one-dimensional exact analytical description of magnetic reconnection with flux pile-up allows for magnetic flux cancellation rates, which are higher than obtained in standard Sweet–Parker-type reconnection. Flux pile-up allows to circumvent small reconnection rates of Sweet–Parker models, caused by low resistivity of the solar plasmas (although due to small ionisation fraction, magnetic Reynolds number in the chromosphere can be as low as 10–102; see for example, Khomenko & Collados 2012; Shelyag et al. 2016).
In this paper we used detailed three-dimensional resistive magneto-hydrodynamic models of the solar (sub-)photosphere and chromosphere with constant resistivity to demonstrate the presence of the magnetic pile-up mechanism. The photospheric data we used was generated with MURaM code and includes magnetic field concentrations of opposite polarities. The magnetic concentrations are allowed to move freely under the photospheric convective flow field and occasionally reconnect.
Obviously, turbulent nature of three-dimensional “realistic” simulations does not allow appearance of local idealised solutions, directly comparable to the analytical models. Nevertheless, if appropriate averaging is applied, the simulations show that naturally generated convective flows in the simulated solar models, while being three-dimensional, produce favourable conditions for forced magnetic reconnection. The flow and magnetic field structure within the reconnection region demonstrate very good qualitative agreement with the magnetic reconnection models with flux pile-up.
We have also demonstrated two regimes of reconnection in magneto-hydrodynamic models of the solar atmosphere. As our simulations suggest, weaker magnetic fields allow for the flux pile-up, while the stronger fields show no magnetic field intensification in proximity of the reconnection region. The latter behaviour is more consistent with the standard Sweet–Parker reconnection regime. Assuming the same magnetic field and plasma flow strength and structure, we expect this behaviour to depend on the value of magnetic diffusivity used in the simulations, with the smaller diffusivities leading to more efficient flux pile-up amplification, and higher diffusivities leading to Sweet–Parker reconnection.
Acknowledgments
The work was supported by the International Exchange programme of Royal Society (UK). VF and GV would like to thank the STFC for financial support. VF, GV, FG and JG thank Royal Society-Newton Mobility Grant NI160149, CIC-UMSNH 4.9 and CONACyT 258726. This work used the DiRAC Data Centric system at Durham University, operated by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility. DiRAC is part of the National E-Infrastructure. This research was undertaken with the assistance of resources and services from the National Computational Infrastructure (NCI), which is supported by the Australian Government. JG gratefully acknowledges DGAPA postdoctoral grant to Universidad Nacional Autónoma de México (UNAM).
References
- Bellot Rubio, L. R., & Beck, C. 2005, ApJ, 626, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J. 2012, in 4th Hinode Science Meeting: Unsolved Problems and Recent Insights, eds. Bellot Rubio, L. R. Reale, F., & Carlsson, M. (San Francisco, CA: ASP), ASP Conf. Ser., 455, 187 [NASA ADS] [Google Scholar]
- Chae, J., Moon, Y.-J., & Pevtsov, A. A. 2004, ApJ, 602, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, A. 1964, Phys. Fluids, 7, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, A. 1965, Phys. Fluids, 8, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Fabling, R. B. 1996, ApJ, 462, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Henton, S. M. 1995, ApJ, 450, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Litvinenko, Y. E. 2012, ApJ, 747, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., Fabling, R. B., Henton, S. M., & Rickard, G. J. 1995, ApJ, 455, L197 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K. P., Bartoe, J.-D. F., Brueckner, G. E., Ewing, J., & Lund, P. 1991, J. Geophys. Res., 96, 9399 [NASA ADS] [CrossRef] [Google Scholar]
- González-Avilés, J. J., Guzmán, F. S., Fedun, V., et al. 2018, ApJ, 856, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., Craig, I. J. D., & Watson, P. G. 2000, Geophys. Astrophys. Fluid Dyn., 93, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Innes, D. E., Inhester, B., Axford, W. I., & Wilhelm, K. 1997, Nature, 386, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Khomenko, E., & Collados, M. 2012, ApJ, 747, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E. 1999, ApJ, 515, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E. 2013, ApJ, 774, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E. 2015, J. Korean Astron. Soc., 48, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Craig, I. J. D. 1999, Sol. Phys., 189, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Craig, I. J. D. 2003, Sol. Phys., 218, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Martin, S. F. 1999, Sol. Phys., 190, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Somov, B. V. 1994, Astron. Lett., 20, 185 [NASA ADS] [Google Scholar]
- Litvinenko, Y. E., Chae, J., & Park, S.-Y. 2007, ApJ, 662, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Livi, S. H. B., Wang, J., & Martin, S. F. 1985, J. Phys., 38, 855 [Google Scholar]
- Martens, P. C., & Zwaan, C. 2001, ApJ, 558, 872 [Google Scholar]
- Martin, S. F. 2012, in Solar Photosphere: Structure, Convection, and Magnetic Fields, ed. Stenflo, J. O. (Dordrecht: Kluwer), IAU Symp., 138, 129 [NASA ADS] [Google Scholar]
- Martin, S. F., Livi, S. H. B., & Wang, J. 1985, J. Phys., 38, 929 [Google Scholar]
- Martin, S. F., Panasenco, O., Engvold, O., & Lin, Y. 2008, Ann. Geophys., 26, 3061 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Del Toro Iniesta, J. C., & Quintero Noda, C. 2011, A&A, 530, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muglach, K. 2008, ApJ, 687, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C. J., Shelyag, S., Mathioudakis, M., et al. 2013, ApJ, 779, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, C. J., Doyle, J. G., & Erdélyi, R. 2016, MNRAS, 463, 2190 [NASA ADS] [CrossRef] [Google Scholar]
- Oldham, K., Myland, J., & Spanier, J. 2009, An Atlas of Functions (New York: Springer) [CrossRef] [Google Scholar]
- Panasenco, O., Martin, S. F., & Velli, M. 2014, Sol. Phys., 289, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Park, S., Chae, J., & Litvinenko, Y. E. 2009, ApJ, 704, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1957, J. Geophys. Res., 62, 509 [Google Scholar]
- Parker, E. N. 1973, J. Plasma Phys., 9, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2000, Magnetic Reconnection: MHD Theory and Applications (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Reid, A., Mathioudakis, M., Scullion, E., et al. 2015, ApJ, 805, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnerup, B. U. O., & Priest, E. R. 1975, J. Plasma Phys., 14, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Mathioudakis, M., & Keenan, F. P. 2012, ApJ, 753, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Khomenko, E., de Vicente, A., & Przybylski, D. 2016, ApJ, 819, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Vissers, G. J. M., Rouppe van der Voort, L. H. M., & Rutten, R. J. 2013, ApJ, 774, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watanabe, H., Vissers, G., Kitai, R., Rouppe van der Voort, L., & Rutten, R. J. 2011, ApJ, 736, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, P. G., & Craig, I. J. D. 2002, Sol. Phys., 207, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, L., Peter, H., He, J., et al. 2015, ApJ, 811, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Yardley, S. L., Green, L. M.,Williams, D. R., van Driel-Gesztelyi, L., Valori, G., & Dacie, S. 2016, ApJ, 827, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, Z., Cao, W., & Ji, H. 2013, ApJ, 790, L4 [Google Scholar]
All Figures
 |
Fig. 1. Dawson function, corresponding to the reconnecting magnetic field profile around the current sheet. The current sheet thickness l was chosen according to the simulation parameters. |
| In the text | |
 |
Fig. 2. Horizontal cuts of the temperature (left panel) and the vertical component of magnetic field (right panel) in the domain, taken at a height of ∼300 km above the continuum formation height. Small-scale temperature enhancements up to 7700 K indicate current sheets in the centres of magnetic reconnection regions. These regions can be clearly seen in the right panel, where magnetic fields of opposite polarities merge. The reconnection region example, shown in Fig. 3, is located at (2,3) Mm. |
| In the text | |
 |
Fig. 3. Algorithm for determining the magnetic field and flow structure around reconnection current sheets, and magnetic field and flow structure around a simulated photospheric reconnection region. Left panel: an example of the averaging algorithm used for diagnostics of the simulated data. The background image is the horizontal cut of the temperature at the height of 300 km above the average continuum formation height. It shows the temperature enhancements in the current sheet region due to the current dissipation. The axes units are grid cells with 6.25 km per grid cell. The green lines are constructed to align with the direction of the strongest change of vertical component of magnetic field at each point of the current sheet. The velocities are projected onto the direction parallel to the strongest gradient direction. Right panel: the vertical component of magnetic field. Arrows indicate the horizontal plasma flow direction. A flow, converging towards the reconnection region is clearly visible. |
| In the text | |
 |
Fig. 4. Reconnection and magnetic flux pile-up. Left column: vertical magnetic field map around the reconnection region. Green boxes identify the averaging regions. Middle and right columns: average vertical magnetic field and the horizontal inflow into the current sheet dependences on the distance from the current sheet, respectively. The first three rows demonstrate the magnetic flux pile-up at the scale predicted by the pile-up reconnection model. The fourth row shows stronger reconnecting magnetic fields and does not show the localised enhancements of the vertical magnetic field in proximity of the current sheet. |
| In the text | |
 |
Fig. 5. Vertical magnetic field component (left panel) and the perpendicular velocity structure in the magnetic flux cancellation region of the cromospheric simulation. |
| In the text | |
 |
Fig. 6. Magnetic field geometry and velocity structure in the reconnection region. The background greyscale image shows the vertical cut (x and z are horizontal and vertical directions respectively) of the vertical component of the magnetic field in the domain. Height z = 0 corresponds to the photospheric level. Solid curves show the magnetic field lines (colours correspond to the magnetic field direction). The horisontal velocity component in the plot corresponds to the velocity, perpendicular to the current sheet. The thin black dash-dotted line shows the height, where the parameters for Fig. 5 were measured. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.