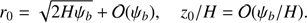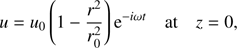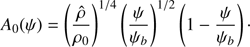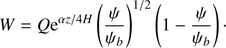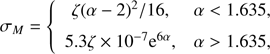| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201833639 | |
| Published online | 27 November 2018 | |
Phase mixing of Alfvén waves in two-dimensional magnetic plasma configurations with exponentially decreasing density
1
School of Mathematics and Statistics (SoMaS), The University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH, UK
e-mail: m.s.ruderman@sheffield.ac.uk
2
Space Research Institute (IKI), Russian Academy of Sciences, Moscow 117810, Russia
3
National Research University Higher School of Economics, Moscow, Russia
Received:
14
June
2018
Accepted:
27
September
2018
We study damping of phase-mixed Alfvén waves propagating in axisymmetric magnetic plasma configurations. We use the linear magnetohydrodynamic (MHD) equations in the cold plasma approximation. The only dissipative process that we take into account is shear viscosity. We reduce the MHD equations describing the Alfvén wave damping to a Klein–Gordon-type equation. We assume that the two terms in this equation, one describing the effect of inhomogeneity and the other the effect of viscosity, are small. Then we use the WKB method to derive the expression describing the wave energy flux attenuation with the height. We apply the general theory to particular equilibria with the exponentially divergent magnetic field lines with the characteristic scale H. The plasma density exponentially decreases with the height with the characteristic scale Hρ. We study the wave damping for typical parameters of coronal plumes and various values of the wave period, the characteristic scale of the magnetic field variation H, and kinematic shear viscosity ν. We show that to have an appreciable wave damping at the height 6H we need to increase shear viscosity by at least six orders of magnitude in comparison with the value given by the classical plasma theory. Another important result is that the efficiency of wave damping strongly depends on the ratio H/Hρ. It increases fast when H/Hρ decreases. We present a physical explanation of this phenomenon.
Key words: hydrodynamics / magnetic fields / magnetohydrodynamics (MHD) / plasmas / waves / Sun: oscillations
© ESO 2018
1. Introduction
Solar coronal heating is one of the most intriguing problems in solar physics. Alfvén wave damping is a popular mechanism for heating the coronal plasma. Alfvén waves can efficiently transport the energy from the lower part of the solar atmosphere to the corona. It was shown by Soler et al. (2017) that torsional Alfvén waves with periods of the order of second are almost completely damp in the chromosphere due to ion-neutral collisions; waves with periods of a few minutes are strongly reflected mainly from the transitional region. However a large part of the energy of waves with the periods of the order of one minute is transmitted in the corona. These latter authors also confirmed the result first obtained by Cally (1983) that the magnetic tube expansion facilitates Alfvén energy transmission in the corona. The main problem in the theory of Alfvén heating is that, for typical coronal conditions, Alfvén waves can propagate through the corona almost without damping because they do not perturb the plasma density.
Heyvaerts & Priest (1983) showed that Alfvén-wave phase mixing can greatly enhance the Alfvén wave damping in weakly dissipative plasmas; it creates large gradients in the direction perpendicular to the wave propagation direction. As a result, the Alfvén wave damping length is proportional to Re1/3 rather than Re as in a homogeneous plasma, where Re is either the viscous or resistive Reynolds number. Because of the possibility of efficient Alfvén wave damping in weakly dissipative plasmas, phase mixing has become a popular mechanism for coronal heating. A review of the recent progress in the theory of coronal heating by waves is given by Arregui (2015).
Although phase mixing greatly enhances the Alfvén wave damping, it is still not sufficiently strong to cause substantial wave damping in the lower part of the solar corona. Because of this researchers started to search for additional mechanisms to further enhance the wave damping. Malara et al. (1996) showed that Alfvén-wave phase mixing can generate compressible perturbations. Non-linear steepening of these perturbations leads to the appearance of shocks. This meachanism was then studied by Nakariakov et al. (1997), Botha et al. (2000), Tsiklauri et al. (2001, 2002, 2003), and Tsiklauri & Nakariakov (2002).
The efficiency of Alfvén wave damping due to phase mixing also depends very much on the geometry of equilibrium. Ruderman et al. (1998) studied the Alfvén wave phase mixing in two-dimensional magnetic plasma configurations using the Wentzel, Kramers, and Brillouin (WKB) method. In particular, they showed that the divergence of the magnetic field lines can substantially enhance the efficiency of the Alfvén wave damping due to phase mixing. While the damping length in an equilibrium with the straight magnetic field lines is proportional to Re1/3, it is proportional to ln(Re) in an equilibrium with the exponentially divergent magnetic field lines. This result was later confirmed by Smith et al. (2007) both analytically and numerically. The enhancement of damping of phase-mixed Alfvén waves was also found by De Moortel et al. (2000) who studied phase mixing of Alfvén waves in a magnetic plasma configuration with radially expanding magnetic field lines and gravitationally stratified plasma. The study of wave propagation in magnetic plasma configurations with divergent magnetic field lines was boosted by the observation that in the chromosphere and lower corona the cross-section area of open magnetic tubes can increase by a few hundred times (Tsuneta et al. 2008).
For waves with periods of the order of one minute that propagate, for example, in plumes in coronal holes, the wave lengths can be comparable with the characteristic scale of variation of background quantities. In this case we cannot use the WKB approximation. Therefore, in general, the study of phase mixing is only possible numerically. However, there is one exception. Analytical study is possible when the waves propagate in non-reflective equilibria, where Alfvén waves propagate without reflection.
Non-reflective wave propagation has been studied in various branches of sciences, including plasma physics (Ginzburg 1970), oceanography (Brekhovskih 1980; Didenkulova et al. 2008; Grimshaw et al. 2010), acoustics (Ibragimov & Rudenko 2004), and atmospheric science (Petrukhin et al. 2011, 2012b). The theory of non-reflective wave propagation has also been applied to solar physics. Petrukhin et al. (2012a) studied non-reflective vertical propagation of acoustic waves in the solar atmosphere. Ruderman et al. (2013) and Petrukhin et al. (2015) studied non-reflective propagation of kink waves along thin magnetic flux tubes.
Recently Ruderman & Petrukhin (2017) and Petrukhin et al. (2018) studied Alfvén wave phase mixing in non-reflective planar and cylindrical magnetic plasma equilibria with exponentially divergent magnetic field lines. Due to high thermal conductivity the temperature in the lower part of the solar corona is almost constant. As a result the density is exponentially decreasing with height. In the planar case Ruderman & Petrukhin (2017) considered equilibria with the plasma density that does not vary in the vertical direction. In the cylindrical case, Petrukhin et al. (2018) considered density profiles approximating density that exponentially decreases with height. However such an approximation was only possible for a very restricted range of parameters.
When the magnetic field configuration is defined, the condition that an equilibrium is non-reflective prescribes the spatial dependence of the equilibrium density, which imposes a very severe restriction on the equilibrium. In particular, equilibria with exponentially divergent magnetic field lines and the density exponentially decreasing with height are not non-reflective. To resolve this problem we substantially modify the method used by Ruderman & Petrukhin (2017) and Petrukhin et al. (2018) and consider weakly reflective equilibria. As a result we greatly expand the set of equilibria where it is possible to study damping of phase-mixed Alfvén waves analytically. In particular, we manage to consider an equilibrium with exponentially divergent magnetic field lines and the density exponentially decreasing with height in the atmosphere.
The paper is organised as follows. In the following section we formulate the problem and present the governing equation describing the Alfvén wave propagation, phase mixing, and damping. In Sect. 3 we develop the general theory of damping of phase-mixed Alfvén waves in weakly reflecting equilibria. In Sect. 4 we apply the general theory to studying damping of phase-mixed Alfvén waves in an equilibrium with exponentially expanding magnetic field lines and the density exponentially decreasing with height. Section 5 contains the summary of obtained results and our conclusions.
2. Problem formulation and governing equation
We study the torsional Alfvén wave propagation in axisymmetric equilibria with all equilibrium quantities dependent on r and z in cylindrical coordinates r, θ, z with the z-axis vertical. The θ-component of the equilibrium magnetic field is zero. The plasma beta in the solar corona is very low, which implies that the equilibrium magnetic field is approximately force-free. A force-free axisymmetric magnetic field with the azimuthal component equal to zero is always potential. Therefore, the equilibrium magnetic field B = (Br, 0, Bz) can be expressed both in terms of magnetic potential ϕ and in terms of the magnetic flux function ψ. As a result, we have
where B0 is a constant equal to the characteristic value of the magnetic field, and H is the characteristic spatial scale of equilibrium quantity variation along the magnetic field lines. Since ψ is defined with accuracy up to an additive constant, we impose the condition that ψ = 0 at r = 0. Below we use ϕ and ψ as new curvilinear coordinates in the θ = constant plane. It follows from Eq. (1) that ∇ϕ ⋅ ∇ψ = 0, meaning that the curvilinear coordinate system (ϕ, ψ) is orthogonal. The ϕ coordinate lines coincide with the magnetic field lines, while the ψ coordinate lines are orthogonal to the magnetic field lines.
Below we only study torsional Alfvén waves. In these waves only the θ-components of the velocity and magnetic field, v and b, are non-zero, while all other quantities remain unperturbed. To describe these waves we use the θ-components of the momentum and induction equation. The only dissipative process that we take into account is shear viscosity, while we neglect resistivity. Since the kinematic shear viscosity and magnetic diffusion are of the same order in the corona, neglecting resistivity can only reduce the efficiency of wave damping by a factor of the order of unity. On the other hand, neglecting resistivity simplifies the analysis enabling us to eliminate the magnetic field perturbation from the governing equations.
In the chromosphere the ion-neutral collisions substantially contribute to the Alfvén wave damping (see review by Ballester et al. 2018, and references therein). However we consider Alfvén wave damping in the corona where the plasma is fully ionised. Consequently, the damping mechanisms related to the ion–neutral collisions, like ambipolar diffusion, do not work there.
The linearised governing equations are
where μ0 is the magnetic permeability of free space, and ν is the kinematic viscosity. Petrukhin et al. (2018) used Eqs. (2) and (3) to derive the equation describing the Alfvén wave propagation,
where u = v/r is the angular velocity and
is the Alfvén speed. We note that in Eq. (4) ϕ and ψ are the independent variables.
Similar to Ruderman & Petrukhin (2017) and Petrukhin et al. (2018) we look for the solution to Eq. (4) in the form
where v0 is an arbitrary constant with the dimension of velocity. We emphasise that this does not impose any condition on the solution; any solution to Eq. (4) can be written in this form. Moreover, we can arbitrarily choose the functions A(ϕ, ψ) and h(ϕ, ψ). We choose these functions as
where V0 = B0(μ0ρ0)−1/2, ρ0 is the density at the coordinate origin, ϕ1(ψ) and A0(ψ) are arbitrary functions, and A0(ψ) satisfies the condition that A0(ψ)r−1 has a non-zero limit as ψ → 0. Petrukhin et al. (2018) showed that with this choice of h and A the function Φ satisfies the equation
where
When ν = 0, Eq. (8) is the Klein–Gordon equation. Equation (8) is used below to study the damping of phase-mixed Alfvén waves. Hence, below we call it the Klein–Gordon-type equation.
3. Damping of phase-mixed Alfvén waves
Now our analysis substantially deviates from that in Petrukhin et al. (2018) who studied the wave damping in non-reflective equilibria and assumed that the second term on the right-hand side of Eq. (8) is independent of ϕ. Here we consider weakly reflective equilibria. In these equilibria the characteristic scale of variation of the coefficient at Φ in Eq. (8) is much larger than the wavelength. Alternatively, we can make a stronger assumption that the term proportional to Φ in Eq. (8) is much smaller than the terms on the left-hand side of this equation. We make this second assumption. We see below that it is sufficient for studying the wave damping in equilibria with the exponentially divergent magnetic field lines and exponentially decreasing density.
In addition, we assume that the first term on the right-hand side of Eq. (8) is much smaller than the terms on the left-hand side, which is equivalent to the assumption that the damping is weak. Here it is worth noting that usually the assumption that damping is weak is considered as a condition that the damping length is much larger than the wavelength. However, the characteristic length of spatial variation of a harmonic wave is not the wavelength but k−1, where k is the wave number. This quantity is about six times smaller than the wavelength. Hence, the wave damping can be considered as weak even when the damping length is of the order of the wavelength.
The assumption that the right-hand side of Eq. (8) is much smaller than its left-hand side enables us to use the WKB method for studying the wave damping. We assume that Alfvén waves are driven at some level in the atmosphere and then propagate along the magnetic field lines. In accordance with this we impose the boundary condition
It follows from Eqs. (6) and (7) that
Now we consider harmonic waves and take all time-dependent quantities proportional to e−iωt. Subsequently, Eq. (8) reduces to
We assume that the characteristic distance of the wave damping is much larger than the characteristic distance of variation of Φ with respect to h. In accordance with this we introduce the slow variable 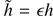 , where ϵ ≪ 1. We recall that this assumption is equivalent to the condition that the wave damping is weak.
, where ϵ ≪ 1. We recall that this assumption is equivalent to the condition that the wave damping is weak.
To characterise the viscosity magnitude, we introduce the Reynolds number Re = HV0/ν (we recall that H is the characteristic spatial scale of variation of the equilibrium magnetic field). We assume that the characteristic wavelength is also H. The assumption that the damping is weak implies that Re ≫ 1. In accordance with this we introduce the scaled kinematic viscosity 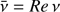 . The relation between ϵ and Re is defined below.
. The relation between ϵ and Re is defined below.
We assume that the second term on the right-hand side of Eq. (8) is small. This is only possible if the characteristic scale of variation of the expression in the brackets in the second term is much larger than H. In accordance with this we introduce the scaled quantity 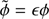 . Now Eq. (12) is transformed to
. Now Eq. (12) is transformed to
where 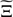 is defined by Eq. (9) with
is defined by Eq. (9) with 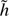 substituted for h. We note that only the external derivative in the second term on the right-hand side of Eq. (13) is with respect to
substituted for h. We note that only the external derivative in the second term on the right-hand side of Eq. (13) is with respect to 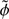 , while the internal derivative is with respect to ϕ because the characteristic scale of variation of A is H.
, while the internal derivative is with respect to ϕ because the characteristic scale of variation of A is H.
Now we use the standard WKB method and look for the solution to this equation in the form (Bender & Orszag 1999)
Substituting this expression to Eq. (13) and using the expression for 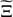 we obtain
we obtain
First, we assume that the first term on the right-hand side is much smaller than the two largest terms on the left-hand side of this equation, which are the last and next-to-last terms. Then we collect the terms of the order of unity in Eq. (15) to obtain
This approximation is usually called the approximation of geometrical optics (e.g. Bender & Orszag 1999); it determines the shape of rays along which the waves propagate. Only considering waves propagating in the positive ϕ-direction, from Eq. (16) we obtain
where we arbitrarily took Θ = 0 at 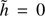 . We emphasise that this does not mean that there is no wave reflection. However, the reflected wave only appears in the higher orders of approximation with respect to ϵ, which is one of the main properties of the WKB method.
. We emphasise that this does not mean that there is no wave reflection. However, the reflected wave only appears in the higher orders of approximation with respect to ϵ, which is one of the main properties of the WKB method.
In the next order approximation we collect terms of the order ϵ. This approximation is usually called the approximation of physical optics. It determines the spatial evolution of the wave amplitude. The first term on right-hand side of Eq. (15) describes the viscous wave damping due to phase mixing. Hence, we define the relation between Re and ϵ in such a way that this term contributes in the approximation of physical optics. In accordance with this we take Re = ϵ−3. Subsequently, we obtain
Using Eqs. (7) and (17) and returning to the original non-scaled variables we transform Eq. (18) to
where G = A/A0 and
We also impose the condition
Obviously, we can assume that Q is real. Equation (20) determines the spatial evolution of the Alfvén wave amplitude. We also use the expressions for the velocity and magnetic field perturbation. Using Eqs. (6), (7), (14), and (17), and recalling that the perturbations are proportional to e−iωt, in the leading-order approximation with respect to ϵ we obtain
Subsequently, we obtain the expression for b: using Eqs. (3), (7), and (22), and the relation B ⋅ ∇ = (B2/B0)∂/∂ϕ yields
To characterise the efficiency of the wave damping, we calculate the variation with the height of the wave energy flux averaged over the wave period through surfaces ϕ = const. A surface ϕ = const is uniquely defined by the coordinate of the point of its intersection with the z-axis. Hence, the energy flux is a function of z. Multiplying Eq. (2) by v, Eq. (3) by b/μ0, and adding the results, we obtain
The expression in the parentheses on the left-hand side of this equation is the wave energy density, while Bvb/μ0 is the density of the wave energy flux. We obtain exactly the same expression for the density of the wave energy flux if we calculate the Pointing flux and only keep the quadratic terms. When ν = 0, Eq. (24) is the energy conservation equation. If we take the average of Eq. (24) with ν = 0 over the wave period, then we obtain that the average density of the wave energy flux is conserved as it should be. The density of the energy flux is directed along the equilibrium magnetic field. Equations (22) and (23) give the complex expressions for v and b. To obtain the physical quantities, we need to take the real parts of these expressions. Subsequently, using Eqs. (22) and (23) we obtain that the magnitude of the average over the period density of the wave energy flux is
where the angle brackets indicate the average over the wave period. Let Σ be the surface ϕ = ϕ* = constant that intersects the z-axis at z*. We assume that the waves propagate in the magnetic tube bounded by the surface ψ = ψb. The wave energy flux through Σ is equal to the wave energy flux density integrated over the part of Σ that is inside this magnetic tube. We denote this part as Σb. Let the equation of Σ be z = z(r). Then we have the identity ϕ(r, z(r)) = constant. Differentiating this identity and using Eq. (1) yields
Using this equation and Eq. (1) we obtain the relation valid on Σ,
We then obtain with the aid of Eqs. (26) and (27) that the elementary part of Σ is
Now, taking into account that the energy flux at Σ is everywhere in the direction normal to this surface, we obtain with the aid of Eqs. (25) and (28) that the average energy flux through the surface Σ is
Below we use Eqs. (19), (20), and (29) to study the Alfvén wave damping for a particular equilibrium.
4. Alfvén wave damping in equilibrium with exponentially divergent magnetic field lines
We now consider an equilibrium with the same magnetic field as in Petrukhin et al. (2018). This magnetic field is defined by
where J0 and J1 are the Bessel functions of the first kind and the zero and first order. The functions ϕ and ψ are given by
We also assume that the equilibrium is isothermal. The equilibrium magnetic field B, density ρ, and pressure p are related by the equation
Using the relation B ⋅ ∇ = (B2/B0)∂/∂ϕ we obtain that the projection of this equation on a magnetic field line is
In accordance with the Clapeyron equation p = (kB/m)ρT, where kB is the Boltzmann constant, m ≈ 0.6 mp in the solar corona, mp is the proton mass, and T is the temperature, and is constant. Using this relation and integrating Eq. (33) we obtain
where Hρ = kBT/mg, α = H/Hρ, and 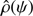 is an arbitrary function. The plasma pressure is then determined by the Clapeyron equation.
is an arbitrary function. The plasma pressure is then determined by the Clapeyron equation.
We recall that one of our assumptions is that the right-hand side of Eq. (8) is much smaller than the left-hand side. The smallness of the first term on the right-hand side is ensured by imposing the condition on the kinematic viscosity ν. The condition that the second term on the right-hand side is much smaller than the left-hand side is written as
where we took into account that Φ is proportional to e−iωt. This equation imposes the lower bound on the value of the frequency and consequently the upper bound on the value of the wave length. In general, the wave reflection is weak and the WKB description of the wave propagation is only possible when the wavelength is much smaller than the characteristic scale of variation of equilibrium quantities. When the wavelength becomes comparable with this characteristic scale the wave reflection is strong and the WKB method does not work. However, there are exceptions. In non-reflective equilibria there is no wave reflection for any wavelength. In weakly reflective equilibria the wave reflection is weak even when the wavelength is comparable with the characteristic scale of variation of equilibrium quantities. We see below that the particular equilibrium that we consider here is of this type.
Using Eqs. (7) and (34) we obtain
Differentiating the expressions for ϕ and ψ with respect to ϕ and using the identities (Abramowitz & Stegun 1964)
where the prime indicates the derivative, we obtain
With the aid of these results we obtain
Using Eqs. (30), (31), (38), and (39) we transform Eq. (35) to
Below we take ϕ1(ψ)= − H and study the wave propagation in a spatially bounded domain 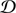 defined by
defined by
We note that the surfaces ϕ = −H and ϕ = −He−6 intersect the z-axis at z = 0 and z = 6H, respectively. The domain 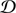 is shown in Fig. 1.
is shown in Fig. 1.
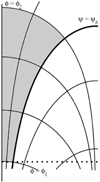 |
Fig. 1. Sketch of domain |
Below we apply our theoretical results to the Alfvén wave propagation in coronal plumes. We take as typical values B = 10 G, the electron number density equal to 1015 cm−3, H ≥ 30 Mm, and the wave period smaller or equal to 60 s. Then we obtain V0 ≈ 700kms−1.
To calculate the dependence of the wave energy flux on the height we must specify two functions, 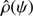 and A0(ψ). We take
and A0(ψ). We take
where 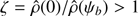 . Let the surface ϕ = −H intersect the tube boundary defined by ψ = ψb at r = r0 and z = z0. Using Eq. (31) we obtain that the quantities r0 and z0 are defined by the equations
. Let the surface ϕ = −H intersect the tube boundary defined by ψ = ψb at r = r0 and z = z0. Using Eq. (31) we obtain that the quantities r0 and z0 are defined by the equations
Below we assume that ψb ≪ H. Then it follows from Eq. (43) that r0 ≪ H and
These results in particular imply that the surface ϕ = −H approximately coincides with its tangent plane z = 0 inside the magnetic tube, and r0 is approximately equal to the radius of the cross-section of magnetic tube by the plane z = 0. Therefore, below we disregard the difference between the plane z = 0 and the surface ϕ = −H. In accordance with this we impose the boundary condition Eq. (11) at z = 0.
We therefore assume that Alfvén waves are driven at z = 0. We take
where u0 = v0/r0. Comparing this expression with Eq. (22), noticing that h = 0 at z = 0, and using the relation r2/r02 = ψ/ψb and Eq. (7) yields
Using this expression and Eq. (34) we obtain from Eq. (22)
We introduce the notation 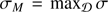 . The numerically calculated dependence of σM on α for ζ = 5 is shown in Fig. 2 by the solid line. The curve showing this dependence consists on two branches. On the left branch σM(α) is a monotonically decreasing function, while it is monotonically increasing on the right branch. We found that this function is very well approximated by
. The numerically calculated dependence of σM on α for ζ = 5 is shown in Fig. 2 by the solid line. The curve showing this dependence consists on two branches. On the left branch σM(α) is a monotonically decreasing function, while it is monotonically increasing on the right branch. We found that this function is very well approximated by
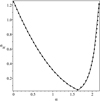 |
Fig. 2. Dependence of σM on α for ζ = 5. The solid line shows the numerically calculated dependence, and the squares show the graph of the approximate dependence σM on α given by Eq. (48). |
This approximate dependence of σM on α for ζ = 5 is shown in Fig. 2 by squares. Using H ≥ 30 Mm, V0 = 700 km s−1, and the wave period smaller or equal to 60 s we obtain ω2H2/V02 ≳ 20, meaning that the inequality (40) is satisfied with a great margin.
We calculated the dependence of the relative wave energy flux, Δ = Π(z)/Π(0) for α = 0.8, ζ = 5, r0/H = 0.1, and various values of wave frequency and kinematic viscosity. It is worth saying a few words about kinematic viscosity. The viscosity in the solar plasma is strongly anisotropic. The Alfvén waves are only affected by the shear viscosity, meaning that ν in Eq. (2) is the kinematic shear viscosity. Ruderman & Petrukhin (2017) and Petrukhin et al. (2018) estimated the characteristic value of kinematic shear viscosity to be 1 m2 s−1. With this value of ν, phase mixing does not cause any damping of Alfvén waves in the low corona. Hence, in our numerical calculations we took ν to be a few orders of magnitude higher than this value. We believe that such enhancement of ν can be caused by plasma turbulence. A substantial discussion of this possibility is given in the following section. The dependence of Δ on z is shown in Fig. 3. We see that there is practically no wave damping at the height 6H when ν = 105 m2 s−1. A notable damping only occurs for ν ≳ 106 m2 s−1. We also see that the damping efficiency increases with the increase of the kinematic viscosity and decrease of the wave period, as it should be.
 |
Fig. 3. Dependence of the relative wave energy flux Δ on the height z. Upper panels: wave period 30 s, lower panels: wave period 60 s. Left panels: H = 30 Mm, right panels: H = 60 Mm. The dotted, solid, dashed, and dash-dotted lines correspond to ν = 105 m2 s−1, 106 m2 s−1, 3 × 106 m2 s−1, and 107 m2 s−1. |
We also calculated the dependence of Δ(6H) on α = H/Hρ for ζ = 5, r0/H = 0.1, ν = 107 m2 s−1, and various values of the wave period and H. The main conclusion that we can make after inspection of Fig. 4 is that there is extremely strong dependence of the wave damping efficiency on H/Hρ. We have already explained this phenomenon in our previous paper (Petrukhin et al. 2018). Due to the exponential divergence of the magnetic field lines the magnetic field magnitude exponentially decreases with the height as e−z/H. The plasma density also decreases with the height as e−z/Hρ. The Alfvén speed is therefore proportional to exp[−z/H(1 − α/2)]. When α < 2, the Alfvén speed decreases with height. As a result, the wave has more time to become phase mixed and damp. It is also obvious that the smaller α is, the stronger the effect of the wave damping enhancement.
 |
Fig. 4. Dependence of Δ(6H) on the ratio H/Hρ for ζ = 5, r0/H = 0.1, and ν = 107 m2 s−1. The solid line corresponds to H = 30 Mm and the wave period 60 s. The dotted line corresponds to H = 60 Mm and the wave period 60 s. The dashed line corresponds to H = 30 Mm and the wave period 30 s. The dash-dotted line corresponds to H = 60 Mm and the wave period 30 s. |
We note that a similar explanation of enhancement of damping efficiency in an equilibrium with the radially expanding magnetic field lines was suggested by De Moortel et al. (2000).
5. Summary and conclusions
In this article we studied the phase mixing and damping of Alfvén waves in two-dimentional axisymmetric magnetic plasma equilibria. In this study we used the linearised MHD equations in the cold plasma approximation. The only dissipative process that we took into account was shear viscosity. The equilibrium magnetic field can be expressed both in terms of the magnetic potential ϕ and flux functions ψ. We used ϕ and ψ as new independent variables and reduced the linearised MHD equations to one equation for the velocity perturbation. Then we further reduced this equation to the equation that becomes the Klein–Gordon equation when there is no viscosity. Hence, we call it the Klein–Gordon-type (KGT) equation.
The left-hand side of the KGT equation has the form of wave equation, while the two terms on the right-hand side describe the effects of inhomogeneity and viscosity. We assumed the right-hand side to be small. To maintain the small size of the term describing the effect of viscosity we assumed the Reynolds number to be large. This is a viable assumption for Alfvén waves with periods of the order of one minute. The assumption that the term describing the effect of inhomogeneity is small is not so obvious because we considered waves with wavelengths of the order of the characteristic scale of inhomogeneity H. Hence, this assumption must be always verified when considering a particular equilibrium. Assuming that the right-hand side of the KGT equation is small we used the WKB method and derived the equation describing the variation of the wave energy flux with the height in the solar atmosphere.
We applied the general theoretical results to a particular equilibrium that can be considered as a model of a plume in a coronal hole. In this model the domain where the Alfvén wave propagates is an expanding magnetic tube. The magnetic field lines diverge exponentially with the characteristic scale H. This results in the expansion of the radius of the magnetic tube cross-section by a plane perpendicular to its axis. The plasma density exponentially decreases with height at the characteristic scale of Hρ. It also decreases from its maximum value at the tube axis to its value in the surrounding plasma. We calculated the dependence of the relative wave energy flux on the height in the solar atmosphere for equilibrium parameters typical for coronal plumes. We considered two wave periods, 30 s and 60 s, two values of the characteristic inhomogeneity scale height, H = 30 Mm and H = 60 Mm, and a few values of kinematic shear viscosity.
We showed that to have notable wave energy dissipation at the height z = 6H we need to increase kinematic shear viscosity by at least six orders of magnitude in comparison with the value given by the classical plasma theory that can be caused by turbulence. To the best of our knowledge, at present there is no observational evidence of turbulence in coronal holes. However, Liu et al. (2014) presented observational evidence of the presence of Alfvénic turbulence in coronal magnetic loops. We hope that similar studies will also eventually reveal the presence of Alfvénic turbulence in coronal holes.
From a theoretical point of view the most obvious candidate for causing the plasma turbulence in coronal holes is the Kelvin–Helmholtz (KH) instability related to shear flows in phase-mixed Alfvén waves. Heyvaerts & Priest (1983) argued that phase-mixed Alfvén waves are only subject to the KH instability in the case of standing waves, while propagating waves are stable. Their conclusion was based on the fact that in standing waves the phase of the magnetic field oscillation is shifted by a quarter of period with respect to the velocity oscillation, and is shifted by half of a period in a propagating wave. As a result, the magnetic field cannot stabilise the KH instability in a standing wave, but can in a propagating wave. However, the analysis by Heyvaerts & Priest (1983) is based on the results obtained for stationary flows. Roberts (1973) studied the stability of an MHD tangential discontinuity with the magnetic field and the velocity having the same direction at the two sides, and the velocity amplitude oscillating harmonically. He found that, in contrast to the case of stationary flow, this discontinuity is always unstable. Hence, the magnetic field parallel to the shear velocity cannot eliminate the KH instability of a tangential MHD discontinuity with oscillating flows no matter how small the velocity amplitude is.
Recently the interest in studying stability of oscillating flows was boosted by the application to the stability of boundaries of oscillating coronal magnetic loops. Terradas et al. (2008) studied the magnetic loop kink oscillation numerically and found that its boundary becomes unstable due to shear motion. This result is in complete agreement with the theory of KH instability of MHD tangential discontinuities with stationary flows. These discontinuities are always unstable when the magnetic field has the same direction at the two sides and the velocity is not parallel to the magnetic field. On the basis of the same theory it was expected that magnetic twist can stabilise the loop boundary because it introduces magnetic shear. However, recent numerical studies by Howson et al. (2017) and Terradas et al. (2018) revealed that the magnetic twist can only reduce the instability increment, but it cannot stabilise the loop boundary. Barbulescu et al. (2018) developed first analytical model of KH instability of the boundary of an oscillating coronal magnetic loop. They modelled this boundary as an MHD tangential discontinuity with the sheared magnetic field and oscillating velocity orthogonal to the magnetic field at both sides of the discontinuity. They also obtained that in contrast to the stationary case the magnetic shear can only reduce the instability increment, but cannot stabilise the discontinuity.
On the basis of all these results we can make a viable assumption that it is intrinsic property of oscillating flow to be subject to the KH instability. The analysis by Heyvaerts & Priest (1983) is only applicable to propagating Alfvén waves in a homogeneous plasma because in that case the flow is stationary in the reference frame moving along the magnetic field lines with the Alfvén speed. Phase-mixed Alfvén waves propagate with different phase speed along different magnetic field lines, which implies that there is no reference frame where the flow is stationary. Hence, we can speculate that propagating phase-mixed Alfvén waves become KH-unstable at some distance from the driver. It is obvious that this distance depends on the wave amplitude and particular geometry of the equilibrium. The results obtained in our paper show that studying the KH instability of phase-mixed Alfvén waves is extremely important for the problem of coronal heating. Due to high complexity of the unperturbed flow this KH instability can only be studied numerically.
Of course, it is also possible that an anomalous shear viscosity appears due to micro-turbulence in plasma that should be described by the kinetic equations. Here however, we do not discuss this problem because it is too far from the topic of this paper.
Finally, we also studied the dependence of the efficiency of the wave energy damping at the height 6H, which corresponds to the lower solar corona. We found that this efficiency quickly increases with a decrease in the ratio H/Hρ.
Acknowledgments
The authors gratefully acknowledge financial support from the Russian Fund for Fundamental Research (RFFR), grant (16-02-00167). M.S.R. acknowledges the support from the STFC grant.
References
- Abramowitz, M., & Stegun, I. 1964, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables (New York: National Bureau of Standards) [Google Scholar]
- Arregui, I. 2015, Phil. Trans. R. Soc. London Ser., 373, 20140261 [Google Scholar]
- Ballester, J. L., Alexeev, I., Collados, M., et al. 2018, Space Sci. Rev., 214, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Barbulescu, M., Ruderman, M. S., Van Doorsselaere, T., & Erdélyi, R. 2018, ApJ, submitted [Google Scholar]
- Bender, C. M., & Orszag, S. A. 1999, Advanced Mathematical Methods for Scientists and Engineers (New York: McGraw-Hill) [CrossRef] [Google Scholar]
- Botha, G. J. J., Arber, T. D., Nakariakov, V. M., & Keenan, F. P. 2000, A&A, 363, 1186 [NASA ADS] [Google Scholar]
- Brekhovskih, L. M. 1980, Waves in Layered Media (New York: Academic Press) [Google Scholar]
- Cally, P. 1983, Sol. Phys., 88, 77 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., Hood, A. W., & Arber, T. D. 2000, A&A, 354, 334 [NASA ADS] [Google Scholar]
- Didenkulova, I., Pelinovsky, E., & Soomere, T. 2008, Proc. Est. Acad. Sci. Eng., 165, 2249 [Google Scholar]
- Ginzburg, V. L. 1970, Propagation of Electromagnetic Waves in Plasma (New York: Pergamon Press) [Google Scholar]
- Grimshaw, R., Pelinovsky, E., & Talipova, T. 2010, J. Phys. Oceanogr., 40, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Heyvaerts, J., & Priest, E. R. 1983, A&A, 117, 220 [NASA ADS] [Google Scholar]
- Howson, T. A., De Moortel, I., Terradas, J., & Antolin, P. 2017, A&A, 607, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ibragimov, N. H., & Rudenko, O. V. 2004, Acoust. Phys., 50, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., McIntosh, S. W., De Moortel, I., Threlfall, J., & Bethge, C. 2014, ApJ, 797, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Malara, F., Primavera, L., & Veltri, P. 1996, ApJ, 459, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., Roberts, B., & Murawski, K. 1997, Sol. Phys., 175, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Petrukhin, N. S., Pelinovsky, E. N., & Batsyna, E. K. 2011, JETP Lett., 93, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Petrukhin, N. S., Pelinovsky, E. N., & Batsyna, E. K. 2012a, Astron. Lett., 38, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Petrukhin, N. S., Pelinovsky, E. N., & Talipova, T. G. 2012b, Izv. Atmos. Ocean. Phys., 48, 169 [CrossRef] [Google Scholar]
- Petrukhin, N. S., Ruderman, M. S., & Pelinovsky, E. N. 2015, Sol. Phys., 290, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Petrukhin, N. S., Ruderman, M. S., & Shurgalina, E. G. 2018, MNRAS, 474, 2289 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B. 1973, J. Fluid Mech., 59, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Petrukhin, N. S. 2017, A&A, 600, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S., Nakariakov, V. M., & Roberts, B. 1998, A&A, 338, 1118 [NASA ADS] [Google Scholar]
- Ruderman, M. S., Pelinovsky, E., Petrukhin, N. S., & Talipova, T. 2013, Sol. Phys., 286, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. G., Tsiklauri, D., & Ruderman, M. S. 2007, A&A, 475, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., & Ballester, J. L. 2017, ApJ, 840, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Andries, J., Goossens, M., et al. 2008, ApJ, 687, L115 [Google Scholar]
- Terradas, J., Magyar, N., & Van Doorsselaere, T. 2018, ApJ, 853, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiklauri, D., & Nakariakov, V. M. 2002, A&A, 393, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsiklauri, D., Arber, T. D., & Nakariakov, V. M. 2001, A&A, 379, 1098 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsiklauri, D., Nakariakov, V. M., & Arber, T. D. 2002, A&A, 395, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsiklauri, D., Nakariakov, V. M., & Rowlands, G. 2003, A&A, 400, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsuneta, S., Ichimoto, K., Katsukawa, Y., et al. 2008, ApJ, 688, 1374 [Google Scholar]
All Figures
 |
Fig. 1. Sketch of domain |
| In the text | |
 |
Fig. 2. Dependence of σM on α for ζ = 5. The solid line shows the numerically calculated dependence, and the squares show the graph of the approximate dependence σM on α given by Eq. (48). |
| In the text | |
 |
Fig. 3. Dependence of the relative wave energy flux Δ on the height z. Upper panels: wave period 30 s, lower panels: wave period 60 s. Left panels: H = 30 Mm, right panels: H = 60 Mm. The dotted, solid, dashed, and dash-dotted lines correspond to ν = 105 m2 s−1, 106 m2 s−1, 3 × 106 m2 s−1, and 107 m2 s−1. |
| In the text | |
 |
Fig. 4. Dependence of Δ(6H) on the ratio H/Hρ for ζ = 5, r0/H = 0.1, and ν = 107 m2 s−1. The solid line corresponds to H = 30 Mm and the wave period 60 s. The dotted line corresponds to H = 60 Mm and the wave period 60 s. The dashed line corresponds to H = 30 Mm and the wave period 30 s. The dash-dotted line corresponds to H = 60 Mm and the wave period 30 s. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



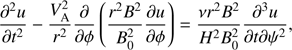
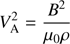
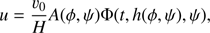
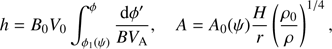
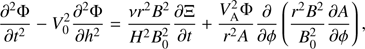
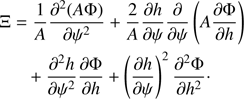
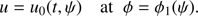
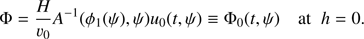
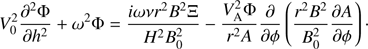
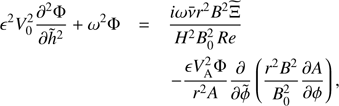
![$$ \begin{aligned} \Phi = Q({\tilde{h}},\psi )\exp [i\epsilon ^{-1}\Theta ({\tilde{h}},\psi )]. \end{aligned} $$](/articles/aa/full_html/2018/12/aa33639-18/aa33639-18-eq20.gif)
![$$ \begin{aligned} \epsilon ^2\frac{\partial ^2 Q}{\partial {\tilde{h}}^2}&+ 2i\epsilon \frac{\partial Q}{\partial {\tilde{h}}}\frac{\partial \Theta }{\partial {\tilde{h}}} + i\epsilon Q\frac{\partial ^2\Theta }{\partial {\tilde{h}}^2} - Q\left(\frac{\partial \Theta }{\partial {\tilde{h}}}\right)^2 + \frac{\omega ^2}{V_0^2} Q \nonumber \\&= -\frac{i\epsilon ^{-2}\omega \bar{\nu }r^2 B^2 Q}{H^2 V_0^2 B_0^2{Re}}\bigg [\bigg (\frac{\partial {\tilde{h}}}{\partial \psi }\bigg )^2\left(\frac{\partial \Theta }{\partial {\tilde{h}}}\right)^2 + \mathcal{O}(\epsilon )\bigg ] \nonumber \\&-\, \frac{\epsilon V_{\mathrm{A}}^2 Q}{r^2 V_0^2 A} \frac{\partial }{\partial \tilde{\phi }}\left(\frac{r^2 B^2}{B_0^2} \frac{\partial A}{\partial \phi }\right)\cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa33639-18/aa33639-18-eq22.gif)
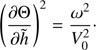
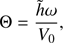
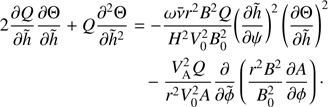
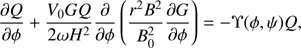
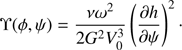

![$$ \begin{aligned} v = v_0 W\exp [i\omega (h/V_0 - t)], \quad W = QA_0(\psi )\left(\frac{\rho _0}{\rho }\right)^{1/4}\cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa33639-18/aa33639-18-eq30.gif)
![$$ \begin{aligned} b = v_0 B\left[\frac{irB}{\omega B_0}\frac{\partial (W/r)}{\partial \phi } - \frac{W}{V_{\mathrm{A}}}\right]\!\exp [i\omega (h/V_0 - t)]. \end{aligned} $$](/articles/aa/full_html/2018/12/aa33639-18/aa33639-18-eq31.gif)
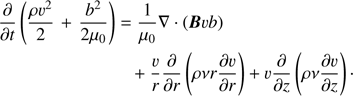
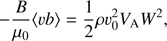
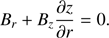
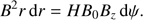
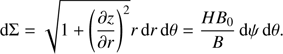
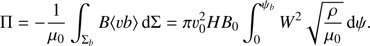

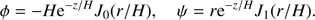
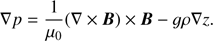
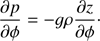
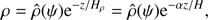
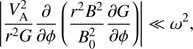
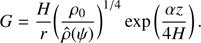
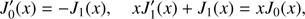
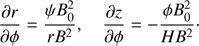
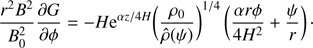
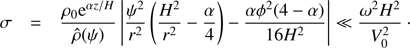
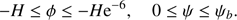
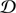
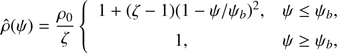
![$$ \begin{aligned} \frac{r_0 J_1(r_0/H)}{J_0(r_0/H)} = \psi _b , \quad z_0 = H\ln [J_0(r_0/H)]. \end{aligned} $$](/articles/aa/full_html/2018/12/aa33639-18/aa33639-18-eq57.gif)