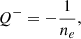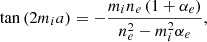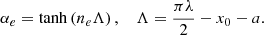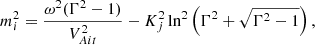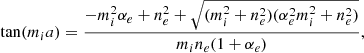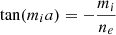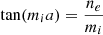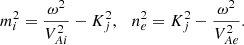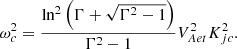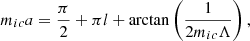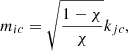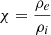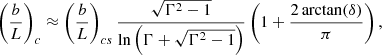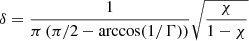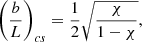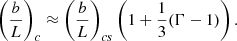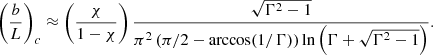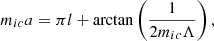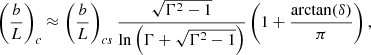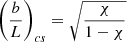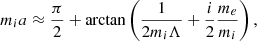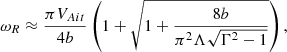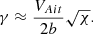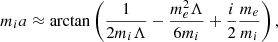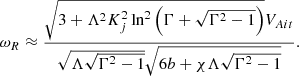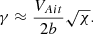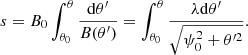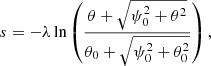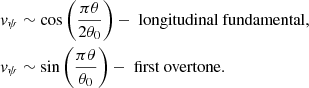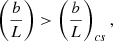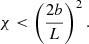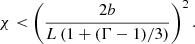| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A353 | |
| Number of page(s) | 11 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202452220 | |
| Published online | 26 November 2024 | |
Fast magnetohydrodynamic oscillations of a coronal loop embedded in a potential coronal arcade
Institute of Applied Astronomy of the Russian Academy of Sciences, Ussuriisk department, nab. Kutuzova 10, St. Petersburg 191187, Russia
⋆ Corresponding author; lopin78@mail.ru
Received:
12
September
2024
Accepted:
22
October
2024
Context. Observations indicate variable widths exhibited by fan coronal loops and flare loops that tend to widen towards the apex. Short-period, quasi-periodic pulsations in solar flares are often interpreted in terms of the fast-sausage oscillations of flare loops and the collective vertical vibrations of arcade loops are attributed with the vertical kink mode. Both phenomena are used as a seismological tool to estimate the physical parameters in the corona.
Aims. We performed an analytical study of fast sausage and kink oscillations in coronal loops, given the effects of loop curvature, expansion, and Alfvén speed variation.
Methods. We modelled a coronal loop as a dense expanding curved magnetic slab embedded within a potential coronal arcade, using a zero-β plasma limit. We obtained the dispersion relation that governs fast waves in the model and studied it both numerically and analytically.
Results. The effects of loop expansion and variable Alfvén speed reduce the cut-off frequency and increase the cut-off wavenumbers for fast sausage and kink waves. Moreover, the principal vertical kink mode has a cut-off and strongly attenuates in the leaky regime. The frequency increase is found to be minor for the global sausage mode both in the trapped and leaky regimes, with a frequency shift within a few percent. We found that in our model, where the Alfvén speed increases from the footpoints to the loop top, the spatial profile of the longitudinal fundamental is broadened and the antinodes of the first overtone are shifted towards the footpoints.
Conclusions. Using the classical expression for the cut-off wavenumber of the global sausage mode in a straight waveguide results in an underestimation of the density contrast constraint in flare loops. Instead, the suggested formula accounting for variations in loop widths provides more accurate results. The frequency of the global sausage mode can be correctly determined with the straight slab model.
Key words: Sun: corona / Sun: oscillations
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Coronal loops constitute visible magnetic structures in the upper solar atmosphere. These traces of coronal magnetic field lines are filled with denser plasma compared to their environment. This feature makes them waveguides for a number of magneto-acoustic wave modes, such as axisymmetric sausage and asymmetric kink fast modes. The theoretical foundation for magnetohydrodynamic (MHD) oscillations in solar waveguides was first established for simple models, including a straight slab or cylinder (see e.g. Edwin & Roberts 1982; Spruit 1982; Roberts et al. 1984, see also Roberts 2019 for comprehensive review). More accurate approaches take into account the effect of plasma stratification along the loops. In the context of the fast kink mode, this problem was considered, for instance, by Andries et al. (2005), Dymova & Ruderman (2005), Erdélyi & Verth (2007), Lopin & Nagorny (2017), whereas Díaz et al. (2007) studied the effect of longitudinal structuring on both kink and sausage fast modes. The transverse density structuring introduces the resonant absorption for kink wave modes in cylindrical loops (e.g. Ruderman & Roberts 2002; Soler et al. 2013) and alters the dispersion properties of fast sausage modes in both slab and cylindrical geometries (e.g. Pascoe et al. 2007; Lopin & Nagorny 2015a,b; Yu et al. 2015). The influence of the magnetic field transverse structure on the fast modes was analysed in various aspects as well. In particular, the fast kink mode was found to be nearly insensitive to the azimuthal component of a loop magnetic field with linear profile (Ruderman 2007; Ruderman & Terradas 2015), whereas it is affected by the localised magnetic twist (Terradas & Goossens 2012). In turn, the dispersion of the global fast sausage mode is strongly modified, when the effect of a magnetic twist is introduced (Giagkiozis et al. 2015; Lopin 2021).
It is also worth noting that coronal loops are essentially curved magnetic structures. The effect of curvature has been previously studied in context of fast wave modes, both numerically and analytically for the cold plasma limit (see Van Doorsselaere et al. 2009 for review). The main finding has been that the curvature introduces the effect of vertical wave leakage, resulting in temporal attenuation of loop oscillations (e.g. Smith et al. 1997; Verwichte et al. 2006). The combined effect of loop curvature and finite plasma-β on fast surface modes of a semicircular loop was found to be minor as long as perpendicular propagation (ky ≠ 0) is ignored (Lopin 2022). Furthermore, observations indicate that the loop cross-section (width) is not constant along their length. Indeed, the coronal magnetic field is detected to diverge with physical height (see e.g. Chen et al. 2014) and the fan-like structure of an active region coronal loops suggests their expansion from the footpoints to apex (Klimchuk 2000; Malanushenko & Schrijver 2013). This effect appears to be especially relevant to the flare loops, where the dynamic phenomena near their summit induce the expansion of a loop cross-section (Zaitsev & Stepanov 1982; Melnikov et al. 2005). The effects of coronal loop expansion alone on kink and sausage oscillations were first studied for models of slab and cylinder with straight axis and variable cross-section (Ruderman et al. 2008; Pascoe et al. 2009). On the other hand, the combination of a coronal loop expansion and curvature is effectively mimicked by considering the field-aligned density enhancements, embedded within curved potential magnetic arcades. So far, this approach was used to numerous numerical simulations of impulsively excited fast kink and sausage oscillations of arcade loops. In particular, Selwa et al. (2006), Gruszecki & Murawski (2008) simulated the vertical kink oscillations in this model, whereas Pascoe & Nakariakov (2016) considered numerically global sausage oscillations. The investigation of sausage and kink oscillations within a model of a curved and expanding slab is of interest for several reasons. The observed quasi-periodic pulsations of flaring plasma are often attributed with the sausage mode oscillations of flare loops (e.g. Melnikov et al. 2005; Kolotkov et al. 2015; Tian et al. 2016; Li et al. 2020). Hence, the development of an adequate theory of this wave mode in solar waveguides such as flare loops is considered to be relevant. Furthermore, the collective vertical kink oscillations of arcade loops could be studied analytically within a similar curved slab model. Given these reasons, it would be actual to carry out an analytical study of fast wave modes in a curved and expanding slab model and to explore the dispersion properties of fast waves upon the model parameters.
In this paper, we consider the combined effect of loop curvature, expansion and Alfvén speed variation on the properties of fast sausage and kink modes, using 2D model of a curved dense slab embedded within a potential magnetic arcade. For the particular case of equilibrium parameters, we plan to obtain the dispersion relations that govern the behavior of fast modes and analyse them both numerically and analytically.
2. Equilibrium model
We consider a 2D potential equilibrium magnetic field to model the coronal arcade. The magnetic field components in Cartesian coordinates are as follows (Oliver et al. 1993; Cadez & Ballester 1994):
and they correspond to the flux function A(x, z) of the form
Here, B0 is a constant, λ is the magnetic scale height and the lateral extent of an arcade structure is πλ. We model an expanding curved coronal loop embedded within a coronal arcade as a field-aligned density enhancement, characterised by the footpoint positions at z = 0 and x = ±x0. The loop semi-extent at the footpoints along the x-axis is a, whereas its semi-width at the apex is b. The sketch of the considered structure is shown in Fig. 1. It is obvious to consider the problem of MHD oscillations in the introduced model using so-called flux coordinates, which are governed by the magnetic field model in Eq. (1). These are as follows:
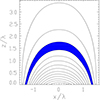 |
Fig. 1. Model of a curved and expanding coronal slab as a density enhancement (blue region) embedded within a potential coronal arcade. Here, z measures the vertical height from the photospheric base at z = 0, and x measures the horizontal extent of a magnetic structure. |
In these coordinates, the curved magnetic field lines transform to straight lines, pointed along the θ-direction and
Here, h = hψ = hθ is the scale factor of coordinate transformations. Furthermore, the loop is given by ψ− ≤ ψ ≤ ψ+, where ψ± define the inner and outer loop boundaries and ψ0 determines the loop axis. Using Eq. (3) we can write the following relations between the introduced parameters
We define the length of the curved coronal loop as a length of its central axis. Using the expression to loop axis in Eq. (5) and the known formula for the length of a curved line, we can obtain the expression to the loop length as
Using similar description to the lower or upper loop boundaries, we can obtain the desired relation between the x-semi-extent of a loop at the footpoints a and the loop semi-width at the apex b. The result is
In particular, considering the actual condition a ≪ x0 and applying the series expansion to the right-hand side of Eq. (7), we obtain
It is also useful to introduce the half-width of a loop at its footpoints d, as it is measured along the direction perpendicular to the loop axis. This parameter generally differs from the x-semi-extent of a loop, because of magnetic field geometry. Simple trigonometric calculations result in the following relation:
and corresponding relation between b and d is
Alternatively, Eq. (10) can be directly obtained with the magnetic flux conservation condition. It is expressed as B0d = Bab, where Ba is the magnetic field strength at the loop apex and according to Eqs. (1) and (3) Ba = B0cos(x0/λ). Substituting this result into the former relation, we arrive at Eq. (10).
We also introduce the expansion factor Γ, which is the ratio of a loop width at the apex to its width at the footpoints, namely,
3. Wave equation and dispersion relation
The linear perturbations in the zero-β plasma are satisfied to the following vector wave equation, written in terms of plasma velocity v (see e.g. Priest 1987) as
Considering the third y-direction to be ignored and v ∼ exp(−iωt), we can reduce this wave equation to the form (Oliver et al. 1993)
written in terms of normal velocity vn = v ⋅ ∇A. Here,
is the Alfvén speed. Using the known expression for the operator ∇2 in the introduced curvilinear coordinate system, we can rewrite Eq. (13) as
At this step, we introduce the scaled field-aligned variable ϕ, given by
and Eq. (15) takes the form
In order to further analytical study, we consider
This is the case when the Alvfén speed grows with physical height z and it satisfies the physical conditions in the solar corona. For the magnetic field model given by Eq. (1), the relation in Eq. (18) is implemented by choosing the density profile ρ = ρ0exp(−4z/λ)/(1 − ψ2/λ2). It follows from Eqs. (5) and (18) that the internal and external Alfvén speeds at the loop footpoints are given by
whereas the internal and external Alfvén speeds at the loop top (apex) are as follows:
It is obvious from Eqs. (18)–(20) that the Alfvén speed grows along the loop from its footpoints toward the apex (see Fig. 2). We note that the adopted model is characterised by the constant value of the transverse Alfvén transit time τAt along the loop. Indeed, it is straightforward to show using the magnetic flux conservation condition and Eqs. (4), (10), and (18) that
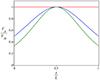 |
Fig. 2. Normalised Alfvén speed profile along the loop axis, shown for the expansion factor Γ = 1 (red line), Γ = 2 (blue curve) and Γ = 3 (green curve). |
where w(θ) and VAi(θ) are the loop semi-width and internal Alfvén speed at distance θ from the loop apex. This feature is similar to that observed in the straight and curved slab models with constant width and Alfvén speed. Furthermore, when varying the expansion factor Γ in our model, the loop semi-width at the apex, b, and the Alfvén speed, VAi, et, at the apex both remain unchanged. Hence, according to Eq. (21), the transverse Alfvén transit time, τAt, remains unchanged as well. However, this is not the case for the longitudinal Alfvén transit time, τAl, governed by the loop length, L, and Alfvén speed distribution along the loop, VA(θ). It is clearly seen in Fig. 2 that the larger expansion factor Γ corresponds to lower Alfvén speed, averaged along the loop and, hence, results in longer τAl. These features of our model are taken into account when interpreting subsequent results.
Substituting Eq. (18) in Eq. (17) we arrive at the following wave equation
Equation (22) is supplemented with the line-tying boundary condition
indicating that the magnetic field lines are anchored within the over dense underlying photosphere for z ≤ 0. The ϕ-component of vψ is represented in the form
where according to the boundary condition in Eq. (23)
j = 0, 1, 2, 3... Here, even values of j correspond to even harmonics, and odd values of j correspond to odd harmonics. In particular, j = 0 corresponds to the longitudinally fundamental mode. It is useful to express kj in terms of physical loop length L, given Eqs. (6) and (11). The result is
where
With ϕ dependences of vψ, given by Eq. (24), Eq. (22) then reduces to the one-dimensional wave equation of the form
Introducing
and considering m2λ2 ≫ 1, we can apply the WKB method to obtain the solutions to Eq. (28). In this case, the general solution is expressed as follows
where
and C1, C2 are arbitrary constants. The validity of the WKB approximation is given by the condition (Bender & Orszag 1978) as
It is straightforward to verify that for mλ ≫ 1 this condition is fulfilled on the entire range of 0 ≤ ψ/λ < 1, excluding for ψ/λ → 1.
We write the solution to Eq. (28) inside the loop as follows
where
The corresponding solution in the upper external region 0 ≤ ψ ≤ ψ+, vanishing as ψ → 0 is given by
where
The solution in the lower external region ψ− ≤ ψ ≤ λ takes the form
This solution is permitted because when neζ is a complex-valued quantity, it prescribes inward waves propagating away from the slab, whereas the factor q1/4(ψ) ensures that vψ0 vanishes as ψ/λ → 1.
We require the natural condition for matching solutions at the loop boundaries, namely,
The second set of boundary conditions requires the continuity of the magnetic pressure perturbations p′m = Bbθ/μ0 at both interfaces and hence, we can write
Using solutions in Eqs. (34), (36) and (38) and boundary conditions in Eqs. (39) and (40) we can obtain the desired dispersion relation. After some algebraic procedures, we arrive at the result
Here, according to Eqs. (5) and (31)
and ζ± = ζ(ψ±). When deriving Eq. (41) we take into account that q1/4(ψ) is the slowly varying function, as it follows from the WKB approach. Given Eqs. (42)–(44), we can rewrite Eq. (41) as follows
where
It is worth noting that expressions to mi and ne are useful to write in terms of internal and external Alfvén speeds, evaluated at the loop apex and wavenumber Kj directly related with the physical loop length L. Using Eqs. (11), (19), (20), and (26) and Eqs. (35) and (37), we obtain
Dispersion relation in Eq. (45) describes both symmetric (sausage) and asymmetric (kink) wave modes in the loop model. Using the trigonometric identity for a tangent function of double argument, Eq. (45) can be rewritten as follows
where
The first and the second factor in Eq. (49) describes the dispersion of asymmetric kink modes and axisymmetric sausage modes, respectively. Hence, the dispersion relations under study are as follows
for the sausage modes and
for the kink modes.
In the following analysis, we will compare the results obtained for our model with those known for the model of a straight slab with constant width. Corresponding dispersion relations for a straight slab are as follows (Edwin & Roberts 1982; Terradas et al. 2005)
for the sausage modes and
for the kink modes, where now
4. Numerical solutions
We carried out the numerical solutions of dispersion relations, given by Eqs. (51), (52), Eqs.(53), and (54) to obtain the qualitative and quantitative characteristics of fast wave dispersion in both curved and expanding and straight slab models.
4.1. Sausage modes
Figure 3 displays the dispersion diagrams of fast sausage modes in a curved slab of length, L, with expansion factor of Γ = 2 and in a straight slab of similar length, L, calculated for the actual range of the aspect ratio b/L and for different density contrasts. The main finding is that the so-called cut-off frequency, separating the trapped and leaky wave regimes decreases in our model with respect to the straight slab, whereas the cut-off wavenumbers increase. It is worth noting that the reference model in our study includes a straight slab of semi-width, b, with an internal Alfvén speed, VAit, which are both equal to their counterparts in the apex of a curved and expanding slab. Obviously, the observed effects are due to the variations of the external Alfvén speed and slab semi-width along its axis, Indeed, the effective values of these parameters are roughly equal to their average values, which are smaller then those in a straight slab. These arguments are confirmed in the analytical study at the rest of this work. Therefore, the curved and expanding slab with apex semi-width b is less effective at trapping the sausage modes (including the global sausage mode) than the straight slab with constant semi-width b. The change of the sausage wave frequencies is more pronounced for the higher transverse order modes and for moderate values of the aspect ratio b/L. The general tendency is that the mode frequencies in our model are larger then those in a straight slab, both in the trapped and in the leaky regimes. These frequency deviations are minor for the global fast sausage mode, which is the mode of the lowest transverse order. In particular, for density contrast χ = 1/25 the frequency deviation in a curved slab with expansion factor Γ = 2 is about of 3% for the aspect ratio of a/L = 0.2 in the trapped regime and about 8% for the aspect ratio b/L = 0.1 in the leaky regime. These deviations remain minor for more contrast loops with χ = 1/50; here, for the aspect ratios of b/L = 0.2 in the trapped regime and b/L = 0.07 in the leaky regime, the frequency differences are within 3% and 4%, respectively. These results are in agreement with the previous numerical simulation of the global sausage mode in a curved and expanding slab, carried out by Pascoe & Nakariakov (2016). In that study, the different model with uniform Alfvén speed was used; nevertheless, the minor changes in frequency of the global sausage mode were found by those authors as well. The reduction in the period of the global sausage mode of about 5% was also found by Pascoe et al. (2009) for the model of a straight slab with variable cross-section. Furthermore, for the global fast sausage mode, the frequency deviation increases with increasing aspect ratio and this is observed at moderate values 0.1 ≤ b/L ≤ 0.5. This implies that the higher longitudinal harmonics of the global sausage mode undergo a more significant increase in frequency compared to a straight slab with constant width. In Fig. 4, we show the dependencies of the change in frequency of the global sausage mode upon the expansion factor, calculated for different values of the aspect ratio, which correspond to both leaky and trapped regimes. These results indicate the larger increase in frequency of the global sausage mode for larger expansion factor and aspect ratio. The frequency deviation from the straight slab model ranges from a few percent to ten percent both in the leaky and trapped regimes, in the actual range of 1 ≤ Γ ≤ 3.
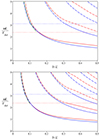 |
Fig. 3. Dependences of the normalised frequencies of the sausage modes upon the aspect ratio, shown for a straight slab (blue curves) and for a curved and expanding slab with expansion factor Γ = 2 (red curves). The calculations were performed for the density contrasts χ = 1/25 (upper panel) and χ = 1/50 (lower panel). The horizontal dotted lines mark the positions of cut-off frequencies in both models. The solid and dashed curves correspond to the trapped and leaky regimes, respectively. The green dashed curves are obtained with approximate relation in Eq. (70). |
 |
Fig. 4. Frequency of the global sausage mode in a curved and expanding slab, ωcs, normalised in terms of the corresponding frequency of a straight slab with uniform cross-section ωss, as a function of the expansion factor, Γ. Calculations were performed for b/L = 0.07 (red dashed curve) in the leaky regime and for b/L = 0.2 (green solid curve), b/L = 0.3 (blue solid curve) in the trapped regime, and for χ = 1/50. |
The aforementioned properties of the global sausage mode indicate the low sensitivity of its frequency (period) to the loop expansion factor Γ both in the leaky regime and in the trapped regime for small and moderate values of the aspect ratio b/L. It is worth noting that an increase in the expansion factor results in a decrease of the Alfvén speed 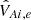 , averaged along the loop length (see e.g. Fig. 2). In particular, for Γ = 2, the averaged Alfvén speed is at least of 30% lower than in a straight and uniform slab, provided that b and VAi, et are both fixed. This increases the longitudinal Alfvén transit time τAl by 30% accordingly. Supposing that the period of the global sausage mode is governed by τAl, we expect it to increase for about these 30%. However, our numerical results show a frequency (period) change of only a few percent for Γ = 2. Moreover, we found the opposite effect – a slight decrease in the oscillation period. Hence, we concluded that the period of the global sausage mode weakly depends on the longitudinal Alfvén transit time. On the other hand, the transverse Alfvén transit time, τAt, remains constant for different expansion factors in our model (see Eq. (21)). This implies that the period of the global sausage mode is mainly governed by τAt both in the leaky and trapped regimes for small and moderate b/L values.
, averaged along the loop length (see e.g. Fig. 2). In particular, for Γ = 2, the averaged Alfvén speed is at least of 30% lower than in a straight and uniform slab, provided that b and VAi, et are both fixed. This increases the longitudinal Alfvén transit time τAl by 30% accordingly. Supposing that the period of the global sausage mode is governed by τAl, we expect it to increase for about these 30%. However, our numerical results show a frequency (period) change of only a few percent for Γ = 2. Moreover, we found the opposite effect – a slight decrease in the oscillation period. Hence, we concluded that the period of the global sausage mode weakly depends on the longitudinal Alfvén transit time. On the other hand, the transverse Alfvén transit time, τAt, remains constant for different expansion factors in our model (see Eq. (21)). This implies that the period of the global sausage mode is mainly governed by τAt both in the leaky and trapped regimes for small and moderate b/L values.
In Fig. 5, we show the transverse profile of the normal velocity perturbations at the loop apex (x = 0), calculated for the global sausage mode and shown with red curve. This profile has axisymmetric structure with a node around the slab axis, which is typical for the global sausage mode.
 |
Fig. 5. Internal transverse profiles of normal velocity perturbation at the loop apex (x = 0), shown for the global sausage mode (red curve) and principal kink mode (blue curve). The set of used parameters: Γ = 2, b/L = 0.15, χ = 1/50 (for the global sausage mode) and χ = 1/10 (for the principal kink mode). |
4.2. Kink modes
In Fig. 6, we show dispersion diagrams obtained for the fast kink modes in a straight slab with uniform width and in a curved and expanding slab with expansion factor Γ = 2. The principal kink mode, which is the mode of the lowest transverse order has a cut-off wavenumber in a curved and expanding slab; thus, it can exist as a trapped or leaky mode. It is worth noting that similar characteristics for the principal kink mode were found in a slab models with asymmetric environment (Zsámberger et al. 2018; Lopin & Nagorny 2020). This is completely different from the properties of this mode in a straight and uniform slab, where the principal kink mode is a trapped mode for any aspect ratio and its phase speed tends to the external Alfvén speed in the limit of b/L → 0. This new feature implies that the vertical kink mode can be subjected to the strong damping due to the wave leakage in a curved and expanding arcade loops with quite small aspect ratio. Furthermore, in the trapped regime, the frequency of the principal kink mode in a curved and expanding slab is slightly lower then in a straight slab with constant width. This frequency difference is within a few percent for moderate values of aspect ratio in the trapped regime. The effect of a curved and expanding slab is more significant to the kink modes of higher transverse order. Their frequencies are higher in our model than in a straight and uniform slab and the observed increase in frequency is in the range of a few tens of percent. The common tendency is the increase of the cut-off wavenumbers in a curved and expanding slab (including the principal kink mode). This is similar to what observed for the fast sausage modes and this indicates that the loop model under study is less effective at trapping the kink modes of different transverse orders than a straight uniform slab.
 |
Fig. 6. Dependences of the normalised frequencies of the kink modes upon the aspect ratio, shown for a straight slab (blue curves) and for a curved and expanding slab with expansion factor of Γ = 2 (red curves). The calculations were performed for the density contrasts χ = 1/5 (upper panel) and χ = 1/10 (lower panel). The horizontal dotted lines mark the positions of cut-off frequencies in both models. The solid and dashed curves correspond to the trapped and leaky regimes, respectively. The green dashed curves are obtained with an approximate relation given by Eq. (73). |
We also calculated the internal transverse profile of perturbed normal velocity at the loop apex for the principal kink mode. It is shown in Fig. 5 with the blue curve. The velocity perturbations have the same sign everywhere inside the slab and this corresponds to our expectations about the principal kink mode.
5. Analytical results
5.1. Cut-off wavenumbers
The so-called cut-off wavenumbers separate the trapped and leaky wave regimes. In the former case, the waves are trapped by the slab and corresponding solutions in the environment are evanescent, that is, they decay far from the slab. In turn, in the leaky wave regime, particularly with respect to our model, the inward propagating waves are supported by the lower external region and this results in attenuation of slab oscillations due to the energy deposition in the environment. These cut-offs are given by the condition ne = 0, implying that
Equation (56) indicates that wave modes in our model become leaky when their phase speed exceeds some effective external Alfvén speed, which is generally lower than the external Alfvén speed in the loop top for Γ > 1. We attribute this with the effect of Alfvén speed variation along the slab, which grows from the footpoints to the apex. It is straightforward to verify that for the actual range of 1 ≤ Γ ≤ 3, this effective external Alfvén speed is roughly equal to the average value, defined as 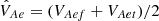 .
.
In order to obtain the desired cut-off wavenumbers for the sausage modes, one need to consider the limit ne → 0 in the right-hand side of Eq. (51) and then use Eq. (56). We obtain the following expressions:
where
and
is the density contrast and l = 0, 1, 2... In particular, l = 0 corresponds to the global sausage mode, which is the symmetric wave mode of the lowest transverse order l. It is more convenient to write Eq. (57) in terms of critical aspect ratio (b/L)c. For the fundamental longitudinal harmonic (j = 0) of the global sausage mode (l = 1), the result is
where
and we introduce (b/L)cs, given by
which is the critical aspect ratio for the global sausage mode in the straight slab of length L and semi-width b (see e.g. Terradas et al. 2005). For the actual range of an expansion factor of 1 ≤ Γ ≤ 3, Eq. (60) can be approximated by the linear function
Figure 7 shows the dependences of the critical aspect ratio upon the expansion factor, calculated with Eqs. (60) and (63). The main finding is that (b/L)c increases as the expansion factor grows. In particular, for Γ = 2 and χ = 1/50, (b/L)c ≈ 1.36(b/L)cs; namely, the critical aspect ratio in curved and expanding loop with expansion factor of 2 is larger for about 40% with respect to the corresponding value in a straight slab with constant width. Thus, curved and expanding loop with apex semi-width b less effectively trap the global sausage mode than loops with similar constant width, b. This is in accordance with our numerical finding. The interpretation of this effect is straightforward. The increase in (b/L)c in a curved and expanding slab is such that the average value, defined as [(b/L)c + (d/L)c]/2, is roughly equal to the critical aspect ratio in a straight and uniform slab (b/L)cs and this condition is valid for the actual range of 1 ≤ Γ ≤ 3. It is obvious that this is due to the fact that curved and expanding loop with apex semi-width b has lower average semi-width then straight slab with semi-width b.
 |
Fig. 7. Dependences of the critical aspect ratio (b/L)c for the global sausage mode against the expansion factor Γ, calculated for different values of the density contrast χ. Solid and dashed curves are obtained with Eqs. (60) and (63) respectively. |
Direct numerical solution of the exact dispersion relation for the kink modes shows that the principal kink mode has a cut-off for Γ > 1. This cut-off wavenumber has the lowest value among all modes. Its analytical expression can be obtained, when considering the limit ne → 0 in Eq. (52). We can obtain
Equation (64) results in the following approximate expression, written in terms of critical aspect ratio (b/L)c for j = 0 as
Figure 8 shows the dependence of critical aspect ratio upon the expansion factor, calculated for different values of the density contrast with Eq. (65). These results indicate that in typical coronal arcade loops of active regions with density contrast 1/5 ≤ χ ≤ 1/3 and aspect ratio 0.02 ≤ b/L ≤ 0.06, the principal kink mode could exist in the leaky regime, even for an expansion factor of Γ ≤ 1.5. This is because the corresponding values of the critical aspect ratio are less than the value that is characteristic for arcade loops. When considering the higher transverse order kink modes, the expression to their cut-offs is as follows
 |
Fig. 8. Dependences of the critical aspect ratio (b/L)c for the principal kink mode against the expansion factor Γ, calculated for different values of the density contrast χ. |
where l = 1, 2, 3… In particular, for the longitudinal fundamental (j = 0) of the l = 1 kink mode, we can obtain the relation to the critical aspect ratio,
where now
is the critical aspect ratio for the l = 1 kink mode in a straight slab of length, L, and semi-width, b. The cut-off wavenumbers for the higher transverse order kink modes increase in the curved and expanding slab, when comparing with their counterparts in the straight slab. This is similar to what is found for symmetric sausage modes.
5.2. Leaky regime
It is of particular interest to perform the analytical study of the global sausage mode and principal kink mode in the leaky regime in order to obtain the expressions to frequencies and damping decrements for these modes in a curved and expanding slab model. This considered to be actual as the aforementioned results indicate that both the principal kink mode in active region arcade loops and the global sausage mode in flaring loops could exist as leaky fast waves.
The properties of the global sausage mode in the leaky regime are found when considering me/mi ≪ 1 in Eq. (51), with ne and tanh(neΛ) being replaced with ime and itan(meΛ), and me2 = −ne2. Taking into account the first two terms of series expansion of the right hand side in Eq. (51), we can write the following expression:
where the right hand side is a complex-valued quantity. Introducing the complex frequency ω = ωR + iγ, where γ is the damping decrement and approximating arctan(x)≈x, we arrive at the results
Equation (70) shows that the frequency of the leaky global sausage mode is defined by the slab width, namely, it is inversely proportional to the transverse Alfvén transit time. This is similar to what is known for this leaky mode in a straight slab. The second term in the square root in the right-hand side of Eq. (70) is a small correction to the mode frequency due to the variation in loop width. The green dashed curves in Fig. 3 are obtained with Eq. (70) and they show a good fitting to the numerical data. The damping decrement given by Eq. (71) has half the value of its counterpart in a straight and uniform slab (see e.g. Terradas et al. 2005). Hence, the leaky global sausage mode is less subjected to attenuation in our loop model. We note that the damping is insensitive to the expansion factor of a loop.
In order to find the properties of the principal kink mode in the leaky regime, we apply the series expansion to the right-hand side of Eq. (52), where ne and tanh(neΛ) are replaced with ime and itan(meΛ), respectively and considering me/mi ≪ 1. Given the two leading order terms, we arrive at the equation
where the right-hand side is a complex-valued quantity. We use the similar technique as above and introduce the complex frequency ω = ωR + iγ. Considering the thin slab limit b/L ≪ 1, we obtain for ωR the following expression:
Equation (73) shows that the frequency of the leaky principal kink mode depends on both the loop length and width and it has the lowest frequency among the other leaky modes. The green dashed curves in Fig. 6 have been obtained with Eq. (73) and they show good fit to the numerical data as well. The damping decrement is as follows
It is straightforward to verify that the damping rate has the similar expression as for the global sausage mode. Figure 9 displays the relative damping rate, γ/ωR, as a function of the expansion factor for different density contrasts. The results indicate very strong damping of the leaky principal kink mode in the case of b/L ≪ 1, because γ/ωR > 1 for typical density contrasts in arcade loops. Therefore, it is unlikely to detect the vertical kink oscillations of expanding arcade loops in the leaky regime. This is similar to what found in previous numerical simulations of vertical kink oscillations in curved and expanding loops (see e.g. Selwa et al. 2006). In those works, the authors detected strong (within the one oscillation period) temporal attenuation of the excited vertical kink oscillations due to the vertical wave leakage.
 |
Fig. 9. Dependences of the relative damping decrement, γ/ωR, for the leaky principal kink mode against the expansion factor, Γ, calculated for different values of the density contrast χ and for b/L = 0.02. |
5.3. Spatial amplitude profiles
It is of interest to consider the spatial structure of the longitudinal fundamental and first harmonic of fast oscillations in our loop model. These modes have an ideal sine (cosine) structure in a straight slab with uniform cross-section. To find the longitudinal profiles, we need to obtain an expression to the distance, s, along the loop axis. It is given by
Evaluating integral in Eq. (75), we arrive at
where ψ0 = λcos(x0/λ) and θ0 = λsin(x0/λ). Using Eqs. (16), (24), and (25) we can write the following expressions for the longitudinal profiles:
Here, θ is expressed in terms of s with Eq. (76). Figure 10 shows the longitudinal profiles of the fundamental mode and first overtone of fast MHD oscillations in our model in comparison with those in a straight and homogeneous slab. The effect of profile broadening is observed for the longitudinal fundamental mode. For the first overtone, its antinodes are shifted to the footpoints of the slab. Both these effects are stronger for larger expansion factor. These properties are identical to those, found in stratified waveguides for the fast kink modes (see e.g. Andries et al. 2005; Verth et al. 2007). Indeed, in our model the loop have both variable cross-section and density, but variations in density are dominant and this results in increasing of the Alfvén speed from the footpoint to the apex. The similar situation occurs in a stratified tube. On the other hand, Pascoe et al. (2009) and Pascoe & Nakariakov (2016) found opposite effects for the amplitudes of the global sausage mode. This is because their models are characterised by the dominance of the magnetic expansion effect, with Alfvén speed either decreasing from the footpoints to apex or remaining constant. Therefore, our results with those obtained by Pascoe et al. (2009) and Pascoe & Nakariakov (2016) show that the Alfvén speed inhomogeneity results in modification of the amplitude profiles of the fundamental mode and first overtone of the global sausage mode. In particular, the density (magnetic field) variation broadens (narrows) the amplitude profile of the fundamental mode and shift the antinodes of the first overtone toward the footpoints (apex) of a loop. The same is true for the higher order fast sausage modes and fast kink modes.
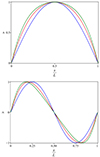 |
Fig. 10. Longitudinal amplitude profiles of the fundamental harmonic (j1 = π/2, top) and first overtone (j2 = π, bottom) in the curved and expanding coronal loop, obtained for the expansion factor Γ = 1.5 (red curves), Γ = 2 (blue curves), and Γ = 3 (green curves). |
6. Relevance of the model and application of the results
The applicability of a curved slab model to coronal structures is justified for the global fast sausage mode, since the identity of its properties in both cylindrical and slab waveguides is well established. The model of a curved and expanding slab is considered an adequate approximation to flare loops, which tend to widen at the apex due to dynamic processes occurring there. Numerous observations of high quality quasi-periodic pulsations in flaring plasma are interpreted in terms of fast sausage oscillations that directly modulate the magnetic field and plasma parameters. Based on this interpretation, a constraint is imposed on the loop aspect ratio
which provides the existence of the global sausage mode in a trapped regime (Nakariakov et al. 2003; Aschwanden et al. 2004). Here, (b/L)cs is given by Eq. (62) for a straight slab model, whereas it differs by a numerical factor for the straight cylinder model. When estimating the visual loop parameters b and L, the inequality in Eq. (78) provides the estimate to the density contrast in oscillating loop (e.g. Srivastava et al. 2008; Su et al. 2012; Chowdhury et al. 2015; Tian et al. 2016)
Our results show that in the loop with non-uniform width, the critical aspect ratio for the global sausage mode, defined with the largest apex width, b, is greater than that in a loop with constant width, b. The following restriction can be obtained from Eqs. (63) and (78):
Hence, using Eq. (79) results in underestimation of the density contrast. In particular, for the expansion factor Γ = 2, the underestimation of the density contrast is of the order of 50%. More accurate results can be obtained with Eq. (80), using visual estimate of the expansion factor, for instance, by measuring loop widths near its apex and bottoms. On the other hand, our results evidence that the inhomogeneities of the loop cross-section and Alfvén speed profile have only minor effect on the frequency (period) of the global sausage mode. Hence, the models of a straight slab or cylinder can be considered adequate to describe the frequencies of fast sausage oscillations in flare coronal loops.
Using the curved slab model in the context of a vertical principal kink mode is possible when considering the collective vertical vibrations of arcade loops. In this case, the vertical width of this structure is much less than its extent along the arcade axis, and the curved slab approach seems appropriate. Then, the observed very strong damping of arcade loop vertical kink oscillations can be interpreted in terms of vertical wave leakage effect.
7. Conclusions
This work explores the properties of fast magnetoacoustic oscillations of a coronal magnetic slab embedded in a potential coronal arcade. The model under study takes into account the effects of a loop curvature and variable loop width, increasing from the footpoints to apex. Furthermore, the effects of both internal and external Alfvén speed variations along the loop are considered. A special choice of equilibrium parameters allowed us to perform the analytical study of oscillations in terms of normal mode analysis in a curved and expanding magnetic slab. Our primary interest has been to study of global sausage and principal kink modes. Our findings are summarised below.
-
We found that in a curved and expanding coronal slab with variable internal and external Alfvén speeds, the cut-off frequencies, separating the trapped and leaky wave regimes, are reduced with respect to their counterparts in a straight and uniform slab. They depend on some effective value of the external Alfvén speed, which is roughly equal to its average value along a loop, for the actual range of the expansion factor of 1 ≤ Γ ≤ 3. Corresponding critical aspect ratios (b/L)c increase as the expansion factor increases. The latter effect is due to the variation of a slab width. Both these results are valid for sausage and kink fast modes and they indicate that the curved and expanding slab with an apex semi-width of b is less effective at trapping the fast modes than the straight and uniform slab of similar semi-width of b.
-
The dispersion diagrams obtained for the sausage modes in a curved and expanding slab show an increase in mode frequencies compared to the case of a straight slab. This change is found minor for the global sausage mode (the sausage mode of the lowest transverse order), with frequency difference in the range of (3 − 10)%, both in the leaky and trapped wave regimes for the actual range of a loop aspect ratio. Furthermore, the frequency of the global sausage mode slightly increases with increasing expansion factor. The effect of a frequency increase is more pronounced for larger values of a loop aspect ratio, namely, this effect is stronger for higher longitudinal harmonics of the global sausage mode. It was shown that the period of the global sausage mode in our model is mainly governed by the transverse Alfvén transit time both in the leaky and trapped wave regime for small and moderate aspect ratios; namely, it depends on the loop width, rather than on its length. In the leaky wave regime, the damping decrement of the global sausage mode is two times less than the corresponding value in a straight uniform slab and this indicates a less strong damping of this mode in a curved and expanding slab.
-
We have found that the principal kink mode (the kink mode of the lowest transverse order) in a model of a curved and expanding slab has the cut-off wavenumber; namely, it can exist in either the trapped or in the leaky regime. This is completely different from its properties in a straight and homogeneous slab, where the principal kink mode is trapped on the entire range of wavenumbers. The critical aspect ratio for this mode has the lowest value among the other fast modes and it depends on both the density contrast and the expansion factor. In the leaky wave regime, the principal kink mode is subjected to a strong attenuation with a relative damping decrement greater than unity. We have also found that the fast kink modes of higher transverse orders undergo a more significant frequency increase than the principal kink mode.
-
It is found that the spatial profiles of the longitudinal fundamental and the first overtone of fast oscillations under study are modified compared to the case of a straight uniform slab. In our model, where the Alfvén speed increases from the footpoints to the apex, the profile of the longitudinal fundamental is broadened and the antinodes of the first overtone are shifted toward the footpoints. It is worth noting that opposite effects were found by Pascoe et al. (2009) and Pascoe & Nakariakov (2016) in a curved and expanding slab models, where the Alfvén speed either decreases from the ends to apex or remains constant. The explanation of this discrepancy is straightforward. In our model, the effect of plasma stratification is dominant, whereas in the models of Pascoe et al. (2009) and Pascoe & Nakariakov (2016), the dominant effect is magnetic field divergence.
As we noted above, the loop model under study most correctly describes the fast sausage mode. In the case of the fast kink mode, the obtained results are applicable when considering kink oscillations of arcade loop structures. A correct description of kink oscillations of individual curved and expanding coronal loops requires the inclusion of the perpendicular propagation effect (ky ≠ 0). This is an issue for the future research.
Acknowledgments
The author thanks to anonymous reviewer for useful suggestions.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Nakariakov, V. M., & Melnikov, V. F. 2004, ApJ, 600, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Bender, C. M., & Orszag, S. A. 1978, Advanced Mathematical Methods for Scientists and Engineers (New York: Mc Grow-Hill) [Google Scholar]
- Cadez, V. M., & Ballester, J. L. 1994, A&A, 292, 669 [NASA ADS] [Google Scholar]
- Chen, F., Peter, H., Bingert, S., et al. 2014, A&A, 564, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chowdhury, P., Srivastava, A. K., Dwivedi, B. N., et al. 2015, Adv. Space Res., 56, 2769 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz, A. J., Donelly, G. R., & Roberts, B. 2007, A&A, 476, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dymova, M. V., & Ruderman, M. S. 2005, Sol. Phys., 229, 79 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1982, Sol. Phys., 79, 239 [NASA ADS] [Google Scholar]
- Erdélyi, R., & Verth, G. 2007, A&A, 462, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giagkiozis, I., Fedun, V., Erdelyi, R., & Verth, G. 2015, ApJ, 810, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Gruszecki, M., & Murawski, K. 2008, A&A, 487, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klimchuk, J. A. 2000, Sol. Phys., 193, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Kolotkov, D. Y., Nakariakov, V. M., Kupriyanova, E. G., Ratcliffe, H., & Shibasaki, K. 2015, A&A, 574, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, B., Antolin, P., Guo, M. Z., et al. 2020, Space Sci. Rev., 216, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Lopin, I. P. 2021, MNRAS, 505, 1878 [NASA ADS] [CrossRef] [Google Scholar]
- Lopin, I. 2022, MNRAS, 514, 4329 [NASA ADS] [CrossRef] [Google Scholar]
- Lopin, I., & Nagorny, I. 2015a, ApJ, 810, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Lopin, I., & Nagorny, I. 2015b, ApJ, 801, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Lopin, I., & Nagorny, I. 2017, AJ, 154, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Lopin, I., & Nagorny, I. 2020, MNRAS, 496, 3035 [NASA ADS] [CrossRef] [Google Scholar]
- Malanushenko, A., & Schrijver, C. J. 2013, ApJ, 775, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Melnikov, V. F., Reznikova, V. E., Shibasaki, K., & Nakariakov, V. M. 2005, A&A, 439, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Melnikov, V. F., & Reznikova, V. E. 2003, A&A, 412, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, R., Ballester, J. L., Hood, A. W., & Priest, E. R. 1993, A&A, 273, 647 [NASA ADS] [Google Scholar]
- Pascoe, D. J., & Nakariakov, V. M. 2016, A&A, 593, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., & Arber, T. D. 2007, A&A, 461, 1149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Nakariakov, V. M., Arber, T. D., & Murawski, K. 2009, A&A, 494, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Priest, E. R. 1987, Solar Magneto-Hydrodynamics (Dordrecht: Reidel Publ. Co.) [Google Scholar]
- Roberts, B. 2019, MHD Waves in the Solar Atmosphere (Cambridge, United Kingdom: Cambridge University Press) [Google Scholar]
- Roberts, B., Edwin, P. M., & Benz, A. O. 1984, ApJ, 279, 857 [CrossRef] [Google Scholar]
- Ruderman, M. S. 2007, Sol. Phys., 246, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [Google Scholar]
- Ruderman, M. S., & Terradas, J. 2015, A&A, 580, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruderman, M. S., Verth, G., & Erdélyi, R. 2008, ApJ, 686, 694 [Google Scholar]
- Selwa, M., Solanki, S. K., Murawski, K., Wang, T. J., & Shumlak, U. 2006, A&A, 454, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, J. M., Roberts, B., & Oliver, R. 1997, A&A, 317, 752 [NASA ADS] [Google Scholar]
- Soler, R., Goossens, M., Terradas, J., & Oliver, R. 2013, ApJ, 777, 158 [Google Scholar]
- Spruit, H. C. 1982, Sol. Phys., 75, 3 [Google Scholar]
- Srivastava, A. K., Zaqarashvili, T. V., Uddin, W., Dwivedi, B. N., & Kumar, P. 2008, MNRAS, 388, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Su, J. T., Shen, Y. D., Liu, Y., Liu, Y., & Mao, X. J. 2012, ApJ, 755, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., & Goossens, M. 2012, A&A, 548, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Oliver, R., & Ballester, J. L. 2005, A&A, 441, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tian, H., Young, P. R., Reeves, K. K., et al. 2016, ApJ, 823, L16 [Google Scholar]
- Van Doorsselaere, T., Verwichte, E., & Terradas, J. 2009, Space Sci. Rev., 149, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Verth, G., Van Doorsselaere, T., Erdélyi, R., & Goossens, M. 2007, A&A, 475, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verwichte, E., Foullon, C., & Nakariakov, V. M. 2006, A&A, 446, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yu, H., Li, B., Chen, S.-X., & Guo, M.-Z. 2015, ApJ, 814, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Zaitsev, V. V., & Stepanov, A. V. 1982, Sov. Astron. Lett., 8, 132 [NASA ADS] [Google Scholar]
- Zsámberger, N. K., Allcock, M., & Erdelyi, A. R. 2018, ApJ, 853, 136 [Google Scholar]
All Figures
 |
Fig. 1. Model of a curved and expanding coronal slab as a density enhancement (blue region) embedded within a potential coronal arcade. Here, z measures the vertical height from the photospheric base at z = 0, and x measures the horizontal extent of a magnetic structure. |
| In the text | |
 |
Fig. 2. Normalised Alfvén speed profile along the loop axis, shown for the expansion factor Γ = 1 (red line), Γ = 2 (blue curve) and Γ = 3 (green curve). |
| In the text | |
 |
Fig. 3. Dependences of the normalised frequencies of the sausage modes upon the aspect ratio, shown for a straight slab (blue curves) and for a curved and expanding slab with expansion factor Γ = 2 (red curves). The calculations were performed for the density contrasts χ = 1/25 (upper panel) and χ = 1/50 (lower panel). The horizontal dotted lines mark the positions of cut-off frequencies in both models. The solid and dashed curves correspond to the trapped and leaky regimes, respectively. The green dashed curves are obtained with approximate relation in Eq. (70). |
| In the text | |
 |
Fig. 4. Frequency of the global sausage mode in a curved and expanding slab, ωcs, normalised in terms of the corresponding frequency of a straight slab with uniform cross-section ωss, as a function of the expansion factor, Γ. Calculations were performed for b/L = 0.07 (red dashed curve) in the leaky regime and for b/L = 0.2 (green solid curve), b/L = 0.3 (blue solid curve) in the trapped regime, and for χ = 1/50. |
| In the text | |
 |
Fig. 5. Internal transverse profiles of normal velocity perturbation at the loop apex (x = 0), shown for the global sausage mode (red curve) and principal kink mode (blue curve). The set of used parameters: Γ = 2, b/L = 0.15, χ = 1/50 (for the global sausage mode) and χ = 1/10 (for the principal kink mode). |
| In the text | |
 |
Fig. 6. Dependences of the normalised frequencies of the kink modes upon the aspect ratio, shown for a straight slab (blue curves) and for a curved and expanding slab with expansion factor of Γ = 2 (red curves). The calculations were performed for the density contrasts χ = 1/5 (upper panel) and χ = 1/10 (lower panel). The horizontal dotted lines mark the positions of cut-off frequencies in both models. The solid and dashed curves correspond to the trapped and leaky regimes, respectively. The green dashed curves are obtained with an approximate relation given by Eq. (73). |
| In the text | |
 |
Fig. 7. Dependences of the critical aspect ratio (b/L)c for the global sausage mode against the expansion factor Γ, calculated for different values of the density contrast χ. Solid and dashed curves are obtained with Eqs. (60) and (63) respectively. |
| In the text | |
 |
Fig. 8. Dependences of the critical aspect ratio (b/L)c for the principal kink mode against the expansion factor Γ, calculated for different values of the density contrast χ. |
| In the text | |
 |
Fig. 9. Dependences of the relative damping decrement, γ/ωR, for the leaky principal kink mode against the expansion factor, Γ, calculated for different values of the density contrast χ and for b/L = 0.02. |
| In the text | |
 |
Fig. 10. Longitudinal amplitude profiles of the fundamental harmonic (j1 = π/2, top) and first overtone (j2 = π, bottom) in the curved and expanding coronal loop, obtained for the expansion factor Γ = 1.5 (red curves), Γ = 2 (blue curves), and Γ = 3 (green curves). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



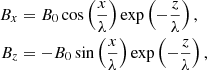
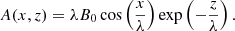
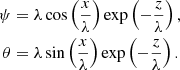
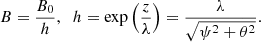
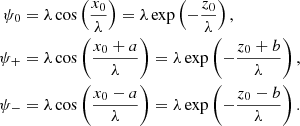
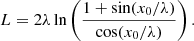
![$$ \begin{aligned} b=-\lambda \ln \left(\frac{\cos [(x_0+a)/\lambda ]}{\cos (x_0/\lambda )}\right). \end{aligned} $$](/articles/aa/full_html/2024/11/aa52220-24/aa52220-24-eq7.gif)
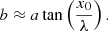
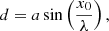
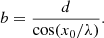
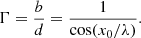
![$$ \begin{aligned} \rho \frac{\partial ^2\mathbf{{v}}}{\partial t^2}=\frac{1}{\mu _0}\{\nabla \times [\nabla \times (\mathbf{{v}}\times \mathbf{{B}})]\}\times \mathbf{{B}}. \end{aligned} $$](/articles/aa/full_html/2024/11/aa52220-24/aa52220-24-eq12.gif)
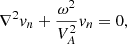
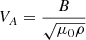
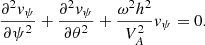
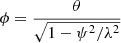
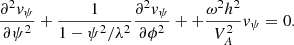
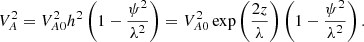
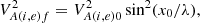
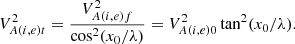
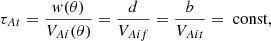
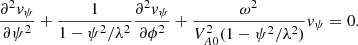
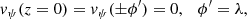
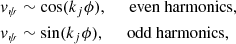
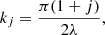
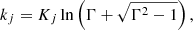
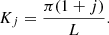
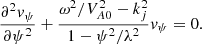
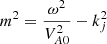
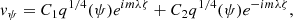
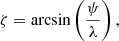
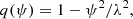
![$$ \begin{aligned} m\lambda \zeta \gg -\ln \left[\left(1-\frac{\psi ^2}{\lambda ^2}\right)^{1/4}\right]. \end{aligned} $$](/articles/aa/full_html/2024/11/aa52220-24/aa52220-24-eq33.gif)
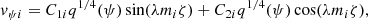
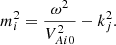
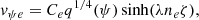
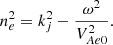
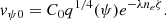
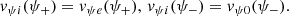
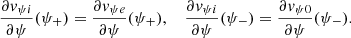
![$$ \begin{aligned} \tan \left[m_i\lambda (\zeta ^+-\zeta ^-)\right]=\frac{m_i\left(Q^+-Q^-\right)}{1+m_i^2Q^+Q^-}. \end{aligned} $$](/articles/aa/full_html/2024/11/aa52220-24/aa52220-24-eq41.gif)
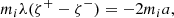
![$$ \begin{aligned}&Q^+=\frac{\tanh (\lambda n_e\zeta ^+)}{n_e}=\frac{1}{n_e}\tanh \left[n_e\left(\frac{\pi \lambda }{2}-x_0-a\right)\right],\end{aligned} $$](/articles/aa/full_html/2024/11/aa52220-24/aa52220-24-eq43.gif)