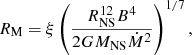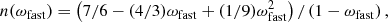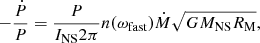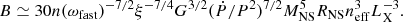| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | L12 | |
| Number of page(s) | 10 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201833442 | |
| Published online | 14 December 2018 | |
Letter to the Editor
NGC 300 ULX1: A test case for accretion torque theory
1
Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
2
Department of Astronomy, Yale University, PO Box 208101 New Haven, CT 06520-8101, USA
e-mail: georgios.vasilopoulos@yale.edu
Received:
16
May
2018
Accepted:
27
November
2018
NGC 300 ULX1 is a newly identified ultra-luminous X-ray pulsar. The system is associated with the supernova impostor SN 2010da that was later classified as a possible supergiant Be X-ray binary. In this work we report on the spin period evolution of the neutron star based on all the currently available X-ray observations of the system. We argue that the X-ray luminosity of the system has remained almost constant since 2010, at a level above ten times the Eddington limit. Moreover, we find evidence that the spin period of the neutron star evolved from ∼126 s down to ∼18 s within a period of about 4 years. We explain this unprecedented spin evolution in terms of the standard accretion torque theory. An intriguing consequence for NGC 300 ULX1 is that a neutron star spin reversal should have occurred a few years after the SN 2010da event.
Key words: X-rays: binaries / galaxies: individual: NGC 300 / stars: neutron / pulsars: individual: NGC 300 ULX1
© ESO 2018
1. Introduction
X-ray binaries are among the most luminous stellar-mass objects that are powered by accretion. A major implication of spherical accretion is that the released radiation can become so luminous that in principle it could halt accretion (at the Eddington limit LEdd). Nevertheless, numerous sources have been observed at X-ray luminosity (LX) levels well above LEdd for a neutron star (NS). These are the so-called ultra-luminous X-ray sources (ULXs; Kaaret et al. 2017). These sources are considered promising candidates for hosting high-stellar-mass black holes. However, the X-ray spectral properties of many ULXs are inconsistent with sub-Eddington accretion models, implying super-Eddington accretion onto stellar-mass objects (Roberts et al. 2016). Remarkably, in recent years pulsations have been discovered from a few such systems (Bachetti et al. 2014; Fürst et al. 2016; Israel et al. 2017b,a). This offers undisputed evidence that at least a few ULXs host highly magnetized NSs. Recently, Koliopanos et al. (2017) revisited a large sample of known ULXs and by taking into account theoretical predictions (e.g. King et al. 2017; Mushtukov et al. 2017) argued that a significant fraction of non-pulsating ULXs may also be powered by a highly magnetized NS.
NGC 300 ULX1 is a newly identified ULX pulsar (ULXP; Carpano et al. 2018, hereafter C18), located in NGC 300 at a distance of 1.88 Mpc (Gieren et al. 2005). The system became active in X-rays and optical in May 2010, when its luminosity rapidly increased causing it to exhibit what was classified as a supernova impostor event (SN 2010da, Binder et al. 2011; Lau et al. 2016). In C18 we showed that in the early 2010 observations the spectrum of the system was mostly affected by partial absorption (i.e. equivalent hydrogen column density NH ∼ 5 × 1023 cm−2), while in the 2016 spectrum the NH of the partial absorption component was significantly lower by a factor of approximately 100. From the analysis of XMM-Newton and NuSTAR data we derived an unabsorbed X-ray luminosity (LX) of 4.7 × 1039 erg s−1 (0.3–30.0 keV), a value consistent with both 2010 and 2016 observations. The temporal analysis of the 2016 X-ray data revealed a spin period (P) of 31.7 s and a spin period derivative (Ṗ) of −5.56 × 10−7 s s−1. In this letter, we discuss the NS spin-period evolution in terms of standard accretion theories and we comment on the derived properties that make NGC 300 ULX1 such an exciting case study among ULXPs.
2. Observational data and analysis
Since its X-ray brightening in 2010, NGC 300 ULX1 has been monitored by most of the modern X-ray observatories; Swift, XMM-Newton, NuSTAR and Chandra. We requested additional Swift monitoring and two Chandra target of opportunity (ToO) observations in order to measure the most recent spin-up rate and LX of the system. Additionally, a NuSTAR ToO observation was performed on January 2018 (Bachetti et al. 2018). For all available X-ray observations standard products were extracted using the latest available software packages and instrument calibration files. For XMM-Newton data reduction we used SAS v16.1.0. NuSTAR and Swift/XRT data were reduced using nupipeline (v0.4.6) and xrtpipeline (v0.13.4) respectively, that can be found in HEASoft 6.22 software (see details in C18). Chandra data reduction was performed with CIAO v4.9 software (Fruscione et al. 2006).
The X-ray spectra were analysed using the xspec (v12.9.0) spectral fitting package (Arnaud et al. 1996). For the fits we used a phenomenological model that best described the high-quality X-ray spectra obtained during three XMM-Newton observations performed in 2010 and 2016 (C18). The continuum model consists of a power law with a high-energy exponential cutoff (Ecut ∼ 6 keV) and a disc black-body component that accounts for emission from the accretion disc. Absorption was modelled by a partial coverage component and an absorption component to account for the local and interstellar absorption, respectively. For each of the analysed spectra we used a Bayesian approach to derive the probability density distributions of the marginalized parameters of the model and the intrinsic LX of NGC 300 ULX1. Additional details about the spectral fitting are provided in Appendix A.
The X-ray light curve of NGC 300 ULX1 is shown in Fig. 1. For simplicity we scaled the LX obtained from our spectral analysis (0.3–10.0 keV) to the LX derived from the simultaneous NuSTAR and XMM-Newton observations in 2016 (LX = 4.7 × 1039 erg s−1; C18). Between 2011 and 2016, only a few observations were performed with collected events consistent with heavily absorbed spectra (see also C18). Due to the low statistics in these observations there is a large degeneracy between the model parameters and especially the disc black-body component cannot be constrained.
 |
Fig. 1. Normalized LX of NGC 300 ULX1, as derived by the fits to the X-ray spectra from Swift (black triangles), XMM-Newton (blue squares), and Chandra (red circles). Values are scaled to 4.7 × 1039 erg s−1, the LX derived by C18 (see text). |
To further investigate X-ray variability we simultaneously fitted all the spectra with low statistics with the same continuum model, letting only the parameters of the absorption components vary for each spectrum. Fixing LX to 4.7 × 1039 erg s−1 and the continuum parameters to the best-fit parameters inferred from the 2016 XMM-Newton observation (see Table 1 in C18) yielded an acceptable fit for all spectra. Therefore, between 2010 and 2018 the observed variability is consistent with changes in LX no greater than a factor of three.
We note that our aim was not to investigate whether our phenomenological model describes the data best, but to put constraints on the LX evolution over the ∼8 yr period following the SN 2010da event. For ULXPs a plethora of models have been used to describe their spectra; some motivated by X-ray pulsars in high-mass X-ray binaries (e.g. Walton et al. 2018), or in the context of optically thick accretion envelopes that has been proposed to explain ULXP spectra (Koliopanos et al. 2017; Mushtukov et al. 2017). A detailed study of all these models is beyond the scope of this letter and will be further addressed in an upcoming publication (Koliopanos et al. 2018).
Given the extreme spin-up rate of the NS in NGC 300 ULX1 reported by C18, P can significantly change within the duration of a typical X-ray exposure (>10 ks). To take this effect into account we performed an accelerated epoch folding (AEF) test (Leahy et al. 1983b) to derive the ephemeris of NGC 300 ULX1. Details about this methodology and its caveats can be found in Appendix B. The complete list of observations and the derived properties of the system are listed in Table B.1. A periodic signal was detected for all observations performed after November 2014, when a period of ∼126.3 s was detected on MJD 56978. The latest analysed observation yielded a period of ∼19 s on MJD 58221 (see Fig. 2).
 |
Fig. 2. Normalized pulse profiles of NGC 300 ULX1. Subplots correspond to different epochs (see Table B.1) and are sorted in decreasing spin period (from top to bottom panels). Pulse profiles derived by Chandra (panels a and e) contain events with energies in the 0.3–8.0 keV band, while those derived from XMM-Newton data (panel c) and Swift (panels b and d) denote the 0.3–10.0 keV range. |
The Swift/XRT monitoring of NGC 300 ULX1 is ongoing. These additional observations cover the period after May 2018 and will be presented in a future study (see also NICER monitoring Ray et al. 2018). However, we have performed a preliminary spectral and temporal analysis and have measured a periodic signal in all of them. The Swift/XRT observations show that LX is still consistent with being almost constant within a factor of less than two until approximately August 2018. The latest detected spin period of NGC 300 ULX1 is ∼17.977 s measured on MJD 58307.3.
3. Results and discussion
We first describe briefly the principles of the interaction between the NS and accretion disc around it (see also review of Lai 2014), and then we apply them to the observational data of NGC 300 ULX1. Throughout the calculations we assume typical values of MNS = 1.4 M⊙ and RNS = 10 km for the NS mass and radius, respectively.
If the inner radius of the Keplerian disc (Rd) is inside the co-rotation radius (Rco), then accretion along the magnetic lines can occur. If the Rd > Rco, accretion is halted by a centrifugal barrier (i.e. propeller regime; Campana et al. 2018). During accretion, we can observationally measure the LX emitted by the accreted material and the change of the NS P. In general, LX is equal to the rate at which gravitational energy of the in-falling matter is released. Nevertheless, the fraction of the gas gravitational potential energy converted to radiation could be different (e.g. radiative inefficient flow; D’Angelo et al. 2015) and model dependent for the environment of the accretion column (Farinelli et al. 2016; West et al. 2017). Therefore we can define neff as the efficiency with which gravitational energy is converted to radiation (Lx = neffG MNSṀ/RNS). To calculate the induced torque onto the NS, we further assume that the accretion disc is truncated at the magnetospheric radius RM due to the strong magnetic field B of the NS:
where the ξ parameter takes a value of ∼0.5 (Campana et al. 2018).
Several models have been proposed for calculating the applied torque onto an accreting NS (e.g. Wang 1987; Ghosh & Lamb 1979; Parfrey et al. 2016). In the early paradigm presented by Ghosh & Lamb (1979), the magnetic field lines permeate through the disc and couple the latter with the NS. Due to the mismatch of the angular velocity of the disc with the NS angular velocity, lines that intersect the disc inside (outside) Rco apply a positive (negative) torque to the NS. The torque due to mass accretion is 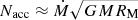 . However, the total torque can be expressed in the form of Ntot = n(ωfast)Nacc where n(ωfast) is a dimensionless function of ωfast = (RM/Rco)3/2, which is known as the fastness parameter. Assuming the magnetic field lines thread through the disc, an assessment of the magnetic stresses (Wang 1995) yields:
. However, the total torque can be expressed in the form of Ntot = n(ωfast)Nacc where n(ωfast) is a dimensionless function of ωfast = (RM/Rco)3/2, which is known as the fastness parameter. Assuming the magnetic field lines thread through the disc, an assessment of the magnetic stresses (Wang 1995) yields:
which simplifies to n(ωfast) = 7/6 for very slow rotators (ωfast ≪ 1). Alternatively, a more physical picture is that the magnetic field lines cannot remain connected to the NS and the spin-down term is due to the enhanced opening of magnetic field lines (see Parfrey et al. 2016). This result is also supported by simulations (Parfrey et al. 2017; Parfrey & Tchekhovskoy 2017). For the range of the derived parameter values of NGC 300 ULX1 (i.e. P, LX, B), the spin-down due to enhanced opening of magnetic field lines is more than two orders of magnitude smaller than the spin-up due to accretion. Therefore, one can safely assume that Ntot = Nacc. We note that all the treatments mentioned above vary only by a normalization factor when applied to “slow rotator” systems away from the propeller transition (i.e. ωfast ≪ 1). In simple terms, for n(ωfast) = 1 the formulation of Ghosh & Lamb (1979) produces the same results as those of Parfrey et al. (2016).
Having a model of the accretion torque we can then compute the spin derivative Ṗ of the NS. For a NS with moment of inertia 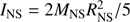 one derives:
one derives:
from where we can solve for the polar magnetic field strength:
We applied Eq. (4) to observations with good statistics where P and Ṗ were computed with high accuracy (i.e. only two epochs). We estimated B to be approximately 1012−13 G (see Table 1). Interestingly, for both epochs we derive the same value for B, which in turn implies that ξ and neff have not changed. The high magnetic field strength is consistent with the findings of Tong & Wang (2019). By using the values of Table 1, we can derive the P-Ṗ evolution of the system assuming constant accretion, as is shown in Fig. 3. NGC 300 ULX1 is clearly still away from the equilibrium (i.e. Ṗ = 0); which when reached will be less than 1 s, assuming constant Ṁ.
Estimation of B under different assumptions for the Wang (1995; W95) and Parfrey et al. (2016; P16) torque models.
 |
Fig. 3. |Ṗ|/P vs. P for NGC 300 ULX1. Solid black lines denote the solution using the W95 approximation while assuming a constant LX. The two solutions based on the derived values from the two data sets (red points) with best statistics (2016 & 2018) presented in Table 1. The Ghosh & Lamb (1979) model prediction is plotted (dotted line) for comparison using the observed 2016 LX. All model lines assume neff = 100%. |
Having an estimate of B we can numerically solve Eq. (3) backwards (and forward) in time from the latest spin period measurement. The only assumption is the history of LX (i.e. Ṁ). Based on the derived spectral properties we argue that after the SN 2010da event, LX (see Fig. 1) only varied by a small factor (i.e. < 3), and the large deviation in the observed flux is mainly caused by a change in absorption (see also C18). The theoretical prediction can then be tested with the observed data. In Fig. 4 we compare the observed spin periods with the theoretical period evolution for a range of Lx values in order to account for small variations of Ṁ. The time axis range and reference date were selected for visualisation purposes and to properly spread the observational points.
 |
Fig. 4. Evolution of the NS spin period of NGC 300 ULX1 since the SN 2010da event (blue vertical dashed line). The black solid line denotes the theoretical prediction assuming a constant accretion rate and stellar torque from disc-magnetosphere interactions (Wang 1995) with efficiency = 1.0, B = 5 × 1012 G and Lx = 4 × 1039 erg s−1. The grey shaded area marks the evolution path for a range of LX, i.e. 3–5 × 1039 erg s−1. The inset plot shows the predicted evolution of the spin period for the subsequent years, with the lone data point being the ∼19 s Swift measurement (MJD 58221). |
Assuming almost steady Ṁ after the SN 2010da event, the only way to explain the spin-period evolution is by an accretion disc formed rotating retrograde with respect to the spin of the NS. Thus, the NS was initially spinning down and at some point the rotation was stopped; after that the NS started to rotate in the opposite direction (Fig. 4). In other words, from an evolutionary point of view, the retrograde disc appears to be a necessary initial condition in order to explain its spin evolution. While this raises questions of how the counter rotation was produced in the first place, the formation of retrograde accretion discs has also been proposed to explain the long-term evolution of spin periods in X-ray binaries (Nelson et al. 1997; Christodoulou et al. 2017). However, for the time window 2010–2015 we can only speculate for the evolution of Ṁ due to lack of observational coverage and because of the high absorption of the X-ray spectrum (see Fig. 3 of C18). Nevertheless, the P and Ṗ measurements during the 2014 Chandra observation are consistent with the constant Ṁ assumption (see Fig. 3), supporting our finding that the decrease of the observed flux between 2010 and 2015 is only due to high absorption. If Ṁ during that period was two orders of magnitude lower than after 2015 then it is possible that there was no NS spin reversal. In this case the NS spin period should have been larger than a few hundred seconds prior to the SN 2010da event.
In general there are multiple ways to maintain the necessary Ṁ to fuel ULXPs. For systems fueled by Roche Lobe (RL) overflow, the accretion flow carries the angular momentum of the orbit. It is therefore implausible for an accretion disc to switch between retrograde and prograde rotation (Chakrabarty et al. 1997), and any change between retrograde and prograde rotation of the NS disc system needs to be due to a change in the direction of the NS rotation. Therefore, for NGC 300 ULX1 it is more plausible that the accretion mechanism was drastically altered during the SN 2010da event, prior to which the NS could have been fueled via wind accretion. A possible explanation for such a phase transition to occur can be an episode of thermal-timescale mass transfer (King et al. 2001). In that case the donor star has a radiative envelope and fills its RL as it expands across the Hertzsprung gap after the wind-fed X-ray phase ends.
However, RL overflow is not the only way to explain such high accretion rates. Supergiant systems and luminous blue variables (LBV) can also exhibit mass loss rates in excess of 10−6 M⊙ yr−1 (Smith 2014), and therefore for a binary system in a moderately close orbit the compact object can capture enough matter to sustain super-Eddington accretion. An LBV is also most probable according to Binder et al. (2016) while other authors have deemed this classification inconclusive (Lau et al. 2016; Villar et al. 2016). We note that many of the arguments used in the classification of the system were based on the decay of the X-ray flux observed after the SN 2010da event. However, the decay in the X-ray flux was most likely a result of rapid increase in X-ray absorption (C18).
4. Conclusions
We have studied the spin period evolution of NGC 300 ULX1, the most extreme spin-up NS powered by an accretion disc. We derived precise measurements of P and Ṗ for different epochs, and applied theoretical models of accretion theory in order to estimate the magnetic field strength of the NS. Even though many of the models assume a geometrically thin disc we find that in the current regime of the system (ωfast ≪ 1) all of them can explain its evolution fairly well. Given the fast spin up of the NS, future observations when the spin period approaches its equilibrium will be of great importance to test different accretion models. However, given the timescale of the period evolution of the NS at the current accretion rate it might take close to one hundred years for the system to reach equilibrium. Finally, we argued that according to theoretical predictions and given the observable properties of the system, the NS has probably exhibited a spin reversal prior to 2014.
Acknowledgments
We would like to thank the editor S. Campana and the anonymous referee for their comments and suggestions which helped us improve this manuscript. We acknowledge the use of public data from Swift, XMM-Newton, Chandra and NuSTAR observatories. We thank the Chandra director Dr. Belinda Wilkes for accepting our DDT request and the CXC team for promptly scheduling the observations. This research has made use of software provided by the Chandra X-ray Center (CXC) in the application package CIAO. We acknowledge the use of the XMM-Newton SAS software, developed by ESA’s Science Operations Centre staff.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Bachetti, M., Harrison, F. A., Walton, D. J., et al. 2014, Nature, 514, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Bachetti, M., Grefenstette, B. W., & Walton, D. J., et al. 2018, ATel, 11282 [Google Scholar]
- Binder, B., Williams, B. F., Kong, A. K. H., et al. 2011, ApJ, 739, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Binder, B., Williams, B. F., Kong, A. K. H., et al. 2016, MNRAS, 457, 1636 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bühlmann, P. 2002, Stat. Sci., 17, 52 [Google Scholar]
- Campana, S., Stella, L., Mereghetti, S., & de Martino, D. 2018, A&A, 610, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpano, S., Haberl, F., & Sturm, R. 2017, A&A, 602, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpano, S., Haberl, F., Maitra, C., & Vasilopoulos, G. 2018, MNRAS, 476, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarty, D., Bildsten, L., Finger, M. H., et al. 1997, ApJ, 481, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Christodoulou, D. M., Laycock, S. G. T., & Kazanas, D. 2017, MNRAS, submitted [arXiv:1704.06364] [Google Scholar]
- D’Angelo, C. R., Fridriksson, J. K., Messenger, C., & Patruno, A. 2015, MNRAS, 449, 2803 [NASA ADS] [CrossRef] [Google Scholar]
- Farinelli, R., Ferrigno, C., Bozzo, E., & Becker, P. A. 2016, A&A, 591, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Fruscione, A., McDowell, J. C., Allen, G. E., et al. 2006, Proc. SPIE, 6270, 62701V [Google Scholar]
- Fürst, F., Walton, D. J., Harrison, F. A., et al. 2016, ApJ, 831, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Gieren, W., Pietrzyński, G., Soszyński, I., et al. 2005, ApJ, 628, 695 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Belfiore, A., Stella, L., et al. 2017a, Science, 355, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Israel, G. L., Papitto, A., Esposito, P., et al. 2017b, MNRAS, 466, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kaaret, P., Feng, H., & Roberts, T. P. 2017, ARA&A, 55, 303 [Google Scholar]
- King, A. R., Davies, M. B., Ward, M. J., Fabbiano, G., & Elvis, M. 2001, ApJ, 552, L109 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., Lasota, J.-P., & Kluźniak, W. 2017, MNRAS, 468, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Koliopanos, F., Vasilopoulos, G., Godet, O., et al. 2017, A&A, 608, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koliopanos, F., Vasilopoulos, G., Buchner, J., Maitra, C., & Haberl, F. 2018, A&A, submitted,[arXiv:1811.06251] [Google Scholar]
- Lai, D. 2014, Eur. Phys. J. Web Conf., 64, 01001 [Google Scholar]
- Lau, R. M., Kasliwal, M. M., Bond, H. E., et al. 2016, ApJ, 830, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., Darbro, W., Elsner, R. F., et al. 1983a, ApJ, 266, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, D. A., Elsner, R. F., & Weisskopf, M. C. 1983b, ApJ, 272, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Mushtukov, A. A., Suleimanov, V. F., Tsygankov, S. S., & Ingram, A. 2017, MNRAS, 467, 1202 [NASA ADS] [Google Scholar]
- Nelson, R. W., Bildsten, L., Chakrabarty, D., et al. 1997, ApJ, 488, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Parfrey, K., & Tchekhovskoy, A. 2017, ApJ, 851, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Parfrey, K., Spitkovsky, A., & Beloborodov, A. M. 2016, ApJ, 822, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Parfrey, K., Spitkovsky, A., & Beloborodov, A. M. 2017, MNRAS, 469, 3656 [NASA ADS] [CrossRef] [Google Scholar]
- Ray, P. S., Guillot, S., Ho, W. C. G., et al. 2018, ArXiv e-prints [arXiv:1811.09218] [Google Scholar]
- Roberts, T. P., Middleton, M. J., Sutton, A. D., et al. 2016, Astron. Nachr., 337, 534 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J. 2004, in AIP Conf. Ser., eds. R. Fischer, R. Preuss, & U. V. Toussaint, 735, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N. 2014, ARA&A, 52, 487 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Tong, H., & Wang, W. 2019, MNRAS, 482, 4956 [NASA ADS] [CrossRef] [Google Scholar]
- Villar, V. A., Berger, E., Chornock, R., et al. 2016, ApJ, 830, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Bachetti, M., Fürst, F., et al. 2018, ApJ, 857, L3 [Google Scholar]
- Wang, Y.-M. 1987, A&A, 183, 257 [NASA ADS] [Google Scholar]
- Wang, Y.-M. 1995, ApJ, 449, L153 [NASA ADS] [Google Scholar]
- West, B. F., Wolfram, K. D., & Becker, P. A. 2017, ApJ, 835, 129 [CrossRef] [Google Scholar]
Appendix A: Spectral analysis of NGC 300 ULX1
C18 have shown that the X-ray spectrum of NGC 300 ULX1 can be described by a partially absorbed power-law and a disc black-body component. By comparing the 2010 and the 2016 XMM-Newton spectra of the system, the authors found that the intrinsic spectrum has not significantly changed and the difference in the observed flux was only due to the heavily absorbed 2010 spectrum. Nevertheless, any model that is composed by a combination of a soft component and a hard (pulsating) component with an exponential cutoff can explain the intrinsic X-ray spectrum. A partial covering absorber should be used to account for the long-term changes of the surrounding material in the binary system (C18).
In the current work, the X-ray spectrum of NGC 300 ULX1 was treated as follows; to model the soft component, we chose a simple disc black-body (diskbb in xspec), for the hard component we used a power-law (powerlaw) modified by a high energy cut-off (highecut). The continuum is absorbed by interstellar material (modeled with tbabs) and a partial covering absorber (pcfabs) that accounts for intrinsic absorption. To mitigate the issues posed by limited statistics we adopted a Bayesian framework to fit the available X-ray spectra (see also; Koliopanos et al. 2018). We used the Bayesian X-ray analysis package (BXA; Buchner et al. 2014) that was specifically designed to test various models in low-statistic spectra. In practice, BXA connects the nested sampling (Skilling et al. 2004) algorithm MultiNest (Feroz et al. 2009) with xspec. BXA explores the parameter space and can be used for parameter estimation (probability distributions of each model parameter and their degeneracies). We use BXA with its default parameters (400 live points and logZ/evidence accuracy of 0.1).
By using this Bayesian framework we are able to fit the phenomenological model described above to the X-ray spectrum of NGC 300 ULX1 and derive a probability density function for LX of the system. Our results probe LX into three different periods; (I) the first 10 days after the SN 2010da event, where LX remained almost constant and the NH and covering fraction of the partial covering component rapidly increased, (II) the following period till 2015, where only a couple of observations were performed and the X-ray spectrum is heavily absorbed (NH > 1024 cm−2) making any LX estimation uncertain, and (III) the period between 2016 and today, where the total NH dropped below 1022 cm−2 and the inclusion of the partial coverage component is not statistically significant in the spectra (i.e. its parameters are not constrained). Our results suggest that NGC 300 ULX1 maintained an almost constant LX (factor of 3) within the eight-year period (2010–2018), except one measurement in 2014, where due to limited statistics we cannot simultaneously constrain both LX and the partial absorber parameters. In any case the upper limit for the LX of the system (as denoted by the 95% percentile of the LX distribution) is only a factor of three lower than the LX derived from the 2016 XMM-Newton observations.
Appendix B: Temporal properties of NGC 300 ULX1: Accelerated epoch folding
Our aim is to study the temporal properties of NGC 300 ULX1 on short time scales. Thus we want to determine both P and Ṗ from a single long observation, or by using multiple short exposures (i.e. snapshots) performed within a couple of days. We extracted the barycentric corrected event arrival times and performed various statistical tests to search for a periodic signal. For individual observations with a high number of events (i.e. XMM-Newton, NuSTAR), we performed an accelerated epoch folding (AEF) test (Leahy et al. 1983b) to derive the ephemeris of the pulsar similar to the work of Fürst et al. (2016). The AEF method uses a grid of trial points in the P-Ṗ plane in order to fold a time series and create a pulse profile, and performs a χ2 test based on the constant signal hypothesis. Therefore, a maximization of the χ2 indirectly supports the presence of a periodic signal. The significance of any detection is then assessed by MCMC simulations. Fake datasets can be created and analysed by the AEF algorithm, the results can then be used to estimate a baseline for the maximum χ2 value we would expect from a non-periodic time series.
For each observation of NGC 300 ULX1 we used a grid of points in the P-Ṗ space to determine the best fit value. We then performed multiple iterations by decreasing the bin size of the grid around the best fit values until we scanned the P-Ṗ plane with sufficient resolution. For the 2016 XMM-Newton and NuSTAR (2016 and 2018) datasets we used a grid of equally spaced points, in linear space for P (∼0.5–1 ms resolution), and in logarithmic space for Ṗ (∼0.002–0.01 resolution). The final grid was smoothed using the four closest neighbours to avoid numerical artifacts. To calculate the uncertainties of the best fit values we introduced an additional step, for each grid point we calculated the pulsed fraction (PF) of the folded pulse profile. In a statistical sense, the uncertainties of the best fit values in the P-Ṗ can be derived as the PF diverges from the best fit value by a factor proportional to the uncertainty (statistical plus 5% systematic) of the pulsed fraction (see Figs. B.2 and B.3). We note that for observations with good statistics this estimation is insensitive to the selected phase-bin size for the pulse profile as long as the number of counts within each phase bin obey Gaussian statistics; For NGC 300 ULX1 (XMM-Newton obsid:0791010101) the PF is 0.603 ± 0.007 and 0.638 ± 0.014 using 10 and 50 phase bins respectively.
 |
Fig. B.1. Left panel: maximum power of the most significant peak of the periodogram as derived for 20 time series that were stretched for different Ṗ/P values for the Chandra observation performed in Nov. 2014. Right panel: periodogram for the most significant detection with Ṗ/P = −8.84 × 10−8 s−1. Horizontal lines correspond to the 32%, 10% and 1% false alarm probability. |
 |
Fig. B.2. Left panel: results of the accelerated search in the 2016 XMM-Newton data of NGC 300 ULX1. Right panel: computed pulsed fraction from the corresponding pulse profiles using 50 phase bins. Contours mark the regions where the pulse profile has decreased by 10% and 50% of its maximum value. |
 |
Fig. B.3. As in Fig. B.2, but for the 2018 NuSTAR data (obsid 90401005002). We note the appearance of “islands” of multiple solutions, but due to the good statistics we are able to avoid any degeneracy. The goodness of fit (i.e. χ2) is computed by using ten phase bins for the folded pulse profile. |
The AEF method can be successfully applied to the two 2018 Chandra observations (obs-ids: 20965 and 20966) that were performed within four days. By analysing each observation separately we can derive an accurate period and an upper limit for the Ṗ (see Table B.1). By combining the events we can measure both P and Ṗ (see Fig. B.4).
Properties of NGC 300 ULX1.
 |
Fig. B.4. As in Fig. B.2, but for the combined Chandra data obtained from MJD 58157–58180. We note the difference in the 50% contour of the pulsed fraction (and the χ2) compared to Fig. B.2. This is an effect of the time gap between the observations. In the case of Swift/XRT due to the observational gaps and the low number of counts it is not possible to derive a unique solution in the P vs. Ṗ plane. The goodness of fit (i.e. χ2) is computed by using ten phase bins for the folded pulse profile. |
By using the AEF method in the 2014 Chandra observation and the Swift/XRT observations performed after 2015 we were also able to measure P and Ṗ. However, these data sets suffer from low statistics and therefore any period search results in large uncertainties. Moreover, Swift data were collected from numerous snapshots over one to two days, and therefore the derived 2D (P-Ṗ plane) periodograms show multiple solutions. This degeneracy is due to the fact that the uncertainty of the derived spin period of each Swift/XRT snapshot is comparable to the spin period change between snapshots. To mitigate these effects we need to use multiple Swift/XRT exposures that span over a duration of days to a week (see Fig. B.5). Unfortunately, most of the Swift/XRT observations performed prior to the discovery of the spin period of NGC 300 ULX1 are not suitable for detailed temporal studies as they were composed by snapshots with short exposures that were performed within ∼24 h. Therefore, we can only compute ΔP for large time intervals (i.e. months-years) and no secular Ṗ for weekly intervals. The results of our analysis are summarised in Table B.1. For some datasets with gaps and low statistics we could not determine a unique set of values due to aliasing and multiple possible solutions (see values marked with “*” in Table B.1).
 |
Fig. B.5. As in the left panel of Fig. B.2, but for the 2014 Chandra data (left panel) and two combined Swift/XRT observations (obsids: 00049834047-8) performed between MJD 58285−9. Due to the low statistics only five phase bins were used for the AEF test. |
At this point we make a note about the ongoing and future monitoring X-ray observations of NGC 300 ULX1 with Swift/XRT that will be presented in a future study. These monitoring observations are repeated with a cadence of 3–4 days. Thus, combining multiple observations performed within a few days we are able to constrain both P and Ṗ using the AEF method. An example of our analysis of these datasets is shown in the right panel of Fig. B.5.
To asses the significance of the observations with low statistics we performed MCMC simulations. We created simulated datasets with similar observational characteristics as the Swift/XRT or Chandra data sets (i.e. number of counts and good time intervals). For each original dataset we performed 106−7 tests by creating 100–1000 fake datasets that were analysed by our AEF algorithm. For all cases, we determined that for the fake datasets the probability of obtaining χ2 values as high as the ones measured in the observed datasets is smaller than ∼10−6 (or 4.8σ).
To further investigate the significance of the detected periods we computed the Lomb-Scargle (LS) periodogram (Leahy et al. 1983a) of the de-accelerated event arrival times. As the recorded arrival times are a result of almost constant acceleration we can transform the time scale during the observation so that the pulsar period will remain constant. The transformation is based on a simple Taylor expansion and can be given by equation:
where t is the detected event time and t′ is the transformed event time. For each observation with low statistics we calculated the LS periodogram for a series of Ṗ/P values while performing white-noise simulations to derive the significance of the detected periods. In Fig. B.1 we show an example of our test for the Chandra observation (obsid: 16029) where the 126 s period was discovered. To estimate the significance of the periodic signal as computed by the LS peridogram we used the block bootstrap method (Bühlmann 2002). Time series was re-sampled with replacement within time blocks of 20 s, while the starting points of the blocks where shuffled. The significance of the periodic signal was then estimated by simulating 10 000 light curves (e.g. see also Carpano et al. 2017).
For completeness we note the following. NGC 300 ULX1 was not active between 2000 and 2005 as it was not detected during four deep (∼40 ks) XMM-Newton observations (obs-ids: 0112800101, 0112800201, 0305860301, 0305860401). Moreover, of particular interest is the 2010 XMM-Newton observation (obsid: 0656780401) with a duration of 18 ks. We performed periodicity tests between 0.1 and 5000 s using a grid of Ṗ/P values, but we could not confirm the presence of any periodic modulation.
To conclude, from our analysis we were able to measure the spin evolution of NGC 300 ULX1 over a period of about 4 years (2014–2018), prior to which no spin measurement could be determined. We were also able to determine the instantaneous P and Ṗ values using the XMM-Newton and NuSTAR 2016 data and the Chandra 2018 data. For all other observations the derived spin periods should be considered as averaged within the exposure duration. Consequently, we can use these values to determine the long-term (secular) spin-up rate of the pulsar, but cannot consider them as derivatives of P at a specific time.
All Tables
Estimation of B under different assumptions for the Wang (1995; W95) and Parfrey et al. (2016; P16) torque models.
All Figures
 |
Fig. 1. Normalized LX of NGC 300 ULX1, as derived by the fits to the X-ray spectra from Swift (black triangles), XMM-Newton (blue squares), and Chandra (red circles). Values are scaled to 4.7 × 1039 erg s−1, the LX derived by C18 (see text). |
| In the text | |
 |
Fig. 2. Normalized pulse profiles of NGC 300 ULX1. Subplots correspond to different epochs (see Table B.1) and are sorted in decreasing spin period (from top to bottom panels). Pulse profiles derived by Chandra (panels a and e) contain events with energies in the 0.3–8.0 keV band, while those derived from XMM-Newton data (panel c) and Swift (panels b and d) denote the 0.3–10.0 keV range. |
| In the text | |
 |
Fig. 3. |Ṗ|/P vs. P for NGC 300 ULX1. Solid black lines denote the solution using the W95 approximation while assuming a constant LX. The two solutions based on the derived values from the two data sets (red points) with best statistics (2016 & 2018) presented in Table 1. The Ghosh & Lamb (1979) model prediction is plotted (dotted line) for comparison using the observed 2016 LX. All model lines assume neff = 100%. |
| In the text | |
 |
Fig. 4. Evolution of the NS spin period of NGC 300 ULX1 since the SN 2010da event (blue vertical dashed line). The black solid line denotes the theoretical prediction assuming a constant accretion rate and stellar torque from disc-magnetosphere interactions (Wang 1995) with efficiency = 1.0, B = 5 × 1012 G and Lx = 4 × 1039 erg s−1. The grey shaded area marks the evolution path for a range of LX, i.e. 3–5 × 1039 erg s−1. The inset plot shows the predicted evolution of the spin period for the subsequent years, with the lone data point being the ∼19 s Swift measurement (MJD 58221). |
| In the text | |
 |
Fig. B.1. Left panel: maximum power of the most significant peak of the periodogram as derived for 20 time series that were stretched for different Ṗ/P values for the Chandra observation performed in Nov. 2014. Right panel: periodogram for the most significant detection with Ṗ/P = −8.84 × 10−8 s−1. Horizontal lines correspond to the 32%, 10% and 1% false alarm probability. |
| In the text | |
 |
Fig. B.2. Left panel: results of the accelerated search in the 2016 XMM-Newton data of NGC 300 ULX1. Right panel: computed pulsed fraction from the corresponding pulse profiles using 50 phase bins. Contours mark the regions where the pulse profile has decreased by 10% and 50% of its maximum value. |
| In the text | |
 |
Fig. B.3. As in Fig. B.2, but for the 2018 NuSTAR data (obsid 90401005002). We note the appearance of “islands” of multiple solutions, but due to the good statistics we are able to avoid any degeneracy. The goodness of fit (i.e. χ2) is computed by using ten phase bins for the folded pulse profile. |
| In the text | |
 |
Fig. B.4. As in Fig. B.2, but for the combined Chandra data obtained from MJD 58157–58180. We note the difference in the 50% contour of the pulsed fraction (and the χ2) compared to Fig. B.2. This is an effect of the time gap between the observations. In the case of Swift/XRT due to the observational gaps and the low number of counts it is not possible to derive a unique solution in the P vs. Ṗ plane. The goodness of fit (i.e. χ2) is computed by using ten phase bins for the folded pulse profile. |
| In the text | |
 |
Fig. B.5. As in the left panel of Fig. B.2, but for the 2014 Chandra data (left panel) and two combined Swift/XRT observations (obsids: 00049834047-8) performed between MJD 58285−9. Due to the low statistics only five phase bins were used for the AEF test. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.