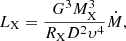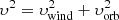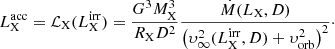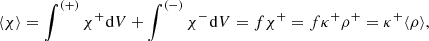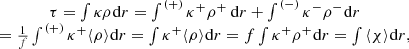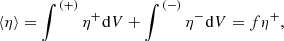| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 14 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833419 | |
| Published online | 11 December 2018 | |
Wind inhibition by X-ray irradiation in HMXBs: the influence of clumping and the final X-ray luminosity
1
Ústav teoretické fyziky a astrofyziky, Masarykova univerzita, Kotlářská 2, 611 37 Brno, Czech Republic
e-mail: krticka@physics.muni.cz
2
Astronomický ústav, Akademie věd České republiky, Fričova 298, 251 65 Ondřejov, Czech Republic
Received:
14
May
2018
Accepted:
8
October
2018
Context. In wind-powered X-ray binaries, the radiatively driven stellar wind from the primary may be inhibited by the X-ray irradiation. This creates the feedback that limits the X-ray luminosity of the compact secondary. Wind inhibition might be weakened by the effect of small-scale wind inhomogeneities (clumping) possibly affecting the limiting X-ray luminosity.
Aims. We study the influence of X-ray irradiation on the stellar wind for different radial distributions of clumping.
Methods. We calculate hot star wind models with external irradiation and clumping using our global wind code. The models are calculated for different parameters of the binary. We determine the parameters for which the X-ray wind ionization is so strong that it leads to a decrease of the radiative force. This causes a decrease of the wind velocity and even of the mass-loss rate in the case of extreme X-ray irradiation.
Results. Clumping weakens the effect of X-ray irradiation because it favours recombination and leads to an increase of the wind mass-loss rate. The best match between the models and observed properties of high-mass X-ray binaries (HMXBs) is derived with radially variable clumping. We describe the influence of X-ray irradiation on the terminal velocity and on the mass-loss rate in a parametric way. The X-ray luminosities predicted within the Bondi-Hoyle-Lyttleton theory agree nicely with observations when accounting for X-ray irradiation.
Conclusions. The ionizing feedback regulates the accretion onto the compact companion resulting in a relatively stable X-ray source. The wind-powered accretion model can account for large luminosities in HMXBs only when introducing the ionizing feedback. There are two possible states following from the dependence of X-ray luminosity on the wind terminal velocity and mass-loss rate. One state has low X-ray luminosity and a nearly undisturbed wind, and the second state has high X-ray luminosity and exhibits a strong influence of X-rays on the flow.
Key words: stars: winds / outflows / stars: mass-loss / stars: early-type / hydrodynamics / X-rays: binaries
© ESO 2018
1. Introduction
X-ray binaries contain a non-degenerate donor star, which deposits part of its mass on the degenerate companion, typically a neutron star or a black hole. This mechanism gives rise to objects which belong to the most luminous X-ray sources in the universe. A class of high-mass X-ray binaries (HMXBs) is powered by accretion of the radiatively driven wind blowing from the non-degenerate star (Davidson & Ostriker 1973; Lamers et al. 1976).
The wind in HMXBs has a very complex structure on various spatial scales. Accretion onto the compact companion proceeds in different forms depending on the strength of the magnetic field of the compact star and on its rotation (see Martínez-Núñez et al. 2017, for a review). On large scales, the primary star wind is strongly influenced by X-ray irradiation originating from the compact companion. Since hot star winds are driven by light absorption in lines of heavier elements, the strong X-ray irradiation affects the line force (Hatchett & McCray 1977; Fransson & Fabian 1980). This results in a complex structure of the flow that has to be studied using numerical simulations (Blondin et al. 1990; Feldmeier et al. 1996; Čechura & Hadrava 2015; El Mellah et al. 2018). The simulations predict the existence of a photoionization wake, which was detected observationally (Kaper et al. 1994).
The complex structure of the flow causes severe problems in numerical simulations. Self-consistent calculation of the radiative force requires determination of ionization and excitation state of the flow, which is far from equilibrium. Therefore, the radiative transfer equation has to be solved together with equations describing ionization and excitation balance (kinetic equilibrium equations). This resulting problem (that allows departures from the LTE) has not yet been solved in its full complexity.
To make the problem tractable, the modelling either simplifies the radiative driving enabling us to unveil the large-scale three-dimensional (3D) flow structure (Blondin et al. 1990), or it solves the wind equations in spherical symmetry (1D) and provides detailed calculation of the radiative force. The latter approach (Krtička et al. 2012, 2015; Sander et al. 2018) is able to estimate binary parameters for which the influence of X-rays becomes important. Wind models with detailed radiative force also show the decrease of the wind velocity due to X-ray irradiation, which was detected observationally (van Loon et al. 2001; Watanabe et al. 2006).
An overly strong X-ray source may even inhibit the wind before it reaches the compact companion and quenches itself. As a result, there is a limit to the X-ray luminosity, which depends on the properties of a given binary system. This can be conveniently displayed in diagrams relating the X-ray luminosity and the optical depth parameter (Krtička et al. 2015). The positions of observed stars in such diagrams appear in the region below the limit of wind inhibition by the X-ray source in agreement with theory. Moreover, many stars appear close to the border of wind inhibition indicating that their X-ray emission may be self-regulated.
The impact of X-rays on the wind flow is also sensitive to the wind mass-loss rate. Recombination is stronger for higher density (higher mass-loss rate), reducing the effect of X-rays. Therefore, a possible reduction of wind mass-loss rate estimates from observations (Najarro et al. 2011; Bouret et al. 2012; Šurlan et al. 2013; Cohen et al. 2014) may pose a problem for wind models with X-ray irradiation. A similar issue also comes from wind modelling, because the global (unified, i.e. including the photosphere) hot star wind models predict mass-loss rates that are lower than the previous theoretical calculations by a factor of between two and five (Krtička & Kubát 2017).
This problem can be alleviated by inclusion of clumping into wind models (Oskinova et al. 2012). Clumping in hot star winds is connected with the appearance of small-scale structures in the wind. This influences the ionization equilibrium (Hamann & Koesterke 1998; Bouret et al. 2003; Martins et al. 2005b; Puls et al. 2006) and the radiative transfer in the case of optically thick clumps either in continuum (Feldmeier et al. 2003) or in lines (Puls et al. 1993; Oskinova et al. 2007; Sundqvist et al. 2010, 2011; Šurlan et al. 2012, 2013). Clumping is considered to be one of the sources of X-ray variability in HMXBs (e.g. Fürst et al. 2010; Oskinova et al. 2012; Manousakis & Walter 2015; Bozzo et al. 2016). The origin of clumping is likely the line-driven wind instability (Lucy & Solomon 1970; Owocki & Rybicki 1984), which may be initiated either in the photosphere by the turbulent motions (Feldmeier et al. 1997; Cantiello & Braithwaite 2011; Jiang et al. 2015) or self-initiated in the wind (Sundqvist et al. 2018).
To understand the effect of clumping on the X-ray ionization, we included clumping into our METUJE wind models (Krtička & Kubát 2017), which also include X-ray irradiation. Inclusion of various physical effects into wind models requires slight modifications of computational strategy. This is reflected in the structure of this paper. Section 2 describes the calculation of global wind models, which neglect wind clumping and X-ray irradiation. The flux from global models is subsequently used in the wind models with various radial distributions of clumping (Sect. 3). The inclusion of X-ray irradiation, as well as wind models that include both clumping and X-ray irradiation, are described in Sect. 4. The implications of our models for the X-ray luminosity of HMXBs are discussed in Sect. 5.
2. Global wind models
The wind modelling is based on our METUJE code (Krtička & Kubát 2017). The code provides global (unified) photosphere-wind models. It solves the radiative transfer equation, the kinetic (statistical) equilibrium equations, and the hydrodynamic equations both in the photosphere and in the wind. The models are calculated assuming that the flow is stationary (time-independent) and spherically symmetric.
We solve the radiative transfer equation in the comoving-frame (CMF) following the method developed by Mihalas et al. (1975). We include line and continuum transitions relevant in atmospheres of hot stars in the radiative transfer equation. The inner boundary condition for the radiative transfer equation is derived from the diffusion approximation, and we assume neither an additional source of radiation in the wind nor irradiation of the outer boundary.
The ionization and excitation states of considered elements (see the list in Krtička & Kubát 2009) are calculated from the kinetic equilibrium equations (also known as NLTE equations). The equations account for the radiative and collisional excitation, deexcitation, ionization, and recombination. A part of the models of ions was adopted from the TLUSTY model stellar atmosphere input data (Lanz & Hubeny 2003, 2007). Because the original TLUSTY ionic models are tailored to stellar atmospheres, additional ionic models are needed for wind modelling. We prepared these additional models using the data from the Opacity and Iron Projects (Seaton et al. 1992; Hummer et al. 1993) and using the level data from NIST (Kramida et al. 2015). For phosphorus the ionic model was prepared using data described by Pauldrach et al. (2001). The bound-free radiative rates are consistently calculated from the CMF mean intensity, while for the bound-bound rates we still use the Sobolev approximation.
To derive the temperature, we use a differential form of the transfer equation deep in the photosphere, while we use an integral form of this equation in the upper layers of the photosphere (Kubát 1996). The electron thermal balance method (Kubát et al. 1999) is applied in the wind. The hydrodynamical equations, that is, the continuity equation, equation of motion, and the energy equation, are solved iteratively. From this we obtain the wind density, velocity, and temperature structure. The radiative force due to line and continuum transitions is calculated in the CMF. The line data for the calculation of the line force were taken from the VALD database (Piskunov et al. 1995; Kupka et al. 1999) with some updates using the NIST data (Kramida et al. 2015).
We calculated wind models for stellar parameters that roughly correspond to typical parameters of O star primaries in HMXBs. We selected two supergiants and two main sequence stars with Teff = 30 000 K and Teff = 37 500 K. Stellar masses and radii of these stars given in Table 1 were derived using relations of Martins et al. (2005a) for main sequence stars and supergiants. We assumed solar chemical composition (Asplund et al. 2009) for our models.
Adopted parameters of the model grid.
3. Wind models with optically thin clumping
3.1. Simplification of wind models
The calculation of global wind models is relatively time consuming. Luckily, the photospheric turbulence does not significantly modify the emergent flux. Therefore, to make the following calculations more tractable, we do not account for the photosphere in the wind models with clumping. Instead, we use the global models to calculate the flux, which we subsequently apply as the lower boundary flux in our wind models with clumping. A similar approach was employed in our previous models that used the core-halo approximation (Krtička et al. 2012). The flux in the global models depends on radius, and we selected such a flux, which leads to a mass-loss rate close to that of the global models.
Because our CMF procedure of the calculation of the radiative force can be used only for monotonic flows and the flow in the presence of the external irradiation may become non-monotonic, we do not use a CMF calculation of the radiative force directly in the following models. Instead, we calculate the ratio of the CMF and Sobolev line force from a wind model without clumping and use this ratio to correct the Sobolev line force in the models with clumping and subsequently also in models with external X-ray irradiation. The Sobolev line force is calculated from actual level populations (Krtička & Kubát 2004, Eq. (25)), which may be influenced by clumping and X-ray irradiation (see Sect. 4).
3.2. General assumptions
The self-consistent way of including clumping into our wind models would require employment of the time-dependent hydrodynamical simulations (Owocki & Rybicki 1984; Feldmeier et al. 1997; Owocki & Puls 1999; Runacres & Owocki 2002; Dessart & Owocki 2005; Feldmeier & Thomas 2017; Sundqvist et al. 2018). However, the self-consistent solution of both NLTE equations and equations of hydrodynamics is likely beyond the possibilities of contemporary computers. To make the task more tractable, we include an approximate effect of local wind inhomogeneities (clumps) into our models.
The basic assumptions under which the clumps are included into our wind models are the following:
-
The whole wind material is concentrated into the spatially organized structures (clumps), the space between individual clumps is void. The clumps are distributed randomly.
-
Each clump is homogeneous.
-
The presence of clumping explicitly affects only the wind density. The wind velocity is assumed to be smooth and a monotonically increasing function of radius.
-
We assume that the clumps are optically thin both in continuum and in lines. This option is also referred to as micro-clumping, that is, the opposite of macro-clumping which accounts for clumps that may be optically thick (Feldmeier et al. 2003; Oskinova et al. 2007).
where ρ− = 0 according to our assumptions. We note that ρ+ is a function of radius. Following Abbott et al. (1981), we introduce the filling factor f as a probability that a given volume element is situated in the clump. The mean quantities are calculated over the volume comprising a large number of clumps. In fact, it would be possible to introduce two types of averaging, that is, the volume one, which is defined for a given instant of time, and the average over a sufficiently long time interval. However, for simplicity, we assume that both approaches are equivalent.
According to these assumptions, the mean wind density ⟨ρ⟩
gives the mass-loss rate that does not explicitly depend on f. We note that ⟨ρ⟩ is also a function of radius. The mean value of the density squared is
Following Peimbert (1968) for example, we introduce the clumping factor as
Using Eqs. (2) and (3) it can be shown that for the case of void space between clumps the clumping factor is the inverse of the filling factor, (5)
(5)
(see also Hamann & Koesterke 1998, where the clumping factor is denoted as D).
The radially dependent mean density ⟨ρ⟩ is the same in the smooth wind as in the clumped wind with the same mass-loss rate (and velocity profile). Consequently, the explicit form of all equations that involve the linear terms in density remains the same. The possibility of clumping is included only in the terms in which the density squared features. In these term it is necessary to formally substitute ρ2 → ⟨ρ2⟩ → Cc⟨ρ⟩2 (see Eq. (4) and, e.g. Abbott et al. 1981; Antokhin et al. 1988; Schmutz 1995; Hamann & Koesterke 1998). The details of the implementation of clumping into our wind code are given in the Appendix.
3.3. Calculated models
We studied two different radial stratifications of clumping. We assumed either constant clumping factor or we adopted the empirical radial clumping stratification from Najarro et al. (2009)
 (6)
(6)
Here υ(r) is the wind radial velocity, υ∞ is the wind terminal velocity, C1 and C4 are the clumping factors close to the star and at large distances from the star, respectively, and C2 and C3 define the radial variations of clumping factor; C2 sets the onset of clumping (in velocity space) and C3 determines the typical velocity at which the clumping factor gradually changes from C1 to C4. Because Eq. (6) may give Cc < 1, we used a lower limit to Cc equal to 1. In comparison with monotonic increase of the clumping factor with r, as adopted in some models (e.g. Bouret et al. 2012), Eq. (6) accounts for the decrease of clumping in outer regions of dense winds (Puls et al. 2006). Motivated by typical values derived in Najarro et al. (2009, 2011), we assume C1 = 10, C2 = 200 km s−1, C3 = 500 km s−1, and C4 = 1.
The dependence of clumping on actual wind velocity in Eq. (6) is not practical for wind simulations. Therefore, within our calculations, we derive Cc using the fit to the wind velocity predicted for smooth wind with Cc = 1 (see Eq. (7)). Given the empirical nature of Eq. (6) with many uncertainties, this change is of minor importance. The radial variations of Cc for individual wind models are given in Fig. 1.
 |
Fig. 1. Radial variation of the clumping factor according to Eq. (6) for individual wind models from Table 1. |
The basic parameters of the wind with clumping are given in Table 2. Clumping favours recombination, which leads to an increase of the radiative force and therefore of the mass-loss rate, because ions with lower charge drive the wind more efficiently (e.g. Krtička et al. 2008). For supergiants we predict on average Ṁ ∼ Cc0.4 for constant clumping factor, while Muijres et al. (2011) predict Ṁ ∼ Cc0.2−0.4, in reasonable agreement. The increase of the mass-loss rate is weaker in the models with radially variable clumping factor after Eq. (6), because the mass-loss rate is determined by conditions close to the star in our models where clumping is weak (see Fig. 1).
Derived wind mass-loss rate Ṁ, wind terminal velocity υ∞, and velocity law fit parameters υ1, υ2, υ3, and γ for models with clumping.
We fitted the radial velocity dependence υ(r) of these models using an analytic formula (we denote the analytic fit by ῦ (r)
where υ1, υ2, υ3, and γ are parameters of the fit given in Table 2 (see also Krtička & Kubát 2011). The radial increase of clumping after Eq. (6) leads to an increase of the line force in the outer wind, which may result in higher wind terminal velocity than in the models with constant clumping factor. Therefore, radially increasing the clumping factor can account for high observed terminal velocities, which are underestimated in global models without clumping (Krtička & Kubát 2017).
We also used the models to derive mean mass-absorption coefficient averaged over radii 1.5 R* − 5 R* and approximated its wavelength dependence as
where λ1 = 20.18, and λ is the value of the wavelength in units of Å. The parameters of the fit a0, a1, b1, a2, and b2 are given in Table 3. The resulting values of 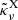 correspond typically within 10–20% to those given in the literature (e.g. Oskinova et al. 2006). It follows that the coefficients of the fit do not significantly depend on clumping in most cases; consequently, clumping does not significantly affect the opacity in the X-ray domain (see Carneiro et al. 2016). This assumption is used to determine mass-loss rates from X-ray line profiles Cohen et al. 2014.
correspond typically within 10–20% to those given in the literature (e.g. Oskinova et al. 2006). It follows that the coefficients of the fit do not significantly depend on clumping in most cases; consequently, clumping does not significantly affect the opacity in the X-ray domain (see Carneiro et al. 2016). This assumption is used to determine mass-loss rates from X-ray line profiles Cohen et al. 2014.
4. Wind models with X-ray irradiation
The inclusion of X-ray irradiation into our wind models closely follows Krtička et al. (2012). In the present study, we aim at the most significant influence of the X-ray irradiation, therefore we solve the wind equation only along a radial ray in the direction of the X-ray source (see Fig. 2). Similarly as for other models with clumping (described in Sect. 3), we use the photospheric flux and the Sobolev line force corrected for CMF radiative transfer to solve wind equations (see Sect. 3.1). Our treatment of the Sobolev line force neglects non-local radiative coupling between absorption zones, which occurs in non-monotonic flows (Rybicki & Hummer 1978; Puls et al. 1993).
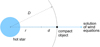 |
Fig. 2. Geometry of the model of a hot star wind irradiated by X-rays from a compact companion. Here D is binary separation, r is radius of studied point in the wind, and d its distance from the compact companion. |
The influence of the compact secondary component is only taken into account by inclusion of external X-ray irradiation, which originates in the wind accretion on the compact component. The X-ray irradiation is introduced as an additional term in the mean intensity Jν
where 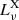 is monochromatic X-ray irradiation luminosity, which after the integration gives the total X-ray luminosity,
is monochromatic X-ray irradiation luminosity, which after the integration gives the total X-ray luminosity, 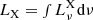 . The frequency distribution of emergent X-rays
. The frequency distribution of emergent X-rays 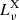 is for simplicity approximated by the power law
is for simplicity approximated by the power law 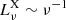 from 0.5 to 20 keV (see Watanabe et al. 2006). The distance of a given point in the wind from the compact companion is d = |D − r| from Fig. 2, D is binary separation, and τν(r) is the optical depth between the given point in the wind and the compact companion,
from 0.5 to 20 keV (see Watanabe et al. 2006). The distance of a given point in the wind from the compact companion is d = |D − r| from Fig. 2, D is binary separation, and τν(r) is the optical depth between the given point in the wind and the compact companion,
where κν is the X-ray mass-absorption coefficient.
The absorption coefficient and the density in Eq. (10) can be derived directly from the actual model. However, we used a simplified approach to avoid possible problems with the convergence of the model. Therefore, for the calculation of the external X-ray irradiation in Eq. (9) we use the optical depth from Eq. (10) calculated with density, velocity, and mass-absorption coefficient in the form of
where υkink is the velocity of the kink that may appear in the wind model (otherwise υkink = ∞), ῦ(r) is the fit Eq. (7) of the wind velocity derived from the models without X-ray irradiation (if the fit ῦ∼(r) > υkink then the value of υkink is taken), and 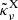 is the radially averaged mass-absorption coefficient given by Eq. (8).
is the radially averaged mass-absorption coefficient given by Eq. (8).
4.1. Influence of clumping on the X-ray wind inhibition
The influence of X-rays on the ionization state of matter with atomic number density n is traditionally described using the ionization parameter ξ = LX/(nd2) introduced by Tarter et al. (1969), see also Hatchett & McCray 1977). Krtička et al. (2015) accounted for the X-ray absorption in the intervening wind via the ξ ∼ e−τν dependence. There is an additional effect in the presence of clumping, because a higher density of material inside the clumps enhances recombination without any impact on photoionization. Therefore, one may expect X-ray ionization to have a weaker effect in clumped media, as shown by Oskinova et al. (2012). We introduce the ionization parameter as
From this we can infer two different ways by which optically thin clumps weaken the effect of wind X-ray photoionization. The direct mechanism (Oskinova et al. 2012) gives ξ ∼ 1/Cc due to the overdensity inside clumps which favours recombination, while the indirect one is connected with variations of the wind mass-loss rate and its influence on n and τν. Because the wind mass-loss rate increases with increasing Cc for optically thin clumps (Muijres et al. 2011, see also Sect. 3.3), all these effects lead to a weaker influence of X-rays on the clumped flow. Moreover, in winds which have high mass-loss rates and which are optically thick in the X-ray domain (τν > 1), the indirect effect is expected to dominate due to the exponential dependence on the optical depth in Eq. (12).
To test the applicability of the ionization parameter Eq. (12) in the case of clumping, we calculated wind models with constant clumping factor Cc = 10 where only the direct effect of clumping affects ξ. This can be achieved only in the models that (without X-ray irradiation) give the same density and velocity structure. To do so, we fixed the mass-loss rate and the terminal velocity of the model without X-ray irradiation to values derived without clumping (and without X-ray irradiation) by a multiplication of the radiative force. The multiplicative factor was different below and above the critical point, because we fixed both the mass-loss rate and the terminal velocity. Thanks to this, we isolated the direct influence of clumping in Eq. (12) and eliminated the indirect influence via n and τν (see Fig. 3). For a low amount of X-ray irradiation or for a distant X-ray source (low ξ), only wind velocity is affected by X-ray irradiation (Krtička et al. 2015; Sander et al. 2018). As a result of X-ray irradiation, higher ionization states become more abundant. For weak X-ray irradiation, the lower ionization states are not significantly affected; consequently, weak X-ray irradiation causes a slight increase of the radiative force and of the wind terminal velocity. However, a stronger X-ray irradiation (with larger ξ) depopulates ions with low charge that mostly drive the wind, and the radiative force and the terminal velocity decrease. This is typically accompanied by the appearance of a kink in the velocity profile where the velocity derivative changes sign. This is demonstrated in Fig. 3, which shows the radial velocity in the models where clumping is allowed to affect the ionization equilibrium only directly. The ionization parameter ξkink at the location of the kink is roughly the same in the models with and without clumping, which demonstrates that Eq. (12) is able to reliably characterize the influence of clumping on X-ray ionization.
 |
Fig. 3. Radial velocity for selected wind models 300-1. The black line denotes the model without either X-ray irradiation or clumping, while blue and red lines denote models with the same X-ray irradiation (with the same LX and D) and different clumping: without clumping (blue solid) and with Cc = 10 (red dashed). Here the clumping is allowed to affect the ionization structure only directly and not via the mean density (mass-loss rate). Overplotted is the value of the ionization parameter Eq. (12) at the location of the velocity kink. Left panel: model with LX = 1036 erg s−1 and D = 200 R⊙. Right panel: model with LX = 1038 erg s−1 and D = 700 R⊙. |
From Fig. 4 it follows that the ionization parameter Eq. (12) reasonably describes the effect of X-ray irradiation even in more realistic models where the clumping affects both the ionization and wind structure. In such models, both the direct and indirect effects of clumping in Eq. (12) come into play. The plots in Fig. 4 show the kink in the velocity profile, where the wind is no longer accelerated due to X-ray ionization. For a given star, Fig. 4 shows that the kink appears for roughly the same critical ionization parameter ξkink ≈ 5 − 25 erg cm s−1 in agreement with Krtička et al. (2015)1.
 |
Fig. 4. Radial velocity for selected wind models. The black line denotes the model without either X-ray irradiation or clumping, while blue, red, and green lines denote models with the same X-ray irradiation (with the same LX and D) but with different clumping: without clumping (blue, solid), with Cc = 3 (red dotted), and with radially dependent clumping factor after Eq. (6) with C1 = 10 (green dashed). Arrows denote the location of the kink in the velocity profile with a corresponding value of the ionization parameter from Eq. (12). Upper left: model 300-1 with LX = 1037 erg s−1 and D = 300 R⊙. Upper right: model 375-1 with LX = 1037 erg s−1 and D = 100 R⊙. Lower left: model 300-5 with LX = 1035 erg s−1 and D = 30 R⊙. Lower right: model 375-5 with LX = 1036 erg s−1 and D = 100 R⊙. |
Figures 3 and 4 also show that clumping weakens the effect of X-ray irradiation. With stronger clumping, the kink in the velocity profile appears at larger distances from the star and at lower wind densities (higher velocities). This has important implications for the regions of wind inhibition as they appear in diagrams of X-ray luminosity versus the optical depth parameter.
4.2. Diagrams of X-ray luminosity versus the optical depth parameter
The diagrams that display X-ray luminosity versus the optical depth parameter were proven to be very effective in estimating the impact of X-rays on the wind (Krtička et al. 2015). The optical depth parameter,
is proportional to the radial optical depth between the stellar surface and the X-ray source. Therefore, it enables us to separate domains according to the type of influence that X-rays have on the wind flow. We use the optical depth parameter defined by Eq. (13) instead of the optical depth, because tX does not depend on energy. The value of tX in Eq. (13) is calculated with mass-loss rate and terminal velocity unaffected by X-rays.
Diagrams of X-ray luminosity versus the optical depth parameter are given in Figs. 5–7 for different clumping factors (see Table 2). The wind is not affected by X-ray irradiation for low LX or for large binary separation. Such models appear in right bottom corner of the LX−tX diagrams as black plus symbols. With increasing LX or with decreasing binary separation, the influence of X-rays becomes stronger and leads to the appearance of the kink in the velocity profile and to a decrease of the terminal velocity marked by red crosses. For a large X-ray luminosity or for a very close X-ray source, the kink approaches the wind critical point2 leading to the wind inhibition (Krtička et al. 2012). Such models appear in the upper left corner of the LX−tX diagrams.
 |
Fig. 5. Diagrams of X-ray luminosity vs. the optical depth parameter Eq. (13) for models without clumping and for individual stars from Table 1. Each point describes models with different LX and D. Individual symbols discriminate between different effects of X-ray ionization on the wind: black plus symbols (+) denote models with negligible influence of X-ray irradiation, while red crosses ( |
Figure 5 displays the case without clumping (Cc = 1). Adding the constant clumping factor (Cc > 1) in Fig. 6 has two effects. The mass-loss rate becomes higher, shifting all models in the diagram towards larger tX , and the boundary marking the wind inhibition retreats towards larger LX with respect to models without clumping. The latter effect once again demonstrates the weakening of the effect of X-ray irradiation with increasing clumping. Similar effects also appear in Fig. 7 for the models with the depth-variable clumping factor given by Eq. (6). However, the shift towards larger tX is shorter than in models with Cc = 3 as a result of the weaker increase of the mass-loss rate.
The parameters of real wind-powered HMXBs should appear outside the region with wind inhibition (the forbidden region). To test this, we collected parameters of HMXBs with Teff > 27 000 K from the literature (see Table 4). We excluded HMXBs with Roche overflow and Be/X-ray binaries powered by disk accretion. Positions of collected stars are also plotted in Figs. 5–7. The X-ray luminosities of HMXBs were derived from the literature. We used the predicted mass-loss rates (Krtička & Kubát 2017, given also in Table 4) and the terminal velocities derived from the stellar parameters, υ∞ = 2.6 υesc = 2.6[2GM*(1−Γ)/R*]1/2 (Lamers et al. 1995) to calculate the optical depth parameter tX of HMXBs in diagrams of LX − tX and in Table 4. In Figs. 6–7 we further corrected the HMXB mass-loss rates for clumping. We multiplied the rates in Table 4 by the ratio of mass-loss rates with and without clumping from Table 2.
Parameters of HMXBs with a neutron star or black hole companion.
Without clumping, many of the stars appear in the region of wind inhibition (see Fig. 5). Contrary to our previous study (Krtička et al. 2015), our results are based on global models, which predict lower mass-loss rates (Krtička & Kubát 2017) and therefore stronger influence of X-rays. As a result of lower mass-loss rates, some stars moved to the region of wind inhibition.
The inclusion of clumping with Cc = 3 does not remove stars from the forbidden region (Fig. 6). The mass-loss rate of model stars (Table 2) as well as the predicted mass-loss rate for the stars from Table 4 increase, causing a shift of the diagram to the right. The predicted wind terminal velocity becomes lower, increasing tX for model stars (see Eq. (13)). Consequently, the location of observed stars shifts into the region of wind inhibition, and as a result of this, a constant clumping factor does not improve the agreement between observations and theory.
Stars are mostly removed from the forbidden region only with the variable clumping factor according to Eq. (6) (Fig. 7). The mass-loss rates slightly increase in comparison with the models without clumping (see Table 2), while the predicted terminal velocity remains large due to the radial increase of clumping. Moreover, with increasing clumping, the influence of X-rays becomes lower and as a result of these effects the positions of observed HMXBs appear outside the region with wind inhibition.
There is direct observational support for the effect of wind inhibition by X-rays. An O9.5 V star BD+53°2790, the optical counterpart to the X-ray source 4U 2206+54, shows peculiar wind with a very low terminal velocity (Blay et al. 2009). This star is located close to the border of the wind inhibition area in Fig. 7 and therefore its peculiar wind can be explained as being the result of X-ray irradiation. Also, X Per appears outside the area of the wind inhibition in this diagram, which is not in conflict with the considered wind accretion in this system (Maitra et al. 2017).
We noticed two stars (not listed in Table 4) that may be located in the area of wind inhibition. For 4U 1538–522, the parameters from Torrejón et al. (2015) predict tX ≈ 0.2 for LX = 2.9×1036 erg s−1. A similar problem appears for XTE J1855–026 and parameters from Falanga et al. (2015). These systems are very compact (distance between the neutron star and the primary is only a small fraction of the radius of the primary) and, possibly, the X-rays are powered by Roche-lobe overflow and not by wind accretion. An alternative explanation is that the assumption of a simple geometry of the problem (see Fig. 2) breaks down for compact systems.
4.3. Wind inhibition in the models with radial dependent clumping: wind parameters and modification of CAK line force
Because the models with radial dependence of a clumping factor according to Eq. (6) (following Najarro et al. 2009) provide the best match with observations, we focus here on models with this approximation of clumping. The decrease of the wind terminal velocity due to X-ray irradiation can be roughly described by a formula that resembles wind β-law (see Fig. A.1),
where υ∞, 0, β1, and β2 are fit parameters. The values of these parameters derived by fitting model terminal velocities as a function of LX and D are given in Table 5. Here L36 = 1036 erg s−1.
The dependence of the model wind mass-loss rate on the X-ray luminosity and on the binary separation is slightly more complicated. The mass-loss rate first slightly increases with increasing LX (by the order of 10%) due to increased radiative force from newly appearing ionization states. However, for even stronger LX the mass-loss rate decreases leading to wind inhibition. The behaviour of the mass-loss rate close to the limit of wind inhibition can be very roughly approximated as
where Ṁ0, s1, and s2 are fit parameters. The values of these parameters derived by fitting predicted mass-loss rates as a function of LX and D are given in Table 5.
Our models were calculated using X-ray irradiation in the radial direction (assuming zero inclination, Fig. 2) but in reality the inclination of incident X-rays might be non-zero (e.g. Krtička et al. 2012). As a result, the terminal velocity and the mass-flux depend on direction. Therefore, Eq. (14) predicts only the terminal velocity in the direction of the compact companion and the quantity Ṁ(LX, D)/(4π) (see Eq. (15)) gives the mass-flux per unit solid angle in this direction.
In Table 6 we provide the radiative force multipliers k and α (Castor et al. 1975; Abbott 1982) corresponding to models with radially dependent clumping after Eq. (6). These force multipliers can be used to approximate the radiative force in hydrodynamical simulations without solving the NLTE problem. The force multipliers describe the strength (k) and slope (α) of the line distribution function (Puls et al. 2000), but we simply selected the multipliers that give the best match with wind mass-loss rate and terminal velocity of models without X-ray irradiation (given in Table 2). We also provide the Q̄ parameter of Gayley (1995), which is more substantially physically motivated and is related to the remaining force multipliers as Q̄ = (1 − α)k (c/υthα]1/(1−α), where the fiducial hydrogen thermal speed is  ).
).
The effect of X-ray irradiation can be roughly included in hydrodynamical models by multiplication of the CAK line force (Eq. (6) of Castor et al. 1975 or Eq. (16) of Pauldrach et al. 1986) by a factor of exp(−ξ/ξkink). Here, ξ can be calculated from Eq. (12) and the mean values of ξkink for individual model stars are given in Table 6.
5. Wind-powered X-ray luminosity
The X-ray luminosity of wind-powered HMXBs stems from the release of the gravitational potential energy during wind accretion. Within the classical Bondi-Hoyle-Lyttleton picture (Hoyle & Lyttleton 1941; Bondi & Hoyle 1944) the accretion luminosity is
where MX and RX are the mass and radius of an accreting object, and υ is its relative velocity, which can be estimated using the orbital velocity of the compact component υorb and the wind velocity at the distance D of the compact component, υwind = υ(D) as
There are two limiting cases: either υ = υ∞ when the wind velocity is not affected by the X-ray source and the wind is accreted at large distances from the non-degenerate star, or υ = υorb in an opposite case. Either way, for a given set of system parameters Eq. (16) gives the maximum X-ray luminosity assuming full conversion of gravitational potential energy to X-rays.
Sander et al. (2018) give a more precise estimate of X-ray luminosity, where instead of the 1/υ4 dependence in Eq. (16), they introduce a dependence of 1/(υ3υwind). However, with this formula the X-ray luminosity formally diverges, LX → ∞ for υwind → 0. This is avoided in reality, because for a very low υwind the wind becomes fully inhibited, does not reach the gravitational well of the compact star and is trapped in the gravitational well of a donor star. Therefore, the wind velocity should be at least roughly υorb to reach the compact star. To account for this effect at least approximately, we keep the 1/υ4 dependence in Eq. (16) which does not diverge for υwind → 0.
The relation between observed and predicted X-ray luminosity according to Eq. (16) for stars from Table 4 is plotted in Fig. 8. Without X-ray wind inhibition (for υ = υ∞), most of the stars are located above the theoretical relation. Although this might be partly due to the fact that the compact object is located close to the massive star where the wind has not yet reached the terminal velocity (Sander et al. 2018), for many objects this would likely mean that their X-ray emission could not be wind-powered. The agreement cannot be significantly improved by increasing the mass-loss rate, because from Eq. (16) the X-ray luminosity scales with mass-loss rate only linearly and an increase of the mass-loss rate by two orders of magnitude (with respect to current models) is not justified.
 |
Fig. 8. Observed X-ray luminosity in comparison with predicted X-ray luminosity Eq. (16) for the stars from Table 4 for two limiting values of relative velocity: υ∞ (red crosses) and υorb (blue plus signs). Line denotes one-to-one relation. |
On the other hand, all stars are located below the maximum theoretical expectation for the case of extreme X-ray wind inhibition (for 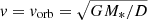 , see Fig. 8 and also Ho & Arons 1987). This is caused by a very strong dependence, LX ∼ υ−4. This shows that current wind mass-loss rate predictions are able to explain the observed X-ray luminosities in HMXBs. Moreover, this is strong observational support for the existence of the wind velocity decrease due to X-ray radiation. Most stars do not reach the maximum X-ray luminosity. There may be several reasons for this: for many stars υ > υorb, for a given star there is a maximum X-ray luminosity due to wind inhibition, and finally the accretion may be suppressed by the compact star itself (Shakura et al. 2012).
, see Fig. 8 and also Ho & Arons 1987). This is caused by a very strong dependence, LX ∼ υ−4. This shows that current wind mass-loss rate predictions are able to explain the observed X-ray luminosities in HMXBs. Moreover, this is strong observational support for the existence of the wind velocity decrease due to X-ray radiation. Most stars do not reach the maximum X-ray luminosity. There may be several reasons for this: for many stars υ > υorb, for a given star there is a maximum X-ray luminosity due to wind inhibition, and finally the accretion may be suppressed by the compact star itself (Shakura et al. 2012).
The decrease of the wind terminal velocity due to X-ray irradiation predicted by Eq. (14) can be used to check the consistency of estimated X-ray luminosities with observations. Inserting υ∞(LX, D) from Eq. (14) calculated for observed X-ray luminosity and scaled by the ratio of the terminal velocity of a given star (after Lamers et al. 1995) and model terminal velocity from Table 2 (for C1 = 10) into Eq. (17), we obtain from Eq. (16) an estimate of X-ray luminosity. These estimates nicely match the observed X-ray luminosities (see Fig. 9).
 |
Fig. 9. X-ray luminosities of stars from Table 4 estimated using Eqs. (16) and (17) inserting the terminal velocity (as υwind) derived from Eq. (14) using observed X-ray luminosities. Plotted as a function of observed X-ray luminosity. Line denotes one-to-one relation. |
Inserting the terminal velocity fit Eq. (14) and mass-loss rate fit Eq. (15) into Eq. (16) for a given D, we derive an equation for the accretion X-ray luminosity as a function of X-ray irradiation luminosity
The irradiating X-rays modify the wind terminal velocity and mass-loss rate, and therefore the accretion luminosity 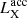 is a function of the irradiation luminosity
is a function of the irradiation luminosity 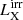 (Fig. 10). For small irradiation luminosities the X-rays do not significantly influence either the terminal velocity or the mass-loss rate. Consequently, the accretion luminosity is almost constant. For higher irradiation luminosities the terminal velocity decreases, which results in an increase of the accretion luminosity. The curves reach a maximum accretion luminosity and start to decrease due to the decrease of the wind mass-loss rate with X-ray luminosity for the case of strong X-ray irradiation. This is nicely illustrated for orbital separations 30 R* and 50 R* in Fig. 10. With decreasing orbital separation the influence of X-rays becomes stronger, which results in the shift of the maximum to lower irradiation luminosities.
(Fig. 10). For small irradiation luminosities the X-rays do not significantly influence either the terminal velocity or the mass-loss rate. Consequently, the accretion luminosity is almost constant. For higher irradiation luminosities the terminal velocity decreases, which results in an increase of the accretion luminosity. The curves reach a maximum accretion luminosity and start to decrease due to the decrease of the wind mass-loss rate with X-ray luminosity for the case of strong X-ray irradiation. This is nicely illustrated for orbital separations 30 R* and 50 R* in Fig. 10. With decreasing orbital separation the influence of X-rays becomes stronger, which results in the shift of the maximum to lower irradiation luminosities.
 |
Fig. 10. Accretion X-ray luminosity according to Eq. (18) as a function of irradiation X-ray luminosity for the model 300-1 (black lines). Labels denote binary separation D. The intersections of straight red line, which denotes one-to-one relation, with black curves correspond to the solution of Eq. (18). |
In a stationary state the irradiation and accretion luminosities are equal, 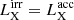 , and are given as a solution of Eq. (18). This is an implicit equation, therefore the solution has to be found numerically. The solution of Eq. (18) can be obtained graphically from Fig. 10 using iterations LX,n+1 = ℒX(LX,n) for n → ∞. According to the Banach fixed-point theorem (Banach 1922), such iterations converge if |dℒX/dLX| < 1. This holds for all curves in Fig. 10 and consequently we can expect that the X-ray emission should be stable even in the presence of X-ray feedback. Therefore, proper treatment of X-ray feedback may suppress large fluctuations of mass-accretion seen in numerical simulations (Blondin et al. 1990). Moreover, as a result of the shape of the curves, there are two types of solution with LX = 1033−1034 erg s−1 and LX = 1036−1037 erg s−1 (Ho & Arons 1987).
, and are given as a solution of Eq. (18). This is an implicit equation, therefore the solution has to be found numerically. The solution of Eq. (18) can be obtained graphically from Fig. 10 using iterations LX,n+1 = ℒX(LX,n) for n → ∞. According to the Banach fixed-point theorem (Banach 1922), such iterations converge if |dℒX/dLX| < 1. This holds for all curves in Fig. 10 and consequently we can expect that the X-ray emission should be stable even in the presence of X-ray feedback. Therefore, proper treatment of X-ray feedback may suppress large fluctuations of mass-accretion seen in numerical simulations (Blondin et al. 1990). Moreover, as a result of the shape of the curves, there are two types of solution with LX = 1033−1034 erg s−1 and LX = 1036−1037 erg s−1 (Ho & Arons 1987).
This dichotomy may provide a natural explanation for the two classes of X-ray binaries, that is, the supergiant fast X-ray transients (SFXTs) and classical supergiant X-ray binaries (sgXBs). The two classes of sgXBs have very similar binary parameters, but differ in strength and variability of their X-ray emission. The X-ray emission of sgXBs is several orders of magnitude stronger on average, while SFXTs show fast and strong variability. This can be explained either by the difference in the wind accretion (Shakura et al. 2012) or by the difference in the wind itself (Giménez-García et al. 2016; Pradhan et al. 2018). The latter explanation is supported by the systematic difference between the absorbing column densities of SFXTs and sgXBs (Pradhan et al. 2018). Based on our models, the differences between sgXBs and SFXTs can be explained by the strength of the X-ray feedback. In a state with low X-ray luminosity, the wind is basically unaffected by X-rays, has a relatively high speed, and from the continuity equation Ṁ = 4πr2 ρυ has a very low density ρ ∼ 1/υ. As a result of the high speed, the accreted amount of mass is low (see Eq. (16)) and as a result of low density the absorbing column is also low, which are characteristic properties of SFXTs. On the other hand, with large X-ray luminosity the wind velocity decreases, increasing the mass-accretion rate and the absorbing column density. The latter corresponds to sgXBs.
The parameters of SFXTs in Table 4 (denoted with index f there) support this picture. Either the optical depth parameter of SFXTs is typically large, tX ≳ 1, or the binaries are located in the bottom part of LX−tX diagrams.
From Fig. 10 it follows that just a small change of binary separation on the order of ten percent may cause transition from the SFXT regime to the sgXB regime. Another parameter that may determine the type of the object is the stellar luminosity, by setting of the wind mass-loss rate or the surface gravity, which determines the terminal velocity. In our explanation we neglected the role of the magnetic field and spin of the neutron star, which may still be important in affecting the mode of accretion (Shakura et al. 2012; Bozzo et al. 2016).
The existence of X-ray luminosity maxima in Fig. 10 is connected with the self-regulated state found in sgXBs (Krtička et al. 2015). For irradiation X-ray luminosities lower than the maximum one, an increase of the X-ray luminosity leads to stronger feedback, lower wind velocities, and stronger X-ray emission. On the other hand, if the irradiation X-ray luminosities overshoot the maximum accretion X-ray luminosity, this leads to a decrease of the wind mass-loss rate and a decrease of the accretion X-ray luminosity.
Sensitivity of wind feedback on orbital and wind parameters may also contribute to the variability of X-ray luminosity on flow timescale τflow ≈ D/υ∞, which is of the order of hours to days. The transitions between states with high and low X-ray luminosity may be triggered by the wind perturbations that include inhomogeneities on small or large scale (Oskinova et al. 2012; David-Uraz et al. 2017).
6. Conclusions
We studied wind inhibition in wind-powered HMXBs. We included the X-ray irradiation into our wind models and studied its effect on the radiative force for various X-ray luminosities and binary separations. As a result of strong X-ray irradiation, the radiative force that drives the wind decreases. This leads to the appearance of a kink in the wind velocity, which reduces the wind terminal velocity. For a very strong X-ray irradiation, the position of the kink approaches the star and the wind may fall back onto the star or the mass-loss may even reduce, leading to wind inhibition.
This wind inhibition may be conveniently studied in diagrams that combine the X-ray luminosity and the optical depth parameter. There was a good agreement between the position of observed stars in the LX versus tX diagrams and the theoretical expectations in our previous models (Krtička et al. 2015). However, more advanced global wind models predict significantly lower wind mass-loss rates, which results in the appearance of stars in the area corresponding to the wind inhibition.
The above agreement can be improved by introducing optically thin clumping (microclumping). Small-scale wind inhomogeneities (clumping) are expected to appear in the winds based on both theory and empirical evidence. Clumping improves the agreement between the expected and observed positions of the stars in the LX versus tX diagrams, because it weakens the effect of X-ray irradiation (as it favours recombination) and leads to an increase of the wind mass-loss rate. We tested different types of radial variations of the clumping factor and the best match between the models and observed properties of HMXBs was derived with the radially variable clumping of Najarro et al. (2009).
Based on our models, we described the influence of X-ray irradiation on the terminal velocity and on the mass-flux in the direction of a compact star in a parametric way. This enabled us to estimate the X-ray luminosities of individual HMXBs from their binary parameters assuming Bondi accretion. Without introducing the wind inhibition, the expected X-ray luminosities are typically lower than observed values by two to three orders of magnitude. However, introducing the reduction of wind velocities due to X-rays, the compact companion accretes a much larger amount of the wind and produces larger X-ray luminosities in agreement with observations.
As a result of the ionizing feedback of X-ray radiation, the equation for the X-ray luminosity within the Bondy-Hoyle-Lyttleton accretion picture becomes implicit. The derived roots however yield a stable solution of this equation. This also implies that the resulting X-ray luminosity can be expected to be stable. Moreover, there are two types of solution. One solution corresponds to weak X-ray irradiation with LX = 1033−1034 erg s−1 and the second solution corresponds to LX = 1036−1037 erg s−1. These two types of solution may provide a natural explanation for the two classes of X-ray binaries, that is, the SFXTs and sgXBs.
We also provide CAK line force multipliers for studied stars and introduce additional parameters that account for the influence of X-ray irradiation. These parameters can be used in hydrodynamical simulations.
The critical point is defined as a point where the speed of the radiative-acoustic Abbott waves is equal to the wind velocity (Abbott 1980; Feldmeier et al. 2008).
Acknowledgments
We thank Dr. J. Puls for comments on the paper and for the discussion on the inclusion of clumping in the wind models. This research was supported by grant GA ČR 18-05665S. Computational resources were provided by the CESNET LM2015042 and the CERIT Scientific Cloud LM2015085, provided under the programme “Projects of Large Research, Development, and Innovations Infrastructures”. The Astronomical Institute Ondřejov is supported by a project RVO:67985815 of the Academy of Sciences of the Czech Republic.
References
- Abbott, D. C. 1980, ApJ, 242, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, D. C. 1982, ApJ, 259, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Abbott, D. C., Bieging, J. H., & Churchwell, E. 1981, ApJ, 250, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Antokhin, I. I., Kholtygin, A. F., & Cherepashchuk, A. M. 1988, AZh, 65, 558 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Banach, S. 1922, Fund. Math., 3, 133 [Google Scholar]
- Blay, P., Ribó, M., & Negueruela, I. 2009, Ap&SS, 320, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Kallman, T. R., Fryxell, B. A., & Taam, R. E. 1990, ApJ, 356, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Bodaghee, A., Tomsick, J. A., Rodriguez, J., et al. 2010, ApJ, 719, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Bodaghee, A., Tomsick, J. A., Rodriguez, J., et al. 2011, ApJ, 727, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Boon, C. M., Bird, A. J., Hill, A. B., et al. 2016, MNRAS, 456, 4111 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Lanz, T., Hillier, D. J., et al. 2003, ApJ, 595, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Bouret, J.-C., Hillier, D. J., Lanz, T., & Fullerton, A. W. 2012, A&A, 544, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouzid, M. Y., Sterken, C., & Pribulla, T. 2005, A&A, 437, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bozzo, E., Stella, L., Ferrigno, C., et al. 2010, A&A, 519, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bozzo, E., Oskinova, L., Feldmeier, A., & Falanga, M. 2016, A&A, 589, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., & Braithwaite, J. 2011, A&A, 534, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carneiro, L. P., Puls, J., Sundqvist, J. O., & Hoffmann, T. L. 2016, A&A, 590, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J., Ribó, M., Ribas, I., et al. 2005, MNRAS, 364, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Čechura, J., & Hadrava, P. 2015, A&A, 575, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaty, S., Rahoui, F., Foellmi, C., et al. 2008, A&A, 484, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, J. S., Goodwin, S. P., Crowther, P. A., et al. 2002, A&A, 392, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, D. J., Sguera, V., Bird, A. J., et al. 2010, MNRAS, 406, L75 [NASA ADS] [Google Scholar]
- Cohen, D. H., Wollman, E. E., Leutenegger, M. A., et al. 2014, MNRAS, 439, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Corbet, R. H. D., Markwardt, C. B., & Tueller, J. 2007, ApJ, 655, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Kaper, L., & Mokiem, M. R. 2005, A&A, 436, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cusumano, G., La Parola, V., Romano, P., et al. 2010, MNRAS, 406, L16 [NASA ADS] [Google Scholar]
- David-Uraz, A., Owocki, S. P., Wade, G. A., Sundqvist, J. O., & Kee, N. D. 2017, MNRAS, 470, 3672 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Dessart, L., & Owocki, S. P. 2005, A&A, 437, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drave, S. P., Clark, D. J., Bird, A. J., et al. 2010, MNRAS, 409, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Drave, S. P., Bird, A. J., Sidoli, L., et al. 2013, MNRAS, 433, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Drave, S. P., Bird, A. J., Sidoli, L., et al. 2014, MNRAS, 439, 2175 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., Sundqvist, J. O., & Keppens, R. 2018, MNRAS, 475, 3240 [NASA ADS] [CrossRef] [Google Scholar]
- Falanga, M., Bozzo, E., Lutovinov, A., et al. 2015, A&A, 577, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier, A., & Thomas, T. 2017, MNRAS, 469, 3102 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, A., Anzer, U., Boerner, G., & Nagase, F. 1996, A&A, 311, 793 [NASA ADS] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Feldmeier, A., Oskinova, L., & Hamann, W.-R. 2003, A&A, 403, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmeier, A., Rätzel, D., & Owocki, S. P. 2008, ApJ, 679, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Fiocchi, M., Bazzano, A., Bird, A. J., et al. 2013, ApJ, 762, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Fransson, C., & Fabian, A. C. 1980, A&A, 87, 102 [NASA ADS] [Google Scholar]
- Fürst, F., Kreykenbohm, I., Pottschmidt, K., et al. 2010, A&A, 519, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gamen, R., Barbà, R. H., Walborn, N. R., et al. 2015, A&A, 583, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gayley, K. G. 1995, ApJ, 454, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R. 2003, in A Massive Star Odyssey: From Main Sequence to Supernova, eds. K. van der Hucht, A. Herrero, & E. Cèsar (San Francisco: ASP), IAU Symp., 91 [Google Scholar]
- Giménez-García, A., Torrejón, J. M., Eikmann, W., et al. 2015, A&A, 576, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giménez-García, A., Shenar, T., Torrejón, J. M., et al. 2016, A&A, 591, A26 [Google Scholar]
- Goossens, M. E., Bird, A. J., Drave, S. P., et al. 2013, MNRAS, 434, 2182 [NASA ADS] [CrossRef] [Google Scholar]
- Götz, D., Falanga, M., Senziani, F., et al. 2007, ApJ, 655, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Hadrava, P., & Čechura, J. 2012, A&A, 542, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiang, Y.-F., Cantiello, M., Bildsten, L., Quataert, E., & Blaes, O. 2015, ApJ, 813, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, W.-R., & Koesterke, L. 1998, A&A, 335, 1003 [NASA ADS] [Google Scholar]
- Harvin, J. A., Gies, D. R., Bagnuolo, Jr., W. G., Penny, L. R., & Thaller, M. L. 2002, ApJ, 565, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- Hatchett, S., & McCray, R. 1977, ApJ, 211, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, A., Puls, J., & Najarro, F. 2002, A&A, 396, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Gabler, R., Vilchez, J. M., & Gabler, A. 1995, A&A, 297, 556 [NASA ADS] [Google Scholar]
- Ho, C., & Arons, J. 1987, ApJ, 316, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1941, MNRAS, 101, 227 [NASA ADS] [Google Scholar]
- Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] [Google Scholar]
- Kaper, L., Hammerschlag-Hensberge, G., & Zuiderwijk, E. J. 1994, A&A, 289, 846 [NASA ADS] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., & NIST ASD Team NIST Atomic Spectra 2015, NIST Atomic Spectra Database (ver. 5.3) [Google Scholar]
- Krtička, J., & Kubát, J. 2004, A&A, 417, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., & Kubát, J. 2009, MNRAS, 394, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Krtička, J., & Kubát, J. 2011, A&A, 534, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., & Kubát, J. 2017, A&A, 606, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krtička, J., Muijres, L., Puls, J., Kubát, J., & de Koter, A. 2008, in The Art of Modeling Stars in the 21st Century, eds. L. Deng, & K. L. Chan (Cambridge: Cambridge Univ. Press), IAU Symp., 252, 283 [NASA ADS] [Google Scholar]
- Krtička, J., Kubát, J., & Skalický, J. 2012, ApJ, 757, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Krtička, J., Kubát, J., & Krtičková, I. 2015, A&A, 579, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kubát, J. 1996, A&A, 305, 255 [NASA ADS] [Google Scholar]
- Kubát, J. 2003, Modelling of Stellar Atmospheres, eds. N. E. Piskunov, W.W. Weiss, & D. F. Gray (San Francisco: ASP), IAU Symp., 210, A8 [Google Scholar]
- Kubát, J., Puls, J., & Pauldrach, A. W. A. 1999, A&A, 341, 587 [NASA ADS] [Google Scholar]
- Kupka, F., Piskunov, N. E., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Lamers, H. J. G. L. M., van den Heuvel, E. P. J., & Petterson, J. A. 1976, A&A, 49, 327 [NASA ADS] [Google Scholar]
- Lamers, H. J. G. L. M., Snow, T. P., & Lindholm, D. M. 1995, ApJ, 455, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2003, ApJS, 146, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- La Parola, V., Cusumano, G., Romano, P., et al. 2010, MNRAS, 405, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B., & Solomon, P. M. 1970, ApJ, 159, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Lutovinov, A., Tsygankov, S., & Chernyakova, M. 2012, MNRAS, 423, 1978 [NASA ADS] [CrossRef] [Google Scholar]
- Lutovinov, A. A., Revnivtsev, M. G., Tsygankov, S. S., & Krivonos, R. A. 2013, MNRAS, 431, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Maitra, C., Raichur, H., Pradhan, P., & Paul, B. 2017, MNRAS, 470, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A., & Walter, R. 2015, A&A, 584, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manousakis, A., Walter, R., & Blondin, J. M. 2012, A&A, 547, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchenko, S. V., Rauw, G., Antokhina, E. A., et al. 2000, MNRAS, 317, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Núñez, S., Kretschmar, P., Bozzo, E., et al. 2017, Space Sci. Rev., 212, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Martins, F., Schaerer, D., & Hillier, D. J. 2005a, A&A, 436, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., et al. 2005b, A&A, 441, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, A. B., Norton, A. J., Clark, J. S., Roche, P., & Negueruela, I. 2011, Bull. Soc. Roy. Sci. Liège, 80, 699 [NASA ADS] [Google Scholar]
- McSwain, M. V., Gies, D. R., Huang, W., et al. 2004, ApJ, 600, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., Kunasz, P. B., & Hummer, D. G. 1975, ApJ, 202, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Moldón, J., Ribó, M., & Paredes, J. M. 2012, A&A, 548, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martocchia, A., Motch, C., & Negueruela, I. 2005, A&A, 430, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muijres, L., de Koter, A., Vink, J., et al. 2011, A&A, 526, A32 [Google Scholar]
- Najarro, F., Figer, D. F., Hillier, D. J., Geballe, T. R., & Kudritzki, R. P. 2009, ApJ, 691, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Najarro, F., Hanson, M.M., & Puls, J. 2011, A&A, 535, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Hamann, W.-R. 2006, MNRAS, 372, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Hamann, W.-R., & Feldmeier, A. 2007, A&A, 476, 1331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Kretschmar, P. 2012, MNRAS, 421, 2820 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Rybicki, G. B. 1984, ApJ, 284, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Owocki, S. P., & Puls, J. 1999, ApJ, 510, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Parkin, E. R., Broos, P. S., Townsley, L. K., et al. 2011, ApJS, 194, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A., Puls, J., & Kudritzki, R. P. 1986, A&A, 164, 86 [NASA ADS] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peimbert, M. 1968, ApJ, 154, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Pellizza, L. J., Chaty, S., & Negueruela, I. 2006, A&A, 455, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Pradhan, P., Bozzo, E., & Paul, B. 2018, A&A, 610, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prat, L., Rodriguez, J., Hannikainen, D. C., & Shaw, S. E. 2008, MNRAS, 389, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Puls, J., Owocki, S. P., & Fullerton, A. W. 1993, A&A, 279, 457 [NASA ADS] [Google Scholar]
- Puls, J., Springmann, U., & Lennon, M. 2000, A&AS, 141, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahoui, F., Chaty, S., Lagage, P.-O., & Pantin, E. 2008, A&A, 484, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribó, M., Negueruela, I., Blay, P., Torrejón, J. M., & Reig, P. 2006, A&A, 449, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, P. 2015, J. High Energy Astrophys., 7, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Ducci, L., Mangano, V., et al. 2014, A&A, 568, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Runacres, M. C., & Owocki, S. P. 2002, A&A, 381, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1978, ApJ, 219, 645 [Google Scholar]
- Sander, A. A. C., Fürst, F., Kretschmar, P., et al. 2018, A&A, 610, A60 [Google Scholar]
- Schmutz, W. 1995, in Wolf-rayet Stars: Binaries; Colliding Winds; Evolution, eds. K. A. van der Hucht, & P. M. Williams (Dordrecht: Kluwer Academic Publishers), IAU Symp., 163, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J., Zeippen, C. J., Tully, J. A., et al. 1992, Rev. Mex. Astron. Astrofis., 23, 19 [NASA ADS] [EDP Sciences] [Google Scholar]
- Sguera, V. 2013, Nucl. Phys. B Proc. Suppl., 239, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Sguera, V., Bird, A. J., Dean, A. J., et al. 2007, A&A, 462, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sguera, V., Drave, S. P., Bird, A. J., et al. 2011, MNRAS, 417, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N., Postnov, K., Kochetkova, A., & Hjalmarsdotter, L. 2012, MNRAS, 420, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Sidoli, L., Esposito, P., Sguera, V., et al. 2013, MNRAS, 429, 2763 [NASA ADS] [CrossRef] [Google Scholar]
- Sierpowska-Bartosik, A., & Bednarek, W. 2008, MNRAS, 385, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Puls, J., & Feldmeier, A. 2010, A&A, 510, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Puls, J., Feldmeier, A., & Owocki, S. P. 2011, A&A, 528, A6 [EDP Sciences] [Google Scholar]
- Sundqvist, J. O., Owocki, S. P., & Puls, J. 2018, A&A, 611, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Kubát, J., Oskinova, L., & Feldmeier, A. 2012, A&A, 541, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Šurlan, B., Hamann, W.-R., Aret, A., et al. 2013, A&A, 559, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sushch, I., de Naurois, M., Schwanke, U., Spengler, G., & Bordas, P. 2012, Fermi Symposium proceedings– eConf C121028 [Google Scholar]
- Tarter, C. B., Tucker, W. H., & Salpeter, E. E. 1969, ApJ, 156, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, T. W. J., Tomsick, J., in ’t Zand, J. J. M., Rothschild, R. E., & Walter, R. 2007, ApJ, 661, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., & Muterspaugh, M. W. 2010, ApJ, 719, 958 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., Chaty, S., Rodriguez, J., et al. 2009, ApJ, 694, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Torrejón, J. M., Schulz, N. S., Nowak, M. A., et al. 2015, ApJ, 810, 102 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. Th., Kaper, L., & Hammerschlag-Hensberge, G. 2001, A&A, 375, 498 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Meer, A., Kaper, L., di Salvo, T., et al. 2005, A&A, 432, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, R., Lutovinov, A. A., Bozzo, E., & Tsygankov, S. S. 2015, A&ARv, 23, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, J., Liu, Q., & Hadrava, P. 2008, AJ, 136, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, S., Sako, M., Ishida, M., et al. 2006, ApJ, 651, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Zurita Heras, J. A., & Chaty, S. 2009, A&A, 493, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zurita Heras, J. A., & Walter, R. 2009, A&A, 494, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Implementation of clumping into the wind code
 |
Fig. A.1. Dependence of the terminal velocity on the binary separation for models from Table 1 with clumping after Eq. (6) for different X-ray luminosities (crosses). Overplotted is the corresponding fit Eq. (14) for different values of LX. |
The mean opacity ⟨χ⟩ in the case of a clumpy medium can be derived from the contributions of clumps (+) and an interclump medium (−),
where κ+ is the opacity per unit of mass in the clumps, ( + ) and ( − ) denote the integration in the clumps only and in the interclump media only, respectively, and where we integrate over a suitably chosen volume V containing a large number of clumps. We assumed a void interclump medium, and consequently χ− = 0. Using the mean opacity it is possible to calculate the optical depth,
where we used Eqs. (1) and (2), and the definition of f. The volume-averaged emissivity is
where we again used the definition of f.
In our models, we solve for the relative occupation numbers Ni = ni/nelem, where ni is the occupation number of a level i and nelem is the number density of a given element (Krtička & Kubát 2004). Consequently, to include the clumping we modified our code in a following way:
-
The electron number density that features in the statistical equilibrium equations (and consequently also in the calculation of the Saha-Boltzmann factors) is taken as Cc⟨ne⟩.
-
The electron number density that features in the free-free emission term is also taken as Cc⟨ne⟩.
-
The electron number density that features in the equations of thermal balance of electrons is taken as Cc⟨ne⟩.
We applied a test devised by J. Puls (priv. comm.) to check for the validity of including clumping. Our code successfully passed the test. Moreover, the ionization parameter Eq. (12) also fulfills the test.
All Tables
Derived wind mass-loss rate Ṁ, wind terminal velocity υ∞, and velocity law fit parameters υ1, υ2, υ3, and γ for models with clumping.
All Figures
 |
Fig. 1. Radial variation of the clumping factor according to Eq. (6) for individual wind models from Table 1. |
| In the text | |
 |
Fig. 2. Geometry of the model of a hot star wind irradiated by X-rays from a compact companion. Here D is binary separation, r is radius of studied point in the wind, and d its distance from the compact companion. |
| In the text | |
 |
Fig. 3. Radial velocity for selected wind models 300-1. The black line denotes the model without either X-ray irradiation or clumping, while blue and red lines denote models with the same X-ray irradiation (with the same LX and D) and different clumping: without clumping (blue solid) and with Cc = 10 (red dashed). Here the clumping is allowed to affect the ionization structure only directly and not via the mean density (mass-loss rate). Overplotted is the value of the ionization parameter Eq. (12) at the location of the velocity kink. Left panel: model with LX = 1036 erg s−1 and D = 200 R⊙. Right panel: model with LX = 1038 erg s−1 and D = 700 R⊙. |
| In the text | |
 |
Fig. 4. Radial velocity for selected wind models. The black line denotes the model without either X-ray irradiation or clumping, while blue, red, and green lines denote models with the same X-ray irradiation (with the same LX and D) but with different clumping: without clumping (blue, solid), with Cc = 3 (red dotted), and with radially dependent clumping factor after Eq. (6) with C1 = 10 (green dashed). Arrows denote the location of the kink in the velocity profile with a corresponding value of the ionization parameter from Eq. (12). Upper left: model 300-1 with LX = 1037 erg s−1 and D = 300 R⊙. Upper right: model 375-1 with LX = 1037 erg s−1 and D = 100 R⊙. Lower left: model 300-5 with LX = 1035 erg s−1 and D = 30 R⊙. Lower right: model 375-5 with LX = 1036 erg s−1 and D = 100 R⊙. |
| In the text | |
 |
Fig. 5. Diagrams of X-ray luminosity vs. the optical depth parameter Eq. (13) for models without clumping and for individual stars from Table 1. Each point describes models with different LX and D. Individual symbols discriminate between different effects of X-ray ionization on the wind: black plus symbols (+) denote models with negligible influence of X-ray irradiation, while red crosses ( |
| In the text | |
 |
Fig. 6. As in Fig. 5, but using a constant clumping factor Cc = 3. |
| In the text | |
 |
Fig. 7. As in Fig. 5, but using the variable clumping factor from Eq. (6) with C1 = 10. |
| In the text | |
 |
Fig. 8. Observed X-ray luminosity in comparison with predicted X-ray luminosity Eq. (16) for the stars from Table 4 for two limiting values of relative velocity: υ∞ (red crosses) and υorb (blue plus signs). Line denotes one-to-one relation. |
| In the text | |
 |
Fig. 9. X-ray luminosities of stars from Table 4 estimated using Eqs. (16) and (17) inserting the terminal velocity (as υwind) derived from Eq. (14) using observed X-ray luminosities. Plotted as a function of observed X-ray luminosity. Line denotes one-to-one relation. |
| In the text | |
 |
Fig. 10. Accretion X-ray luminosity according to Eq. (18) as a function of irradiation X-ray luminosity for the model 300-1 (black lines). Labels denote binary separation D. The intersections of straight red line, which denotes one-to-one relation, with black curves correspond to the solution of Eq. (18). |
| In the text | |
 |
Fig. A.1. Dependence of the terminal velocity on the binary separation for models from Table 1 with clumping after Eq. (6) for different X-ray luminosities (crosses). Overplotted is the corresponding fit Eq. (14) for different values of LX. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




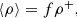
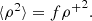
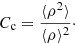
![$$ \begin{aligned}&\tilde{v}(r)= \left[v_1\left(1-\frac{R_*}{r}\right)+v_2\left(1-\frac{R_*}{r}\right)^2+ v_3\left(1-\frac{R_*}{r}\right)^3\right]\nonumber \\&\qquad \;\times \left\{1-\exp \left[-\gamma \left(1-\frac{r}{R_*}\right)^2\right]\right\} , \end{aligned} $$](/articles/aa/full_html/2018/12/aa33419-18/aa33419-18-eq7.gif)
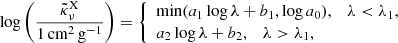
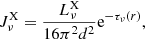
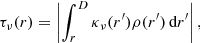
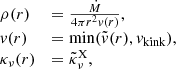
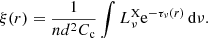
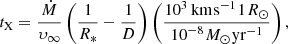



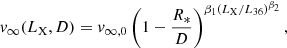
![$$ \begin{aligned} \dot{M}({L_{\rm X}},D)=\dot{M}_0\left[1-\exp \left(-\frac{\left(D-R_*\right)^2}{s_1({L_{\rm X}}/L_{36})^{s_2}}\right)\right], \end{aligned} $$](/articles/aa/full_html/2018/12/aa33419-18/aa33419-18-eq21.gif)