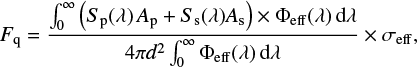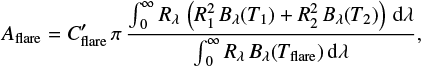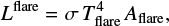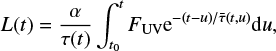| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 6 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201834116 | |
| Published online | 16 November 2018 | |
X-ray and UV emission of the ultrashort-period, low-mass eclipsing binary system BX Trianguli
1
Hamburger Sternwarte, Gojenbergsweg 112, 21029, Hamburg, Germany
e-mail: vperdelwitz@hs.uni-hamburg.de
2
Astronomical Institute, Slovak Academy of Sciences, 059 60, Tatranská Lomnica, Slovakia
Received:
22
August
2018
Accepted:
4
September
2018
Context.Close binary systems provide an excellent tool for determining stellar parameters such as radii and masses with a high degree of precision. Due to the high rotational velocities, most of these systems exhibit strong signs of magnetic activity, postulated to be the underlying reason for radius inflation in many of the components.
Aims.We extend the sample of low-mass binary systems with well-known X-ray properties.
Methods.We analyze data from a singular XMM-Newton pointing of the close, low-mass eclipsing binary system BX Tri. The UV light curve was modeled with the eclipsing binary modeling tool PHOEBE and data acquired with the EPIC cameras was analyzed to search for hints of orbital modulation.
Results.We find clear evidence of orbital modulation in the UV light curve and show that PHOEBE is fully capable of modeling data within this wavelength range. Comparison to a theoretical flux prediction based on PHOENIX models shows that the majority of UV emission is of photospheric origin. While the X-ray light curve does exhibit strong variations, the signal-to-noise ratio of the observation is insufficient for a clear detection of signs of orbital modulation. There is evidence of a Neupert-like correlation between UV and X-ray data.
Key words: stars: activity / stars: coronae / binaries: eclipsing / X-rays: individuals: BX Tri / stars: low-mass
© ESO 2018
1. Introduction
The increasing number of well-studied close eclipsing binary (EB) systems with low-mass components, partly driven by large-scale exoplanet search programs (see, e.g., Borucki et al. 2010; Neuhäuser et al. 2011), has opened up the opportunity to benchmark stellar evolutionary models such as those developed by Baraffe et al. (2015) and Feiden & Chaboyer (2012). Utilizing light curves and radial velocity data, stellar parameters such as radius and mass can be determined to a higher degree of precision than for single stars. Various authors, such as Ribas (2006), López-Morales (2007), and Morales et al. (2010), have shown that evolutionary models can underestimate the radii of low-mass components of EBs by as much as 15% and overestimate their temperatures by up to 5%. Although several phenomena have been proposed as the underlying reason (Feiden 2015), there seems to be a correlation between the deviations and magnetic activity (López-Morales 2007; Morales et al. 2010; Feiden & Chaboyer 2012). Most of these close EBs are known to be tidally locked and therefore exhibit high levels of activity caused by their rapid rotation. Based on surface magnetic flux levels published in Reiners (2012), Feiden & Chaboyer (2013) have computed an empirical scaling law between the X-ray luminosity LX of a star (based on ROSAT all-sky survey data; Voges et al. 1999) and its magnetic flux Φ, allowing the incorporation of magnetic fluxes derived from X-ray observations into evolutionary models.
With the advent of the large X-ray facilities XMM-Newton (Jansen et al. 2001) and Chandra (Weisskopf et al. 2000) it is possible to use longer pointings of EBs to derive more accurate values for L X and eliminate systematic errors such as flaring events and phase-dependent modulation. Furthermore, in the same way that photometric light curves in the optical regime provide a precise value for the shape and extent of the photosphere, X-ray observations enable the study of coronal extent and structure previously limited to the sun (Güdel et al. 2001, 2005).
In this paper, we analyze a singular XMM-Newton observation of the close, low-mass binary system BX Tri to search for orbital modulations in the UV and X-ray regime and derive a precise estimate of the X-ray luminosity of the system. The paper is structured in the following way. After summarizing previous studies on the system in Sect. 2, we describe the observations and data products in Sect. 3. The data analysis and results are then presented in Sect. 4, and we give a summary and conclusion of our findings in Sect. 5.
2. BX Tri: Previous knowledge
BX Tri was first identified as a short-period variable star by Norton et al. (2007) and classified as a W UMa-type binary by Dimitrov & Kjurkchieva (2010), who find that it consists of a 0.51 M⊙ primary and a 0.26 M⊙ secondary with a separation of 1.28 R⊙ and an orbital period of 0.19 d, making it one of the closest known binary systems comprised of main sequence stars, below the short-period limit of eclipsing binaries of 0.22 d given by Rucinski & Pribulla (2008).
Like most close binary systems, BX Tri exhibits strong magnetic activity in photospheric, chromospheric, and coronal indicators. Strong chromospheric activity was reported in Hα (Dimitrov & Kjurkchieva 2010) and in Hβ and Hγ (Zhang et al. 2014). These authors also find stable configurations of large spots as well as high flare rates. The system is identified with the RASS source 1RXS J022050.7+332049 by Norton et al. (2007) with a count rate of 0.07 ± 0.02 cts−1 and was found to be a variable X-ray source by Fuhrmeister & Schmitt (2003). When applying the empirical conversion formula derived by Schmitt et al. (1995) the detected ROSAT count rate corresponds to a flux of FX = 4.4 × 10−13 erg s−1 cm−2; when using the bolometric luminosities given in Dimitrov & Kjurkchieva (2010), this corresponds to log(L X/Lbol) = −3.2, close to the saturation limit of −3.13 (Wright et al. 2011). Gaia DR2 (Gaia Collaboration 2018) states a parallax of 18.83 ± 0.05 mas (corresponding to a distance of 53.11 ± 0.14 pc) and confirms the finding of Dimitrov & Kjurkchieva (2011) that BX Tri has a visual companion (** LDS 3372) at a separation of 1.2″.
 |
Fig. 1. Mass-radius diagram of EB components. Data are adapted from Kraus et al. (2011), Cruz et al. (2018), and the DEBCat catalog (Southworth 2015). Primary components are displayed as black symbols, secondaries as gray. The two components of BX Tri are displayed with the parameters determined by Dimitrov & Kjurkchieva (2010). The solid line represents a 1 Gyr isochrone model by Chabrier et al. (2000). |
As is the case in many active M Dwarfs, the radius of one of the components is enlarged substantially with respect to model predictions. Figure 1 shows the mass-radius relationship of close binary systems based on data from Kraus et al. (2011), Southworth (2015), and Cruz et al. (2018), as well as the two components of BX Tri, assuming the values derived by Dimitrov & Kjurkchieva (2010). A comparison to a 1 Gyr isochrone model (Chabrier et al. 2000) shows that most stars within the sample are significantly enlarged with respect to model predictions.
Lohr et al. (2013) found period variations of dP/dt = (−0.030 ± 0.007) s yr−1(Lohr, priv. comm.) with a 4σ significance level based on SuperWASP data (Pollacco et al. 2006). The system parameters derived by Dimitrov & Kjurkchieva (2010) and Zhang et al. (2014) are listed in Table 1.
System parameters of BX Tri.
3. Observations
Observations of BX Tri were carried out with XMM-Newton on 2013 July 19 (Obs. ID 0720180101) for a duration of 43 ks with the optical monitor (OM) and 35 ks with the EPIC detectors, covering two full periods of the system. All data were reduced using the XMM-Newton SCIENCE ANALYSIS SYSTEM (SAS) version 14.0.0. and barycentric correction was carried out.
All EPIC cameras were operated in full frame mode using the medium filter. In order to detect eclipses or other signs of periodicity, light curves were extracted for an energy range of 0.2−5 keV for all EPIC detectors and binned to 100 s time intervals. Throughout the exposure the background level was substantial, but particularly towards the end of the pointing, the X-ray data quality deteriorated significantly and all EPIC detectors switched off 35 ks into the observation. Since the Reflection Grating Spectrometer (RGS) spectra exhibit a low signal-to-noise ratio, spectroscopy was performed with the EPIC detectors only.
The XMM-Newton OM (Mason et al. 2001) observed in fast mode setting using the UVW1 filter (effective wavelength of 291 nm and effective width of 83 nm) in order to acquire data in the ultraviolet. Data reduction was performed with the SAS OM pipeline OMFCHAIN and light curves were binned to 60 s intervals. Figure 2 shows the light curves of the entire observation in the UV (upper panel) and X-ray range (lower panel). Both wavelength regimes exhibit significant flaring events, with the count rates rising by a factor of 7 in the UV and 4 in the X-ray. In Fig. 2 these flaring regions, determined by visual inspection, are marked with shaded areas, along with solid and dashed lines representing the locations of primary and secondary eclipses.
 |
Fig. 2. XMM-Newton light curves of BX Tri. Upper panel: OM UVW1 data. Lower panel: co-added EPIC light curves for the energy range 0.2–5 keV. The position of the primary and secondary eclipses based on the ephemerides given by Zhang et al. (2014) are marked by solid and dashed vertical red lines. Flaring regions excluded from the light curve analysis described in Sects. 4.1 and 4.2 are indicated as shaded areas. |
A first look at the OM light curve gives the impression that primary eclipses are present at phases 0.0 and 1.0, while the third at phase 2.0 is obscured by a fading flare. The secondary eclipses, however, appear to be indistinguishable from noise. A similar inspection of the X-ray light curve yields no obvious signs of orbital modulation.
4. Data analysis and results
In this section we discuss the analysis of the UV and X-ray light curves as well as EPIC spectra. For this purpose, both the UV and X-ray light curves were phase-folded according to the ephemerides derived by Dimitrov & Kjurkchieva (2010), and the orbital modulations in both wavelength regimes were utilized to draw conclusions on the origin of the UV emission as well as the distribution of the coronal plasma. We then conclude the section with a discussion of the flaring events.
4.1. UV range
As a first approach to analyzing the UV light curve we compare it to model predictions based on the PHOEBE code (Prša & Zwitter 2005). Optical light curves and RV data of BX Tri from Dimitrov & Kjurkchieva (2010) were fitted following the procedure described in their publication, and subsequently removing the two spots from the model. The OM UVW1 light curve was then added as an additional data set, omitting the flaring regions indicated by shaded areas in Fig. 2. For this purpose, we added the XMM-Newton OM UVW1 filter1 to the set of PHOEBE filter curves. Since the van Hamme limb darkening coefficients (van Hamme 1993) utilized by PHOEBE cover the spectral range in question, we could then compare the model predictions to the observed UV light curve. The resulting light curve, along with the PHOEBE model predictions, is displayed in Fig. 3.
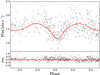 |
Fig. 3. Optical monitor light curve folded with the period given by Zhang et al. (2014). The solid red line represents the PHOEBE model and the residuals between the flux and the unshifted model are displayed in the bottom panel. Regions with flaring events were omitted. |
While the residuals show slight systematics around the primary eclipse, the artificial light curve yields a good approximation of the data, indicating that the modeling of eclipses in the UV with PHOEBE works well. The flux in the UVW1 filter at quarter phase based on the model light curve was determined to be (6.72 ± 0.04) × 10−13 erg s−1 cm2, and the flux during primary eclipse to be (4.5± 0.01) × 10−13 erg s−1 cm2. Here we used the conversion factor of 4.76 × 10−16 erg cm2 Å cnt as stated on the SAS website2. A geometrical model assuming two spheres yields a primary eclipse depth of around 10%, which is below the observed variation, indicating that Roche geometry and heating effects play an important role in the modeling of the system. We compare the out-of-eclipse flux to a theoretical flux prediction based on a PHOENIX (Hauschildt et al. 1999) composite model with temperatures T1/T2 = 3700/3100 K, surface gravities log g = 4.5/5.0, and solar metallicities. The model spectra S(λ) of the primary and secondary component are multiplied with the respective stellar surfaces and folded with the OM effective area. The theoretical flux prediction at quarter phase can then expressed as
where 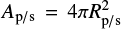 are the surfaces of the pri mary and secondary component, Φeff(λ) is the effective area of the UVW1 filter (Talavera 2009), d = 53.11 pc is the distance of BX Tri, and σeff = 830 Å is the effective width of the filter.
are the surfaces of the pri mary and secondary component, Φeff(λ) is the effective area of the UVW1 filter (Talavera 2009), d = 53.11 pc is the distance of BX Tri, and σeff = 830 Å is the effective width of the filter.
This approximation yields an out-of-eclipse flux of F q = 5.20 × 10−13 erg s−1 cm2, which corresponds to 77% of the measured flux. Since this approach neglects Roche geometry and surface heating effects, both of which should increase the predicted flux, we conclude that at least three-quarters of the UV flux is of photospheric origin since the PHOENIX models do not include chromospheric emission. Since the PHOEBE model and the PHOENIX spectra both give a good approximation of the observed UV flux, we assume that both components contribute to the UV emission, despite the absence of clear secondary eclipses in the light curve.
 |
Fig. 4. Observed-calculated eclipse minima of BX Tri. Archival data from Zhang et al. (2014) are marked with green crosses, those from Lohr et al. (2013) and Lohr (priv. comm.) with black dots. The DWARF project data (Pribulla et al. 2012) are displayed as blue diamonds. The XMM-Newton OM minimum is highlighted in red. The best-fit quadratic function based on the visual data is displayed as a broken line and yields a period change of (−0.018 ± 0.003) s yr−1. |
Using a least-squares analysis, we determined the phase of the primary eclipse in the folded light curve. Assuming the ephemerides given in Zhang et al. (2014), we find a substantial phase shift in the OM data of 0.029 ± 0.009 phases corresponding to (483 ± 153) s. Here the error was determined using a Monte Carlo approach, displacing the flux values within the respective error range and determining the best-fit phase shift for each draw. The standard deviation of the phase shifts was adopted as the error value. In order to compare this phase shift to observed-calculated (O-C) data acquired in the optical regime, we combine data derived by Lohr et al. (2013), Zhang et al. (2014), and Pribulla et al. (2012). The resulting O-C diagram is displayed in Fig. 4, along with a quadratic fit of all available optical data. We find a significant period change of (−0.024 ± 0.005) s yr−1 in the optical O–C data, which is consistent with an updated value of (−0.030 ± 0.007) s yr−1 derived by Lohr et al. (2013) and Lohr (priv. comm.). The O–C value of the UV minimum does not fit the trend of the optical data within the margins of error. This indicates that the emitting material is not distributed in a spherically symmetric way across the surface of each stellar component, which is in agreement with Dimitrov & Kjurkchieva (2010), who found large spots in the photospheres of the binary.
4.2. X-ray range
As a first attempt to identify orbital modulation, we phase-folded the entire EPIC PN light curve. While the result shown in Fig. 5 shows eclipse-like modulations at the location of the primary and secondary eclipse, a closer look at the lower panel of Fig. 2 reveals that this impression is caused by two large flaring events. An increase in flare rates at quarter-phase has been observed in the optical regime in other binary systems (Gao et al. 2016).
The same light curves were then phase-folded after removal of the large flaring events by visual inspections (shaded regions in Fig. 2). The resulting light curve is shown in Fig. 6 and does not exhibit any clear signs of eclipses.
If we assume both stars to be magnetically saturated (LX/Lbol = 10−3.13), the distribution of the coronal emission then follows the ratio of the bolometric luminosities, or 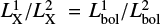 . Even under optimal conditions for the detection of eclipses, i.e., with no coronal extent above the photosphere, the depth of primary and secondary eclipse would be on the order of 0.015 cts s−1 and 0.007 cts s−1, respectively, which is well below the noise level of the light curve.
. Even under optimal conditions for the detection of eclipses, i.e., with no coronal extent above the photosphere, the depth of primary and secondary eclipse would be on the order of 0.015 cts s−1 and 0.007 cts s−1, respectively, which is well below the noise level of the light curve.
For an estimate of the coronal scale height, a higher signal-to-noise ratio would be required.
Without the presence of eclipses, we cannot determine the contribution of each stellar corona to the overall X-ray luminosity. Considering that both components are extremely fast rotators, we can make the reasonable assumption that the secondary component also exhibits coronal activity and contributes to the X-ray emission.
 |
Fig. 5. Complete EPIC PN light curve of BX Tri folded with the period derived by Zhang et al. (2014). The black dots represent the full light curve with a binning of 100 s (error bars were omitted for clarity), while the blue diamonds display the phase-binned light curve. |
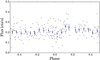 |
Fig. 6. EPIC PN light curve of BX Tri folded with the period derived by Zhang et al. (2014) after flare removal. The black dots represent the filtered light curve with a binning of 100 s (error bars were omitted for clarity), while the blue diamonds show the phase-binned light curve. |
Time-resolved spectroscopy
We divided the EPIC data into nine time intervals centered on times corresponding to quarter phases and extracted the individual spectra. Spectral analysis was performed with XSPEC version 12.8.1 (Arnaud 1996) by simultaneously fitting MOS1, MOS2, and PN spectra with an apec model with two plasma temperatures. Table 2 contains the center phase of the time intervals, the time span relative to the start of the observation, as well as temperatures and emission measures of the two plasma components. The reduced χ2 of all spectral fits was below 1.2, indicating that the two-temperature plasma model describes the coronal emission well. Figure 7 shows the plasma temperatures and emission measures derived from time-resolved spectroscopy, which exhibit no signs of periodicity but rather follow the trend of the X-ray light curve, which we attribute to the presence of large flares during the observation.
We determined the quiescent X-ray luminosity by extracting the spectrum for the region between the first secondary and second primary eclipse (corresponding to phase 0.75 in Table 2), which is unaffected by larger flares, yielding LX = (9.29 ± 0.07)⋅1028 erg s−1 in the energy range 0.2−5 keV, or log(LX/Lbol) = −3.4.
Results of the time-resolved spectroscopy.
4.3. Flaring events
Zhang et al. (2014) report a flare rate of BX Tri of νf = 0.11 h−1 in the optical regime, which among close, low-mass EBs is only surpassed by YY Gem with ν f = 0.22 h−1 (Doyle & Mathioudakis 1990). During the XMM-Newton observation of BX Tri described in this paper, three large and several small flaring events occurred. All of these events appear first in the UV light curve and are then echoed in the X-ray regime where the decay time is much greater, which is characteristic of the X-ray emitting material filling the coronal loops.
In order to obtain an estimate of the emitting area and total energy of the two flares (t1 = 3.4 ks and t2 = 29 ks after the start of the EPIC observations) we followed the approach of Shibayama et al. (2013) and estimated the area as
where 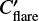 is the ratio of the flare peak and quiescent count rates, Ri are the stellar radii, Rλ is the XMM-Newton OM response curve, and Bλ(Ti) are the Planck curves at the effective and flare temperature. Here we used the value of Tflare = 9000 K stated by Kretzschmar (2011) as the flare temperature. With count rate ratios of
is the ratio of the flare peak and quiescent count rates, Ri are the stellar radii, Rλ is the XMM-Newton OM response curve, and Bλ(Ti) are the Planck curves at the effective and flare temperature. Here we used the value of Tflare = 9000 K stated by Kretzschmar (2011) as the flare temperature. With count rate ratios of 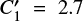 and
and 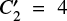 , we estimated the flare area to be Aflare ≈ 4.8 × 1018 cm2, or 0.08% of the combined stellar surface, for the first flare and Aflare ≈ 1.1 × 1019 cm2, or 0.17% of the combined stellar surface, for the second.
, we estimated the flare area to be Aflare ≈ 4.8 × 1018 cm2, or 0.08% of the combined stellar surface, for the first flare and Aflare ≈ 1.1 × 1019 cm2, or 0.17% of the combined stellar surface, for the second.
 |
Fig. 7. Plasma temperatures (upper panel) and emission measures (lower panel) derived from time-resolved spectroscopy. The black diamonds represent the higher temperatures, the gray circles the lower temperatures of the two-temperature apec model fit. |
We were then able to derive the bolometric flare luminosities via
where σ is the Stefan–Boltzmann constant, and arrived at peak luminosities of 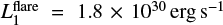 and
and 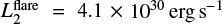 .
.
Finally, we investigated the existence of a Neupert-like effect. The Neupert effect (Neupert 1968) originally described a correlation between microwave and soft X-ray emission. It is of interest with regard to flare energetics, and has also been proposed by Parker (1988) as a contributor to coronal heating.
Our effort was limited by the high background level and the read-out gaps in the OM data, and we limited it to the flaring event occurring 3.4 ks after the beginning of the observation. We followed the formalism of Guedel et al. (1996) and compared the generalized Neupert effect
where L denotes the X-ray luminosity, α is a proportionality constant, τ is the thermal decay parameter, and FUV is the flux in the UVW1 filter. Figure 8 shows the UVW1 light curve (upper panel), the X-ray light curve (black dots, lower panel), and the X-ray count rate derived via Eq. (4) (red solid line, lower panel). While the derived X-ray light curve follows the general trend of the observed data, the quality of the approximation is diminished by the occurrence of smaller flares after the large peak, and by a read-out gap in the OM data at the beginning of the flare. Due to the lower quality approximation and the low count rates in the X-ray regime it is not possible to study delay times between UV and X-ray flares in a manner similar to Mitra-Kraev et al. (2005).
5. Summary and conclusions
We performed a detailed analysis of data from a XMM-Newton observation of the close, low-mass eclipsing binary system BX Tri. Based on the OM fast mode data acquired with the UVW1 filter, we were able to model the UV emission with PHOEBE and conclude that at least three-quarters of the UV flux originates in the stellar photosphere. A comparison with optical O–C data indicates an inhomogeneous distribution of emitting material likely caused by spot modulation.
In the X-ray regime we found that the signal-to-noise ratio was insufficient to detect orbital modulation and to derive a unique solution of the coronal distribution and scale heights. In comparison to the close M-dwarf binary YY Gem, which exhibits clear eclipses in the X-ray regime (Güdel et al. 2001; Stelzer et al. 2002), the X-ray luminosity and orbital inclination of BX Tri are less favorable for such an analysis.
The quiescent, out-of-eclipse X-ray luminosity of the system was determined to be LX = (9.29 ± 0.07) × 1028 erg s−1, or log(LX/Lbol) = −3.4, placing BX Tri near the magnetic saturation limit of log(LX/Lbol)= −3.13. We find that the large flaring events during the observation dominate both the X-ray light curve and the parameters of the coronal plasma derived via time-resolved spectroscopy. We determined that there is evidence of a Neupert-like relation between the UV and X-ray light curve and estimated the X-ray luminosities of two larger flaring events. While secondary eclipses are absent in the UV and X-ray light curves, we stipulate that both stellar components contribute to the observed flux in the two wavelength regimes.
 |
Fig. 8. Flaring event at t = 3.4 ks in the UVW1 filter (upper panel) and the X-ray regime (lower panel). The solid line in the lower panel represents the modeling of a Neupert-like effect according to Eq. (4). |
Acknowledgments
Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. VP acknowledges funding through the DFG Research Training Group 1351. JR acknowledges funding through DLR grant 50QR1605. SC acknowledges support from DFG project SCH 1382/2-1. This work was supported by project VEGA 2/0031/18. We thank M.E. Lohr for supplying us with updated data from the SuperWASP analysis.
References
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz, P., Diaz, M., Birkby, J., et al. 2018, MNRAS, 476, 5253 [NASA ADS] [CrossRef] [Google Scholar]
- Dimitrov, D., & Kjurkchieva, D. 2011, AJ, 17, 39 [Google Scholar]
- Dimitrov, D. P., & Kjurkchieva, D. P. 2010, MNRAS, 406, 2559 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, J. G., & Mathioudakis, M. 1990, A&A, 227, 130 [NASA ADS] [Google Scholar]
- Feiden, G. A. 2015, in Living Together: Planets, Host Stars and Binaries, eds. S. M. Rucinski G. Torres, & M., Zejda, ASP Conf. Ser., 496, 137 [NASA ADS] [Google Scholar]
- Feiden, G. A., & Chaboyer, B. 2012, ApJ, 757, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Feiden, G. A., & Chaboyer, B. 2013, ApJ, 779, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., & Schmitt, J. H. M. M. 2003, A&A, 403, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, Q., Xin, Y., Liu, J.-F., Zhang, X.-B., & Gao, S. 2016, ApJS, 224, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Güdel, M., Audard, M., Magee, H., et al. 2001, A&A, 365, L344 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güdel, M., Telleschi, A., Skinner, S. L., Audard, M., et al. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata G. A. J.Hussain, & B. Battrick, ESA SP, 560, 605 [NASA ADS] [Google Scholar]
- Guedel, M., Benz, A. O., Schmitt, J. H. M. M., & Skinner, S. L. 1996, ApJ, 471, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kraus, A. L., Tucker, R. A., Thompson, M. I., Craine, E. R., & Hillenbrand, L. A. 2011, ApJ, 728, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Kretzschmar, M. 2011, A&A, 530, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lohr, M. E., Norton, A. J., Kolb, U. C., et al. 2013, A&A, 549, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Morales, M. 2007, ApJ, 660, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, K. O., Breeveld, A., Much, R., et al. 2001, A&A, 365, L36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mitra-Kraev, U., Harra, L. K., Güdel, M., et al. 2005, A&A, 431, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morales, J. C., Gallardo, J., Ribas, I., et al. 2010, ApJ, 718, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Neuhäuser, R., Errmann, R., Berndt, A., et al. 2011, Astron. Nachr., 332, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Neupert, W. M. 1968, ApJ, 153, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. J., Wheatley, P. J., West, R. G., et al. 2007, A&A, 467, 785 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Pollacco, D. L., Skillen, I., Collier Cameron, A., et al. 2006, PASP, 118, 1407 [NASA ADS] [CrossRef] [Google Scholar]
- Pribulla, T., Vaňko, M., Ammler-von Eiff, M., et al. 2012, Astron. Nachr., 333, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A. 2012, Living Rev. Sol. Phys., 9, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I. 2006, in Astrophysics of Variable Stars, eds. C. Aerts, & C. Sterken, ASP Conf. Ser., 349, 55 [NASA ADS] [Google Scholar]
- Rucinski, S. M., & Pribulla, T. 2008, MNRAS, 388, 1831 [NASA ADS] [Google Scholar]
- Schmitt, J. H. M. M., Fleming, T. A., & Giampapa, M. S. 1995, ApJ, 450, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2015, in Living Together: Planets, Host Stars and Binaries, eds. S. M. Rucinski G. Torres, & M. Zejda, ASP Conf. Ser., 496, 164 [NASA ADS] [Google Scholar]
- Stelzer, B., Burwitz, V., Neuhäuser, R., Audard, M., & Schmitt, J. H. M. M. 2002, in Stellar Coronae in the Chandra and XMM-NEWTON Era, eds. F. Favata, & J. J. Drake, ASP Conf. Ser., 277, 215 [NASA ADS] [Google Scholar]
- Talavera, A. 2009, Ap&SS, 320, 177 [NASA ADS] [CrossRef] [Google Scholar]
- van Hamme, W. 1993, AJ, 106, 2096 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Weisskopf, M. C., Tananbaum, H. D., & Van Speybroeck, L. P. 2000, in X-Ray Optics, Instruments, and Missions III, eds. J. E. Truemper, & B. Aschenbach, Proc. SPIE, 4012, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, N. J., Drake, J. J., Mamajek, E. E., & Henry, G. W. 2011, ApJ, 743, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L.-Y., Pi, Q.-F., & Yang, Y.-G. 2014, MNRAS, 442, 2620 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Mass-radius diagram of EB components. Data are adapted from Kraus et al. (2011), Cruz et al. (2018), and the DEBCat catalog (Southworth 2015). Primary components are displayed as black symbols, secondaries as gray. The two components of BX Tri are displayed with the parameters determined by Dimitrov & Kjurkchieva (2010). The solid line represents a 1 Gyr isochrone model by Chabrier et al. (2000). |
| In the text | |
 |
Fig. 2. XMM-Newton light curves of BX Tri. Upper panel: OM UVW1 data. Lower panel: co-added EPIC light curves for the energy range 0.2–5 keV. The position of the primary and secondary eclipses based on the ephemerides given by Zhang et al. (2014) are marked by solid and dashed vertical red lines. Flaring regions excluded from the light curve analysis described in Sects. 4.1 and 4.2 are indicated as shaded areas. |
| In the text | |
 |
Fig. 3. Optical monitor light curve folded with the period given by Zhang et al. (2014). The solid red line represents the PHOEBE model and the residuals between the flux and the unshifted model are displayed in the bottom panel. Regions with flaring events were omitted. |
| In the text | |
 |
Fig. 4. Observed-calculated eclipse minima of BX Tri. Archival data from Zhang et al. (2014) are marked with green crosses, those from Lohr et al. (2013) and Lohr (priv. comm.) with black dots. The DWARF project data (Pribulla et al. 2012) are displayed as blue diamonds. The XMM-Newton OM minimum is highlighted in red. The best-fit quadratic function based on the visual data is displayed as a broken line and yields a period change of (−0.018 ± 0.003) s yr−1. |
| In the text | |
 |
Fig. 5. Complete EPIC PN light curve of BX Tri folded with the period derived by Zhang et al. (2014). The black dots represent the full light curve with a binning of 100 s (error bars were omitted for clarity), while the blue diamonds display the phase-binned light curve. |
| In the text | |
 |
Fig. 6. EPIC PN light curve of BX Tri folded with the period derived by Zhang et al. (2014) after flare removal. The black dots represent the filtered light curve with a binning of 100 s (error bars were omitted for clarity), while the blue diamonds show the phase-binned light curve. |
| In the text | |
 |
Fig. 7. Plasma temperatures (upper panel) and emission measures (lower panel) derived from time-resolved spectroscopy. The black diamonds represent the higher temperatures, the gray circles the lower temperatures of the two-temperature apec model fit. |
| In the text | |
 |
Fig. 8. Flaring event at t = 3.4 ks in the UVW1 filter (upper panel) and the X-ray regime (lower panel). The solid line in the lower panel represents the modeling of a Neupert-like effect according to Eq. (4). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.