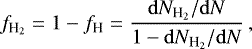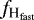| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 7 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201834008 | |
| Published online | 15 November 2018 | |
Production of atomic hydrogen by cosmic rays in dark clouds
1
INAF – Osservatorio Astrofisico di Arcetri,
Largo E. Fermi 5,
50125
Firenze,
Italy
e-mail: padovani@arcetri.astro.it
2
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstr. 1,
85741
Garching,
Germany
3
Scuola Normale Superiore,
Piazza dei Cavalieri 7,
56126
Pisa,
Italy
Received:
3
August
2018
Accepted:
11
September
2018
Context. Small amounts of atomic hydrogen, detected as absorption dips in the 21 cm line spectrum, are a well-known characteristic of dark clouds. The abundance of hydrogen atoms measured in the densest regions of molecular clouds can only be explained by the dissociation of H2 by cosmic rays.
Aims. We wish to assess the role of Galactic cosmic rays in the formation of atomic hydrogen, for which we use recent developments in the characterisation of the low-energy spectra of cosmic rays and advances in the modelling of their propagation in molecular clouds.
Methods. We modelled the attenuation of the interstellar cosmic rays that enter a cloud and computed the dissociation rate of molecular hydrogen that is due to collisions with cosmic-ray protons and electrons as well as fast hydrogen atoms. We compared our results with the available observations.
Results. The cosmic-ray dissociation rate is entirely determined by secondary electrons produced in primary ionisation collisions. These secondary particles constitute the only source of atomic hydrogen at column densities above ~1021 cm−2. We also find that the dissociation rate decreases with column density, while the ratio between the dissociation and ionisation rates varies between about 0.6 and 0.7. From comparison with observations, we conclude that a relatively flat spectrum of interstellar cosmic-ray protons, such as suggested by the most recent Voyager 1 data, can only provide a lower bound for the observed atomic hydrogen fraction. An enhanced spectrum of low-energy protons is needed to explain most of the observations.
Conclusions. Our findings show that a careful description of molecular hydrogen dissociation by cosmic rays can explain the abundance of atomic hydrogen in dark clouds. An accurate characterisation of this process at high densities is crucial for understanding the chemical evolution of star-forming regions.
Key words: dust, extinction / ISM: clouds / atomic processes / molecular processes
© ESO 2018
1 Introduction
The formation of molecular hydrogen occurs on dust grains in molecular clouds through the reaction between two hydrogen atoms. Because this is an exothermic process, H2 is then released into the gas phase. Depending on the position in the cloud (or on the amount of visual extinction measured inward from the cloud edge), two processes determine the destruction of H2 and the restoration of the atomic form: photodissociation that is due to interstellar (hereafter IS) UV photons, and dissociation due to cosmic rays (hereafter CRs). In the diffuse part of molecular clouds, UV photons regulate the abundance of atomic hydrogen by dissociating H2, while in the densest parts, IS UV photons are blocked by dust absorption as well as by H2 line absorption (Hollenbach et al. 1971). In the deepest parts of the cloud, CRs dominate the destruction of molecular hydrogen.
A wealth of studies has been carried out to characterise the origin of the atomic hydrogen component in dense environments (e.g. McCutcheon et al. 1978; van der Werf et al. 1988; Montgomery et al. 1995; Li & Goldsmith 2003; Goldsmith & Li 2005), but the rate of CR dissociation was always assumed to be constant (i.e., independent of the position in the cloud) or was simply neglected. In this paper, we wish to explore the role of CRs in more detail, especially after the latest data release of the Voyager 1 spacecraft (Cummings et al. 2016), which showed that the measured proton and electron fluxes are not able to explain the values of the CR ionisation rate estimated in diffuse clouds (e.g. Indriolo et al. 2015; Phan et al. 2018). In our previous work (e.g. Padovani et al. 2009, 2013, 2018; Padovani & Galli 2013; Ivlev et al. 2015) we postulated the presence of a low-energy component in the IS CR proton spectrum, with which it is possible to recover the high ionisation rates observed in diffuse clouds.
We treat a cloud as a semi-infinite slab. This simplification is completely justified for our purposes for the following reasons. First, attenuation of IS UV photons occurs in a thin gas layer near the cloud surface (with a visual extinction of AV ≈ 1−3 mag), that is, at column densities much lower than those characterising the line-of-sight thickness of a cloud. Second, CRs propagate through a cloud along the local magnetic field. The latter assumption is always valid since the Larmor radius of sub-relativistic CRs is much smaller than any characteristic spatial scale of the cloud (Padovani & Galli 2011) and the correlation length of the magnetic field (Houde et al. 2009). Therefore, regardless of the field geometry, we can measure the coordinate along the local field line and treat this as a one-dimensional problem (Padovani et al. 2018). The CR ionisation rate is then a function of the effective column density, measured along the field line. To facilitate the presentation of our results, we assume the line-of-sight and the effective column densities to be the same. These considerations can be generalised to a slab of a finite thickness by adding IS particles that enter the cloud from the opposite side; however, given a strong attenuation, this addition is only important for clouds with column densities of ≈ 1022 cm−2 or lower (increasing the ionisation and dissociation rates in the cloud centre by up to a factor of 2).
The paper is organised as follows: in Sect. 2, we discuss the main processes of H2 dissociation by CR protons, electrons, and fast hydrogen atoms, and compute the resulting dissociation rate as a function of the column density, in Sect. 3, we present equations to compute the fractions of atomic and molecular hydrogen, in Sect. 4, we compare our theoretical findings with available observations, and in Sect. 5, we discuss implications for our outcomes and summarise the most important results.
2 CR dissociation reactions with H2
We considered dissociation processes induced by CR primary and secondary electrons, CR protons, and fast hydrogen atoms colliding with molecular hydrogen. A schematic diagram of different dissociation paths is depicted in Fig. 1.
 |
Fig. 1 Dissociation diagram showing the three main processes of atomic hydrogen production. Labels “diss” and “e.c.” refer to dissociation and electron capture, respectively. |
2.1 Electron impact
Electrons can produce atomic hydrogen by exciting five electronic states of the H2 triplet (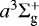 ,
, 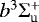 , c3 Πu,
, c3 Πu, 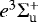 , and d3 Πu), followed by dissociation. While the radiativedecay from the state
, and d3 Πu), followed by dissociation. While the radiativedecay from the state 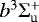 is fully dissociative, the decay from
is fully dissociative, the decay from 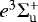 contributes to dissociation at 20%, and dissociation from the other states is negligible. There is also a contribution from the H2 singlet state, but the respective cross section peaks at about 40−50 eV with a maximum value of 3.02 × 10−18 cm2, which is a factor ≈20 lower than the peak value of the triplet-state cross section. Thus, the dissociation cross section by electron impact is given by
contributes to dissociation at 20%, and dissociation from the other states is negligible. There is also a contribution from the H2 singlet state, but the respective cross section peaks at about 40−50 eV with a maximum value of 3.02 × 10−18 cm2, which is a factor ≈20 lower than the peak value of the triplet-state cross section. Thus, the dissociation cross section by electron impact is given by
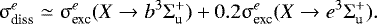 (1)
(1)
2.2 Proton impact
Atomic hydrogen can also be produced by protons, by direct dissociation of H2 from the vibrational state v = 0. The H2 excitation cross sections by electrons, 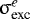 , and the dissociation cross section by protons,
, and the dissociation cross section by protons, 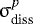 , have been parameterised by Janev et al. (2003) as
, have been parameterised by Janev et al. (2003) as
![\begin{equation*}\upsigma(E) = \frac{a}{E^{\upalpha_{1}}}\left[1-\left(\frac{E_{0}}{E}\right)^{\upalpha_{2}}\right]^{\upalpha_{3}}\times{10^{-16}~\textrm{cm}^{2}}\,, \end{equation*}](/articles/aa/full_html/2018/11/aa34008-18/aa34008-18-eq9.png) (2)
(2)
with the energy E in eV. In Table 1, we list the values of factor a, exponents α1,2,3, and the energy threshold E0 for the respective cross sections.
2.3 Effect of fast hydrogen atoms
Figure 2 shows that dissociation cross sections peak at very low energy, about 8 and 15 eV for protons and electrons, respectively, which means that the processes that regulate the distributions of different species in this energy range require close study. In Appendix A, we demonstrate that CR protons are efficiently neutralised at low energies because of electron capture (see also Chabot 2016). This generates a flux of fast H atoms (hereafter Hfast) that in turn creates fast H+ ions (secondary CR protons) through reaction (A.3). We computed the equilibrium distributions of protons and Hfast atoms, finding that below ≈ 104 eV, less than 10% of (non-molecular) hydrogen is in the form of H+ (see Fig. A.2), so that the dissociation by Hfast (reaction A.4) must be taken into account. The corresponding cross section, 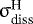 (Dove & Mandy 1986; Esposito & Capitelli 2009) is also plotted in Fig. 2.
(Dove & Mandy 1986; Esposito & Capitelli 2009) is also plotted in Fig. 2.
 |
Fig. 2 Energy dependence of the dissociation cross sections by protons (blue), electrons (red), and fast hydrogen atoms (green) colliding with molecular hydrogen. |
2.4 CR dissociation rate
The rate of dissociation due to primary and secondary CRs and Hfast atoms, occurring at the total column density N, is given by
 (3)
(3)
where jk is the differential flux of CR particles k, 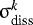 is the dissociation cross section, and k = p, e, H_fast. In the semi-infinite slab geometry, the factor ℓ is equal to 1 for primary CRs and Hfast, and equal to 2 for secondary electrons (because the latter are produced isotropically). The final expression for the dissociation rate is obtained by averaging over the pitch-angle distribution of the incident CRs (see Eq. (45) in Padovani et al. 2018).
is the dissociation cross section, and k = p, e, H_fast. In the semi-infinite slab geometry, the factor ℓ is equal to 1 for primary CRs and Hfast, and equal to 2 for secondary electrons (because the latter are produced isotropically). The final expression for the dissociation rate is obtained by averaging over the pitch-angle distribution of the incident CRs (see Eq. (45) in Padovani et al. 2018).
In the following we assume the same IS CR proton and electron spectra as in Ivlev et al. (2015) and Padovani et al. (2018). For CR protons we adopt two different models: the first, model  , is an extrapolation of the Voyager 1 observations to lower energies; the second, model
, is an extrapolation of the Voyager 1 observations to lower energies; the second, model 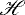 , is characterised by an enhanced flux of low-energy protons with respect to Voyager 1 data. Models
, is characterised by an enhanced flux of low-energy protons with respect to Voyager 1 data. Models 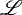 and
and 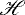 can be regarded as the lower and upper bound, respectively, of the average Galactic CR proton spectrum, since the corresponding CR ionisation rates encompass the values estimated from observations in diffuse clouds (e.g. Indriolo et al. 2015; Neufeld & Wolfire 2017). For CR electrons, we use a single model based on the latest Voyager results, which show that the electron flux varies at E ≲ 100 MeV as ∝ E−1.3 (Cummings et al. 2016). Figure 3 shows the partial contributions to the dissociation rate of primary CR protons and electrons, Hfast atoms, and secondary electrons. The latter is computed following Eq. (16) in Ivlev et al. (2015). In Fig. 3, we also show the corresponding visual extinction, AV = 5.32 × 10−22 (N∕cm−2). Clearly, ζdiss is entirely dominated by low-energy secondary electrons that are produced during the propagation of primary CRs.
can be regarded as the lower and upper bound, respectively, of the average Galactic CR proton spectrum, since the corresponding CR ionisation rates encompass the values estimated from observations in diffuse clouds (e.g. Indriolo et al. 2015; Neufeld & Wolfire 2017). For CR electrons, we use a single model based on the latest Voyager results, which show that the electron flux varies at E ≲ 100 MeV as ∝ E−1.3 (Cummings et al. 2016). Figure 3 shows the partial contributions to the dissociation rate of primary CR protons and electrons, Hfast atoms, and secondary electrons. The latter is computed following Eq. (16) in Ivlev et al. (2015). In Fig. 3, we also show the corresponding visual extinction, AV = 5.32 × 10−22 (N∕cm−2). Clearly, ζdiss is entirely dominated by low-energy secondary electrons that are produced during the propagation of primary CRs.
In previous work (e.g. Li & Goldsmith 2003; Goldsmith & Li 2005), ζdiss has usually been assumed to be equal to the CR ionisation rate, ζion (which in turn did not depend on N). In Fig. 4 we show that ζdiss and ζion exhibit very similar behaviour: they decrease monotonically with N; the ratio ζdiss∕ζion can be as low as ≈ 0.63 at low column densities (N ≈ 1019 cm−2), depending on the assumed spectrum of IS CR protons. This ratio rapidly approaches the constant value of ≈ 0.7, and at N ≳ 1022 cm−2 becomes independent of the column density and the IS proton spectrum. The values of ζdiss and ζion are comparable because secondary electrons provide the main contribution to both processes. We note that the ionisation rate was computed by taking into account the presenceof Hfast atoms (see Eq. (B.1)) that contribute to the production of 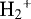 ions through reaction (A.2) at energies below ≈104 eV. However, this process is only marginally important for model
ions through reaction (A.2) at energies below ≈104 eV. However, this process is only marginally important for model 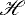 below N ≈ 1021 cm−2, and is always negligible for model
below N ≈ 1021 cm−2, and is always negligible for model 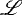 (see Appendix B). Figure 4 also shows the photodissociation rate, ζpd = D0χa, computed following Draine (2011).
(see Appendix B). Figure 4 also shows the photodissociation rate, ζpd = D0χa, computed following Draine (2011).
 |
Fig. 3 CR dissociation rate for models |
 |
Fig. 4 Top panel: CR dissociation rates (ζdiss, solid lines), CR ionisation (ζion, dashed lines), and photodissociation (ζpd, purple dotted line) for models |
3 Balance equation
Goldsmith & Li (2005) and Goldsmith et al. (2007) presented a time-dependent modelling of the H abundance in molecular clouds and introduced the concept of the atomic-to-molecular hydrogen ratio, 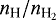 , as a clock of the evolutionary stage of a cloud. In particular, Goldsmith & Li (2005) modelled observations of
, as a clock of the evolutionary stage of a cloud. In particular, Goldsmith & Li (2005) modelled observations of 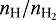 in five dark clouds, concluding that the characteristic time required to reach a steady-state
in five dark clouds, concluding that the characteristic time required to reach a steady-state 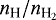 ratio is close to the cloud ages. In the following, we consider the steady-state solution, keeping in mind that time dependence may still affect the interpretation of the observational data (see Sect. 4).
ratio is close to the cloud ages. In the following, we consider the steady-state solution, keeping in mind that time dependence may still affect the interpretation of the observational data (see Sect. 4).
In steady state, the balance between H2 formation and destruction processes gives
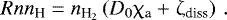 (4)
(4)
Here, 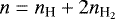 is the total volume density of hydrogen, R is the H2 formation rate coefficient, D0 is the unattenuated photodissociation rate, χa is the attenuation factor for dust absorption and H2-self shielding, and ζdiss is the CR dissociation rate. In the following we assume R = 3 × 10−17 cm3 s−1 (Jura 1975) and D0 = 2 × 10−11G0 s−1 (Draine 2011, taking into account a semi-infinite slab geometry), where G0 is the far-UV (FUV) radiation field in Habing units (Habing 1968). Unless specified otherwise, we adopt G0 = 1. The attenuation factor is usually written in the form
is the total volume density of hydrogen, R is the H2 formation rate coefficient, D0 is the unattenuated photodissociation rate, χa is the attenuation factor for dust absorption and H2-self shielding, and ζdiss is the CR dissociation rate. In the following we assume R = 3 × 10−17 cm3 s−1 (Jura 1975) and D0 = 2 × 10−11G0 s−1 (Draine 2011, taking into account a semi-infinite slab geometry), where G0 is the far-UV (FUV) radiation field in Habing units (Habing 1968). Unless specified otherwise, we adopt G0 = 1. The attenuation factor is usually written in the form
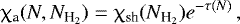 (5)
(5)
where 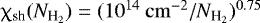 is the H2 self-shielding factor (Tielens 2010, valid for
is the H2 self-shielding factor (Tielens 2010, valid for 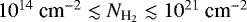 ) and τ(N) = σgN is the dust attenuation. Here,
) and τ(N) = σgN is the dust attenuation. Here, 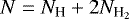 is the total column density of hydrogen and σg = 1.9 × 10−21 cm2 is the average value of the FUV dust grain absorption cross section for solar metallicity (Draine 2011).
is the total column density of hydrogen and σg = 1.9 × 10−21 cm2 is the average value of the FUV dust grain absorption cross section for solar metallicity (Draine 2011).
Assuming nH∕n = dNH∕dN and  , Eq. (4) becomes
, Eq. (4) becomes
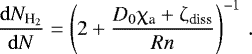 (6)
(6)
The fractions of atomic and molecular hydrogen can be expressed as
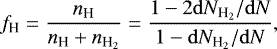 (7)
(7)
respectively. In the next section we describe in detail all the processes that contribute to the dissociation of molecular hydrogen.
4 Comparison with observations
Li & Goldsmith (2003) performed a survey of dark clouds in the Taurus-Perseus region, and reported the detection of H I narrow self-absorption features. This allowed them to compute the atomic and molecular hydrogen fraction (Eqs. (7) and (8)). They concluded that a relevant fraction of atomic hydrogen is mixed with H2 in the densest part of a cloud that is shielded from the IS UV flux.
At high column densities typical of dark clouds, the attenuation factor χa in Eq. (4) is so large that the UV photodissociation is inefficient, and the observed  ratios can only be explained by CR dissociation. In Sect. 2.4, we showed that ζdiss ≈ 0.7ζion at typical column densities of dark clouds (≈ 1022 cm−2); more importantly, ζdiss is not constant, but decreases with N (e.g. Padovani et al. 2009, 2018).
ratios can only be explained by CR dissociation. In Sect. 2.4, we showed that ζdiss ≈ 0.7ζion at typical column densities of dark clouds (≈ 1022 cm−2); more importantly, ζdiss is not constant, but decreases with N (e.g. Padovani et al. 2009, 2018).
We computed the fraction of atomic and molecular hydrogen expected at different column densities (Eqs. (7) and (8)) to evaluate the effect of CR dissociation on the abundance of atomic hydrogen in dark clouds. For the total volume density n in Eq. (4), we used the average value of 5 × 103 cm−3 computed by Li & Goldsmith (2003), to which we added an error of 2.6 × 103 cm−3 (the standard deviation for the observed values).
Figure 5 shows the comparison between our models and the observations by Li & Goldsmith (2003). As expected, UV photodissociation alone cannot explain the observed 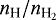 ratios because of the attenuation at high column densities. More notably, a CR spectrum based on the extrapolation of the Voyager data (model
ratios because of the attenuation at high column densities. More notably, a CR spectrum based on the extrapolation of the Voyager data (model 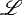 ) fails to reproduce the majority of the observations, and only a spectrum enhanced at low energies (such as model
) fails to reproduce the majority of the observations, and only a spectrum enhanced at low energies (such as model 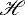 ) can explain this.The latter fact corroborates the need of a low-energy tail in the IS CR flux of protons, also required to explain the high CR ionisation rates in diffuse clouds (e.g. Padovani et al. 2009; Indriolo et al. 2015).
) can explain this.The latter fact corroborates the need of a low-energy tail in the IS CR flux of protons, also required to explain the high CR ionisation rates in diffuse clouds (e.g. Padovani et al. 2009; Indriolo et al. 2015).
The large spread in the observed values of fH probably reflects a broad variety of environments in dark clouds, including variations in the density and IS UV radiation field, for instance see e.g. Bialy & Sternberg (2016). In this work we assume a H2 formation rate of R = 3 × 10−17 cm3 s−1 (see Sect. 3). We note that Li & Goldsmith (2003) used R = 6.5 × 10−18 cm3 s−1, which is a factor of ≈5 smaller thanour value. A lower R implies a lower ionisation rate needed to reproduce the observations. This explains why, using a constant dissociation rate equal to the ionisation rate of 3 × 10−17 s−1, they found fH ≈ 1.5 × 10−3. However, R is strongly dependent on the condition of each cloud; for example, in photodissociation regions, where the large abundance of polycyclic aromatic hydrocarbons favours the formation of H2, R can increase by one order of magnitude (Habart et al. 2004). Variations in the grain size distribution may also change the value of R by a factor of ~ 3 (Goldsmith & Li 2005). Draine (2011) suggests 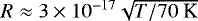 cm3 s−1, but even assuming T as low as 10 K, we find fH ≈ 10−3 at N ≈ 1022 cm−2 for a Voyager-like spectrum (model
cm3 s−1, but even assuming T as low as 10 K, we find fH ≈ 10−3 at N ≈ 1022 cm−2 for a Voyager-like spectrum (model  ). As a consequence, a higher flux of low-energy CR protons (model
). As a consequence, a higher flux of low-energy CR protons (model  ) is still needed to explain the higher
) is still needed to explain the higher  ratios. This conclusion remains unchanged even if G0 is increased by up to two orders of magnitude, since the UV field is exponentially attenuated in the range of column densities of the observed dark clouds (2 × 1021 cm−2 ≲ N ≲ 2 × 1022 cm−2).
ratios. This conclusion remains unchanged even if G0 is increased by up to two orders of magnitude, since the UV field is exponentially attenuated in the range of column densities of the observed dark clouds (2 × 1021 cm−2 ≲ N ≲ 2 × 1022 cm−2).
We also recall that as mentioned in Sect. 3, some of the observed clouds may not necessarily have reached a steady-state  ratio (Goldsmith & Li 2005; Goldsmith et al. 2007). In this case, model
ratio (Goldsmith & Li 2005; Goldsmith et al. 2007). In this case, model  could not be completely ruled out because if these clouds are younger, they will have a higher
could not be completely ruled out because if these clouds are younger, they will have a higher 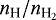 ratio than predicted by our steady-state assumption.
ratio than predicted by our steady-state assumption.
 |
Fig. 5 Atomic hydrogen fraction vs. the total column density of hydrogen (bottom scale) and visual extinction (top scale). Observations from Li & Goldsmith (2003) are shown as solid orange circles. Coloured stripes represent our results for the case of photodissociation only (purple), and models |
5 Discussion and conclusions
Dissociation of H2 into atomic hydrogen by CRs in dark clouds can have important consequences for the chemical evolution of dense regions in the clouds. Atomic hydrogen is the most mobile reactive species on the surface of bare dust grains and icy mantles, and therefore it is crucial to accurately determine its abundance. The higher fH values predicted in this work imply a more efficient hydrogenation of molecular species on grain surfaces. In particular, hydrogenation of CO, which freezes out onto grains at densities above a few 104 cm−3 (e.g. Caselli et al. 1999), follows the sequence (e.g. Tielens & Hagen 1982)
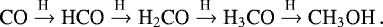 (9)
(9)
This leads to efficient production of formaldehyde (H2CO) and methanol (CH3OH; Vasyunin et al. 2017) on very short timescales. Hence, even if dissociation by energetic particles takes place, CO cannot be returned to the gas phase because it is rapidly converted into methanol. If the products of dissociation do not move very far from their formation site (Shingledecker et al. 2018), methanol is ejected from the surface because the exothermicity of chemical reactions (9) is partially channelled into kinetic energy through a process known as reactive desorption (Garrod et al. 2007). On the other hand, ammonia (NH3), which is synthesised onto grains through the hydrogenation sequence (e.g. Hiraoka et al. 1995; Fedoseev et al. 2015)
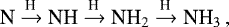 (10)
(10)
can, in principle, return to the gas phase upon surface dissociation followed by reactive desorption. These considerations could help in explaining the observational evidence that NH3 (unlike CO) does not appear to deplete towards the central regions of dense cores, despite its high binding energy. To verify this hypothesis, the consequences of an enhanced abundance of atomic hydrogen in chemical models need to be evaluated.
We point out that CR dissociation is not only limited to H2, but could occur for other molecular species as well, both in the gas phase and on/in ices mantles, with potentially significant consequences in the chemical composition of dense cloud cores and dark clouds.
To summarise, we studied the role of CRs in determining the fractional abundance of atomic hydrogen in dark clouds. The main results are listed below.
- (i)
The CR dissociation rate, ζdiss, is primarily determined by secondary electrons produced during the primary CR ionisation process. These secondary electrons can efficiently dissociate H2 and represent the only source of atomic hydrogen at column densities higher than ≈1021 cm−2, regulating the
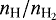 ratio in dark clouds.
ratio in dark clouds. - (ii)
ζdiss entering the balance Eq. (4) is not equal to the ionisation rate ζion, as assumed in some previous work. We find that the ratio ζdiss∕ζion varies between ≈0.63 and ≈0.7, depending on the column density range, while ζion is a decreasing function of the column density.
- (iii)
Even given the uncertainties in the values of H2 formation rate, temperature, total hydrogen volume density, and IS UV radiation field for each cloud, only a CR proton spectrum enhanced at low energies (such as our model
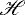 ) is capable of reproducing the upper values of measured fH under the assumption of steady state. We note that neither model
) is capable of reproducing the upper values of measured fH under the assumption of steady state. We note that neither model 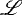 nor model
nor model 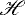 is able toreproduce the entire set of observational data: the spread in the values of fH at any given column density must be attributed to time dependence or to individual characteristics of each cloud. For example, tangled magnetic field lines and/or higher volume densities would result in a stronger CR attenuation and thereforein a lower fH.
is able toreproduce the entire set of observational data: the spread in the values of fH at any given column density must be attributed to time dependence or to individual characteristics of each cloud. For example, tangled magnetic field lines and/or higher volume densities would result in a stronger CR attenuation and thereforein a lower fH. - (iv)
An accurate description of H2 dissociation in dense environments is essential because many chemical processes (such as CO hydrogenation and its depletion degree onto dust grains, or formation of complex organic molecules) critically depend on the abundance of atomic hydrogen.
Acknowledgements
The authors wish to thank the referee, Paul Goldsmith, for his careful reading of the manuscript and insightful comments that considerably helped to improve the paper. M.P. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 664931. A.F. acknowledges support from the ERC Advanced Grant INTERSTELLAR H2020/740120. The authors thank Fabrizio Esposito for sending us his results for the H2 dissociation cross section by atomic hydrogen impact.
Appendix A Equilibrium distribution of protons and Hfast atoms at low energies
Because of the process of electron capture at low energies, CR protons interacting with H2 are efficiently neutralised,
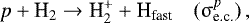 (A.1)
(A.1)
creating fast H atoms. In parentheses we list the cross section of the respective process. At the same time, Hfast atoms reacting with H2 yield

The electron capture by protons, reaction (A.1), and the reaction of Hfast self-ionisation, reaction (A.3), are catastrophic processes, since the respective projectile particles disappear after such collisions. The reactions of H2 ionisation and dissociation by Hfast atoms, reactions (A.2) and (A.4), respectively, are continuous loss processes, where the projectile kinetic energy decreases only slightly after each collision. The efficiency of continuous energy losses is generally characterised by the projectile stopping range (see, e.g. Padovani et al. 2009).
For our calculations,  is taken from Rudd et al. (1983),
is taken from Rudd et al. (1983), 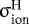 is adopted from Phelps (1990) and Kunc & Soon (1991),
is adopted from Phelps (1990) and Kunc & Soon (1991), 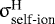 is computed by Stier & Barnett (1956), van Zyl et al. (1981), and Phelps (1990), and
is computed by Stier & Barnett (1956), van Zyl et al. (1981), and Phelps (1990), and 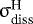 is taken from Dove & Mandy (1986) and Esposito & Capitelli (2009). In Fig. A.1, we plot the cross sections and the inverse of the proton stopping range,
is taken from Dove & Mandy (1986) and Esposito & Capitelli (2009). In Fig. A.1, we plot the cross sections and the inverse of the proton stopping range, 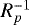 , versus the respective projectile energy. We see that
, versus the respective projectile energy. We see that  is much larger than
is much larger than 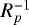 for 102 eV ≲ E ≲ 105 eV, which implies that continuous loss processes cannot significantly affect the balance between protons and Hfast atoms at these energies. The equilibrium ratio of the Hfast and proton fluxes is then given by
for 102 eV ≲ E ≲ 105 eV, which implies that continuous loss processes cannot significantly affect the balance between protons and Hfast atoms at these energies. The equilibrium ratio of the Hfast and proton fluxes is then given by
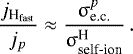 (A.5)
(A.5)
 |
Fig. A.1 Cross sections of processes governing equilibrium distributions of protons and fast hydrogen atoms at low energies: electron capture by p (A.1, dotted blue line), ionisation of H2 by Hfast (A.2, short dashed orange line), self-ionisation of Hfast (A.3, long dashed red line), and H2 dissociation by Hfast (A.4, solid green line). The inverse of the proton stopping range, |
This allows us to calculate the fractions of Hfast atoms,
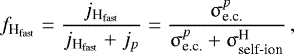 (A.6)
(A.6)
and protons,  . Figure A.2 shows that for energies below ≈104 eV, only less than 10% of non-molecular hydrogen is in the form of protons. This means that H2 ionisation at these energies is dominated by Hfast atoms via reaction (A.2).
. Figure A.2 shows that for energies below ≈104 eV, only less than 10% of non-molecular hydrogen is in the form of protons. This means that H2 ionisation at these energies is dominated by Hfast atoms via reaction (A.2).
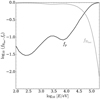 |
Fig. A.2 Fraction of non-molecular hydrogen in neutral ( |
Appendix B Ionisation by Hfast atoms
As shown in Appendix A, the ionisation at energies below ≈ 104 eV is mostly driven by Hfast atoms. To take this effect into account, we use the following expression for the H2 ionisation rate by CR protons:
![\begin{eqnarray*}\upzeta_{\textrm{ion}}^{p}(N)&=&2\uppi\int \bigg\{j_{p}(E,N)\left[\upsigma^{p}_{\textrm{ion}}(E)+\upsigma^{p}_{\textrm{e.c.}}(E)\right]\\\nonumber &&+j_{{\textrm{H}_{\textrm{fast}}}}(E,N)\upsigma^{\textrm{H}}_{\textrm{ion}}(E)\bigg\}\mathrm{d} E\,, \end{eqnarray*}](/articles/aa/full_html/2018/11/aa34008-18/aa34008-18-eq62.png) (B.1)
(B.1)
where 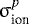 is the H2 ionisation cross section by proton impact (Rudd et al. 1985). It turns out, however, that the difference between the ionisation rates computed from Eq. (B.1) taking into account Eq. (A.5) and assuming
is the H2 ionisation cross section by proton impact (Rudd et al. 1985). It turns out, however, that the difference between the ionisation rates computed from Eq. (B.1) taking into account Eq. (A.5) and assuming 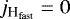 is very small: for N≈ 1019 cm−2, the difference is ≈5% and ≈40% for models
is very small: for N≈ 1019 cm−2, the difference is ≈5% and ≈40% for models 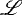 and
and 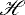 , respectively. At higher column densities, it rapidly decreases and becomes negligible for both models above ≈ 1021 cm−2. This result justifies the assumption
, respectively. At higher column densities, it rapidly decreases and becomes negligible for both models above ≈ 1021 cm−2. This result justifies the assumption  made previously for calculating the ionisation.
made previously for calculating the ionisation.
References
- Bialy, S., & Sternberg, A. 2016, ApJ, 822, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Chabot, M. 2016, A&A, 585, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cummings, A. C., Stone, E. C., Heikkila, B. C., et al. 2016, ApJ, 831, 18 [Google Scholar]
- Dove, J. E., & Mandy, M. E. 1986, ApJ, 311, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Esposito, F., & Capitelli, M. 2009, J. Phys. Chem. A, 113, 15307 [CrossRef] [Google Scholar]
- Fedoseev, G., Ioppolo, S., Zhao, D., Lamberts, T., & Linnartz, H. 2015, MNRAS, 446, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., & Li, D. 2005, ApJ, 622, 938 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Li, D., & Krčo M. 2007, ApJ, 654, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., Walmsley, C. M., & Pineau des Forêts, G. 2004, A&A, 414, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 20, 120 [NASA ADS] [Google Scholar]
- Hiraoka, K., Yamashita, A., Yachi, Y., et al. 1995, ApJ, 443, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., Werner, M. W., & Salpeter, E. E. 1971, ApJ, 163, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Houde, M., Vaillancourt, J. E., Hildebrand, R. H., Chitsazzadeh, S., & Kirby, L. 2009, ApJ, 706, 1504 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Ivlev, A. V., Padovani, M., Galli, D., & Caselli, P. 2015, ApJ, 812, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Janev, R. K., Reiter, D., & Samm, U. 2003, Collision Processes in Low-Temperature Hydrogen Plasmas (Jlich, Germany: Forschungszentrum, Zentralbibliothek), 188 [Google Scholar]
- Jura, M. 1975, ApJ, 197, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Kunc, J. A., & Soon, W. H. 1991, J. Chem. Phys., 95, 5738 [NASA ADS] [CrossRef] [Google Scholar]
- Li, D., & Goldsmith, P. F. 2003, ApJ, 585, 823 [NASA ADS] [CrossRef] [Google Scholar]
- McCutcheon, W. H., Shuter, W. L. H., & Booth, R. S. 1978, MNRAS, 185, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, A. S., Bates, B., & Davies, R. D. 1995, MNRAS, 273, 449 [NASA ADS] [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2017, ApJ, 845, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., & Galli, D. 2011, A&A, 530, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., & Galli, D. 2013, in Cosmic Rays in Star-Forming Environments, eds. D. F. Torres, & O. Reimer, Astrophysics and Space Science Proceedings, 34, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Hennebelle, P., & Galli, D. 2013, A&A, 560, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Ivlev, A. V., Galli, D., & Caselli, P. 2018, A&A, 614, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phan, V. H. M., Morlino, G., & Gabici, S. 2018, MNRAS, 480, 5167 [NASA ADS] [Google Scholar]
- Phelps, A. V. 1990, J. Phys. Chem. Ref. Data, 19, 653 [NASA ADS] [CrossRef] [Google Scholar]
- Rudd, M. E., Goffe, T. V., Dubois, R. D., Toburen, L. H., & Ratcliffe, C. A. 1983, Phys. Rev. A, 28, 3244 [NASA ADS] [CrossRef] [Google Scholar]
- Rudd, M. E., Kim, Y.-K., Madison, D. H., & Gallagher, J. W. 1985, Rev. Mod. Phys., 57, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Shingledecker, C. N., Tennis, J., Le Gal, R., & Herbst, E. 2018, ApJ, 861, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Stier, P. M., & Barnett, C. F. 1956, Phys. Rev., 103, 896 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2010, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [Google Scholar]
- van der Werf, P. P., Goss, W. M., & Vanden Bout P. A. 1988, A&A, 201, 311 [NASA ADS] [Google Scholar]
- van Zyl, B., Le, T. Q., & Amme, R. C. 1981, J. Chem. Phys., 74, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Vasyunin, A. I., Caselli, P., Dulieu, F., & Jiménez-Serra, I. 2017, ApJ, 842, 33 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Dissociation diagram showing the three main processes of atomic hydrogen production. Labels “diss” and “e.c.” refer to dissociation and electron capture, respectively. |
| In the text | |
 |
Fig. 2 Energy dependence of the dissociation cross sections by protons (blue), electrons (red), and fast hydrogen atoms (green) colliding with molecular hydrogen. |
| In the text | |
 |
Fig. 3 CR dissociation rate for models |
| In the text | |
 |
Fig. 4 Top panel: CR dissociation rates (ζdiss, solid lines), CR ionisation (ζion, dashed lines), and photodissociation (ζpd, purple dotted line) for models |
| In the text | |
 |
Fig. 5 Atomic hydrogen fraction vs. the total column density of hydrogen (bottom scale) and visual extinction (top scale). Observations from Li & Goldsmith (2003) are shown as solid orange circles. Coloured stripes represent our results for the case of photodissociation only (purple), and models |
| In the text | |
 |
Fig. A.1 Cross sections of processes governing equilibrium distributions of protons and fast hydrogen atoms at low energies: electron capture by p (A.1, dotted blue line), ionisation of H2 by Hfast (A.2, short dashed orange line), self-ionisation of Hfast (A.3, long dashed red line), and H2 dissociation by Hfast (A.4, solid green line). The inverse of the proton stopping range, |
| In the text | |
 |
Fig. A.2 Fraction of non-molecular hydrogen in neutral ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.