| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 9 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201834243 | |
| Published online | 24 October 2018 | |
Letter to the Editor
Linear radio size evolution of μJy populations
1 INAF – Istituto di Radioastronomia, Via Gobetti 101, 40129 Bologna, Italy
e-mail: bondi@ira.inaf.it
2 INAF – Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, Via Gobetti 93/3, 40129 Bologna, Italy
3 Department of Physics, Faculty of Science, University of Zagreb, Bijenička cesta 32, 10002 Zagreb, Croatia
4 Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
5 Argelander Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
6 International Max Planck Research School of Astronomy and Astrophysics at the Universities of Bonn and Cologne, Bonn, Germany
7 National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA, 22903 USA
Received:
14
September
2018
Accepted:
5
October
2018
We investigate the linear radio size properties of the μJy populations of radio-selected active galactic nuclei (AGN) and star-forming galaxies (SFGs) using a multi-resolution catalog based on the original VLA-COSMOS 3 GHz 0.″75 resolution mosaic and its convolved images (up to a resolution of 2.″2). The final catalog contains 6399 radio sources above a 3 GHz total flux density of ST > 20 μJy (median ⟨ST⟩=37 μJy), with redshift information (median ⟨z⟩=1.0), and multi-wavelength classification as SFGs, radio-excess AGN (RX-AGN), or non-radio-excess AGN (NRX-AGN). RX-AGN are those whose radio emission exceeds the star formation rate derived by fitting the global spectral energy distribution. We derive the evolution with redshift and luminosity of the median linear sizes of each class of objects. We find that RX-AGN are compact, with median sizes of ∼1–2 kpc and increasing with redshift, corresponding to an almost constant angular size of 0.″25. NRX-AGN typically have radio sizes a factor of 2 larger than the RX-AGN. The median radio size of SFGs is about 5 kpc up to z ∼ 0.7, and it decreases beyond this redshift. Using luminosity-complete subsamples of objects, we separately investigate the effect of redshift and luminosity dependance. We compare the radio sizes of SFGs with those derived in the rest-frame far-infrared (FIR) and UV bands. We find that SFGs have comparable sizes (within 15%) in the radio and rest-frame FIR, while the sizes measured in the UV-band are systematically larger than the radio sizes.
Key words: galaxies: fundamental parameters / galaxies: active / galaxies: evolution / radio continuum: galaxies
© ESO 2018
1. Introduction
While the Hubble Space Telescope (HST) has revealed the morphological properties and sizes in the UV and optical rest-frame for galaxies up to redshift ∼7 (e.g., Ferguson et al. 2004; Hathi et al. 2008; Oesch et al. 2010; Ono et al. 2013; van der Wel et al. 2014; Shibuya et al. 2015), the radio size distribution in the submillijanksy (μJy) regime for different galaxy types is currently not well known. This information is crucial in several aspects. The determination of the linear radio size evolution as a function of redshift in star-forming galaxies (SFGs) traces the spatial extent of star formation through cosmic time; this is a key ingredient for understanding galaxy formation and evolution and, for instance, for testing the paradigm of inside-out growth (e.g., Mo et al. 1998). Moreover, given that one problem affecting the measurement of the UV/optical sizes of SFGs is the obscuration of the inner regions (e.g., Nelson et al. 2016), radio sizes provide complementary measurements that are not affected by obscuration. For active galactic nuclei (AGN), the size of the radio-emitting region provides information on the radio emission mechanisms in different types of AGN and is possibly related to the accretion efficiency of the central black hole. Distinguishing the contributions of the AGN and SF-related radio emission is critical for investigating the feedback mechanisms.
Furthermore, an accurate knowledge of the intrinsic radio size distribution is necessary to correct the observed differential source counts and luminosity functions for incompleteness due to the resolution bias (e.g., Bondi et al. 2003). Differential source counts derived from different surveys show a scatter that is larger than the quoted errors for flux densities ≲200 μJy (e.g., de Zotti et al. 2010; Padovani 2016), which, in addition to cosmic variance, is generally explained as being due to the different corrections applied to compensate for the resolution bias in different surveys (Condon 2007; Heywood et al. 2013). We can expect that SFGs and AGN have different radio size distributions and consequently different corrections for resolution bias, even in the same flux density range. This is also relevant for the predictions of the numbers of SFGs and AGN for future surveys with the Square Kilometer Array (SKA) and its precursors (e.g., Novak et al. 2018; Mancuso et al. 2017; Bonaldi et al. 2019).
The determination of radio sizes of μJy sources is challenging, and previous studies have suffered from small statistics, incomplete classification that did not separate SFGs from AGN, and a correlation between the estimated sizes and angular resolution.
For instance, Murphy et al. (2017) derived a median FWHM major axis of ∼0.″17 ± 0.″03 from a sample of 32 sources imaged with the Very Large Array (VLA) at 10 GHz with a resolution of ≃0.″22 and a sensitivity of 0.57 μJy beam−1. When the same image tapered to 1.″0 resolution is used, the median size increases to 0.″75 ± 0.″17 (see Table 2 in Murphy et al. 2017). The larger sizes of the sources derived from the tapered image can be due to the lower resolution, but for some sources, it is likely that faint extended emission is resolved out in the full resolution, while it is detected in the tapered image, as suggested by the comparison of the total flux densities at both resolutions. In the same field, Guidetti et al. (2017) used sensitive (σ ≃ 3 μJy beam−1) 5.5 GHz observations with a resolution of ∼0.″5 and obtained a catalog of 94 radio sources classified as AGN or SFGs using X-ray luminosity and IR colors, finding a median FWHM major axis of 0.″2–0.″3 for the AGN and 0.″8 for the SFGs. Recently, Cotton et al. (2018) derived the angular size distribution of μJy radio sources from a sample of ∼800 sources obtained from sensitive (σ ∼ 1 μJy beam−1) VLA observations at 3 GHz of the Lockman Hole with 3.″0 and 0.″66 resolutions. The angular sizes are estimated from the brightness ratio at the two resolutions, and should be regarded as equivalent to circular Gaussian FWHM. Cotton et al. (2018) find that the median size is ∼0.″3–0.″4 (see Table 4 in their paper).
This Letter presents for the first time the linear radio size properties and its redshift and luminosity evolution for a large sample (more than 6000) of μJy radio sources classified as AGN or SFGs.
2. A multi-resolution catalog of radio-selected SFGs and AGN
The 3 GHz multi-resolution (MR) catalog is compiled using the full-resolution (0.″75) catalog and catalogs obtained from radio images convolved to coarser resolutions. The MR catalog lists 6399 radio sources with flux densities above 20 μJy, a spectroscopic or photometric redshift, and a multi-wavelength classification as SFGs1 or AGN (Delvecchio et al. 2017; Smolčić et al. 2017a). AGN are further divided into radio-excess (RX) or non-radio-excess (NRX) sources. RX-AGN are those whose radio emission exceeds (by more than 3σ at any given redshift) the star formation rate (SFR) derived by fitting the global spectral energy distribution (Delhaize et al. 2017; hereafter D17). The total number of sources in each class is listed in Table A.2. The details on how the MR catalog is obtained are given in Appendix A, and the procedure used to derive the angular size of the radio sources is described in Appendix B.
3. Linear size evolution of μJy populations
Sources in each class (SFG, NRX-AGN, and RX-AGN) were binned in redshift and 3 GHz total luminosity (L3 GHz), and for each bin, the Kaplan-Meier median estimator of the FWHM linear size was derived using the ASURV statistical package that implements the methods described by Feigelson & Nelson (1985) and Isobe et al. (1986) to properly handle censored data. The median sizes with the 1σ errors are reported in Tables D.1 and D.2 and are shown in Fig. 1.
 |
Fig. 1. Median linear size as a function of redshift (left panel) and 3 GHz radio luminosity (right panel) for the different classes of μJy radio sources (see the inset legend and text for details). The dashed lines in the left panel correspond to a constant angular size of 0.″25 (lower line) and 0.″45 (upper line). |
The RX- and NRX-AGN have significantly different sizes of up to z ∼ 2.5 or L3 GHz ∼ 1024 W Hz−1. RX-AGN are systematically more compact with median FWHM values, increasing with redshift or luminosity, in the range ∼1–2 kpc corresponding to an almost constant angular size of 0.″25 (see the lower dashed line in the left panel of Fig.1). The median linear size of NRX-AGN steadily increases from z ∼ 0 up to z ∼ 0.7 (or to L3 GHz ∼ 1023 W Hz−1), converging to a roughly constant value of ∼3–4 kpc up to the highest redshift (luminosity). NRX-AGN are a factor of ∼2 more extended than RX-AGN up to z ∼ 1 or L3 GHz ∼ 1023.5, and the median size is consistent with a constant angular size of 0.″45 (see the upper dashed line in Fig. 1).
The median linear size of the SFGs has a peak at z ∼ 0.6 (or L3 GHz ∼ 1022.5 W Hz−1), corresponding to a value of ∼4.8 kpc, followed by a steady decrease at higher redshift or luminosity. The rise of the median linear size of SFGs up to z ∼ 0.6 is, at least partly, the result of the resolution bias. Even if our MR catalog corrects partly for this effect, this approach is limited by the lower sensitivity of the convolved images with respect to the full resolution image (see Table 2 in D17). The solid lines in Fig. 2 (left panel) show the expected maximum angular size for a ≥5σ detection as a function of total flux for three convolved images. This size is calculated using the geometric mean of Eqs. (2) and (3) in Smolčić et al. (2017b). The plot shows that when only sources with ST ≥ 20 μJy (as for our MR catalog) are selected, we can recover all the sources with an intrinsic size of ≲0.″8. To detect sources as large as 1.″5 (corresponding to a linear size of 4.8 kpc at z ∼ 0.2), we could use the 1.″2 resolution image, but we would need to raise the completeness limit to ST ≳ 30 μJy.
 |
Fig. 2. Left panel: maximum detectable angular size resulting from the combined effects of r.m.s sensitivity and total flux density selection limit for images with 0.″75 (grey line), 1.″2 (magenta line) and 1.″5 resolution (pink line). The maximum angular size is estimated from the ratio ST/5σ using the geometric mean of the two limiting cases (see text). Right panel: redshift evolution of the median linear sizes of three different samples of SFGs: the blue points are the same as in Fig. 1 and correspond to radio sources with 3 GHz total flux density ST > 20 μJy, while the purple squares and magenta triangles correspond to subsamples with ST > 30 μJy and ST > 40 μJy, respectively. |
Therefore, even using the convolved images, we can expect to miss sources with intrinsic sizes of ∼5 kpc at low (z < 0.5) redshift. We tested this conclusion by restricting our sample to sources with ST > 30 μJy and ST > 40 μJy and repeated the analysis for the SFGs and NRX-AGN. The results for the SFGs are shown in Fig.2 (right panel): for z > 1 the median sizes are not significantly affected by different cuts in ST, while for z ≲ 0.7 we indeed find larger median sizes using only sources with ST > 30 μJy. A threshold of ST > 40 μJy does not produce a further significant change in the median sizes. The NRX-AGN exhibit no significant differences in the median sizes regardless of the cut in the total flux density. Therefore, while we find evidence of an increase in the median radio linear sizes for the NRX-AGN from z ∼ 0 to z ∼ 0.7, the radio size of the μJy population of SFGs is consistent with being constant at a value of ∼5–6 kpc up to z ∼ 1 followed by a steady decrease thereafter.
These results confirm, with a much improved statistics, the sizes derived from Guidetti et al. (2017) for SFGs and AGN. If we consider all our sources together (no distinction between SFGs and AGN), as done in Cotton et al. (2018) and Murphy et al. (2017), we obtain a median linear size of 3.58 ± 0.05 kpc that corresponds to ≃0.″45 at z = 1 (the median redshift of our sources). This value is comparable with that found by Cotton et al. (2018) when we take into account that we measure the size along the major axis, while they derive an equivalent circular size. The more compact sizes found by Murphy et al. (2017) can be partly intrinsically due to the energy-dependent propagation of electrons producing the synchrotron emission at 10 GHz and 3 GHz (e.g., Murphy et al. 2012) and partly due to selection effects caused by the higher resolution (0.″22) of the 10 GHz observations.
4. Discussion
4.1. AGN sizes
We find that the radio emission of the μJy RX-AGN is dominated by a compact radio source (∼0.″25), most likely the radio nucleus. This is consistent with the results obtained from Very Long Baseline Array (VLBA) observations (Herrera Ruiz et al. 2017). The MR catalog includes 405 RX-AGN detected by the 1.4 GHz VLBA observations at milliarcsec resolution (Herrera Ruiz et al. 2017). While the percentage of RX-AGN is only 26% in the entire MR catalog, almost 87% of the sources detected by the VLBA observations are RX-AGN. The VLBA observations are biased toward the most compact sources. Both RX- and NRX-AGN detected by the VLBA have median sizes of ∼1.5 kpc. The VLBA-detected RX-AGN have the same median size as the entire RX-AGN population in the MR catalog. Conversely, the NRX-AGN with a VLBA detection are about a factor of 2 more compact than the NRX-AGN in the MR catalog, and as noted by Herrera Ruiz et al. (2017), they display a systematically higher radio emission than that expected from star formation, but not enough to be above the threshold we assumed to be classified as RX-AGN.
To separate the effects of L3 GHz and redshift on the median radio sizes, we selected subsamples of RX-AGN fully complete in L3 GHz at three different redshift intervals (0.6 < z < 1.0, 1.0 < z < 1.8, 1.8 < z < 3.0). The complete bins in L3 GHz are 1022.9 < L3 GHz < 1023, 5, 1023.5 < L3 GHz < 1024.0, 1024.0 < L3 GHz < 1024.5.
The median linear radio size derived from the luminosity-complete subsamples of RX-AGN are shown in Fig. 3 (left panel). We find that redshift is the dominant parameter ruling the increase in radio sizes. At lower redshifts (z ≲ 1), RX-AGN are compact (< 2 kpc), and the most luminous sources are the most compact ones. These properties are consistent with those of FR0 sources observed in the local Universe (Baldi et al. 2015). FR0 sources are expected to be more numerous at z ∼ 1 (Whittam et al. 2016) and in surveys selected at frequencies above 1.4 GHz. We find that ∼25% of the μJy sources in our MR catalog can indeed be regarded as FR0, a significant percentage of the μJy population that should be considered when modeling the μJy radio sky (Whittam et al. 2017). Moreover, the median sizes of subsamples that are complete at higher luminosity confirm the overall trend of Fig. 1: RX-AGN at z ≳ 2 have significantly larger radio sizes (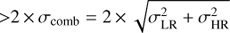 kpc for 1024.0 < L3 GHz < 1024.5), comparable to those of NRX-AGN, than RX-AGN at z ≲ 1 with the same L3 GHz. This is consistent with the bulk of RX-AGN at z ≳ 2 being radiatively efficient AGN (see Appendix A.3) hosted in blue SFGs, as recently found by Delvecchio et al. (2018), in contrast to what is observed at z ≲ 1, where RX-AGN are instead radiatively inefficient AGN within red and passive galaxies. The more extended radio emission in z ≳ 2 RX-AGN can be produced by star formation and/or by a radio jet component that might be able to develop only in objects with higher redshift or luminosity. The two processes are not mutually exclusive and might be related through AGN feedback (e.g., Silk 2013). It is interesting to note that the median radio size of z ≳ 2 RX-AGN is comparable to the optical size of the quiescent galaxies at z ∼ 2 (Szomoru et al. 2012; van Dokkum et al. 2015). Furthermore, Fig. 4 confirms that the most compact RX-AGN are hosted in the most massive galaxies (Sadler et al. 1989; Wrobel & Heeschen 1991; Nyland et al. 2016; Baldi et al. 2018), while median linear radio sizes of RX-AGN are larger in galaxies with lower stellar mass, suggesting a possible link between the build-up of a massive galaxy and the presence of a compact radio core.
kpc for 1024.0 < L3 GHz < 1024.5), comparable to those of NRX-AGN, than RX-AGN at z ≲ 1 with the same L3 GHz. This is consistent with the bulk of RX-AGN at z ≳ 2 being radiatively efficient AGN (see Appendix A.3) hosted in blue SFGs, as recently found by Delvecchio et al. (2018), in contrast to what is observed at z ≲ 1, where RX-AGN are instead radiatively inefficient AGN within red and passive galaxies. The more extended radio emission in z ≳ 2 RX-AGN can be produced by star formation and/or by a radio jet component that might be able to develop only in objects with higher redshift or luminosity. The two processes are not mutually exclusive and might be related through AGN feedback (e.g., Silk 2013). It is interesting to note that the median radio size of z ≳ 2 RX-AGN is comparable to the optical size of the quiescent galaxies at z ∼ 2 (Szomoru et al. 2012; van Dokkum et al. 2015). Furthermore, Fig. 4 confirms that the most compact RX-AGN are hosted in the most massive galaxies (Sadler et al. 1989; Wrobel & Heeschen 1991; Nyland et al. 2016; Baldi et al. 2018), while median linear radio sizes of RX-AGN are larger in galaxies with lower stellar mass, suggesting a possible link between the build-up of a massive galaxy and the presence of a compact radio core.
 |
Fig. 3. Median FWHM radio size for a subsample of RX sources (left panel) and SFGs (right panel) complete in 3 GHz luminosity (L3 GHz) in the redshift bins listed in the legends. |
 |
Fig. 4. Median FWHM radio size of AGN with RX-AGN and NRX-AGN as a function of the host galaxy stellar mass. |
The accessible range in radio luminosity of NRX-AGN here is too limited to repeat the same analysis on luminosity-complete subsamples as performed on the RX-AGN. The NRX-AGN do not show a decrease in radio size in the most massive objects (Fig. 4), suggesting that the build-up of the galaxy is not associated with the emerging of a compact and bright radio core. The median radio size in NRX-AGN is consistent with radio emission (or at least most of it) being spread across the galactic disk and probably not being related to the AGN detected from the multi-wavelength diagnostics, but rather originating by star formation processes.
4.2. SFGs sizes
Figure 1 shows a significant decrease in the median radio size with redshift (or luminosity) in SFGs for z ≳ 1. To separate the dependence on redshift and luminosity, we considered subsamples of sources complete in L3 GHz at a given redshift, as was done for the RX-AGN. The results are shown in Fig. 3 (right panel). We note that at a fixed redshift, the median radio size decreases with increasing L3 GHz: SFGs with higher L3 GHz have a more centrally peaked surface brightness that can be either due to a nuclear starburst or a low-luminosity radio AGN that is not detected by the multi-wavelength diagnostics. This is in agreement with the higher fraction of AGN found in the most extreme starburst galaxies (e.g., Bonzini et al. 2015). Figure 3 also shows a hint for more extended SFGs at higher redshifts at a given L3 GHz.
To compare the radio sizes of SFGs to those derived in the rest-fame FIR and optical-UV bands by Fujimoto et al. (2017; F17), Tadaki et al. (2017; T17), and Shibuya et al. (2015; S15), we converted the measured FWHM of the radio major axis into the circularized effective radius (Re, see Appendix C).
F17 and T17 derived the rest-frame far-infrared (FIR) size of the star-forming regions that are obscured by large amount of dust using ALMA observations of 1034 and 12 sources, respectively. The SFGs from F17 are split into three redshift bins (z = 1–2, 2–4, and 4–6), while the 12 sources from T17 are all within 2.2 < z < 2.5.
In the optical-UV, the most updated and comprehensive study of galaxy Re is presented by S15 using HST observations for a sample of ∼190 000 galaxies at z = 0 − 10. This study is an extension of that published by van der Wel et al. (2014), who provided similar and consistent results. S15 derived a best-fit relation to the median size evolution with redshift for three different ranges of UV luminosity for different statistics (median, average, and mode). We used the median fit obtained for the UV-bright galaxies (−24 < MUV < −21), corresponding to stellar masses in the range 10.0 ≲ log(M/M⊙)< 11.0. This is consistent with the median stellar mass of log(M/M⊙)=10.6 derived for the hosts of our radio-selected SFGs.
In Fig. 5 we plot the median Re values derived in the radio, FIR, and UV bands, and the best-fit median size evolution curve obtained by S15 (Re = Bz(1 + z)βz, with Bz = 4.05 and βz = − 0.78).
 |
Fig. 5. Redshift evolution of the circularized effective radius Re for SFGs with z > 1. Blue filled circles are the radio Re from our sample of radio-emitting SFGs, magenta triangles and green squares are the rest-frame FIR Re from Fujimoto et al. (2017; F17) and Tadaki et al. (2017; T17), purple diamonds are the UV median values from Shibuya et al. (2015; S15). The errors on the radio Re also include the dispersion of the axial ratio median value we used to convert into circularized effective radius. The solid line is the best-fit median size evolution derived for Re in the UV-band for UV-luminous SFGs by S15, given by Re = Bz(1 + z)βz, with Bz = 4.05 and βz = −0.78. |
The radio sizes derived from our sample of SFGs are systematically smaller (by less than 15%), but agree within the errors with the sizes measured in the rest-frame FIR by F17. We note that for spiral galaxies in the local Universe the radio sizes are generally larger than those measured in the FIR (e.g., Bicay & Helou 1990; Murphy et al. 2006, 2008), because the synchrotron-emitting electrons are diffused out of the galactic disk, but at high redshift, the inverse-Compton losses will dominate the diffusion, and the radio emission is expected to be confined within the star-forming regions. A similar difference is observed to the rest-frame UV sizes for SFGs at z ≳ 2, while the offset between the radio and UV sizes increases at lower redshifts, becoming 30% at z ∼ 1. UV measurements may be affected by dust obscuration, in particular, an increased dust attenuation in the central regions as has been suggested to be typical in SFGs at z ∼ 2 (Tacchella et al. 2018), would produce larger UV sizes than those that could be recovered without a significant radially dependent obscuration.
5. Summary
We have presented an analysis of the linear radio size evolution for a sample of more than 6000 μJy radio sources classified as SFGs, non-radio-excess AGN (NRX-AGN) and radio-excess AGN (RX-AGN) from the COSMOS 3 GHz Large Program Survey, using a multi-resolution radio catalog. The results can be summarized as follows:
-
We find compelling evidence that RX-AGN, NRX-AGN, and SFGs at a μJy flux density level have distinct median linear sizes with different redshift (or luminosity) evolutions. The sizes of RX-AGN increase with redshift (or 3 GHz radio luminosity) up to z ∼ 2, with values in the range 1–2 kpc, corresponding to an almost constant angular sizes of 0.″25. NRX-AGN show systematically larger sizes than those of RX-AGN, with a more complex evolution with redshift or luminosity. From z ∼ 0 to z ∼ 0.6, the median linear size of RX-AGN steadily increases up to ∼3–4 kpc and is consistent with being constant at higher redshifts. SFGs, after correcting for the resolution bias, have a larger and approximately constant median size (∼5 kpc) from z ∼ 0.2 up to z ∼ 1, followed by a decrease at higher redshifts. At z ∼ 2.5, the median size of SFGs is comparable to that of the NRX-AGN.
-
Our results are consistent, but with much improved statistics, with those recently reported by Guidetti et al. (2017) and Cotton et al. (2018), while we find larger sizes than those derived at 10 GHz with 0.″2 resolution by Murphy et al. (2017). This difference is probably partly intrinsic because of the energy-dependent propagation of synchrotron -emitting electrons at 10 GHz and 3 GHz, and is partly due to selection effects caused by the higher angular resolution of the 10 GHz observations.
-
To distinguish the effect of redshift and luminosity, we have selected subsamples of sources that are complete in L3 GHz at each redshift bin. Considering only RX-AGN in the redshift range 0.6 < z < 1.0, we find that higher luminosity objects are more compact. Moreover, at a given L3 GHz, the RX-AGN at higher redshift are more extended than those at lower redshift. The median radio size of RX-AGN at z ∼ 2.5 is a factor of 2.4 larger than the median size of local (z ≲ 1) RX-AGN. While the radio emission in local RX-AGN originates from a compact radio core, at high redshift (z ≳ 2), the RX-AGN are significantly more extended in the radio, and part of this radio emission could be associated with star formation. The median radio size of high-redshift RX-AGN (≃2.9 kpc) is comparable to the optical size of quiescent galaxies at z ∼ 2. We also find a clear anticorrelation between the stellar mass content and the radio sizes in RX-AGN: smaller radio sizes are present in the most massive hosts, while the less massive (and typically high -redshift) galaxies have larger radio sizes. The radio sizes of NRX-AGN do not significantly depend on the stellar mass of the host galaxy.
-
Considering only SFGs with z > 0.8 that are complete in L3 GHz at each redshift, we find that the most luminous SFGs are more compact, while at a given L3 GHz, the SFGs at higher redshift are more extended.
-
The radio linear sizes of SFGs at z ≳ 1 agree (within 15%) with the rest-frame FIR sizes published by F17 and T17. The same is true for the rest-frame UV sizes of SFGs at z ≳ 2, while at lower redshifts the discrepancy is larger (at z ≲ 1 radio sizes are ∼30% smaller than UV sizes).
In this paper we use SFG for the objects classified as clean SFG in Smolčić et al. (2017a), i.e., sources without a radio excess.
Acknowledgments
VS acknowledges support from the European Union’s Seventh Frame-work program under grant agreement 337595 (ERC Starting Grant, “CoSMass”). BM and EJA acknowledge support by the Collaborative Research Centre 956, sub-project A1, funded by the Deutsche Forschungsgemeinschaft (DFG). EJA acknowledges support of the Collaborative Research Center 956, subproject A, funded by the Deutsche Forschungsgemeinschaft (DFG).
References
- Baldi, R. D., Capetti, A., & Giovannini, G. 2015, A&A, 576, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldi, R. D., Williams, D. R. A., McHardy, I. M., et al. 2018, MNRAS, 476, 3478 [NASA ADS] [CrossRef] [Google Scholar]
- Bicay, M. D., & Helou, G. 1990, ApJ, 362, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Bonaldi, A., Bonato, M., Galluzzi, V., et al. 2019, MNRAS, 482, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, M., Ciliegi, P., Zamorani, G., et al. 2003, A&A, 403, 857 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonzini, M., Mainieri, V., Padovani, P., et al. 2015, MNRAS, 453, 1079 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 2007, in Deepest Astronomical Surveys, eds. J. Afonso,H. C. Ferguson,B. Mobasher, & R. Norris, ASP Conf. Ser., 380, 189 [NASA ADS] [Google Scholar]
- Cotton, W. D., Condon, J. J., Kellermann, K. I., et al. 2018, ApJ, 856, 67 [NASA ADS] [CrossRef] [Google Scholar]
- de Zotti, G., Massardi, M., Negrello, M., & Wall, J. 2010, A&ARv, 18, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Delhaize, J., Smolčić, V., Delvecchio, I., et al. 2017, A&A, 602, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Smolčić, V., Zamorani, G., et al. 2017, A&A, 602, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delvecchio, I., Smolčić, V., Zamorani, G., et al. 2018, MNRAS, 481, 4971 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, H. C., Dickinson, M., Giavalisco, M., et al. 2004, ApJ, 600, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Ouchi, M., Shibuya, T., & Nagai, H. 2017, ApJ, 850, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Guidetti, D., Bondi, M., Prandoni, I., et al. 2017, MNRAS, 471, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, C. A., Murphy, T., Curran, J. R., et al. 2012, MNRAS, 425, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Hathi, N. P., Jansen, R. A., Windhorst, R. A., et al. 2008, AJ, 135, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera Ruiz, N., Middelberg, E., Deller, A., et al. 2017, A&A, 607, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heywood, I., Jarvis, M. J., & Condon, J. J. 2013, MNRAS, 432, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., & Nelson, P. I. 1986, ApJ, 306, 490 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Mancuso, C., Lapi, A., Prandoni, I., et al. 2017, ApJ, 842, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Mo, H. J., Mao, S., & White, S. D. M. 1998, MNRAS, 295, 319 [Google Scholar]
- Murphy, E. J., Helou, G., Braun, R., et al. 2006, ApJ, 651, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Helou, G., Kenney, J. D. P., Armus, L., & Braun, R. 2008, ApJ, 678, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Porter, T. A., Moskalenko, I. V., Helou, G., & Strong, A. W. 2012, ApJ, 750, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Momjian, E., Condon, J. J., et al. 2017, ApJ, 839, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, E. J., van Dokkum, P. G., Momcheva, I. G., et al. 2016, ApJ, 817, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Novak, M., Smolcic, V., Schinnerer, E., et al. 2018, A&A, 614, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nyland, K., Young, L. M., Wrobel, J. M., et al. 2016, MNRAS, 458, 2221 [NASA ADS] [CrossRef] [Google Scholar]
- Oesch, P. A., Bouwens, R. J., Carollo, C. M., et al. 2010, ApJ, 709, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Ono, Y., Ouchi, M., Curtis-Lake, E., et al. 2013, ApJ, 777, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P. 2016, A&ARv, 24, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Sadler, E. M., Jenkins, C. R., & Kotanyi, C. G. 1989, MNRAS, 240, 591 [NASA ADS] [Google Scholar]
- Sanders, D. B., Salvato, M., Aussel, H., et al. 2007, ApJS, 172, 86 [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 2013, ApJ, 772, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Delvecchio, I., Zamorani, G., et al. 2017a, A&A, 602, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017b, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolčić, V., Novak, M., Delvecchio, I., et al. 2017c, A&A, 602, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Szomoru, D., Franx, M., & van Dokkum, P. G. 2012, ApJ, 749, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Tacchella, S., Carollo, C. M., Förster Schreiber, N. M., et al. 2018, ApJ, 859, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Tadaki, K.-I., Genzel, R., Kodama, T., et al. 2017, ApJ, 834, 135 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Franx, M., van Dokkum, P. G., et al. 2014, ApJ, 788, 28 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Nelson, E. J., Franx, M., et al. 2015, ApJ, 813, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Whittam, I. H., Riley, J. M., Green, D. A., et al. 2016, MNRAS, 457, 1496 [NASA ADS] [CrossRef] [Google Scholar]
- Whittam, I. H., Jarvis, M. J., Green, D. A., Heywood, I., & Riley, J. M. 2017, MNRAS, 471, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Wrobel, J. M., & Heeschen, D. S. 1991, AJ, 101, 148 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Building a multi-resolution catalog
The VLA-COSMOS 3 GHz Large Project produced a final image with a median rms sensitivity of 2.3 μJy beam−1 over a field of 2 square degrees with a resolution of 0.″75 and a catalog of about 11 000 radio sources ≥5σ (Smolčić et al. 2017b). This catalog allowed us to derive the radio source counts down to a flux density of about 10 μJy (Smolčić et al. 2017b,a) and even deeper, extrapolating from the derived luminosity function for different classes of objects (Smolčić et al. 2017c; Novak et al. 2018). The subarcsecond resolution of the VLA-COSMOS 3 GHz observations is an advantage for a proper optical counterpart identification, but has two relevant disadvantages affecting radio sources with intrinsic angular sizes > 0.″75:
-
For moderately resolved sources, the total flux density (and consequently the angular size) in the catalog can be underestimated.
-
A significant number of heavily resolved sources can be completely missed because the catalog is selected on the peak flux density.
The original full-resolution mosaic has been convolved, producing a set of images and associated catalogs, with increasingly coarser resolutions. All the catalogs were generated using the software blobcat developed by Hales et al. (2012), as detailed in Smolčić et al. (2017b).
To derive an estimate of the size of the radio-emitting region, we decided to adopt the following procedure. The first step was to compile a multi-resolution (MR) catalog based on the full-resolution catalog and on the catalogs derived from the convolved images to recover the correct flux and size of the moderately resolved sources (see Appendix A.1), and as many as possible of the heavily resolved ones that are undetected in the full-resolution 3 GHz catalog (Appendix A.2). The program blobcat does not provide a measure for the size, therefore the second step was to fit all the resolved sources in the MR catalog, assuming a Gaussian brightness distribution, using the prescription that the peak and total fluxes from the fits must be consistent with the values derived by blobcat (Appendix B).
A.1. Sources detected at full resolution
We started from the 3 GHz radio source counterpart catalog containing all the 9161 objects detected with a signal-to-noise ratio (S/N) greater than 5 at a resolution of 0.″75 and an optical/infrared (OIR) counterpart assigned either in the COSMOS2015 (Laigle et al. 2016), i-band (Capak et al. 2007), or IRAC catalogs (Sanders et al. 2007), as described in Smolčić et al. (2017a). We selected 8864 sources within the region of 2 square degrees with right ascension (RA) and declination (DEC) in the range 149.41134< RA (deg) < 150.8271 and 1.49862< DEC (deg) < 2.91286. In this region, 59 radio sources are classified as multiple, and they were treated differently, leaving a total of 8805 single-component sources.
For each of these sources we identified counterparts (best match within a 1″ search radius) in the 5σ radio catalogs obtained from the convolved radio mosaics at resolutions of 0.″90, 1.″20, 1.″50, 1.″80, and 2.″20. When a source had a counterpart in a lower resolution catalog (starting from 0.″90), we calculated the difference between the total flux densities reported in the two catalogs (lower–higher resolution). If this difference was 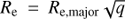 , where σcomb is defined through σLR and σHR, the total flux density errors of the lower and higher resolution catalogs, then the lower resolution was selected as the best resolution. For each source, we iterated this comparison to all the counterparts in catalogs with increasingly lower resolutions (from 0.″90 to 2.″20). In this way, we associated a best resolution and a corresponding total flux density with each source detected at full resolution. This is the MR catalog for the single-component radio sources. About 20% of the sources detected at full resolution have a best resolution > 0.″75. The number of sources whose total flux density is affected by this procedure and the best resolution adopted in the MR catalog is reported in Table A.1. The same procedure could not be applied to the 59 multi-components sources. For these sources the total flux in the MR catalog was measured on the 1.″5 resolution convolved image using the same method as we employed to derive the flux for the original catalog.
, where σcomb is defined through σLR and σHR, the total flux density errors of the lower and higher resolution catalogs, then the lower resolution was selected as the best resolution. For each source, we iterated this comparison to all the counterparts in catalogs with increasingly lower resolutions (from 0.″90 to 2.″20). In this way, we associated a best resolution and a corresponding total flux density with each source detected at full resolution. This is the MR catalog for the single-component radio sources. About 20% of the sources detected at full resolution have a best resolution > 0.″75. The number of sources whose total flux density is affected by this procedure and the best resolution adopted in the MR catalog is reported in Table A.1. The same procedure could not be applied to the 59 multi-components sources. For these sources the total flux in the MR catalog was measured on the 1.″5 resolution convolved image using the same method as we employed to derive the flux for the original catalog.
Number of sources at each resolution in the multi-resolution catalog.
A.2. Sources undetected at full resolution
So far, we have only considered the radio sources with OIR counterparts detected in the full-resolution mosaic. As previously noted and discussed in D17, a non-negligible number of sources with intrinsic sizes > 0.″75 could be missing from this catalog as a result of the resolution bias. As a first step, we followed the method used by D17 selecting 449 infrared selected sources with a > 5σ radio counterpart in at least one of the catalogs of the convolved radio images up to a resolution of 2.″2. These IR sources are from a 24 μm prior-based catalog of Herschel-detected sources (≥5σ detection in at least one of the Herschel bands at the position of the prior) matched to the COSMOS2015 photometric catalog (Laigle et al. 2016) with a search radius of 1″ (see D17 for more details). Then, we cross-correlated the COSMOS2015 and i-band catalogs with the radio catalogs derived from the 0.″9, 1.″2, and 1.″5 resolution-convolved images, finding 457 new radio sources (not included by D17) that are detected in at least one of the convolved radio images and with an OIR counterpart within 0.″8. We did not use the 1.″2 resolution-convolved images as the small number of sources (∼10) that could be added from these images could be significantly affected by spurious identifications. All these 906 sources that are not included in the 3 GHz radio source counterpart catalog (Smolčić et al. 2017a) based on the full-resolution radio mosaic (Smolčić et al. 2017b) were added to the MR catalog by applying the same method as discussed above to derive for each one its best resolution and the corresponding total flux density.
 |
Fig. A.1. Redshift and 3 GHz total flux density distributions for 6399 radio sources in the final multi-resolution catalog. The black line shows the distribution of the whole sample, while color-coded lines show the distributions of different populations as reported in the inset legend. |
A.3. A multi-resolution catalog
Following the steps outlined in the previous sections, we obtained a catalog of 9770 radio sources with OIR counterparts. From this catalog we selected only those sources that fulfilled the following criteria. First, we were interested in investigating the evolution of the linear sizes of different populations of radio sources, therefore we selected only those with a measured redshift (photometric or spectroscopic) and for which it was possible to derive a classification as star-forming galaxy (SFG) or AGN based on their multiwavelength (X-ray to FIR) properties. The criteria used to separate these classes are detailed in Delvecchio et al. (2017) and Smolčić et al. (2017a). AGN were further divided into radio-excess (RX) or non-radio-excess (NRX) sources. Sources showing a radio-excess are defined as those whose radio emission exceeds by more than 3σ at any given redshift the star formation rate derived from the IR through spectral energy distribution (SED) fitting (see Smolčić et al. 2017b, and D17). Based on the multi-wavelength analysis and SED-fitting reported in Delvecchio et al. (2017), Smolčić et al. (2017a), about 90% (30%) of NRX-AGN (RX-AGN) are moderate-to-high luminosity AGN, so-called HLAGN, and the remaining 10% (70%) are low-to-moderate luminosity AGN, also known as MLAGN. With a reasonable degree of approximation, HLAGN are radiatively efficient AGN and MLAGN are radiatively inefficient AGN. Here, by definition, SFGs are always NRX sources (i.e., are only those classified as clean SFG in Smolčić et al. 2017a).
Number of radio sources in each class in the final MR catalog.
Second, we restricted the following analysis to sources with a total flux density at 3 GHz of S3 GHz > 20 μJy. The reason for this choice was that ∼90% of the sources with S3 GHz < 20 μJy are classified as unresolved in the original catalog because of their low S/N, compared to ∼35% of the sources with ST > 20 μJy. For all sources with a best resolution of 0.″75 in the MR catalog, we maintained the classification into resolved or unresolved that we derived for the full-resolution catalog. All the other sources, those originally detected at full resolution but with a best resolution corresponding to a convolved image and those found only in the convolved images, were classified as resolved, regardless of the original classification.
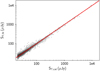 |
Fig. A.2. Total flux density from a Gaussian fit vs. total flux density from the MR catalog for all the 6340 single-component sources. The solid line is the equal flux line. |
With these criteria, we obtained an MR catalog listing 6340 single-component and 59 multi-component radio sources. Each source in the MR catalog has an associated best resolution and a total flux density measured in the best-resolution image. The number of radio sources divided into different classes is listed in Table A.2. The redshift and 3 GHz total flux density distributions for the whole sample of 6399 sources are shown in Fig. A.1. The overall median 3 GHz total flux density and redshift are ⟨ST⟩=37 μJy and ⟨z⟩=1.0, respectively.
Appendix B: Deriving the angular sizes
To derive the angular size of each single-component source, we fit a two-dimensional Gaussian component on its best-resolution image. We started fitting all the sources by setting the peak flux to the MR catalog value and not allowing it to vary. To test the reliability of the fit, we compared the total flux from the fit with that from the MR catalog. All sources whose total flux density from the fit was different by more than 25% from the value in the MR catalog were fit again, allowing the peak flux to vary. For about 90% of the fitted sources, the flux density from the fit agreed with that derived from blobcat, while the remaining 10% of the sources had a total flux derived from the Gaussian fit that was systematically lower than the flux reported in the catalog. Typically, these sources are heavily resolved and/or strongly asymmetric. In these cases, blobcat is more efficient in recovering the total flux because it is based on the flood fill, or thresholding, alghorithm (Hales et al. 2012, and references therein), which isolates blobs by selecting all pixels above an S/N threshold, without any a priori assumption on the surface brightness distribution. On the other hand, Gaussian fits produce more reliable results for slightly resolved sources, as their surface brightness distribution can be well approximated by a Gaussian. We solved this discrepancy by fitting these sources on a lower resolution image and obtained more reliable fits and a much better agreement between the fitted and cataloged total flux densities. A small number of fits (< 1%) produced clearly incorrect results, and they had to be fit manually with a more subtle selection of the starting parameters.
Figure A.2 shows the comparison between the total flux from the MR catalog (ST, cat) and the total flux from the one-component Gaussian fit (ST, fit) for the 6340 single-component sources,. Defining R = ST, cat/ST, fit as the ratio between the two flux densities, the median value of R is 1.00, with a median absolute deviation (MAD) of 0.06. Using a Gaussian fit, with the procedure described above, we were able to reproduce with excellent agreement the total flux densities in the catalog that are derived using the flood-fill alghorithm. From the Gaussian fits we obtained the angular sizes for each source. For the sources classified as resolved, we used as size measurement the fitted FWHM of the major axis deconvolved by the beam of the image we used for the fit. For the unresolved sources, the upper envelope curve in Fig. 9 from Smolčić et al. (2017b) gives the upper limit of the total-to-peak flux densities as a function of the S/N. As discussed in Smolčić et al. (2017b), the ratio between total and peak flux densities can be used to estimate the angular size of a radio source in two limiting approximations: a source with a circular geometry (major and minor axis are equal), or a source with a highly elongated geometry in just one direction (minor axis equals zero). We set the upper limit of the sizes of sources that were classified as unresolved to the geometric mean of the two limiting cases. Finally, for the 59 sources classified as multiple, we estimated the angular size by measuring the source extension directly in the 1.″50 resolution mosaic, which has been found to be the most appropriate for very extended sources.
Appendix C: Converting from Gaussian FWHM into circularized effective radius
Radial profiles in SFGs are often fit by an exponential disk or Sersic profile. For a proper comparison, we therefore converted our linear or angular FWHM into the equivalent radius, Re, major, which is the radius containing half of the emitted light along the semimajor axis, using the relation FWHM ≃ 2.43 Re, major (Murphy et al. 2017). We note that this relation is formally valid for an exponential disk profile (Sersic index n = 1), while the derived fit values of the Sersic index can have a large spread and even the median values are typically > 1. Furthermore, the data we wish to compare with use the circularized equivalent radius (hereafter referred to as Re) to measure the size. The relation to convert Re, major into Re is 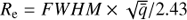 , where q is the axial ratio. For our sources we proceeded in the following way. First we derived an average axial ratio, q̄, for the resolved sources (using a 2σ limit for the minor axis when undetermined by the fit). Then, the circularized Re for the resolved sources was calculated as
, where q is the axial ratio. For our sources we proceeded in the following way. First we derived an average axial ratio, q̄, for the resolved sources (using a 2σ limit for the minor axis when undetermined by the fit). Then, the circularized Re for the resolved sources was calculated as 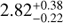 , while for the upper limits, Re = FWHM/2.43.
, while for the upper limits, Re = FWHM/2.43.
Appendix D: Additional tables
Median FWHM radio size redshift evolution of μJy populations.
Median FWHM radio size luminosity evolution of μJy populations.
All Tables
All Figures
 |
Fig. 1. Median linear size as a function of redshift (left panel) and 3 GHz radio luminosity (right panel) for the different classes of μJy radio sources (see the inset legend and text for details). The dashed lines in the left panel correspond to a constant angular size of 0.″25 (lower line) and 0.″45 (upper line). |
| In the text | |
 |
Fig. 2. Left panel: maximum detectable angular size resulting from the combined effects of r.m.s sensitivity and total flux density selection limit for images with 0.″75 (grey line), 1.″2 (magenta line) and 1.″5 resolution (pink line). The maximum angular size is estimated from the ratio ST/5σ using the geometric mean of the two limiting cases (see text). Right panel: redshift evolution of the median linear sizes of three different samples of SFGs: the blue points are the same as in Fig. 1 and correspond to radio sources with 3 GHz total flux density ST > 20 μJy, while the purple squares and magenta triangles correspond to subsamples with ST > 30 μJy and ST > 40 μJy, respectively. |
| In the text | |
 |
Fig. 3. Median FWHM radio size for a subsample of RX sources (left panel) and SFGs (right panel) complete in 3 GHz luminosity (L3 GHz) in the redshift bins listed in the legends. |
| In the text | |
 |
Fig. 4. Median FWHM radio size of AGN with RX-AGN and NRX-AGN as a function of the host galaxy stellar mass. |
| In the text | |
 |
Fig. 5. Redshift evolution of the circularized effective radius Re for SFGs with z > 1. Blue filled circles are the radio Re from our sample of radio-emitting SFGs, magenta triangles and green squares are the rest-frame FIR Re from Fujimoto et al. (2017; F17) and Tadaki et al. (2017; T17), purple diamonds are the UV median values from Shibuya et al. (2015; S15). The errors on the radio Re also include the dispersion of the axial ratio median value we used to convert into circularized effective radius. The solid line is the best-fit median size evolution derived for Re in the UV-band for UV-luminous SFGs by S15, given by Re = Bz(1 + z)βz, with Bz = 4.05 and βz = −0.78. |
| In the text | |
 |
Fig. A.1. Redshift and 3 GHz total flux density distributions for 6399 radio sources in the final multi-resolution catalog. The black line shows the distribution of the whole sample, while color-coded lines show the distributions of different populations as reported in the inset legend. |
| In the text | |
 |
Fig. A.2. Total flux density from a Gaussian fit vs. total flux density from the MR catalog for all the 6340 single-component sources. The solid line is the equal flux line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


