| Issue |
A&A
Volume 618, October 2018
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 11 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201833430 | |
| Published online | 16 October 2018 | |
Extragalactic radio source stability and VLBI celestial reference frame: insights from the Allan standard deviation⋆
1
Laboratoire d’Astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire, 33615 Pessac, France
e-mail: cesar.gattano@u-bordeaux.fr
2
SYRTE, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, LNE, Paris, France
3
NVI, Inc., Goddard Space Flight Center, 61A, Greenbelt, Maryland, USA
Received:
15
May
2018
Accepted:
6
July
2018
Aims. We investigate the composition of the noise in coordinate time series of several hundreds of extragalactic radio sources monitored by the geodetic VLBI program since 1979. The noise type is identified at all available timescales longer than one year, following the observational history of the source.
Methods. We computed the Allan standard deviation of coordinate time series and developed a Monte Carlo test to evaluate the influence of the irregular sampling and error on data onto the noise type identification. We classified the radio sources into three categories depending on their type of noise and taking into account the dominating noise at different timescales: from the category AV0, which contains sources with a stable behavior at all timescales, to the category AV2, which contains sources whose coordinates are dominated by random walks at the longest timescales.
Results. We found that almost no source exhibited “idealized” white noise. Only 5% of the 647 sources we studied belong to the category AV0 (stable sources). Moreover, we found that this class contains sources with relatively short observational histories, suggesting that after some years, a source whose astrometric position has shown a stable behavior is likely to become unstable. This questions the existence of the stable source paradigm and adds complementary information in the crucial task of selecting sources on which to base the axes of the celestial reference frame.
Key words: techniques: interferometric / astrometry / reference systems
The data table is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/618/A80
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The celestial reference frame (CRF) is a cornerstone of several scientific domains connected to astrometry and geosciences. In its current realization by very long baseline interferometry (VLBI), the second realization of the International Celestial Reference Frame (ICRF2) is based on precise positions of thousands of extragalactic radio sources (see Fey et al. 2015, and references therein). An accurate CRF opens the door to millimeter-level geodetic measurements (e.g., Earth rotation), insights into the internal structure of Earth (e.g., Mathews et al. 2002), and into testing of General Relativity and alternative theories with VLBI (Le Poncin-Lafitte et al. 2016, and references therein). The arrival of the Gaia Celestial Reference Frame (Gaia-CRF2; Mignard et al. 2018), which is first time that two independent CRF realizations with similarly high accuracies can be compared, also allows comparisons between the positions of the common objects at several frequencies. This adds insights into the physics of quasars (Kovalev et al. 2017), reference frames (Shabala et al. 2014), and the complex structure consisting of one or several black holes (Roland et al. 2013).
Geodetic VLBI has measured the positions of thousands of radio sources since 1979. Fey et al. (2015) determined an internal precision of the ICRF2 and claimed a noise floor (best positional accuracy) of 0.04 mas. They reported that the stability of the ICRF axes is close to 0.02 mas. The same authors recommended a set of 295 so-called “defining sources” that are supposed to best verify the no-net rotation condition. These sources were selected on the basis of their rms (rescaled by the χ2), which is a quantity that does not account for time variability of the position or of the noise type and amplitude, although such a variability may result from distinct underlying physical processes occurring at different epochs.
For this reason, we propose to use the Allan standard deviation (Allan 1966), which provides a means for measuring the amplitude of the noise as a function of the timescale, and thereby to separate different types of noise that coexist in a time series. Initially conceived to characterize the stability of time and frequency standards, the Allan standard deviation has been used in geodesy for about two decades and was raised in several works aiming at selecting suitable radio sources to define stable celestial frame axes (Gontier et al. 2001; Feissel-Vernier 2003; Feissel-Vernier et al. 2007; Malkin 2016; Le Bail et al. 2016). Nevertheless, most of the cited studies considered the Allan standard deviation at one given timescale (generally one year). Here, we explore the noise type for all available timescales following the length of the observational time span. We note that the Allan standard deviation is also used for the analysis of extragalactic radio source activity through the variable radio or optical flux we receive (see, e.g., Taris et al. 2018).
In this study, we use up-to-date coordinate time series of radio sources observed in the framework of the permanent geodetic VLBI monitoring program. Their computation is presented in Sect. 2. Our method, which is based on the Allan standard deviation, for characterizing the type of noise within the series is described in Sect. 3. We also propose a stability index based on the Allan standard deviation that could be used as a complement to the stability index constructed by Fey et al. (2015). Finally, Sect. 4 is devoted to a discussion of the results.
2. Coordinate time series
We used 6396 diurnal VLBI sessions made available at the data center of the International VLBI Service for geodesy and astrometry (IVS; Nothnagel et al. 2017). Earth orientation parameters and rates were estimated once per session. Station coordinate differences with respect to ITRF 2014 (Altamimi et al. 2016, including post-seismic nonlinear terms for some stations) were estimated as global parameters with no-net rotation and no-net translation conditions applied to the positions and velocities of a group of 38 stations. All station positions were corrected for tridimensional displacements due to oceanic and atmospheric loading using FES2004 (Lyard et al. 2006) and output from the Atmospheric Pressure Loading Service (APLO; Petrov & Boy 2004). Antenna thermal deformations were obtained in Nothnagel (2009). A priori dry zenith delays were estimated from local pressure values and then mapped to the elevation using the Vienna Mapping Function (Böhm et al. 2006). Wet zenith delays, north and east troposphere gradients, and quadratic clock drift coefficients were estimated every 10 min, 6 h, and 20 min, respectively. Our data reduction model complies with the IERS Conventions 2010 (Petit & Luzum 2010).
To obtain coordinate time series for all sources observed in these sessions, we used a method inspired by previous works of Ma et al. (1998), for instance, and various posterior works. We ran the solution 11 times. In each solution, we treated the positions of a subset of sources as local parameters, while the remaining source coordinates were treated as global parameters, including a large part of the 295 ICRF2 defining sources to which we applied uniformly a no-net rotation (NNR) constraint. In the first solution, all 295 defining sources were considered global parameters. All other sources were also considered global parameters except for the 39 special handling sources, as listed in the ICRF2; for the latter, we obtained their coordinate time series. Then, each successive solution 2–11 aimed at producing time series for one-tenth of all the other sources, including one-tenth of the 295 defining sources, whose coordinates were downgraded as session parameters, while the positions of the remaining nine-tenth were estimated as global parameters.
We obtained coordinate time series for 4895 sources. In these time series, we excluded estimates resulting from reduction of fewer than three observations (i.e., three VLBI delays). We also considered as outliers data points whose distance to the mean computed on a two-year window, which is centered on the epoch of the tested data point, was larger than six times the series standard deviation computed on the same window.
We did not correct our computed time series for specific patterns such as linear drift or periodic signal. A significant linear drift could be the result of structure effect that occurs on timescales longer than the VLBI source observational history, or they might be due to Galactic aberration, as explained by Kovalevsky (2003). The latter imprints a glide of the distant objects toward the Galactic center at a rate of about 5 μas yr−1, which is too small to affect our study significantly. Hypothetical periodic signal may be detected if there is a binary black hole within the active galactic nuclei (AGN; e.g. Roland et al. 2013). Because these possible signals are more probably due to the intrinsic physic of the sources, we include them in the analysis by our classification method and patterns like this might be evaluated as unstable astrometric behavior. Although the Allan standard deviation is first devoted to characterizing the noise content of a signal (more details in the next section), it is also sensitive to these specific patterns.
 |
Fig. 1. The four-quadrant plot shows (left panels) coordinate time series with their standard deviation given by the blue area and (right panels) the Allan standard deviation as a function of the averaging timescale (black solid line, see Eq. (1)), where the colored background indicates the behavior of the dominating noise (stable in gray, unstable in red, intermediate in pink), the black dotted lines represent the interval of confidence (at 90%) on the estimated Allan standard deviation at each timescale, and the gray lines represent the boundaries of deciles as computed from the Monte Carlo test (an explanation of the principle is given in Sect. 3.3 and additional information is provided in Sect. 3.4). The percentage in the top right corner gives the probability that the source is AV0. Additional figures are available in Appendix A. |
3. Source stability
3.1. Allan standard deviation
There are several estimators of the Allan standard deviation. We used the overlapping estimator (see, e.g., Howe et al. 1981), which increases the number of variance samples. Given a time series y of length N and mean sampling time τ0, the squared overlapping Allan standard deviation (Allan variance) is given by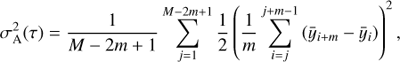 (1)
(1)
wherein the 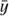 are computed as the weighted mean of every y samples within a considered time interval τ = mτ0 (the value of τ is also called the timescale, given in the abscissa in the right plots of Fig. 1). The weight associated with a given y sample is taken as the inverse of its squared standard errors. These weights enable taking into account the uneven distribution of the uncertainties in the y samples during the process. M is the total number of
are computed as the weighted mean of every y samples within a considered time interval τ = mτ0 (the value of τ is also called the timescale, given in the abscissa in the right plots of Fig. 1). The weight associated with a given y sample is taken as the inverse of its squared standard errors. These weights enable taking into account the uneven distribution of the uncertainties in the y samples during the process. M is the total number of 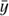 samples that can be computed considering the separation fixed to τ0 between them, given the length of the initial time series y and regardless of the initial sampling of y. In other words, M is the number of times we can move the averaging window of length τ from the beginning to the end of the time series y with a time step τ0.
samples that can be computed considering the separation fixed to τ0 between them, given the length of the initial time series y and regardless of the initial sampling of y. In other words, M is the number of times we can move the averaging window of length τ from the beginning to the end of the time series y with a time step τ0.
Some windows may contain too few data points to return a reliable averaged value or return even no data at all. In such a case, we considered the window as empty and did not include the averaged value when computing the sample variance, that is, the bracketed term of Eq. (1). If D is the number of missing points due to empty windows, M − 2m + 1 − D is the number of variance samples taken into account when computing the whole Eq. (1) for a variance estimation at time-scale τ (a point in the black curve in the right plots in Fig. 1). We computed the Allan standard deviation for m between 3 and N/3.
We can then determine an interval of confidence on σA using the algorithm of Greenhall & Riley (2003), who proposed a general method for several variance estimators and several types of noise. In our case, the first step was to compute the equivalent degree of freedom ν (Eq. (6) in Greenhall & Riley 2003) of the applied overlapped Allan standard deviation estimator (following Sect. 3 in Greenhall & Riley 2003, with d = 2, F = m and S = m). As explained by the authors, it has been observed empirically that for these estimators (and therefore for the overlapped Allan standard deviation estimator as well), 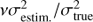 has a
has a 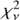 distribution. The interval of confidence can then be obtained by
distribution. The interval of confidence can then be obtained by 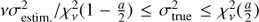 . We used a 90% interval (a = 0.1) in order to fix error bars on σA. We show the error bars computed under the hypothesis of a dominating white noise at all timescales.
. We used a 90% interval (a = 0.1) in order to fix error bars on σA. We show the error bars computed under the hypothesis of a dominating white noise at all timescales.
The relation between the noise color and the slope of the Allan standard deviation σA when represented versus the sampling time in log-log scale is shown in Table 1:
-
a slope of −0.5 characterizes white noise,
-
a slope of 0 characterizes pink (also flicker) noise, and
-
a slope of 0.5 characterizes red noise (also random walk).
Correspondence between the type of noise, associated with a color given by the exponent of the power-law-type spectral density function, and the drift observed in the Allan standard deviation as a function of the timescale represented log scale.
3.2. Source categorization
We qualified the stability of sources using the Allan variance as discussed previously. We split the sources into three categories following the sequence of the dominating noise at each timescale.
-
AV0: most stable astrometric behavior. The condition to be classified as AV0 is not to be dominated by unstable noise (slope larger than +0.25) such as red noise at any timescale.
-
AV1: intermediate astrometric stability. AV1 is dominated by unstable noise at some timescales, but stable noise (slope lower than −0.25) such as white noise dominates on the longest timescales appreciable considering the observational history of the source.
-
AV2: least stable behavior. All sources whose longest timescales are dominated by an unstable noise.
The category AV0 is identified to the most stable sources, although the wording “stable” employed here mainly has a statistical meaning and is not entirely related to the physics of the radio sources. The determination of the position of theses sources generally improves as the timescale increases. Sources in the category AV1 are also prone to improvement. On the other hand, AV2 sources suffer degradation as the timescale increases.
3.3. Rehabilitation
The question to answer is how the Allan standard deviation is affected by the irregularity of the original data. In other words, whether an unstable noise signature might be due to the irregular sampling instead of to the intrinsic nature of the source. To answer this question, we developed a statistical validation test based on Monte Carlo simulations that aims at determining the probability that deviating slopes of the log of Allan standard deviation versus log of timescale inducing an AV1/2 classification are caused by a white-noise process irregularly sampled and therefore should be classified as AV0.
We simulated 1000 white-noise processes with the method of Box & Muller (1958) distributed in time following the original sampling of the tested time series. Then, we computed the corresponding Allan standard deviations whose scatter provides an empirical error that can be attributed to the irregular sampling. The scatter resulting from the Monte Carlo test is represented by several gray lines in the right plots of Fig. 1 that link the decile boundaries of the distribution (minimum value – 10% – … – 90% – maximum value) at each timescale.
For example, assuming a variation in the trend of the Allan standard deviation that leads to the conclusion that this is a red-noise domination rather than white noise. Results from the Monte Carlo test may suggest that the Allan standard deviation stays closer to the white-noise median than at least a certain percentage of the simulated white noises at all timescales. This percentage is quantified by comparing our observation to the resulting scatter of the 1000 Allan standard deviation graphs computed from the simulated white noises. If this percentage is high, the white-noise domination is more probable.
This test has been made to estimate the probability of a white-noise domination because it is the desired behavior for a source to be selected as a source that defines the celestial reference frame. It should therefore not be used to reject sources from the AV0 category because these sources might show some small deviation from the white-noise trend, such as a flicker (pink) noise behavior. Such a behavior is neither stable or unstable, therefore it does not cause change in a source between the categories in our classification. A consequence of this is that an AV0 source can have a zero chance of rehabilitation from the Monte Carlo test because there is no need to rehabilitate it. Its behavior, as complex as it can be, has already been associated with a stable behavior in our classification.
Conversely, thanks to this test, each of the non-stable sources (AV1/2) therefore has a certain probability to truly be a stable source (AV0) if the computed probabilities on both coordinates are considered sufficiently high by a user. The following section provides concrete examples to illustrate this principle of rehabilitation.
In summary, the automatic process first produces a certain distribution of VLBI sources in our classification without taking the rehabilitation process into account. Then, we (or a user) define a certain rehabilitation threshold for which all AV1/2 sources presenting probabilities computed by the Monte Carlo test that are higher than this threshold on both coordinates are rehabilitated into the AV0 category. Finally, we determine the final distribution in our classification by taking into account these transfers.
 |
Fig. 2. Number of sources in each category as a function of the rehabilitation threshold. |
3.4. Examples
Figures 1 and A.1 show coordinate times series in the left plots and the Allan standard deviation in the right plots for eight sources of different “flavors”. Similar plots for all VLBI sources are publicly available1.
For 1611+343, the Allan standard deviation on both coordinates clearly shows an unstable behavior at all timescales, implying that the source is in the AV2 category. Comparison with the scatter gray plot resulting from the Monte Carlo test reveals that a white-noise regime cannot explain the observed behavior, which means that 1611+343 cannot be rehabilitated into the AV0 category.
For 1803+784, the Allan standard deviations globally show a stable behavior (combination of white and flicker noise), but an unstable behavior appears at marginal timescales (mainly in the declination for timescales longer than seven years). This source is therefore initially classified as an AV2 source. Nevertheless, the Allan standard deviations remain within the scatter lines of the Monte Carlo test, suggesting that the white-noise regime may still remain a white-noise regime at long timescales and the colored-noise regime that appears may be an artifact due to irregular sampling. The probability of this is 24% in right ascension and 12% in declination. This means that if we consider a rehabilitation threshold of 12% or lower, 1803+784 is classified as an AV0 source after rehabilitation. OJ287 is another similar example.
Finally, source 2234+282 shows evident random jumps in its time series that induce a major flicker noise domination with some marginal random walk domination. Then, at sufficiently long timescales, a white-noise regime dominates. Such a source is classified as an AV2 source only due to the marginally unstable behavior. Even if it cannot be rehabilitated into the AV0 category, this source is a good example to illustrate the boundary between AV0 and AV1/2 sources.
To illustrate the general panorama, Fig. 2 displays the number of sources observed in more than 20 sessions in a period longer than five years falling into each category for different rehabilitation thresholds. Of these 647 sources, 34 are AV0, 431 are AV1, and 182 are AV2 before rehabilitation. The median time span is 21.6 years for AV0, 25.7 years for AV1, and 25.5 years for AV2. The median number of sessions is 39, 154, and 80, for AV0, AV1, and AV2, respectively. The correlation coefficient between the time-series time span and the number of sessions in logarithm is about 0.6.
These numbers suggest that on the basis of the current VLBI observational history, (i) very few sources behave as white/flicker noise over timescales of several years to several tens of years, and (ii) even though some sources show such a white/flicker noise in a restricted time span (as suggested by the smaller number of sessions characterizing the AV0 sources), they are likely to show an unstable signature at longer timescales. A somewhat speculative corollary of these remarks could be that all sources are intrinsically AV1 or AV2: a sufficient observational history only has to be accumulated to have access to some displacements of the radio center. In other words, all sources are (potentially) unstable if they are observed for a sufficiently long time-span.
The rehabilitation process has the potential of mitigating this conclusion by introducing a level of confidence on the action of classification. Nevertheless, Fig. 2 shows that the rehabilitation threshold needs to be quite low to obtain a significantly different distribution. With a threshold of 60%, the distribution becomes 70 AV0, 406 AV1, and 171 AV2. The AV0 population (280 sources) becomes comparable to that of AV1/2 sources (247+120 sources) only when the rehabilitation threshold is reduced at 20%. Moreover, the rehabilitation process accentuates the observed tendencies on the time span of the series and on the number of sessions, meaning that it is preferentially the less frequently observed AV1/2 sources that are rehabilitated into the AV0 category. This consolidates the above conclusion and corollary.
 |
Fig. 3. Illustration of the computation of the lowest maximizing white noise (LMWN), represented by the thick blue lines for the source OJ287. LMWN is the lowest −0.5 sloped straight line that maximizes the source coordinate Allan standard deviation functions with respect to the timescale τ. |
 |
Fig. 4. Comparison between the stability index a based on the LMWN and (top panel) the classical rms-based indice r (middle panel), the observation time span, and (bottom panel) the declination. The horizontal bars represent the first (left extremity) and the third (right extremity) quartiles. The larger disk indicates the median. |
3.5. Lowest maximizing white noise and stability index
In the ICRF2 work (Fey et al. 2015), a stability index was defined as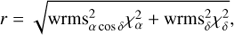 (2)
(2)
where 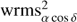 and
and 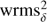 are the weighted standard deviations of the position in right ascension and declination, respectively, and
are the weighted standard deviations of the position in right ascension and declination, respectively, and 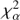 and
and 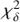 are their reduced χ2. This stability index has the advantage to summarize the source in one single number. Nevertheless, both the noise type and the time variability were ignored.
are their reduced χ2. This stability index has the advantage to summarize the source in one single number. Nevertheless, both the noise type and the time variability were ignored.
The Allan standard deviation here is, by definition, timescale dependent and cannot be represented by a single number. However, a conservative possibility consists of considering the lowest white-noise amplitude for which the associated theoretical Allan standard deviation, hereafter referred to as lowest maximizing white noise (LMWN), maximizes the Allan standard deviation at all timescales longer than one year. The LMWN is therefore a simple function of the timescale τ. Figure 3 provides an illustration of the computation of the two LMWN on both coordinates, represented by their theoretical Allan standard deviation function with respect to the timescale (thick blue lines) in the case of source OJ287 (last source presented in Fig. A.1).
A pair of two LMWN functions for each coordinate represents the behavior of a hypothetical source for which one can say that the actual source is more stable at all timescales. For comparison between sources, we propose to compare their LWMN at a same given timescale: we arbitrarily chose ten years. A conservative limit on the source stability can be computed as the quadratic sum of the LMWN(10 yr) of each coordinates. Similarly to the rms-based index r, we define a stability index based on the LMWN by (3)
(3)
Figure 4 shows how the indices r and a compare to each other, as well as the dependency of a on the time span of the series and declination. The correlation between a and r is about 0.7. The median a index is 0.14, 0.11, and 0.15 mas for AV0, AV1, and AV2, respectively, and the median r index is 0.50, 0.40, and 0.50 mas for AV0, AV1, and AV2, respectively. The differences between AV0 and AV1 suggest that the AV0 category might contain sources whose motion is interpreted as white noise because a large dispersion hides the random walks that often occur at the level of a few 0.1 mas. This dispersion can be due to the intrinsic nature of the source or to observational factors (low-resolution network).
When compared against the time span of the series, it appears that AV0 sources correspond to a median time span of about 21 years, whereas AV1 and AV2 are relevant for longer series of about or more than 25 years. This result again suggests that random walk dominates all radio sources if the observing time is long enough to capture it.
The index a tends to be larger for southern declinations. This reflects recurring results of VLBI astrometry (e.g., zonal errors) that are likely due to a north-south network asymmetry and probably not to the intrinsic nature of the sources.
 |
Fig. 5. Number of sources (top panels) in each category vs. the ICRF2 source category and (bottom panels) in the AV0 class as a function of the rehabilitation threshold. |
 |
Fig. 6. Comparison between the stability index a based on the LMWN and (top left panel) the flux at 8.4 GHz, (top right panel) the B magnitude, (bottom left panel) the radio-to-optical distance deduced from the comparison between the ICRF2 positions and Gaia DR1, and (bottom right panel) the redshift. The horizontal bars indicate the second (from the left extremity) and the third (to the right extremity) quartiles. The larger disk indicates the median. |
4. Discussion and conclusion
Figure 5 displays the number of ICRF2 sources observed in more than 20 sessions falling into the AV0, AV1, and AV2 categories before any rehabilitation (top) and restricted to the AV0 category as a function of the rehabilitation threshold (bottom). Most of the ICRF2 sources are AV1/2. In other words, the Allan standard deviation shows that most of the sources are unstable and only very few of them can be considered as behaving as white noise. This assertion is still true for ICRF2 defining sources in similar proportions. This distribution can be understood by taking into account that the defining sources were chosen on the basis of (i) their small standard deviation and structure index, (ii) their declination, and (iii) their number. As described above, a low standard deviation does not necessarily mean that a source is stable because of the existence of subtle random walk motions. Concerning items (ii) and (iii), some of the defining sources were chosen to increase the number of sources at southern declinations, even though most had a short observational history (observed in only a few tenths of sessions since the beginning of VLBI for the less frequently observed sources). All the defining sources are being observed regularly (with an observation target of 6–12 good observations per year) since the release of ICRF2. The statistical behavior of some of the poorly observed ICRF2 sources has evolved as a random walk since they were observed more frequently.
A comparison of the source category and the LMWN with photometric and astrometric data reveals some trends (Fig. 6). B magnitudes, redshift, and fluxes at 8.4 GHz were taken as recorded in the Large Quasar Astrometric Catalog (Gattano et al. 2018). AV0 sources tend to have a lower flux (median of 0.5 Jy) than AV1 and AV2 (median flux close to 0.7 Jy). No contrast was seen in magnitude. Interestingly, when we focus on the comparison of median values (filled circles in Fig. 6), AV0 sources tend to have a higher redshift (median close to 1.4) than AV1/2 sources (median close to 1.1). On the other hand, however, the point cloud dispersion (the horizontal bars) is equivalent for the three-source category, which means that a conclusion in any sense is difficult to advocate. All this suggests that most stable sources are generally fainter at radio wavelengths and that the astrometric instabilities can be linked to intrinsic events in the radio source that boost the flux at both optical and radio wavelengths, as advocated in Shabala et al. (2014). It is still an open question whether we need to search for stable sources that lie farther away since no compelling or reliable argument was found in this study.
The contrast to the radio-to-optical distance taken between ICRF2 and Gaia DR2 positions (Mignard et al. 2018) is not particularly revealing. The median angular distance between Gaia and VLBI is slightly larger than 1 mas.
To conclude, our analysis of the coordinate time series of VLBI-observed radio sources with the Allan standard deviation allows us to classify the sources into three categories, from the most stable that behave as white noise to those showing random walk. The most stable category, called AV0, contains only 5% of the 647 sources we studied. We showed that the “stable” sources are generally fainter in radio flux. An important remark is that these sources correspond to shorter time series, suggesting that no source can be considered to be really stable: when monitored over several decades, an intrinsic phenomenon that behaves like a random walk is very likely to be detected. The radio sources will be regularly reassessed to account for the variability in AGN that can affect the astrometric position. Three to six months is a reasonable compromise between the typical evolution timescale of AGN and the new information provided by new VLBI sessions (typically one to three sessions per week).
Arias & Bouquillon (2004) showed that the subset of radio sources selected by Feissel-Vernier (2003) on the basis of the one-year Allan standard deviation was more stable than the set of defining sources of the ICRF1 (Ma et al. 1998). Future investigations will be dedicated to celestial reference frame prototypes that are realized using the stability information as provided by the Allan standard deviation.
Acknowledgments
This work has been partially supported by a CNES post-doctoral grant.
References
- Allan, D. W. 1966, IEEE Proc., 54, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Altamimi, Z., Rebischung, P., Métivier, L., & Collilieux, X. 2016, J. Geophys. Res. Solid Earth, 121, 6109 [Google Scholar]
- Arias, E. F., & Bouquillon, S. 2004, A&A, 422, 1105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhm, J., Werl, B., & Schuh, H. 2006, J. Geophys. Res., 111, 2406 [Google Scholar]
- Box, G. E. P., & Muller, M. E. 1958, Ann. Math. Stat., 29, 610 [CrossRef] [Google Scholar]
- Feissel-Vernier, M. 2003, A&A, 403, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feissel-Vernier, M., de Viron, O., & Le Bail, K. 2007, Earth Planets Space, 59, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Fey, A. L., Gordon, D., Jacobs, C. S., et al. 2015, AJ, 150, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Gattano, C., Andrei, A. H., & Coelho, B. 2018, A&A, 614, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gontier, A.-M., Le Bail, K., Feissel, M., & Eubanks, T. M. 2001, A&A, 375, 661 [Google Scholar]
- Greenhall, C., & Riley, W. 2003, in Proc. 35th Annual Precise Time and Time Interval Systems and Applications Meeting, 267 [Google Scholar]
- Howe, D. A., Allan, D. W., & Barnes, J. A. 1981, in Proc. on the 35th Annual Symp. on Frequency Control, 1 [Google Scholar]
- Kovalev, Y. Y., Petrov, L., & Plavin, A. V. 2017, A&A, 598, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bail, K., Gordon, D., & Ma, C. 2016, in International VLBI Service for Geodesy and Astrometry 2016 General Meeting Proceedings: “New Horizons with VGOS”, eds. D. Behrend, K. D. Baver, & K. L. Armstrong, 288 [Google Scholar]
- Le Poncin-Lafitte, C., Hees, A., & Lambert, S. 2016, Phys. Rev. D, 94, 125030 [NASA ADS] [CrossRef] [Google Scholar]
- Lyard, F., Lefevre, F., Letellier, T., & Francis, O. 2006, Ocean Dyn., 56, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, C., Arias, E., Eubanks, T., et al. 1998, AJ, 116, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Malkin, Z. 2016, IEEE Trans. Ultrason. Ferroelectr. Freq. Control, 63, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, P. M., Herring, T. A., & Buffett, B. A. 2002, J. Geophys. Res., 107, 2068 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F., & Klioner, S. 2012, A&A, 547, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignard, F., Klioner, S., Lindegren, L., et al. 2018, A&A, 616, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nothnagel, A. 2009, J. Geod., 83, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Nothnagel, A., Artz, T., Behrend, D., & Malkin, Z. 2017, J. Geod., 91, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Petit, G., & Luzum, B. 2010, IERS Technical Note, 36, 1 [NASA ADS] [Google Scholar]
- Petrov, L., & Boy, J.-P. 2004, J. Geophys. Res., 109, 3405 [Google Scholar]
- Roland, J., Britzen, S., Caproni, A., et al. 2013, A&A, 557, A85 [Google Scholar]
- Shabala, S. S., Rogers, J. G., McCallum, J. N., et al. 2014, J. Geod., 88, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Taris, F., Damljanovic, G., Andrei, A., et al. 2018, A&A, 611, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A:
Additional figures
 |
Fig. A.1. Additional examples as Fig. 1. Each four-quadrant plot shows (left panel) coordinate time series with their standard deviation given by the blue area and (right panel) the Allan standard deviation as a function of the averaging timescale (black solid line, see Eq. (1)), where the colored background indicates the behavior of the dominating noise (stable in gray, unstable in red, intermediate in pink), the black dotted lines represent the interval of confidence (at 90%) on the estimated Allan standard deviation at each timescale, and the gray lines represent the boundaries of deciles as computed from the Monte Carlo test (an explanation of the principle is given in Sect. 3.3 and additional information is provided in Sect. 3.4). The percentage in the top right corner gives the probability that the source is AV0. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
All Tables
Correspondence between the type of noise, associated with a color given by the exponent of the power-law-type spectral density function, and the drift observed in the Allan standard deviation as a function of the timescale represented log scale.
All Figures
 |
Fig. 1. The four-quadrant plot shows (left panels) coordinate time series with their standard deviation given by the blue area and (right panels) the Allan standard deviation as a function of the averaging timescale (black solid line, see Eq. (1)), where the colored background indicates the behavior of the dominating noise (stable in gray, unstable in red, intermediate in pink), the black dotted lines represent the interval of confidence (at 90%) on the estimated Allan standard deviation at each timescale, and the gray lines represent the boundaries of deciles as computed from the Monte Carlo test (an explanation of the principle is given in Sect. 3.3 and additional information is provided in Sect. 3.4). The percentage in the top right corner gives the probability that the source is AV0. Additional figures are available in Appendix A. |
| In the text | |
 |
Fig. 2. Number of sources in each category as a function of the rehabilitation threshold. |
| In the text | |
 |
Fig. 3. Illustration of the computation of the lowest maximizing white noise (LMWN), represented by the thick blue lines for the source OJ287. LMWN is the lowest −0.5 sloped straight line that maximizes the source coordinate Allan standard deviation functions with respect to the timescale τ. |
| In the text | |
 |
Fig. 4. Comparison between the stability index a based on the LMWN and (top panel) the classical rms-based indice r (middle panel), the observation time span, and (bottom panel) the declination. The horizontal bars represent the first (left extremity) and the third (right extremity) quartiles. The larger disk indicates the median. |
| In the text | |
 |
Fig. 5. Number of sources (top panels) in each category vs. the ICRF2 source category and (bottom panels) in the AV0 class as a function of the rehabilitation threshold. |
| In the text | |
 |
Fig. 6. Comparison between the stability index a based on the LMWN and (top left panel) the flux at 8.4 GHz, (top right panel) the B magnitude, (bottom left panel) the radio-to-optical distance deduced from the comparison between the ICRF2 positions and Gaia DR1, and (bottom right panel) the redshift. The horizontal bars indicate the second (from the left extremity) and the third (to the right extremity) quartiles. The larger disk indicates the median. |
| In the text | |
 |
Fig. A.1. Additional examples as Fig. 1. Each four-quadrant plot shows (left panel) coordinate time series with their standard deviation given by the blue area and (right panel) the Allan standard deviation as a function of the averaging timescale (black solid line, see Eq. (1)), where the colored background indicates the behavior of the dominating noise (stable in gray, unstable in red, intermediate in pink), the black dotted lines represent the interval of confidence (at 90%) on the estimated Allan standard deviation at each timescale, and the gray lines represent the boundaries of deciles as computed from the Monte Carlo test (an explanation of the principle is given in Sect. 3.3 and additional information is provided in Sect. 3.4). The percentage in the top right corner gives the probability that the source is AV0. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


