| Issue |
A&A
Volume 617, September 2018
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833346 | |
| Published online | 12 September 2018 | |
Tunnelling dominates the reactions of hydrogen atoms with unsaturated alcohols and aldehydes in the dense medium
1
Institute for Theoretical Chemistry, University Stuttgart,
Pfaffenwaldring 55,
70569
Stuttgart, Germany
2
Leiden Institute of Chemistry, Gorlaeus Laboratories, Leiden University,
PO Box 9502,
2300 RA
Leiden, The Netherlands
e-mail: a.l.m.lamberts@lic.leidenuniv.nl
Received:
2
May
2018
Accepted:
6
June
2018
Hydrogen addition and abstraction reactions play an important role as surface reactions in the buildup of complex organic molecules in the dense interstellar medium. Addition reactions allow unsaturated bonds to be fully hydrogenated, while abstraction reactions recreate radicals that may undergo radical–radical recombination reactions. Previous experimental work has indicated that double and triple C–C bonds are easily hydrogenated, but aldehyde –C=O bonds are not. Here, we investigate a total of 29 reactions of the hydrogen atom with propynal, propargyl alcohol, propenal, allyl alcohol, and propanal by means of quantum chemical methods to quantify the reaction rate constants involved. First of all, our results are in good agreement with and can explain the observed experimental findings. The hydrogen addition to the aldehyde group, either on the C or O side, is indeed slow for all molecules considered. Abstraction of the H atom from the aldehyde group, on the other hand, is among the faster reactions. Furthermore, hydrogen addition to C–C double bonds is generally faster than to triple bonds. In both cases, addition on the terminal carbon atom that is not connected to other functional groups is easiest. Finally, we wish to stress that it is not possible to predict rate constants based solely on the type of reaction: the specific functional groups attached to a backbone play a crucial role and can lead to a spread of several orders of magnitude in the rate constant.
Key words: astrochemistry / ISM: clouds / ISM: molecules / molecular processes
© ESO 2018
1 Introduction
In the dense molecular clouds of the interstellar medium, the low temperatures (10–20 K) result in the freeze-out of atoms and molecules on the surface of dust grains. There they can diffuse and finally react with each other. In particular, hydrogenation reactions of the type H + A →HA that result in the formation of fully saturated species can be facilitated by the uptake of the excess energy by a third body, the dust grain. For instance, the hydrogenation of the triply bonded carbon monoxide molecule, CO, leads to the formation of first formaldehyde, H 2CO, and finally methanol, CH 3OH (Tielens & Hagen 1982; Hiraoka et al. 1998; Watanabe & Kouchi 2002; Fuchs et al. 2009). Carbon–carbon double and triple bonds can also be hydrogenated, starting from acetylene, C 2H 2, leading to ethylene, C 2H 4, and ethane, C 2H 6 (Bennett & Mile 1973; Kobayashi et al. 2017).
By adding more carbon and oxygen atoms to the backbone, this leads to the study of complex organic molecules (COMs). For instance, not only methanol, but also acetaldehyde, vinyl alcohol (tentative), and ethanol have been detected (Ball et al. 1970; Gottlieb 1973; Zuckerman et al. 1975; Turner & Apponi 2001). However, in the variety of C 3H nO species, the unsaturated molecules, propynal, propenal, and propanal have indeed been detected (Irvine et al. 1988; Hollis et al. 2004), but propanol has not (yet) been observed. Various other molecules with three carbon atoms and one oxygen atom have also been seen, such as propylene oxide, acetone, and cyclopropenone (Hollis et al. 2006; McGuire et al. 2016; Lykke et al. 2017).
It is now well known that methanol is mainly formed on the surfaces of dust grains through successive hydrogenation of carbon monoxide. Implementing these routes in models indeed allows reproducing the observed abundances (Boogert et al. 2015; Walsh et al. 2016; An et al. 2017). However, for acetaldehyde and ethanol, surface hydrogenation reactions alone do not seem to explain the relative abundances in young stellar objects (Bisschop et al. 2008). Furthermore, Loison et al. (2016) suggested that both propynal and cyclopropenone are exclusively formed in the gas phase. In an attempt to be able to link the various unsaturated C 3H nO molecules to propanol, which is fully saturated, Jonusas et al. (2017) performed hydrogenation experiments at low temperature under ultra-high vacuum conditions. They found that under their conditions and for a total H fluence of 2.7 × 1018 cm−2 s−1, the aldehyde group, –HC = O, could not be reduced to the alcohol form. This may seem to be in line with the non-detection of propanol. However, it should be kept in mind that this only considers one reaction route. Moreover, while laboratory experiments are very useful in determining reaction pathways, it is difficult, if not impossible, to determine exact reaction rate constants that can be used in astrochemical models. These rate constants are highly needed in order to determine which pathways dominate the formation ofcertain molecules.
Here, we further characterise the hydrogenation reactions starting from propynal and successively leading to propanol. We take a computational approach and make use of density functional theory benchmarked against coupled cluster theory in combination with instanton theory to quantify the various reaction rate constants involved. Moreover, not only hydrogen addition reactions are possible, but the degree of saturation can also decrease as a result of hydrogen abstraction reactions. Both types of reactions are studied here, leading to a total of 29 reactions under consideration.
Section 2 gives an overview of the computational methods used, both the underlying electronic structure calculations and the basics of instanton theory. In Sect. 3, the molecules under study are introduced along with the main reaction paths, subsequently, the calculated rate constants are discussed in comparison to the experimental work of Jonusas et al. (2017). Finally, we provide astrochemically relevant conclusions in Sect. 4.
2 Methods
2.1 Electronic structure
The potential energy surface was described by density functional theory (DFT). Following the benchmark calculations performed by Kobayashi et al. (2017), the MPWB1K functional (Zhao & Truhlar 2004) in combination with the basis set def2-TZVP (Weigend et al. 1998) was chosen. The energy and gradient calculations were carried out in NWChem version 6.6 (Valiev et al. 2010). An additional benchmark was performed for the activation and reaction energies of the four hydrogen addition reactions of propenal by comparing to single-point energy calculations at CCSD(T)-F12/VTZ-F12 level (Knowles et al. 1993, 2000; Deegan & Knowles 1994; Adler et al. 2007; Peterson et al. 2008; Knizia et al. 2009) in Molpro version 2012 (Werner et al. 2012). For an accurate calculation of the rate constant, a good description of the barrier region is crucial. The differences between coupled cluster and DFT activation energies are only ± 2 kJ mol−1; see Appendix A. We note that Álvarez-Barcia et al. (2018) showed that the multi-reference character for H addition to a C=O functional group is small and CCSD(T)-F12 values can be used as a reference.
The general procedure is the same for each selected mole- cule. Geometry optimisations are carried out for the separated reactant, product, and transition structures and verified by the appropriate number of imaginary frequencies. A transition structure is characterised by the Hessian bearing exactly one negative eigenvalue. To confirm that the found transition structure connects the desired reactant and product an intrinsic reaction coordinate (IRC) search is conducted. From the end-point of the IRC, a re-optimisation is performed to obtain the pre-reactive complex (PRC).
All calculations were performed with DL-find (Kästner et al. 2009) within Chemshell (Sherwood et al. 2003; Metz et al. 2014). IRC searches were performed using the algorithm described by Meisner et al. (2017b) and Hratchian & Schlegel (2004).
2.2 Reaction rate constants
Reaction rate constants were calculated using instanton theory (Langer 1967; Miller 1975; Callan & Coleman 1977; Coleman 1977), which has been proven to provide accurate tunnelling rates down to very low temperatures (Kästner 2014; Meisner & Kästner 2016). Instanton theory treats the quantum effects of atomic movements by Feynman path integrals. The instanton path can be seen as a periodic orbit in the upside-down potential connecting the reactant and product states at a given temperature. This path is located by a Newton–Raphson optimisation scheme. More details on our implementation of instanton theory are given in Rommel et al. (2011), Rommel & Kästner (2011), and McConnell & Kästner (2017). Reactant partition functions in the bimolecular cases were calculated as products of the partition functions of both separated reactants. For the unimolecular case, the partition function of the respective PRC was used. To model the reaction on a surface, the rotational partition function in the unimolecular case is assumed to be constant during the reaction. Such an implicit surface model (Meisner et al. 2017a) covers the effect of the ice surface, where the rotation on the surface is suppressed. In principle, this approximation holds as long as the interaction between the surface and the admolecules is weak, as is the case for a CO-rich ice mantle and the C3HnO molecules studied here. The instanton calculations were performed in a stepwise cooling scheme, starting with instanton discretisation by 40 images and increasing the number of images for lower temperatures, if necessary. The initial temperature was chosen just below the crossover temperatureTc (Gillan 1987), since canonical instanton theory is not applicable above it. The crossover temperature is defined as
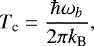 (1)
(1)
where ωb is the absolute value of the imaginary frequency at the transition state, ℏ is the reduced Planck constant, and kB is the Boltzmann constant. It provides an estimate of the temperature below which tunnelling dominates the rate constant. Instantons were optimised to a residual gradient below 10−8 au. A path of the transition structure elongated along the unstable mode was chosen as the initial guess for the calculation of the first instanton of each reaction. For every subsequent cooling step, the geometry of the preceding instanton was used as the initial configuration for the optimisation. Optimised instantons can be used to calculate both bi- and unimolecular rate constants by using the respective reactant partition function. In this work we focus on unimolecular rate constants, since these are related to the Langmuir–Hinshelwood surface reaction mechanism that is relevant at the low temperatures present in dense clouds in the ISM. All instantons were calculated down to the temperature of 60 K.
3 Results
We first introduce the five investigated molecules and their possible reactions along with DFT calculations of the activation and reaction energies. Subsequently, we discuss the calculated rate constants for all exothermic reactions. Finally, we relate the calculated rate constants to previous experimental observations (Jonusas et al. 2017).
3.1 Selected molecules
We performed calculations for hydrogen addition and abstraction reactions of five unsaturated organic molecules, each containing an aldehyde group, alcohol group, carbon double or triple bond. These are, starting from the most unsaturated molecule, propynal, propargyl alcohol, propenal, allyl alcohol, and propanal. In order to simplify the nomenclature of possible reaction paths, each carbon atom of the selected molecules is labelled as depicted in Fig. 1.
The mass of the migrating particles, the height, and the width of the barrier are three important parameters that have impact on quantum tunnelling. Since all reactions we study here are hydrogen addition or abstraction reactions, the effective mass can be considered to be similar in all cases. Activation and reaction energies excluding (EA and Er, respectively) and including (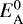 and
and 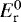 , respectively) zero-point vibrational energy (ZPE) were calculated relative to the PRC. They are given, along with the crossover temperatures, in Table 1.
, respectively) zero-point vibrational energy (ZPE) were calculated relative to the PRC. They are given, along with the crossover temperatures, in Table 1.
The barriers for hydrogen addition reactions, including zero-point energies, lie between 8.2 and 41.1 kJ mol−1. The highest activation energies were observed for the hydrogen addition on the O atom of the aldehyde group in accordance with results obtained for glyoxal and glycoaldehyde by Álvarez-Barcia et al. (2018). The lowest barriers are found for hydrogen additions to the C3 atom of either a double or triple bond. Activation energies for the hydrogen abstraction reactions are generally somewhat higher than those for hydrogen addition reactions and range from 13.8 to 67.0 kJ mol−1. The hydrogen abstraction reaction with the highest activation energy is the one at the C3 position for all molecules, while abstraction at C1 is comparatively easy. The C3 hydrogen abstraction reactions of propynal and propargyl alcohol are highly endothermic (on the order of 130 kJ mol−1), and thus are not considered in the following. A PRC structure could not be found for hydrogen abstraction at the C3 -atom from propynal and propargyl alcohol. Thus, we used the separated molecules as reference.
For moderately endothermic reactions, like hydrogen abstraction from C2 and C3 for propenal and allyl alcohol, no rate constants were calculated since they are very low at low-temperature conditions. Tunnelling can be expected to only occur through the exothermic fraction of the barrier. The three reactions that become exothermic when including zero-point energy, on the other hand, are also discussed in the following sections.
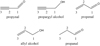 |
Fig. 1 Investigated molecules, containing carbon double or triple bonds, and aldehyde or alcohol groups: propynal, propargyl alcohol, propenal, allyl alcohol, and propanal. Carbon atoms are enumerated starting from the one nearest to the functional group. |
3.2 Rate constants
All calculated rate constants here concern reactions between closed-shell molecules and hydrogen atoms. The resulting radicals can subsequently react with another radical, for example, a hydrogen atom through generally barrier-less, radical-recombination reactions. Thus, in the overall process, the rate constants we provide here are rate limiting, unless the orientation of the reactants prevents reactions from taking place.
The temperature-dependent unimolecular rate constants calculated below the crossover-temperature by canonical instanton theory are given in Fig. 2 for both the hydrogen addition and hydrogen abstraction reactions. We note that the deviation from the smooth curves visible in panel d, for instance, is thought to be due to numerical errors, and these irregularities are thus not physically meaningful. For numerical values, we refer to Appendix C. The plots are ordered according to the bond type, that is, addition to carbon double and triple bonds in Figs. 2a and b, addition to the aldehyde C and O atoms in panel c, and abstraction reactions in panels d and e. The rate constants for different reaction paths range over almost 16 orders of magnitude; the y-axis scales in Fig. 2 vary.
The rate constant does not only depend on the barrier height, but also on the shape of the barrier. The easiest estimation for that is the curvature of the classical transition state (Gillan 1987), which can be extracted from the crossover temperatures given in Table 1. A high crossover temperature indicates a thin barrier. The full IRC paths for the reactions of the hydrogen atoms with the investigated molecules are presented in Appendix B. We note that at low impact energies, that is, when the temperature is low, the shape of the barrier along the IRC may be distinctly different from that at the classical transition state (see Fig. B.1).
Comparing the hydrogen addition reactions to the C3 atoms for the double and triple bonds, Figs. 2a and b, we find that addition to the double bonds is faster than to the triple bonds, in accordance with results obtained for C2 H2 and C2 H4 (Kobayashi et al. 2017). Moreover, addition to the C3 atom is generally the fastest reaction pathway compared to the other possibilities within the same molecules. This in turn is in agreement with the activation energies presented in Table 1, since these reactions have the lowest energy barriers.
The rate constants for the hydrogenation of the aldehyde group show the lowest reactivity, as depicted in Fig. 2c, regardless of whether the addition takes place at the carbon or oxygen atom. Although the barriers for addition to O atoms are higher, they are somewhat narrower (except for propanal), as can be seen in Fig. B.1c. This leads to the observed crossing of the rate constants around 100 K. In the high-temperature regime, the addition to O is slower, but at lower temperatures, the barrier width dominates the tunnelling behaviour, as explained above, and indeed the hydrogen addition to O surpasses the addition to C1. The hydrogenation of the oxygen atom of propanal has a much higher and therefore broader barrier than the other molecules, leading to much lower rate constants.
The hydrogen abstraction rate constants vary strongly among the selected molecules, as can be seen in Figs. 2d and e. The rate constants for hydrogen abstraction from C1 reversely follow the activation energy and crossover temperature values presented in Table 1. In other words, the instanton rate constants run parallel to each other, but their values are shifted according to the barrier height, since the barrier shape is very similar. The three abstraction reactions that are exothermic only when considering the ZPE have very similar barrier heights, resulting in similar rate constants at high temperature. At low temperature, especially the abstraction of a hydrogen atom from the alcohol group of propargyl alcohol is notable, where the rate constant decreases steeply with decreasing temperature as a result of its much wider barrier at low impact energies (see Fig. B.1e).
From the above it becomes clear that it is not possible to extrapolate rate constants from small test systems directly to other molecules that may contain the same bond type, but different functional groups. The easiest example to demonstrate this is the H-addition to carbon double or triple bonds, where previous calculations on C 2H 2 and C 2H 4 differ by up to two orders of magnitude from those calculated here for the C 3H nO species. Furthermore, the hydrogen abstraction reactions also clearly show that although the barrier shapes are very similar, the barrier height differs so much between the five molecules considered here that the rate constants also spread over three orders of magnitude.
Activation energies EA and reaction energies Er of hydrogen addition and abstraction reactions for the investigated molecules in kJ mol−1 relative to the PRC.
 |
Fig. 2 Instanton rate constants for the reactions of hydrogen atoms with the investigated molecules. Panel a: hydrogen additions to carbon double bonds. Values for C2 H2 and C2 H4 are taken from Kobayashi et al. (2017). Panel b: hydrogen addition to carbon triple bonds. Panel c: hydrogen additions to aldehyde groups. Panel d: hydrogen abstractions from C1 and C2. Panel e: hydrogen abstractions from C3 and O (exothermic due to ZPE). |
3.3 Comparison with experiments
We briefly sketch the main experimental results per molecule as obtained by Jonusas et al. (2017) and comment how our calculated rate constants relate to their experiments. We note that experiments were carried out at 10 K, whereas our low-temperature rate constants are calculated at 60 K. Overall, we find good agreement with the experimental data.
Propynal. Experiments show that the hydrogenation of propynal directly leads to the formation of propanal, leaving propenal as a short-lived species. Furthermore, hydrogen addition to the aldehyde group of the propynal was proposed not to lead to propargyl alcohol.
The calculated rate constants for the hydrogenation of the C3 carbon atom of propenal are at least one order of magnitude higher than those for the hydrogenation of the C3 carbon atom of propynal. This supports the experimental results of propenal as short-lived species. Addition at the C2 atom or abstraction from the C1 atom have lower values for the rate constant, and therefore we expect the addition to the C3 carbon to be followed by a barrier-less addition to the C2 carbon as a second step. Finally, hydrogenation of the aldehyde group of propynal is indeed much slower than the hydrogenation of the carbon double or triple bonds and is therefore not competitive.
Propenal. Experimentally, hydrogenation of propenal only leads to the reduction of the carbon double bond.
We find very similar results as for propynal, that is, the rate constant for addition to the aldehyde group is several orders of magnitude lower than for hydrogen addition to the C3 carbon atom. Both addition to C2 and abstraction from C1 are slower as well, suggesting that again addition to the C3 carbon is the dominant pathway.
Propanal. The experimental hydrogenation of propanal did not lead to propanol formation.
For the reaction of the hydrogen atom with propanal, the possibilities are addition to the aldehyde C or O atom or abstraction from C1, C2, or C3. Out of these, the fastest reaction by more than three order of magnitude is abstraction from the C1 carbon atom. This may lead to a cycle of H abstraction and subsequent barrier-less H addition reactions on the same carbon atom, leading to a net zero result. It is expected that because of such a cycle, indeed no propanol could be formed during the experiments.
Allyl alcohol and propargyl alcohol. Experimentally, the hydrogenation of propargyl alcohol ice leads mainly to allyl alcohol, although no further reaction to propanol is observed. Hydrogenation of a pure allyl alcohol sample, on the other hand, did lead to the formation of propanol. It was furthermore concluded that the activation energy is higher for the hydrogenation of the triple bond of propargyl alcohol than for the double bond of allyl alcohol.
Calculated rate constants and barrier relations are similar to those discussed above, that is, faster hydrogenation for double bonds than for triple bonds. The C1 hydrogen abstraction reaction from propargyl alcohol may compete with both the C2 and C3 hydrogen addition reactions, which can lead to an even slower reduction of the triple bond. Hydrogen abstraction from the OH group of the alcohols is slower than all competing reactions in both cases.
We wish to stress that experimental non-detection or the low values for the calculated rate constants do not imply that a reaction does not take place on interstellar timescales. This may in particular be important when specific reactive sites are blocked as a result of the orientation on an ice surface.
Finally, as for the formation of propanol in the solid state in the interstellar medium, hydrogenation of aldehydes with three carbon atoms does not seem to be an efficient route. However, other surface routes may still be available, such as the recombination of C 2H n and CH 2OH fragments.
4 Conclusions
Unimolecular reaction rate constants have been calculated and are provided for hydrogen addition and abstraction reactions from propynal, propargyl alcohol, propenal, allyl alcohol, and propanal and are thus available to be implemented in both rate-equation and kinetic Monte Carlo models aimed at studying the formation of COMs at low temperatures. Our results are generally in agreement with ultra-high vacuum experiments.
Specifically, we can say that hydrogen addition to the C3 atom is fastest, most notable for double bonds. However, addition to the C3 atom for carbon triple bonded molecules is still faster than addition to either the C1 or O atom of the aldehyde group.
For selected molecules, hydrogen abstraction reactions are in competition with addition reactions, overall slowing down the saturation of unsaturated bonds. However, on average, abstraction reactions have higher energy barriers and can also be endothermicin some cases.
Not only are hydrogen addition and abstraction in competition with each other, but the larger the molecules are, hydrogen diffusion starts to play a role as well in diffusion from on side of the molecule to another.
Finally, every molecule is unique, and therefore it is not wise to use small model systems to extrapolate rate constants for large molecules with similar bond types. Compare for instance the values for C2 H2 and C2 H4 vs. those forthe molecules studied here.
Acknowledgements
This project was financially supported by the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 646717, TUNNELCHEM) for V.Z., M.M., and J.K., and the Alexander von Humboldt Foundation, the Netherlands Organisation for Scientific Research (NWO) via a VENI fellowship (722.017.008) and COST Action CM1401 via a STSM for TL.
Appendix A Benchmark
Relative energies with respect to the separated reactants of the bimolecular hydrogen addition reactions for the propenal molecule without vibrational ZPE.
Appendix B IRC: Classical reaction paths
The IRC paths for the reactions of hydrogen atoms with the investigated molecules are presented in Fig. B.1. For the hydrogen addition reactions, IRCs are ordered according to the bond type. The barrier widths are similar for reactions proceeding at the same bond type. Additionally, a comparison with the hydrogenation energy barriers of C2 H2 and C2 H4 was carried out. Although the IRCs indeed follow a similar trend qualitatively, quantitative, differences in the barrier height are present.
For the hydrogen abstractions from the C1 site, all reactions are exothermic. The hydrogen abstractions from the alcohol group for allyl and propargyl alcohol become exothermic when including zero-point energy, but have very high activation energies. For the hydrogen abstraction from the alcohol group of propargyl alcohol, the additional structure rearrangement after the reaction contributes to the exothermicity. We note that the IRCs look quite different in terms of the width, although the only difference in the molecule is the existence of a double or triple bond. Again, this shows that it is not easily possible to extrapolate reaction energetics by reactions on the similar functional groups.
 |
Fig. B.1 IRCs for the reactions of hydrogen atoms with the investigated molecules. Panel a: hydrogen additions to carbon double bonds. Panel b: hydrogen additions to carbon triple bonds. Panel c: hydrogen additions to aldehyde groups. Values for C2 H2 and C2 H4 are taken from Kobayashi et al. (2017). Panel d: hydrogen abstractions from C1 and C2. Panel e: hydrogen abstractions from C3 and O (exothermic due to ZPE). |
Appendix C Rate constant values
Instanton rate constants for the hydrogen addition to propynal.
Instanton rate constants for the hydrogen abstraction from propynal.
Instanton rate constants for the hydrogen addition to propargyl alcohol.
Instanton rate constants for the hydrogen abstraction from propargyl alcohol.
Instanton rate constants for the hydrogen addition to propenal.
Instanton rate constants for the hydrogen abstraction from propenal.
Instanton rate constants for the hydrogen addition to allyl alcohol.
Instanton rate constants for the hydrogen abstraction from allyl alcohol.
Instanton rate constants for the hydrogen addition to propanal.
Instanton rate constants for the hydrogen abstraction from propanal.
References
- Adler, T. B., Knizia, G., & Werner, H.-J. 2007, J. Chem. Phys., 127, 221106 [NASA ADS] [CrossRef] [Google Scholar]
- Álvarez-Barcia, S., Russ, P., Kästner, J., & Lamberts, T. 2018, MNRAS, 479, 2007 [NASA ADS] [CrossRef] [Google Scholar]
- An, D., Sellgren, K., Boogert, A. C. A., Ramírez, S. V., & Pyo, T.-S. 2017, ApJ, 843, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Ball, J. A., Gottlieb, C. A., Lilley, A. E., & Radford, H. E. 1970, ApJ, 162, L203 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, J. E., & Mile, B. 1973, J. Chem. Soc., Faraday Trans., 1, 1398 [CrossRef] [Google Scholar]
- Bisschop, S. E., Jørgensen, J. K., Bourke, T. L., Bottinelli, S., & van Dishoeck E. F. 2008, A&A, 488, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boogert, A. A., Gerakines, P. A., & Whittet, D. C. 2015, ARA&A, 53, 541 [Google Scholar]
- Callan, C. G., & Coleman, S. 1977, Phys. Rev. D, 16, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, S. 1977, Phys. Rev. D, 15, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Deegan, M. J. O., & Knowles, P. J. 1994, Chem. Phys. Lett., 227, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillan, M. J. 1987, J. Phys. C, 20, 3621 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A. 1973, in Molecules in the Galactic Environment, eds. M. A. Gordon, & L. E. Snyder (New York, NY: Wiley-Interscience), 181 [Google Scholar]
- Hiraoka, K., Miyagoshi, T., Takayama, T., Yamamoto, K., & Kihara, Y. 1998, ApJ, 498, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Møllendal, H. 2004, ApJ, 610, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Hollis, J. M., Remijan, A. J., Jewell, P. R., & Lovas, F. J. 2006, ApJ, 642, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Hratchian, H. P., & Schlegel, H. B. 2004, J. Chem. Phys., 120, 9918 [NASA ADS] [CrossRef] [Google Scholar]
- Irvine, W. M., Brown, R. D., Cragg, D. M., et al. 1988, ApJ, 335, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Jonusas, M., Guillemin, J.-C., & Krim, L. 2017, MNRAS, 468, 4592 [NASA ADS] [CrossRef] [Google Scholar]
- Kästner, J. 2014, WIREs Comput. Mol. Sci., 4, 158 [CrossRef] [Google Scholar]
- Kästner, J., Carr, J. M., Keal, T. W., et al. 2009, J. Phys. Chem. A, 113, 11856 [CrossRef] [Google Scholar]
- Knizia, G., Adler, T. B., & Werner, H.-J. 2009, J. Chem. Phys., 130, 054104 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, P. J., Hampel, C., & Werner, H.-J. 1993, J. Chem. Phys., 99, 5219 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, P. J., Hampel, C., & Werner, H.-J. 2000, J. Chem. Phys., 112, 3106 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., Hidaka, H., Lamberts, T., et al. 2017, ApJ, 837, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, J. 1967, Ann. Phys., 41, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J.-C., Agúndez, M., Marcelino, N., et al. 2016, MNRAS, 456, 4101 [Google Scholar]
- Lykke, J. M., Coutens, A., Jørgensen, J. K., et al. 2017, A&A, 597, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McConnell, S., & Kästner, J. 2017, J. Comput. Chem., 38, 2570 [CrossRef] [Google Scholar]
- McGuire, B. A., Carroll, P. B., Loomis, R. A., et al. 2016, Science, 352, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Meisner, J., & Kästner, J. 2016, Angew. Chem., Int. Ed., 55, 5400 [Google Scholar]
- Meisner, J., Lamberts, T., & Kästner, J. 2017a, ACS Earth Space Chem., 1, 399 [Google Scholar]
- Meisner, J., Markmeyer, M. N., Bohner, M. U., & Kastner, J. 2017b, Phys. Chem. Chem. Phys., 19, 23085 [CrossRef] [Google Scholar]
- Metz, S., Kästner, J., Sokol, A. A., Keal, T. W., & Sherwood, P. 2014, WIREs Comput. Mol. Sci., 4, 101 [CrossRef] [Google Scholar]
- Miller, W. H. 1975, J. Chem. Phys., 62, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, K. A., Adler, T. B., & Werner, H.-J. 2008, J. Chem. Phys., 128, 084102 [NASA ADS] [CrossRef] [Google Scholar]
- Rommel, J. B., & Kästner, J. 2011, J. Chem. Phys., 134, 184107 [NASA ADS] [CrossRef] [Google Scholar]
- Rommel, J. B., Goumans, T. P. M., & Kästner, J. 2011, J. Chem. Theory Comp., 7, 690 [NASA ADS] [CrossRef] [Google Scholar]
- Sherwood, P., de Vries, A. H., Guest, M. F., et al. 2003, J. Mol. Struct.: THEOCHEM, 632, 1 [Google Scholar]
- Tielens, A. G. G. M., & Hagen, W. 1982, A&A, 114, 245 [Google Scholar]
- Turner, B. E., & Apponi, A. J. 2001, ApJ, 561, L207 [NASA ADS] [CrossRef] [Google Scholar]
- Valiev, M., Bylaska, E., Govind, N., et al. 2010, Comput. Phys. Commun., 181, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Loomis, R. A., Öberg, K. I., et al. 2016, ApJ, 823, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, N., & Kouchi, A. 2002, ApJ, 571, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Weigend, F., Häser, M., Patzelt, H., & Ahlrichs, R. 1998, Chem. Phys. Lett., 294, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., & Schütz, M. 2012, WIREs Comput. Mol. Sci., 2, 242 [CrossRef] [Google Scholar]
- Zhao, Y., & Truhlar, D. G. 2004, J. Phys. Chem. A, 108, 6908 [CrossRef] [Google Scholar]
- Zuckerman, B., Turner, B. E., Johnson, D. R., et al. 1975, ApJ, 196, L99 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Activation energies EA and reaction energies Er of hydrogen addition and abstraction reactions for the investigated molecules in kJ mol−1 relative to the PRC.
Relative energies with respect to the separated reactants of the bimolecular hydrogen addition reactions for the propenal molecule without vibrational ZPE.
All Figures
 |
Fig. 1 Investigated molecules, containing carbon double or triple bonds, and aldehyde or alcohol groups: propynal, propargyl alcohol, propenal, allyl alcohol, and propanal. Carbon atoms are enumerated starting from the one nearest to the functional group. |
| In the text | |
 |
Fig. 2 Instanton rate constants for the reactions of hydrogen atoms with the investigated molecules. Panel a: hydrogen additions to carbon double bonds. Values for C2 H2 and C2 H4 are taken from Kobayashi et al. (2017). Panel b: hydrogen addition to carbon triple bonds. Panel c: hydrogen additions to aldehyde groups. Panel d: hydrogen abstractions from C1 and C2. Panel e: hydrogen abstractions from C3 and O (exothermic due to ZPE). |
| In the text | |
 |
Fig. B.1 IRCs for the reactions of hydrogen atoms with the investigated molecules. Panel a: hydrogen additions to carbon double bonds. Panel b: hydrogen additions to carbon triple bonds. Panel c: hydrogen additions to aldehyde groups. Values for C2 H2 and C2 H4 are taken from Kobayashi et al. (2017). Panel d: hydrogen abstractions from C1 and C2. Panel e: hydrogen abstractions from C3 and O (exothermic due to ZPE). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


