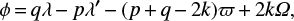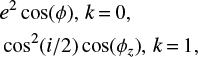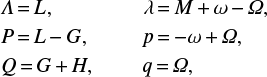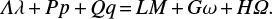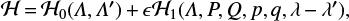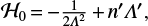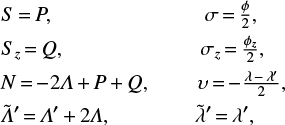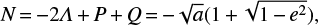EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 617 (September 2018) A&A, 617 (2018) A114 Full HTML
Free Access
Issue
A&A
Volume 617, September 2018
Article Number A114
Number of page(s) 8
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/201833019
Published online 28 September 2018

© ESO 2018

1. Introduction

All of the major planets and a significant portion of the asteroids have orbits around the Sun with an inclination i < 90° when viewed from above the north ecliptic pole of our solar system (Wiegert et al. 2017). However, small bodies on retrograde orbits do exist in the solar system, such as irregular satellites that have eccentric, highly inclined or even retrograde orbits around their giant planets (Jewitt & Sheppard 2003). Although the origins of these mysterious retrograde objects are not yet clear, they are generally believed to have been captured from heliocentric orbit during the final phase of planetary accretion (Pollack et al. 1979; Heppenheimer & Porco 1977). Halley-type comets (HTCs) provide us with some good candidates to study the dynamics of retrograde objects, while their origin has long been a matter of debate (Emel’yanenko & Bailey 1998; Fernandez & Gallardo 1999; Wiegert & Tremaine 1999; Nurmi et al. 2002; Fouchard et al. 2014; Olsson-Steel 1988; Levison et al. 2001, 2006; Fernandez et al. 2016). Minor bodies in retrograde orbits are rare in our solar system. Among the 753 782 small bodies found so far, only 93 are in retrograde motion1. In recent years, research into heliocentric retrograde orbital motion has gradually grown but lots of details have remained uncertain. Morais & Namouni (2013a) identified some asteroids trapped into retrograde resonance for thousands of years with Jupiter and Saturn. Greenstreet et al. (2012) suggested that the retrograde orbits inside Jupiter’s heliocentric path may be produced through the gravitational interaction of Jupiter and Saturn. Surprisingly, after the discovery of the first retrograde extrasolar planet, which is known as HAT-P-7b (Narita et al. 2009; Winn et al. 2009), Triaud et al. (2010) identified some other exoplanets on retrograde orbits. Interestingly, Chen et al. (2016) identified a new retrograde trans-Neptunian object (TNO), nicknamed Niku, which is confirmed to be in 7/9 mean motion resonance with Neptune by Morais & Namouni (2017b). These findings further stimulate the researchers’ interest in retrograde motion. Understanding the dynamics of the retrograde minor bodies is significant for the study of the mechanisms and origins of the major and minor planets on retrograde orbits.

More than 7000 trojans have been discovered until now, which are locked into stable prograde co-orbit motion with Jupiter. Some trojans of other planets including Earth, Mars, Uranus, and Neptune2 have also been observed in recent years, such as the Earth’s first trojan, 2010 TK7 (Connors et al. 2011), but no Saturn trojans have ever been identified (Hou et al. 2014). Interestingly, a retrograde co-orbit motion was not found until recently. In recent years, some theoretical work on these mysterious orbits has verified that the co-orbit retrograde motion can be stable. Morais & Namouni (2013b) developed a semi-analytical model for retrograde co-orbit motion through the averaged unexpanded disturbing function. They confirmed later that there is a great potential for retrograde orbits trapped in co-orbit resonance (Namouni & Morais 2015). The stability and properties of spatial co-orbital motion have been studied by Morais & Namouni (2016) from numerical simulations. The authors confirmed that a stable co-orbit motion can exist regardless of the orbital inclination, which, of course, includes the retrograde case.

The recent discovery of the first asteroid trapped in retrograde co-orbit resonance with Jupiter, 2015 BZ509, has renewed interest in the search for such mysterious objects (Wiegert et al. 2017). Asteroid 2015 BZ509 is the first asteroid in retrograde co-orbit resonance with a planet of our solar system, and it has long-term stability. Wiegert et al. (2017) suggest that this asteroid can keep this stable resonant state for about a million years. The retrograde co-orbit resonance with Jupiter protects it from disruptive close encounters with the other planets. Through numerical simulations, Namouni & Morais (2017) have found that 2015 BZ509 lies almost exactly at the capture efficiency peak. Indeed, Morais & Namouni (2013a) have found that 2006 BZ8 could enter into co-orbit retrograde resonance with Saturn in the future. From numerical simulations, Namouni & Morais (2015) showed that asteroids on retrograde motion are more easily captured in mean motion resonances than those on prograde motion. In this paper, we identify the dynamics of the centaurs that have co-orbit retrograde orbits around Saturn by numerical simulations, trying to find some new small bodies in co-orbit retrograde resonance with the giant planets of our solar system.

The article is structured as follows: in Sect. 2, we introduce the main properties of the retrograde mean motion resonance, and the co-orbit retrograde resonance is discussed in detail. Section 3 gives a full description of the numerical model used in our study. In Sect. 4, we show the general statistical results of our numerical simulations and analyze the complicated resonant states we observed. In Sect. 5, we analyze the phase-space portrait of the co-orbit retrograde resonance and present a comparison between the results obtained from the semi-analytical model and the numerical simulations. Our conclusions and some discussion are given in the last section.

2. Retrograde co-orbit resonance

A retrograde mean motion resonance between a small body and a planet (denoted by superscript symbol ′) occurs when pn − qn′ ≈ 0, where p and q are both positive integers, and n and n′ are the mean motion frequencies of the small body and the planet, respectively. We call such resonance a retrograde p/q resonance or p/−q resonance.

To determine whether these minor bodies are in retrograde co-orbit resonances with Saturn, we have to first get the correct expression of the particular resonant angles defined by the Fourier expansion of the disturbing function (Murray & Dermott 1999). For retrograde mean motion resonance, Morais & Namouni (2013b) presented a transformation of the relevant resonant term for the corresponding retrograde resonance to keep with the conventional definition of osculating orbital elements in prograde motion. The expression of the longitude of the pericenter becomes ϖ = ω – Ω, while the mean longitude of the asteroid becomes λ = M + ω − Ω, where ω, Ω, and M are the argument of pericenter, the longitude of the ascending node, and the mean anomaly, respectively.

Morais & Namouni (2013a,b, 2016) reported that the resonant angles for the p/−q resonance have the forms

(1)

where p, q, and k are positive integers. The equation p + q ≥ 2k must be satisfied, and the lowest order terms are proportional to cos2k(i/2)ep + q − 2k, where i and e are respectively the inclination and the eccentricity of the small body. The resonant term corresponding to k = 0 will be the dominant one for the nearly coplanar retrograde motion because of cos(i/2) ≈ 0. In particular, for retrograde co-orbit resonance, the lowest order resonant terms are proportional to

(2)

where ϕ = λ – λ′ – 2ϖ and ϕz = λ − λ′ + 2Ω are two resonant angles of the 1/−1 resonance. When we study the centaurs in 1/−1 resonance with Saturn, we also consider the possibility of the centaurs in 2/−5 resonance with Jupiter as the positions of Jupiter and Saturn are near the 5/2 resonance.

3. Descriptions concerning the numerical model

To find all of the small bodies in 1/−1 resonance with Saturn, we use the JPL (Jet Propulsion Laboratory) Small-Body Database Search Engine3 to search for small bodies with retrograde orbits (inclination i > 90°) and semi-major axes ranging from 9.3 au to 9.8 au (the semi-major axis of Saturn is aSaturn = 9.54 au). There are four centaurs that meet our limitations: 2006 RJ2, 2006 BZ8, 2012 YE8, and 2017 SV13. We studied centaurs on retrograde orbits, which are usually believed to be strongly chaotic because of their giant-planet crossing orbit. The discovered centaurs mainly have two kinds of dynamical evolution (Bailey & Malhotra 2009; Volk & Malhotra 2013): random walk and resonance sticking. Jewitt (2005) suggested that the most obvious origin of these selected small bodies among damocloids (Jupiter Tisserand’s parameter T < 2) would be an Oort Cloud or Halley-type comet.

We numerically integrate the motions of these centaurs in the solar system using the MERCURY (Chambers 1999) package with an accuracy parameter 10−12. The Burlisch-Stoer integrator is employed while considering all the gravity of the eight planets throughout the integration. As listed in Tables 1 and 2, the uncertainty parameters U4 of 2006 RJ2, 2006 BZ8, 2012 YE8, and 2017 SV13 according to the Minor Planet Center are 5, 0, 5, and 4, respectively. To exclude the influence of uncertainties in the orbit determination, we generated 1000 clone orbits (include the nominal one) for each selected centaur by standard deviations (1-σ uncertainties), which correspond to Gaussian distribution around the nominal orbit. We integrate the nominal and clone orbits over a 40 000 yr period from −10 000 yr to 30 000 yr around the present day.

Table 1.

Nominal orbital elements at JED2458000.5 of 2006 RJ2.

Table 2.

Nominal orbital elements at JED2458000.5 of 2006 BZ8, 2012 YE8, 2017 SV13.

4. Crucial statistical results of numerical simulations

To evaluate the particular resonant state of each candidate, we focus on the fractions of clones trapped in 1/−1 resonance, currently in 1/−1 resonance, and trapped in 1/−1 resonance over 10 000 yr with Saturn, respectively. The crucial statistical results of numerical simulations include the properties of each candidate in 1/−1 mean motion resonance with Saturn and are given in Table 3. The following section gives detailed descriptions of the dynamical states of the four centaurs under consideration.

Table 3.

Numerical statistics about fraction of clones for four centaurs under study.

Centaur 2006 RJ2 was discovered on 14 September 2006 and was designated as a centaur. As shown in Table 1, the centaur has an orbit with large inclination and eccentricity. As shown in Fig. 1, the nominal orbit of 2006 RJ2 is currently in a long-term stable 1/−1 resonance with Saturn. In fact, the fourth panel of Fig. 1 shows that libration of the resonant angle ϕ is of large amplitude and is centered on 0°, which confirms that the nominal orbit of 2006 RJ2 is in 1/−1 resonance with Saturn. The oscillation of the resonant angles for most of the clones of 2006 RJ2 also behaves in a similar way. As shown in Table 3, 906 clones are trapped in retrograde co-orbit resonance and 752 clones among them keep this resonant state over 10 000 yr. Above all, a majority of (805/1000) clones are shown to be in co-orbit resonance at the present time. Therefore, these results seem to suggest that 2006 RJ2 is very likely a retrograde co-orbital centaur of Saturn, and that this finding is not accidentally due to uncertainties in the orbit determination. From this, it is probable that 2006 RJ2 is another minor body apart from 2015 BZ509 in retrograde co-orbit resonance with the giant planets. The last panel of Fig. 1 shows that the resonance protects the centaur from close encounters with the giant planets. In fact, the minimum distance in a close encounter with the giant planets is always larger than two Hill’s radii during the whole integration time span. A brief capture in the 2/−5 resonance with Jupiter after the centaur exits the 1/−1 resonance is also possible (363/1000 clones). The path of centaur 2006 RJ2 in Saturn’s rotating frame is shown in Fig. 2. When viewed from above the plane of Saturn’s orbit (Fig. 2a), the motion of 2006 RJ2 has a typical type of trisectrix curve defined by Morais & Namouni (2017a). Morais & Namouni (2016) have confirmed by numerical investigations that this trisectrix motion of 2006 RJ2 can be long-term stable if it is influenced only by Saturn.

thumbnail Fig. 1.

Properties of the nominal orbit of 2006 RJ2. From top to lower panel: semimajor axis a and location of exact 1/−1 resonance with Saturn; eccentricity e; inclination i; angle for nearly coplanar motion involving 1/−1 resonance with Saturn ϕ; 2/−5 resonant angle with Jupiter ϕ2; argument of pericenter ω; the minimum distance in close encounters with Jupiter and Saturn within three Hill’s radii of the planet is represented by red plus and green square, respectively.

thumbnail Fig. 2.

Path of the Centaur 2006 RJ2 in the frame that rotates with Saturn. X, Y, and Z are the cartesian axes of the Saturn’s rotating frame. The X-axis points from Sun to Saturn and Z-axis is vertical to Saturn’s orbital plane. Saturn is presented as the green filled circle. Panel a: path of 2006 RJ2 in Saturn’s rotating frame viewed from the Z-axis direction. The black dotted curve is the Saturn’s orbit in the inertial reference frame. Panel b: motion of 2006 RJ2 viewed from the Y-axis direction. The blue curve represents the motion of 2006 RJ2 above the Saturn’s orbital plane while the red curve means the opposite.

Now, we focus on the other three potential retrograde co-orbital centaurs of Saturn, 2006 BZ8, 2012 YE8, and 2017 SV13, which have retrograde orbits around Saturn and may be captured in the 1/−1 resonance within the whole integration time span. Table 2 shows their orbital elements and the 1-σ uncertainties at JED2458000.5. Centaur 2006 BZ8 has been confirmed to be in 2/−5 resonance with Jupiter (libration around 180°) (Morais & Namouni 2013a). Moreover, as listed in Table 3, our numerical statistical results show that this centaur has a low probability of currently being in a 1/−1 resonant state with Saturn (9/1000), which is not mentioned in Morais & Namouni (2013a). Moreover, as shown in Fig. 3, we choose one of the best clones captured in a 1/−1 resonant state. Our statistical results indicate that capture in 1/−1 resonance with Saturn (libration around 0°) within a 40 000 yr integration time span is possible (878/1000 clones), and 38 clones among them are captured in 1/−1 resonant state over 10 000 yr. Morais & Namouni (2013a) suggested that 2006 BZ8 is in Lidov–Kozai secular resonance; we find that 2006 BZ8 is locked in a Lidov–Kozai mechanism (the argument of pericenter ω librates around 0°) at present and will exit at around 120 000 yr5. The main dynamical properties of the Lidov–Kozai mechanism for retrograde orbits (i > 90°) outside the mean motion resonances are identical with the symmetrical prograde orbits with inclination 180 − i. Kozai (1962) studied the secular evolution of a test particle (a = 3 au) in the main asteroid belt while considering the effect of Jupiter only. Thomas & Morbidelli (1996) used the semi-analytical method to study the Lidov–Kozai dynamics around the main belt (a = 3 au) and the Kuiper belt (a = 45 au) by considering the effects of the four giant planets. Gronchi & Milani (1999) introduced an example (a = 7 au) to analyze the Lidov–Kozai dynamics on centaurs. They pointed out that for orbits with a moderate value of maximum orbital inclination (imax = 25°), the argument of pericenter ω librates around 0° or 180°. For even larger imax, there will be new libration regions where ω = 90° or 270° and large eccentricity. However, there are as yet no systematic studies on the role of the Lidov–Kozai mechanism in minor bodies near giant planets. We will analyze in detail the effects of Lidov–Kozai dynamics on retrograde centaurs near giant planets in our future work. It is interesting to note that in the restricted three-body model (Sun-Saturn-2006 BZ8), the centaur 2006 BZ8 is in 1/−1 resonance with Saturn very well for over 10 000 yr. A similiar result is obtained in the Sun-Jupiter-2006 BZ8 model where the Centaur is in 2/−5 resonance with Jupiter. We will try to analyze this interesting phenomenon in our future work.

thumbnail Fig. 3.

Cloned orbit of 2006 BZ8 chosen as one of best clones captured in 1/−1 resonance. The basic meaning of this figure is the same as Fig. 1.

Centaur 2012 YE8 (Fig. 4) is currently near the 2/−5 resonance with Jupiter and the 1/−1 resonance with Saturn at the same time. Close approaches to Saturn and Jupiter may lead the centaur to enter or exit the resonant states. Since its orbit is far from the planar case, we consider two possible 1/−1 resonant angles (ϕ and ϕz). In our numerical integrations for 2012 YE8, as listed in Table 3, 140/1000 clones are currently in 1/−1 resonance with Saturn (libration around 0°), 426 clones are trapped in this resonant state, and 100 clones among them have relative long-term stability. Meanwhile, 268/1000 clones are captured in the 2/−5 resonance with Jupiter (libration around 180°), most often occurring between −10 000 yr and −5000 yr and from 15 000 yr to 25 000 yr. The argument of pericenter ω is always close to 0° over the integration timespan, which means a Lidov–Kozai secular resonance5.

thumbnail Fig. 4.

Cloned orbit of 2012 YE8. Since its orbit is far from the planar case, another 1/−1 resonant angle with Saturn ϕz is included. The other basic meaning of this figure is the same as Fig. 1.

Centaur 2017 SV13 was discovered on 17 September 2017 and designated as a centaur. Different from the other three centaurs, 2017 SV13 has a near-vertical orbit. As shown in Fig. 5, 2017 SV13 is another suitable candidate to be in 1/−1 resonance with Saturn. Almost all of the clones (998/1000 clones) are captured in 1/−1 resonance with Saturn (libration around 0°), and the resonant state of 626 clones among them last beyond 10 000 yr. Meanwhile, 434 clones are shown to be in retrograde co-orbit resonance at present, and clones are always expected in a 1/−1 resonant state between the 5000 yr and 15 000 yr time span. These results make 2017 SV13 another good candidate for Saturn’s retrograde co-orbital centaur. After leaving the 1/−1 resonance around 15 000 yr, 595/1000 clones will be captured in 2/−5 resonance with Jupiter (libration around 180°). The motion is not in Lidov–Kozai secular resonance presently but will be briefly captured in the Lidov–Kozai mechanism (the argument of pericenter ω librates around ±90°)5.

thumbnail Fig. 5.

Cloned orbit of 2017 SV13. Since its orbit is far from the planar case, another 1/−1 resonant angle with Saturn ϕz is included. In the last panel, the minimum distance in close encounters with Jupiter and Uranus within three Hill’s radii of the planet is represented by red plus and cyan cross, respectively. The other basic meaning of this figure is the same as Fig. 1.

5. Phase-space portrait of 1/−1 mean motion resonance

To confirm that the centaurs may be captured in 1/−1 resonance with Saturn, this section is devoted to the construction of the theory of the retrograde mean motion resonance, and the phase-space portrait of 1/−1 mean motion resonance specifically. Following the method introduced by Huang et al. (2018) to analyze the dynamics of 1/−1 resonance, firstly we introduce the following retrograde Poincare variables,

(3)

where 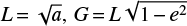, H = G cos i. The canonical variables L, M, G, ω, H, Ω are usually called the Delaunay variables. These new retrograde Poincare variables are different from those given by Murray & Dermott (1999). However, it is easy to check that the following contact transformation relationship holds:

(4)

So the new retrograde Poincare variables are a set of canonical action-angle variables. The 1/−1 mean motion resonant Hamiltonian for the circular restricted three-body model is given by Morbidelli (2002),

(5)

where

(6)

is the main term, and ℋ1 is the disturbing term. To study the dynamics of Hamiltonian (5), we introduce a set of canonical action-angle variables as follows:

(7)

where σ and σz are the critical angles of the retrograde mean motion resonance. If we restrict our retrograde motion to the planar case i = 180°, the second resonant angle ϕz can be neglected and then Sz or Q is always equal to 0. Besides, it is obvious that N is constant of motion for ℋ, whose expression is now

(8)

which defines a curve in the a−e plane. Thus the Hamiltonian of the planar case only depends on one critical angle σ. The new integrable Hamiltonian reads 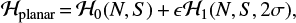(9)

As for the disturbing term ϵℋ1, we numerically evaluate its value by averaging over all fast angles (Morbidelli 2002). Then we can calculate the value of Eq. (9) on the e−ϕ plane. We apply this planar 1/−1 resonance semi-analytical model to the first asteroid in 1/−1 resonance with Jupiter, 2015 BZ5096, which has a nearly coplanar orbit. We can predict its motion in a numerical model very well (Fig. 6).

thumbnail Fig. 6.

Phase-space portrait of 1/−1 mean motion resonance with Jupiter associated with orbital elements of asteroid 2015 BZ509, presented in e−ϕ polar space. The variance of color and contours represent level curves of the ℋplanar (Eq. 9). The red scatter diagram presents the results of the numerical integration in the N-body numerical model, while the yellow dashed line denotes the collision curve with the perturber.

As shown in Tables 1 and 2, the inclinations of 2006 RJ2 and 2006 BZ8 are both close to 180°. We can apply this planar semi-analytical model to these two centaurs to evaluate their dynamical motions. The e−ϕ diagram for 2006 RJ2 is presented in Fig. 7. We notice that the motion of 2006 RJ2 in the numerical model is predicted pretty accurately by the planar semi-analytical model. The motion of the centaur is just around the ideal equilibrium point of the 1/−1 resonance. The curves given by the numerical integration correspond to the large-amplitude libration as defined by Murray & Dermott (1999). The phase-space portrait of 2006 BZ8 after capture in 1/−1 resonance is also presented in Fig. 8. The motion in the numerical model is not predicted as accurately as 2006 RJ2 due to the non-negligible impact of Jupiter. However, it also belongs to the scale of large-amplitude libration around the ideal equilibrium point. As shown in Figs. 6 and 8, the collision curve slices the entire phase space into different region. This work further verifies the 1/−1 resonant state of 2006 RJ2 and 2006 BZ8. We will research the theory of retrograde mean motion resonance that can apply to three-dimensional cases in a future work.

thumbnail Fig. 7.

Phase-space portrait of 1/−1 mean motion resonance with Saturn associated with orbital elements of centaur 2006 RJ2, presented in e−ϕ polar space. The basic meaning of this figure is the same as Fig. 6. We confine the plot range of the eccentricity to (0.7, 0.78) for better visual presentation.

thumbnail Fig. 8.

Phase-space portrait of 1/−1 mean motion resonance with Saturn associated with orbital elements of centaur 2006 BZ8. The basic meaning of this figure is the same as Fig. 6. We confine the plot range of the eccentricity to (0.62, 0.75) for better visual presentation.

6. Conclusions

Morais & Namouni (2016) predicted that stable co-orbit resonances exist at all inclinations, but an asteroid in stable retrograde co-orbit resonance with a planet was not discovered until the first identified asteroid in 1/−1 resonance with Jupiter, 2015 BZ509 (Wiegert et al. 2017). In this paper, we identify four potential retrograde co-orbital centaurs of Saturn. The statistical results of 1000 clones (including nominal orbit) of each candidate by numerical simulations are given in Table 3. According to our statistical results, 2006 RJ2 is the best candidate to be currently in a 1/−1 mean motion resonance with Saturn, as another minor body found in retrograde co-orbit resonance with the planet after 2015 BZ509. Centaur 2017 SV13 is another important potential candidate whose clones are always captured in this particular resonant state during the whole integration time span. Moreover, 2012 YE8 and 2006 BZ8 are also centaurs of interest but their current and long-term 1/−1 resonant state with Saturn is less likely.

Our findings suggest that small bodies in retrograde co-orbit resonance with giant planets may be more common in our solar system than previously expected. The existence of these mysterious small bodies may give us a kind of unique perspective to study co-orbital motion in our solar system. As for small bodies on planet-crossing orbits such as centaurs, Fernandez et al. (2016), Bailey & Malhotra (2009), and Namouni & Morais (2015) suggested that those locked in stable resonances have longer lifetimes than others. That is to say, the centaurs in retrograde co-orbit resonance we identified here, 2006 RJ2, 2006 BZ8, 2012 YE8, and 2017 SV13, may belong to the most dynamically stable objects among centaurs. This is significant for research into the origin of centaurs and their dynamical evolution.

The dynamics of the planar retrograde co-orbit resonance are studied through the averaged Hamiltonian. We introduce a useful integrable approximation for planar 1/−1 resonance and confirm the 1/−1 resonant states by the comparison of the phase-space portrait of the semi-analytical model and the numerical results. The planar 1/−1 resonance semi-analytical model can predict the motion of 2015 BZ509 (its inclination is close to 180°) quite well. The real motions of 2006 RJ2 and 2006 BZ8 (after capture in 1/−1 resonance) in the solar system are just around the ideal equilibrium points of the 1/−1 resonance given by the planar semi-analytical model. These results further verify our findings from the numerical simulations. Namouni & Morais (2017) confirmed that the efficiency of co-orbit capture at large retrograde inclination is an intrinsic feature of co-orbital resonance. Therefore, this planar semi-analytical model can provide a good approximation to the real motion of most small bodies in 1/−1 resonance with the planets.

Centaurs are small bodies of the solar system on long-term unstable orbits with a semi-major axis between those of the outer planets. As a result, these retrograde centaurs that wander radially between the outer planets have a high “chance” of being captured in co-orbit resonance because of the frequent close encounters with giants planets.

The conclusions of our present study encourage the search for such minor bodies on a larger scale to analyze the origins and evolution of these mysterious objects. Our results imply that retrograde mean motion resonance plays a crucial role in the dynamical evolution of centaurs on retrograde orbits. In this regard, the findings of this paper are useful for understanding the origin and dynamical evolution of centaurs and damocloids on retrograde orbits.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11772167)

1

Minor Planet Center; https://www.minorplanetcenter.net/iau/MPCORB.html, retrieved 18 January 2018.

2

Until now, one Earth trojan, nine Mars trojans, one Uranus trojan and 17 Neptune trojans have been discovered. This data are taken from the website of JPL Small-Body Database Search Engine, retrieved 5 May 2018.

3

JPL Small-Body Database Search Engine; https://ssd.jpl.nasa.gov/sbdb_query.cgi

4

The uncertainty parameter is defined by the Minor Planet Center on a scale of 0–9, 9 being very uncertain.

5

Longer integrations have been done to confirm these results.

6

Orbital elements of 2015 BZ509 taken from JPL Small-Body Database Search Engine; https://ssd.jpl.nasa.gov/sbdb_query.cgi, retrieved on January 2018.

References

  1. Bailey, B. L., & Malhotra, R. 2009, Icarus, 203, 155 [NASA ADS] [CrossRef] [Google Scholar]
  2. Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  3. Chen, Y.-T., Lin, H. W., Holman, M. J., et al. 2016, AJ, 827, L24 [NASA ADS] [CrossRef] [Google Scholar]
  4. Connors, M., Wiegert, P., & Veillet, C. 2011, Nature, 475, 481 [NASA ADS] [CrossRef] [Google Scholar]
  5. Emel’yanenko, V. V., & Bailey, M. E. 1998, MNRAS, 298, 212 [NASA ADS] [CrossRef] [Google Scholar]
  6. Fernandez, J. A., & Gallardo, T. 1999, in Evolution and Source Regions of Asteroids and Comets, eds. J. Svoren, E. M. Pittich, & H. Rickman, IAU Colloq. 173, 327 [NASA ADS] [Google Scholar]
  7. Fernandez, J. A., Gallardo, T., & Young, J. D. 2016, MNRAS, 461, 3075 [NASA ADS] [CrossRef] [Google Scholar]
  8. Fouchard, M., Rickman, H., Froeschlé, C., & Valsecchi, G. B. 2014, Icarus, 231, 99 [NASA ADS] [CrossRef] [Google Scholar]
  9. Greenstreet, S., Gladman, B., Ngo, H., Granvik, M., & Larson, S. 2012, AJ, 749, L39 [Google Scholar]
  10. Gronchi, G. F., & Milani, A. 1999, A&A, 341, 928 [NASA ADS] [Google Scholar]
  11. Heppenheimer, T. A., & Porco, C. 1977, Icarus, 30, 385 [NASA ADS] [CrossRef] [Google Scholar]
  12. Hou, X. Y., Scheeres, D. J., & Liu, L. 2014, MNRAS, 437, 1420 [NASA ADS] [CrossRef] [Google Scholar]
  13. Huang, Y., Li, M., Li, J., & Gong, S. 2018, AJ, 155, 262 [NASA ADS] [CrossRef] [Google Scholar]
  14. Jewitt, D. 2005, AJ, 129, 530 [NASA ADS] [CrossRef] [Google Scholar]
  15. Jewitt, D. C., & Sheppard, S. S. 2003, Nature, 423, 261 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
  17. Levison, H. F., Dones, L., & Duncan, M. J. 2001, AJ, 121, 2253 [NASA ADS] [CrossRef] [Google Scholar]
  18. Levison, H. F., Duncan, M. J., Dones, L., & Gladman, B. J. 2006, Icarus, 184, 619 [NASA ADS] [CrossRef] [Google Scholar]
  19. Morais, M. H. M., & Namouni, F. 2013a, MNRAS, 436, L30 [NASA ADS] [CrossRef] [Google Scholar]
  20. Morais, M. H. M., & Namouni, F. 2013b, Celest. Mech. Dyn. Astron., 117, 405 [NASA ADS] [CrossRef] [Google Scholar]
  21. Morais, M. H. M., & Namouni, F. 2016, Celest. Mech. Dyn. Astron., 125, 91 [NASA ADS] [CrossRef] [Google Scholar]
  22. Morais, H., & Namouni, F. 2017a, Nature, 543, 635 [NASA ADS] [CrossRef] [Google Scholar]
  23. Morais, M. H. M., & Namouni, F. 2017b, MNRAS, 472, L1 [NASA ADS] [CrossRef] [Google Scholar]
  24. Morbidelli, A. 2002, Modern Celestial Mechanics: Aspects of Solar System Dynamics [Google Scholar]
  25. Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge Univ. Press) [Google Scholar]
  26. Namouni, F., & Morais, M. H. M. 2015, MNRAS, 446, 1998 [NASA ADS] [CrossRef] [Google Scholar]
  27. Namouni, F., & Morais, H. 2017, Comput. Appl. Math. [Google Scholar]
  28. Narita, N., Sato, B., Hirano, T., & Tamura, M. 2009, PASJ, 61, L35 [NASA ADS] [Google Scholar]
  29. Nurmi, P., Valtonen, M. J., Zheng, J. Q., & Rickman, H. 2002, MNRAS, 333, 835 [NASA ADS] [CrossRef] [Google Scholar]
  30. Olsson-Steel, D. 1988, MNRAS, 234, 389 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pollack, J. B., Burns, J. A., & Tauber, M. E. 1979, Icarus, 37, 587 [NASA ADS] [CrossRef] [Google Scholar]
  32. Thomas, F., & Morbidelli, A. 1996, Celest. Mech. Dyn. Astron., 64, 209 [NASA ADS] [CrossRef] [Google Scholar]
  33. Triaud, A. H. M. J., Collier Cameron, A., Queloz, D., et al. 2010, A&A, 524, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Volk, K., & Malhotra, R. 2013, Icarus, 224, 66 [NASA ADS] [CrossRef] [Google Scholar]
  35. Wiegert, P., & Tremaine, S. 1999, Icarus, 137, 84 [NASA ADS] [CrossRef] [Google Scholar]
  36. Wiegert, P., Connors, M., & Veillet, C. 2017, Nature, 543, 687 [NASA ADS] [CrossRef] [Google Scholar]
  37. Winn, J. N., Johnson, J. A., Albrecht, S., et al. 2009, AJ, 703, L99 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Nominal orbital elements at JED2458000.5 of 2006 RJ2.

In the text
Table 2.

Nominal orbital elements at JED2458000.5 of 2006 BZ8, 2012 YE8, 2017 SV13.

In the text
Table 3.

Numerical statistics about fraction of clones for four centaurs under study.

In the text

All Figures

thumbnail Fig. 1.

Properties of the nominal orbit of 2006 RJ2. From top to lower panel: semimajor axis a and location of exact 1/−1 resonance with Saturn; eccentricity e; inclination i; angle for nearly coplanar motion involving 1/−1 resonance with Saturn ϕ; 2/−5 resonant angle with Jupiter ϕ2; argument of pericenter ω; the minimum distance in close encounters with Jupiter and Saturn within three Hill’s radii of the planet is represented by red plus and green square, respectively.
In the text
thumbnail Fig. 2.

Path of the Centaur 2006 RJ2 in the frame that rotates with Saturn. X, Y, and Z are the cartesian axes of the Saturn’s rotating frame. The X-axis points from Sun to Saturn and Z-axis is vertical to Saturn’s orbital plane. Saturn is presented as the green filled circle. Panel a: path of 2006 RJ2 in Saturn’s rotating frame viewed from the Z-axis direction. The black dotted curve is the Saturn’s orbit in the inertial reference frame. Panel b: motion of 2006 RJ2 viewed from the Y-axis direction. The blue curve represents the motion of 2006 RJ2 above the Saturn’s orbital plane while the red curve means the opposite.
In the text
thumbnail Fig. 3.

Cloned orbit of 2006 BZ8 chosen as one of best clones captured in 1/−1 resonance. The basic meaning of this figure is the same as Fig. 1.
In the text
thumbnail Fig. 4.

Cloned orbit of 2012 YE8. Since its orbit is far from the planar case, another 1/−1 resonant angle with Saturn ϕz is included. The other basic meaning of this figure is the same as Fig. 1.
In the text
thumbnail Fig. 5.

Cloned orbit of 2017 SV13. Since its orbit is far from the planar case, another 1/−1 resonant angle with Saturn ϕz is included. In the last panel, the minimum distance in close encounters with Jupiter and Uranus within three Hill’s radii of the planet is represented by red plus and cyan cross, respectively. The other basic meaning of this figure is the same as Fig. 1.
In the text
thumbnail Fig. 6.

Phase-space portrait of 1/−1 mean motion resonance with Jupiter associated with orbital elements of asteroid 2015 BZ509, presented in e−ϕ polar space. The variance of color and contours represent level curves of the ℋplanar (Eq. 9). The red scatter diagram presents the results of the numerical integration in the N-body numerical model, while the yellow dashed line denotes the collision curve with the perturber.
In the text
thumbnail Fig. 7.

Phase-space portrait of 1/−1 mean motion resonance with Saturn associated with orbital elements of centaur 2006 RJ2, presented in e−ϕ polar space. The basic meaning of this figure is the same as Fig. 6. We confine the plot range of the eccentricity to (0.7, 0.78) for better visual presentation.
In the text
thumbnail Fig. 8.

Phase-space portrait of 1/−1 mean motion resonance with Saturn associated with orbital elements of centaur 2006 BZ8. The basic meaning of this figure is the same as Fig. 6. We confine the plot range of the eccentricity to (0.62, 0.75) for better visual presentation.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.