| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A280 | |
| Number of page(s) | 8 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/202348985 | |
| Published online | 22 July 2024 | |
Physical parameters and orbital evolution of asteroids in retrograde orbits
Chorzow Astronomical Observatory,
41-500
Chorzow,
Poland
e-mail: astrobit@ka.onet.pl
Received:
17
December
2023
Accepted:
28
May
2024
Context. We studied the dynamical orbital and physical evolution of all 21 numbered and 13 selected unnumbered asteroids in retrograde orbits.
Aims. Based on all published observations of studied asteroids in retrograde orbits, we computed their starting orbital elements, absolute magnitudes, and diameters, together with the non-gravitational parameters A2 and da/dt.
Methods. Using publicly available orbital computation methods, we studied the dynamical evolution of orbital elements and the physical parameters of asteroids: rotation period, spin direction, and the non-gravitational parameters A2.
Results. Lyapunov times (LT) for studied asteroids are short, from 60 to 36 496 yr, with a mean of 5978. Without considering non-gravitational effects, LT is longer: values range from 328 to 63 165 yr, with a mean of 6392. Over the next 10 Myr and beyond, the rotation period of the studied asteroids P decreases by approximately 8%. Moreover, 15% of the clones slow down.
Conclusions. The starting spin distribution becomes flatter, with only one large maximum in the range (0–5) deg containing 279 clones (i.e. approximately 13%). However, the non-gravitational parameter da/dt has a maximum value of around (0–0.04)× 10−5 au day−2 .
Key words: astrometry / celestial mechanics
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The discovery in 1999 of the first asteroid in a retrograde orbit was so unusual that the name suggested for it was ‘Dioretsa’, the reverse of the word ‘asteroid’. 20461 Dioretsa (1999 LD31) is the first of the 162 currently known numbered (see Minor Planet Center database search)1 minor planets in the Solar System with a retrograde motion (Schmadel 2006). The approved naming convention was published by the Minor Planet Center on 1 May 2003 (M.P.C. 48396)2.
When we started studying this asteroid group around 2008, we only had 22 discovered objects, of which a few were numbered. A few of the studied objects were later reclassified as comets. Despite this, the number of classified asteroids in retrograde orbit is constantly increasing, and today (24 April 2024), we observe 162 of them, including 22 that are numbered. In this article, we target all 21 known numbered asteroids in retrograde orbits (data were updated on 25 February 2022), as mentioned in our previous article (Wlodarczyk 2022). In addition, we studied 13 selected, unnumbered retrograde asteroids (Table 1).
We continued our work detailed in Wlodarczyk (2022), including Kankiewicz & Włodarczyk (2021); Kankiewicz & Wlodarczyk (2020); Kankiewicz (2020); Kankiewicz & Włodarczyk (2018a); Kankiewicz & Włodarczyk (2018b, 2017, 2014, 2010a,b). Current research on the behaviour of asteroids in retrograde orbits is detailed in Valsecchi et al. (2022). The authors discuss direct-retrograde orbit flips during planetary close encounters. They also show the role of the Tisserand parameter and methods of searching known asteroids and comets, which can flip to retrograde motion due to encounters with an outer planet. They also computed critical values of the semi-major axis for inclination flipping. Namouni (2024) investigated the injection process of asteroids in the context of the three-body problem. The authors identified two injection modes: one corresponding to Tisserand parameter values (T > 0.1), which equivalently represents prograde inclinations, and another associated with (T ≤ 0.1), indicating polar and retrograde inclinations. Morais & Namouni (2022) try to explain how the stability borders of the 2/1 and 1/2 retrograde resonances are connected to the geometry of the resonant orbits. In this study, we focused on the physical parameters of asteroids in retrograde orbits and their evolution. We studied physical parameters such as their rotation periods, spin behaviour, and the parameters of non-gravitational A2. In particular, we studied physical parameters such as their rotation periods, spin behaviour, and non-gravitational parameters. We also examined their Lyapunov times (LT).
We used the publicly available OrbFit 5.0.73 software. The orbital and physical parameters of the asteroids were added, which we calculated from the new Novakovic & Fenucci (2022) software. We studied the behaviour of asteroids in retrograde orbits over next 10 Myr.
The non-gravitational parameter A2 depends on the Yarkovsky effect, the thermal re-emission of absorbed solar radiation. The non-gravitational acceleration arises from the anisotropic re-emission of solar energy absorbed at thermal wavelengths. The Yarkovsky effect acts on the semi-major axis, a. The drift of the semi-major axis 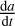 depends on the obliquity of the asteroid, γ the bulk density ϱ, and the diameter D of the asteroid Chesley et al. (2014):
depends on the obliquity of the asteroid, γ the bulk density ϱ, and the diameter D of the asteroid Chesley et al. (2014):
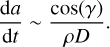 (1)
(1)
According to Farnocchia et al. (2013), we computed the Yarkovsky effect as a transverse acceleration, given by the formula 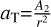 , where r represents the heliocentric distance and A2 is a function of the physical quantities of the asteroid. According to Farnocchia et al. (2013), the semi-major axis drift of asteroid is
, where r represents the heliocentric distance and A2 is a function of the physical quantities of the asteroid. According to Farnocchia et al. (2013), the semi-major axis drift of asteroid is
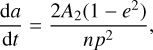 (2)
(2)
where e is the eccentricity, n is the mean motion, and p is the semi latus rectum. As shown in Farnocchia et al. (2013), A2 can be computed using the physical parameters of an asteroid or by fitting observations. The last method was used when we computed an asteroid’s orbit with small uncertainties. We then solved seven orbital parameters instead of the previous six. The Near Earth Objects Dynamical Side (NEODyS ) team has developed the software OrbFit v.5.0 and higher versions4, which computes both non-gravitational parameters 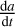 or A2. We used this publicly available software and computed the non-gravitational parameters.
or A2. We used this publicly available software and computed the non-gravitational parameters.
We observed the effects of the radiation pressure on small, irregularly shaped asteroids, which consist of two components as was pointed out in Durech et al. (2024). The first component is a smaller torque caused by directly reflected sunlight in the optical band and a more significant component due to the asteroid’s recoil of the thermally emitted radiation. Rubincam (2000) introduced the acronym YORP, which stands for the Yarkovsky-O’Keefe-Radzievski-Paddack effect. More YORP effects are in Vokrouhlický et al. (2015).
2 Starting orbital elements
We have filtered the numbered asteroid with orbital inclination i >90 deg from the JPL NASA Small-Body Database Query5 (updated 25 February 2022, at the beginning of our integration). As of 7 December 2023, compared to our starting database (25 February 2022), the number of numbered asteroids in retrograde orbits has remained the same, at 21.
However, the number of unnumbered asteroids in retrograde orbits increased from 137 to 145. The additional eight asteroids have typical retrograde orbits. They are not important for our study. The starting orbital elements of the 137 asteroids were obtained from the ASTDyS database6. Using the freely available software OrbFit 5.0.7, we computed the orbital elements of asteroids from Table 1 for the epoch starting MJD59600=21 January 2022 and the absolute magnitude H with its uncertainty. In addition, we computed the diameter of each asteroid D according to Harris (1998)
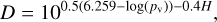 (3)
(3)
where H denotes the absolute magnitude and pv the geometric albedo.
The procedure for calculating the evolution of orbital and physical parameters is presented in Fig. 1. It is described in detail below.
 |
Fig. 1 Procedure for calculating the orbital evolution of asteroids and the physical parameters of retrograde orbits. |
2.1 Non-gravitational parameter A2
As previously mentioned, we computed the absolute magnitude H with its error ΔH using the OrbFit software. We determined the geometric albedo pv from Wide-field Infrared Survey Explorer (WISE) X data using JPL NASA’s analysis.
Up to 10 October 2023, albedos of only five numbered retrograde asteroids and ten unnumbered ones have been published. We took the mean of the five albedos of numbered asteroids, which gives an albedo value of 0.074, and used it for the albedo of the remaining retrograde asteroids. In some cases, we used the known albedo of unnumbered retrograde asteroids. Table 1 shows the selected starting orbital elements and physical parameters of the 21 numbered and 13 unnumbered asteroids in retrograde orbits. We computed the non-gravitational parameter A2 using the publicity available software OrbFit 5.0.7 on the NEODyS website7.
Table 1 presents records data from JPL with asteroids in retrograde orbits with condition codes better than 2. x This is similar to the MPC “U” parameter orbit uncertainty code between 0 and 9, with 0 being good and 9 being highly uncertain. Nine of 34 asteroids have an exact non-gravitational parameter A2 (these are recorded in blue font). They have an uncertainty value of dA2 less than A2. Based on the WISE data, the mean albedo value of the five numbered is 0.0740. This albedo value was applied to the remaining retrograde asteroids whose albedo values were unknown. We computed the following values: H, D, P, A2, dA2, and partially, the albedo.
First, we compared our A2 computations of selected asteroids with those that were published in Hung et al. (2023). Results are presented in Table 2.
The differences in the computed values of the non-gravitational parameter A2 are mainly related to the length of the observational arc. Our results are based on all published observations and the results of Hung et al. (2023) on the shorter arc. The qualitative results are almost the same. The NASA JPL does not publish the A2 parameter for any numbered asteroid in a retrograde orbit, except ’Oumuamua (A/2017 U1), which has been described as hyperbolic, where A2 = (1.42.4)10−8 au day−2 (updated 7 October 2023).
We found many published A2 for asteroids in prograde orbits, including 167 numbered asteroids with a known non-gravitational parameter A2. If we include non-numbered asteroids, we have a total number of 258. The non-gravitational parameters A2 lie mainly within a range from −10−13 to 10−13 au day−2. The NASA JPL provides the A2 value for 259 comets with values of the order of 10−8–10−9 au day−2 (i.e. they are several orders greater than for asteroids). In some cases, the calculated value of A2 for retrograde asteroids is of the order of a comet (i.e. several orders of magnitude greater than asteroids moving in orbits with i < 90 deg).
Data referenced to Epoch MJD59000.0 (JD2459000.5), corresponding to 31 May 2020.
2.2 Known rotational periods of asteroids
According to JPL8 among 1 283 023 asteroids (updated on 10 October 2023), 34 103 asteroids have known rotation periods, of which 29 428 asteroids have H ≤ 16 mag and rotation period P, between 0.00083 h and 4812 h. As the above mentioned link shows, in many cases, presented rotation periods are taken from the Ondrejov Asteroid Photometry Project9 and are based on less than complete coverage, so the period may be wrong by 30 per cent. We generally focused on asteroids with absolute magnitudes (H) falling within the range of 7.45≤H ≤ 16.8 mag in order to study asteroids in retrograde orbits from Table 1. Only two out of 105 known asteroids with i ≥ deg (of which 19 are numbered) have a known value for the rotation period. Table 3 presents data on these two asteroids. Both bodies were studied in our work and presented with the other asteroids in Table 1. The top left figure shows asteroid 2006 BZ8 with P10h (see Fig. 2).
Moreover, as shown in Fig. 2, 17 346 asteroids with P ≤ 10 h are illustrated in the left middle figure, and 792 asteroids with P ≤ 2 h are shown in the right middle figure. The bottom figures present asteroids with the perihelion distance of q ≤ 3 au, whereas the left figure shows results for asteroids with an absolute magnitude of H ≤ 16 mag; asteroids with rotational period P ≤ 2 h are shown in the right figure. The bottom left figure shows the asteroids in two regions, separated by q = 1.3 au (Fig. 2). Beyond this threshold, there are near-Earth asteroids (NEAs) with a wide range of H values.
As mentioned, we present P versus q dependence in the bottom right figure. In the NEA region, we observe a small number of asteroids with P between 0 and 0.5 h, while the P range of many asteroids at over q = 1.3 au is between 0.5 and 2 h.
As of 10 October 2023, there are 34 103 asteroids with listed rotation periods (P), including 32 594numberedasteroids. Among these, 29 248 asteroids fall within the studied range of absolute magnitudes (7.45 < H < 16.8; i.e. from the studied H range) and have known P. Therefore, we can fit the rotation periods (P) in hours as follows:
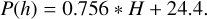 (4)
(4)
We used this formula (4) to calculate the values for the rotation period P for all asteroids in retrograde orbits listed in Table 1, except for the two with known rotation periods (Table 3). Interestingly, the mean P from the range of 7.45 < H < 16.8 of numbered asteroids is 34.56 h.
Non-gravitational parameter A2 of selected asteroids compared with those in (1).
Asteroids in retrograde orbits with known rotation periods and within the studied range of 7.45 ≤ H ≤ 16.8 mag.
3 Orbital evolution
Using the freely available OrbFit software, we can track the orbital evolution of asteroids. To achieve this, 101 clones or virtual asteroids (VAs) were calculated for each of the 34 studied asteroids using the Milani multiple solution methods with the OrbFit 5.0.7 software. We used the υfcc17 error model (Vereš et al. 2017). The computed VA sets were then inserted into the Orbit9 programme, which is implemented within the OrbFit package.
Next, we used the mercury software described in Novakovic & Fenucci (2022). As mentioned in10 and in11, this is a modified version of the N-body code mercury developed by Chambers (1999), which includes the Yarkovsky and YORP effects to account for the dynamics of small Solar System objects.
The Yarkovsky effect, as detailed by Bottke et al. (2006) and Chesley et al. (2003), includes diurnal and seasonal components that produce a shift in the semi-major axis of the asteroid. To study the motion of asteroids and comets under the influence of the Yarkovsky effect, we used the non-gravitational parameters A2 and da/dt. As a seventh parameter during orbit determination, A2 and da/dt can be determined, together with six other orbital parameters (i.e. Keplerian elements). In Włodarczyk (2018), we computed several non-gravitational parameters, including A2 and da/dt.
The method used in the present work has the advantage of simultaneously showing the evolution of rotation period P, the obliquity γ, and da/dt of the studied asteroids.
In the starting file Yarkovsky, we used typical values for the physical parameters associated with this type of asteroid, as partially presented in Fenucci & Novaković (2022):
Thermal conductivity K (W m−1 K−1) = 0.001;
Heat capacity C (J kg−1 K−1) = 800;
Absorption coefficient α (usually set to 1);
Emissivity є (usually set to 1);
Diameter D (m), from Eq. (1);
Density ρ equal 1300 (kg m−3) for all asteroids in retrograde orbits, as presented in Table 4 with a high inclination in Cibulková et al. (2014);
Obliquity γ (degrees) = for the first clone = 0, and the following 100 clones differ from the previous one by 180/101 deg = 1.782 deg;
Rotation period P (h) is from Eq. (2).
As starting parameters in the YORP file:
-
Yorp_flag = 1
(i.e., includes the spin-axis evolution due to the YORP effect);
-
Stoc_yorp_flag = 1
includes the stochastic YORP;
-
Step_user = 1.0
Timestep for the spin-axis integration (i.e. equal 1.0 yr – the minimum value for this integrator);
-
dt_out = 1.0
Timestep for printing output on a file;
One year.
The time between the two outputs was 10–50 yr. We used from 1 000 000 to 200 000 output numbers at job termination, which gives 10 Myr forward integration. We used a sampling ratio of the filter equal to 20. Thus, we obtained 34 forward orbital evolution packets covering all the asteroids studied in Table 1. After a specific duration, denoted as T, the integration was halted as the first individual clone was ejected from the Solar System when its semi-major axis exceeded 100 au. The dynamic compactness time is shown in Table 5 in Col. T.
Many asteroids, including those in retrograde orbits, have close approaches (CAs) with planets. CAs can be a source of chaotic motion for asteroids. Chaos can be measured using LT. The Lyapunov exponent or Lyapunov characteristic exponent (LCE) characterises the separation rate of initially infinitesi-mally close trajectories (nearby orbits). Two nearby trajectories in phase space with the initial separation δX0 diverge in time by
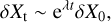 (5)
(5)
where λ is the Lyapunov exponent. We computed the LCE according to the method presented by Kneževic & Ninkovic (2005). Similarly, we used this method in Wlodarczyk et al. (2014). The computed LT presented in Table 5 is, on the whole, short, and as a consequence, the orbits of the retrograde asteroids can be classified as very chaotic. Our previous paper (Włodarczyk 2022) reports these results.
Table 1 contains 9 of 34 asteroids with an exact A2, (i.e. about 26%); they have an uncertainty value of dA2 less than A2 (blue font). Interestingly, the number of asteroids with a nominal A2 > 0 is the same as those with A2 < 0 (17 asteroids each).
Table 5 shows dynamic compactness time T and the LT calculated for 21 numbered asteroids on retrograde orbits, both without considering the Yarkovsky effect (i.e. gravitational effects only, indicated with a ‘grav. index’) and with the Yarkovsky effect (marked with a ‘yark. Index’). We previously presented the results of T and LT calculations without the Yarkovsky effects for integration period 2 Myr in Włodarczyk (2022). Here, we present the results of the calculations for an integration period of 10 Myr, considering the Yarkovsky effect. Only 21 numbered asteroids are available for comparison with the results of the 2 Myr integrations from the previous study Włodarczyk (2022).
Table 5 and Fig. 3 show that the LT values calculated without considering the Yarkovsky effect are more significant than those with the Yarkovsky effect.
According to the fit in Fig. 3
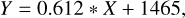 (6)
(6)
where X denotes LT computed without the Yarkovsky effect and Y with the Yarkovsky effect, both in years.
It is important to note that although the impact of the Yarkovsky effect on large asteroids is minimal, its influence becomes visible over a long period. Moreover, the accuracy of the A2 calculation has little impact on the value of LT (see asteroids in bold font). We calculated LT by averaging the LT values for each clone at the end of the integration period, thus averaging the errors.
 |
Fig. 2 Known physical parameters of asteroids. Asteroids in retrograde orbit are red stars, while the others are blue stars. |
Most numerous non-gravitational parameter da/dt populations among the clones of the 21 numbered retrograde asteroids after a 10 Myr integration forward.
 |
Fig. 3 Correlation between LT computed without and with the Yarkovsky effect for asteroids in retrograde orbits. |
4 Long-time orbital and physical evolution
Figure 4 presents the physical parameters of all 2121 clones of 21 studied retrograde asteroids (101 clones for each asteroid) after 10 Myr forward integration. We present their rotation period P, γ (spin axis), and non-gravitational parameter da/dt. After the 10 Myr period, these three physical parameters showed significant differentiation. Additional details are provided in Tables 6– 4. We divided the entire range of these parameters into a series of intervals:
Computed rotation period, P: 50 intervals of 2 h each
Computed gamma: range of 180 deg in 36 intervals of five degrees each
Computed non-gravitational parameter, da/dt: 40 intervals of 0.04 au Myr−1 × 105 each.
Finally, we counted how many data points fall within each interval. Tables 6–4 list the ranges with the largest populations.
The histogram of asteroid rotation periods, P, is multimodal. There are maxima of rotation periods close to their starting intervals (i.e. near 30 h). However, there are also intervals with an increased population of clones, specifically around 0 and 35 h, and a large group of asteroids with P = 1000 h. This result indicates that these asteroids do not rotate, encompassing approximately 333 of the total 2121 clones. Noteworthy is the large number of asteroids with short rotation periods, with 101 clones having P ≤ 10 h. Hence, it can be concluded that changes in rotation periods are dynamic over the relatively short period of 10 Myr. Regarding the second parameter, the spin axis (gamma) of the asteroid, we divided the entire range of values into a series of 36 intervals, each 5 deg of gamma, summing up to 180 deg, and then counted the values falling into each interval. Table 7 presents the first five intervals.
Continuing our research, we again calculated a substantial number of 2121 starting clones. We maintained a precision of 180/101 deg (approximately every 1.8 deg) for the starting spins. The initial distribution was flat, with each bin containing the same number of clones. The histogram shows the number of clones in 5-deg intervals (180/5 = 36 intervals). Calculations showed that 279 clones had the most significant spin in the 0–5 deg range. The remaining bins usually contain about 4–50 clones.
The histogram for the third physical parameter, the non-gravitational effect da/dt, is symmetrical concerning da/dt = 0. This can be seen in Fig. 4 (lower panel). We divided the entire final da/dt range into a series of intervals, each 0.04 au Myr−1 ×10−5. Table 4 gives the number of clones with selected da/dt. More clones have positive da/dt values–about twice as many as negative ones (1419 versus 655). Details are shown in Table 4 for the largest of the 20 intervals on both sides of da/dt=0. Our calculations show that over the period 10 Myr, the clones move outside the Solar System (da/dt ≥ 0) au Myr−1. However, it is also necessary to consider unnumbered asteroids in retrograde orbits and wait to discover further asteroids in retrograde orbits.
Selected dynamical parameters of the 21 numbered asteroids in retrograde orbits during 2 Myr and 10 Myr forward integration.
 |
Fig. 4 Physical parameters of all 2121 clones of the 21 numbered retrograde asteroids studied after 10 Myr forward integration. da/dt values in the bottom panel are in 10−5 au Myr−1. |
5 Conclusions
Adding the Yarkovsky and YORP effects to the equations of motion of asteroids in retrograde orbits reveals that their orbital evolutions and physical parameters are highly dynamic. We found that their LT are relatively short, ranging from several hundred to tens of thousands of years. However, without considering non-gravitational effects, LT is longer, as shown by comparing our results with previous work (Włodarczyk 2022).
Over a period of 10 Myr, the rotation periods P of asteroids decrease by approximately 8%, and 15% of clones experience a slowdown. The spin distribution becomes flattened, with a significant maximum in the range of 0–5 deg containing 279 clones (about 13%).
The non-gravitational parameter da/dt shows a maximum around (0–0.04)×10−5 au day−2.
Rotation periods become partially shortened, and 333 clones (about 15% of all clones) slow down.
Of all 2121 clones (21 asteroids, 101 clones each), we observed an almost evenly flattened distribution of the spin population, with approximately 50 clones per bin and one large maximum, 279 clones in the 0–5 deg range. The non-gravitational parameter (da/dt) has a maximum around (0– 0.04)×10−5 au Myr−1.
The evolution of orbital elements and physical parameters of the 21 asteroids in retrograde orbits is highly dynamic over a period of 10 Myr. Therefore, it is essential to include the Yarkovsky and YORP effects when studying the orbital and physical evolution of asteroids in retrograde orbits.
Most numerous populations of rotation periods among the clones of the 21 numbered asteroids in retrograde orbits after a 10 Myr forward integration.
Most numerous gamma (spin axis) populations among the clones of the 21 numbered asteroids in retrograde orbits after a 10 Myr forward integration.
Acknowledgements
The author thanks Dr. Eva Plávalová for carefully improving the manuscript. I want to thank the Space Research Center of the Polish Academy of Sciences in Warsaw for granting access to its computer cluster.
Data availability. All starting data of orbital elements and the source code of the OrbFit software were accessed from https://ssd.jpl.nasa.gov/tools/sbdb_query.html#results, https://minorplanetcenter.net/db_search and https://newton.spacedys.com/astdys/.
References
- Bottke, W. F., Vokrouhlicky, D., Rubincam, D. P., & Nesvorny D. 2006, AREPS, 34, 157 [NASA ADS] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [Google Scholar]
- Chesley, S. R., Ostro, S. J., Vokrouhlicky, D., et al. 2003, Science, 302, 1739 [NASA ADS] [CrossRef] [Google Scholar]
- Chesley, S. R., Farnocchia, D., Nolan, M. C., et al. 2014, Icarus, 235, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cibulková, H., Broz, M., & Benavidez, P. G. 2014, Icarus, 241, 358 [CrossRef] [Google Scholar]
- Durech, J., Vokrouhlicky, D., Pravec, P., et al. 2024, A&A, 682, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farnocchia, D., Chesley, S. R., Vokrouhlicky, D., et al. 2013, Icarus, 224, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fenucci, M., & Novakovic, B. 2022, Serb. Astron. J., 204, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W. 1998, Icarus, 131, 291 [Google Scholar]
- Hung, D., Tholen, D. J., Farnocchia, D., & Spoto F. 2023, PSJ, 4, 215 [NASA ADS] [Google Scholar]
- Kankiewicz, P. 2020, Planet. Space Sci., 191, 105031 [NASA ADS] [CrossRef] [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2010, Protecting the Earth against Collisions with Asteroids and Comet Nuclei, Proceedings of the International Conference “Asteroid-Comet Hazard 2009”, eds. A. M. Finkelstein, W. F. Huebner, & V. A. Shor (St. Petersburg: Nauka), 52 [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2010, Protecting the Earth against Collisions with Asteroids and Comet Nuclei, Proceedings of the International Conference “Asteroid-Comet Hazard 2009”, eds. A. M. Finkelstein, W. F. Huebner, & V. A. Shor (St. Petersburg: Nauka), 268 [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2014, XXXVI Polish Astronomical Society Meeting, Proceedings of the conference held 11-14 September, 2013, eds. A. Rózanska & M. Bejger, Polish Astron. Soc., 167 [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2017, MNRAS, 468, 4143 [NASA ADS] [CrossRef] [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2018, Polish Astron. Soc., 7, 132 [NASA ADS] [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2018, Planet. Space Sci., 154, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2020, VizieR Online Data Catalog, J/A+A/646/A182 [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2020, Polish Astron. Soc., 10, 97 [NASA ADS] [Google Scholar]
- Kankiewicz, P., & Wlodarczyk, I. 2021, A&A, 646, A182 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kneževic, Z., & Ninkovic, S. 2005, Dynamics of Populations of Planetary Systems, Proc. of IAU Colloquium 197, eds. Z. Knezevic & A. Milani (Cambridge: Cambridge University Pres), 187 [Google Scholar]
- Morais, M. H. M., & Namouni, F. 2013, MNRAS, 436, L30 [Google Scholar]
- Morais, M. H. M., & Namouni, F. 2022, Computat. Appl. Math., 35, 881 [Google Scholar]
- Namouni, F. 2024, MNRAS, 527, 4889 [Google Scholar]
- Novakovic, B., & Fenucci, M. 2022, EPSC Abstr., 16, 620 [NASA ADS] [Google Scholar]
- Rubincam, D. P. 2000, Icarus, 148, 2 [Google Scholar]
- Schmadel, L. D. 2006, Dictionary of Minor Planet Names, addendum to 5th Edition: 2003-2005, Prepared on behalf of Commission 20 under the auspices of the International Astronomical Union (Berlin: Springer), VIII+343 [Google Scholar]
- Valsecchi, G. B., Rickman, H., Morbidelli, A., et al. 2022, A&A, 667, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vereš, P., Farnocchia, D., Chesley, S. R., & Chamberlin, A. B. 2017, Icarus, 296, 139 [CrossRef] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015, Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 509 [Google Scholar]
- Włodarczyk, I., 2018, Polish Astron. Soc., 7, 141 [Google Scholar]
- Włodarczyk, I. 2022, MNRAS, 516, 6116 [CrossRef] [Google Scholar]
- Włodarczyk, I., Cernis, K., Boyle, R. P., & Laugalys, V. 2014, MNRAS, 438, 2621 [CrossRef] [Google Scholar]
All Tables
Asteroids in retrograde orbits with known rotation periods and within the studied range of 7.45 ≤ H ≤ 16.8 mag.
Most numerous non-gravitational parameter da/dt populations among the clones of the 21 numbered retrograde asteroids after a 10 Myr integration forward.
Selected dynamical parameters of the 21 numbered asteroids in retrograde orbits during 2 Myr and 10 Myr forward integration.
Most numerous populations of rotation periods among the clones of the 21 numbered asteroids in retrograde orbits after a 10 Myr forward integration.
Most numerous gamma (spin axis) populations among the clones of the 21 numbered asteroids in retrograde orbits after a 10 Myr forward integration.
All Figures
 |
Fig. 1 Procedure for calculating the orbital evolution of asteroids and the physical parameters of retrograde orbits. |
| In the text | |
 |
Fig. 2 Known physical parameters of asteroids. Asteroids in retrograde orbit are red stars, while the others are blue stars. |
| In the text | |
 |
Fig. 3 Correlation between LT computed without and with the Yarkovsky effect for asteroids in retrograde orbits. |
| In the text | |
 |
Fig. 4 Physical parameters of all 2121 clones of the 21 numbered retrograde asteroids studied after 10 Myr forward integration. da/dt values in the bottom panel are in 10−5 au Myr−1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


