| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833071 | |
| Published online | 28 August 2018 | |
Estimating the equation of state from measurements of neutron star radii with 5% accuracy
1
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, ul. Bartycka 18, 00-716, Warsaw, Poland
e-mail msieniawska@camk.edu.pl, bhaskell@camk.edu.pl, bejger@camk.edu.pl
2
APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/Irfu, Observatoire de Paris, Sorbonne Paris Cité, 75205 Paris Cedex 13, France
Received:
22
March
2018
Accepted:
20
May
2018
Context. Observations of heavy (⋍2 M⊙) neutron stars, such as PSR J1614−2230 and PSR J0348+0432, in addition to the recent measurement of tidal deformability from the binary neutron-star merger GW170817, place interesting constraints on theories of dense matter. Currently operating and future observatories, such as the Neutron star Interior Composition Explorer (NICER) and the Advanced Telescope for High ENergy Astrophysics (ATHENA), are expected to collect information on the global parameters of neutron stars, namely masses and radii, with an accuracy of a few percent. Such accuracy will allow for precise comparisons of measurements to models of compact objects and significantly improve our understanding of the physics of dense matter.
Aims. The dense-matter equation of state is still largely unknown. We investigate how the accuracy of measurements expected from the NICER and ATHENA missions will improve our understanding of the dense-matter interior of neutron stars.
Methods. We compared global parameters of stellar configurations obtained using three different equations of state: a reference (SLy4 EOS) and two piecewise polytropes manufactured to produce mass-radius relations indistinguishable from an observational point of view, i.e. within the predicted error of radius measurement. We assumed observational errors on the radius determination corresponding to the accuracies expected for the NICER and ATHENA missions. The effect of rotation was examined using high-precision numerical relativity computations. Because masses and rotational frequencies might be determined very precisely in the most optimistic scenario, only the influence of observational errors on radius measurements was investigated.
Results. We show that ±5% errors in radius measurement lead to ~10% and ~40% accuracy in central parameter estimations for low-mass and high-mass neutron stars, respectively. Global parameters, such as oblateness and surface area, can be established with 8–10% accuracy, even if only compactness (instead of mass and radius) is measured. We also report on the range of tidal deformabilities corresponding to the estimated masses of GW170817 for the assumed uncertainty in radius.
Key words: equation of state / dense matter / stars: neutron
© ESO 2018
1. Introduction
Neutron stars (NS) are the most extreme material objects in the Universe. Formed in the aftermath of core-collapse supernovae, some few thousands are currently known. Most of these are seen as pulsars. These rotating compact objects allow astronomers to perform direct measurements of global parameters of NSs and, indirectly, to investigate the properties of dense matter in their interiors, which is in a state that is impossible to reproduce in terrestrial conditions. High-precision observations compared with theoretical models for the equation of state (EOS) of dense matter in NSs are currently the only way to study physics in such extreme conditions.
Precise determinations of the masses of PSR J1614−2230 (Demorest et al. 2010; Fonseca et al. 2016; Arzoumanian et al. 2018) and PSR J0348+0432 (Antoniadis et al. 2013) have set an observational bound on the maximum mass of a NS not lower than about 2 M⊙ and have constrained theoretical models of the EOS. Present determinations of NS radii R are roughly between 10 and 15 km (for a review, see e.g. Özel & Freire 2016; Fortin et al. 2016), but because of systematic errors uncertainties on the values are still large (see e.g. Heinke et al. 2014; Fortin et al. 2015; Elshamouty et al. 2016; Miller & Lamb 2016; Haensel et al. 2016). Additionally, GW170817, the recent first direct detection of gravitational waves from the final orbits of a relativistic binary NS system (Abbott et al. 2017a) yielded tidal deformability parameter measurements that disfavour radii larger than 14 km at 1.4 M⊙.
Ongoing and future missions such the Neutron star Interior Composition Explorer (NICER; Arzoumanian et al. 2014) and Advanced Telescope for High ENergy Astrophysics (ATHENA; Motch et al. 2013) are or will be able to measure NS gravitational masses and radii with accuracies of a few percent. Generally, the radius R and gravitational mass M measurement methods consist of
-
Pulse profile modelling related to brightness variations from the non-uniform surface of the NS. Such fluctuations may be caused by hot and cold spots, originated by magnetic field in rotation-powered pulsars or by non-uniform thermonuclear burning on the surface of an X-ray burster (see e.g. Özel et al. 2016; Sotani 2017). According to Psaltis et al. (2014) and Psaltis & Özel (2014), an uncertainty of ≲5% in the NS radius measurements is feasible, assuming that the rotational frequency of the object is in the range 300–800 Hz, and sufficiently long observations are possible (106 counts in the pulse profile). However, other authors pointed out that realistic observational errors might be larger, even up to 10% (see e.g. Lo et al. 2013; Miller & Lamb 2016) and may depend strongly on the geometry of the system. Nevertheless, in our work we decided to assume 5% accuracy as an optimistic scenario.
To break the degeneracy, four quantities have to be measured: the amplitude of the bolometric flux oscillation, amplitude of its second harmonic, amplitude of the spectral colour oscillation, and phase difference between the bolometric flux and colour oscillation. These requirements can be fulfilled by the NICER mission’s long exposure time and/or by combining pulse profile modelling methods with other measurements; for example X-ray pulse modelling from ATHENA and mass determination from radio timing. For lower spins (≲300 Hz), the amplitude of the second harmonic is too low to perform a full analysis. In this case only measurements of the compactness M/R are possible. For much higher spins (≳800 Hz), higher order multipoles that become important in the modelling and solutions of the field equations are EOS dependent.
-
Observations of Eddington-limited X-ray bursts from accreting NSs, which may put constraints on the maximum radius of the compact object (see e.g. Galloway et al. 2008).
-
Fitting spectra with an appropriate atmosphere model to observations of the quiescent emission from low-mass X-ray binaries. This method was proposed by van Paradijs (1979) and improved since that time using realistic NS atmospheres, relativistic NS models, and ray tracing (e.g. Vincent et al. 2018). A recent analysis by Steiner et al. (2018) suggests NS radii between 10 and 14 km.
-
Detections of gravitational waves from NS binary systems, allowing for measurements of NS masses and radii from both observations of the late inspiral (Bejger et al. 2005; Damour et al. 2012; Abbott et al. 2017a) and postmerger (e.g. Bauswein et al. 2015, 2017; Abbott et al. 2017b; Margalit & Metzger 2017; Annala et al. 2018; Rezzolla et al. 2018).
All these methods are necessarily limited by their intrinsic measurement errors. The current state of the art is such that in several cases mass can be measured with much smaller errors than radii. We focus on future measurements of radii and in particular on how the planned radius measurement accuracy reflects on the ability to discriminate similar M(R) relations obtained using different NS interior prescriptions (that is, based on different EOSs). Specifically, we manufacture stable M(R) sequences for parametric (piecewise-polytropic) EOSs and compare these to a reference sequence of configurations based on the SLy4 EOS (Douchin & Haensel 2001). In this test case we investigate ways of telling apart the M(R) relations that are indistinguishable because of observational errors in the radius measurement; we assume these errors are equal to 5% of the radius of the reference configuration based on the SLy4 EOS (the M(R) sequences of the piecewise-polytropes that trace the ΔR = ±5% outline of the SLy4 EOS non-rotating M(R) sequence). We also study various spin frequency cases: from non-rotating objects to extremely rapidly spinning sources to check if rotation aids the discrimination between various functionals of the EOS (mass, radius, quadrupole moment, and moment of inertia). In addition, we study cases in which the rotation rate is not known, and quantify the magnitude of the errors on the EOS parameters related to the radius measurement error and/or the lack of spin frequency measurement.
The paper is composed as follows. In Sect. 2 we present the EOS models, that is the numerical methods used to obtain the rigidly rotating sequences of configurations, and list the global NS parameters of interest. Section 3 contains the results. Section 4 presents the discussion and conclusions.
2. Methods and equations of state
The state of matter is relatively well known below the nuclear saturation density ρs = 2.7 × 1014 g cm−3. Above this density several competing theories describing the EOS of dense matter exist (for a textbook review, see e.g. Haensel et al. 2007). In order to compare the effects of the uncertainty in the radius measurement on the EOS, we choose as the reference the SLy4 EOS (Douchin & Haensel 2001), which is consistent with recent radius and mass constraints described in the introduction. Furthermore, we select two parametric EOSs, named Model1 and Model2, manufactured to be barely consistent with the expected radius uncertainty measurement with respect to the non-rotating reference model.
Model1 and Model2 EOSs are constructed using the SLy4 prescription of the crust for densities lower than the nuclear saturation density and with three piecewise relativistic polytropes,
for higher densities, where P(n) and ɛ(n) denote the pressure and mass-energy density as function of the baryon density n, and κi, γi, and mbi are the pressure coefficient, polytropic index (characterizing the stiffness of the EOS at given density), and baryon mass for a given polytropic ith segment (i = 1, …, 3). Index γi is a parameter of choice, and κi and mbi are fixed for a polytropic segment by the mechanical and chemical equilibrium.
In this study we limit ourself to stationary, axisymmetric, rigidly rotating NS configurations. Non-rotating static NS solutions are obtained by solving the Tolman-Oppenheimer-Volkoff (TOV) equations (Oppenheimer & Volkoff 1939; Tolman 1939). Sequences of rotating stars parametrized by the spin frequency f and the EOS parameter at the stellar centre (e.g. the central pressure Pc) are obtained by solving coupled partial differential equations using a multi-domain spectral methods library LORENE1 (Langage Objet pour la RElativité NumériquE; Gourgoulhon et al. 2016) nrotstar code (Bonazzola et al. 1993; Gourgoulhon et al. 1999, 2010). The accuracy of the solutions is inspected by checking the validity of the 2D general-relativistic virial theorem (Bonazzola & Gourgoulhon 1994). Global parameters describing the NS are gravitational and baryon masses M and Mb, angular momentum J and quadrupole moment Q; their definition can be found in Bonazzola et al. (1993) and Gourgoulhon (2010). From electromagnetic observations one obtains some estimation of the flux from the stellar surface, F∞ ∝ T4R2, proportional to its effective temperature T and the size R of the star. For a rotating star its visible size and radius are not uniquely defined as they depend on many factors, such as the viewing angle, compactness, rotation rate, and physical parameters of the atmosphere (see e.g. Vincent et al. 2018 for details); in order to compare configurations rotating with different rates we adopt the mean radius 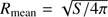 , where S is the surface area of the star, as a sufficiently good approximation.
, where S is the surface area of the star, as a sufficiently good approximation.
We also compare the tidal deformabilities related to different models. The tidal deformability λ, which represent the reaction of the star on the external tidal field (such as that in a tight binary system) were obtained in the lowest order approximation by integrating the TOV equations supplemented by an additional equation for the second tidal Love number k2 (Flanagan & Hinderer 2008; Van Oeveren & Friedman 2017), λ = 2R5k2/3, where k2 is the quadrupole Love number (Love 1911) and R is the non-rotating star radius. We use the normalized value of the parameter, Λ = λ(GM/c2)−5.
3. Results
Parametric models, denoted Model1 and Model2, are chosen in such a way to produce non-rotating M(R) relations tracing the ΔR = ±5% outline of the SLy4 EOS non-rotating M(R) sequence; they are plotted in the left panel in Fig. 1. At the present moment the data analysis methods allow us to treat objects with rotational frequency ≲800 Hz, as was mentioned in the Sect. 1. Nevertheless, one can expect that future theoretical and observational progress will enable studies of NSs with larger spins. We therefore research a broader range of spin frequencies, 0–1400 Hz, as shown in the right panel in Fig. 1. The EOSs parameters are collected in Table 1. In addition to the required difference in radius, we select the parameters such that the maximum mass Mmax > 2 M⊙, and the speed of sound, 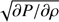 , is always smaller than the speed of light c for stable configurations.
, is always smaller than the speed of light c for stable configurations.
 |
Fig. 1. Right panel: Range of central densities ρc for stars rotating with the frequency f up to 1400 Hz. Left panel: Non-rotating configurations for the SLy4 EOS (red), Model1 EOS (green), and Model2 EOS (blue), following the ΔR = ±5% uncertainty in the radius measurement (grey region). |
Parameters of the three polytropes employed for the EOSs of Model1 and Model2 (indices correspond to the number of the polytrope).
3.1. Non-rotating neutron stars
The pressure-density P(ρ) relations for non-rotating configurations are presented in Fig. 2. The two lower panels show the differences between the reference SLy4 model, Model1 (lower panel), and Model2 (middle panel). Model1 is initially stiffer than the SLy4 EOS, which provides a larger radius. For higher densities Model2 becomes stiffer, which is necessary to reach the desired maximum mass.
 |
Fig. 2. Upper panel: P(ρ) profiles corresponding to the M(R) relations from the left panel of Fig. 1, with the SLy4 model denoted by a red solid line, Model1 by a green dashed line, and Model2 by a blue dash-dotted line. Thick semi-transparent lines denote P(ρ) ranges for the two components of the GW170817 binary neutron star system (Abbott et al. 2017a, with mass estimates using the low-spin priors). We also plot the pressure difference between the SLy4 model and Model1 (dashed green line, middle panel) and Model2 (dash-dotted blue line, lower panel). |
3.2. Slowly-spinning neutron stars
As was mentioned in the Sect. 1, a full pulse profile analysis cannot be performed for NSs with rotational frequencies ≲300 Hz because the signal cannot be distinguished from a sinusoid and its second harmonic is too weak to perform a Fourier decomposition. As a consequence, only compactness can be measured and is defined as C = 2GM/Rmeanc2 ratio, where G is the gravitational constant, and c is the speed of light. We analyse the influence of the measured compactness on global and central NS parameters.
In Fig. 3 we show the compactness as a function of the NS surface area. Selected values of constant ρc are also indicated. Configurations with C ≳ 0.6 are possible only for Model2. Additionally, if in addition to C the rotational frequency f is also known, the NS surface area can be estimated with ~10% accuracy for all values of C and f . Unfortunately, obtaining the central parameters, such as the central density ρc, is difficult when only the compactness, instead of M and R, is known. For example, a central density ρc = 0.7 × 1015g cm−3 spans C between 0.2 and 0.3.
 |
Fig. 3. Compactness vs. surface area for three EOSs: SLy4 (solid red), Model1 (dashed green), and Model2 (dash-dotted blue), for two rotational frequencies: 0 Hz (thin lines) and 1200 Hz (thick lines). Lines of constant central density are indicated in grey (dark grey for SLy4, medium grey for Model2, and light grey for Model1). Corresponding values of the central density are given on the left side of the plot (in units of 1015g cm−3). |
3.3. Unknown rotational frequency
We limit our analysis of rotating stars to axisymmetric, rigidly rotating, stable cases (frequencies below the Keplerian frequency). We have studied a wide range of possible spin frequencies and central parameters, as shown in the right panel on the Fig. 1. The fastest known pulsar, PSR J1748−2446ad (Hessels et al. 2006), rotates at 716 Hz. However, to fully cover the possible parameter space, we survey spin frequencies much higher than this current limit, up to 1200 Hz, which is just above the spin frequency of 1122 Hz that is suggested for XTE J1739−285 (reported by Kaaret et al. 2007, but not a confirmed burst oscillation frequency). The typical accuracy of the results, monitored by the GRV2 virial error, is of the order of 10−6. Figure 4 shows stable configurations for the three models: no rotation (left panel), 700 Hz (middle panel), and 1200 Hz (right panel). For the 700 Hz spin frequency, the M(R) relations for Model1 and Model2 go beyond the shaded region representing the tentative observational errors. The deviation is stronger for less-massive stars, ≲1.4 M⊙. As expected, for extremely rapidly rotating NSs (1200 Hz) only objects with large masses, ≈2 M⊙, are able to counterbalance the centrifugal force; all stable Model1 and Model2 configurations are outside the ΔR = ±5% region. In the following, we discuss the scenario in which, when the measurements of spin are uncertain, configurations of different EOS and spin may have the same mass and radius. Such ambiguous configurations are indicated with symbols on Fig. 4.
 |
Fig. 4. Stable mass-radius relations for three models: SLy4 model (red solid line), Model1 (green dashed line), Model2 (blue dash-dotted line), and three spin frequencies: 0 Hz (left panel), 700 Hz (middle panel), and 1200 Hz (right panel). Shaded regions correspond to ΔR = ±5% of radii measurements for the non-rotating SLy4 model. We note that some lines of stable configurations with different EOS and f , but similar masses and radii can cross each other. Such cases are denoted by markers: black dots correspond to Rmean ≈ 10.6 km and M ≈ 2.05 M⊙, red stars to Rmean ≈ 11.9 km and M ≈ 1.76 M⊙, green diamonds to Rmean ≈ 12.5 km and M ≈ 1.06 M⊙, and blue triangles to Rmean ≈ 11.9 km and M ≈ 0.91 M⊙. Models with a fixed mass and radius may thus belong to configurations with different EOS, depending on the value of the spin. This adds additional ambiguity to the determination of the EOS from mass and radius measurements, if the rotation rate of the star is not known. |
For example, at Rmean ≈ 10.6 km and M ≈ 2.05 M⊙ (denoted by a black dot), three different NSs are possible: a non-rotating configuration described by Model1, the reference model SLy4 rotating at f = 700 Hz, and Model2 at f = 1200. Such a setup corresponds to a situation in which the masses and radii are determined, but the spin frequency is unknown, for example for a NS in a binary system for which bursts are observed, but which is not observed as a pulsar. We compare these configurations in the P(nb) plane in Fig. 5.
 |
Fig. 5. P(nb) profiles for NSs indicated in Fig. 4 with corresponding markers. Objects have the same M and R, but different spin frequencies f and EOSs. |
This illustrates the importance of the spin information for the inference of the EOS from observations. The most extreme example is shown in the left panel of Fig. 5: the accuracy of the estimation of the central density between Model1 with f = 0 Hz, and Model2 with f = 1200 Hz is approximately 40%. Additionally, the pressure difference between the Model1 ( f = 0 Hz) and SLy4 (f = 700 Hz) configurations is almost 20%. Other properties of the NSs from this case are shown in Table 2: the surface area 𝒮, oblateness 𝒪, T/W ratio, and the angular momentum J. Interestingly, the configuration described by Model1 ( f = 0 Hz) has almost the same surface area 𝒮 as the fast-spinning ( f = 1200 Hz) Model2 configuration. In the other panels of Fig. 5, less extreme cases are presented; their differences between central pressures are around 10%.
The influence of rotation on the global parameters, such as the oblateness 𝒪 and surface area 𝒮, differs between low-mass and massive NSs, as shown in Figs. 6 and 7. Grey vertical lines correspond to PSR J1748−2446ad. As expected, from these two figures one can notice that NSs with masses ≈1 M⊙ reach the mass-shedding frequency much faster (≈750 Hz for Model1 and ≈850 Hz for Model2) than in the case of massive NSs. If PSR J1748−2446ad is a light NS, its oblateness is between ≈0.73 and 0.83. In other words, a ΔR = ±5% accuracy in the radius measurement leads to ±8% accuracy in 𝒪 and to ±10% accuracy in 𝒮 estimation. For stars with M ≈ 2 M⊙, the dependence of oblateness on EOSs is much weaker: at the spin frequency of PSR J1748−2446ad the oblateness is around 0.95 for all three models (±1% accuracy). For the faster rotation, f ≈ 1200 Hz, the error of the 𝒪 increases up to ±11%.
 |
Fig. 6. Oblateness 𝒪 vs. rotational frequency for SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 1 M⊙ and 2 M⊙ masses. The frequency of PSR J1748−2446ad (716 Hz) is shown with the grey vertical line. |
 |
Fig. 7. Surface area 𝒮 vs. rotational frequency for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 1 M⊙ and 2 M⊙ masses. |
The NS surface area for masses M ≈ 1 M⊙ is almost constant with increasing rotational frequency. A significant increase of 𝒮 appears for f ≳ 650 Hz, close to the mass-shedding limit. Massive NSs are also not very susceptible to centrifugal force deformations. Significant deformations occur at ≈1000 Hz. For the whole range of f (for NSs with M ≈ 1 M⊙ and M ≈ 2 M⊙), 𝒮 changes about ±10%. For PSR J1748−2446ad, for which the mass is unknown, the error in the surface area estimation is large: 𝒮 for Model2 2 M⊙ NS is twice as small as for Model1 1 M⊙ NS. As was mentioned in Sect. 3.2, a precise measurement of compactness 𝒞 leads to a ±10% accuracy in the surface area estimation, if f is known. This is comparable with the result that we get for low-mass NSs with unknown spins.
We also investigate central EOS parameters (pressure Pc, density ρc and the baryon density nc) for various masses, spin frequencies, and EOS models. Their behaviour as a function of f strongly depends on the M: for low-mass stars central EOS parameters are almost the same for a broad range of f (Fig. 8). For M = 1 M⊙, for all EOSs and f , Pc ≈ 7 × 1035 dyn cm−2 with negligible errors, ρc ≈ 0.75 × 1015 g cm−3 ±10% and nc ≈ 4.1 × 0.1 fm−3±15%. For NSs with masses ≈ 2M⊙, above few hundreds Hz, the decrease in the values of central parameters, with increasing rotational frequency, is rather fast especially for Model2. For example, the difference in Pc between 0 Hz and 1400 Hz configurations is almost five times smaller (Fig. 8). This case, once again, shows the importance of the knowledge of f . Large uncertainties also exist abetween the interiors of various models: the difference between SLy4 and Model2 is ~40% in Pc and ~35% in ρc and nc. The difference between SLy4 and Model1 is slightly less: ~27% in Pc and ~20% in ρc and nc. Compared to global parameters 𝒪 and 𝒮, estimates of Pc, ρc and nc result in larger differences. For larger spin frequencies, the central parameters converge to similar values.
 |
Fig. 8. Central pressure vs. rotational frequency for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dashed-dotted blue line) for 1 M ⊙ and 2 M ⊙ masses. |
3.4. Known rotational frequency
In Fig. 9, the relation between central pressure Pc and mass M is shown for different spin frequencies. The value Pc slowly increases up to the mass ≈1.9 M⊙, whereas for higher M the growth of Pc(M) is rapid. This is reflected in the uncertainty of the central parameters: for M ≲ 1.9 M⊙, the differences between models for Pc and ρc, are ≲10%; this value increases up to 30% when f is unknown). For objects with higher masses (≳1.9 M⊙), uncertainties in Pc are around 50%, if f is known, and increase to 85% if f is unknown. The increasing uncertainty in central parameters at higher masses is related to the softening of the M(Pc) curve due to general-relativistic effects near to the maximum mass. Although massive stars are much more interesting from the point of view of the dense-matter EOS, they are more challenging to study than low-mass NSs.
 |
Fig. 9. Central pressure as a function of mass for the SLy4 model (red), Model1 (green), Model2 (blue), for rotational frequencies 0 Hz (solid), 700 Hz (dashed), and 1200 Hz (dashed-dotted). |
In Fig. 10, the global angular momentum J for NSs with M = 1 M⊙ and 2 M⊙ is shown. For a specified mass, results for all three models are very similar for frequencies ≲1000 Hz. Above this point one can observe a fast increase in J until the object reaches a Keplerian frequency. Differences between models for low-mass and slowly rotating massive NS are much smaller than for rapidly rotating massive stars. The largest differences, about ±20%, are present for sub-millisecond rotation rates.
 |
Fig. 10. Angular momentum vs. rotational frequency for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 1 M⊙ and 2 M⊙ masses. |
According to Yagi & Yunes (2013a) there exists a universal (independent of the EOS) relation between the quadrupole moment Q and the moment of inertia I. It might be used, for example, to determine rotational frequencies of NSs or distinguish between so-called normal NSs and strange stars (see e.g. Urbanec et al. 2013; Yagi & Yunes 2013a), or employed in the description of binary NS inspiral waveforms. We use the following normalization: Ī = I/M3 and Q̄ = Q/(M3χ2), where M is gravitational mass, χ = J/M2, and J is angular momentum of the object. Our results presented in Fig. 11 show the Ī–Q̄ relation for the three models for two different spin frequencies: 700 and 1200 Hz. The results are consistent with the I–Q relation. This is especially true for massive stars (occupying the lower right corner of Fig. 11), which are less deformed by the centrifugal force.
 |
Fig. 11. Normalized moment of inertia Ī vs. normalized quadrupole moment Q̄ for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 700 Hz and 1200 Hz spin frequencies. |
3.5. Radius measurements with ±10% uncertainty
As mentioned in Sect. 1, ±5% errors in R may be considered too optimistic and a ±10% uncertainty is a more realistic value (Lo et al. 2013; Miller & Lamb 2016). In order to study this case two additional piecewise polytropic EOSs with the SLy4 EOS crust were constructed. The parameters of the Model3 and Model4 EOSs are collected in Table 3.
Parameters of the three polytropes employed for the EOSs of Model3 and Model4 (indices correspond to the number of the polytrope).
Model3 and Model4 were chosen to reproduce ΔR = ±10% errors of the radius measurements of the non-rotating reference SLy4 model. Results, as before, depend on the NS mass. Trends are similar to the ±5% case; NSs with masses ≈1 M⊙ are more favourable for the estimations of the central parameters such as Pc, ρc, nc, whereas massive stars produce small errors in the determination of global parameters such as 𝒪 and 𝒮. As expected, most of the uncertainties increase with increasing ΔR.
For low-mass NSs, the accuracy of the 𝒪 determination is comparable with the result for the ΔR = ±5% assumption; the oblateness for NSs with masses ≈1 M⊙ depends weakly on the accuracy of the R measurements. For massive NSs, the 𝒪 uncertainty is ≈3% for the frequency of the fastest known pulsar and ≈18% for 1200 Hz (for the ±5% case the values were 1% and 11%, respectively). The errors in the estimation of the surface area 𝒮 do not depend on frequency: for the whole spin range they are similar and around 22% (twice what they are in the case of ΔR = ±5%).
As expected, uncertainties in the central parameters are smaller for low-mass stars. For NSs with M ≈ 1 M⊙: Pc ≈ 7 × 1035 dyn cm−2 with negligible errors (similar as for ΔR = ±5%), ρc ≈ 0.75 × 1015 g cm−3 ±30% (10% in case ΔR = ±5%) and nc ≈ 4.1 × 0.1 fm−3 ±30% (15% in case ΔR = ±5%). For massive stars again one can observe a very fast decrease in the central values with frequency, especially for Model4. An example of the central density ρc as a function of the rotational frequency, for all five models 2 M⊙ NS, is shown in Fig. 12. Differences between SLy4 and Model4 are 64% in Pc, 38% in ρc, and 32% in nc; differences between SLy4 and Model3 are 33% in Pc, 19% in ρc, and 15% in nc.
 |
Fig. 12. Central density ρc vs, rotational frequency for the SLy4 EOS (red), Model1 EOS (green), Model2 EOS (blue), Model3 EOS (purple), and Model4 EOS (orange), for 2 M⊙. |
3.6. Tidal deformability
We also investigate the recent gravitational-wave estimate of the tidal deformabilities in the GW170817 binary NS system. Fig. 13 reproduces the Λ1 − Λ2 relation for the deformabilities in the range of masses corresponding to the measured chirp mass 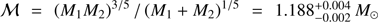 and the range of component masses in the case of low-spin priors, M1 = 1.36−1.60 M⊙ and M2 = 1.17−1.36 M⊙ (the definition of the tidal deformability Λ was introduced in Sect. 2). For the three EOS models discussed in this work, the difference in radius ΔR = ±5% is consistently reflected in the ΔΛ values, which are between 250 for 1.17 M⊙, and 50 for 1.6 M⊙. Increasing ΔR by a factor of two gives a two times larger ΔΛ. This trend can be understood by analysing Fig. 2, where the P(ρ) ranges for GW170817 component masses are shown, and in Fig. 13, where the relation between R, M, Λ, and k2 are plotted. The EOSs yield, to first approximation, a constant difference in the stellar radius and have similar stiffness in the relevant mass ranges, which is reflected in the k2 values, while the difference in Λ between models is dominated by the M−5 term. Regular behaviour of Λ with R and M may be exploited to approximately reproduce R, given Λ and M values. A linear relation R ≈ a(M)Λ + b(M) (km), where
and the range of component masses in the case of low-spin priors, M1 = 1.36−1.60 M⊙ and M2 = 1.17−1.36 M⊙ (the definition of the tidal deformability Λ was introduced in Sect. 2). For the three EOS models discussed in this work, the difference in radius ΔR = ±5% is consistently reflected in the ΔΛ values, which are between 250 for 1.17 M⊙, and 50 for 1.6 M⊙. Increasing ΔR by a factor of two gives a two times larger ΔΛ. This trend can be understood by analysing Fig. 2, where the P(ρ) ranges for GW170817 component masses are shown, and in Fig. 13, where the relation between R, M, Λ, and k2 are plotted. The EOSs yield, to first approximation, a constant difference in the stellar radius and have similar stiffness in the relevant mass ranges, which is reflected in the k2 values, while the difference in Λ between models is dominated by the M−5 term. Regular behaviour of Λ with R and M may be exploited to approximately reproduce R, given Λ and M values. A linear relation R ≈ a(M)Λ + b(M) (km), where 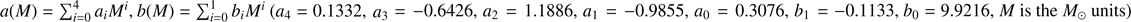 recovers the values of radii R for the models considered here with an error of typically 0.1 km.
recovers the values of radii R for the models considered here with an error of typically 0.1 km.
 |
Fig. 13. Upper row, left panel: Comparison of tidal deformabilities Λ for stellar component masses compatible with the GW170817 observation (assuming low-spin priors; Abbott et al. 2017a). The shaded area denotes the estimated 90% confidence region corresponding to the measurement. Right panel: Stellar mass as a function of tidal deformability Λ, for the mass range between 1.15 M⊙ and the Mmax. Lower row, left panel: Tidal deformability Λ as a function of stellar radius; points denote 1.2, 1.4, and 1.6 M⊙ (from upper to lower). Approximate formula denoted in the text is represented by black dotted curves. Right panel: Mass as a function of the k2 tidal Love number. |
4. Discussion
In this work we have estimated how much information about the EOS parameters can be drawn from current and future measurements of neutron star radii, assuming a target accuracy of about 5%. To address this question, we have compared the widely accepted SLy4 EOS (Douchin & Haensel 2001), treated as a reference EOS, with two parametric EOSs designed to yield TOV M(R) sequences with ±5% of the SLy4 radius.
We also considered the influence of rigid axisymmetric rotation on the global properties of the NSs and their central EOS parameters. In some cases, certain configurations may mimic othes with different rotational frequencies and EOSs. We show that even if M is established precisely and errors are present only in the measurement of R, the lack of the information about f might lead to 40% error in central pressure estimation (see Figs. 4 and 5).
Rapid rotation may be a crucial factor in the distinction between NSs with different EOSs. For spins comparable with the rotational frequency of the fastest known pulsar (716 Hz for PSR J1748−2446ad), the radii deviate by more than 5% from the reference SLy4 radius for stars with masses ≲1.4 M⊙, whereas for f = 1200 Hz the radius difference is larger than 5% for the whole available NS mass range. As expected, for low-mass stars, rotation manifests itself strongly by deforming the star, but the central parameters are almost unchanged. A 5% accuracy in the measurement of R leads to 8–10% errors in the estimation of the stellar oblateness 𝒪 and surface area 𝒮. Even if the rotational frequency of these stars is unknown, their central properties can be established with ±10% accuracy. For more massive stars, with masses ≈2 M⊙ and known rotational frequency f , the uncertainties are much higher, up to 40%.
For cases when only compactness can be measured (e.g. because of the slow rotation of the object), it is possible to estimate surface area with ~10% accuracy for sources with known spin frequency.
We take as an example PSR J1748−2446ad, and show how limited our reconstruction of the properties of a compact object is, when only its rotational frequency is known. Assuming, for the sake of an example, that the SLy4 EOS is the true EOS, one can expect that the oblateness lies between 0.72 and 0.97 for masses between 1 and 2 M⊙. If we assume ±5% observational uncertainty on radius, it leads to an ≈30% accuracy in the determination of ρc, ≈20% for nb and ≈50% accuracy for Pc, if this object is massive. If its mass is only ≈1 M⊙, the central parameters for various models are very similar to each other.
We repeated our study for the ΔR = 10% case. As expected, uncertainties on the central and global parameters increase. Oblateness 𝒪 can be estimated with ≲18% and 𝒮 with ≈22% error, which are approximately twice the measurement uncertainties of the ±5% case. The accuracy of the estimation of the central parameters depends on the NS mass. For low-mass stars Pc can be estimate with negligible errors, and ρc and nc with ≈30% uncertainties. For massive NSs errors are up to 64% in Pc, 38% in ρc, and 32% in nc. These results suggest that increasing ΔR by a factor of two decreases the accuracy of the estimation of the NS central parameters by a factor of ~2–3.
We also estimate the effect of the radius uncertainty on the tidal deformability Λ, using as an example the estimated masses of the components from the GW170817 event (Abbott et al. 2017a). The ±5% radius difference of the parametric models with respect to the SLy4 model results in ΔΛ between 250 at 1.17 M⊙ and 50 at 1.6 M⊙ (these values are two times higher for ΔR = ±10%), and since the EOSs possess similar stiffness in the relevant regimes and hence similar behaviour of the tidal Love numbers k2 (Figs. 2 and 13), the ΔΛ is mostly influenced by the dependence of Λ on mass M.
Linking the NS global parameters with the properties of the dense matter EOS is an area of active effort in view of forthcoming observational results. An extensive study on the full currently allowed range of NS radii will be the subject of future work.
Acknowledgments
We acknowledge Prof. J. L. Zdunik for his implementation of the tidal Love numbers in the TOV equation and Prof. T. Güver for useful comments and suggestions. MS and MB were partially supported by the Polish NCN grants no. 2014/14/M/ST9/00707 and 2016/22/E/ST9/00037. BH and MB acknowledge support from the European Union’s Horizon 2020 research and innovation programme under grant agreements No. 70271 and No. 653477, respectively. We acknowledge partial support by the “PHAROS” COST action CA 16214. This research was completed using free and open software (LORENE, gnuplot, python: matplotlib, numpy and scipy).
References
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2017a, Phys. Rev. Lett., 119, 161101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abbott, B. P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) 2017b, ApJ, 851, 1 [CrossRef] [Google Scholar]
- Annala, E., Gorda, T., Kurkela, A., & Vuorinen, A. 2018, Phys. Rev. Lett., 120, 172703 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Antoniadis, J., Freire, P. C. C., Wex, N., et al. 2013, Science, 340, 448 [Google Scholar]
- Arzoumanian, Z., Gendreau, K. C., & Baker, C. L., et al. 2014, Proc. SPIE 9144, Space Telescopes and Instrumentation 2014: Ultraviolet to Gamma Ray, 914420 [Google Scholar]
- Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., et al. 2018, ApJS, 235, 37 [CrossRef] [Google Scholar]
- Bauswein, A., Stergioulas, N., & Janka, H.-T. 2015, ArXiv e-prints [arXiv:1503.08769] [Google Scholar]
- Bauswein, A., Just, O., Janka, H.-T., & Stergioulas, N. 2017, ApJ, 850, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Bejger, M., Gondek-Rosińska, D., Gourgoulhon, E., et al. 2005, A&A, 431, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonazzola, S., & Gourgoulhon, E. 1994, CQG, 11, 1775 [NASA ADS] [CrossRef] [Google Scholar]
- Bonazzola, S., Gourgoulhon, E., Salgado, M., & Marck, J. A. 1993, A&A, 278, 421 [NASA ADS] [Google Scholar]
- Damour, T., Nagar, A., & Villain, L. 2012, Phys. Rev. D, 85, 123007 [NASA ADS] [CrossRef] [Google Scholar]
- Demorest, P. B., et al. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elshamouty, K. G., Heinke, C. O., Morsink, S. M., Bogdanov, S., & Stevens, A. L. 2016, ApJ, 826, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Flanagan, É. É., & Hinderer, T. 2008, Phys. Rev. D, 77, 021502 [NASA ADS] [CrossRef] [Google Scholar]
- Fonseca, E., Pennucci, T. T., Ellis, J. A., et al. 2016, ApJ, 832, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Fortin, M., Zdunik, J. L., Haensel, P., & Bejger, M. 2015, A&A, 576, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fortin, M., Providência, C., Raduta, Ad. R., et al. 2016, Phys. Rev. C, 94, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Galloway, D. K., Özel, F., & Psaltis, D. 2008b, Mon. Not. Roy. Astron. Soc., 387, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Gourgoulhon, E. 2010, ArXiv e-prints [arXiv:1003.5015] [Google Scholar]
- Gourgoulhon, E., Haensel, P., Livine, R., et al. 1999, A&A, 349, 851 [Google Scholar]
- Gourgoulhon, E., Grandclément, P., Marck, J. A., Novak, J., & Taniguchi, K. 2016, Astrophysics Source Code Library, [record ascl:1608.018] [Google Scholar]
- Haensel, P., Potekhin, A. Y., Yakovlev, D. G., 2007, Astrophysics and Space Science Library, (New York: Springer), 326 [Google Scholar]
- Haensel, P., Bejger, M., Fortin, M., & Zdunik, J. L. 2016, Eur. Phys. J. A, 52, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinke, C. O., et al. 2014, MNRAS, 444, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Hessels, J. W. T., Ransom, S. M., Stairs, I. H., et al. 2006, Science, 311, 1901 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kaaret, P., Prieskorn, Z., In’t Zand, J. J. M., et al. 2007, AJ, 657, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Lo, K. H., Miller, M. C., Bhattacharyya, S., & Lamb, F. K. 2013, AJ, 776, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Margalit, B., & Metzger, B. D. 2017, ApJ, 850, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, M. C., & Lamb, M. C. 2016, Eur. Phys. J. A, 52, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motch, C., Wilms, J., Barret, D., et al. 2013, ArXiv e-prints [arXiv:1306.2334] [Google Scholar]
- Love, A. E. H. 1911, Some Problems of Geodynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Özel, F., & Freire, P. 2016, ARA&A, 54, 401 [Google Scholar]
- Özel, F., Psaltis, D., Arzoumanian, Z., Morsink, S., & Bauböck, M. 2016, AJ, 832, 92 [CrossRef] [Google Scholar]
- Psaltis, D., & Özel, F. 2014, AJ, 792, 2 [Google Scholar]
- Psaltis, D., Özel, F., & Chakrabarty, D. 2014, AJ, 787, 136 [Google Scholar]
- Rezzolla, L., Most, E. R., & Weih, L. R. 2018, ApJ, 852, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Sotani, H. 2017, Phys. Rev. D, 96, 104010 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Heinke, C. O., Bogdanov, S., et al. 2018, MNRAS, 476, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Tolman, R. C. 1939, Phys. Rev., 55, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Urbanec, M., Miller, J. C., & Stuchlík, Z. 2013, MNRAS, 433, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Bejger, M., Ró˙zańska, A., et al. 2018, ApJ, 855, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Van Oeveren, E. D., & Friedman, J. L. 2017, Phys. Rev. D, 95, 083014 [NASA ADS] [CrossRef] [Google Scholar]
- van Paradijs, J. 1979, AJ, 234, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Yagi, K., & Yunes, N. 2013a, Science, 341, 365 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Parameters of the three polytropes employed for the EOSs of Model1 and Model2 (indices correspond to the number of the polytrope).
Parameters of the three polytropes employed for the EOSs of Model3 and Model4 (indices correspond to the number of the polytrope).
All Figures
 |
Fig. 1. Right panel: Range of central densities ρc for stars rotating with the frequency f up to 1400 Hz. Left panel: Non-rotating configurations for the SLy4 EOS (red), Model1 EOS (green), and Model2 EOS (blue), following the ΔR = ±5% uncertainty in the radius measurement (grey region). |
| In the text | |
 |
Fig. 2. Upper panel: P(ρ) profiles corresponding to the M(R) relations from the left panel of Fig. 1, with the SLy4 model denoted by a red solid line, Model1 by a green dashed line, and Model2 by a blue dash-dotted line. Thick semi-transparent lines denote P(ρ) ranges for the two components of the GW170817 binary neutron star system (Abbott et al. 2017a, with mass estimates using the low-spin priors). We also plot the pressure difference between the SLy4 model and Model1 (dashed green line, middle panel) and Model2 (dash-dotted blue line, lower panel). |
| In the text | |
 |
Fig. 3. Compactness vs. surface area for three EOSs: SLy4 (solid red), Model1 (dashed green), and Model2 (dash-dotted blue), for two rotational frequencies: 0 Hz (thin lines) and 1200 Hz (thick lines). Lines of constant central density are indicated in grey (dark grey for SLy4, medium grey for Model2, and light grey for Model1). Corresponding values of the central density are given on the left side of the plot (in units of 1015g cm−3). |
| In the text | |
 |
Fig. 4. Stable mass-radius relations for three models: SLy4 model (red solid line), Model1 (green dashed line), Model2 (blue dash-dotted line), and three spin frequencies: 0 Hz (left panel), 700 Hz (middle panel), and 1200 Hz (right panel). Shaded regions correspond to ΔR = ±5% of radii measurements for the non-rotating SLy4 model. We note that some lines of stable configurations with different EOS and f , but similar masses and radii can cross each other. Such cases are denoted by markers: black dots correspond to Rmean ≈ 10.6 km and M ≈ 2.05 M⊙, red stars to Rmean ≈ 11.9 km and M ≈ 1.76 M⊙, green diamonds to Rmean ≈ 12.5 km and M ≈ 1.06 M⊙, and blue triangles to Rmean ≈ 11.9 km and M ≈ 0.91 M⊙. Models with a fixed mass and radius may thus belong to configurations with different EOS, depending on the value of the spin. This adds additional ambiguity to the determination of the EOS from mass and radius measurements, if the rotation rate of the star is not known. |
| In the text | |
 |
Fig. 5. P(nb) profiles for NSs indicated in Fig. 4 with corresponding markers. Objects have the same M and R, but different spin frequencies f and EOSs. |
| In the text | |
 |
Fig. 6. Oblateness 𝒪 vs. rotational frequency for SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 1 M⊙ and 2 M⊙ masses. The frequency of PSR J1748−2446ad (716 Hz) is shown with the grey vertical line. |
| In the text | |
 |
Fig. 7. Surface area 𝒮 vs. rotational frequency for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 1 M⊙ and 2 M⊙ masses. |
| In the text | |
 |
Fig. 8. Central pressure vs. rotational frequency for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dashed-dotted blue line) for 1 M ⊙ and 2 M ⊙ masses. |
| In the text | |
 |
Fig. 9. Central pressure as a function of mass for the SLy4 model (red), Model1 (green), Model2 (blue), for rotational frequencies 0 Hz (solid), 700 Hz (dashed), and 1200 Hz (dashed-dotted). |
| In the text | |
 |
Fig. 10. Angular momentum vs. rotational frequency for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 1 M⊙ and 2 M⊙ masses. |
| In the text | |
 |
Fig. 11. Normalized moment of inertia Ī vs. normalized quadrupole moment Q̄ for the SLy4 model (solid red line), Model1 (dashed green line), and Model2 (dash-dotted blue line) for 700 Hz and 1200 Hz spin frequencies. |
| In the text | |
 |
Fig. 12. Central density ρc vs, rotational frequency for the SLy4 EOS (red), Model1 EOS (green), Model2 EOS (blue), Model3 EOS (purple), and Model4 EOS (orange), for 2 M⊙. |
| In the text | |
 |
Fig. 13. Upper row, left panel: Comparison of tidal deformabilities Λ for stellar component masses compatible with the GW170817 observation (assuming low-spin priors; Abbott et al. 2017a). The shaded area denotes the estimated 90% confidence region corresponding to the measurement. Right panel: Stellar mass as a function of tidal deformability Λ, for the mass range between 1.15 M⊙ and the Mmax. Lower row, left panel: Tidal deformability Λ as a function of stellar radius; points denote 1.2, 1.4, and 1.6 M⊙ (from upper to lower). Approximate formula denoted in the text is represented by black dotted curves. Right panel: Mass as a function of the k2 tidal Love number. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.