| Issue |
A&A
Volume 616, August 2018
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 11 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201732060 | |
| Published online | 22 August 2018 | |
The consequences of a nearby supernova on the early solar system
1
Leiden Observatory, Leiden University,
PO Box 9513,
2300
RA,
Leiden,
The Netherlands
e-mail: spz@strw.leidenuniv.nl
2
Centrum Wiskunde & Informatica,
Science Park 123,
1098
XG Amsterdam,
The Netherlands
3
Department of Astrophysics/IMAPP, Radboud University Nijmegen,
PO Box 9010,
6500
GL Nijmegen,
The Netherlands
4
Konkoly Observatory, Research Centre for Astronomy and Earth Sciences, Hungarian Academy of Sciences,
1121
Budapest,
Hungary
Received:
6
October
2017
Accepted:
10
April
2018
If the Sun was born in a relatively compact open cluster (half-mass radius ≲3 pc) with ≳103 stars, it is quite likely that a massive (≳10 M⊙) star was nearby when it exploded in a supernova. The repercussions of a supernova can be rather profound, and the current solar system may still bear the scars of this traumatic event. The truncation of the Kuiper belt and the tilt of the ecliptic plane with respect to the Sun’s rotation axis could represent such signatures. We simulated the effect of a nearby supernova on the young solar system using the Astrophysical Multipurpose Software Environment (AMUSE). Our calculations are realized in two subsequent steps in which we study the effect of the supernova irradiation on the circumstellar disk and the effect of the impact of the nuclear blast-wave which arrives a few decades later. We find that the blast wave of our adopted supernova exploding at a distance of 0.15–0.40 pc and at an angle of 35°–65° with respect to the angular-momentum axis of the circumsolar disk would induce a misalignment between the Sun’s equator and its disk to 5.°6 ± 1.°2, consistent with the current value. The blast of a supernova truncates the disk at a radius between 42 and 55 au, which is consistent with the current edge of the Kuiper belt. For the most favored parameters, the irradiation by the supernova as well as the blast wave heat the majority of the disk to ≳1200 K, which is sufficiently hot to melt chondrules in the circumstellar disk. The majority of the planetary system may have been affected by a nearby supernova. Some of its repercussions, such as truncation and tilting of the disk, may still be visible in the current planetary system topology. The amount of material from the supernova blast wave that is accreted by the circumstellar disk is too small by several orders of magnitude to explain the current abundance of the short-lived radionuclide 26Al.
Key words: methods: numerical / planets and satellites: dynamical evolution and stability
© ESO 2018
1 Introduction
Stars are expected to form in clustered environments (Lada & Lada 2003) and the Sun is probably no exception (Portegies Zwart 2009). From dynamical considerations with the hypothesis that the Sun’s circumstellar disk survived close encounters, the proto-solar cluster was ~ 1 pc in size, contained ~ 103 stars, and ultimately became gravitationally unbound (Portegies Zwart 2009). In this dense stellar environment, several massive ≳ 20M⊙ stars must have been present and one star was probably close when it exploded in a supernova (Lichtenberg et al. 2016; Nicholson & Parker 2017).
The repercussions of a nearby supernova may be profound Close & Pittard (2017), and it’s effect has been studied using grid-based hydrodynamical simulations by Ouellette et al. (2007), who injected a slab of dense gas at 400 km s−1 perpendicular to a 40au circumstellar disk. They found that the disk accretes ~ 1% of the slab, which is insufficient to explain the abundance of 26Al in the early solar system. This is a short-lived radionuclide (t1∕2 = 0.717 Myr) whose initial abundance corresponds to a 26Al /27Al ratio of 5 × 10−5, as inferred from excesses of its decay product, 26Mg, in meteoritic materials such as calcium- and aluminium-rich inclusions (CAIs; Jacobsen et al. 2008b). Iron-60 (t1∕2 = 2.62 Myr) is another short-lived radionuclide (SLR) of interest because its presence in the early solar system could indicated the occurrence of (one or more) nearby core-collapse supernovae during formation. However, its initial abundance is highly uncertain, with recently reported values ranging from 60Fe/56Fe ~ 10−8, which would not require one or more local supernovae (Tang & Dauphas 2012, 2015), up to ~ 10−7–10−6 (Mishra & Chaussidon 2014; Telus et al. 2018), which would require more than one supernova. The traditional view is, therefore, that 26Al originated from a ~25 M⊙ star that exploded as a supernova (Meyer 2005; Looney et al. 2006); however due to the potential difficulty for supernovae to match the 60Fe/26Al ratio in the early solar system, other sources have also been suggested, such as Wolf-Rayet stars (Gaidos et al. 2009; Gounelle & Meynet 2012; Dwarkadas et al. 2017). In the framework of accretion of supernova ejecta by a protoplanetary disk, to solve the problem of the overly small accretion efficiency, Ouellette et al. (2007, 2010) proposed that the radionuclides 26Al and 60Fe were completely condensed into large (μm size) dust grains, which have a much higher injection efficiency.
We revisit this problem to study the more intricate interaction between the supernova irradiation and its blast wave and the Sun’s circumstellar disk, in particular when both do not perfectly align. Another reason to revisit this problem is to investigate to what extent today’s anomalously small disk 42–55 au, in comparison to the 100–400 au disks found in nearby star-forming regions (Vicente & Alves 2005), could be the result of the truncation by the blast wave of a nearby supernova. We report on our findings in two sections, Sect. 2 where we discuss the effect of the supernova radiation on the circumstellar disk and Sect. 3 where we discuss the hydrodynamics of the blast wave hitting the disk; we discuss the results and consequences in Sect. 4.
2 Effect of the supernova irradiation
For the supernova explosion distances we are interested in, the first impact to which the nearby proto-planetary disk is exposed will be the intense radiation emitted in the early stages of the supernova. This radiation can ionize and heat the disk material and even disrupt the disk. In order to assess the extent of this heating and whether the disk survives, we start by calculating the effect of the supernova irradiation on the disk using a combined hydrodynamics and radiative transfer solver.
We start each simulation by generating the young solar system composed of a 1 M⊙ star and a 0.01 M⊙ gaseous disk with an inner radius of rmin = 1 au and an outer radius of rmax = 100 au. In Fig. 1 we present the geometry of our simulation setup, and Fig. 2 shows three projections of the initial disk.
The mid-plane temperature profile for a disk in a steady state and with constant viscosity follows a power law, Tc ∝ r−p, and the surface density profile 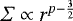 between a few and ~ 100 au (Shakura &Sunyaev 1973). For planet-forming disks in steady state p ≃ 0.5 (Armitage 2011) and surface density profile is roughly ∝ r−1. This profile is consistent with the surface densities of protoplanetary disks observed in the Ophiuchus star-formingregion (Andrews et al. 2009, 2010). We adopt a power-law density profile with exponent − 1 (with temperature profile ∝ r−0.5) with Savronov-Toomre Q-parameter qout = 25 (Safronov 1960; Toomre 1964), for which the disk at least marginally stable throughout. The temperature of this disk ranges from 19 K (at the rim) to about 165 K in the central regions. In Fig. 3 we present the disk temperature along three planes. At t = 0, when we start our calculations, the supernova is ignited at a distance d and with anangle Θ with respect to the locus of the disk (Θ = 0° indicates right above the disk). In Fig. 1, we present a schematic presentation of the simulation. We performed calculations for a grid in distance to the supernova d = 0.05 pc, 0.1, 0.15, 0.2, 0.3, 0.4 and 0.6 pc, and angle of the disk Θ = 15° to 75° in steps of 15°.
between a few and ~ 100 au (Shakura &Sunyaev 1973). For planet-forming disks in steady state p ≃ 0.5 (Armitage 2011) and surface density profile is roughly ∝ r−1. This profile is consistent with the surface densities of protoplanetary disks observed in the Ophiuchus star-formingregion (Andrews et al. 2009, 2010). We adopt a power-law density profile with exponent − 1 (with temperature profile ∝ r−0.5) with Savronov-Toomre Q-parameter qout = 25 (Safronov 1960; Toomre 1964), for which the disk at least marginally stable throughout. The temperature of this disk ranges from 19 K (at the rim) to about 165 K in the central regions. In Fig. 3 we present the disk temperature along three planes. At t = 0, when we start our calculations, the supernova is ignited at a distance d and with anangle Θ with respect to the locus of the disk (Θ = 0° indicates right above the disk). In Fig. 1, we present a schematic presentation of the simulation. We performed calculations for a grid in distance to the supernova d = 0.05 pc, 0.1, 0.15, 0.2, 0.3, 0.4 and 0.6 pc, and angle of the disk Θ = 15° to 75° in steps of 15°.
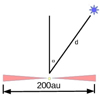 |
Fig. 1 Geometry of the experimental setup. The circumestellar disk is represented near the bottom with a diameter of 200 au. The exploding star (blue star to the top right) at a distance d and with angle Θ with respectto the disk’s angular momentum axis. |
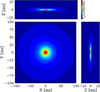 |
Fig. 2 Mid-plane density distribution of the protoplanetary disk with a top view in the middle and side views to the right and top. The density is color coded, the coding scheme is presented to the top right of the figure. The density extrema range from 10−12.9 g cm−3 to 10−9.97 g cm−3. |
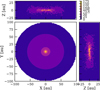 |
Fig. 3 Top view of the protoplanetary disk from three sides, the top view (x-y) image in the middle and two size aspects to the right and top. The colors represent temperature, and the coding is represented by the bar to the top right. |
2.1 The supernova light curve
For the supernova light curve, we adopt the multiple power-law fits to observed supernovae by Sanders et al. (2015). We use fit parameters for supernovae PS1-10a and PS1-11aof (referred to henceforth as SN10a and SN11aof, respectively) from their Table 3, because the light curves as well as the mass of the ejecta are well constrained for these two. The former peaks at a luminosity of 2.3 ×1042 erg s−1 (almost 108.8 L⊙) approximately 10 days after the supernova, whereas the latter reaches its peak of 1.1 ×1043 erg s−1 (almost 109.8 L⊙) approximately 26 days after the supernova explosion is initiated. We compare the light curves of these two supernovae in Fig. 4. From the fits to the light curves, Sanders et al. (2015) derive masses for the ejecta of 6.0 M⊙ for SN10a and 23.5 M⊙ for SN11aof.
The temperature of the supernova before hydrogen recombination in the remnant is very high. The temperature decays quickly withtime and up to about 100 days after the explosion follows the relation
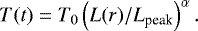 (1)
(1)
Here T0 = 15 000 K and α = 1∕3 (Faran et al. 2018). We adopt this temperature evolution in our calculations.
 |
Fig. 4 Light curves and disk temperatures for the type IIp supernovae SN11aof (left panel) and SN10a (right panel). The dashed blue curves with the scales in blue to the left of the respective panels give the luminosity of the supernova, and are power-law fits from Sanders et al. (2015). The red curves give the mean temperature of the disk at distances of 0.1, 0.2, 0.3 and 0.4 pc (from left to right). For the latter, we present curves (bottom to top curve) for an inclination of 15°, 30°, 45°, 60° and 75°. For the distance of 0.1 pc, we only show the disk temperature for the inclination angle of 75°, and for the other two distances at 15°. In the right-hand panel, we show the same curves but for supernova SN10a. The thin green line (to the upper right) indicates a cooling of 0.3 K h−1, which is consistent with the cooling after the supernova radiation has heated the disk for SN11aof. In Sect. 4.1, we discuss the effect of the heating on structure of vitreous chondrules in the disk. |
2.2 The combined hydrodynamics with radiative transfer solver
The first part of the calculation is composed of a hydrodynamics solver for the circumstellar disk and a radiative transfer code for irradiating the disk.
The hydrodynamics is addressed with the smoothed particles hydrodynamics (SPH) code Fi (Hernquist & Katz 1989; Gerritsen & Icke 1997; Pelupessy et al. 2004). We performed a series of test calculations for the hydrodynamics of the protoplanetary disk using 103 particles, doubling the number of particles to 107, and these reached convergence at a few times 104 particles. Based on this validation experiment we decided to perform all further calculations with 105 SPH particles.
The radiative transfer calculations are performed with SPHRay (Ritzerveld & Icke 2006; Altay et al. 2008, 2011). This is a classic Monte-Carlo ray-tracing code meant for integrating rays through the interpolated SPH density distribution. The radiative transfer code requires the ionizing luminosity of the radiative source to be expressed in photons per second. We set each photon to deposit 20 eV, which for SN11aof, which has a peak luminosity of 109.8 L⊙ results in ~ 7.6 × 1056 photons s−1. For the energy spectrum of the photons, we assume a power-law index of − 3. As soon as the outflow material blocks the central source, the spectrum becomes softer, but since we are mostly interested in the hard and hot phase shortly after the onset of the supernova, we ignore this. Absorption is computed from the transfer equation in each cell, upon which re-emission creates new sources. The transfer equation is solved using a semi-implicit iteration scheme (Iliev et al. 2006). In Sect. 4.2 we discuss the effect of adding dust to the radiative transfer solution.
The two codes are combined using the Astronomical Multipurpose Software Environment (AMUSE for short; Portegies Zwart 2011; Portegies Zwart et al. 2013; Pelupessy et al. 2013). AMUSE is a component library dedicated to multi-scale and multi-physics astronomical calculations. Details on the code can be found in the associated textbook by Portegies Zwart & McMillan (2017).
The two codes are combined in the main event loop by taking subsequent steps in the radiative transfer and hydrodynamics codes. The loop starts with half a step in the radiative transfer code. This calculation is followed by one full step in the hydrodynamics, and a finishing second half-step in the radiative transfer. During these steps, the positions, velocities, densities, pressure, internal energy, and degree of ionization are communicated between the radiative transfer and the hydrodynamics solvers. This coupling strategy is called interlaced temporal discretization in the AMUSE framework (Portegies Zwart & McMillan 2017), which is a form of operator splitting (Wisdom & Holman 1991; Pelupessy et al. 2013).
We performed a series of test calculations with a step size of 1 day, halving the step size by factors of two until we reached time steps of 10 min; convergence was reached at a step size of about 2 h. Based on these validation experiments we decided to perform all further calculations with a conservative step size of 1 h.
We performed a series of radiative transfer test-calculations using 105 rays per time step (1 h at a distance of 0.1 pc), doubling again until we reached 109 rays per time step, and convergence was reached at about 106 rays per time step. Based on this validation experiment we decided to perform all further calculations with 107 rays per time step.
The adopted backward difference solver for the combined evolution of the temperature and abundances of chemical species includes photo ionization, collisional ionization, recombination, photo heating and atomic cooling (Altay et al. 2008). The adopted chemical model includes an approximation for the H2 chemistry taking into account photo-ionization of the H2 molecule. The frequency and flux of the incoming radiation are calculated using the underlying supernova model and assuming a thermalized spectrum.
The production calculations were performed on a 192-core X86-E7 workstation and took about a month per run.
2.3 Results on the irradiation of the circumstellar disk
The intense radiation of a bright supernova explosion increases the average temperature in the disk. In Fig. 4 we present the results of several calculations of the combined solver, hydrodynamics plus radiative transfer. We present various curves for a range of angles and distances to both supernovae. In Fig. 5 we present a single top view of the temperature in the disk’s midplane as it is illuminated and heated by supernova SN11aof from a distance of 0.2 pc at an angle of θ = 60°. In Fig. 6 we present three more images of the same disk and supernova simulations at different epochs.
Temperatures in excess of ~ 1200 K are sufficient to melt chondrules without vaporizing them (Davis & Richter 2005). In Fig. 7 (see also Fig. 14 where we included the effect of dust), we present the temperature of the disk when it is hottest as a function of the distance to the supernova d and the impact angle Θ. In our simulations, temperatures of 1500–2000 K are reached when the supernova exploded at a distance of 0.13–0.44 pc for SN11aof and ~ 0.05–0.18 pc for SN10a (for a discussion on the effect of dust in the circumstellar disk, see Sect. 4.2). The dependence of the peak mean temperature on the inclination angle Θ is not very strong unless the irradiation happens almost edge on (Θ ≳ 70°) when self-shielding effects become strong. The disk would vaporize if the temperature were even higher; there is no observational evidence for this, however.
After the main irradiation, when the supernova starts to dim, the circumstellar disk material cools down to the equilibrium state. The cooling rate in this phase is of the order of 0.3 K h−1 (see the green line to the right in Fig. 4). After ~ 3 yr, the radiation of the supernova has dropped below ~ 105 L⊙ at which moment we stop the radiative transfer calculation. The further thermal evolution of the disk is addressed by integrating the thermal evolution using a semi-analytic approximation for the cooling curve (Gerritsen & Icke 1997).
 |
Fig. 5 View of the midplanet temperature of the circumstellar disk at the moment supernova SN11aof reaches its maximum. The supernova exploded at a distance of 0.2 pc and at an angle of θ = 60°. In Fig. 6, we present several face-on temperature distributions of the same disk at different moments in time. |
 |
Fig. 6 Top view of the mid-plane temperature of the circumstellar disk at four epochs: the start of the simulation (left most image), at 26 days after the onset of supernova SN11aof, about 100 days after the supernova and about 2 yr later, when the disk has almost completely cooled down again (right-most image). Each image was taken from the simulation where the supernova exploded at a distance of 0.2 pc and at an angle of θ = 60°. See Fig. 5 for the temperature scale. |
 |
Fig. 7 Peak mean temperature of the disk (contours) due to the supernova radiation as a function of the distance to a supernova (d in parsec) and the impact angle (Θ in degrees, measured from the disk’s angular-momentum axis). The adopted type IIp supernovae, SN11aof (left), has a peak luminosity of 1.1 × 1043 erg s−1 and SN10a (right) has a peak luminosity of 2.3 × 1042 erg s−1. Evaporation of the bulk of the solids in the proto-planetary disk is achieved when the irradiation heats it to a mean temperature of ≳ 1500 K. The two shaded regions indicate the range in distance for which the Sun’s obliquity is consistent with the currently observed value of 5.°6 ± 1.°2 (blue with “\\” hashes), and for which the disk is truncated to 42–55 au (green with “//” hashes). This area is indicated in Figs. 11 and 12 with a blue polygon. The most promising part of parameter space is where the two hashed areas overlap because that is where both criteria are met. |
 |
Fig. 8 Surface density profile of the proto planetary disk at two moments in time for two supernovae SN10a (green) and the much brighter SN11aof (red). The former was at a distance of d = 0.1 pc and with an impact angle of Θ = 60°, the latter at a distance of d = 0.4 pc and with an angle of Θ = 15°. The dark blue curve indicates the surface density distribution of the known planetesimals in the solar system (see http://minorplanetcenter.net/data). The total mass of the Sun’s planetesimal disk was normalized to the initial disk mass in our simulations (0.01 M⊙). The initial density profile of the disk (light blue) is the same for each model. The thin periwinkle-colored horizontal line indicates the minimum disk-mass we adopted, truncating the solar system’s disk at about 55 au. |
 |
Fig. 9 Radial distribution of the inclination of particles bound to the disk shortly after the moment at which the supernova blast-wave impacts (blue), 100 days after the supernova shell hits the disk (green), and at the end of the simulation (yellow) for simulation of SN11aof at a distance of d = 0.4 pc and θ = 45°. The bullet points give the inclinations of the eight known planets. |
 |
Fig. 10 The median inclination of the protoplanetary disk as a function of time since the supernova explosion of supernova SN11aof at a distance of 0.2 pc for a range of impact angles of 15° to 75°. The two horizontal dotted lines indicate the dispersion along the mean inclination of the current solar system with respect to the Sun’s equatorial plane. |
 |
Fig. 11 Fraction of the surviving disk that is heated to a temperature ≳ 1500 K by the supernova blast wave (scale to the right) for SN11aof (left) and SN10a (right). The enclosed area indicates the initial parameter space for which the observed obliquity and the disk size are satisfactorily reproduced by the simulations (see Fig. 7). The hashed subset of this area indicates for which parameters the disk is also heated to a temperature ≳ 1500 K by the supernova radiation. The non-hashed area to the lower right indicates for which parameters the disk is sufficiently truncated and tilted by the blast wave but the supernova flash-induced temperature is insufficient to melt corundum. |
 |
Fig. 12 Disk enrichment mass-fraction as function of the distance to the supernova and its angle with respect to the proto-planetary disk’s rotation axis for SN11aof (left) and SN10a (right). The colored contours give the amount of accreted mass from the supernova remnant as a fraction of the mass of the surviving disk (scale to the right). The enclosed and shaded regions are as in Fig. 11. The small top-left area of the hashed region which overlaps with an enrichment of at least mshell ∕Mdisk ≳ 10−3 satisfies all the criteria of the model. The absence of a hashed region in the left panel indicates that there is no consistent solution across all requirements in our simulations for SN10a. |
 |
Fig. 13 Relative temperature as a function of the dust fraction, for inlincation Θ = 0 and at a distance of 0.2 pc. |
 |
Fig. 14 Peakmean temperature of the disk (contours) due to the supernova radiation as a function of the distance to a supernova (d in parsec) and the impact angle (Θ in degrees, measured from the disk’s angular-momentum axis). The adopted type IIp supernovae, SN11aof (left), has a peak luminosity of 1.1 × 1043 erg s−1 and SN10a (right) has a peak luminosity of 2.3 × 1042 erg s−1. The two shaded regions indicate the range in distance for which the Sun’s obliquity is consistent with the currently observed value of 5.°6 ± 1.°2 (blue with “//” hashes), and for which the disk is truncated to 42–55 au (green with hashes). This area is indicated in Fig. 12 with a blue polygon. The most promising part of parameter space is where the two hashed areas overlap because this is where both criteria are met. |
3 The arrival of the blast wave
3.1 The effect of the supernova blast wave on the disk
The outflow velocity of the two supernovae is ~ 104 km s−1 for SN10a and 5400 km s−1 for SN11aof. At such a short distance (≲ 1 pc), this outflowis still in the free expansion phase, and the blast wave hits 10–100 yr after the initiation of the supernova. By that time, the disk has cooled down to Tdisk ~ 100 K. The morphology of the disk is hardly affected by the irradiation of the supernova (see Fig. 8) because the heating and cooling by the supernova radiation proceeded so quickly.
Instead of following the entire supernova blast wave, which would be difficult for performance arguments and numerical stability, we initiate the hot gas at a distance of 10 au from the nearest point in the circum-stellar disk. With this adopted distance and the velocity of the blast wave, it takes 3–100 days before the shock front of the supernova traverses the entire disk, depending on the impact angle and the supernova blast- wave velocity.
The hot shell is initialized as a cylinder directed at the solar system. This cylinder has a radius of rshell = 150 au, to assure that the entire circumstellar disk is engulfed. The mass along the shell is distributed homogeneously. Along the cylinder axis, we adopt a density profile with the peak nearest to the solar system dropping-off linearly in log density with a characteristic scale of 200 au along the far side. The total mass in the cylinder is
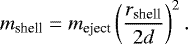 (2)
(2)
As a consequence, the mass and density of the impacting shell of SN10a at a distance of d = 0.1 pc is comparable to that of SN11aof at a distance of d = 0.2 pc.
The temperature of the shell at a distance of 10 au from the exploding star is Teject = 9 × 107 K, but by the time the gas reaches the solar system it has cooled to (Spicer et al. 1990)
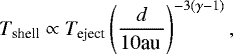 (3)
(3)
which for d = 0.1 pc results in Tshell ≃ 9500 K, and about 1800 K at a distance of d = 0.4 pc. Here we adopted γ = 7∕5. The sound speed in the shell is about cs ≃ 5.8 km s−1, which is negligible compared to the speed of the shell. As a consequence, the shape of the shell front remains intact if it traverses the disk without obstruction.
The supernova outflow of hot gas hits the disk with an angle Θ with respect to the rotation axis of the disk (see Fig. 1). The blast wave takes a few weeks to pass, during which the disk heats again to high temperatures; it harasses the disk and injects small amounts of blast wave material. Each of these processes has profound consequences for the disk structure and further evolution. About 100 days after first contact between the disk and the supernova shell, the disk mass reaches its final value. After this moment, the temperature and density profile of the disk change very little. We check this by continuing several calculations to 4 yr after the shell impact, but most calculations are stopped around 200 days after first contact. Further analysis is performed by averaging over the last ten snapshots of the simulations, each 1 day apart.
The supernova blast-wave injects energy into the disk. This excess energy results in its heating and ablation, the effect of which we discuss in the following section. The amount of energy injected depends on the distance to the supernova and the incident angle. The amountof kinetic energy injected into the disk is generally about an order of magnitude smaller than the amount of kinetic energy lost by the blast wave material. The amount of energy gained by the disk varies between and ranges from 3.0 × 1045 erg at 0.1 pc to 2.8 × 1043 erg at 0.6 pc, and follows ΔEkin ≃ 1042.5−3u erg, with u = log10(d∕pc).
3.2 Disk stripping
Ram-pressure stripping by the blast wave has a strong effect on the size of the disk (see also Wijnen et al. 2016). If the supernova occurs within ~ 0.05 pc, most of the disk is obliterated. We consider these results as not being representative for the solar system because this is hardly reconcilable with the current size of the planetary system and the edge of the Kuiper belt. At a distance of 0.15–0.4 pc, however, the disk is truncated at about 42 to 55 au almost irrespective of the supernova, although there is a strong correlation with the impact angle Θ. Such a disk size is consistent with the current extent of the Kuiper belt. In Fig. 7, the green “//” hashed area indicates the area for which the circumstellar disk was truncated in these limits.
In Fig. 8, we present the surface density profile of the disk that is hit by the blast wave at two moments in time: the moment the blast wave hits the disk (light blue curve) and 4 yr after the impact. The latter is presented for two models, one for SN10a at a distance of 0.1 pc and with an impact angle of 60° (rather edge-on), and for SN11aof at a distance of 0.4 pc and with an impact angle of 15° (almost face-on).
After such an extended harassment by the supernova blast wave, the outer parts of the disk have been stripped, up to a distance of about 50 au from the host star. The disk between ~ 10 au and ~ 50 au is depleted whereas within the inner ~ 10 au the disk is hardly affected.
For comparison, we present an estimate of the density profile of the solar system’s planetesimal disks (dark blue). Here we simply assume that each planetesimal contributes equally to the local density and that the solar system’s disk has a total mass of 0.01 M⊙, equivalent to the initially adopted mass of the circumstellar disk.
3.3 Tilting the disk
The disk is not deformed uniformly by the passing blast wave, but the periphery and the part of the disk closest to the supernova are more strongly affected than the inner parts. This interaction between the supernova blast-wave and the disk material causes the latter to tilt, orienting itself perpendicular to the flow due to the interaction between the momentum of the gas and the inclined disk (Wijnen et al. 2017).
For each simulation, we calculate the inclination of the disk with respect to the initial inclination for each particle. We adopt the median of the inclination of all particles bound to the disk as the global disk inclination and a radial profile is determined by calculating the median inclination in a co-moving bin of 500 particles.
The initial radial distribution in inclinations is rather flat and near i ≃ 0°. At a later time, the distribution of orbital inclinations increases, with higher inclination at greater distance from the central star. We demonstrate this in Fig. 9 where we present the radial distribution of the inclination for the simulation with supernova SN11aof at a distance of d = 0.4 pc and at an angle of Θ = 45° at three moments in time. The trend of an increased inclination with disk radius is general for the simulations, and in this example matches reasonably well with the inclinations observed in the solar system (see also Fig. 9). The radial increase is expected from a theoretical perspective because the timescale for tilting the disk is shorter at greater distance from the star (Wijnen et al. 2017). Wijnen et al. (2017) also suggested that a nearby supernova could have this effect on the Sun’s protoplanetary disk, and could potentially explain the observed angle between the Ecliptic and the Sun’s equatorial plane of ~ 5.°6 ± 1.2 (Beck & Giles 2005). In Fig. 7 we indicate this range with the blue hashed area.
In Fig. 10 we present the evolution of the inclination of the disk as a function of time from the moment the supernova blast-wave hits the outer disk edge (about 36.9 yr after the supernova) up to the moment where the blast wave has completely passed the disk (about 100 days later). The presented calculations are for a distance of d = 0.2 pc from supernova SN11aof. When this supernova occurred at an impact angle Θ ≲ 45°, the final tilt of the disk exceeded the observed obliquity of the Sun. The solution here must be degenerate. It is evident from Fig. 10 that shallow impact angles are more effective in tilting the disk. The timescale on which eccentricity, and therefore also the inclination, changes ∝ 1∕(sin(Θ)cos(Θ)), which has a minimum at45°. For larger inclinations, the flow is less effective in increasing the momentum due to the smaller projected surface area of the disk with respect to the incoming flow, while for smaller inclinations the force in the plane of the disk that increases the eccentricity is smaller. However, in order to precisely match the observed Sun’s obliquity of ~ 5.6° would require the supernova impact angle to be of the same order, which leaves a very small range of possible impact angles. We did, however, not consider the effect of very small Θ ≲ 10° supernova impact angles.
When the supernova occurs with a high impact angle of Θ ≳ 65°, the disk hasno time to reorient itself into the supernova blast-wave. In these cases, and at a distance of 0.2 pc from the supernova, the disk does not tilt to the observed value. Only for an angle of ~ 60° to ~ 50° is the disk tilt consistent with the observed value of 5.6 ± 1.2° (indicated by the horizontal dotted lines in Fig. 10).
3.4 Heating the disk
With a temperature of Tshell ≃ 9500 K, the blast wave material is extremely hot when it interacts with the disk. As a result, the disk itself will also be heated to high temperatures, although this heating is not very efficient due to the low density of the blast wave. In Fig. 11, we present the mass-fraction of the disk that is heated to ≳ 1500 K by the supernova blast-wave. We also present the overlapping regions where the disk is truncated to 42–55 au and tilted to 5.6 ± 1.2°. Both supernovae have such an overlapping area in the initial parameter space. The blue-hashed area in the left panel of Fig. 11 indicates where the temperature induced by the supernova radiation exceeds 1500 K. Only supernova SN11aof is able to heat the disk to this range. In the overlapping regions, a fraction of 0.3–0.4 of the disk is heated to sufficiently high temperatures to melt.
3.5 Accretion from the blast wave
A small amount of material from the nuclear blast wave is deposited in the Sun’s proto planetary disk. We illustrate this in Fig. 12 for both supernova SN11aof and SN10a. The enclosed region indicates the area in distance to the supernova and impact angle for which the truncation of the disk due to the passing blast wave and the obliquity of the Sun with respect to the disk is consistent with the observations. The absence of a hashed region for SN10a (right panel) indicates that in no part of the initial parameter space does the irradiation temperature of the disk due to the supernova explosion reach a temperature ≳ 1500 K.
For a nearby supernovae, d ≲ 0.12 pc, the amount of accreted material can exceed 10−5 of the bound disk mass, but this fraction drops rapidly with distance, which is consistent with earlier simulations by Ouellette et al. (2007). A similar trend is visible for SN11aof, however the amount of accreted material is considerably larger. For this latter supernova, the disk mass can be enriched with ≳ 10−6 up to a distance of ~ 0.2 pc, whereas for SN10a, this amount is only achieved at a distance of ≲ 0.12 pc. These results are consistent with earlier calculations of disk enrichment by a nearby supernova (Ouellette et al. 2007; Close & Pittard 2017).
4 Discussion
We simulated the supernova explosion and its effect on the circumstellar disk in two stages. In the first stage in Sect. 2, we perform the radiative transfer calculation coupled to a hydrodynamical simulation in order to study the effect of the irradiation of the supernova explosion on the Sun’s protoplanetary disk. In the second stage in Sect. 3, we study the effect of the hot nuclear blast wave from the supernova ejecta on the previously heated disk.
Our simulations are carried out with the AMUSE software framework, which is specifically designed for such simulations with multiple physical domains and scales. In our approach, we coupled a radiative transfer solver with a hydrodynamics (SPH) code and made them co-operate by interlaced temporal discretization. We performed extensive resolution and convergence tests to assure that the individual codes produce satisfactory results, and we tested the coupled codes for consistency. It remains difficult, however, to validate and verify such intricately coupled problems in which no analytic solution is available. The complications are caused by the lack of a proper chemistry model and a number of assumptionsabout the temperture-coupling of grain and gas and the state of the protoplanetary disk (i.e. gaseous with some dust without ongoing planet formation). Apart from the obvious theoretical extrapolations, no such analytic solutions are readily available for the problem at hand. Considering the stability of our results under small changes of input physics and model parameters we at least argue that the results presented here are robust and consistent.
The chain of events, that is, first the heating of the disk by the supernova radiation, followed by the blast wave and the consequent heating, stripping and the injection of the supernova processed material, may have had important consequences for the formation and evolution of the solar system. Above, we argue that the inclination of the ecliptic with respect to the Sun’s equatorial plane and the truncation of the current Kuiper belt could be the result of a nearby supernova. Here we further discuss some of the more speculative implications, regarding the chemical evolution of the early solar system.
4.1 The heating of the disk
In the range of distances and incident angles which satisfy the observed size and tilt, the disk is heated to about 1500 K (see the hashed regions in Figs. 7, 11 and 12). After the heating, the disk rapidly cools to ~ 100 K. A few decades later, the supernova outflow material heats a considerable fraction of the disk again to a comparable temperature. In our model, a fraction of the solids with up to ~ 1 m size and the surfaces of larger solids present in the Sun’s circum-stellar disk would then be heated to ≳ 1500 K twice, once by radiation and again a few decades later by the injection of the hot nuclear blast-wave.
The second episode of heating is less global for the disk because it casts a shadow on itself. In Fig. 11, we show that only a fraction of the disk is heated, which is the result of the self-shadowing of the disk. Supernova SN10a is less bright than SN11aof and the total mass in the blast wave is smaller. Because the out-flowing material has a higher velocity, the fraction of the disk-mass that is heated is comparable.
After the blast wave has passed, the temperature of the disk drops again, resulting in a cooling rate of about 3–30 K h−1. The mean temperature ≳ 1500 K reached in the disk reported here for both interactions (radiation and blast wave) is interesting because we can speculate if it may be related to the still-elusive physical process responsible for the existence of chondrules (Alexander et al. 2008). These are the major components of most meteorites and consist of free-floating millimeter-size droplets that were liquified at high temperatures. The origin of the possible flash-heating events that liquified the chondrules is unknown and we cannot exclude that this may be related to local effects resulting from the global disk-supernova interaction investigated here. Another interesting feature of chondrules is their cooling rates of 0.5–1000 K h−1 (Connelly et al. 2012), which is considerably slower than expected for isolated particles. This may imply that during the cooling phase they were embedded into hot gas, which would be a natural consequence of being heated by the supernova blast wave.
On the other hand, the observations that chondrules exhibit a wide range of ages and were probably being processed several times also require an explanation. Our models would naturally account for two heating events in short succession. However, it cannot be excluded that in a relatively dense cluster, more than one supernova exploded nearby the proto-solar disk. More detailed studies are required to ascertain if this supernova origin for the heating, needed to explain the existence of chondrules, may be feasible.
4.2 The effect of the presence of dust in the circumstellar disk on its temperature
The calculations in Sect. 2.3 were performed using the ray-tracing radiative transfer code SPHRay without support for dust extinction. The presence of dust is expected to reduce the temperature because it is efficient for storing and subsequently re-radiating the heat. To test this hypothesis, we perform a new set of calculations in which we include the effect of dust in the effective cross section per hydrogen atom:
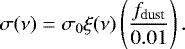 (4)
(4)
Here we adopt a constant of ξ(ν) = 3 and σ0 = 5.0 × 10−22 cm−2. In Fig. 13, we present the effect of the dust-to-gass mass fraction on the temperature of the circumstellar disk at the peak of the supernova luminosity (26 days after the supernova for SN11aof, and 10 days after for SN10a). In these cases, we adopted Θ = 0 and a distance of 0.2 pc. The effect of dust is to generally reduce the mean temperature of the disk at any moment, although weonly present the peak mean temperature in Fig. 13. For a small dust fraction of fdust ≲ 10−7 the temperaturesaturates to the no-dust case presented in Sect. 2.3, but for higher dust fractions the temperature drops by up to about 20%.
We repeated the calculations in Sect. 2.3 with a constant gas-to-dust ratio fdust = 0.01. The results of these calculations are presented in Fig. 14. The presence of dust in the circumstellar disk results in an overall lower mean temperature over the entire parameter space in Θ and d. These differences may have a profound effect on the disk chemistry, but for our discussion, the effect is not profound and does not affect our conclusions.
4.3 The accretion of short-lived radionuclids
In order to explain the abundance of 26Al observed in the early solar system, a certain fraction of material from the supernova needs to be incorporated in the disk. From the derived value of the 26Al/27Al ratio of 5 × 10−5 (Jacobsen et al. 2008b) and the recommended 27Al abundance of the proto-sun of 6.26× 10−5 (adopting a value of 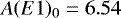 , Lodders et al. 2009) the early solar system disk of 0.01 M⊙ is expected to be enriched by a relative mass-fraction of m26_Al∕mdisk ≃ 3 × 10−9 of 26Al. A 25 M⊙ star has a 26Al yield of ~ 5 × 10−5 M⊙ (Tur et al. 2010; Lugaro et al. 2014). In order to be able to accrete the observed amount of 26Al by the supernova blast-wave a total mass fraction of maccreted∕mdisk ≃ 6 × 10−5 M⊙ has to be accreted, which exceeds the fraction of mass accreted in our simulations (see Fig. 12).
, Lodders et al. 2009) the early solar system disk of 0.01 M⊙ is expected to be enriched by a relative mass-fraction of m26_Al∕mdisk ≃ 3 × 10−9 of 26Al. A 25 M⊙ star has a 26Al yield of ~ 5 × 10−5 M⊙ (Tur et al. 2010; Lugaro et al. 2014). In order to be able to accrete the observed amount of 26Al by the supernova blast-wave a total mass fraction of maccreted∕mdisk ≃ 6 × 10−5 M⊙ has to be accreted, which exceeds the fraction of mass accreted in our simulations (see Fig. 12).
Considering this value and the amount of material accreted by the circumstellar disk (see Fig. 12) we conclude that only for an extremely nearby supernova, ≲ 0.1 pc, and at a relatively small angle with respect to the disk, ≲ 40°, can a sufficient amount of 26Al be accreted. The disadvantage of such a nearby supernova would be the almost complete obliteration of the disk. Our result is consistent with the earlier calculations of Ouellette et al. (2007); Nicholson & Parker (2017) who argue that injecting SLRs into a protosolar disk from a nearby supernova is not straightforward and may require an early condensation of 26Al in large dust grains that can be accreted more easily by the disk (Ouellette et al. 2010).
The abundance of 60Fe in the early solar system may be too low to allow for a nearby supernova, although the possibility of such an abundance is still actively debated. It is difficult to separate 27Al and 60Fe in supernova ejecta because these two nuclei are produced in the same regions (Timmes et al. 1995; Limongi & Chieffi 2006). Furthermore, proof that both nuclei are produced by massive stars is provided by γ-ray spectroscopic observations (Diehl 2013). The flux ratio observed 60Fe/27Al of roughly 0.15 (Wang et al. 2007) corresponds to an abundance ratio of 0.55, which is a few to orders of magnitude higher than the ratios measured for the early solar system. This indicates that the early solar system did not sample the average Galactic content of SLRs. In addition, evolutionary models for massive stars have some difficulties to avoid overproducing even the Galactic ratio (Limongi & Chieffi 2006; Sukhbold et al. 2016; Austin et al. 2017).
Following Ouellette et al. (2010), we can still assume that the required amount of 26Al was incorporated into the early solar system because it was carried into the disk inside large dust grains. In this case, if the highest observed values for 60Fe are representative of the early solar system, then the scenario of disk injection from the supernova is still plausible. Even in that case, however, it is not clear to what extent the shock-wave of the interaction between the supernova and the disk can be responsible for the origin of chondrules.
To answer this question we consider timescales. Aluminum-26 is observed to be present in the oldest components of meteorites, which are called calcium-aluminum inclusions (Jacobsen et al. 2008a), and are distributed within the entire disk (Villeneuve et al. 2009) with abundance ratios varying at least within a factor of two (Larsen et al. 2011). Chondrules, on the other hand, are expected to have formed over a timescale of a few million years, beginning with the moment the first CAIs formed (Connelly et al. 2012). This implies that the first heating event modeled here could not have contributed to the production of chondrules since it occurred before the 26Al survival within the blast wave responsible for the second heating event. The first heating event may still have been responsible for the melting of some CAIs (only those which are 26Al -poor). The CAIs also show igneous features, but for this, there seems to be no clear relation to chondrules (e.g., Needham et al. 2017). If the interaction with the blast wave was responsible for both the origin of SLRs and the heating event that produced the oldest chondrules, then we are left with the problem that future heating events are needed to produce chondrules for the next several million years. If these were also supernova related, then they should have been poor in 26Al, otherwise the abundance variations in chondrules would have been considerably larger.
It appears difficult to argue that the same supernova that is responsible for the presence of 26Al in the early solar system was also responsible for the shock waves responsible for the formation of chondrules. As we have demonstrated here, the interaction between a supernova and a disk that could have injected SLRs into the early solar system would also have heated a considerable fraction of the disk to temperatures sufficiently high to melt even the hardest dust grains. This would have profound consequences for the further chemical evolution of the disk. At this moment we do not know what these consequences could be; this remains to be studied.
Another important issue to consider is that supernova SN11aof was produced by a star of at least 25 M⊙. Such massive stars take less then 8 million years to evolve. This is longer than the age spread of < 3 Myr observed in the nearby star-forming regions W3 (Bik et al. 2012) and the Orion Nebular Cluster (Jeffries et al. 2011). Although this would indicate a rather prolonged disk lifetime, it is consistent with recent findings regarding the average disk lifetime of planetary systems being longer than 10 Myr, as observed in the Large Magellanic Cloud (De Marchi et al. 2010), or the presence of a disk around the ~ 12 Myr-old star TW Hydra (Nomura et al. 2016). We therefore argue that by the time a nearby star exploded, the Sun and its disk may still have had anage similar to that of the exploding star, including the uncertainty in the spread in the star-formation history.
4.4 Implications for other planetary systems
For the planetary systems that are born in clusters of 500 to 104 stars, the interaction between a supernova blast-wave and the circumstellar disk may be rather common. Although we only cover a rather limited parameter space in terms of supernova type, distance, and incident angle, we compare the distribution of observed inclinations with the simulations.
We used the last ten snapshots for each simulation in the grid of parameter space (d and Θ) to constructa cumulative distribution of the measured inclination. We weighted the simulations based on the distance and inclination. For the distance, we adopted a Plummer (1911) distribution with a characteristic length of 1.0pc. The underlying assumption is that the star cluster, at an age of 10 Myr, resembles a Plummer distribution with the exploding star in the cluster center. The inclinations were weighted with cos (Θ).
For the observed systems, we adopt the Kepler database1 from July 2017. We selected the systems for which the rotation of the parent star and the inclination of at least one planet was observed. In a subsequent pass we selected the 189 systems for which this inclination angle was 1° < i < 15°. Their cumulative distribution is presented in Fig. 15 (blue curve). The simulated distributions (red and yellow curves in Fig. 15) are statistically indistinguishable and differ from the observed distribution (with a Kolmogorov-Smirnoff (Kolmogorov 1954) p-value of 1.1%). The Kepler systems to which we compare, however, are all relatively tight compared to our 100 au sized disks, and, in addition, the interaction with a supernova blast-wave is probably not the only mechanism that can induce a tilt in a circumstellar disk. Other mechanisms that may be important in affecting the obliquity of the star with respect to its planetary disk include close stellar encounters and secular dynamics, both of which are probably important in the same environment (Cai et al. 2017).
 |
Fig. 15 Cumulative distribution of the inclination for observed planetary systems (blue) with our two supernova models SN11aof (red) and SN10a (yellow). The two simulated distributions are statistically indistinguishable (p-value = 0.47), and both distributions have a lower consistency when compared with the observations (p-value ~ 0.011). |
5 Conclusions
We performed radiative transfer and hydrodynamical simulations of the interaction between a supernova and a Sun-like star with a circumstellar disk. The calculations are performed using the AMUSE software environment and all the scripts used in this manuscript are available at the package website2.
We have discussed the relevance of our model to cosmochemistry constraints, that is, to the presence of SLRs in the early solar system and to the shock heating events possibly responsible for the origin of chondrules. We confirm, as argued by Ouellette et al. (2007), that the amount of SLRs with which a protoplanetary disk would be enriched is too small to explain their abundance in the solar system. They argue that the incorporation of 26Al and 60Fe in large dust grains would allow these elements to stick to the disk, but they do not explain why 60Fe would be underabundant in this process. More detailed models of the local impact of the heat generated by the supernova-disk interaction are needed to assess if this may play a role in the origin of chondrules.
We identified two distinct physical consequences that provide independent constraints on the distance between the exploding star and the solar system, and on the relative inclination angle of the supernova with respect to the disk’s angular momentum axis. The solar system’s circumstellar disk is sensitive to these parameters via the ablation of the circumstellar disk and the tilt induced by the blast wave of the supernova shell. Using simulations to compare the observed disk size and obliquity of the Sun with respect to the ecliptic, we then constrain the type of supernova, its distance, and the angle with respect to the Sun’s circumstellar disk. Consistent results between observations and simulations are obtained when the supernova occurs at a distance of 0.15 ≲ d ≲ 0.40 pc, and at an angle of 35° ≲Θ ≲ 65°. We only tried two supernovae; both are of type IIp, and it is hard to be conclusive, but we prefer supernova SN11aof because it is brighter and has a higher-density mass outflow, but at a somewhat lower velocity than SN10a. We also confirm that the amount of blast-wave material that is accreted by the circumstellar disk is insufficient to explain the enrichment of short-lived radionuclides.
Considering all constraints, we tend to prefer the brighter supernova SN11aof to explain the temperature evolution of the protoplanetary disk, the Sun’s obliquity, and the outer disk radius. This supernova would have occurred at a distance of 0.15–0.25 pc and from an angle of 52° to 66°. However, if the temperature cannot be used to constrain the initial conditions we have to relax the viable initial parameter space to d≃ 0.15 to 0.40 pc and Θ ≃ 35° to about 66°.
Acknowledgements
It is a pleasure to thank Ignas Snellen, Vincent Icke, Mher Kazandjian, and Xander Tielens, Guido de Marchi, Marco Delbo, Shu-Ichiro Inutsuka and Eiichiro Kokubo. This work was supported by the Netherlands Research School for Astronomy (NOVA), NWO (grant #621.016.701 [LGM-II]) and by the European Research Council (ERC) under the EU Horizon 2020 research and innovation programme (grant agreement No 724560) through ERC Consolidator Grant “RADIOSTAR” to M.L.
References
- Alexander, C. M. O., Grossman, J. N., Ebel, D. S., & Ciesla, F. J. 2008, Science, 320, 1617 [NASA ADS] [CrossRef] [Google Scholar]
- Altay, G., Croft, R. A. C., & Pelupessy, I. 2008, MNRAS, 386, 1931 [NASA ADS] [CrossRef] [Google Scholar]
- Altay, G., Croft, R. A. C., & Pelupessy, I. 2011, Astrophysics Source Code Library [record ascl:1103.009] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2011, ARA&A, 49, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Austin, S. M., West, C., & Heger, A. 2017, ApJ, 839, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, J. G., & Giles, P. 2005, ApJ, 621, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Bik, A., Henning, T., Stolte, A., et al. 2012, ApJ, 744, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, M. X., Kouwenhoven, M. B. N., Portegies Zwart, S. F., & Spurzem, R. 2017, MNRAS, 470, 4337 [NASA ADS] [CrossRef] [Google Scholar]
- Close, J. L., & Pittard, J. M. 2017, MNRAS, 469, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Connelly, J. N., Bizzarro, M., Krot, A. N., et al. 2012, Science, 338, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, A. M., & Richter, F. M. 2005, Condensation and Evaporation of Solar System Materials, eds. A. M. Davis, H. D. Holland, & K. K. Turekian (Amsterdam: Elsevier B. V.), 407 [Google Scholar]
- De Marchi, G., Panagia, N., & Romaniello, M. 2010, ApJ, 715, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, R. 2013, Rep. Prog. Phys., 76, 026301 [NASA ADS] [CrossRef] [Google Scholar]
- Dwarkadas, V. V., Dauphas, N., Meyer, B., Boyajian, P., & Bojazi, M. 2017, ApJ, 851, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Faran, T., Nakar, E., & Poznanski, D. 2018, MNRAS, 473, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E., Krot, A. N., & Huss, G. R. 2009, ApJ, 705, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Gerritsen, J. P. E., & Icke, V. 1997, A&A, 325, 972 [NASA ADS] [Google Scholar]
- Gounelle, M., & Meynet, G. 2012, A&A, 545, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernquist, L., & Katz, N. 1989, ApJS, 70, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Iliev, I. T., Ciardi, B., Alvarez, M. A., et al. 2006, MNRAS, 371, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobsen, B., Yin, Q.-z., Moynier, F., et al. 2008a, Earth Planet. Sci. Lett., 272, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobsen, S. B., Chakrabarti, R., Ranen, M. C., & Petaev, M. I. 2008b, Lunar Planet. Sci. Conf., 39, 1999 [Google Scholar]
- Jeffries, R. D., Littlefair, S. P., Naylor, T., & Mayne, N. J. 2011, MNRAS, 418, 1948 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. N. 1954, Dolk Akad. Nauk SSSR, 98, 527 [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Larsen, K. K., Trinquier, A., Paton, C., et al. 2011, ApJ, 735, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Lichtenberg, T., Parker, R. J., & Meyer, M. R. 2016, MNRAS, 462, 3979 [NASA ADS] [CrossRef] [Google Scholar]
- Limongi, M., & Chieffi, A. 2006, ApJ, 647, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt-Börnstein, New Series VI/4B, 34, Chapter 4.4. [Google Scholar]
- Looney, L. W., Tobin, J. J., & Fields, B. D. 2006, ApJ, 652, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Lugaro, M., Heger, A., Osrin, D., et al. 2014, Science, 345, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, B. S. 2005, ASP Conf. Ser., 341, 515 [NASA ADS] [Google Scholar]
- Mishra, R. K., & Chaussidon, M. 2014, Earth Planet. Sci. Lett., 398, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Needham, A. W., Messenger, S., Han, J., & Keller, L. P. 2017, Geochim. Cosmochim. Acta, 196, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholson, R. B., & Parker, R. J. 2017, MNRAS, 464, 4318 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., Tsukagoshi, T., Kawabe, R., et al. 2016, ApJ, 819, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ouellette, N., Desch, S. J., & Hester, J. J. 2007, ApJ, 662, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Ouellette, N., Desch, S. J., & Hester, J. J. 2010, ApJ, 711, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Pelupessy, F. I., van der Werf, P. P., & Icke, V. 2004, A&A, 422, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelupessy, F. I., van Elteren, A., de Vries, N., et al. 2013, A&A, 557, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plummer, H. C. 1911, MNRAS, 71, 460 [CrossRef] [Google Scholar]
- Portegies Zwart, S. F. 2009, ApJ, 696, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Portegies Zwart, S. 2011, Astrophysics Source Code Library [record ascl:1107.007] [Google Scholar]
- Portegies Zwart, S. & McMillan, S. 2017, Astrophysical Recipes: The Art of AMUSE (AAS IOP Astronomy) [Google Scholar]
- Portegies Zwart, S., McMillan, S. L. W., van Elteren, E., Pelupessy, I., & de Vries N. 2013, Comput. Phys. Commun., 183, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Ritzerveld, J., & Icke, V. 2006, Phys. Rev. E, 74, 026704 [NASA ADS] [CrossRef] [Google Scholar]
- Safronov, V. S. 1960, Ann. Astrophys., 23, 979 [Google Scholar]
- Sanders, N. E., Soderberg, A. M., Gezari, S., et al. 2015, ApJ, 799, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Spicer, D. S., Maran, S. P., & Clark, R. W. 1990, ApJ, 356, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Tang, H., & Dauphas, N. 2012, Lunar Planet Sci. Conf., 43, 1703 [NASA ADS] [Google Scholar]
- Tang, H., & Dauphas, N. 2015, ApJ, 802, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Telus, M., Huss, G. R., Nagashima, K., Ogliore, R. C., & Tachibana, S. 2018, Geochim. Cosmochim. Acta, 221, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., Woosley, S. E., Hartmann, D. H., et al. 1995, ApJ, 449, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Tur, C., Heger, A., & A.M., S. 2010, Proc. 11th Symposium on Nuclei in the Cosmos, 46 [Google Scholar]
- Vicente, S. M., & Alves, J. 2005, A&A, 441, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villeneuve, J., Chaussidon, M., & Libourel, G. 2009, Science, 325, 985 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, W., Harris, M. J., Diehl, R., et al. 2007, A&A, 469, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijnen, T. P. G., Pols, O. R., Pelupessy, F. I., & Portegies Zwart S. 2016, A&A, 594, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijnen, T. P. G., Pelupessy, F. I., Pols, O. R., & Portegies Zwart S. 2017, A&A, 604, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
see amusecode.org and github.com/amusecode
All Figures
 |
Fig. 1 Geometry of the experimental setup. The circumestellar disk is represented near the bottom with a diameter of 200 au. The exploding star (blue star to the top right) at a distance d and with angle Θ with respectto the disk’s angular momentum axis. |
| In the text | |
 |
Fig. 2 Mid-plane density distribution of the protoplanetary disk with a top view in the middle and side views to the right and top. The density is color coded, the coding scheme is presented to the top right of the figure. The density extrema range from 10−12.9 g cm−3 to 10−9.97 g cm−3. |
| In the text | |
 |
Fig. 3 Top view of the protoplanetary disk from three sides, the top view (x-y) image in the middle and two size aspects to the right and top. The colors represent temperature, and the coding is represented by the bar to the top right. |
| In the text | |
 |
Fig. 4 Light curves and disk temperatures for the type IIp supernovae SN11aof (left panel) and SN10a (right panel). The dashed blue curves with the scales in blue to the left of the respective panels give the luminosity of the supernova, and are power-law fits from Sanders et al. (2015). The red curves give the mean temperature of the disk at distances of 0.1, 0.2, 0.3 and 0.4 pc (from left to right). For the latter, we present curves (bottom to top curve) for an inclination of 15°, 30°, 45°, 60° and 75°. For the distance of 0.1 pc, we only show the disk temperature for the inclination angle of 75°, and for the other two distances at 15°. In the right-hand panel, we show the same curves but for supernova SN10a. The thin green line (to the upper right) indicates a cooling of 0.3 K h−1, which is consistent with the cooling after the supernova radiation has heated the disk for SN11aof. In Sect. 4.1, we discuss the effect of the heating on structure of vitreous chondrules in the disk. |
| In the text | |
 |
Fig. 5 View of the midplanet temperature of the circumstellar disk at the moment supernova SN11aof reaches its maximum. The supernova exploded at a distance of 0.2 pc and at an angle of θ = 60°. In Fig. 6, we present several face-on temperature distributions of the same disk at different moments in time. |
| In the text | |
 |
Fig. 6 Top view of the mid-plane temperature of the circumstellar disk at four epochs: the start of the simulation (left most image), at 26 days after the onset of supernova SN11aof, about 100 days after the supernova and about 2 yr later, when the disk has almost completely cooled down again (right-most image). Each image was taken from the simulation where the supernova exploded at a distance of 0.2 pc and at an angle of θ = 60°. See Fig. 5 for the temperature scale. |
| In the text | |
 |
Fig. 7 Peak mean temperature of the disk (contours) due to the supernova radiation as a function of the distance to a supernova (d in parsec) and the impact angle (Θ in degrees, measured from the disk’s angular-momentum axis). The adopted type IIp supernovae, SN11aof (left), has a peak luminosity of 1.1 × 1043 erg s−1 and SN10a (right) has a peak luminosity of 2.3 × 1042 erg s−1. Evaporation of the bulk of the solids in the proto-planetary disk is achieved when the irradiation heats it to a mean temperature of ≳ 1500 K. The two shaded regions indicate the range in distance for which the Sun’s obliquity is consistent with the currently observed value of 5.°6 ± 1.°2 (blue with “\\” hashes), and for which the disk is truncated to 42–55 au (green with “//” hashes). This area is indicated in Figs. 11 and 12 with a blue polygon. The most promising part of parameter space is where the two hashed areas overlap because that is where both criteria are met. |
| In the text | |
 |
Fig. 8 Surface density profile of the proto planetary disk at two moments in time for two supernovae SN10a (green) and the much brighter SN11aof (red). The former was at a distance of d = 0.1 pc and with an impact angle of Θ = 60°, the latter at a distance of d = 0.4 pc and with an angle of Θ = 15°. The dark blue curve indicates the surface density distribution of the known planetesimals in the solar system (see http://minorplanetcenter.net/data). The total mass of the Sun’s planetesimal disk was normalized to the initial disk mass in our simulations (0.01 M⊙). The initial density profile of the disk (light blue) is the same for each model. The thin periwinkle-colored horizontal line indicates the minimum disk-mass we adopted, truncating the solar system’s disk at about 55 au. |
| In the text | |
 |
Fig. 9 Radial distribution of the inclination of particles bound to the disk shortly after the moment at which the supernova blast-wave impacts (blue), 100 days after the supernova shell hits the disk (green), and at the end of the simulation (yellow) for simulation of SN11aof at a distance of d = 0.4 pc and θ = 45°. The bullet points give the inclinations of the eight known planets. |
| In the text | |
 |
Fig. 10 The median inclination of the protoplanetary disk as a function of time since the supernova explosion of supernova SN11aof at a distance of 0.2 pc for a range of impact angles of 15° to 75°. The two horizontal dotted lines indicate the dispersion along the mean inclination of the current solar system with respect to the Sun’s equatorial plane. |
| In the text | |
 |
Fig. 11 Fraction of the surviving disk that is heated to a temperature ≳ 1500 K by the supernova blast wave (scale to the right) for SN11aof (left) and SN10a (right). The enclosed area indicates the initial parameter space for which the observed obliquity and the disk size are satisfactorily reproduced by the simulations (see Fig. 7). The hashed subset of this area indicates for which parameters the disk is also heated to a temperature ≳ 1500 K by the supernova radiation. The non-hashed area to the lower right indicates for which parameters the disk is sufficiently truncated and tilted by the blast wave but the supernova flash-induced temperature is insufficient to melt corundum. |
| In the text | |
 |
Fig. 12 Disk enrichment mass-fraction as function of the distance to the supernova and its angle with respect to the proto-planetary disk’s rotation axis for SN11aof (left) and SN10a (right). The colored contours give the amount of accreted mass from the supernova remnant as a fraction of the mass of the surviving disk (scale to the right). The enclosed and shaded regions are as in Fig. 11. The small top-left area of the hashed region which overlaps with an enrichment of at least mshell ∕Mdisk ≳ 10−3 satisfies all the criteria of the model. The absence of a hashed region in the left panel indicates that there is no consistent solution across all requirements in our simulations for SN10a. |
| In the text | |
 |
Fig. 13 Relative temperature as a function of the dust fraction, for inlincation Θ = 0 and at a distance of 0.2 pc. |
| In the text | |
 |
Fig. 14 Peakmean temperature of the disk (contours) due to the supernova radiation as a function of the distance to a supernova (d in parsec) and the impact angle (Θ in degrees, measured from the disk’s angular-momentum axis). The adopted type IIp supernovae, SN11aof (left), has a peak luminosity of 1.1 × 1043 erg s−1 and SN10a (right) has a peak luminosity of 2.3 × 1042 erg s−1. The two shaded regions indicate the range in distance for which the Sun’s obliquity is consistent with the currently observed value of 5.°6 ± 1.°2 (blue with “//” hashes), and for which the disk is truncated to 42–55 au (green with hashes). This area is indicated in Fig. 12 with a blue polygon. The most promising part of parameter space is where the two hashed areas overlap because this is where both criteria are met. |
| In the text | |
 |
Fig. 15 Cumulative distribution of the inclination for observed planetary systems (blue) with our two supernova models SN11aof (red) and SN10a (yellow). The two simulated distributions are statistically indistinguishable (p-value = 0.47), and both distributions have a lower consistency when compared with the observations (p-value ~ 0.011). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


