| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A171 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833225 | |
| Published online | 06 August 2018 | |
Modeling optical and UV polarization of AGNs
V. Dilution by interstellar polarization and the host galaxy
Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, 67000
Strasbourg, France
e-mail: frederic.marin@astro.unistra.fr
Received:
13
April
2018
Accepted:
23
May
2018
Context. One of the main challenges for polarimetric observations of active galactic nuclei (AGN) is to properly estimate the amount of parasitic light that contaminates the polarization signal. Removing this unpolarized flux is a complex task that has only been achieved in a couple of objects.
Aims. In this fifth paper of the series, we present a new version of the Monte Carlo code STOKES that accounts for dilution by interstellar polarization and host starlight in radiative transfer modeling.
Methods. We upgraded our code by including spectral energy distribution (SED) templates for a set of representative host galaxies. The unpolarized light emitted by those hosts alters the observer polarization while being coherently radiatively coupled to the AGN structure. We also included in our analysis tool a routine that may add, depending on the user’s objectives, an interstellar component.
Results. Using a generic AGN model, we illustrate how interstellar polarization and starlight dilution impact the observed polarimetric signal of AGN. We applied our code to NGC 1068, an archetypal edge-on AGN and demonstrate that STOKES can reproduce its SED, the expected wavelength-dependent polarimetric signatures, and the observed high-angular resolution polarimetric maps. Using the flexibility of the code, we derived several intrinsic parameters such as the system inclination and the torus opening angle.
Conclusions. The new version of our publicly available code now allows observers to better prepare their observations, interpret their data and simulate the three-dimensional geometry and physics of AGN in order to probe unresolved structures. Additionally, the radiative interaction between the host and the AGN can be used to probe the co-evolution of the system.
Key words: galaxies: active / galaxies: Seyfert / polarization / radiative transfer / scattering
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Spectropolarimetric observations of active galactic nuclei (AGN) have completely changed our understanding of those objects. The discovery of broad Balmer and Fe II emission lines in the polarized spectrum of NGC 1068, with approximately the same polarization position angle and linear polarization degree that of the continuum, allowed Miller & Antonucci (1983) and Antonucci & Miller (1985) to reunite the spectroscopically separated type-1 and type-2 AGN classes. A type-1 Seyfert galaxy is a lower-luminosity AGN, usually found in spiral galaxies, that often has two sets of emission lines in its spectrum: narrow lines such as [O III] λ5007 or [S II] λ6716, 6731, with a width of several hundred of km s−1, and broad lines such as the Balmer series or Mg II λ2798 lines, with widths up to 104 km s−1. A type-2 Seyfert galaxy lacks the broad line component, similarly to the so-called Narrow Line Seyfert-1s (Osterbrock 1989; Goodrich 1989; Véron-Cetty et al. 2001). If for the latter the reason is unknown, it was proven thanks to spectropolarimetry that a Seyfert-1 core is hidden in probably all type-2 AGN, the difference being due to an orientation effect (Antonucci 1993). Due to the anisotropic geometric configuration of AGN, a type-2 observer would not see the central engine as its line-of-sight is obscured by an equatorial, optically thick, geometrically thick dusty region. This “torus” is responsible for the different polarization angle we see in type-1s and type-2s (Antonucci 1984), and blocks the emission coming from the central Keplerian region of AGN producing the broad lines (Peterson & Wandel 1999; Gaskell 2009). It is only thanks to spectropolarimetry that the dust-obscured signal of AGN cores can be revealed in type-2 Seyferts: light perpendicularly scatters along the polar direction towards the observer and carries the broad line signatures in its Stokes parameters.
Perpendicular scattering of optical photons leads to high polarization degrees since polarization depends on the cosine squared of the scattering angle. We thus naturally expect highly polarized spectra for type-2 AGN as they are seen along the equatorial direction. Nevertheless the usual linear continuum polarization we observe is less than a few percent (e.g., Kay 1994; Ramos Almeida et al. 2016). This is intriguing as the broad lines are detected in polarized flux. Where is the polarization much greater than 10% that we expected? Miller & Antonucci (1983) showed that those high polarization degrees are, in fact, present but dilution by additional sources strongly reduces the observed polarization. Hiltner (1949) and Hall (1949) discovered that interstellar extinction is birefringent and that the interstellar extinction increases greatly towards the ultraviolet (UV). Interstellar polarization (ISP) is to be accounted for, since the trajectory of photons through the local galactic medium is impacted by the alignment of dust grains and produces a foreground contamination. Hence, any observations of distant sources might be altered by ISP. This can be estimated by looking at the polarization of Galactic stars in the same field of view than the AGN (Miller & Goodrich 1990), or by using plots of the E-vector of polarization over the entire sky (Mathewson & Ford 1970). On the other hand, starlight from the host galaxy is a major contributor to the contamination of polarized spectra of type-2 AGN: since the nucleus is hidden, a large fraction of the observed flux comes from stellar sources and the final polarization decreases. This is less problematic for the case of type-1 AGN as the central engine is directly visible through the torus funnel and radiation from the accretion disk dominates the host starlight. However, for Seyfert-2s, it becomes a major challenge to estimate the true scattered component of light. It is possible to remove the starlight contribution using a galaxy template super-imposed on high-resolution polarized spectra. By carrying out subtractions at various flux ratios between the template host and the polarized spectrum, it is possible to find a flux ratio that provides a simultaneous cancellation of all the stellar features. This was the technique used by Miller & Antonucci (1983), who found that the true continuum polarization of NGC 1068 is polarized at P = 16% ± 2%. The wavelength-independence of the polarization continuum was also a proof for the dominance of Thomson scattering in the optical band. However, not all archival polarimetric observations were achieved in high resolution spectropolarimetric modes. To correct for interstellar and host dilution the observed narrowband and filter-integrated polarimetric observations, reverse engineering is needed.
This is the purpose of our upgrade. We aim to provide a simulation tool that can fit any near-infrared, optical and ultraviolet polarimetric observations of AGN and provide a good estimation of its true scattered polarization. To do so, we include a variety of galaxy templates to be accounted for in AGN simulations. The flux ratio between the AGN central engine and the host can be arbitrarily chosen by the user to fit the data and retrieve the true polarization. We present in Sect. 2 an overview of the current code version and explain the upgrade we included in the newest version. We show in Sect. 3 several examples of polarimetric simulations, both in photometry, spectropolarimetry, and polarization imaging, to highlight the necessity of accounting for ISP and starlight contribution. We discuss the potential future use of our code in Sect. 4 and conclude our paper in Sect. 5.
2. STOKES upgrade
STOKES is a Monte Carlo code that was first presented in Goosmann & Gaskell (2007). Its main goal is to reproduce the observed near-infrared, optical and ultraviolet polarization of AGN. The most important part of this radiative transfer code is that it accounts for radiative coupling between the different three-dimensional emitting and scattering regions. Multiple scattering has a profound impact on the net polarization we observe and several specific features seen in polarimetry cannot be reproduced without multiple scattering (see, e.g., Young 2000; Smith et al. 2002 who numerically reproduced the polarization variations observed in broad emission lines). Multiple scattering is thus essential, and it is also the backbone of our new numerical improvements.
2.1. Overview of the code performances
The previous version (v1.2) of STOKES is able to handle photon emission with a variety of spectral shapes (power-law, thermal emission, …) originating from any number of geometrical sources that can be located anywhere in the three-dimensional environment. The photons then travel in straight lines (relativistic effects are yet to be included in the vicinity of the central black hole) until they encounter a medium whose size, composition, temperature, and velocity can be fully parametrized by the user. Depending on the photon energy and the opacity of the matter, radiation can travel through the medium, be scattered, absorbed and potentially re-emitted several times. The code registers the photon time delay due to multiple scattering and follows each photon until it is absorbed or escapes from the model region. Awebof virtual detectors (scaled in cosine along the polar direction) registers the photons at all viewing angles (including potential azimuthal bins). The photon polarization is stored using the Stokes parameters I, Q, U, and V. The I parameter stands for the intensity, Q and U are used to characterize the linear polarization, and V characterizes the circular polarization.
The code’s output is given in a specific format that can be processed with the ANALYZE tool that is provided with the code1. The ANALYZE routine computes the total flux, the total, linear and circular polarization degrees (P = P lin + P circ), the polarization position angle Ψ and the polarized flux (total flux times P). A convention used since the first paper of our series is to consider the polarization to be parallel when the E-vector is aligned with the projected symmetry axis of the model (i.e. Ψ = 90°). We sometimes denote the difference between parallel and perpendicular polarization by the sign of the polarization percentage. P is negative if Ψ = 90° and P is positive if Ψ = 0°.
Over the past decade, the code has been improved in many ways. It is now equipped with an imaging routine that can have any required spatial resolution (Marin et al. 2012), it can also account for fragmented regions made of several thousands spherical clumps (Marin et al. 2015), and it coherently computes the time delays and cross-correlation of light between the total and unpolarized fluxes (Rojas Lobos et al. 2018). The code has been implemented with faster computing routines to allow swifter runs. An overview of the science cases were STOKES was applied is presented in Marin & Goosmann (2014).
2.2. Interstellar polarization
Hiltner (1949) and Hall (1949) showed that light reaching us through the interstellar medium is polarized. In the interstellar medium the dust grains, which are known to be elongated (Hildebrand & Dragovan 1995), can be aligned by the interstellar magnetic field. The aligned grains block the light waves that are polarized parallel to the long axis of the grains, and let the polarized waves pass perpendicularly to the long axis of the grains. This dichroic extinction is responsible for an interstellar polarization that can reach up to 5% (Mathewson & Ford 1970). This polarized signal can easily dilute or overwhelm the polarization signal of type-1 AGN, which is known to be weak (often less than 2%) due to their symmetric morphology (Marin et al. 2012). It is particularly important to include this feature in STOKES to allow the user to check whether the polarimetric signal observed is truly due to the AGN. As we show in Sect. 3, constraints on the inclination angle of the AGN can also be deduced thanks to comparisons between observations and modeling that accounts for interstellar polarization.
To include interstellar polarization, we follow the seminal work of Serkowski et al. (1975). The authors investigated the wavelength dependence of interstellar linear polarization for ~180 stars with a variety of photometric filters. By doing so, they produced a well-known empirical formula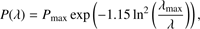 (1)
(1)
where λ max is the wavelength at which the maximum interstellar linear polarization P max occurs. From observations, Serkowski et al. (1975) determined that λ max = 5450 Å. We illustrate different interstellar polarization signatures in Fig. 1 for different values of P max. The optical band suffers the most from this parasitic component and observations in the ultraviolet or infrared bands must be favored. The empirical law of Serkowski et al. (1975) is now implemented in analyze. The user has to enter the values of λ max, P max and Ψ ISP. The parameter Ψ ISP was not investigated by Serkowski et al. (1975) but it has some importance since it can alter the observed polarization position angle of the AGN polarized flux, even when the magnitude of interstellar polarization is small. Hoffman et al. (2005) studied how such uncertainties may affect the observed polarization angle and found that the intrinsic position angle differs from the observed one by
 |
Fig. 1. Examples of ultraviolet-to-infrared interstellar polarization levels for different values of P max. The value of λ max is fixed to 5450 Å. |
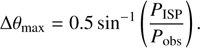 (2)
(2)
We thus decided to also account for the variation of the total polarization position angle by introducing in our code the parameter Ψ ISP that can be easily derived from the previous equation.
2.3. Host starlight
Dilution by starlight is the major contributor to the weakening of the observed AGN polarization. Galaxies contain large amounts of hot gas that are detected thanks to intense emission lines, and stars are responsible for the continuum spectrum and the absorption lines. There is a vast collection of galaxy classes that are divided into groups based on their visual appearance (Hubble 1936; de Vaucouleurs 1959; Sandage 1975; van den Bergh 1998). However AGN are mostly found in the heart of early-type spiral galaxies (Sa–Sb, Heckman et al. 1978). Large surveys of well-resolved nearby AGN confirmed this trend but also demonstrated that Seyfert host galaxies often show signs of morphological irregularities, most probably caused by tidal interactions (Simkin et al. 1980; MacKenty 1990). Not all Seyferts show a large-scale stellar bar within the spiral host galaxy (Deo et al. 2006) and (Kelm & Focardi 2001) have shown that about 70% of both Seyfert-1 and Seyfert-2 classes are preferably detected in spirals. Chen & Hwang (2017) also discovered that Seyfert-1 galaxies are mainly located in bulge-dominant galaxies while type-2s are more often detected in disk galaxies. However, since both classes are dominated by large bulge fractions, late type host galaxies cannot be excluded. For this reason, we included in STOKES the possibility to use a variety of host galaxy templates that cover a large fraction of the galaxy morphological classification. We extracted the templates of four galaxy types (E/S0, Sbc, Scd, and Im) from the public code HYPERZ (Bolzonella et al. 2000) and included them in our code. The host templates, see Fig. 2, cover the 90–100 000 Å band. They are soft-coded in STOKES, which means that the user can erase the source file and replace the input spectrum with its own galaxy spectral energy distribution (SED). An automatic procedure rebins the host spectrum according to the required resolution set by the user. Since stars principally emit unpolarized or mildly polarized light, and since the vectorial superposition of the many polarization angles from all the stars of the galaxy will be null, the common assumption of unpolarized host radiation is used in our code. However, scattering of starlight by dust, molecules and electrons in the galactic medium may produce an observable amount of polarization that depends on the orientation of the host plane (Simmons & Audit 2000; Stil et al. 2009). In our model, it is therefore possible to fill the host galaxy region with dust and/or electrons to re-create such conditions. Finally, the fraction of host starlight with respect to the AGN intrinsic flux, integrated over the considered waveband, is required before starting the code.
 |
Fig. 2. Templates of four classes of host galaxy extracted from (Bruzual & Charlot 1993) and extended towards the ultraviolet and infrared bands by Bolzonella et al. (2000). The four templates are: an elliptical or lenticular galaxy (E/S0, in red), a spiral galaxy with very loose spiral arms (Sbc, in yellow), a spiral galaxy (Scd, in blue), and an highly irregular galaxy (Im, in green). |
2.4. Quantitative assessment
We illustrate how ISP and starlight dilution can alter the observed total flux and polarization of a cosmic source in Fig. 3. We simulated four different AGN observations that account for (1) only the AGN flux, (2) the AGN flux plus ISP, (3) the AGN flux plus the host starlight, and (4) the AGN flux plus the host and the ISP. We set the ratio of AGN photons to host photons to 50% for this experiment. The top row of Fig. 3 shows that the ISP has no impact on the observed AGN flux (the black and violet lines are superimposed, similarly to the red and orange lines). The host starlight has very little influence on the observed spectrum of type-1 objects, since emission from the accretion disk dominates. On the other hand, we see that the host overshadows most of the AGN flux for type-2 objects. The ultraviolet band is less affected due to the dimming of starlight photons in this waveband but the optical and near-infrared bands are completely dominated by the host. Looking at the polarization degree (Fig. 3, middle panels), we see that type-1 polarization is only marginally affected by starlight dilution in the optical band. The ISP, however, can completely cover the AGN polarization. At equatorial inclinations the presence of ISP is completely over-shadowed by the high polarization degrees due to perpendicular scattering of disk photons in the polar outflows. Without host contamination P can be as high as 53%. When starlight is added, the polarization degree is strongly weakened. It is no longer constant and shows the highest values in the ultraviolet band, such as observed by Code et al. (1993). The overall polarization degree is strongly affected and reduced to P less than 10% in the ultraviolet, and less than 3% in the optical. Those values correspond to the numerous polarimetric observations of type-2s achieved by Kay (1994). Finally, the polarization position angle is not affected by the host starlight at polar inclinations, but the ISP can induce a wavelength-dependent variation (Fig. 3, bottom panels). For equatorial inclinations, only the combination of starlight dilution plus interstellar polarization may affect Ψ.
 |
Fig. 3. Impact of ISP and starlight dilution on the AGN total flux (top), polarization degree (middle) and polarization angle (bottom). Two different inclinations are shown: a polar orientation (left) and an equatorial inclination (right). Four AGN models are shown. In black is an AGN model without parasitic light (the kind of model that STOKES was able to produce until this paper). In violet is a model that accounts for ISP, in red a model that accounts for host starlight only, and in orange an AGN model that accounts for both the host and ISP. The interstellar polarization is parametrized with the following numerical values: P max = 1.4%, λ max = 5450 Å, and Ψ ISP = 44°. |
Overall, we have seen that removing both the ISP and the host contamination is necessary to uncover the true polarization originating from the AGN. While correcting for interstellar polarization is achievable (yet it requires observations of standard stars), accounting for host starlight is more tricky. Radiative transfer models account for both diluting sources are thus needed to uncover the true scattered polarization.
3. Examples of NGC 1068 modeling
In order to demonstrate how our newest code version can help to disentangle the true AGN polarized light from parasitic light, we run STOKES for a realistic test case. We focus on one specific target for this study: NGC 1068. This archetypal Seyfert-2 galaxy has been the most observed in terms of polarization and archival data allow us to efficiently compare our simulations to observations. Details of the model are listed in Table 1. Each free parameter is described and referenced in the consecutive subsections. In addition, since it is an AGN seen at a relatively large inclination (70–80°, Hönig et al. 2007; Fischer et al. 2013, 2014; Marin 2016), it is an ideal target to evaluate the fraction of polarization dilution in dust-obscured AGN.
Components of the NGC 1068 model, its host galaxy and the interstellar polarization.
3.1. Spectral energy distribution
We begin by modeling the 1000–10 000 Å SED of NGC 1068 (Fig. 4). To represent the host galaxy contribution, we use the Sbc template presented in Sect. 2.3. This template is consistent with the morphological classification of the host of NGC 1068, such as discovered by Balick & Heckman (1985). The authors also highlighted the importance of starburst activity in the SED of NGC 1068 that impacts the observed fluxes at wavelengths larger than 1 μm. The resulting host SED nicely fit the fluxes observed with large aperture detectors that are listed in the NASA/IPAC Extragalactic Database, see the first panel of Fig. 4. The AGN continuum is modeled using an isotropic power-law spectral energy distribution F * ∝ ν −α with = 1. This continuum is the scattered component of the intrinsic flux that is blocked along the equatorial plane by an obscuring dust screen, usually referred to as a torus. The scattered continuum originates from polar scattering of disk photons. This simple model allows us to reproduce the observed AGN flux that can only be detected with small aperture instruments (≤1″), see the second panel of Fig. 4. Finally, the combination of the two components allow us to reproduce the observed SED of NGC 1068 at apertures close to 8”. Assuming a distance of ~14.4 Mpc, 1″ corresponds to 72 pc; thus an 8” aperture isolates the first 576 pc around the nucleus, where both the host and the AGN contribute to the observed flux. Hence, because of the inclusion of host starlight templates, STOKES is now possible to properly compute and reproduce the observed SED of AGN, while accounting for the aperture effects.
 |
Fig. 4. Decomposition of the ultraviolet, optical and near-infrared SED of the Seyfert-2 galaxy NGC 1068, including multi-aperture flux measurements taken from the NASA/IPAC Extragalactic Database (NED). Dust re-emission by the AGN circumnuclear region is not accounted for as it only becomes preponderant at λ > 1 μm. |
3.2. Continuum linear polarization
We pursued our study of NGC 1068 by investigating its continuum polarization. To do so, we construct a physical model of the AGN by setting a power-law continuum source at its center with the same characteristics as the ones described in Sect. 3.1. Around this central source, we implemented a scattering disk that is representative of the accretion flow between the torus and the accretion disk (Smith et al. 2002). This structure is marginally optically thin (τ V = 1), fully ionized and extends from 0.001–0.1 pc (Marin et al. 2012). It has a flared structure with a half-opening angle of 20° from the equatorial plane (ibid.). At larger distances from the source, we set up the dusty circumnuclear region using a flared disk filled with Milky Way dust. The structure is optically thick (τ V 50) and extends from 0.1–5 pc. The inner radius is set by the dust sublimation radius (Barvainis 1987; Kishimoto et al. 2007) and the outer rim corresponds to the expected size of AGN tori (Siebenmorgen et al. 2015; Marin et al. 2015). The half-opening angle of the torus is fixed to 45° (Sazonov et al. 2015). Finally, along the polar direction, biconical outflows are collimated by the torus funnel. They extend up to 100 pc and they are filled with electrons and their radial optical depth is fixed to τ V = 1 (Osterbrock 1989). See Table 1 for a summary of the model parameters. It is a generic model based on the Unification Scheme presented by Antonucci (1993), yet such modeling has been very successful in reproducing observational polarimetric measurements (Marin et al. 2012, 2015). Our goal is not to perfectly reproduce the spectropolarimetric signal of NGC 1068, but rather show whether the unified scheme gives a consistent comparison between observations and simulations, and to show how STOKES can help to fit data. Around the AGN, we added a host galaxy using the Sbc template presented in the previous section. The flux ratio between the two radiation sources is fixed according to the estimation made by Miller & Antonucci (1983) who concluded that “no more than 15% of the light at 4000Å could come from stars earlier than type F”. Radiation from the host may scatter onto the AGN, coupling the radiation field in a consistent way. Finally, an interstellar polarization of 0.5% at 0° was added on the detector plane, following the measurements of Miller & Antonucci (1983) and the all-sky polarization maps of Mathewson & Ford (1970).
We show in Fig. 5 the resulting continuum flux, polarization degree and polarization angle produced by STOKES for the same model but using the old and new versions of the code. The observed spectra (in black) are extracted from Miller’s publication using WebPlotDigitizer, a polyvalent and free software to extract spectra from old astronomical publications (Marin et al. 2017). Since STOKES records the net polarization at all inclinations, we tested all the spectra. The best fit between observations and our model is obtained for an inclination of 67.5 ± 2.5°, shown in red in Fig. 5. We see that the continuum level is found to be very similar to the observed continuum flux, albeit with small differences at longer wavelengths. This is mainly due to the absence of emission lines whose wings contribute to the continuum. There is a great agreement between the observed starlight-contaminated polarization degree P and the continuum polarization simulated with STOKES, both in percentage and wavelength-dependence. This agreement could not be obtained with the previous version of the code since dilution was not accounted for. The observed polarization level was too high in comparison to observations. Our new version of STOKES allows us to subtract the starlight component to the linear polarization, enabling us to reproduce the scattering-induced polarization estimated by Miller & Antonucci (1983). The wavelength-independence of P is due to electron scattering and nicely reproduces the observational work of the authors. The polarization position angle (compared to the position angle of the radio structure in NGC 1068) is perpendicular (hence equal to 0° using our polarimetric convention), similarly to the observed value.
 |
Fig. 5. Total flux, linear polarization degree P and polarization position angle Ψ resulting from the modeling of NGC 1068 including ISP and starlight dilution by a Sbc host galaxy. In black are the observations by Miller & Antonucci (1983) and in red are the Monte Carlo simulations. The solid line corresponds to the model with starlight dilution and the dashed line is the polarization degree without host contamination. |
We have demonstrated with our modeling that it is possible to reproduce both the total and polarized components of AGN using the latest code implementations. Such work was not previously possible without using crude first-order approximations for flux and polarization dilution. Now, not only can the code fit data with a physical model, but it is also possible to derive the inclination angle of the AGN. Using a simple yet reliable AGN model, we derived an inclination angle for the AGN core that is consistent with previous estimations (Marin 2016). However we found a small degeneracy between the inclination angle and the half-opening angle of the dusty circumnuclear structure. Varying the height of the dust component (with respect to the equatorial plane) impacts the inclination angle at which the total flux and polarization degree fit the observational data the best. The degeneracy is not linear and is only revealed due to multiple scattering. For each AGN, a set of models must be run in order to evaluate the uncertainties on the inclination angle and torus geometry. This is beyond the scope of this paper, which aims to present the numerical tool needed for such an extensive analysis.
3.3. Polarimetric maps
NGC 1068 was also extensively observed in imaging polarization thanks to the Hubble Space Telescope (HST) and various other telescopes. Recently Gratadour et al. (2015) undertook high angular resolution polarization imaging of the first 5” around NGC 1068. Using the infrared camera IRDIS installed in the SPHERE instrument on the Very Large Telescope, Gratadour et al. (2015) achieved 60 mas H and K
′ band polarimetric maps of the central region of NGC 1068. Similar, yet less resolved, imaging polarimetric campaigns were achieved by, for example, Capetti et al. (1995a, b) and Weinberger et al. (1999). In order to demonstrate the code’s capabilities of reproducing such observations, we ran STOKES with a 200 × 200 spatial resolution binning covering the first 300 pc around the nucleus. We implemented a de Vaucouleurs profile for the emission of the central parts of the host galaxy since the bugle region of spiral galaxies can be well approximated by an elliptical model (de Vaucouleurs 1948). The surface brightness of the host is then modeled using the following equation: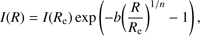 (3)
(3)
with R e the radius of the isophote containing half the galaxy luminosity, b = 1.999n−0.327 and n = 4. Following the NGC 1068 host galaxy observations of Tanaka et al. (2017) we fix R e = 1500 pc. The host galaxy size ranges from 5 to 3000 pc in our model and the fraction of starlight in the observed total continuum flux is set to 0.82 at 5075 Å, such as measured by Miller & Antonucci (1983). Finally, we fill the host disk with dusty grains so that the vertical density structure is optically thin.
We present the monochromatic (λ = 5000 Å) polarization maps of NGC 1068 in Fig. 6. The top left map displays the spatial distribution of the total flux. The core of the picture is saturated due to the strong central emission of the host galaxy. The de Vaucouleurs emission profile is clearly visible, with decreasing fluxes observed at larger distances from the central bins. The top and bottom parts of the polar outflows are almost detected as host photons from the background are scattered away from the observer’s line-of-sight by electrons in the polar wind, hence contrasting the sharp borders of the outflows. The rest of the AGN cannot be detected as the image is entirely dominated by the central photon flux. Compared to real total flux images of the central parts of NGC 1068 (see Fig. 1 in Gratadour et al. 2015) our simulations are quite successful in reproducing the observed flux distribution of AGN. Similarly, the spatial distribution of polarization fraction appears to be dominated by the polar components of the model (Fig. 6, top right). Scattering of disk emission by polar material naturally produces high polarization degrees, thus explaining the 10–20% polarization within the winds. The northern part of the ejection flow (which is inclined towards the observer) has a polarization distribution that is not homogeneous due to projection effects. The central part of the winds is more strongly polarized than the edges, where the volumetric amount of matter is significantly smaller than along the polar axis, resulting in less light-matter interaction. Lower scattering probability and host depolarization leads to smaller observed polarization degrees, but a particular contrast is visible along the edges of the polar flow. Due to the de Vaucouleurs flux distribution, dilution is less important at larger distances and the finite size of the outflow naturally shows higher P. This is in perfect agreement with the observed distribution of polarization fraction in NGC 1068 (Gratadour et al. 2015). The polarized flux map (Fig. 6, bottom left) shaves off the stellar fluxes and highlights the AGN regions that present the highest amounts of flux and/or polarization degree. The central part of the image, where the supermassive black hole resides, is among the dominant sources of polarized fluxes but this is not due to a direct view towards the accretion disk. It is a combination effect of (1) high polarization fractions due to scattering of disk emission by the bases of the polar cones, (2) polarization from starlight by host dust grains, and (3) strong stellar fluxes originating from the inner radius of the host extending up to the AGN torus. The cumulated effects of high fluxes and high polarization clearly highlight the central region. The edges of the polar winds also show high polarized fluxes, which is a border effect. Finally the map of the polarization position angles (Fig. 6, bottom right) shows a centro-symmetric component that is clearly visible on the edges of the lower wind cone (the upper cone showing the same signatures at larger distances, where dilution by the host becomes less important). This is a clear signature of scattered emission from the central engine. This pattern has already been already observed by Gratadour et al. (2015) and confirms the assumptions of the authors about the origin of this structure. The direction of the polarization angle pinpoints the source of emission and allows us to retrieve the location of the hidden nucleus (Axon et al. 1996; Capetti et al. 1997; Kishimoto 1999).
 |
Fig. 6. Monochromatic (λ = 5000 Å) polarization maps of NGC 1068. Top left: total flux, top right: fraction of polarization, bottom left: polarized flux, bottom right: polarization angle. In the case of the total and polarized fluxes the color bar is in arbitrary units. |
Our numerical polarimetric maps of NGC 1068 have shown very strong agreement with the observed flux and polarization distribution. The addition of a starlight component allows us to reproduce the expected amount of polarization and helps us to create realistic predictions for future observations. The possibility to extract polarimetric information of individual photons is the key to interpret the data. STOKES is able to decompose the results in order to better understand the contribution of each model component to the net polarization. Hence, by using the newest version of the code, it is possible to fit and interpret high-angular resolution polarimetric data in a reliable way.
4. Discussion
4.1. Deriving the intrinsic polarization of type-2 AGN
The new features we included in our code grant large possibilities to interpret data and fit observations. In particular, Kay (1994) have shown that interpreting type-2 polarization is problematic due to the strong diluting effects of the host. Yet, using STOKES, it is now possible to retrieve the real amount of scattered light from the AGN only. For this purpose, the same simulation must be run in two modes: with and without host dilution. Since the degree of polarization is a geometric value, it is independent on the photon flux and thus a direct comparison between the polarization properties of the two models allows us to estimate the intrinsic polarization from the AGN. To compare the photometric and spectroscopic results, it is necessary to parametrize the bolometric fraction emitted by the different components. This is implemented by specifying the number of radiation sources and their relative strengths. A different technique to evaluate the true polarimetric signal of edge-on AGN was used in Marin (2014) and consists of dividing the polarized flux of the AGN by the total flux across the broad emission lines. Only the broad lines polarization is a reliable indicator of the polarization of the scattered component but broad lines are, by definition, not detected in the total flux spectra of type-2 so proxies had to be used. With STOKES it is now possible to overcome this problem. Polarized spectra are preferable but narrowband polarimetric informations can also be used. We stress that degeneracies are still present, but coupling total flux, polarization degree and polarization position angle information allows one to better constrain the unknown AGN parameters than with spectroscopy only. The addition of timing information is also crucial to remove further degeneracies (Gaskell et al. 2012; Rojas Lobos et al. 2018). To narrow the uncertainties, observations of the host galaxy are needed in order to derive the fraction of starlight to the total flux. Miller & Antonucci (1983) have proven that it is possible to estimate this fraction by varying the ratio of the AGN and host spectra in order to cancel the absorption lines from stars. SED reconstruction from archival data is another alternative way but correction of the observed fluxes for aperture-dependence is crucial Marin (in prep.).
4.2. The AGN-starburst connection
The numerical implementation of a galactic structure around the AGN has additional beneficial effects. It was shown in Sect. 3.3 that the host galaxy can be modeled with various geometries and compositions, which allows us to implement radial distributions of emitting sources. The long-standing problem of the interplay between star formation and AGN activity may thus be explored. It is well known that there is a tight relationship between the accretion activity of supermassive black holes and the evolution of their host galaxies (Cattaneo et al. 1999; Ferrarese & Merritt 2000; Tremaine et al. 2002) but it is often difficult to separate the contribution of the AGN from starburst light. The mixing between the two can be probed using emission-line ratio diagnostics. In particular, Davies et al. (2014a, b) found a smooth transition from AGN-dominated emission in the center of the host to pure star-forming activity at larger galacto-centric distances. The relative contributions of star formation and AGN activity across AGN host galaxies tells us about the evolutionary mechanisms of galaxies and allow us to probe the condition of the interstellar medium over cosmic time (Davies et al. 2017). Optical and near-infrared polarimetric observations of starburst-dominated AGN are less common, but Brindle et al. (1991) undertook a study of 27 starburst and interacting galaxies. Among other results, they found that their polarization is very low, that is ≤1%, and decreases with increasing wavelength. The most likely physical mechanism to produce such low, wavelength-dependent polarization degrees is the transmission of light through aligned dust grains. The dichroic explanation is also favored by Draper et al. (1994) to explain the observed the optical polarization of NGC 1808. The polarization degree is found to decrease with increasing radial distances from the center of NGC 1808 and, similarly to the radial-dependent emission-line ratio diagnostics of Davies et al. (2014a), a radial-dependent polarimetric investigation can be undertaken with STOKES in the future. It will be possible to test whether low ionization nuclear emission region (LINER) ultraluminous infrared galaxies (ULIRG) are necessarily starburst-dominated (Antonucci 2002).
4.3. Extension towards the infrared
A critical limit of the code is that it is only valid up to 1 μm, where dust thermal re-emission starts (Sanders et al. 1989; Wilkes 2004). This hampers any investigation of the infrared polarization of AGN. The infrared band holds several key information on the physics of AGN, the host galaxy’s nuclear environments, and the evolution of the system through time. In particular it is the best waveband to test the alignment of dust grains by parsec-scale magnetic fields. Lopez-Rodriguez et al. (2015) measured the J’ and K’ polarization of NGC 1068 and found that the large infrared polarization (7.0 ± 2.2%) is likely due to a 4–150 mG magnetic field, depending on several physical assumptions. To probe the galactic magnetic field direction and strength, infrared polarimetric modeling is thus mandatory. STOKES was used as a comparison point between several radiative transfer codes that work in the near and mid-infrared, such as skirt (Peest et al. 2017) or MontAGN (Grosset et al. 2016, 2018; Marin et al. 2017). The results are in good agreement around 1 μm and it is possible to couple those codes with STOKES for a first-order estimation of the ultraviolet-to-infrared polarization of a given AGN model. However no other code than STOKES is able to handle such detailed physics, nor our newest implementations (starlight and ISP). Hence the development of STOKES towards the infrared is among the priorities for the next updates.
5. Conclusions
We present a new version of STOKES, a Monte Carlo code that allows one to simulate the radiative transfer of photons in a complex, three-dimensional environment. The main features we included to the code are the real yet parasitic components that dilute the observed signal of AGN : interstellar polarization and starlight photons from the host galaxy. It is well known that AGN polarimetric observations suffer from those extra components that can alter or even overshadow the true scattered AGN radiation. Our code now handles these two aspects in order to allow for fast and easy interpretation of observed results, together with a better understanding of the physical processes occurring at small scales. We have applied our code to NGC 1068, an archetypal type-2 AGN whose polarimetric signal is dominated by the host galaxy. We began by successfully reproducing the SED of the system at several scales (from nuclear fluxes to large apertures). Then, we used a generic model to emulate the spectropolarimetric signal of the AGN. Compared to archival data our code is now able to reproduce the wavelength-dependent total flux and polarized flux, together with the correct polarization angle. We also determined a putative inclination angle of the core engine that matches previous estimations. Finally, we used STOKES to reproduce the observed high-angular resolution polarization maps of NGC 1068. Our maps show a very detailed agreement with observations, replicating the generic flux and polarization levels together with small scales polarimetric features. Until our new code version, such fitting was not possible and simple first-order corrections had to be done to estimate the diluting impact of the host galaxy.
In conclusion, the new version of STOKES, that will shortly be available through its dedicated website2, will help observers to better estimate the expected polarization from a source prior to any observation. Observational results will be easily compared to simulations that now account for multiscale dilution by the host. By running grids of models it will be possible to constrain several unknown AGN parameters such as the system inclination, the size and geometry of the reprocessing regions, or the true scattered polarization from the inner components. We also highlight the fact that our code is not restricted to AGN, but can be applied to any cosmic sources that suffers from host and interstellar contamination.
Acknowledgments
The author would like to thank René W. Goosmann for his comments on the text, Ariane Lançon for her advises on galaxy structures and physics, and Mari Kolehmainen for proof-reading this paper. This work was supported by the Centre national d’études spatiales (CNES) who funded this project through to the post-doctoral grant “Probing the geometry and physics of active galactic nuclei with ultraviolet and X-ray polarized radiative transfer”.
References
- Antonucci, R. R. J. 1984, ApJ, 278, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Antonucci, R. 2002, in Astrophysical. Spectropolarimetry, eds. J. Trujillo-Bueno, F. Moreno-Insertis, & F. Sánchez, 151 [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Axon, D. J., Capetti, A., Macchetto, F., Sparks, W. B., & Boksenberg, A. 1996, Vistas Astron., 40, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Balick, B., & Heckman, T. 1985, AJ, 90, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [Google Scholar]
- Brindle, C., Hough, J. H., Bailey, J. A., Axon, D. J., & Sparks, W. B. 1991, MNRAS, 252, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, A. G., & Charlot, S. 1993, ApJ, 405, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., Axon, D. J., Macchetto, F., Sparks, W. B., & Boksenberg, A. 1995, ApJ, 446, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., Macchetto, F., Axon, D. J., Sparks, W. B., & Boksenberg, A. 1995b, ApJ, 452, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Capetti, A., Macchetto, F. D., & Lattanzi, M. G. 1997, Ap&SS, 248, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Haehnelt, M. G., & Rees, M. J. 1999, MNRAS, 308, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-C., & Hwang, C.-Y. 2017, Ap&SS, 362, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Code, A. D., Meade, M. R., Anderson, C. M., et al. 1993, ApJ, 403, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Kewley, L. J., Ho, I.-T., & Dopita, M. A. 2014a, MNRAS, 444, 3961 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Rich, J. A., Kewley, L. J., & Dopita, M. A. 2014b, MNRAS, 439, 3835 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Groves, B., Kewley, L. J., et al. 2017, MNRAS, 470, 4974 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1948, Ann. Astrophys., 11, 247 [Google Scholar]
- de Vaucouleurs, G. 1959, Handb. Phys., 53, 275 [Google Scholar]
- Deo, R. P., Crenshaw, D. M., & Kraemer, S. B. 2006, AJ, 132, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draper, P. W., Scarrott, S. M., & Stockdale, D. P. 1994, Ap&SS, 216, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., & Schmitt, H. R. 2013, ApJS, 209, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., Schmitt, H. R., & Turner, T. J. 2014, ApJ, 785, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 2009, New Astron. Rev., 53, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M., Goosmann, R. W., Merkulova, N. I., Shakhovskoy, N. M., & Shoji, M. 2012, ApJ, 749, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Goodrich, R. W. 1989, ApJ, 342, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Goosmann, R. W., & Gaskell, C. M. 2007, A&A, 465, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratadour, D., Rouan, D., Grosset, L., Boccaletti, A., & Clénet, Y. 2015, A&A, 581, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grosset, L., Marin, F., Gratadour, D., et al. 2016, in Proc. Annual meeting SF2A 2016, eds. C. Reylé, J. Richard, L. Cambrésy, et al., 57 [Google Scholar]
- Grosset, L., Rouan, D., Gratadour, D., et al. 2018, A&A, 612, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, J. S. 1949, Science, 109, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Balick, B., & Sullivan, III, W. T. 1978, ApJ, 224, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H., & Dragovan, M. 1995, ApJ, 450, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Hiltner, W. A. 1949, Science, 109, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffman, J. L., Chornock, R., Leonard, D. C., & Filippenko, A. V. 2005, MNRAS, 363, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Beckert, T., Ohnaka, K., & Weigelt, G. 2007, in The Central Engine of Active Galactic Nuclei, eds. L. C. Ho, & J.-W. Wang, ASP Conf. Ser., 373, 487 [Google Scholar]
- Hubble, E. P. 1936, Realm of the Nebulae [Google Scholar]
- Kay, L. E. 1994, ApJ, 430, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Kelm, B., & Focardi, P. 2001, in QSO Hosts and Their Environments, eds. I. Márquez, J. Masegosa, A. del Olmo, L. Lara, E. García, & J. Molina, 229 [Google Scholar]
- Kishimoto, M. 1999, ApJ, 518, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Beckert, T., & Weigelt, G. 2007, A&A, 476, 713 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lopez-Rodriguez, E., Packham, C., Jones, T. J., et al. 2015, MNRAS, 452, 1902 [NASA ADS] [CrossRef] [Google Scholar]
- MacKenty, J. W. 1990, ApJS, 72, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F. 2014, MNRAS, 441, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F. 2016, MNRAS, 460, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F., & Goosmann, R. W. 2014, in SF2A-2014: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. J. Ballet, F. Martins, F. Bournaud, R. Monier, & C. Reylé, 103 [Google Scholar]
- Marin, F., Goosmann, R. W., & Gaskell, C. M. 2015, A&A, 577, A66 [Google Scholar]
- Marin, F., Goosmann, R. W., Gaskell, C. M., Porquet, D., & Dovčiak, M. 2012, A&A, 548, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marin, F., Rohatgi, A., & Charlot, S. 2017, in SF2A-2017: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, P. Di Matteo, F. Herpin, et al. 113 [Google Scholar]
- Mathewson, D. S., & Ford, V. L. 1970, MmRAS, 74, 139 [Google Scholar]
- Miller, J. S., & Antonucci, R. R. J. 1983, ApJ, 271, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. S., & Goodrich, R. W. 1990, ApJ, 355, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Mill Valley, CA: University Science Books), 422 [Google Scholar]
- Peest, C., Camps, P., Stalevski, M., Baes, M., & Siebenmorgen, R. 2017, A&A, 601, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., & Wandel, A. 1999, ApJ, 521, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Martínez González, M. J., Asensio Ramos, A., et al. 2016, MNRAS, 461, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas Lobos, P. A., Goosmann, R. W., Marin, F., & Savić, D. 2018, A&A, 611, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandage, A. 1975, in Classification and Stellar Content of Galaxies Obtained from Direct Photography, eds. A. Sandage, M. Sandage, & J. Kristian (University of Chicago Press), 1 [Google Scholar]
- Sanders, D. B., Phinney, E. S., Neugebauer, G., Soifer, B. T., & Matthews, K. 1989, ApJ, 347, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Sazonov, S., Churazov, E., & Krivonos, R. 2015, MNRAS, 454, 1202 [NASA ADS] [CrossRef] [Google Scholar]
- Serkowski, K., Mathewson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., Heymann, F., & Efstathiou, A. 2015, A&A, 583, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simkin, S. M., Su, H. J., & Schwarz, M. P. 1980, ApJ, 237, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Simmons, J. F. L., & Audit, E. 2000, MNRAS, 319, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. E., Young, S., Robinson, A., et al. 2002, MNRAS, 335, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Stil, J. M., Krause, M., Beck, R., & Taylor, A. R. 2009, ApJ, 693, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, I., Yagi, M., & Taniguchi, Y. 2017, PASJ, 69, 90 [NASA ADS] [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 1998, Galaxy Morphology and Classification. (Cambridge, New York: Cambridge University Press) [Google Scholar]
- Véron-Cetty, M.-P., Véron, P., & Gonçalves, A. C. 2001, A&A, 372, 730 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weinberger, A. J., Neugebauer, G., & Matthews, K. 1999, AJ, 117, 2748 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. 2004, in AGN Physics with the Sloan Digital Sky Survey, eds. G. T. Richards, & P. B. Hall, ASP Conf. Ser., 311, 37 [NASA ADS] [Google Scholar]
- Young, S. 2000, MNRAS, 312, 567 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Components of the NGC 1068 model, its host galaxy and the interstellar polarization.
All Figures
 |
Fig. 1. Examples of ultraviolet-to-infrared interstellar polarization levels for different values of P max. The value of λ max is fixed to 5450 Å. |
| In the text | |
 |
Fig. 2. Templates of four classes of host galaxy extracted from (Bruzual & Charlot 1993) and extended towards the ultraviolet and infrared bands by Bolzonella et al. (2000). The four templates are: an elliptical or lenticular galaxy (E/S0, in red), a spiral galaxy with very loose spiral arms (Sbc, in yellow), a spiral galaxy (Scd, in blue), and an highly irregular galaxy (Im, in green). |
| In the text | |
 |
Fig. 3. Impact of ISP and starlight dilution on the AGN total flux (top), polarization degree (middle) and polarization angle (bottom). Two different inclinations are shown: a polar orientation (left) and an equatorial inclination (right). Four AGN models are shown. In black is an AGN model without parasitic light (the kind of model that STOKES was able to produce until this paper). In violet is a model that accounts for ISP, in red a model that accounts for host starlight only, and in orange an AGN model that accounts for both the host and ISP. The interstellar polarization is parametrized with the following numerical values: P max = 1.4%, λ max = 5450 Å, and Ψ ISP = 44°. |
| In the text | |
 |
Fig. 4. Decomposition of the ultraviolet, optical and near-infrared SED of the Seyfert-2 galaxy NGC 1068, including multi-aperture flux measurements taken from the NASA/IPAC Extragalactic Database (NED). Dust re-emission by the AGN circumnuclear region is not accounted for as it only becomes preponderant at λ > 1 μm. |
| In the text | |
 |
Fig. 5. Total flux, linear polarization degree P and polarization position angle Ψ resulting from the modeling of NGC 1068 including ISP and starlight dilution by a Sbc host galaxy. In black are the observations by Miller & Antonucci (1983) and in red are the Monte Carlo simulations. The solid line corresponds to the model with starlight dilution and the dashed line is the polarization degree without host contamination. |
| In the text | |
 |
Fig. 6. Monochromatic (λ = 5000 Å) polarization maps of NGC 1068. Top left: total flux, top right: fraction of polarization, bottom left: polarized flux, bottom right: polarization angle. In the case of the total and polarized fluxes the color bar is in arbitrary units. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


